2. 哈尔滨工程大学 水下机器人技术重点实验室, 黑龙江 哈尔滨 150001
2. Science and Technology on Underwater Vehicle Laboratory, Harbin Engineering University, Harbin 150001, China
水面舰船航行时在艉部会形成不均匀伴流场,工作在船后的螺旋桨会因此产生周期性变化的力,即为激振力[1]。螺旋桨激振力主要分为两类,即轴承力和表面力。以叶频为基频的脉动力和力矩作用在桨叶上并通过轴系传到船体,称之为轴承力;通过流体传递给船表面的压力,称为表面力。航行于水面的船体在周期性激振力的作用下会出现一定程度的振动,船体振动对船上的仪器设备会产生不良影响,使其不能正常运转甚至寿命减短;伴随船体振动产生的噪声更是会危及船上工作人员的身体健康,干扰水下生物的的正常生活从而破坏生态环境,影响军用舰艇的声隐身性能[2-3]。傅慧萍计算了3100TEU船体尾部螺旋桨诱导的船体表面脉动压力,并探讨了网格对计算结果的影响,结果表明采用MRF方法最容易收敛且推力扭矩计算精度最高,细化网格以及增加内迭代次数可以去除由于非定常本身引起的高频振荡成分[4]。叶金铭等提出了空泡螺旋桨诱导的双桨船脉动压力预报方法,该方法计入空泡的影响,并考虑了左右螺旋桨之间的相位差对脉动压力计算的影响,计算结果表明同时考虑双桨的相互影响时,相位差的影响不可忽略,并建议在进行双桨船脉动压力的试验测量时,必须注意双桨之间相位差的影响[5]。N.Abbas等采用URANS-LES混合模型对螺旋桨与船体的相互影响效应进行了数值模拟,计算结果表明采用该方法得到的力与力矩的脉动存在较强的峰值,比工程方法得到结果的三倍还要多[6]。Ye等对空气含量对空泡螺旋桨诱导的脉动压力的影响进行了实验研究,试验中对螺旋桨的空泡形态进行了观察,对船体脉动压力进行了测量。实验结果表明,气体含量对片状空泡基本没有影响,对气泡空化和稍涡空化影响较大。脉动压力的幅值随着气体含量的减少而增加[7]。Hanshin Seol提出了一种对螺旋桨非定常片空泡进行计算的方法,即发展的时域预报方法,并将计算结果与基于势流理论得到的结果以及实验数据进行了比较,结果表明该方法可以提供合理的预报结果,并与实验值吻合较好[8]。
随着计算机软硬件和CFD技术的飞速发展,基于雷诺平均方法且考虑粘性的复杂物体绕流场的数值模拟已经基本得到解决。目前正在向高雷诺数及湍流直接数值模拟方向发展,而船舶水动力性能计算发展到现在,也已经从最开始的不考虑自由液面的船桨一体计算,发展到可以直接进行模型尺度下考虑粘性和自由液面的船桨整体计算,但在进行船桨整体CFD计算时,考虑船体姿态变化的不多,大多只进行固定状态下船桨整体计算。然而船舶在实际航行中,必然会发生升沉和纵倾,因此模拟真实条件下的自航实验是非常有必要的[9-10]。本文基于RANS方法以KCS船和KP505桨为研究对象,采用六自由度运动模型、叠加旋转模型以及重叠网格技术,进行了固定状态和自由度开放状态下的数值自航实验,对船体周围绕流场以及螺旋桨激振力进行了对比分析。
1 船桨一体数值计算方法 1.1 控制方程不可压缩牛顿流体的运动满足连续性方程和动量守恒方程[11]:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0$ | (1) |
| $\begin{array}{l} \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}\cdot\\ \left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {{u_i}\prime {u_j}\prime } } \right) + {S_j} \end{array}$ | (2) |
式中:ui和uj是速度分量的时均值(i, j=1, 2, 3),p是压力的时均值, ρ为流体密度,μ为动力粘性系数,
本文数值计算的控制方程采用基于压力的耦合求解,其中对流项采用二阶迎风格式进行空间离散,耗散项采用二阶中心差分格式进行离散[12]。由于考虑到模型壁面剪切力的影响,为了能够较好地模拟强逆压梯度流场,本文所采用的是SST(shear stress transport)k-ω模型[13],该模型混合了k-ω模型和k-ω模型的优势,能够计算流动分离区域,是目前二方程湍流模型中最为先进的模型之一,在粘性绕流场的计算方面有很好的优势。自由液面采用VOF(volume of fluids)方法[14]进行捕捉。
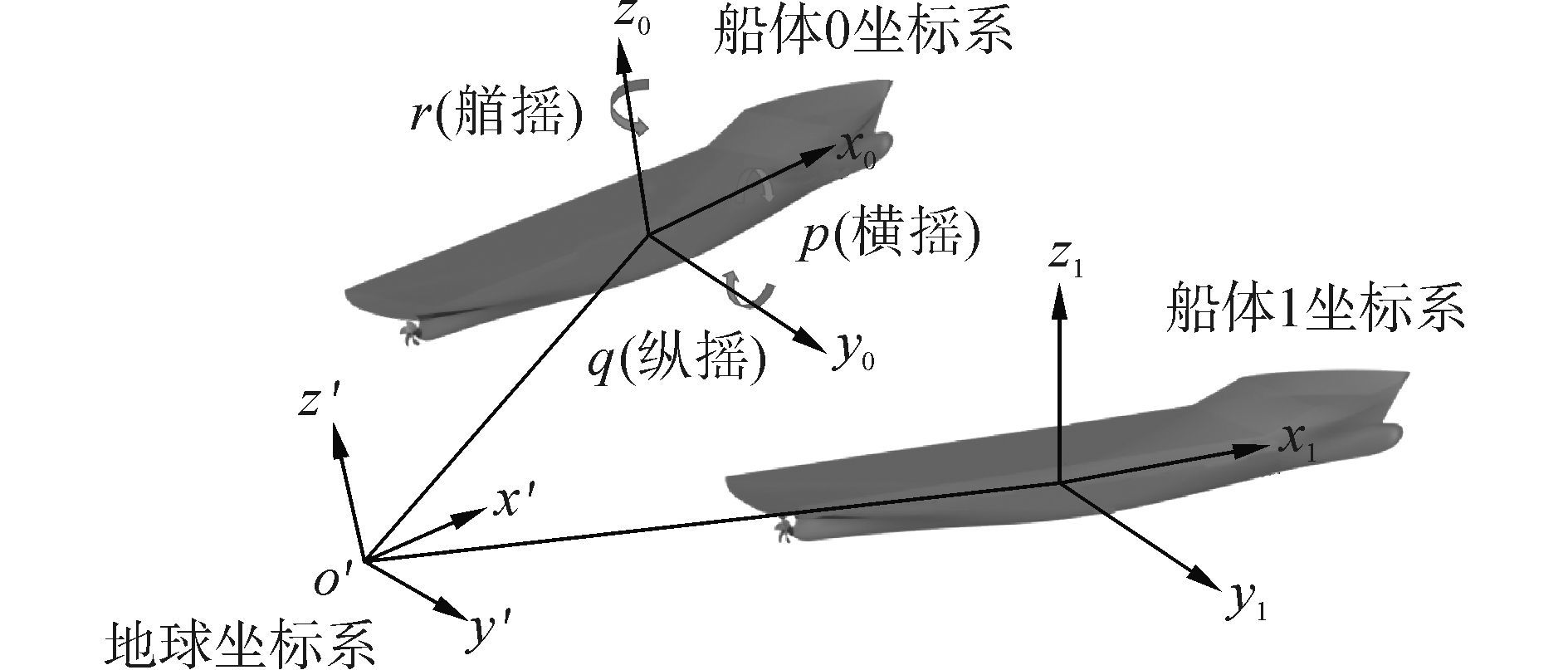
1.3 运动模型本文计算采用六自由度运动模型(DFBI rotation and translation)和叠加旋转模型(DFBI superposed rotation)实现自由度开放状态下的数值自航试验。六自由度运动模型采用两个坐标系统求解六自由度方程,即初始坐标系统(地球坐标系统)和非初始坐标系统(船体坐标系统),初始坐标系统可以定义在地球或者是相对地球匀速运动的物体上。非初始坐标系统定义在船体上,并且随着船体的运动平动或者转动。如图 1所示,两个坐标系统在计算的开始是对齐的,x轴正方向从船艉指向船艏,y轴正方向为从左舷指向右舷的方向,z轴正方向为垂直向上。六自由度运动方程见参考文献[15]。
|
图 1 船体与地球坐标系统示意图 Fig.1 Description of ship and earth systems |
模拟自由度放开状态下船舶自航的难点在于如何实现螺旋桨随船运动,如果在计算中仅仅使用六自由度运动模型实现船体升沉和纵倾两个自由度的运动,会造成船桨分离,为了实现放开升沉和纵倾两个自由度下的船桨一体数值自航,必须使用叠加旋转模型。叠加旋转模型可以将一个固定物体的旋转运动叠加到DFBI运动上去,该模型可以使得螺旋桨依附于船体上,使螺旋桨随船产生升沉和纵倾成为可能。
2 计算模型及网格 2.1 计算模型本文选取KCS船与KP505桨为研究对象,其主要参数见表 1和表 2。本文的实验数据来源于2005年东京CFD会议[16]。
| 表 1 KCS船主要参数 Tab.1 Main particulars of KCS ship |
| 表 2 KP505桨主尺度 Tab.2 Main particulars of propeller KP505 |
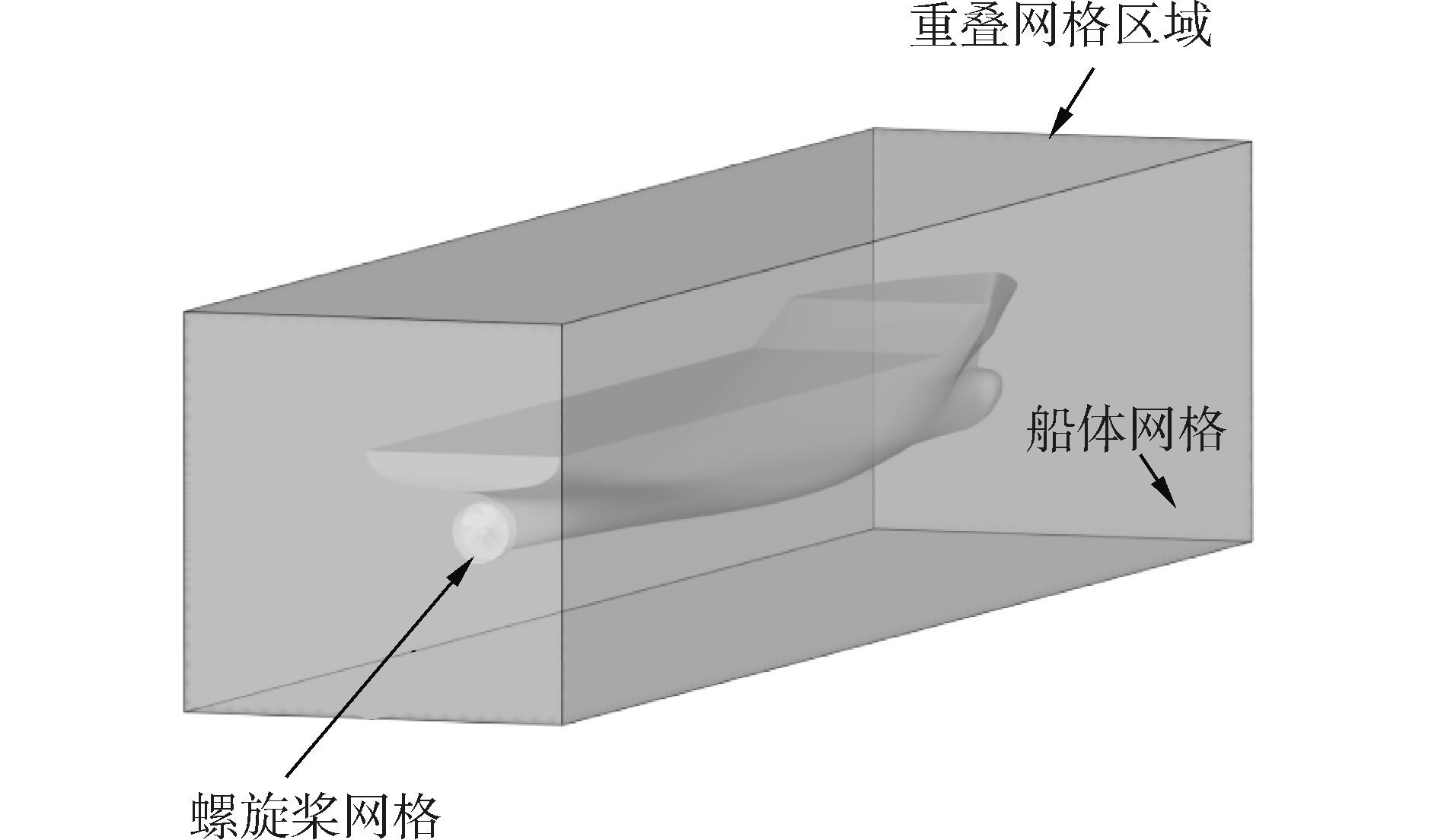
图 2为本文船桨一体数值自航实验的重叠网格布局和边界条件,为了模拟升沉和纵倾两个自由度放开的情况,在船桨一体计算中应用了重叠网格。嵌套在背景网格中的重叠网格区域中包含有船体与螺旋桨,船后的旋转域中包含有螺旋桨网格,螺旋桨绕桨轴旋转,如图 3所示。

|
图 2 边界条件 Fig.2 Boundary conditions |
|
图 3 重叠网格区域 Fig.3 Overset mesh region |
“重叠网格”又叫“嵌套网格”,在进行自由度放开条件下的数值自航实验时,随着升沉和纵倾幅度的增大,普通的动网格方法如网格变形方法和网格再生方法会出现网格的异常变形和网格重新生成的低效率问题。重叠网格在解决CFD计算中的两相流问题时,可以保证自由液面的网格分辨率,并且突破了大幅度运动时网格的局限性,能有效地解决非定常问题的计算。重叠网格在船舶CFD中的应用可以实现船舶六自由度运动的模拟。应用VOF法对自由液面进行追踪,可以实现船舶兴波过程中船艏碎波模拟和船舶升沉以及纵倾的模拟。因此本文应用VOF法和重叠网格进行固定状态与自由度开放条件下的船桨整体计算。
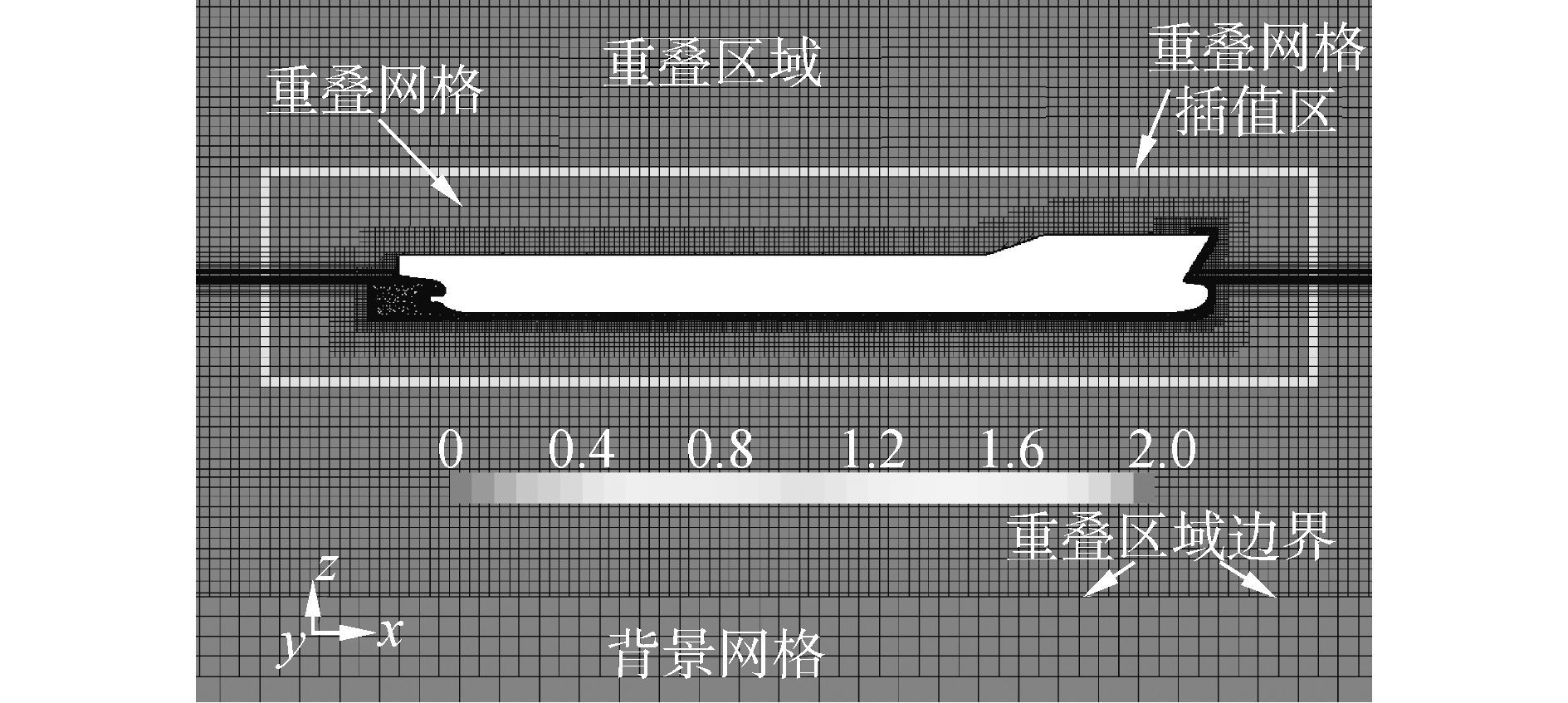
图 4为本文的计算网格,即带有边界层与重叠网格的切割体网格,计算网格整体分为背景网格区域与重叠网格区域,在进行网格划分时,背景网格中重叠区域的网格大小要与重叠网格区域边界的网格尺寸大小一致,且重叠网格的运动区域要限制在重叠区域内。图 5为船体和螺旋桨网格分布。
|
图 4 重叠网格分布 Fig.4 Distribution of overset mesh |

|
图 5 船桨一体网格分布 Fig.5 Mesh distribution of hull-propeller |
船模航速设置为2.196 m/s,螺旋桨转速为9.5 r/s,计算的时间步长取螺旋桨旋转一度所需要的时间,即为3×10-4 s。表 3给出了固定状态与自由度开放状态下船桨一体系统水动力计算值与实验值对比,固定状态下,螺旋浆推力、扭矩和船本阻力的计算误差分别为2.29%、1.58%和4.56%,自由度开放状态下,螺旋浆推力、扭矩和船本阻力的课类分别为2.50%、1.19%和2.63%,二者在螺旋桨推力与扭矩方面相比实验值误差均在3%以内,且相差不多,但是二者在船体阻力计算结果上有明显差异,自由度开放状态阻力计算结果更为接近实验值,是因为其在计算过程中充分考虑了船体姿态变化。
| 表 3 固定状态与自由状态计算值与实验值对比 Tab.3 Comparison of calculation values for fixed and open freedom condition with experiment data |
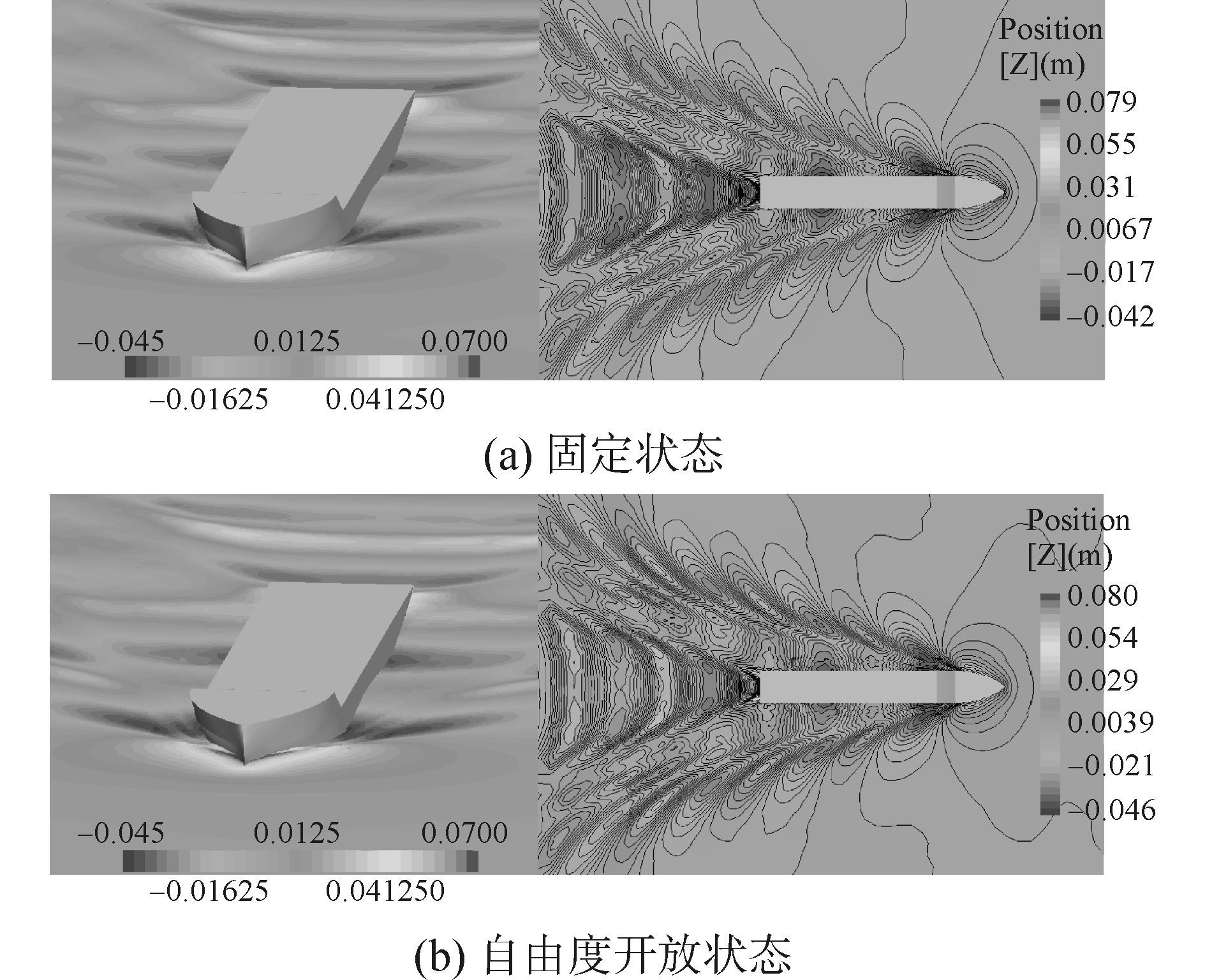
图 6为固定状态与自由度开放状态下的自由液面波形图,从图中可以看出,二者自由表面波形几乎一致。相比于自由度开放状态,自由度固定状态的波形等高线更为光顺;另外通过对比可以发现,自由度是否开放对艏部波形有一定的影响,在自由度开放时,船舶兴起波浪的范围更大;二者船艉波形基本保持一致。
|
图 6 自由液面波形 Fig.6 Free surface waves |
图 7为船艏Vx/V0=0.9涡结构分布图,颜色分布为Vx/V0=0.9。从图中可以清晰的看到船艏部球鼻艏兴波涡结构、艏肩涡等涡结构。自由度放开状态相比于固定状态具有一定的球鼻艏埋艏现象,球鼻艏处吃水相对较大,球鼻冲起的船艏部兴波较自由度固定状态下小,引起的船艏球鼻艏兴波涡结构较固定状态小。自由度放开状态下,由于船舶具有埋艏纵倾,船舶艏部与自由表面相交部分吃水面积相比自由度固定状态下大,船艏肩涡区域较自由度固定状态下大。

|
图 7 船艏涡结构分布(Vx/V0=0.9) Fig.7 Vortical structures of the ship bow (Vx/V0=0.9) |
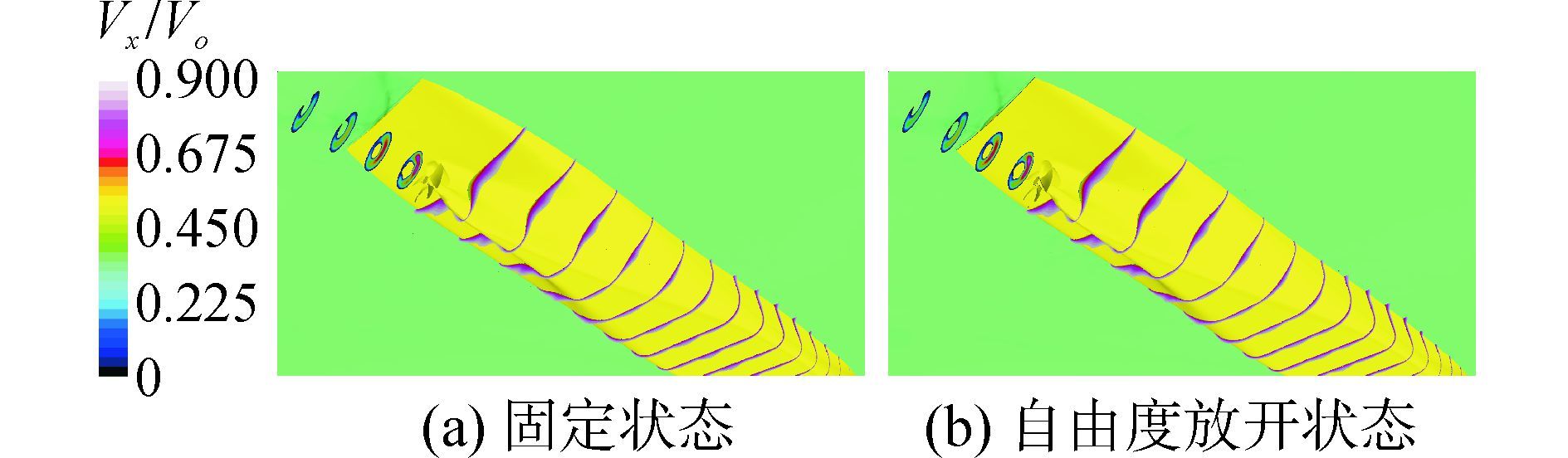
图 8给出了以切片形式表示的船舶边界层分布图,颜色分布为限制到Vx/V0=0.9的轴向速度,从图中可以看出,自由度固定状态与自由度开放状态的桨前船身速度边界层差异不大。自由度固定状态与自由度开放状态的螺旋桨尾流在远离螺旋桨后都迅速恢复成自由流,其中自由度放开状态下的螺旋桨尾流的平均轴向速度稍大于自由度固定状态。
|
图 8 边界层和螺旋桨尾流对比 Fig.8 Comparison figure of boundary layer and free wake of propeller |
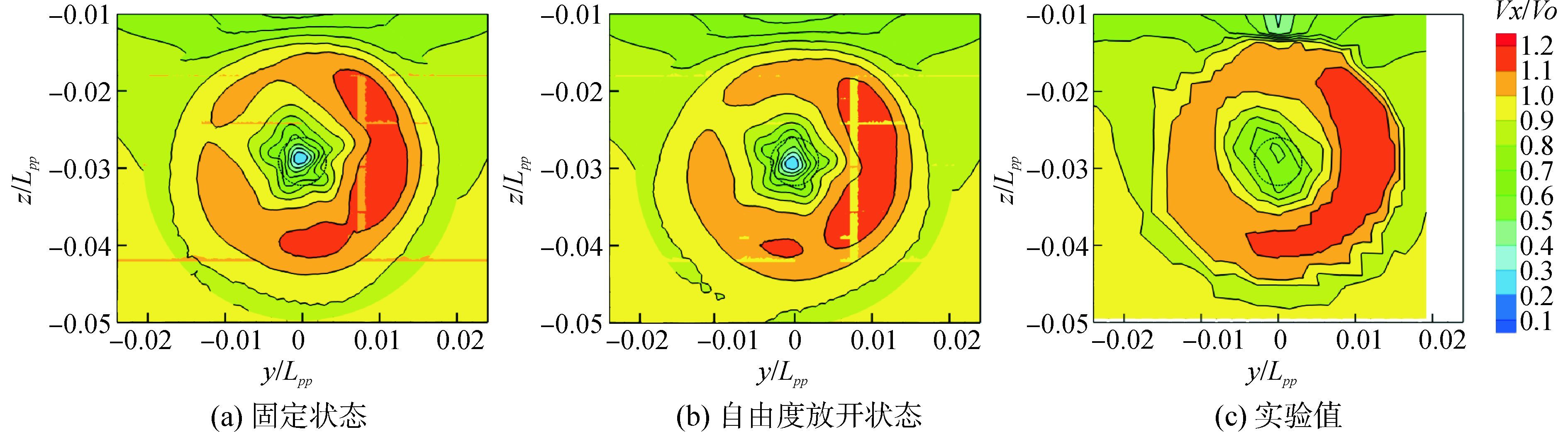
螺旋桨盘面下游x/Lpp=0.005 9处以船舶航速进行无量纲化的轴向速度分布云图如图 9所示。通过对比实验值,自由度放开状态与固定状态下的计算都捕捉到了螺旋桨尾流的非对称特性,以及位于右舷方向的速度最高区,这里螺旋桨诱导的动量最大。二者都准确预报了由于螺旋桨桨毂导致的动量损失,在截面中心可以观察到较强的毂涡。二者轴向速度的分布总体上与实验值符合较好,但自由度放开状态相比于固定状态更好的捕捉到了截面中心区域的轴向速度分布。
|
图 9 螺旋桨盘面下游轴向速度分布(x/Lpp=0.005 9) Fig.9 Axial velocity contours downstream of the propeller plane (x/Lpp=0.005 9) |
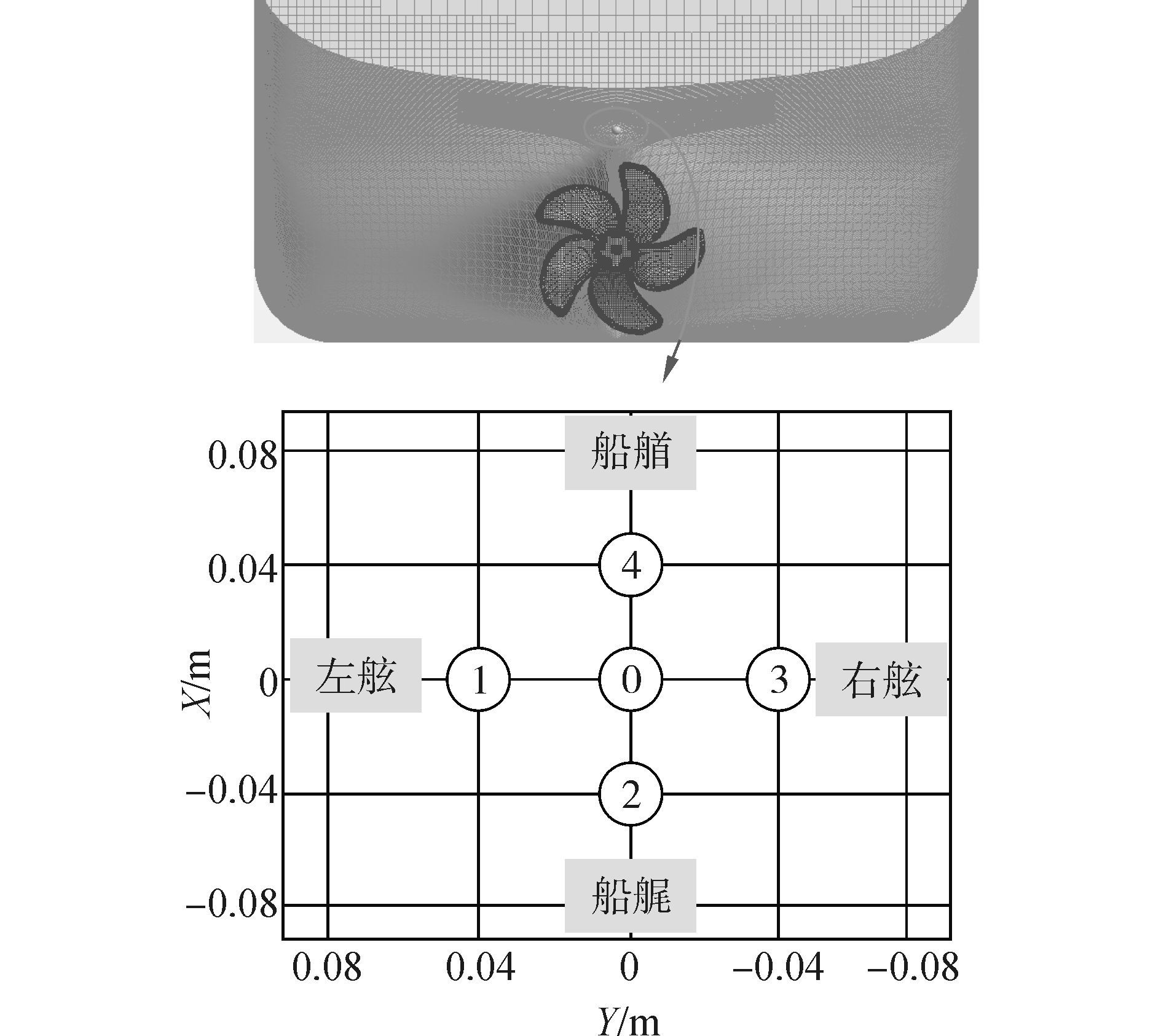
为了研究自由度开放状态与固定状态下船桨一体计算时的螺旋桨激振力,采取在船艉螺旋桨上方靠近船体表面Z=-0.043 8 m平面上(Z=0 m为水线面)设置5个观测点的方法,通过监测这5个观测点上的脉动压力时历变化,来反应螺旋桨在两种不同工作状态时脉动压力的变化规律。其中P0位于螺旋桨旋转中心的正上方,5个观测点可默认是5个无限小的面,然后记录这些面上的压强变化,5个测点的具体分布如图 10所示。需要说明的是,固定状态时,这5个测点的绝对坐标不会发生变化;而在进行自由度开放状态下的计算时,由于船体姿态的变化,这5个测点的绝对坐标会发生变化,但是其相对船体和螺旋桨的位置始终保持一致,计算过程中其坐标在船体坐标系下进行给定,保持其相对船体重心的位置不变。待计算收敛后开始监测5个测点位置处的总压。
|
图 10 测点布置图 Fig.10 Measuring points arry |
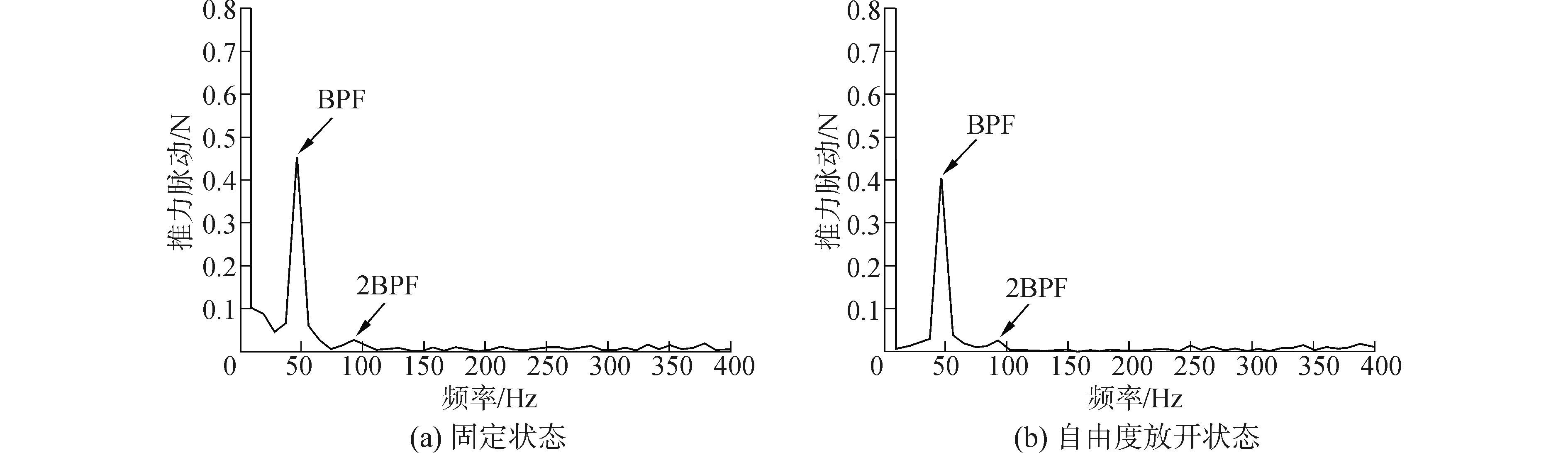
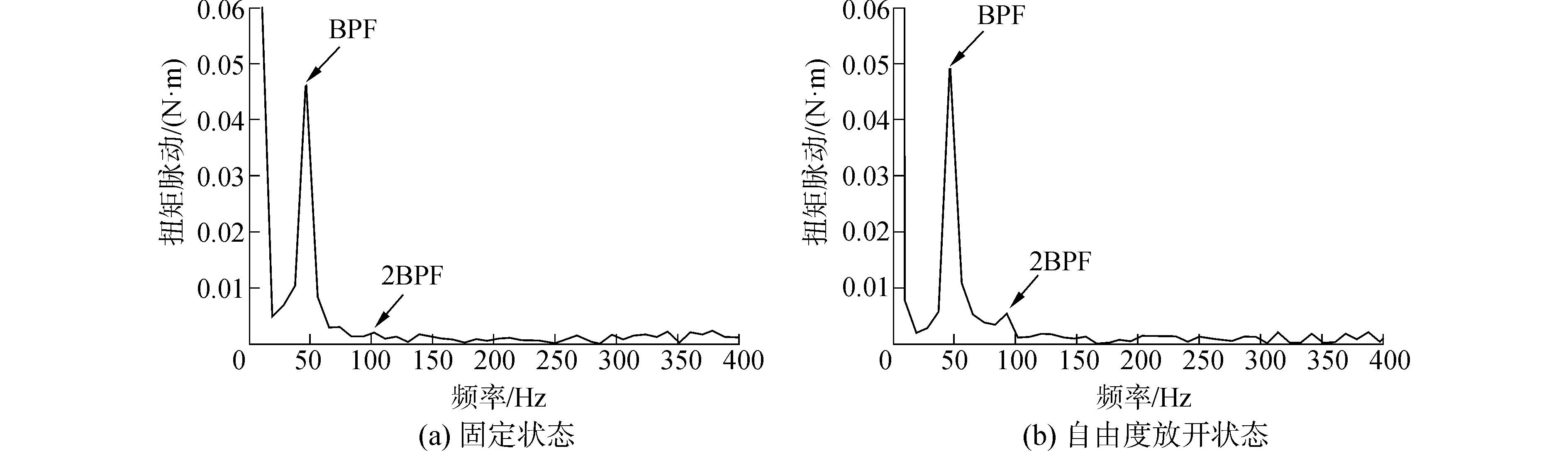
对螺旋桨推力、扭矩的时域值进行快速傅里叶变换(FFT),设置采样频率与时间步长一致为3×10-4,将船后螺旋桨推力和扭矩的时域信号转化为频域信号,两种状态下船后螺旋桨的推力和扭矩频域曲线分别如图 11、12所示。从图中可以看出,船后螺旋桨的轴承力在叶频BPF(47.5 Hz)整数倍处均呈现不同程度的峰值,以叶频处峰值为最大,然后逐渐衰减,400 Hz以后其峰值基本可以忽略不计,脉动幅值频率分布较为广泛,在200 Hz以后仍呈现出不同程度的小波峰,说明其高频振荡成分不可忽略。固定状态与自由度开放状态下的螺旋桨推力与扭矩在一阶叶频处的峰值相差不太多,固定状态计算模型船后螺旋桨的推力在一阶叶频处的峰值大于自由度开放状态计算模型。固定状态计算模型船后螺旋桨的扭矩在一阶叶频处的峰值小于自由度开放状态计算模型。
|
图 11 螺旋桨推力脉动频域 Fig.11 Frequency domain figure of propeller thrust fluctuation |
|
图 12 螺旋桨扭矩脉动频域 Fig.12 Frequency domain figure of propeller torque fluctuation |
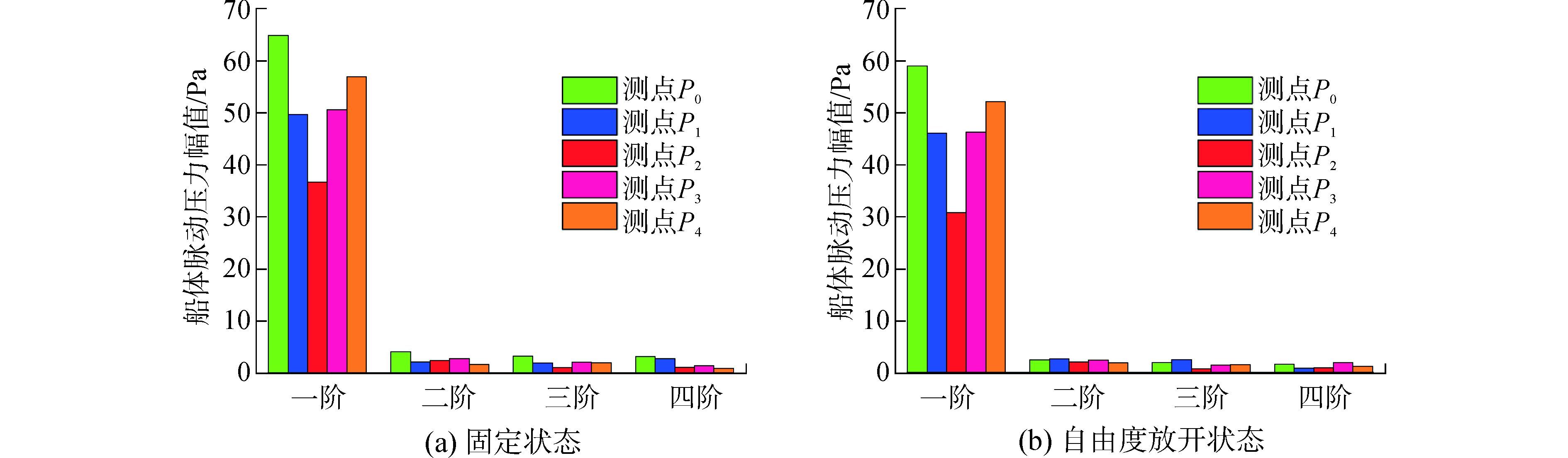
对各个监测点的压强变化进行快速傅里叶变换(FFT变换),设置采样频率与时间步长一致为3×10-4,将各个监测点压强变化的时域信号转化为频域信号,即可得到叶频整数倍处的脉动压力峰值,固定状态与自由度放开状态下船艉各阶脉动压力幅值的条形图如图 13所示。从叶频处脉动压力值来看,位于螺旋桨前方的P2点处脉动压力幅值明显小于其他几个监测点,这是由于自由液面的兴波以及水流经过螺旋桨后的扰流作用导致的结果,而位于螺旋桨正上方测点P0值最大,这是因为P0距离桨叶梢最近,故而P0测点的脉动压力值也会最大,位于右舷的P3测点的值稍大于P1测点是因为KP505桨的右旋造成的。固定状态模型船艉各个测点的脉动压力幅值的规律与自由度放开状态模型基本保持一致。
|
图 13 船艉各阶脉动压力幅值 Fig.13 Each order of stern fluctuating pressure amplitude |
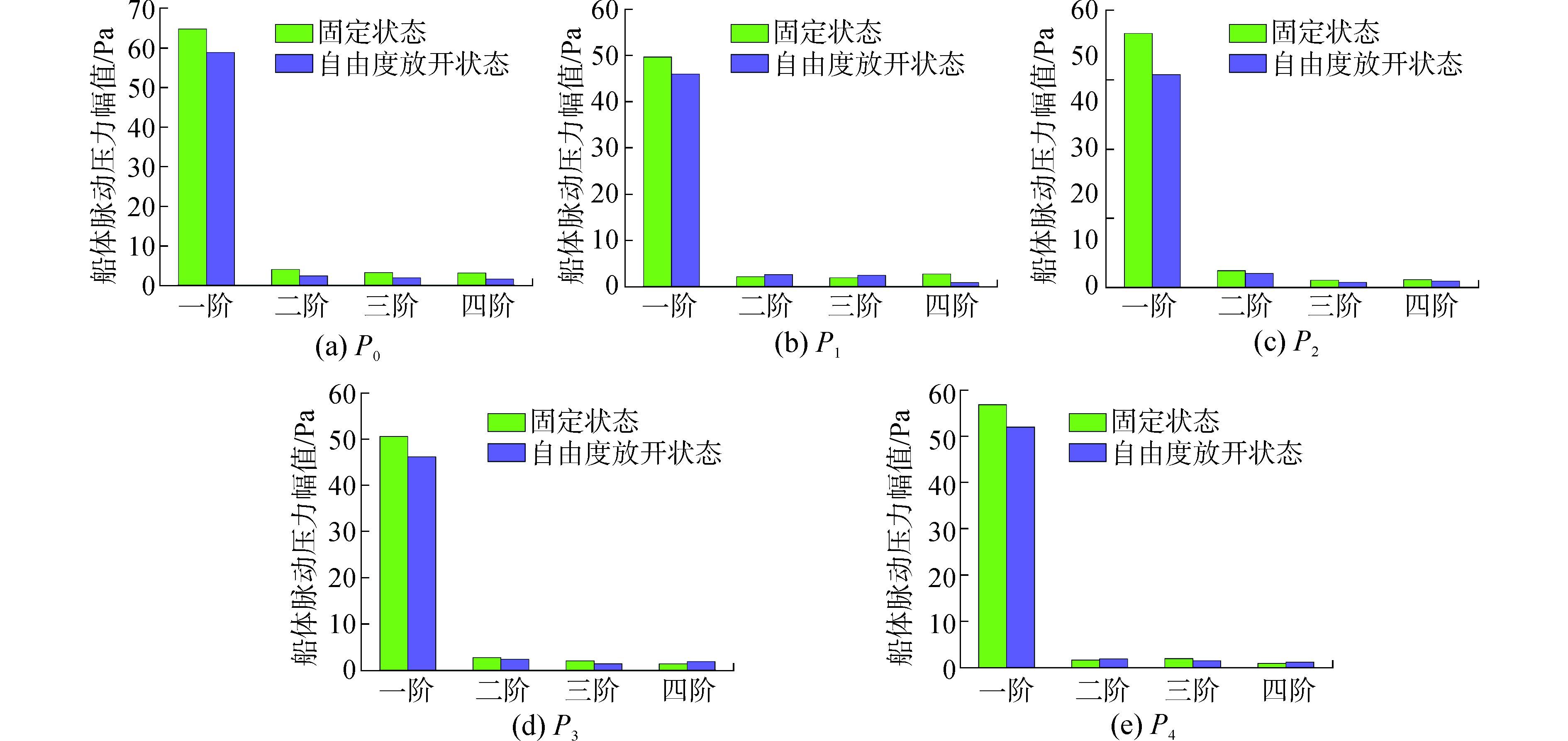
固定状态与自由度放开状态下船艉测点各阶脉动压力对比如图 14所示,因为一阶脉动压力为最主要成分,所以只关注一阶脉动压力。从图中可以看出,各个测点自由度开放状态下的一阶脉动压力幅值均小于固定状态。这就意味着,往往以固定模型为基准的数值自航实验,其船艉脉动压力预报相比于自由度开放状态存在一定的过度预报现象,这可能是由于自由度放开条件下,船模存在一定艏倾的原因。
|
图 14 两种状态船艉测点各阶脉动压力对比 Fig.14 Comparison of each order of stern fluctuating pressure at the measuring points for the two conditions |
1) 对于航行于水面的舰船,船体姿态的变化会导致以约束模型为基准的数值计算与实际情况有所差别。本文基于重叠网格技术,应用六自由度运动模型与叠加旋转模型实现了自由度开放状态下的KCS自航计算,该方法能够避免由于船体运动造成流场网格扭曲与计算发散等问题,具有较好的稳定性,并且该方法充分考虑了船体姿态的影响。
2) 通过与约束状态下的模型计算结果对比,发现二者在绕流场以及螺旋桨诱导的激振力方面存在差异。自由度放开状态相比固定状态,船舶埋艏纵倾,导致二者船艏兴波和尾流场存在差异;固定状态与自由度开放状态下的螺旋桨推力与扭矩在一阶叶频处的峰值相差不多,固定状态计算模型船后螺旋桨的推力在一阶叶频处的峰值大于自由度开放状态的计算模型。固定状态计算模型船后螺旋桨的扭矩在一阶叶频处的峰值小于自由度开放状态计算模型。各个测点自由度开放状态下的一阶脉动压力幅值均小于固定状态。
3) 往往以固定模型为基准的数值自航实验进行的船艉脉动压力预报相比于自由度开放状态存在一定的过度预报现象。因此在对螺旋桨诱导的船艉脉动压力进行数值预报时,应用本文采用的放开自由度的数值计算方法能更好的模拟真实环境中,由于船舶姿态发生变化时的船舶水动力性能,并能对船桨减振降噪工作提供更有效的指导。
| [1] |
LEE J H, LEE K J, PARK H G, et al. Possibility of air-filled rubber membrane for reducing hull exciting pressure induced by propeller cavitation[J]. Ocean engineering, 2015, 103: 160-170. DOI:10.1016/j.oceaneng.2015.04.073 ( 0) 0)
|
| [2] |
李亮, 王超, 孙盛夏, 等. 船桨舵一体的螺旋桨激振力数值预报分析[J]. 武汉理工大学学报:交通科学与工程版, 2015(4): 768-772. LI Liang, WANG Chao, SUN Shengxia, et al. Numerical prediction analysis of propeller exciting force for hull-propeller-rudder system[J]. Journal of Wuhan University of Technology:transportation science & engineering, 2015(4): 768-772. (  0) 0)
|
| [3] |
GAGGERO S, TANI G, VIVIANI M, et al. A study on the numerical prediction of propellers cavitating tip vortex[J]. Ocean engineering, 2014, 92(92): 137-161. ( 0) 0)
|
| [4] |
傅慧萍. 船桨整体及螺旋桨诱导的船体表面脉动压力计算[J]. 哈尔滨工程大学学报, 2009, 30(7): 728-734. FU Huiping. Numerical study of methods for predicting interal hull and propeller and propeller-induced hull surface pressure fluctuations[J]. Journal of Harbin Engineering University, 2009, 30(7): 728-734. (  0) 0)
|
| [5] |
叶金铭, 熊鹰, 孙海涛, 等. 空泡螺旋桨诱导的双桨船脉动压力数值预报[J]. 哈尔滨工程大学学报, 2013, 34(5): 568-574. YE Jinming, XIONG Ying, SUN Haitao, WANG Zhanzhi. Numerical prediction of pressure fluctuations induced by cavitating propeller on twin-screw ship[J]. Journal of Harbin Engineering University, 2013, 34(5):568-574. http://heuxb.hrbeu.edu.cn/oa/DArticle.aspx?type=view&id=201110060 (  0) 0)
|
| [6] |
ABBAS N, KORNEV N, SHEVCHUK I, et al. CFD prediction of unsteady forces on marine propellers caused by the wake nonuniformity and nonstationarity[J]. Ocean engineering, 2015, 104: 659-672. DOI:10.1016/j.oceaneng.2015.06.007 ( 0) 0)
|
| [7] |
YE J, XIONG Y, FANG L I, et al. Experimental study of effects of air content on cavitation and pressure fluctuations[J]. Journal of hydrodynamics, Ser. B, 2010, 22(5): 634-638. DOI:10.1016/S1001-6058(09)60097-4 ( 0) 0)
|
| [8] |
SEOL H. Time domain method for the prediction of pressure fluctuation induced by propeller sheet cavitation:numerical simulations and experimental validation[J]. Ocean engineering, 2013, 72: 287-296. DOI:10.1016/j.oceaneng.2013.06.030 ( 0) 0)
|
| [9] |
郭春雨, 王恋舟, 赵庆新, 等. 一种计及姿态变化的船舶阻力预报方法[J]. 船舶工程, 2015(1): 31-34. GUO Chunyu, WANG Lianzhou, ZHAO Qingxin, et al. Approach of ship resistance prediction with consideration of hull gesture[J]. Ship engineering, 2015(1): 31-34. (  0) 0)
|
| [10] |
CASTIGLIONE T, STERN F, BOVA S, et al. Numerical investigation of the seakeeping behavior of a catamaran advancing in regular head waves[J]. Curriculum teaching material & method, 2013, 112(112): 64-74. ( 0) 0)
|
| [11] |
WILCOX D C. Turbulence modeling for CFD [M]. DOW Industries, Inc. La Can ada, 1994. http://www.academia.edu/15512767/Simulation_of_Particle_Deposition_in_an_Idealized_Mouth_with_Different_Small_Diameter_Inlets
( 0) 0)
|
| [12] |
WEISS J M, SMITH W A. Preconditioning applied to variable and constant density flows[J]. AIAA journal, 1995, 33(11): 2050-2057. DOI:10.2514/3.12946 ( 0) 0)
|
| [13] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA journal, 1994, 32(9): 1598-1605. ( 0) 0)
|
| [14] |
HIRT C W, NICHOLS B D. Volume of fluid(VOF)method for the dynamics of free boundary[J]. Compute Phys, 1981, 39: 201-225. DOI:10.1016/0021-9991(81)90145-5 ( 0) 0)
|
| [15] |
CARRICA P M, CASTRO A M, STERN F. Self-propulsion computations using a speed controller and a discretized propeller with dynamic overset grids[J]. Journal of marine science & technology, 2010, 15(4): 316-330. ( 0) 0)
|
| [16] |
CHAO Y, KARL K. Numeric propulsion for the KCS coutainer ship[C]//Proceedings of CFD workshop Tokyo 2005. Tokyo, 2005:539-547.
( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


