导管桨由螺旋桨和具有流线形剖面的导管组合而成,导管的存在能够显著改善工作在船后的螺旋桨的伴流场,并产生一定的额外推力,对提高重载荷船舶的螺旋桨效率效果尤为明显[1],因此,导管桨在现代水面和水下船只上得到了广泛应用。
随着对导管桨研究的不断深入,人们已经开发了多种方法来研究导管桨的水动力性能。Feiten等利用试验的方法对导管桨进行了研究[2]。基于薄翼假设,Khatib利用升力面方法研究了导管和螺旋桨之间的水动力干扰问题[3]。随着面元法的兴起,开始将面元法技术应用于导管桨水动力性能的求解。韩宝玉等采用迭代方法计算了导管桨的定常水动力性能[4-5]。杨晨俊等用面元法来计算导管,涡格法来计算螺旋桨,通过迭代过程考虑二者之间的的相互影响,计算了敞水中导管螺旋桨的水动力性能[6]。为了修正线型尾涡模型的误差,Kawakita根据试验结果,建立了非线性尾涡模型并利用该模型研究了导管桨的水动力性能[7]。Kinnas等运用边界元法计算并分析了导管桨周围流动的时域特征[8]。Sanchez-Caja等考虑了流体的粘性,用计算流体力学方法分析了不可压缩流体中导管桨的水动力性能[9]。解学参等基于面元法,迭代计算了导管和螺旋桨之间的相互影响,并分析了其内部流场的速度分布特征[10]。胡健等在分析影响导管桨水动力性能的几个关键因素时,运用面元法,并根据计算结果,从水动力性能角度来对这些要素的组合进行优化[11]。
以往对导管桨的流场计算大部分采用了势流理论的方法,这种方法的本质特点是忽略了流体粘性。对于螺旋桨,由于其以很高的速度运转,雷诺数很大,基本可以忽略粘性的影响,但是由于导管的雷诺数相对较小,采用势流方法进行计算会带来很大的误差。近年来,CFD方法在导管桨的水动力计算中获得了较多的应用。Park等在计算了带有定子的导管螺旋桨周围的流场时采用了CFD方法[12]。崔立新等运用CFD方法对导管桨的定常和非定常水动力性能进行了理论计算[13]。以往对于导管桨的大部分CFD数值计算采用的是非结构网格划分方法,虽然与结构网格划分方法相比,更容易生成网格,但计算周期长,且计算结果不够准确。为了有效地缩短计算周期,提高计算结果的准确性,本文采用全结构网格方法研究了均匀来流中导管桨的定常水动力性能和斜流中导管桨的非定常水动力性能。
1 数值模型的建立 1.1 计算模型及网格划分本文采用的计算模型为JD7704型导管+Ka4-55型螺旋桨,盘面比为AE/A0=0.55,螺距比为P/D=1.0,其主要参数见表 1和表 2,三维模型如图 1(a)所示。
| 表 1 JD7704型导管主要参数 Tab.1 Main particulars of JD7704 duct |
| 表 2 Ka4-55螺旋桨主要参数 Tab.2 Main particulars of Ka4-55 propeller |

|
图 1 计算域及导管桨的网格示意图 Fig.1 Gridding sketch of the computational domain and ducted propeller |
整个计算域被分为包含螺旋桨的旋转域和包含导管的静止域两个部分,均采用结构化网格划分形式,图 1(a)为总体计算域的网格布置形式,外静止域半径为3D(D为螺旋桨直径),计算域入口与螺旋桨桨盘面的距离为4D,计算域出口与螺旋桨桨盘面的距离为5D。对于结构化网格,其六面体形状越接近于正方体,奇异性越好,网格质量越好。从图 1(b)可以看出,导管桨的面网格基本接近于矩形,说明本文的网格划分方法很好地控制了网格的质量。
1.2 边界条件将大域的入口设置为速度入口,出口设置为质量出口,在导管表面上,边界条件设为固壁,无滑移。螺旋桨所处的旋转域采用MRF法[17],具体设置如表 3所示。
| 表 3 数值模型的及计算参数 Tab.3 Numerical model and the computational variables |
导管桨的导管和螺旋桨之间虽然存在着相对运动,但是由于导管是一个回转体,轴向均匀来流中不同位置桨叶和导管之间的影响是相同的,因此可以将该问题当成定常问题处理。
图 2给出了不同进速下螺旋桨的敞水性能,其中螺旋桨的推力系数KTp,转矩系数KQp和导管的推力系数KTd,转矩系数KQd定义表示为
| ${K_{Tp}} = \frac{{{T_p}}}{{\rho {n^2}{D^4}}}$ | (1) |
| ${K_{Qp}} = \frac{{{Q_p}}}{{\rho {n^2}{D^5}}}$ | (2) |
| ${K_{Td}} = \frac{{{T_d}}}{{\rho {n^2}{D^4}}}$ | (3) |
| ${K_{Qd}} = \frac{{{Q_d}}}{{\rho {n^2}{D^5}}}$ | (4) |
螺旋桨的进速系数:
| $J = \frac{{{V_A}}}{{nD}}$ | (5) |
式中:Tp为螺旋桨的推力,Qp为螺旋桨的转矩,Td为导管的推力,Qd为导管的转矩,n为转速,D为螺旋桨的直径,ρ为流体的密度。在此定义KT=KTp+KTd,KQ=KQp+KQd。
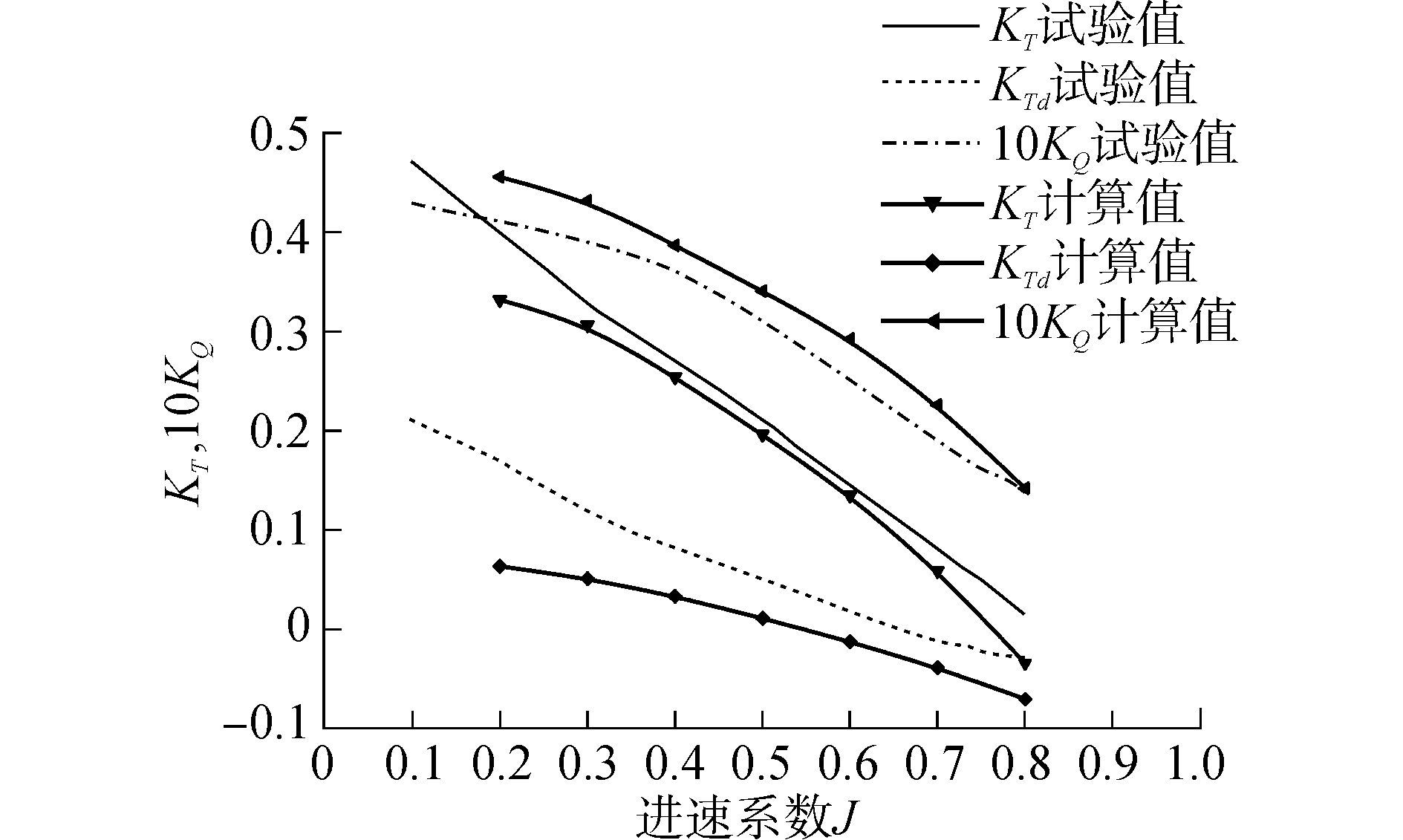
将数值计算结果与试验值进行对比,其结果如图 2所示。
|
图 2 JD7704+Ka4-55导管桨敞水性能 Fig.2 Open water performance of JD7704+Ka4-55 ducted propeller |
从图 2可以看出,对于Ka4-55型螺旋桨,本文中CFD模拟的计算值与试验值吻合较好。
本文还使用RNG k-ε湍流模型对上述导管桨进行了模拟,壁面函数为标准壁面函数。以进速系数J=0.5时为例,将使用了RNG k-ε湍流模型的计算结果与使用SST k-ω的计算结果相比较,结果见表 4。
| 表 4 J=0.5时不同湍流模型计算结果对比 Tab.4 Results comparison of different turbulent models as J=0.5 |
由表 4可以看出,使用RNG k-ε湍流模型的计算结果与使用SST k-ω湍流模型的计算结果的精度均在可接受范围内。
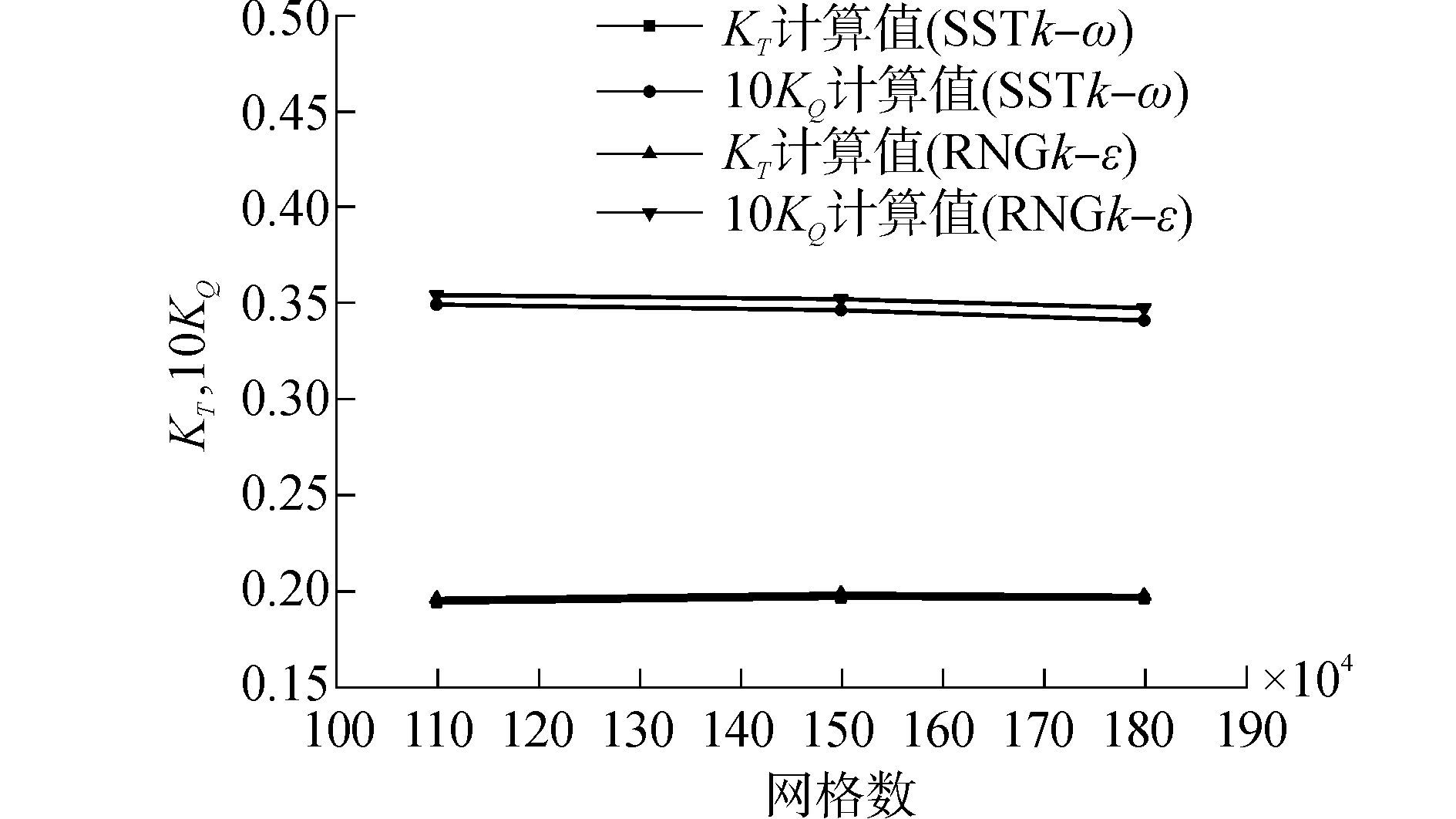
为了验证计算结果相对于网格和计算模型的收敛性,图 3分别计算了当划分网格数为110万、150万、180万,湍流模型为SST k-ω和RNG k-ε,进速系数J=0.5时六种情况下的推力系数KT和转矩系数KQ,将其计算结进行对比。
|
图 3 J=0.5时不同网格数计算结果对比 Fig.3 Comparison of the numerical results with different grid numbers as J=0.5 |
从图 3可以看出,本文所采用的两种模型,当划分网格数分别为110万、150万、180万时,计算值基本保持不变,由此本文的计算结果关于网格数量和湍流模型是收敛的。在以下分析中,均采用180万网格,湍流模型为SST k-ω。
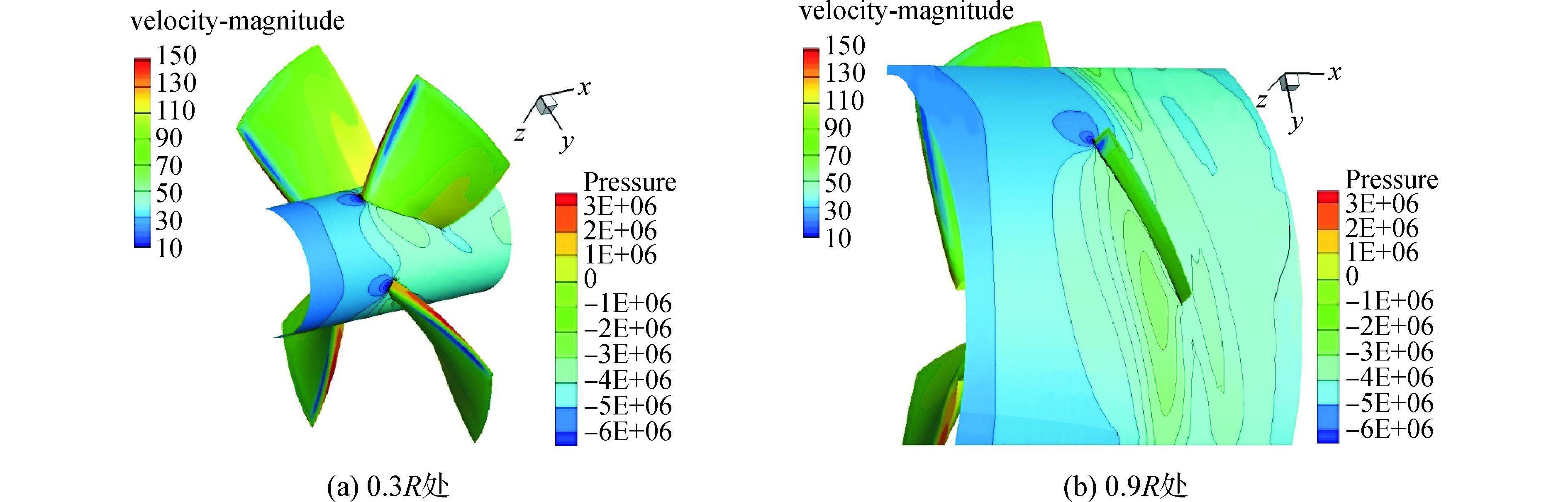
2.2 桨叶压力分布图 4是进速系数J=0.2、来流速度为10 m/s、螺旋桨转速为10 r/s时,导管桨桨叶的压力分布及0.3R、0.9R位置圆柱面的速度分布图。
|
图 4 J=0.2时桨叶压力分布和不同半径处速度分布 Fig.4 Blade pressure distribution and velocity distribution at different radius as J=0.2 |
从图 4可以看出,在粘性的作用下,流体在螺旋桨叶片导边处的速度最小,而压力取得最大值;当流体沿着螺旋桨叶背向随边运动时,速度逐渐增大,使得在叶背上的压力减小而形成低压区,由叶面和叶背的压力差形成沿着负x方向的推力。随着进速系数的增大,叶面与叶背的压力差越来越小,由螺旋桨所产生的推力越来越小。在不同的圆柱截面上,桨前方的流体和速度比较小,而后方比较大,速度最小值出现在桨叶导缘附近。
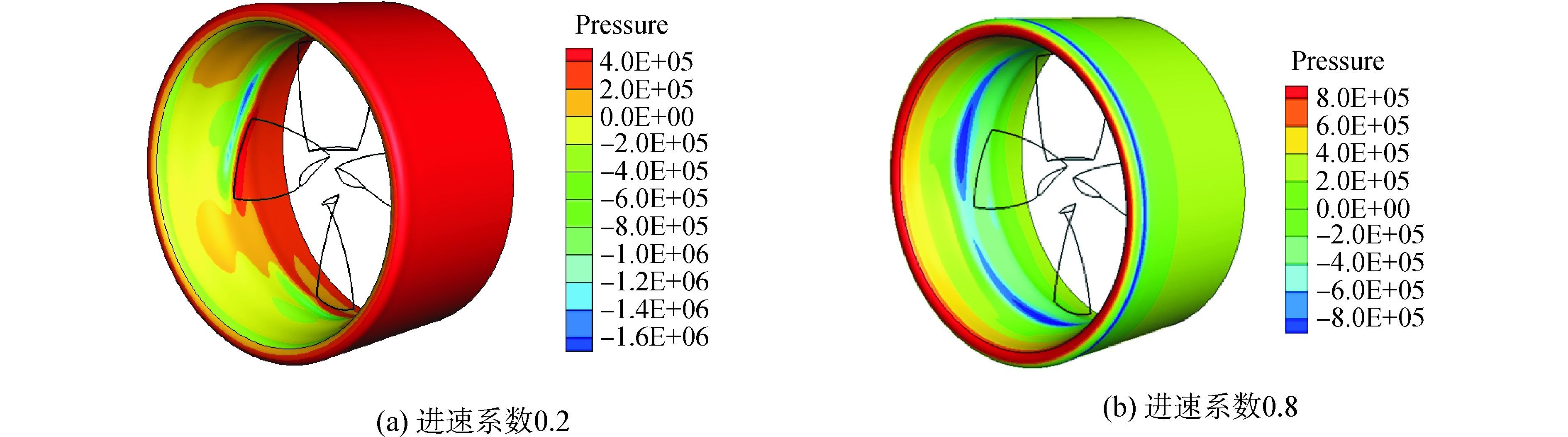
2.3 导管推力的机理分析图 5分别为当进速系数J=0.2、来流速度为10 m/s、螺旋桨转速为10 r/s,和进速系数J=0.8、来流速度为40 m/s、螺旋桨转速为10 r/s两种工况时,导管的压力分布图。
|
图 5 不同进速系数时导管表面压力 Fig.5 Pressure distribution of the duct at different J |
从图 5(a)可以看出,在进速系数J=0.2时导管外壁压力分布比较均匀,由此可知导管外壁产生的轴向力即推力基本可以忽略。受螺旋桨的影响,导管内壁的压力分布非常复杂,其基本特征是内壁前半部分的压力较小,后半部分压力较大。由于导管内壁和轴向具有一定的夹角,其表面合力会在轴向产生一个很大的分量,此分量即为导管产生的推力。如图 5(b)所示,J=0.8时导管表面的压力分布趋势恰恰相反,导管内壁前半部分压力较大,后半部分压力较小,其合力的轴向分量和低进速时相反,此时导管上产生的阻力,这就是导管桨在推轮、拖轮等低航速、重载荷船舶上广泛运用的主要原因之一。
比较图 5(a)和图 5(b),可以看出,当J=0.2时,在螺旋桨叶梢前面附近的导管内壁上形成一个很明显的低压区,而叶梢后面附近的导管内壁上形成一个很明显的高压区;当J=0.8时,相同位置的低压区仍然存在,而高压区消失,这也说明螺旋桨载荷对导管的受力存在巨大的影响。
2.4 导管对螺旋桨水动力性能的影响为了计算导管对螺旋桨水动力性能的影响,本文分别对导管的型值在长度方向和半径方向进行了改变。在长度方向对导管分别拉伸为原尺寸的1.2、1.4、1.6倍,在半径方向对导管分别扩大为原尺寸的1.2、1.4、1.6倍,对6组模型进行三维建模并计算,当进速系数J=0.5时,计算结果图 5、6所示。
|
图 6 导管长度对螺旋桨水动力性能的影响 Fig.6 Effect of duct length on the hydrodynamic performance of propeller |
从图 6中可以看出,随着导管沿着长度方向拉伸倍数的增加,导管桨桨叶的推力系数和转矩系数均逐渐减小,由于对导管沿长度方向进行了拉伸,导管首缘处和尾缘处的形变会比原来更为明显,因此导管的推力系数有所增大,但转矩系数基本保持不变。随着导管沿着长度方向拉伸倍数的增加,导管螺旋桨整体的推力系数和转矩系数均逐渐减小。上述变化均在沿长度方向拉伸为原尺寸的1.0~1.2倍时较为明显,当拉伸为1.2~1.6倍时,效果改变不显著。
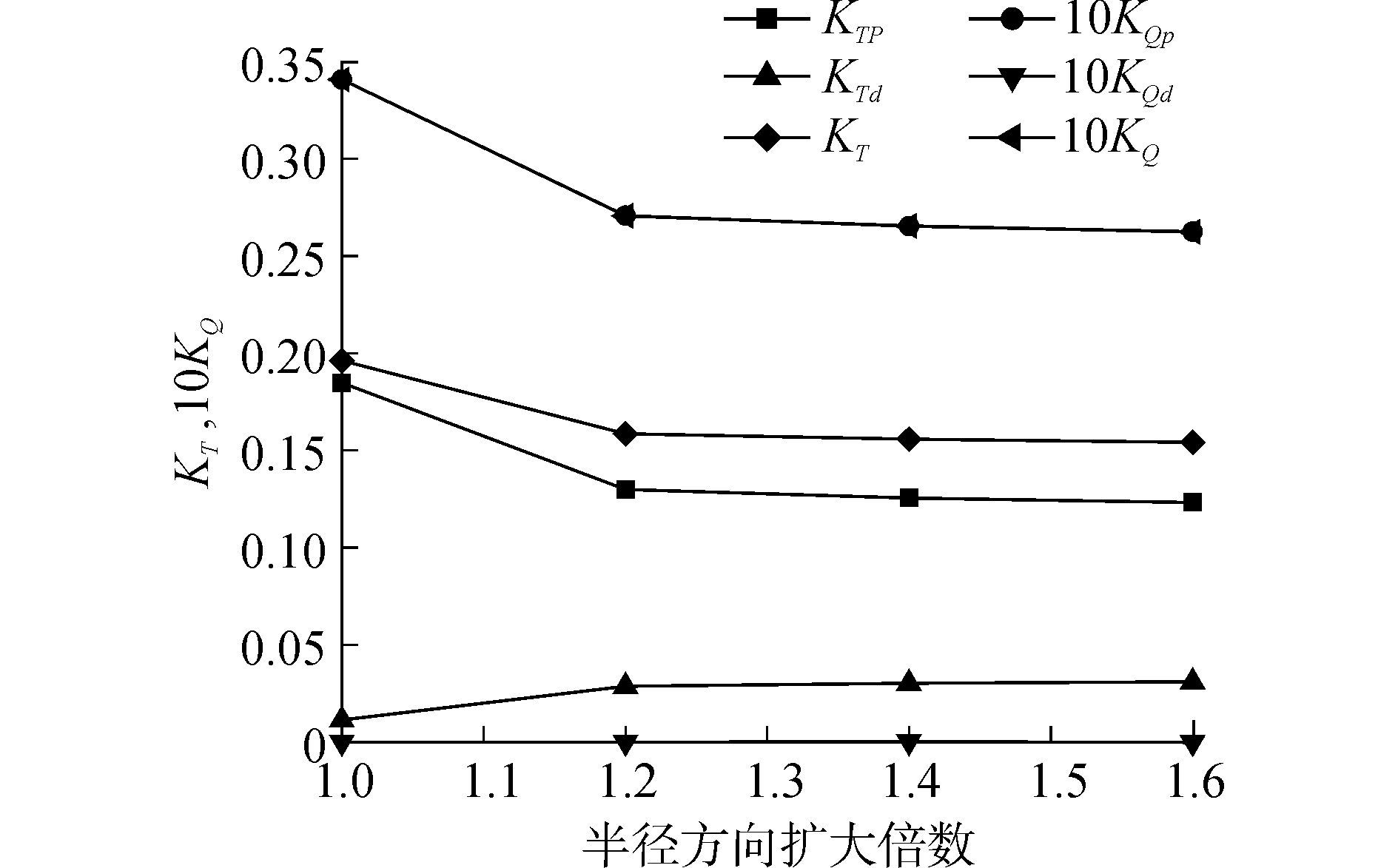
从图 7中可以看出,当沿着半径方向扩大为原尺寸的1.0~1.2倍时,导管桨桨叶,导管桨整体的推力系数和转矩系数稍有减小,当扩大为1.2~1.6倍时,随着导管沿着半径方向扩大倍数的增加,导管桨桨叶,导管桨整体的推力系数和转矩系数均增大。当沿着半径方向扩大为原尺寸的1.0~1.4倍时,导管的推力系数逐渐减小,当扩大为1.6倍时,由于导管的尺度较大,导管的推力系数稍有增加,但在整个变化过程中,导管的转矩系数基本保持不变。
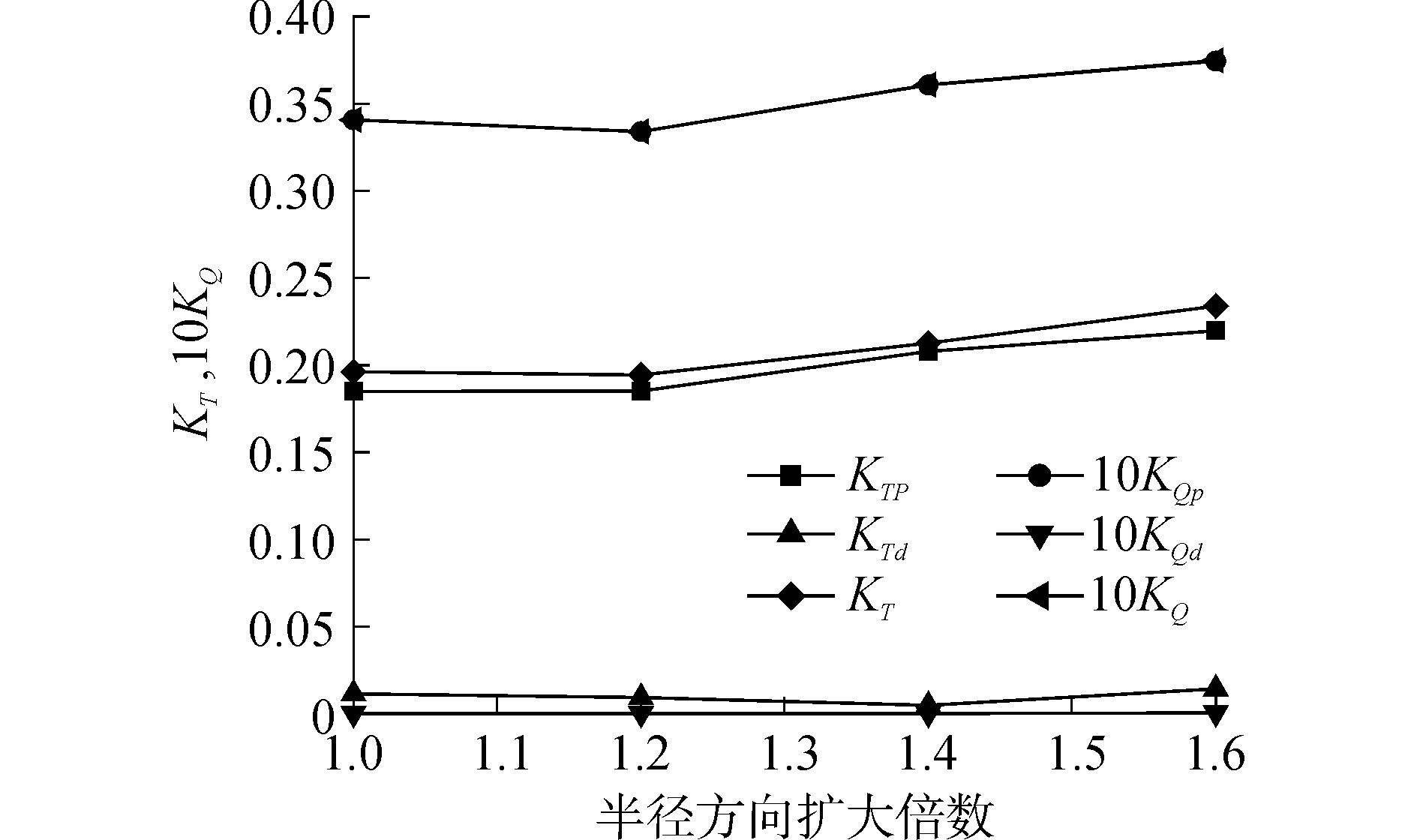
|
图 7 导管半径对螺旋桨水动力性能的影响 Fig.7 Effect of duct radius on the hydrodynamic performance of propeller |
在轴向均匀来流中,虽然螺旋桨和导管之间存在相对运动,但是由于导管是回转体,该问题仍然可以当成是定常的,因此在旋转域中采用运动参考系,即在旋转域中螺旋桨不动、坐标系运动,螺旋桨相对坐标系产生旋转。但是当来流和轴向存在一定的夹角时,该问题就变成了非定常问题,因此在旋转域中采用滑移网格的方法,螺旋桨运动、坐标系不动,螺旋桨相对坐标系产生旋转。
本文通过非定常方法,对在进速系数J=0.5,螺旋桨转速为10 r/s,来流速度为25 m/s,有Z轴负方向速度分量,倾斜角度为7.5°的斜流中,有导管和无导管两种情况下单个桨叶(0°时,桨叶的位置为Y轴正方向)的水动力性能进行了对比分析,计算结果如图 8所示。

|
图 8 7.5°斜流中对螺旋桨水动力性能的变化 Fig.8 Variation of hydrodynamic forces of the propeller in 7.5° oblique flow |
从图 8中可以看出,在斜流中,有导管和无导管两种情况下单桨叶的推力系数和转矩系数均呈周期性变化,其变化周期与螺旋桨的旋转周期相同。由于导管的作用,在有导管时桨叶的推力系数和转矩系数的幅值变化范围明显比无导管情况下小,且无导管情况下桨叶的推力系数和转矩系数更大,说明导管的存在能够显著减小螺旋桨在斜流工况下运作时推力和转矩的脉动。
斜流中无导管时螺旋桨叶背、叶面的压力分布如图 9所示。
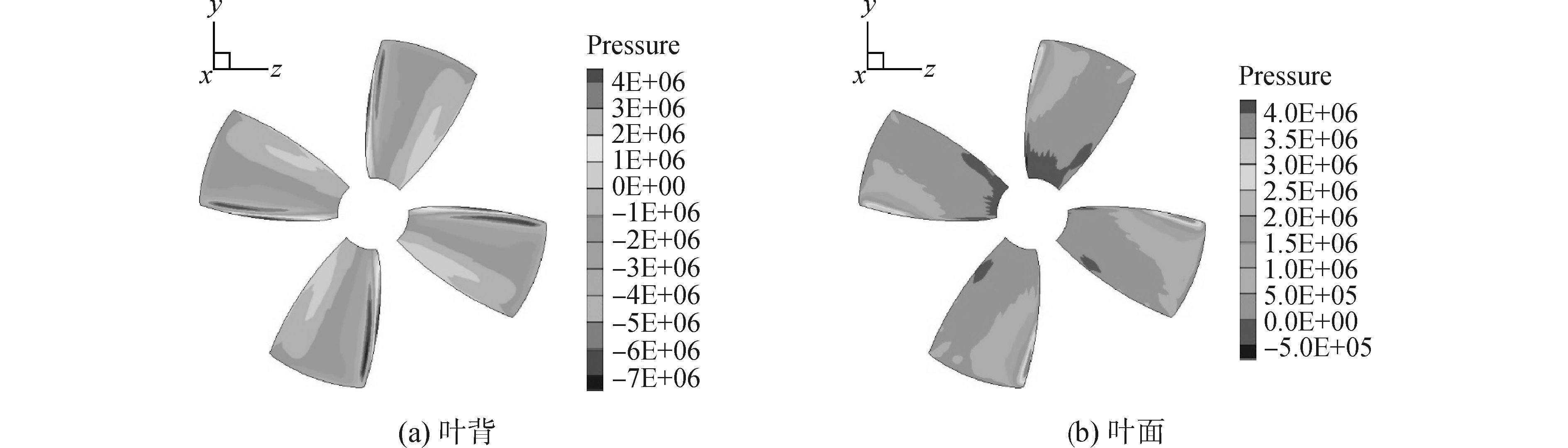
|
图 9 7.5°斜流中无导管螺旋桨叶表面压力分布 Fig.9 Pressure distribution of the propeller without duct in the 7.5° oblique flow |
斜流中导管桨桨叶叶背、叶面的压力分布如图 10所示。

|
图 10 7.5°斜流中有导管螺旋桨叶表面压力分布 Fig.10 Pressure distribution of the propeller with duct in the 7.5° oblique flow |
从图 9、10中可以看出,受到斜流的影响,非定常计算中导管桨不同桨叶的压力分布是不同的,而在定常计算中,导管桨不同桨叶的压力分布基本一致。本文所设置的斜流角度为7.5°,在此角度下,可以看出不同螺旋桨叶表面压力变化不十分明显,但是,仍然可以发现无导管时不同桨叶表面的压力差明显大于有导管时的压力差,因此其推力和转矩的变化也比较明显。
斜流中导管桨导管的压力分布如图 11所示。从图 11中可以看出,在螺旋桨叶梢前面附近的导管内壁上形成一个很明显的低压区,且由于斜流的作用,导管内外壁面上的压力分布不均匀。
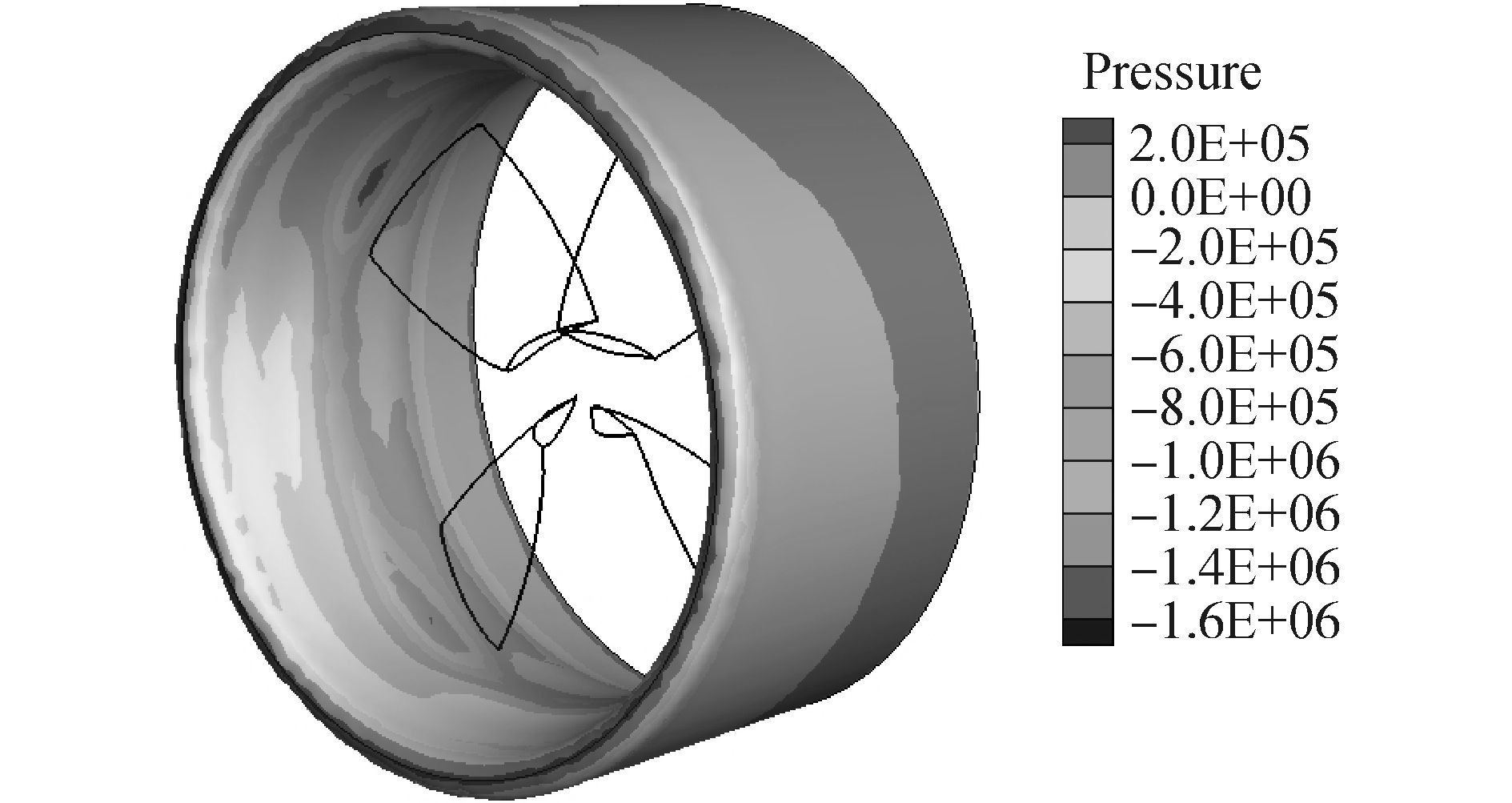
|
图 11 斜流中导管压力分布图 Fig.11 Pressure distribution of duct in the oblique flow |
斜流中,沿桨轴方向、取距离桨盘面前x/R=0.56位置处的截面,分别给出导管桨导管内桨前流场轴向、径向及切向速度分布图。
5 结论1) 通过网格数量和湍流模型的收敛性计算结果与试验值的对比,验证了本文所采用的数值模型和湍流模型的准确性和可靠性。在低进速下由导管和螺旋桨所产生的推力较大,在高进速下螺旋桨的推力减小,且导管产生阻力。
2) 导管桨的推力系数和转矩系数均呈周期性变化,其周期值与螺旋桨的旋转周期相同,导管的存在能够显著减小螺旋桨在斜流工况下运作时推力和转矩的脉动。
| [1] |
BORENSTEIN J, KOREN Y. Histogramic in-motion mapping for mobile robot obstacle avoidance[J]. IEEE transactions on robotics and automation, 1991, 7(4): 535-539. DOI:10.1109/70.86083 ( 0) 0)
|
| [2] |
FEITEN W, BAUER R, LAWITZKY G. Robust obstacle avoidance in unknown and cramped environments[C]//IEEE International Conference on Robotics and Automation, 1994:2412-2417. https://www.researchgate.net/publication/235412274_Foundations_of_Parameterized_Trajectories-based_Space_Transformations_for_Obstacle_Avoidance
( 0) 0)
|
| [3] |
KHATIB M. Sensor-based motion control for mobile robots[C]//5th International Symposium on Applied Computational Intelligence and Informatics. Timisoara, Romania, 2009.
( 0) 0)
|
| [4] |
韩宝玉, 熊鹰, 叶金铭. 面元法预估导管螺旋桨定常性能的一种简便方法[J]. 船海工程, 2007, 36(3): 42-45. HAN Baoyu, XIONG Ying, YE Jinming. A simple method to predict the steady performance of ducted propeller with surface panel method[J]. Ship & ocean engineering, 2007, 36(3): 42-45. (  0) 0)
|
| [5] |
刘小龙, 王国强. 导管螺旋桨定常性能预估的基于速度势的面元法[J]. 船舶力学, 2006, 10(3): 26-35. LIU Xiaolong, WANG Guoqiang. A potential based panel method for prediction of steady performance of ducted propeller[J]. Journal of ship mechanics, 2006, 10(3): 26-35. (  0) 0)
|
| [6] |
杨晨俊, 王国强. 导管螺旋桨定常性能理论计算[J]. 上海交通大学学报, 1997, 31(11): 36-39. YANG Chenjun, WANG Guoqiang. Theoretical prediction of the steady performance of ducted propellers[J]. Journal of Shanghai Jiao Tong University, 1997, 31(11): 36-39. (  0) 0)
|
| [7] |
KAWAKITA C. A surface panel method for ducted propellers with new wake model based on velocity measurements[J]. Journal of the society of naval architects of Japan, 1992, 1992(172): 187-202. DOI:10.2534/jjasnaoe1968.1992.172_187 ( 0) 0)
|
| [8] |
KINNAS S, HSIN C Y, KEENAN D. A potential based panel method for the unsteady flow around open and ducted propellers[C]//Eighteenth Symposium on Naval Hydrodynamics.[S.l.], 1991.
( 0) 0)
|
| [9] |
SANCHEZ-CAJA A, RAUTAHEIMO P, SIIKONEN T. Simulation of incompressible viscous flow around a ducted propeller using a RANS equation solver[C]//Proceedings of the 23rd Symposium on Naval Hydrodynamics.[S.l.], 2000.
( 0) 0)
|
| [10] |
解学参, 黄胜, 胡健, 等. 导管桨内部流场的数值计算[J]. 哈尔滨工程大学学报, 2009, 30(1): 7-12. XIE Xuesen, HUANG Sheng, HU Jian, et al. Inner flow field calculations for ducted propellers[J]. Journal of Harbin Engineering University, 2009, 30(1): 7-12. (  0) 0)
|
| [11] |
胡健, 黄胜, 马骋, 等. 影响导管桨内部流场的几个因素[J]. 天津大学学报, 2009, 42(4): 340-344. HU Jian, HUANG Sheng, MA Chi, et al. Several influence factors for the inner flow field of ducted propeller[J]. Journal of Tianjin University, 2009, 42(4): 340-344. (  0) 0)
|
| [12] |
PARK W G, JUNG Y R, KIM C K. Numerical flow analysis of single-stage ducted marine propulsor[J]. Ocean engineering, 2005, 32(10): 1260-1277. DOI:10.1016/j.oceaneng.2004.10.022 ( 0) 0)
|
| [13] |
崔立新. 导管螺旋桨的水动力性能及噪声性能预报[D]. 哈尔滨工程大学, 2013. CUI Lixin. Prediction of hydrodynamic performances and noise of ducted propeller[D]. Harbin:Harbin Engineering University, 2013. (  0) 0)
|
| [14] |
项立银, 陈杨. 结构化与非结构化网格融合技术研究[J]. 雷达与对抗, 2012, 32(3): 53-55. XIANG Liyin, CHEN Yang. A study on structured and unstructured grid fusion technology[J]. RADAR & ECM, 2012, 32(3): 53-55. (  0) 0)
|
| [15] |
PAN G, CHENG B, ZHANG P, et al. Coupling design and performance analysis of rim-driven integrated motor propulsor[C]//OCEANS 2016-Shanghai. IEEE, 2016:1-6.
( 0) 0)
|
| [16] |
MULJOWIDODO K, ADI N, PRAYOGO N, et al. Design and testing of underwater thruster for SHRIMP ROV-ITB[J]. Indian Journal of geo-marine sciences, 2009, 38(3): 338-345. ( 0) 0)
|
| [17] |
周水清, 孔繁余, 王志强, 等. 基于结构化网格的低比转数离心泵性能数值模拟[J]. 农业机械学报, 2011, 42(7): 66-69. ZHOU Shuiqing, KONG Fanyu, WANG Zhiqiang. Numerical simulation for low specific-speed centrifugal pump with structured grid[J]. Transaction of the Chinese Society for Agricultural Machinery, 2011, 42(7): 66-69. (  0) 0)
|
| [18] |
杨春蕾, 朱仁传, 缪国平, 等. 基于CFD方法的船/桨/舵干扰数值模拟[J]. 水动力学研究与进展A辑, 2011, 26(6): 667-673. YANG Chunlei, ZHU Renchuan, MIAO Guoping. CFD-based numerical simulation of hull/propeller/rudder interaction[J]. Chinese journal of hydrodynamics (series A), 2011, 26(6): 667-673. (  0) 0)
|
| [19] |
胡磊, 谭廷寿. 大侧斜螺旋桨敞水性能分析[J]. 船海工程, 2010, 39(1): 41-44. HU Lei, TAN Tingshou. Analysis of open water performance of the high-skew propeller[J]. Ship & Ocean Engineering, 2010, 39(1): 41-44. (  0) 0)
|
| [20] |
陈庆光, 徐忠, 张永建. RNG湍流模型在冲击射流数值计算中的应用[J]. 力学与实践, 2002, 24(6): 21-24. CHEN Qingguang, XU Zhong, ZHANG Yongjian. Application of RNG turbulence models on numerical computations of an impinging jet flow[J]. Mechanics in Engineering, 2002, 24(6): 21-24. (  0) 0)
|
| [21] |
杨从新, 巫发明, 张玉良. 基于滑移网格的垂直轴风力机非定常数值模拟[J]. 农业机械学报, 2009, 40(6): 98-102. YANG Chongxin, WU Faming, ZHANG Yuliang. Numerical simulation on unsteady rotated flow of a vertical axis wind turbine based on moving meshes[J]. Transaction of the Chinese society for agricultural machinery, 2009, 40(6): 98-102. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


