在使用GPS获取大气可降水量(PWV)的过程中,需要将天顶湿延迟转换为PWV所需的转换因子Π,其中重要的参数就是Tm,该参数对GPS-PWV精度的影响甚大。因此,利用气象参数建立起适用于当地的高精度Tm模型是获取GPS-PWV的关键[1]。
目前,采用无线电探空的大气廓线资料进行积分可获取最为精确的Tm值,但由于其高昂的运行成本和较低的时空分辨率,绝大多数GPS测站并没有与探空站共址[2-4]。为获得高精度的Tm值,国内外学者进行了大量研究。Bevis等[5]首次分析了地表温度Ts与Tm的相关性,并提出适用于中纬度地区的Tm-Ts线性回归模型。然而,由于大气湿廓线的快速时空变化,Tm-Ts的关系可能随地理位置和季节发生变化,且研究表明,Bevis模型在全球范围内的表现并不均衡[6]。王皓等[7]利用香港探空站2007~2017年的数据建立了香港地区的Tm回归模型,并考虑了季节性的影响。Yao等[8]考虑了季节性和地势变化,利用多源参数建立了全球范围内的加权平均温度模型。
为获取日本区域高精度的GPS-PWV,本文利用2014~2018年ERA-Interim数据建立考虑季节性改正的日本区域Tm模型,并利用实测数据分析模型的精度。
1 数据与Tm获取 1.1 数据介绍本文使用欧洲中期天气预报中心(ECMWF)提供的ERA-Interim全球再分析数据,其持续提供覆盖对流层和平流层不同空间分辨率的6 h气象参数。ERA-Interim全球再分析数据包括地面、近地面、等压面等各类与气象有关的参数,其中等压面分为1~37层,大气压强从1 000 hPa逐层递减至1 hPa,顶层高度可达到50 km左右(http://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/),数据整体质量较高。
1.2 日本区域Tm获取对流层加权平均温度可由测站上空的水汽压e和绝对气温T沿天顶方向积分得到[9]:
| $ {T_m} = \frac{{\mathop \smallint \limits^{} {\kern 1pt} \left( {e/T} \right){\rm{d}}z}}{{\mathop \smallint \limits^{} {\kern 1pt} \left( {e/{T^2}} \right){\rm{d}}z}} $ | (1) |
式中,e和T分别为测站天顶方向上的水汽压(hPa)和绝对温度(K),z为测站上空的垂直高度(m)。
由于大气水汽基本分布在地面上空12 km以内的区域,而ERA-Interim中的全球大气再分析资料可提供该高度范围内的气温和湿度等大气廓线信息,根据这些廓线信息可将式(1)离散化,通过数值积分的形式计算出Tm,即
| $ {{T}_{m}}=\overset{{}}{\mathop{\sum }}\, \frac{\left( {{z}_{2}}-{{z}_{1}} \right)e}{T}/\overset{{}}{\mathop{\sum }}\, \frac{\left( {{z}_{2}}-{{z}_{1}} \right)e}{{{T}^{2}}} $ | (2) |
式中,z1和z2分别为上、下观测层的高度值(m),e和T分别为上、下观测层的平均水汽压(hPa)和平均温度(K)。水汽压可通过下式计算:
| $ {{e}_{s}}=6.105\cdot \text{exp}\left[ 25.22\cdot \frac{T-273.15}{T}-5.31\cdot \text{ln}\frac{T}{273.15} \right] $ | (3) |
| $ e=\left( \text{RH}\cdot {{e}_{s}} \right)/100 $ | (4) |
式中,T为温度(K),RH为相对湿度(%)。
基于以上公式,本文采用2014~2018年ERA-Interim数据中的等压面气温、相对湿度和位势构建日本区域加权平均温度模型,并考虑其季节性改正。
2 日本区域加权平均温度建模大多数情况下无法获取详细的大气水汽压和温度垂直剖面情况,但可以利用ERA-Interim中的分层温度和相对湿度数据通过数值积分公式和插值方法得到GPS测站的Tm[10]。本文依据前人对Tm和Ts关系的研究,首先分析Tm-Ts的相关性,建立与气象因素相关的线性回归模型,再对模型残差进行季节性改正,从而获得日本区域精化后的Tm模型。
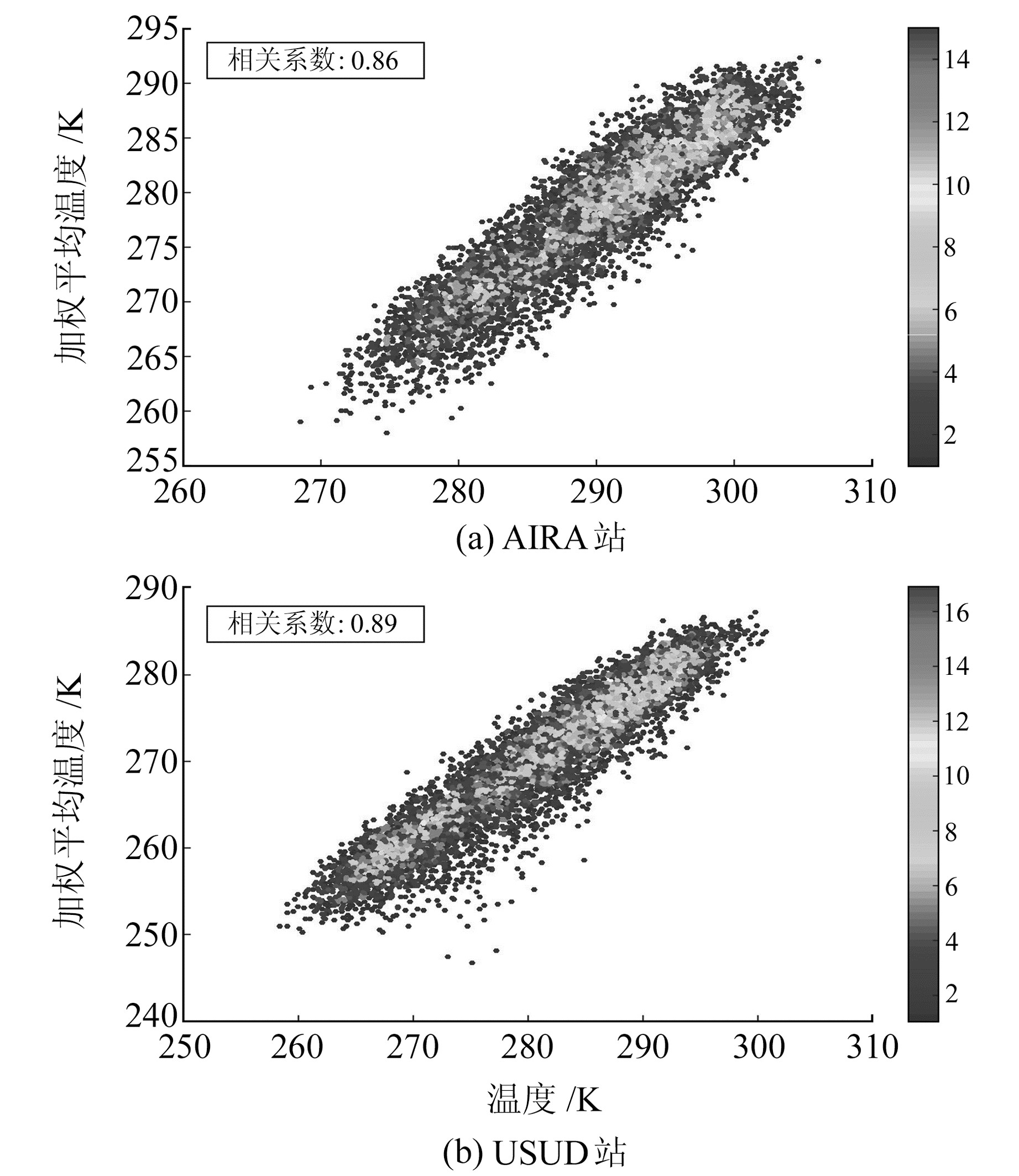
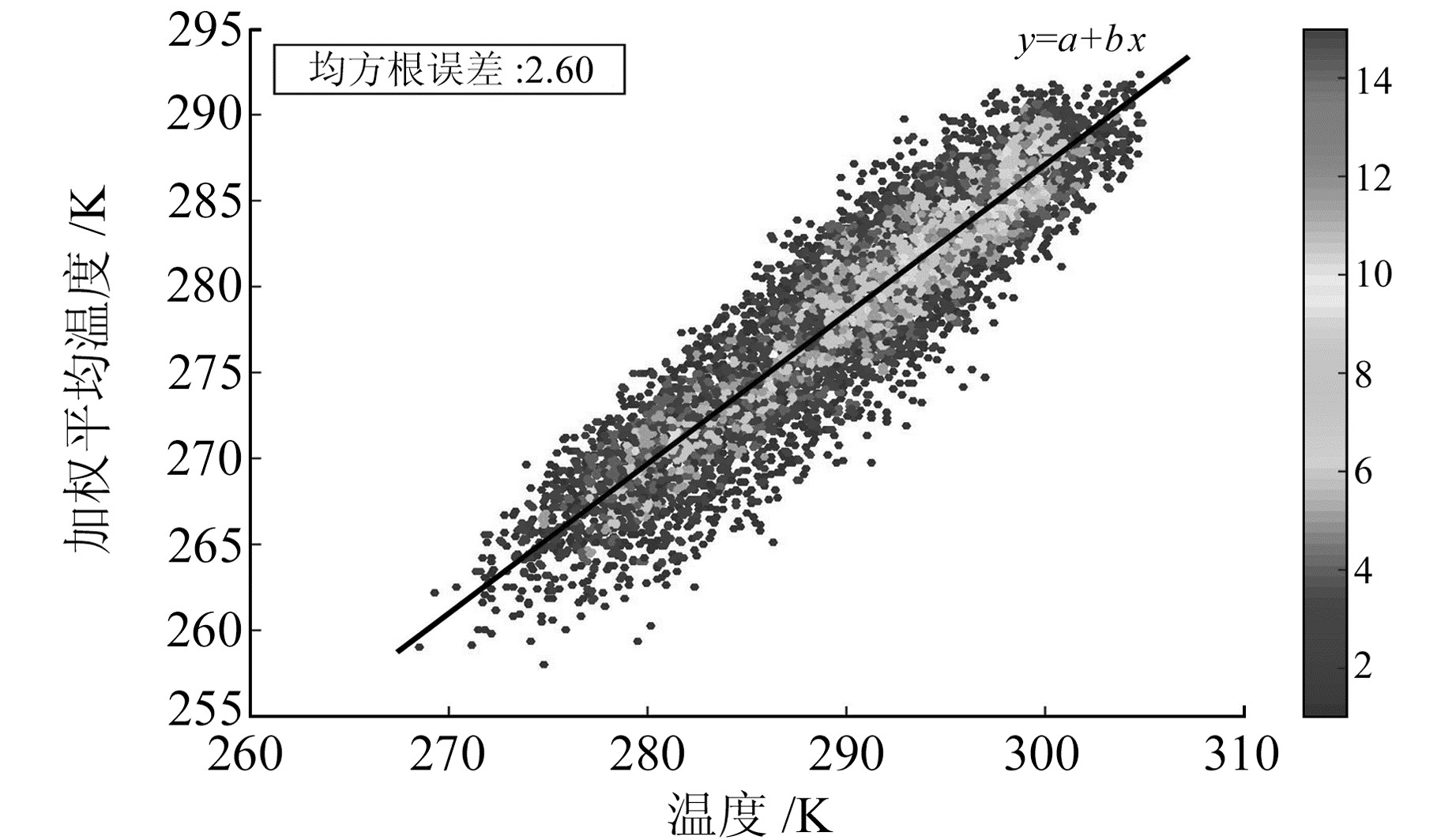
2.1 加权平均温度与地表温度的关系Tm与Ts具有非常高的相关性[11],因此利用2014~2018年的ERA-Interim数据对日本区域GPS测站的Tm和Ts之间的关系进行简要的分析。图 1为2个GPS测站2014~2018年Tm与Ts的散点图,可以看出,2个测站的Tm与Ts都具有明显的线性相关性,相关系数分别为0.86和0.89。用简单公式Tm=a+b×Ts(式中,a取25.94,b取0.870 5)对AIRA站的数据进行拟合,结果见图 2。
|
图 1 2014~2018年AIRA站和USUD站Tm相对于Ts的散点图 Fig. 1 Scatter plots of Tm versus Ts at AIRA and USUD stations from 2014 to 2018 |
|
图 2 AIRA站2014~2018年Tm相对于Ts的散点图及拟合直线 Fig. 2 Scatter plot of Tm versus Ts and fitting line at AIRA station from 2014 to 2018 |
由于不同地区的气象条件有所差异,本文计算了日本区域所有GPS测站的Tm-Ts回归模型系数,利用克里金插值算法进行插值,获取了日本地区的Tm-Ts线性回归模型,并与Bevis线性模型进行对比,结果见表 1。表中,B-Tm为Bevis线性模型,J-Tm为各GPS测站的加权平均温度模型。统计结果表明,J-Tm模型的偏差和均方根误差都小于B-Tm模型,精度提高约16%。
|
|
表 1 2018年各模型和积分Tm间的偏差和均方根误差统计 Tab. 1 Statistics of bias and root mean square error between each model and integral Tm in 2018 |
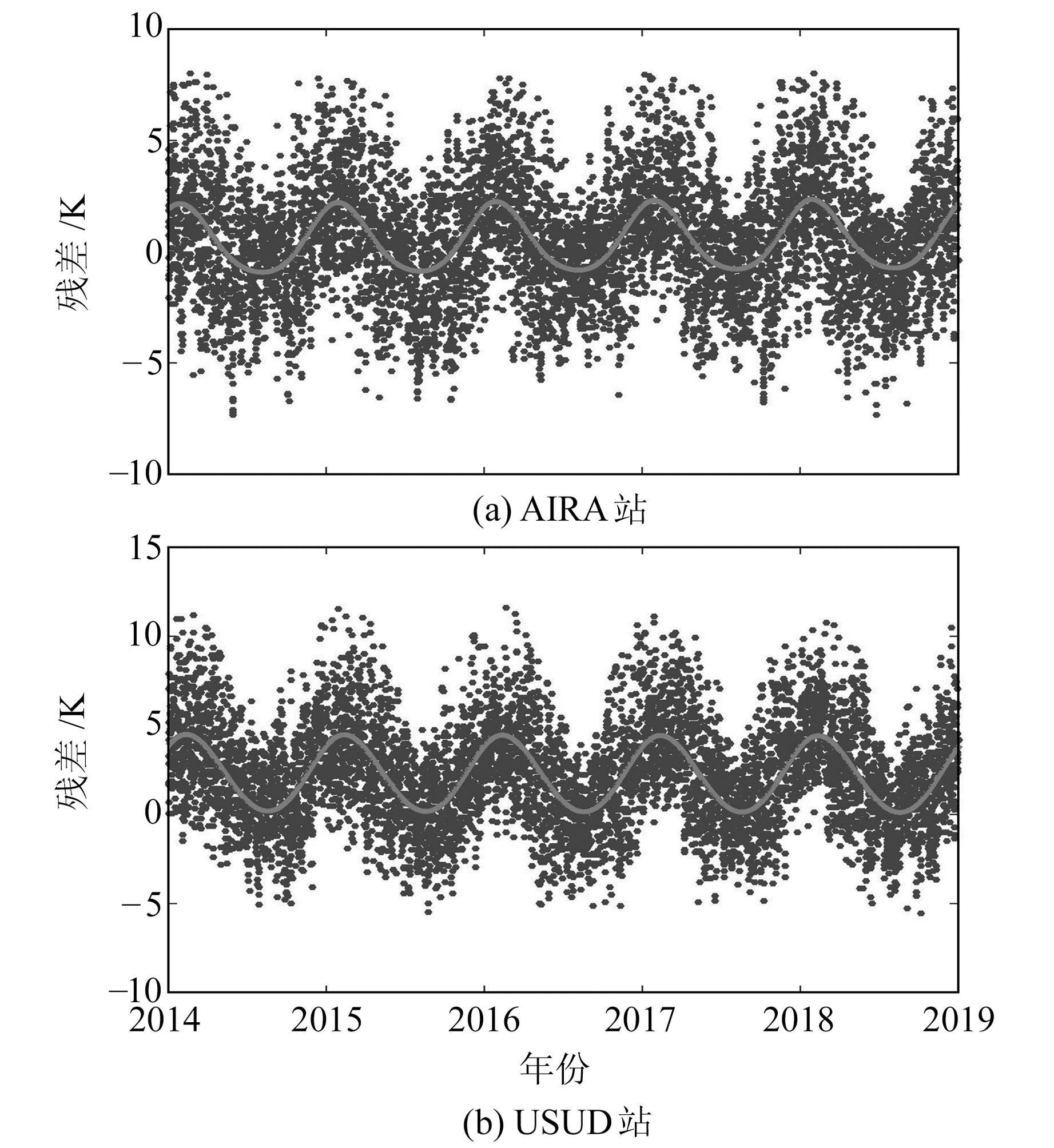
Yao等[12]研究发现,Tm模型的残差存在很强的季节性信号,因此首先对J-Tm模型残差的季节性信号进行探测。图 3展示了2014~2018年AIRA站和USUD站J-Tm模型的残差序列(分别用相应的模型值减去积分值),图中的曲线为拟合曲线,可以看出,残差具有明显的季节性变化,可采用周期函数去拟合残差,增强模型精度。大量学者为了减弱误差存在的季节性变化的影响,对J-Tm模型的残差进行再次建模,以对原有的J-Tm模型进行补偿[7]。Lagler等[13]通过年周期和半年周期去拟合残差,改进了GPT模型,得到GPT2模型;Zhang等[14]研究了年周期、半年周期和日周期来拟合Tm模型,以提高建模精度。
|
图 3 2014~2018年AIRA站和USUD站J-Tm模型残差时间序列 Fig. 3 Residual time series of J-Tm models at AIRA and USUD stations from 2014 to 2018 |
为更清晰地说明J-Tm模型误差的周期性变化,采用周期函数分别对积分Tm和J-Tm模型计算的Tm进行拟合,结果见图 4(以AIRA站和USUD站为例)。可以看出,虽然J-Tm模型的Tm与积分Tm的结果具有较为一致的变化趋势,但并未完全重合,仍然存在部分偏差,而偏差部分正好与J-Tm模型的周期性残差对应。

|
图 4 AIRA站和USUD站拟合的积分Tm与J-Tm模型的Tm时间序列 Fig. 4 Time series of fitted integral Tm and J-Tm models Tm at AIRA and USUD stations |
事实上,这一季节性变化可直接在Tm模型中加以考虑。本文利用年周期、半年周期和日周期对J-Tm模型进行改进,给出能够减弱这种周期性误差影响的新Tm模型,称为J-Tm-Ⅰ模型,具体形式为:
| $ \begin{align} & {{T}_{m}}\left( {{T}_{s}}\text{, doy, hou}{{\text{r}}_{\text{UTC}}} \right)\text{=} \\ & Q\text{ }\!\!\times\!\!\text{ }{{T}_{s}}\text{+}C\text{+HF}\left( \text{doy, hou}{{\text{r}}_{\text{UTC}}} \right) \\ & \text{HF}\left( \text{doy, hou}{{\text{r}}_{\text{UTC}}} \right)\text{=}{{a}_{\text{0}}}\text{+} \\ & {{a}_{\text{1}}}\text{cos}\left( \frac{\text{doy}}{\text{365}\text{.25}}\text{2 }\!\!\pi\!\!\text{ } \right)\text{+}{{b}_{\text{1}}}\text{sin}\left( \frac{\text{doy}}{\text{365}\text{.25}}\text{2 }\!\!\pi\!\!\text{ } \right)\text{+} \\ & {{a}_{\text{2}}}\text{cos}\left( \frac{\text{doy}}{\text{365}\text{.25}}\text{4 }\!\!\pi\!\!\text{ } \right)\text{+}{{b}_{\text{2}}}\text{sin}\left( \frac{\text{doy}}{\text{365}\text{.25}}\text{4 }\!\!\pi\!\!\text{ } \right)\text{+} \\ & \text{ }\!\!~\!\!\text{ }{{a}_{\text{3}}}\text{cos}\left( \frac{\text{hou}{{\text{r}}_{\text{UTC}}}}{\text{24}}\text{2 }\!\!\pi\!\!\text{ } \right)\text{+}{{b}_{\text{3}}}\text{sin}\left( \frac{\text{hou}{{\text{r}}_{\text{UTC}}}}{\text{24}}\text{2 }\!\!\pi\!\!\text{ } \right) \\ \end{align} $ | (5) |
式中,Ts为地表温度,Q为Tm和Ts的回归系数,C为线性模型中的截距,doy为年积日,hourUTC为UTC时间,a0为线性模型中Tm残差的平均值,(a1, b1)、(a2, b2)、(a3, b3)分别为Tm残差的年周期、半年周期和日周期振幅。利用GPS测站的Tm、Ts、年积日和UTC时间,通过最小二乘原理求解出a0、(a1, b1)、(a2, b2)和(a3, b3),最终建立日本区域精化后的Tm模型。
2.3 J-Tm-Ⅰ模型的验证利用2014~2018年ERA-Interim数据建立新的Tm模型,即J-Tm-Ⅰ模型,再利用2018年ERA-Interim数据的积分Tm进行验证,并与B-Tm模型和J-Tm模型比较,结果见表 2。由表 1和2可知,J-Tm-Ⅰ模型精度相对于B-Tm模型和J-Tm模型分别提高约37%和25%,这应该是考虑了季节性变化的结果。
|
|
表 2 2018年J-Tm-Ⅰ模型和积分Tm间的偏差和均方根误差统计 Tab. 2 Statistics of bias and root mean square error between J-Tm-Ⅰ model and integral Tm in 2018 |
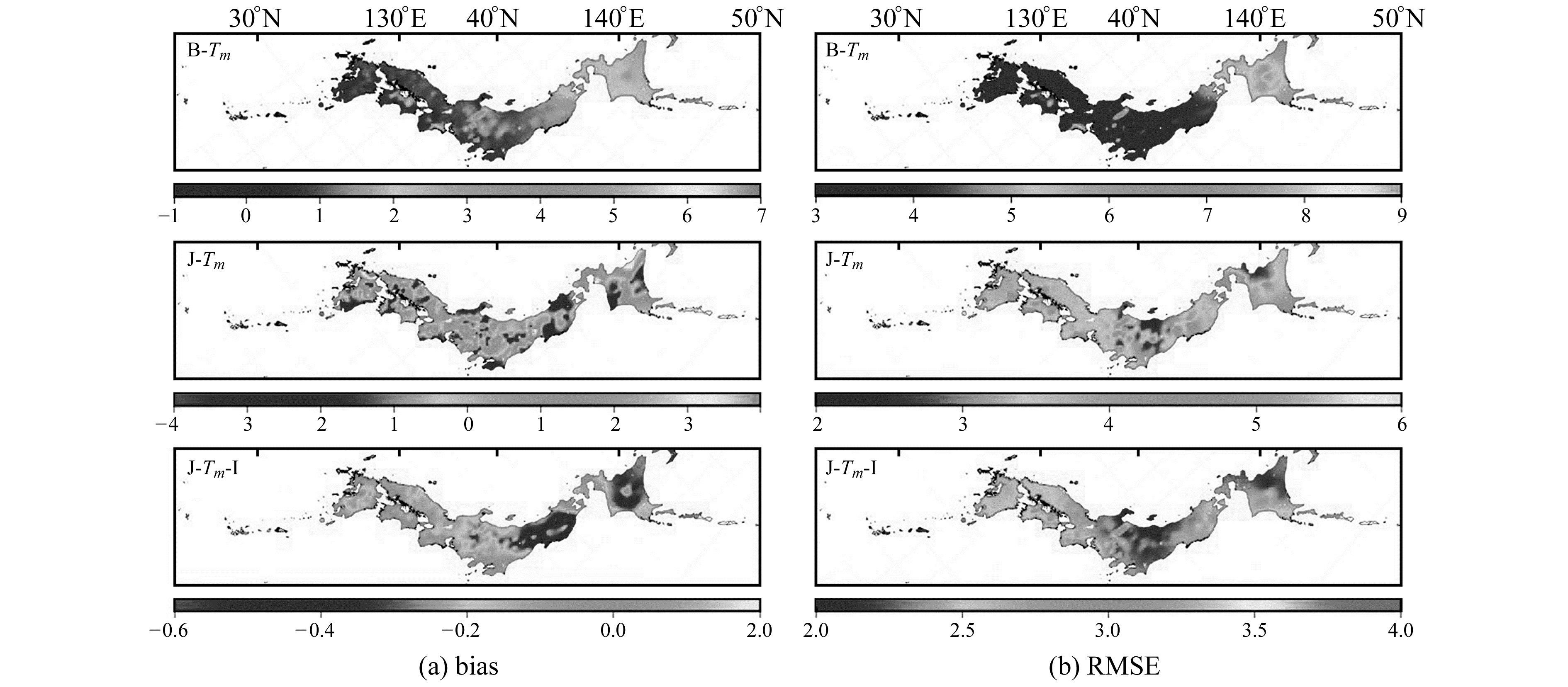
图 5为B-Tm、J-Tm和J-Tm-Ⅰ模型误差的分布情况。可以看出,B-Tm模型和J-Tm模型在日本北海道、富山、宫城地区存在较大偏差,而J-Tm-Ⅰ模型在这些地区的偏差均较小, 这是因为J-Tm-Ⅰ模型考虑了季节性变化,弥补了B-Tm模型和J-Tm模型在这些区域无法准确估算Tm的缺陷。从整个日本范围来看,J-Tm-Ⅰ模型的均方根误差均小于4 K。
|
图 5 2018年各模型与积分Tm间偏差和均方根误差的分布情况 Fig. 5 Distribution of bias and root mean square error between each model and integral Tm in 2018 |
另外,由于探空站的积分Tm精度较高,本文还利用与GPS测站邻近的无线电探空站来验证J-Tm-Ⅰ模型,并与B-Tm模型和J-Tm模型比较,结果见图 6。从图中也可以看出,J-Tm-Ⅰ模型较B-Tm模型和J-Tm模型均有改善,其均方根误差均小于4 K。
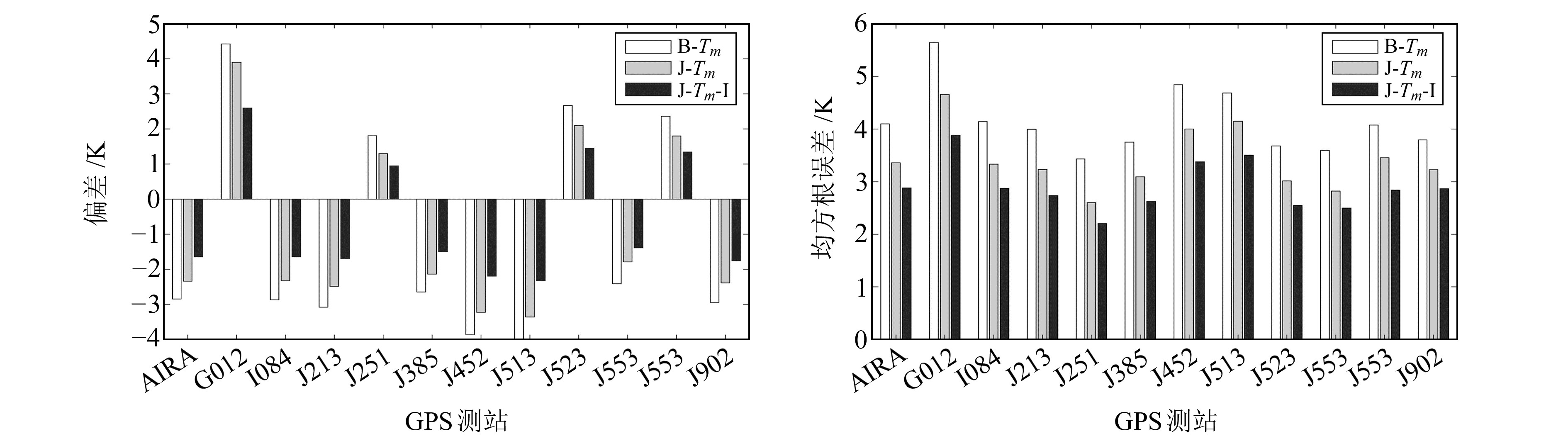
|
图 6 2018年各模型与12个邻近探空站积分Tm间的平均偏差和均方根误差 Fig. 6 Mean bias and root mean square error between each model and 12 adjacent sounding stations integral Tm in 2018 |
图 7为AIRA站和USUD站2014~2018年采用J-Tm-Ⅰ模型计算的Tm残差时间序列,图中点为Tm残差,曲线为拟合曲线。从图中可以进一步看出,J-Tm-Ⅰ模型的残差不存在明显的系统性变化,相对于J-Tm模型(图 3),J-Tm-Ⅰ模型Tm残差的季节性现象明显减弱,残差分布更为合理。
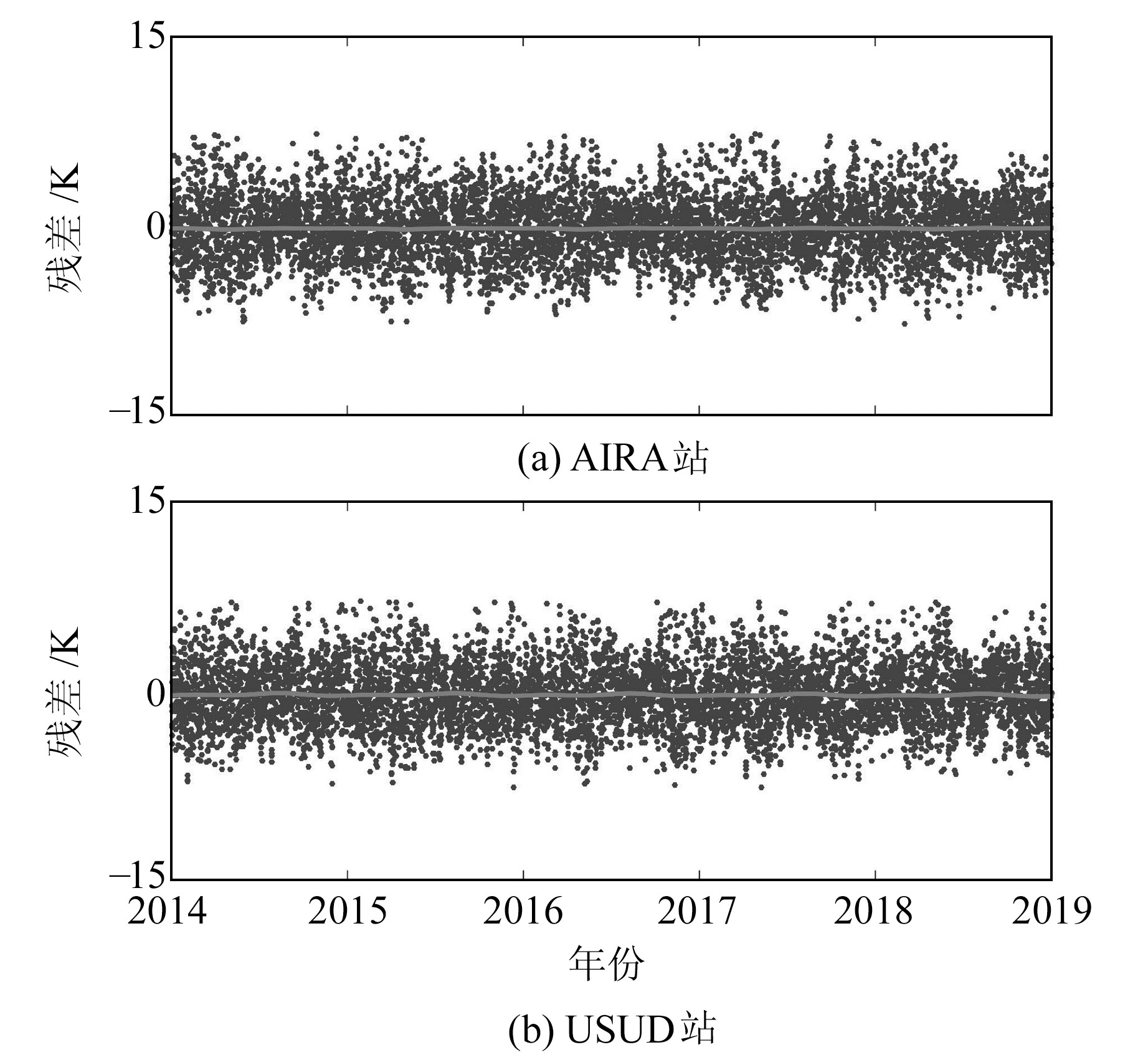
|
图 7 2014~2018年AIRA和USUD站J-Tm-Ⅰ模型残差时间序列 Fig. 7 Residual time series of J-Tm-Ⅰ model at AIRA and USUD stations from 2014 to 2018 |
本文先利用ERA-Interim全球再分析数据建立了一种适合日本区域的Tm-Ts线性回归模型J-Tm,在此基础上顾及模型残差的季节性信号,对J-Tm模型进行季节性改正,提出J-Tm-Ⅰ模型,再采用探空资料对建立的模型在日本区域的精度和适用性进行评估与分析,得出以下结论:
1) Tm和Ts有很强的相关性,利用该相关性建立Tm与Ts的线性回归模型J-Tm,其精度比广泛使用的B-Tm模型提高约16%。
2) 对J-Tm模型与积分Tm的误差进行分析,发现误差存在季节性变化。对J-Tm模型进行季节性改正,得到的J-Tm-Ⅰ模型削弱了季节性变化的影响,精度比B-Tm模型和J-Tm模型提高约37%和25%,证明J-Tm-Ⅰ模型具有一定的优越性。
3) 将B-Tm模型、J-Tm模型和J-Tm-Ⅰ模型与探空站的积分Tm进行比较,结果表明,J-Tm-Ⅰ模型较B-Tm模型和J-Tm模型有所改善。
| [1] |
李黎, 樊奕茜, 王亮, 等. 湖南地区加权平均温度的影响因素分析及建模[J]. 大地测量与地球动力学, 2018, 38(1): 48-52 (Li Li, Fan Yiqian, Wang Liang, et al. Influence Analysis of Multi-Factor on Weighted Average Temperature and Its Modeling in Hunan Region[J]. Journal of Geodesy and Geodynamics, 2018, 38(1): 48-52)
(  0) 0) |
| [2] |
Wang J H, Rossow W B, Zhang Y C. Cloud Vertical Structure and Its Variations from a 20-Yr Global Rawinsonde Dataset[J]. Journal of Climate, 2000, 13(17): 3 041-3 056 DOI:10.1175/1520-0442(2000)013<3041:CVSAIV>2.0.CO;2
(  0) 0) |
| [3] |
Wang Z Y, Zhou X H, Liu Y X, et al. Precipitable Water Vapor Characterization in the Coastal Regions of China Based on Ground-Based GPS[J]. Advances in Space Research, 2017, 60(11): 2 368-2 378 DOI:10.1016/j.asr.2017.09.017
(  0) 0) |
| [4] |
Jiang P, Ye S R, Chen D Z, et al. Retrieving Precipitable Water Vapor Data Using GPS Zenith Delays and Global Reanalysis Data in China[J]. Remote Sensing, 2016, 8(5): 389 DOI:10.3390/rs8050389
(  0) 0) |
| [5] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology:Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research Atmospheres, 1992, 97(D14): 15 787-15 801 DOI:10.1029/92JD01517
(  0) 0) |
| [6] |
黄良珂, 李琛, 王浩宇, 等. 基于GPT2w模型计算中国地区对流层加权平均温度的精度分析[J]. 大地测量与地球动力学, 2019, 39(5): 496-501 (Huang Liangke, Li Chen, Wang Haoyu, et al. Precision Analysis of the Tropospheric Weighted Mean Temperature Derived from GPT2w Model over China[J]. Journal of Geodesy and Geodynamics, 2019, 39(5): 496-501)
(  0) 0) |
| [7] |
王皓, 赵兴旺. 香港地区大气加权平均温度建模与研究[J]. 全球定位系统, 2019, 44(1): 119-124 (Wang Hao, Zhao Xingwang. Modeling and Research on Atmospheric Weighted Mean Temperature in Hongkong[J]. GNSS World of China, 2019, 44(1): 119-124)
(  0) 0) |
| [8] |
Yao Y B, Zhang B, Xu C Q, et al. Improved One/Multi-parameter Models That Consider Seasonal and Geographic Variations for Estimating Weighted Mean Temperature in Ground-Based GPS Meteorology[J]. Journal of Geodesy, 2014, 88(3): 273-282
(  0) 0) |
| [9] |
Davis J L, Herring T A, Shapiro I I, et al. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length[J]. Radio Science, 1985, 20(6): 1 9531-1 607
(  0) 0) |
| [10] |
Kibrom E A, Elias L, Frédéric M, et al. Spatial-Temporal Variations of Water Vapor Content over Ethiopia: A Study Using GPS Observations and the ECMWF Model[J]. GPS Solutions, 2017, 21(1): 89-99 DOI:10.1007/s10291-015-0508-7
(  0) 0) |
| [11] |
Yao Y B, Zhang B, Xu C Q, et al. Analysis of the Global Tm-Ts Correlation and Establishment of the Latitude-Related Linear Model[J]. Chinese Science Bulletin, 2014, 59(19): 2 340-2 347 DOI:10.1007/s11434-014-0275-9
(  0) 0) |
| [12] |
Yao Y B, Zhu S, Yue S Q. A Globally Applicable, Season-Specific Model for Estimating the Weighted Mean Temperature of the Atmosphere[J]. Journal of Geodesy, 2012, 86(12): 1 125-1 135 DOI:10.1007/s00190-012-0568-1
(  0) 0) |
| [13] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1 069-1 073 DOI:10.1002/grl.50288
(  0) 0) |
| [14] |
Zhang H X, Yuan Y B, Li W, et al. GPS PPP-Derived Precipitable Water Vapor Retrieval Based on Tm/Ps from Multiple Sources of Meteorological Data Sets in China[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(8): 4 165-4 183 DOI:10.1002/2016JD026000
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


