2. 湖南科技大学资源环境与安全工程学院,湖南省湘潭市桃园路,411201;
3. 湖南省气象台,长沙市芙蓉南路四段196号,410118
GPS气象学主要研究从GPS信号的时间延迟(结合若干地面气象参数)来反演大气水汽含量[1-2]。水汽是大气层中最活跃的成分,水汽含量变化与降水量大小紧密相关。中性大气天顶延迟(ZTD)分为干、湿两个分量,可以通过GPS数据联合解算出来。其中干分量(ZHD)可以利用地面气象参数通过公式解算精确获得,大气延迟减去干延迟便得到湿延迟(ZWD),湿延迟乘以一个转换系数便可以得到大气水汽含量[3]。在转换系数中,大气加权平均温度(Tm)是关键参数,湿延迟转换为水汽的精度主要取决于Tm的精度。
在确定Tm的方法中,由于气象探空站点分布稀疏,数值预报产品的应用也受到一定的限制,目前一般采用经验方法。Bevis等[1]根据美国27°~65°N范围内的8 718次探空记录,回归出Bevis公式(Tm=70.2+0.72Ts),均方差为4.74 K。这种方法的最大优点是估算Tm简便,只有一个参量Ts,且由Ts的地理和季节变化反映出了Tm的地理和季节变化。但由于我国地域辽阔,东西向、南北向跨度很大,地形地貌复杂多样,气候类型多变,同时Tm具有纬度和季节性变化[4],此模型应用于其他地区误差会增大。对此,我国陆续开展了对Tm与Ts及各种气象要素的研究。单九生、吕弋培等[5-6]利用线性回归法分别建立了江西及成都地区的大气加权平均温度模型;王晓英等[7]利用香港探空站2003~2009年数据分季节回归了春夏秋冬Tm计算模型;李国翠等[8]建立了华北地区基于地面气象要素的单因子和多因子回归方程;龚绍琦[9]对全国按气候分区和季节分区分别建立了单因子和多因子Tm回归模型。以上研究的目的是分析当地的Tm与Ts及各种气象要素的变化特性,建立适合本地区的单因子或多因子Tm模型。
湖南省气象局和湖南省国土厅自2011年建立HNCORS参考站网以来[10],基于HNCORS的地基GPS气象学已提上应用日程,但湖南省还没有适合的本地化Tm计算模型。本文将利用湖南省长沙、怀化、郴州3个探空站2012~2014年的探空数据建立湖南地区的本地化Tm多因子模型,并对该模型的内符合和外符合精度进行分析,论证其可用性,为湖南地区的地基GPS水汽遥感奠定应用基础。
1 数据处理方法为满足实际应用需要,国内外学者提出4种获取Tm的方法:近似积分法、常数法(取Tm=281 K)、Bevis公式法和数值积分法[11]。常数法比较简单,但精度最低,结果并不可靠;近似积分法的实现还需其他附加条件,参数不易确定,实现较难且精度较低;Bevis公式利用美国27°~65°N范围内8 718次的探空站资料建立,满足Tm的实时性要求,是目前应用最广泛的Tm计算模型,但Tm具有纬度和季节性变化,应用到其他地区误差会增大;数值积分法最精确,也较容易实现,且数值积分中的逼近误差和气象元素误差综合影响也较小[5-6, 11]。综上比较,我们在建立湖南地区本地化模型时采用数值积分法[11]:
| $ {{T}_{m}}=\frac{\sum\limits_{l}^{n}{\left( \frac{{{e}_{i}}}{{{T}_{i}}} \right)}\Delta {{h}_{i}}}{\sum\limits_{l}^{n}{\left( \frac{{{e}_{i}}}{T_{i}^{2}} \right)}\Delta {{h}_{i}}} $ | (1) |
式中,ei为第i层大气的平均水汽压(hPa),Ti为第i层大气的平均温度(K),Δhi为第i层大气层的厚度(km),ei、ei-1、Ti、Ti-1分别为大气层上界和下界的水汽压和气温:
| $ \frac{{{e}_{i}}}{{{T}_{i}}}=\frac{\frac{{{e}_{i}}}{{{T}_{i}}}+\frac{{{e}_{i-1}}}{{{T}_{i-1}}}}{2} $ | (2) |
| $ \frac{{{e}_{i}}}{T_{i}^{2}}=\frac{\frac{{{e}_{i}}}{T_{i}^{2}}+\frac{{{e}_{i-1}}}{T_{i-1}^{2}}}{2} $ | (3) |
式中,水汽压并不是直接观测量,只能通过露点温度和饱和水汽压公式间接计算得到。这里选用2008年世界气象组织建议采用的饱和水汽压计算公式[10]:
| $ e=6.112{\text{exp}}\left( 17.62\mathit{t}/243.12+t \right) $ | (4) |
选择2012-01-01~2014-12-31湖南地区长沙、怀化、郴州3个探空站的探空资料以及对应的地面气象资料,探空资料包括每日08:00和20:00大气垂直方向的位势高度、大气压、气温、露点、风向和风速,地面气象资料主要包括气压、露点、气温,数据来自国家气象信息中心。
2.2 影响因子分析在许多地基GPS水汽遥感研究中,Tm与地面温度Ts、水汽压es自然对数和地面大气压Ps都有着一定的相关性[9]。本研究的数据统计分析结果也表明,Tm与Ts、es和Ps都具有良好的线性相关性。图 1(a)为Tm与Ts的散点图,其相关系数为0.90;图 1(b)为Tm与es的散点图,其相关系数为0.88,具有良好的正相关;图 1(c)为Tm与Ps的散点图,二者相关系数为-0.56,呈较好的负相关。因此,各因子的回归系数以Ts最高,说明近地气温Ts对Tm的估算贡献最大,水汽压es次之,大气压Ps最小。

|
图 1 Tm与Ts、es、Ps相关性分析 Fig. 1 Correlation analysis between Tm and Ts, es, Ps |
利用2012年的探空数据,采用多元线性拟合方法,分别对长沙、怀化和郴州3个探空站的Ts、es和Ps与Tm作相关性分析,可得其误差方程为:
| $ \mathit{\boldsymbol{V}}=\left[1\ \ \ \ {{T}_{s}}\ \ \ \ {{P}_{s}}\ \ \ \ {{e}_{s}} \right]\ \left[\begin{align} &a \\ &b \\ &c \\ &d \\ \end{align} \right]-{{T}_{m}}~ $ | (5) |
利用最小二乘原理VTPV=min,将从3个探空站数据得到的Tm真值和Ts、es和Ps代入方程,即可得到各系数a、b、c、d的值。因此,湖南地区的本地化三因子模型为:
| $ \begin{align} &{{T}_{m}}=0.783\ 7{{T}_{s}}-0.143\ 0{{e}_{s}}- \\ &\ \ \ \ 0.063\ 4{{P}_{s}}+115.950\ 6 \\ \end{align} $ | (6) |
利用以上相同的方法,在式(1)中仅引入Ts,则可以拟合出对应的基于Ts的单因子模型:
| $ {{T}_{m}}=0.645\ 5{{T}_{s}}+89.946\ 6 $ | (7) |
如果式(1)中引入Ts和es,则双因子模型为:
| $ {{T}_{m}}=0.831\ 6{{T}_{s}}-0.148\ 3{{e}_{s}}-39.246\ 0 $ | (8) |
利用2012~2014年湖南地区长沙、怀化、郴州3个探空站实测大气探空数据,首先是用2012年大气探空数据来建立湖南地区单因子、双因子和多因子本地化模型,同时利用本地化模型来预测2013~2014年的Tm值,并将本地单因子模型与Bevis模型及龚绍琦[10]等所建立的全国单因子Tm模型所预测的结果进行对比。
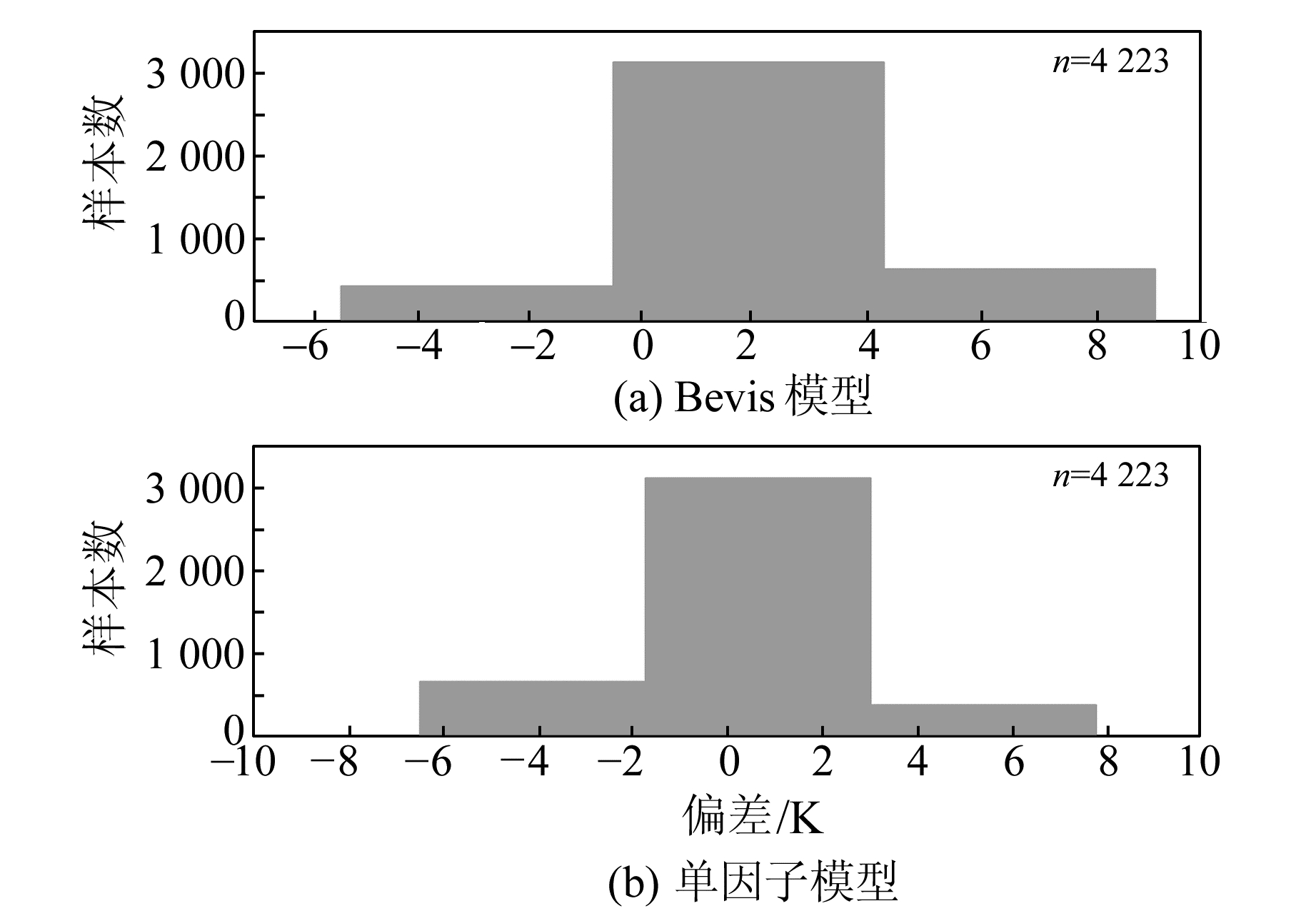
由图 2中的预测值与参考值(探空数据计算的Tm)的偏差统计直方图可见,Bevis模型的偏差主要分布在0~4 K之间,而本地化Tm模型的偏差主要分布在-2~3 K之间,可见本地化模型更加精确。图 3给出的分别是长沙、怀化、郴州3地的Tm趋势图和偏差图,更加直观地表现出本地化模型的精度比Bevis和全国模型更高、更加接近真值, 进一步证明了本地化模型的精度较高。
|
图 2 单因子模型偏差统计 Fig. 2 Statistical histogram of deviations between Bevis and single-factor models |

|
图 3 Bevis、全国和湖南本地化单因子Tm模型对比及其偏差 Fig. 3 Comparisons among Bevis, national and local single-factor Tm models |
由表 1(单位K)可知,湖南省本地化模型在各个精度标准上皆优于Bevis模型。其中,本地化模型平均偏差比Bevis模型低0.1 K;同时也优于龚绍琦所建立的全国Tm模型,其对应的标准差也优于Bevis和全国Tm模型。这说明本地化Tm模型很好地校正了Bevis和全国Tm模型存在的系统偏差,更符合实际,可应用于湖南地区的Tm值估算。
|
|
表 1 单因子Tm模型精度分析 Tab. 1 Accuracy comparison of single-factor Tm models |
根据§2.2的分析,大气加权平均温度与地面温度和水汽压存在正相关性,并与大气压呈负相关性。这里将Tm与Ts、es、Ps进行多因子回归分析,分别建立湖南本地化双因子、三因子模型,并将其与单因子模型进行对比分析。
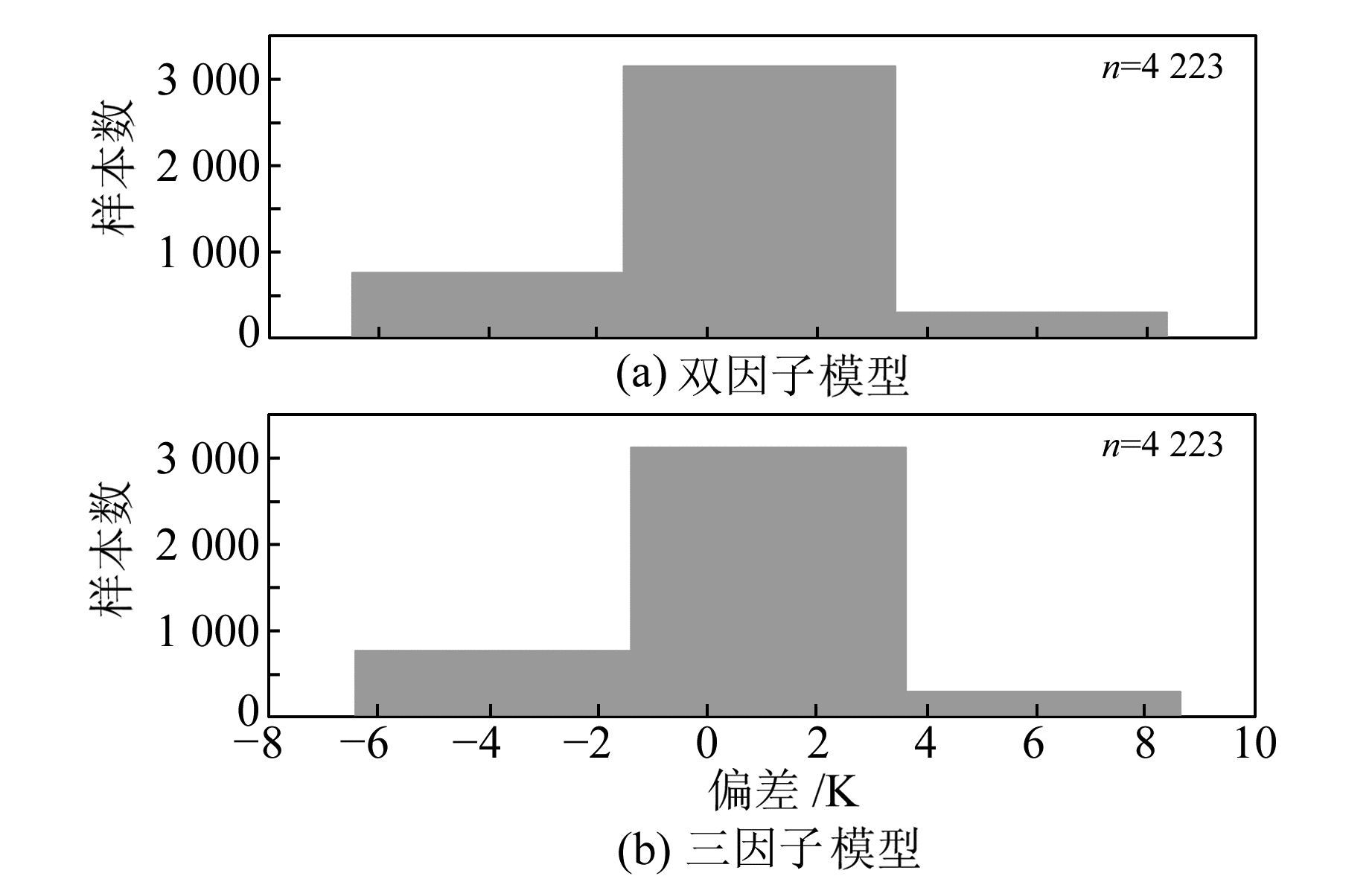
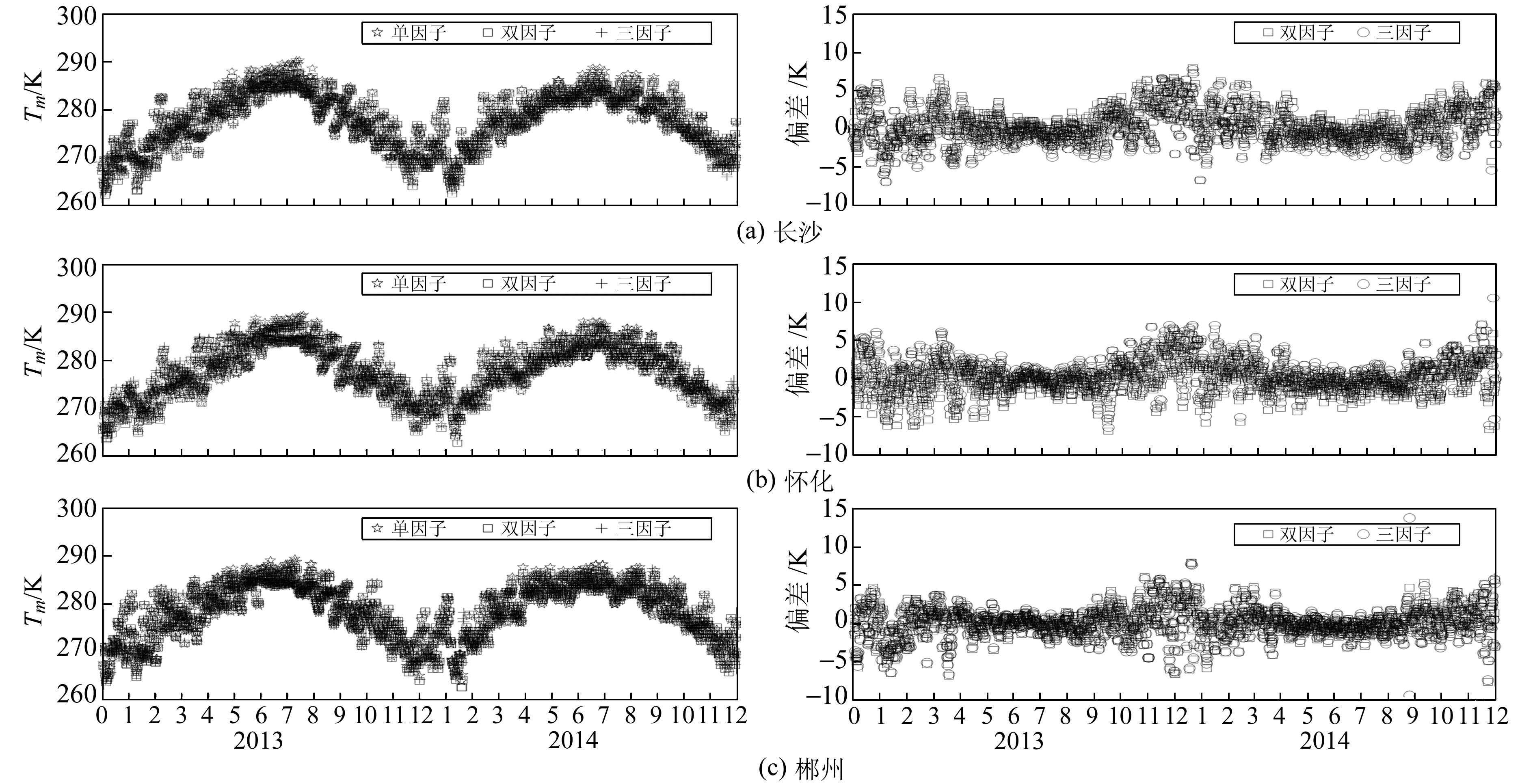
图 4是双因子和三因子Tm模型预测Tm值与参考值(探空数据计算的Tm)的偏差统计直方图。可以看出,双因子与三因子模型的偏差值都主要集中在-2~2 K之间,相比单因子模型的- 2~3 K分布更加集中且精度更高。图 5给出了双因子和三因子模型所预测的2013~2014年Tm及其与参考值之间的偏差。从偏差值上来看,两者的偏差基本上是重合的,说明双因子和三因子Tm模型的预测效果基本相同。
|
图 4 双因子和三因子偏差统计 Fig. 4 Statistical histogram of deviations between two-factor and three-factor |
|
图 5 单因子、双因子和三因子模型对比及其偏差 Fig. 5 Comparisons of single-factor, two-factor and three-factor Tm models |
从表 2(单位K)的单因子、双因子与三因子Tm模型精度统计分析表可以看出,双因子与三因子的平均偏差和标准差几乎相等,说明双因子模型就已达到三因子模型的精度要求。但双因子和三因子模型的标准差为2.85,低于单因子的3.07,说明其精度略高于单因子模型。当然,在实际的应用中,可以根据地面气象资料的丰缺程度来选择是使用单因子或是多因子模型。
|
|
表 2 多因子Tm模型精度对比分析 Tab. 2 Accuracy comparison of multi-factor Tm models |
1) 大气加权平均温度Tm与地面温度Ts和水汽压es存在较强的正相关性,Tm与Ts的相关系数为0.89,与es的相关系数为0.88;而与大气压P0呈负相关性,其相关系数为-0.55。
2) 利用湖南地区长沙、怀化、郴州3个探空站2012年的探空资料,采用数值积分法和最小二乘原理建立了湖南地区的单因子本地化模型:Tm=0.645 5Ts+89.946 6。与真值相比,其平均偏差和标准差分别为1.79 K和3.07 K,各项指标均比Bevis模型好,说明单因子本地化Tm模型优于Bevis模型,更加接近真值,符合实际应用。
3) 双因子与三因子模型所计算出的平均偏差基本相当,标准差均为2.85 K,表明二者预测Tm的精度相等,因此无需建立三因子本地化模型。而相较于单因子模型,多因子Tm模型的平均偏差和标准差均较小,表明其精度更高。因此,湖南地区可以根据地面气象资料的丰缺程度来选择是使用单因子模型或是双因子模型。
| [1] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
| [2] |
Duan J, Bevis M, Fang P, et al. GPS Meteorology: Direct Estimation of the Absolute Value of Precipitable Water[J]. Journal of Applied Meteorology, 1996, 35(6): 830-838 DOI:10.1175/1520-0450(1996)035<0830:GMDEOT>2.0.CO;2
(  0) 0) |
| [3] |
姚宜斌, 郭健健, 张豹, 等. 湿延迟与可降水量转换系数的全球经验模型[J]. 武汉大学学报:信息科学版, 2016, 41(1): 45-51 (Yao Yibin, Guo Jianjian, Zhang Bao, et al. A Global Empirical Model of the Conversion Factor Between Zenith Wet Delay and Precipitable Water Vapor[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 45-51)
(  0) 0) |
| [4] |
Lan Z, Zhang B, Geng Y. Establishment and Analysis of Global Gridded Tm-Ts Relationship Model[J]. Geodesy and Geodynamics, 2016, 7(2): 101-107 DOI:10.1016/j.geog.2016.02.001
(  0) 0) |
| [5] |
单九生, 邹海波, 刘熙明, 等. GPS/MET水汽反演中Tm模型的本地化研究[J]. 气象与减灾研究, 2012, 35(1): 42-46 (Shan Jiusheng, Zou Haibo, Liu Ximing, et al. Localization Studies of Tm Model in Derivating the GPS/MET Precipitable Water over Jiangxi[J]. Meteorology & Disaster Reduction Research, 2012, 35(1): 42-46)
(  0) 0) |
| [6] |
吕弋培, 殷海涛, 黄丁发, 等. 成都地区大气平均温度建模及其在GPS/PWV计算中的应用研究[J]. 测绘科学, 2008, 33(4): 103-105 (Lü Yipei, Yin Haitao, Huang Dingfa, et al. Modeling of Weighted Mean Atmospheric Temperature and Application in GPS/PWV of Chengdu Region[J]. Science of Surveying and Mapping, 2008, 33(4): 103-105)
(  0) 0) |
| [7] |
王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报:信息科学版, 2011, 36(4): 412-415 (Wang Xiaoying, Dai Ziqiang, Cao Yunchang, et al. Weighted Mean Temperature Tm Statistical Analysis in Ground-Based GPS in China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 412-415)
(  0) 0) |
| [8] |
李国翠, 李国平, 杜成华, 等. 华北地区地基GPS水汽反演中加权平均温度模型研究[J]. 南京气象学院学报, 2009, 32(1): 81-86 (Li Guocui, Li Guoping, Du Chenghua, et al. Weighted Mean Temperature Models for Mapping Zenith Wet Delays onto Precipitable Water in North China[J]. Journal of Nanjing Institute of Meteorology, 2009, 32(1): 81-86)
(  0) 0) |
| [9] |
龚绍琦. 中国区域大气加权平均温度的时空变化及模型[J]. 应用气象学报, 2013, 24(3): 332-334 (Gong Shaoqi. Temporal and Spatial Variation of Regional Atmospheric Weighted Average Temperature in China and Its Model[J]. Journal of Applied Meteorology, 2013, 24(3): 332-334 DOI:10.11898/1001-7313.20130309)
(  0) 0) |
| [10] |
胡立新, 汤仲安. 湖南CORS建设的战略构思与对策思考[J]. 测绘工程, 2009, 18(3): 61-64 (Hu Lixin, Tang Zhong'an. The Stratagems and Tactics on Hunan Continuously Operating Reference System Construction[J]. Engineering of Surveying and Mapping, 2009, 18(3): 61-64)
(  0) 0) |
| [11] |
刘焱雄, 陈永奇, 刘经南. 利用地面气象观测资料确定对流层加权平均温度[J]. 武汉测绘科技大学学报, 2000, 25(5): 400-404 (Liu Yanxiong, Chen Yongqi, Liu Jingnan. Determination of Weighted Mean Tropospheric Temperature Using Ground Meteorological Measurement[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(5): 400-404)
(  0) 0) |
2. School of Resource Environment and Safety Engineering, Hunan University of Science and Technology, Taoyuan Road, Xiangtan 411201, China;
3. Hunan Provincial Meteorological Bureau, 196 Forth Segment of South-Furong Road, Changsha 410118, China
 2018, Vol. 38
2018, Vol. 38

