2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006;
3. 武汉大学卫星导航定位技术研究中心,武汉市珞喻路129号,430079;
4. 广西壮族自治区水利电力勘测设计研究院,南宁市民主路1-5号,530023
利用GPS监测大气水汽(PWV)时,对流层加权平均温度(Tm)是一个极为重要的参数。Tm值可通过探空资料或全球大气再分析资料等气象数据计算得到,但为了方便GPS水汽监测,常构建一个区域或全球经验模型进行计算。Bevis等[1]利用全球多个探空站数据首次构建Tm与地表温度(Ts)的函数模型。随后,诸多学者在分析Tm与Ts、水汽压(es)和地表气压(Ps)等气象参数相关性的基础上,分别构建区域或全球Tm经验模型[2-5],但这些模型需要实测的气象参数,限制了其在GPS实时水汽监测中的应用。
为满足GPS实时水汽探测的要求,Emardson[6]首先在欧洲地区建立了与纬度和季节相关的Tm模型(Emardson模型)。该模型不需要实测气象参数,可广泛应用于实时的GPS水汽监测。姚朝龙等[7]、刘立龙等[8]将Emardson模型分别在中国低纬度地区和新疆地区进行精化,取得了良好效果。诸多学者致力于全球Tm经验模型的构建且取得一系列的成果[9-14],这些模型在全球均表现出各自的优越性和较高的精度,但鲜有文献对上述全球模型在中国地区的适用性予以评价。
Tm作为GPS水汽监测的关键因子,在GPS实时水汽监测中主要通过模型获取。GPT2w模型作为目前最先进的全球对流层延迟改正模型之一,在全球可获得较高的Tm精度,但在中国地区计算的Tm精度尚无文献予以分析。本文联合全球大地观测系统(GGOS)Atmosphere格网Tm产品和探空站资料对中国地区GPT2w模型计算的Tm精度进行评估,分析GPT2w模型在中国地区的适用性。
1 GPT2w模型和数据来源 1.1 GPT2w模型简介GPT2w模型是由Böhm等[11]提出的一个全球经验对流层格网模型,可提供水平分辨率1°×1°和5°×5°的对流层湿延迟、对流层干延迟、地表温度、地表气压和Tm等对流层参数。Tm的计算公式为:
| $ \begin{aligned} T_{m}^{r}=& \beta_{0}+\beta_{1} \cos \left(2 \pi \frac{\operatorname{doy}}{365.25}\right)+\beta_{2} \sin \left(2 \pi \frac{\operatorname{doy}}{365.25}\right)+\\ & \beta_{3} \cos \left(4 \pi \frac{\operatorname{doy}}{365.25}\right)+\beta_{4} \sin \left(4 \pi \frac{\operatorname{doy}}{365.25}\right) \end{aligned} $ | (1) |
式中,Tmr表示格网点处的Tm值,doy表示年积日,βi(i=0, 1, 2, 3, 4)表示模型系数。分别将1°×1°和5°×5°两种分辨率的对流层格网模型简称为GPT2w-1和GPT2w-5。目标点处Tm的值通过周边4个格网点处的Tm值利用双线性插值计算得到。
1.2 数据源介绍本文选取覆盖中国地区的2015年GGOS Atmosphere格网产品和89个探空站资料来进行GPT2w模型计算Tm的精度检验。
GGOS Atmosphere的Tm格网产品是利用欧洲中尺度天气预报中心(ECMWF)提供的再分析资料计算得到的,以水平分辨率为2°×2.5°(纬度×经度)、时间分辨率为6 h的全球格网形式提供。研究表明,GGOS Atmosphere格网产品具有较高的精度。
美国俄怀明大学向全球免费提供超过1 500个无线电探空站资料(http://weather.uwyo.edu/upperair/sounding.html)。探空站资料分为气压层和地表层信息,时间分辨率为12 h,其中气压层信息包含温度、相对湿度和位势高等参数,地表层信息包含大气水汽含量(PWV)和测站位置等参数。探空站处的Tm值可通过探空站的气压层信息积分获得[12-14]。
2 GPT2w模型计算Tm的精度评估Tm不仅是水汽监测的关键因子,也是GPT2w模型计算对流层湿延迟(ZWD)的重要参数,其精度将直接影响ZWD和PWV计算的精度。本文主要选取覆盖中国地区的GGOS Atmosphere的Tm格网产品和位于中国地区的89个探空站资料评估GPT2w模型计算Tm的精度,采用偏差(bias)和均方根误差(RMS)2种精度指标来检验GPT2w模型计算的Tm,表达式为:
| $ \mathrm{bias}=\frac{1}{N} \sum\limits_{i=1}^{N}\left(X_{m}^{M_{i}}-X_{m}^{R_{i}}\right) $ | (2) |
| $ \mathrm{RMS}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(X_{m}^{M_{i}}-X_{m}^{R_{i}}\right)^{2}} $ | (3) |
式中,XmMi表示模型计算值,XmRi表示参考值,N表示样本数。
2.1 利用GGOS Atmosphere Tm格网产品进行精度分析Yao等[13]利用全球341个探空站资料对GGOS Atmosphere提供的Tm格网产品的精度进行检验,结果表明,Tm格网产品具有较高的精度,可作为构建高精度Tm模型的数据源。本文利用覆盖中国地区的2015年Tm格网产品(时间分辨率为6 h)作为参考值,对GPT2w模型计算的Tm进行精度检验,结果见表 1(单位K)和图 1。
|
|
表 1 利用2015年GGOS Atmosphere格网Tm检验GPT2w模型的精度统计 Tab. 1 Statistical results of GPT2w model validated by using GGOS Atmosphere grid Tm data from 2015 |

|
图 1 2015年GGOS格网产品评估中国地区GPT2w模型计算Tm的年均bias和RMS分布 Fig. 1 The distribution of annual bias and RMS error of Tm derived from GPT2w model validated by using gridded Tm data from 2015 in China |
由表 1可知,GPT2w-5和GPT2w-1模型在中国地区计算Tm的年均bias分别为0.19 K和0.23 K,GPT2w-5模型的最大年均bias为17.6 K,最小年均bias为-13.5 K,而GPT2w-1模型的最大年均bias小于GPT2w-5模型;GPT2w-5和GPT2w-1模型在中国地区计算Tm的年均RMS分别为4.5 K和3.8 K,GPT2w-5模型表现出更大的最大年均RMS。图 1表明,在中国西部部分地区(尤其在西藏地区)GPT2w-5模型表现出较大的正bias,GPT2w-1模型也表现出一定的正bias;同时,GPT2w-5和GPT2w-1模型均表现出较大的年均RMS。由于GPT2w模型在计算Tm时未考虑高程改正,因此在地形起伏较大的中国西部地区表现出较大的偏差。在中国东北地区,GPT2w模型也出现相对较大的年均RMS,主要原因是Tm在该地区具有较为显著的日均周期[15],而GPT2w在建模时并未顾及Tm的日周期变化。综上所述,GPT2w-1模型的性能优于GPT2w-5模型,GPT2w模型可以通过提高模型参数的水平分辨率改善Tm的计算精度。
2.2 利用探空站资料进行精度分析探空站提供的大气分层剖面信息均为实测值,是当前精度最为可靠的大气分层资料,常用于验证大气模型和其他再分析资料。为进一步检验GPT2w模型在中国地区Tm的计算精度,本文均匀选取中国地区89个探空站2015年的探空数据(分布见图 2),以积分法计算的各探空站Tm值作为参考值来评价GPT2w模型的精度,统计GPT2w模型计算Tm的年均bias和RMS,结果见表 2(单位K)和图 3。

|
图 2 中国地区探空站点位分布 Fig. 2 Distribution of the 89 radiosonde stations in China |
|
|
表 2 利用2015年探空站资料检验GPT2w模型的精度统计 Tab. 2 Statistical results of GPT2w model validated by using radiosonde data from 2015 |
|
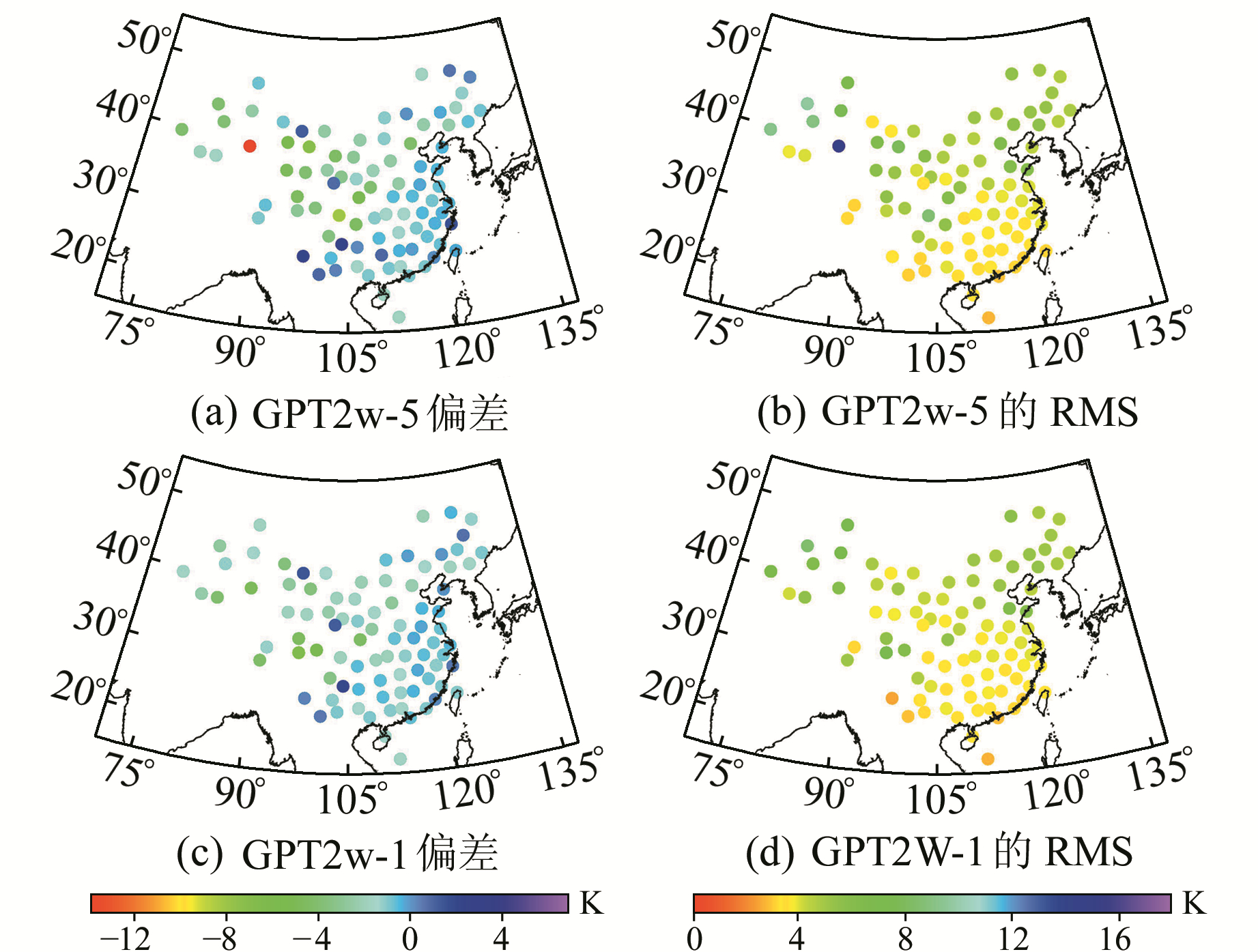
图 3 2015年探空资料评估中国地区GPT2w模型计算Tm的年均bias和RMS分布 Fig. 3 The distribution of annual bias and RMS error of Tm derived from GPT2w model validated by using radiosonde data from 2015 in China |
由表 2可知,在中国地区GPT2w-5和GPT2w-1模型均表现出明显的负偏差,年均bias值分别为-1.7 K和-1.4 K;GPT2w-5和GPT2w-1模型的bias最小值分别为-13.9 K和-6.6 K,表明GPT2w-1模型比GPT2w-5更稳定。同时,GPT2w-5和GPT2w-1模型的年均RMS分别为4.8 K和4.4 K,而GPT2w-5的最大RMS为14.4 K,说明GPT2w-1模型的性能要高于GPT2w-5。
由图 3可知,GPT2w-5和GPT2w-1模型在中国西部的部分地区均出现较大偏差,其他地区偏差则较小。GPT2w-5和GPT2w-1模型在中国北部地区和西南地区均表现出较大的年均RMS误差,而在南部低纬度地区和东南部地区年均RMS误差则较小,主要原因是西部地区受地形起伏大和北部地区存在显著的Tm日均周期。而在南部低纬度地区和东南部地区,Tm的变化振幅低于中纬度地区,在该区域易于对Tm进行精确模型化,因此,GPT2w模型在这两个地区具有较好的精度。为进一步说明GPT2w-5和GPT2w-1模型的精度,对中国地区89个探空站的年均bias和RMS进行统计,结果见图 4。
|
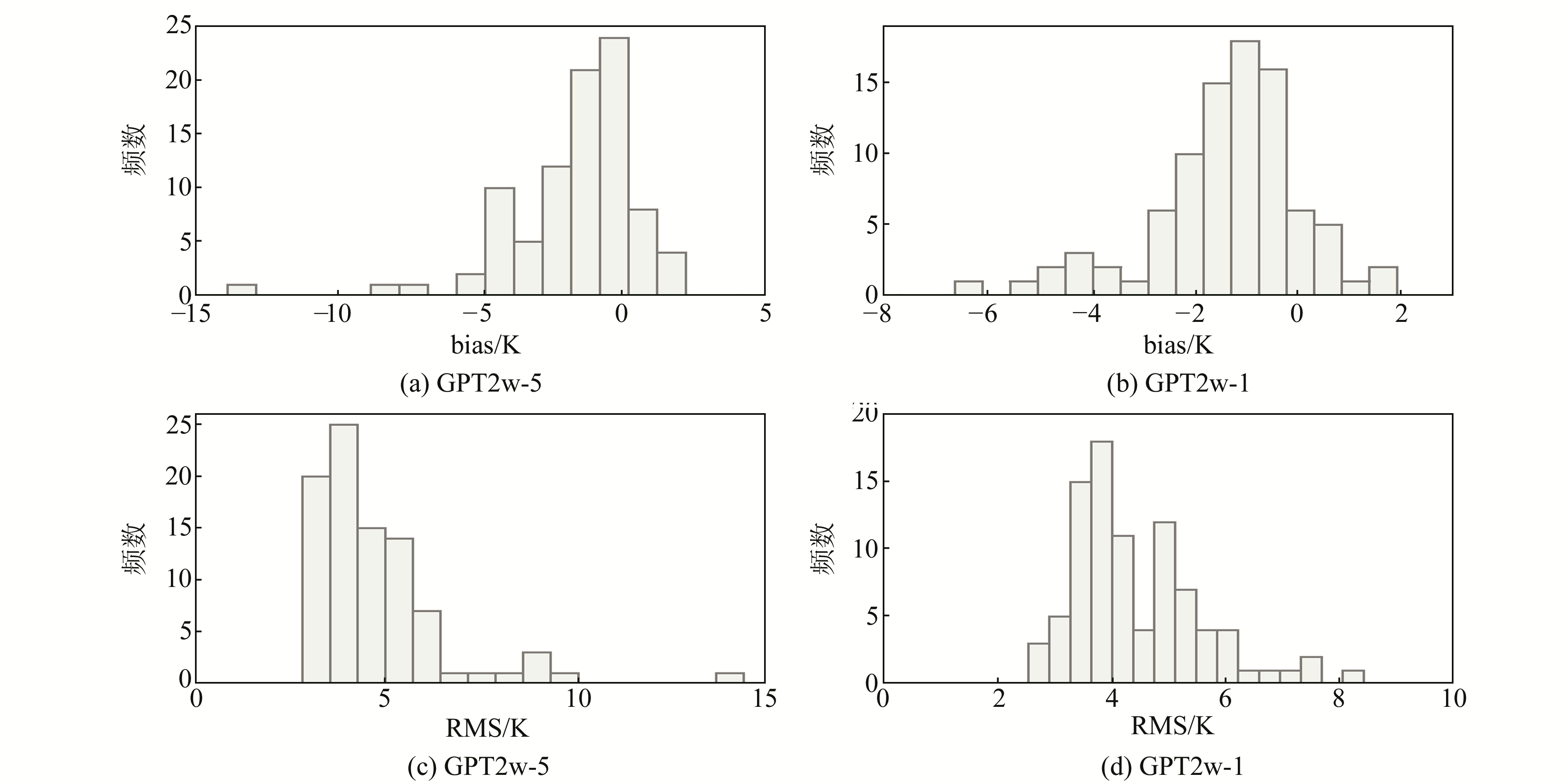
图 4 中国地区GPT2w模型计算Tm的年均bias和RMS分布直方图 Fig. 4 Histogram of bias and RMS of Tm derived from GPT2w model tested by using radiosonde data from 2015 in China |
由图 4可知,GPT2w模型表现出明显的负偏差,GPT2w-5模型的偏差比GPT2w-1更显著。此外,GPT2w-1模型的RMS误差分布比GPT2w-5集中,进一步表明GPT2w-1模型的性能比GPT2w-5更稳定。为分析GPT2w模型的季节性变化,对89个探空站对应的日均bias和RMS取均值,得到2015年中国地区bias和RMS的时间序列,结果见图 5。
|
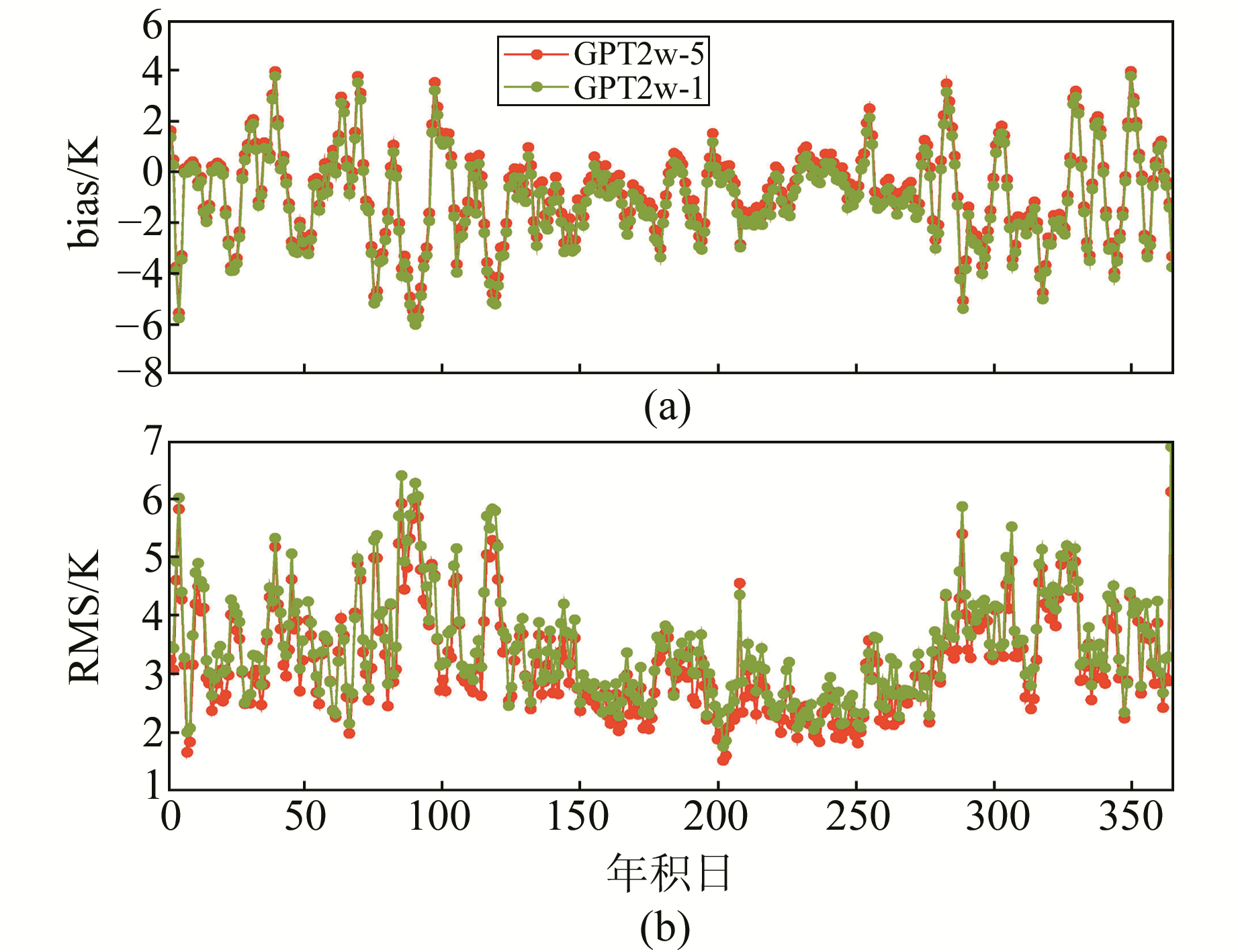
图 5 中国地区GPT2w模型计算Tm的2015年日均bias和RMS时序变化 Fig. 5 The results of Tm derived from GPT2w model validated using radiosonde data during different doy in China |
由图 5可知,GPT2w模型在1 a中的大部分时间里表现为显著的负偏差,在春季和冬季的偏差较大。同时,GPT2w模型的RMS误差在春季和冬季也较大、在夏季较小,主要是由于中国地区的大多数探空站位于中纬度地区,而在这些地区Tm的变化振幅表现为夏季小、冬季大。
相关研究表明,Tm的变化与高程和纬度具有较大的相关性[4, 6-7]。为分析中国地区GPT2w模型计算Tm的bias、RMS与高程的变化关系,本文对89个探空站按照高程进行分类,即<500 m、500~1 000 m、1 000~1 500 m、1 500~2 000 m和>2 000 m,结果见图 6。
|
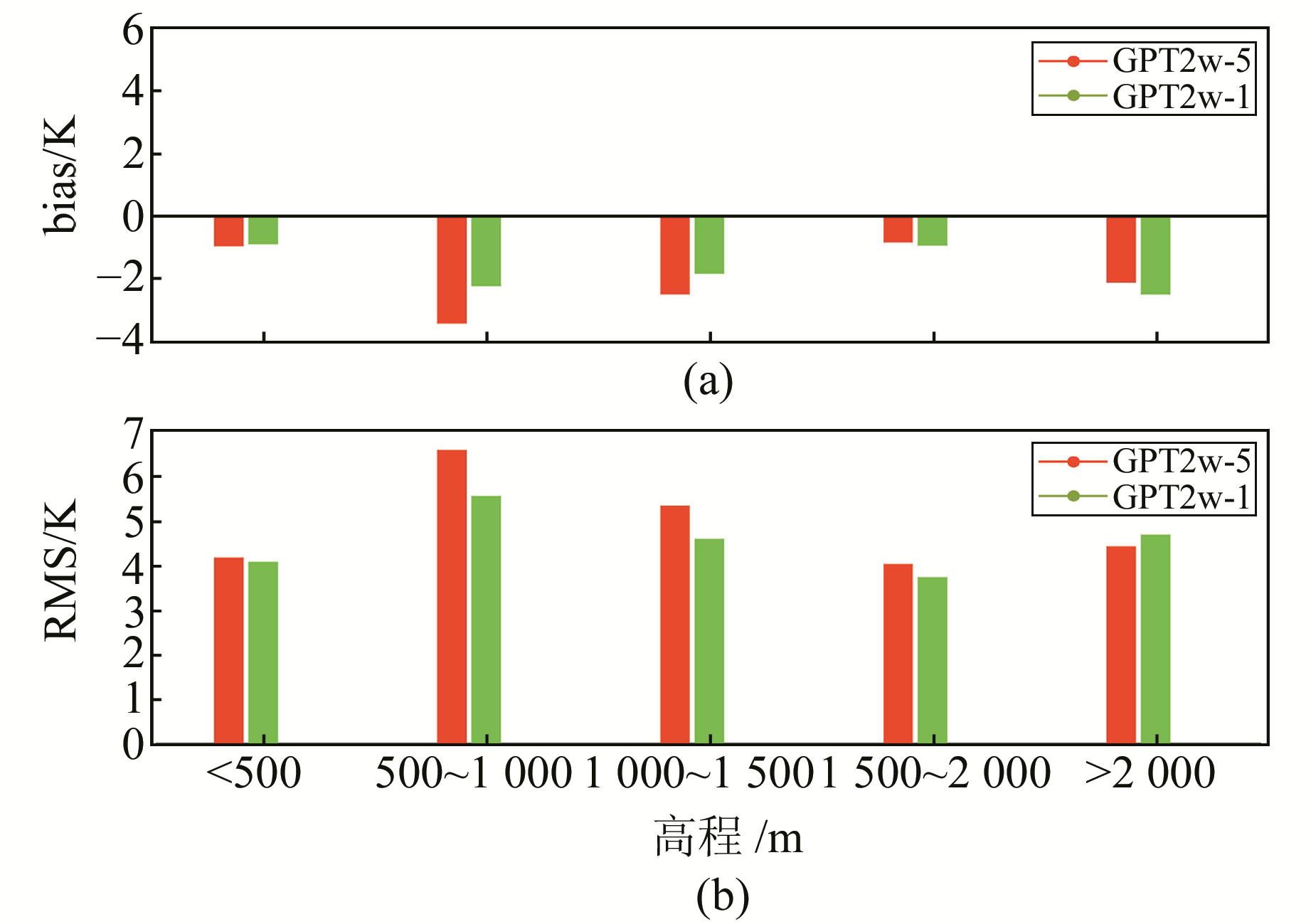
图 6 中国地区GPT2w模型计算Tm的bias和RMS随高程变化统计 Fig. 6 Results of bias and RMS of the Tm derived GPT2w model at different altitude ranges in China |
由图 6(a)可知,GPT2w-5和GPT2w-1模型在每个高程范围内均表现为显著的负偏差,进一步说明GPT2w模型在中国地区具有显著的系统偏差。由图 6(b)可以看出,当高程在500~1 000 m范围内时,GPT2w模型出现较大的RMS误差,这个高程范围内的探空站多数分布在中国西南地区和新疆地区;而在1 500~2 000 m范围内探空站数量较少,GPT2w模型的RMS误差相对较小。综上,在高程500~1 500 m范围GPT2w模型表现出较大的RMS误差。
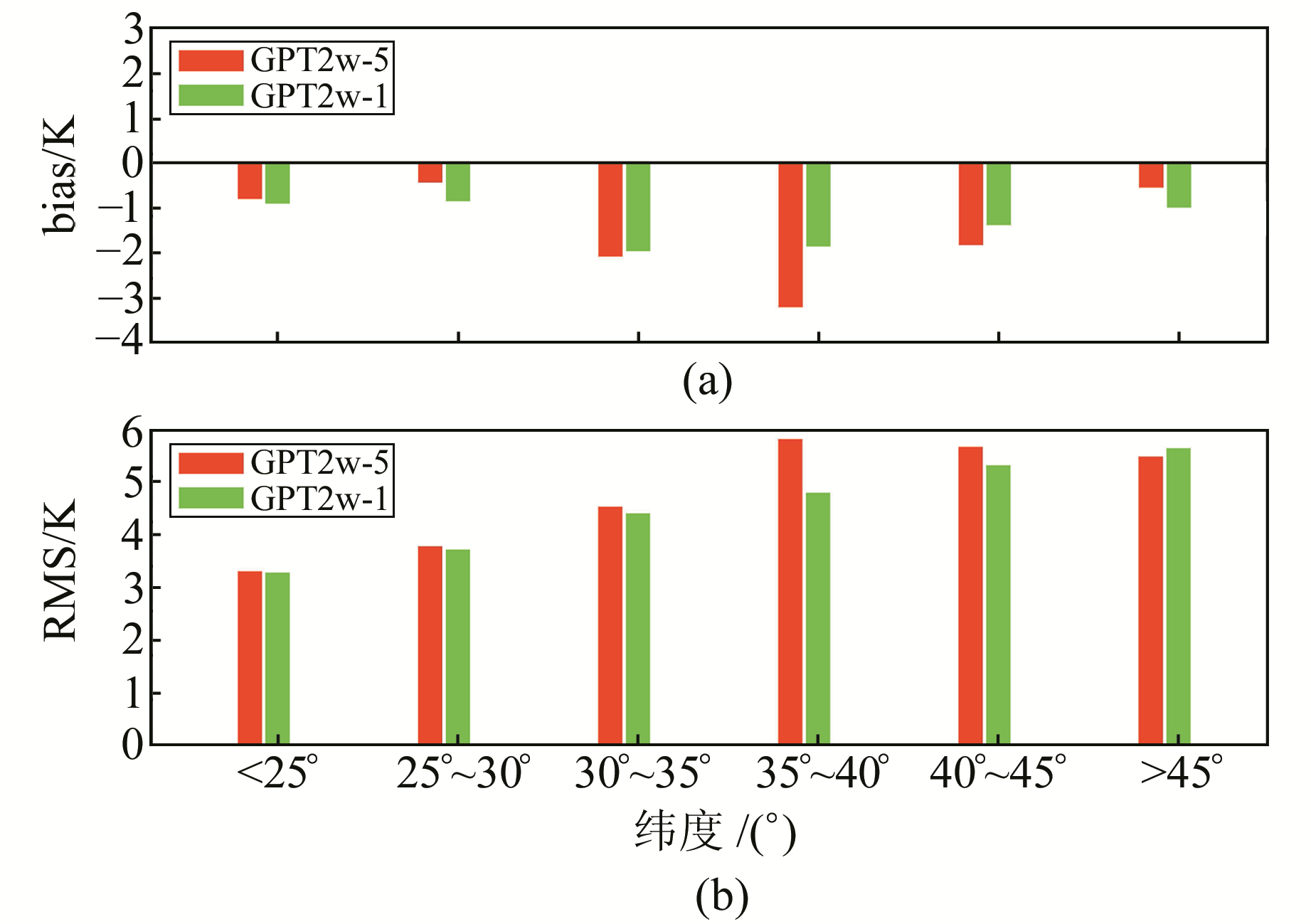
为进一步分析中国地区GPT2w模型计算Tm的bias、RMS与纬度的变化关系,本文对89个探空站按照5°的纬度间隔进行分类,结果见图 7。
|
图 7 中国地区GPT2w模型计算Tm的bias和RMS随纬度变化统计 Fig. 7 Results of bias and RMS of the Tm derived GPT2w model at different latitude ranges in China |
由图 7(a)可以看出,GPT2w模型在各个纬度范围仍然表现为显著的负偏差,其中30°~40°的纬度范围偏差较大,主要是由于该纬度范围包含较多西部地区的探空站。由图 7(b)可知,GPT2w模型计算Tm的RMS误差表现为明显的随纬度增加而增大,主要原因是低纬度地区的Tm变化振幅要低于中纬度地区[5]。
3 结语GPT2w模型作为目前较为先进的对流层延迟改正模型之一,可提供包含Tm在内的多个对流层关键参数,评价其在中国地区计算Tm的精度具有重要的现实意义。本文利用2015年覆盖中国地区的GGOS Atmosphere格网产品和位于中国地区的探空站资料评价GPT2w模型计算Tm的精度和适用性,结果表明:
1) GPT2w-1模型的精度和稳定性优于GPT2w-5,GPT2w通过提高参数的水平分辨率可改善模型的精度;
2) GPT2w模型在中国地区计算的Tm表现出明显的系统误差,日均bias和RMS误差具有显著的季节性变化,春冬季较大、夏季较小;
3) GPT2w模型计算的Tm在中国西部地区和东北地区表现出较大误差,主要是受地形起伏大和显著的Tm日周期变化影响。此外,Tm的年均RMS表现出明显的空间特性,高程在500~1 500 m范围时相对较大,且RMS随纬度增加而增大。
总之,GPT2w模型在中国低海拔地区使用可保证较高的精度,在应用时建议使用GPT2w-1模型。由于GPT2w模型在计算Tm时未顾及高程的改正,且其模型表达式忽略了Tm的日周期变化,因此,下一步可对GPT2w模型在高程上进行精化,进一步提升GPT2w模型的性能。
| [1] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
| [2] |
李建国, 毛节泰, 李成才, 等. 使用全球定位系统遥感水汽分布原理和中国东部地区加权"平均温度"的回归分析[J]. 气象学报, 1999, 57(3): 283-292 (Li Jianguo, Mao Jietai, Li Chengcai, et al. The Approach to Remote Sensing of Water Vapor Based on GPS and Linear Regression Tm in Eastern Region of China[J]. Acta Meteorologica Sinica, 1999, 57(3): 283-292 DOI:10.3969/j.issn.1001-7313.1999.03.004)
(  0) 0) |
| [3] |
Liu L L, Yao C L, Wen H Y. Empirical Tm Modeling in the Region of Guangxi[J]. Geodesy and Geodynamics, 2012, 3(4): 47-52 DOI:10.3724/SP.J.1246.2012.00047.1
(  0) 0) |
| [4] |
姚宜斌, 张豹, 许超钤, 等. Tm-Ts的相关性分析及全球纬度相关的线性关系模型构建[J]. 科学通报, 2014, 59(9): 816-824 (Yao Yibin, Zhang Bao, Xu Chaoqian, et al. Analysis of the Global Tm-Ts Correlation and Establishment of the Latitude-Related Linear Model[J]. Chinese Science Bulletin, 2014, 59(9): 816-824)
(  0) 0) |
| [5] |
Yao Y B, Zhang B, Xu C Q, et al. Improved One/Multi-Parameter Models That Consider Seasonal and Geographic Variations for Estimating Weighted Mean Temperature in Ground-Based GPS Meteorology[J]. Journal of Geodesy, 2014, 88(3): 273-282 DOI:10.1007/s00190-013-0684-6
(  0) 0) |
| [6] |
Emardson T R, Derks H J P. On the Relation between the Wet Delay and the Integrated Precipitable Water Vapour in the European Atmosphere[J]. Meteorological Applications, 2000, 7(1): 61-68 DOI:10.1017/S1350482700001377
(  0) 0) |
| [7] |
姚朝龙, 罗志才, 刘立龙, 等. 顾及地形起伏的中国低纬度地区湿延迟与可降水量转换关系研究[J]. 武汉大学学报:信息科学版, 2015, 40(7): 907-912 (Yao Chaolong, Luo Zhicai, Liu Lilong, et al. On the Relation between the Wet Delay and the Water Precipitable Vapor in Consideration of Topograghic Relief in the Low-Latitude Region of China[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 907-912)
(  0) 0) |
| [8] |
刘立龙, 陈香萍, 封海洋, 等. 新疆地区Emardson大气水汽转换系数适用性分析[J]. 大地测量与地球动力学, 2016, 36(5): 434-437 (Liu Lilong, Chen Xiangping, Feng Haiyang, et al. Analysis of the Applicability of the Emardson Model for Transformation Coefficient of Water Vapor in the Region of Xinjiang[J]. Journal of Geodesy and Geodynamics, 2016, 36(5): 434-437)
(  0) 0) |
| [9] |
Yao Y B, Zhu S, Yue S Q. A Globally Applicable, Season-Specific Model for Estimating the Weighted Mean Temperature of the Atmosphere[J]. Journal of Geodesy, 2012, 86(12): 1125-1135 DOI:10.1007/s00190-012-0568-1
(  0) 0) |
| [10] |
陈鹏, 陈家君. 利用NCEP再分析资料建立全球大气加权平均温度模型[J]. 大地测量与地球动力学, 2014, 34(3): 133-136 (Chen Peng, Chen Jiajun. Establishment of Global Atmospheric Weighted Average Temperature Model Using NCEP Reanalysis Data[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 133-136)
(  0) 0) |
| [11] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w)[J]. GPS Solut, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [12] |
Yao Y B, Zhang B, Yue S Q, et al. Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Geodesy, 2013, 87(5): 439-448 DOI:10.1007/s00190-013-0617-4
(  0) 0) |
| [13] |
Yao Y B, Xu C Q, Zhang B, et al. GTm-Ⅲ: A New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapor[J]. Geophysical Journal International, 2014, 197(1): 202-212 DOI:10.1093/gji/ggu008
(  0) 0) |
| [14] |
Huang L K, Jiang W P, Liu L L, et al. A New Global Grid Model for the Determination of Atmospheric Weighted Mean Temperature in GPS Precipitable Water Vapor[J]. Journal of Geodesy, 2019, 93(2): 159-176 DOI:10.1007/s00190-018-1148-9
(  0) 0) |
| [15] |
Zhang H X, Yuan Y B, Li W, et al. GPS PPP-Derived Precipitable Water Vapor Retrieval Based on Tm/Ps from Multiple Sources of Meteorological Data Sets in China[J]. Journal of Geophysical Research: Atmosphere, 2017, 122(8): 4165-4183 DOI:10.1002/2016JD026000
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China;
3. GNSS Research Center, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
4. Guangxi Water and Power Design Institute, 1-5 Minzhu Road, Nanning 530023, China
 2019, Vol. 39
2019, Vol. 39


