2. 上海航天电子技术研究所, 上海 201109;
3. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
4. 地球空间信息协同创新中心, 湖北 武汉 430079
2. Shanghai Aerospace Electronic Technology Research Institute, Shanghai 201109, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
4. Collaborative Innovation Center Of Geospatial Technology, Wuhan 430079, China
近年来,随着我国空间技术的飞速发展,光学卫星的影像质量不断提高,获取更加便捷,成本逐渐降低,已成为高分辨率对地观测系统的重要组成部分。伴随着空间分辨率的不断提升,光学卫星影像的清晰度和解析能力不断增强,其细节信息更加丰富。然而,卫星在发射过程中由于应力释放、成像环境变化等因素,其成像参数会发生变化,直接使用地面实验室检校的参数无法获取准确的几何精度(以资源三号下视相机为例,基于实验室检校参数的成像模型精度在公里级别)。因此,在“看得清”的基础上,如何使其“测得准”则成了充分发挥高分辨率光学卫星影像性能和应用潜力的一个关键问题。
在轨几何定标是提高卫星影像无控几何质量的有效手段,同时也是光学卫星几何预处理的必要步骤。目前,常用的几何定标方法是利用从定标场参考数据匹配的密集控制点,采用后方交会的方法实现内外系统误差参数的高精度解算,且国内外现役的大多数卫星均采用该方法进行标定。针对SPOT-5卫星,法国空间中心(CNES)利用分布世界各地的地面定标场,对SPOT-5卫星进行了在轨定标,定标后单影像平面定位精度达到50 m(RMS)[1]。对于世界上首颗高分辨率商业遥感卫星IKONOS,美国空间成像公司、美国国家宇航局等组织成立了几何定标小组,利用Lunar lake、Railroad Valley、Dark Brooking、Denver等定标场,对星上载荷的几何成像参数进行了严格检校,最终实现了无控制条件下平面12 m(RMS)和高程10 m(RMS)的几何精度,利用少量控制点即可满足1:10 000比例尺地形图测绘的精度要求[2-5]。针对OrbView-3号卫星,文献[6]同样基于几何定标场对其全色相机进行了定标,进而将Orb-View3号卫星全色相机的平面定位精度提高到了15 m(CE90),高程精度提高到了10 m(CE90),且无明显的内部畸变[6]。在光学卫星在轨几何定标方面,国内学者同样做了大量的工作,文献[7—8]将相机安装角和探元指向角分别作为待定标参数,利用嵩山定标场的高精度参考数据对ZY-1号02C卫星的全色相机进行了在轨几何定标,结果表明,经过在轨几何定标后,影像的无控几何精度从定标前1500 m提高到定标后100 m左右[7-8]。同样,在ZY-3号卫星发射后,文献[9—13]利用河南嵩山定标场对其进行了在轨几何定标与精度验证,标定后资源三号卫星下视影像无控定位精度提高到了15 m左右,并且验证了ZY-3号卫星三线阵相机符合零畸变的设计要求[9-13]。相似的基于定标场的方法目前已经应用于国内外许多卫星,例如ALOS、GeoEye-1、IRS-P6、KOMPSAT-2、TH-1等[14-18]。总的来说,这种方法已发展成熟,并取得了较好的工程应用效果。然而,这种方法由于过度依赖地面定标场而存在固有的缺陷,主要体现在以下4个方面:①昂贵的定标场建设和维护成本提高了在轨几何定标的代价;②随着卫星影像幅宽的增大,从已有的参考数据匹配的控制点的分布已经无法满足在沿CCD(charge-coupled device)线列方向覆盖卫星影像的需求,这无疑会降低在轨标定的精度;③过境定标场区域的无云影像的选取受天气影响较大,加之卫星较长的重访周期会进一步降低在轨几何定标的时效性;④定标场数据通常采用航空摄影测量的方式生产,因此卫星影像与参考数据影像之间的异源匹配精度一定程度会影响几何内定标的精度。
针对传统方法在无定标场条件下的局限性,本文提出一种基于稀少控制点的光学遥感卫星在轨几何定标方法,在传统后方交会定标方法的基础上引入重叠影像之间的相对约束条件,利用沿CCD方向不少于50%重叠的影像对(覆盖相机视场范围)和稀少控制点即可进行相机参数的高精度标定,其中,重叠影像之间的同名光线空间相交的几何关系可构建相机视场中“探元-探元”的几何约束条件,进而实现在无定标场条件下对相机内方位元素的精确标定,而稀少控制点的绝对约束条件主要用来标定外参数,同时改善由于缺少绝对约束条件造成的内定标模型病态的问题。因而,本文方法无须从定标场参考影像上匹配密集控制点,摆脱了传统定标方法对于定标场数据的依赖,大大降低在轨几何定标成本,并有利于提高在轨几何定标的时效性。
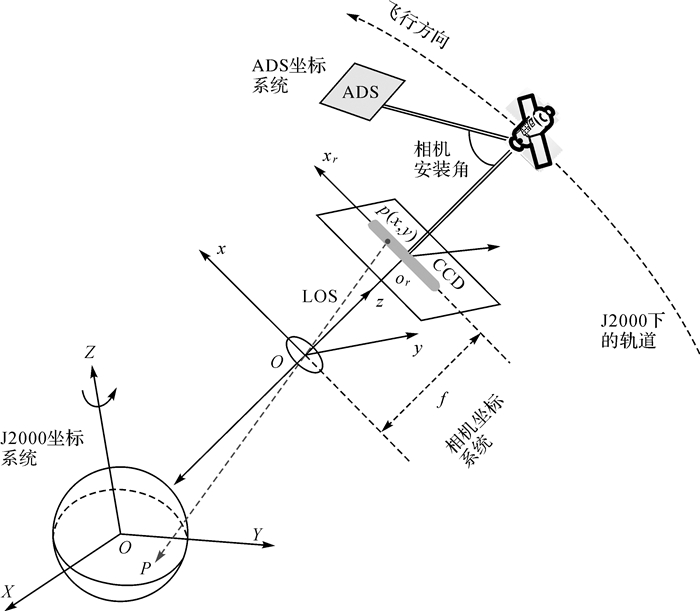
1 几何定标模型构建 1.1 成像模型构建线阵推扫成像的光学卫星的成像原理如图 1所示,图中or-xryr、o-xyz和O-XYZ分别表示焦平面坐标系、相机坐标系和空间固定惯性坐标系,f为相机的主距,物方点P为相机坐标系坐标为(x, y, z)的探元p在某成像时刻拍摄的目标点。此时线阵排列的电荷耦合元件CCD通过将中心投影方式传入的光学信号转换为电信号来获取每个像元的灰度DN值,在CCD成像的同时,姿态测量系统ADS和轨道测量系统(GPS系统)以一定的频率测量每个时刻姿态测量系统在惯性坐标系J2000下的姿态和GPS天线中心在地心直角坐标系WGS-84下的位置矢量。
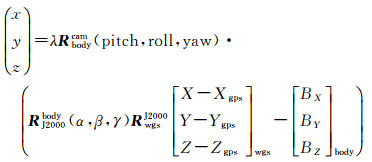
基于线阵光学卫星的成像原理可建立起每个CCD探元和其成像时刻所拍摄的物方点之间的严格对应关系,其严格成像模型如式(1)所示
 (1)
(1)
式中,(x, y, z)为CCD探元在相机坐标系中的坐标,(X, Y, Z)与(Xgps, Ygps, Zgps)分别表示该探元对应的物方点及GPS天线相位中心在WGS-84坐标系下的坐标;RwgsJ2000、RJ2000body、Rbodycam分别代表WGS-84坐标系到J2000坐标系的旋转矩阵、J2000坐标系到卫星本体坐标系的旋转矩阵、卫星本体坐标系到相机坐标系的旋转矩阵;(BX, BY, BZ)body代表从传感器投影中心到GPS天线相位中心的偏心矢量在卫星本体坐标系下的坐标。
1.2 几何定标模型构建在轨几何定标的本质是对影响成像模型精度的系统误差参数进行标定[19]。成像过程中系统误差参数主要可分为两类:外部系统误差参数和内部系统误差参数。外部系统误差参数可广义归纳为卫星本体(星敏)坐标系和相机坐标系3轴之间的夹角(pitch, roll, yaw),基于这3个夹角建立的广义安装矩阵Rbodycam可用于建立卫星本体和相机本体之间的关系。内部系统误差参数主要包括相机的主点、主距、探元尺寸及光学畸变参数等众多内部参数。因此,光学卫星的在轨几何标定的目的就是通过补偿这些参数来改正成像模型中存在的几何误差。
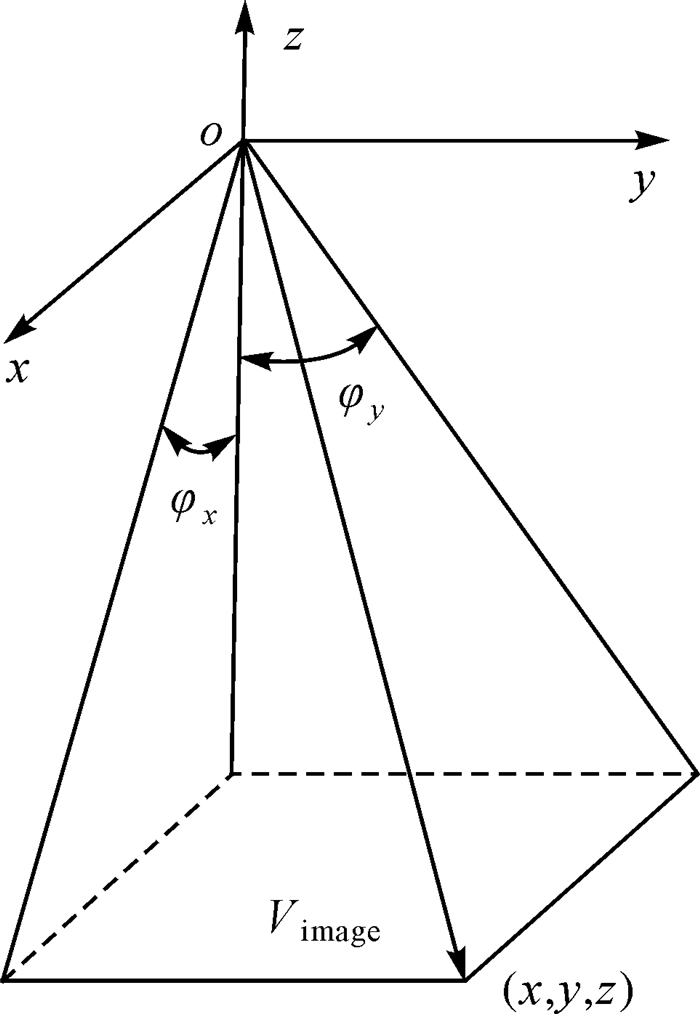
根据上述分析,外定标需要解算的参数即为卫星本体与相机本体之间的3个安装角,而内定标需要解算的参数却需要经过一定的优化来解决严格内参数模型存在的问题。严格物理模型是基于光学相机成像机理所构建,各类参数具有明确的物理意义,但是,某些参数之间存在着强相关性,这一点对于具有窄视场角、长焦距及线阵CCD的光学卫星相机尤为突出[20],因此在定标中直接解算这些参数势必会造成解算的不稳定。此外,卫星载荷镜头设计工艺复杂,在轨成像环境恶劣,基于布朗模型的严格内参数模型可能存在一定程度的欠拟合的问题,因此,本文采用一种指向角模型作为内定标模型,如图 2所示。
|
| 图 2 每个探元的指向角 Fig. 2 Viewing-angle of the CCD detector |
每个CCD探元在相机坐标系o-xyz中的指向Vimage可由其指向角(φx, φy)根据式(2)精确确定
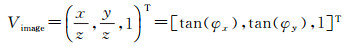 (2)
(2)
然而,对于CCD上的每个探元均解算其指向角是没有必要的,可采用多项式来拟合每个CCD探元的指向角,由于光学遥感卫星的长焦距、窄视场的设计特点,高阶畸变在所有误差中所占的比例有限,一个三阶的探元指向角模型通常足以准确描述每个探元的光线指向,如式(3)所示
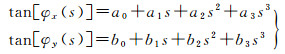 (3)
(3)
式中,s代表探元号; (ai, bi)(i=0, 1, 2, 3)为指向角模型的系数。
本模型是对严格物理模型进行参数正交化的结果,模型参数可认为是具有相关性的物理参数的一组正交基,每项系数等效或部分等效于严格物理模型中一个或者多个畸变参数对相机内部几何畸变的影响。最后,将指向角模型引入到严格成像模型(1)中,即可构建线阵推扫光学卫星的在轨几何定标模型,如式(4)
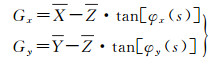 (4)
(4)
式中
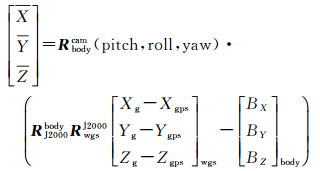
模型中,未知参数不但包括外定标参数(pitch, roll, yaw)、内定标参数(ai, bi)(i=0, 1, 2, …, 3),还包括每对同名点对应的物方大地坐标(B, L, H)。
2 定标参数的稳健解算分步解算定标参数更适合本文的所提出的定标方法,同时也更适合实际的在轨应用,主要原因如下:①本文方法在解算内外参数时所利用的条件不同,模型处理方式不同,因此更适合分开处理;②对于处于低轨道的卫星,其在轨运行时内参数较稳定,因此在卫星生命周期内,内参数通常只标定几次即可,而外参数随时间变化较大,标定后一段时间影像的定位精度会有所衰减,需要以一定的频率对其进行时序化的标定[21],因此,将内外参数分开处理更符合实际应用需求。
采用先外后内的分步解算方法,首先,基于影像覆盖区域的稀少控制点进行外定标,然后在解算的外参数确定的坐标框架基础上进行内定标,内定标不但需要控制点的约束,还需要影像之间同名点的约束,其中,同名点的相对约束条件用来反演高阶参数,而控制点的绝对约束条件主要用于解算模型中的常数项同时保证内定标的稳健解算,具体如下。
2.1 基于稀少控制点的外定标解算在外定标解算时仅需要使用影像覆盖区域的稀少控制点即可。此时,将内参数的设计值XI0作为真值,利用外参数的初值XE0=(pitch0, roll0, yaw0)对定标模型进行线性化,可得到第i个控制点的误差方程如下
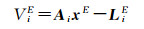 (5)
(5)
式中
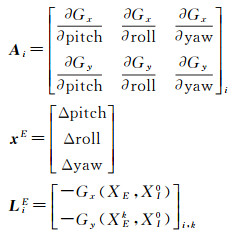
式中,xE是外参数的改正值;LiE是利用内参数的设计值XI0和外参数的当前值XE计算得到的第i个控制点的差值向量。
最后,利用最小二乘方法即可得到每次迭代解算中外参数改正值的最优估计
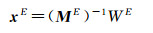 (6)
(6)
式中
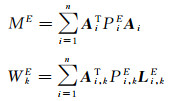
式中,n是控制点的个数。
最小二乘解算是一个迭代过程,每次迭代后需要根据解算的改正数更新外参数,当连续两次解算的结果差值小于一个限差时,解算结束。
2.2 附加高程约束的内定标稳健解算传统方法在解算内参数时需要通过在沿CCD方向匹配均匀分布的一定数量的密集控制点来保证内定标的精度,因此,仅使用稀少控制点无法精确地估计内参数。而重叠影像同名点之间的相互约束条件又与相机内参数模型中的常数项相互独立,因此,当仅使用影像之间的同名点相互约束条件进行内定标时,会造成内参数解算方程秩亏,无法收敛。鉴于此,在内定标时需要同时使用两种约束进行联合求解。此时,同名像点的相互约束条件用来估计高阶参数,而稀少控制点的绝对约束条件主要用来估计内参数中的常数项,进而保证解算的稳定性。基于此,理论上在内定标解算时仅需一个控制点即可。
在外定标中解算的外参数XE的基础上进行内定标,利用内参数的初值XI0对定标模型进行线性化,对于控制点采用与外定标相同的方法进行线性化并建立误差方程,这里不再赘述。而对于同名点,在线性化时未知参数不但包括待解算的内参数,还包括同名点对应的物方坐标。然而,内参数的值与同名点对应的高程值是高度相关的[22-23],因此,当二者在定标解算中均为未知数时,势必导致改化法方程系数矩阵的秩亏,进而造成平差参数解算无法达到最优估计。针对该问题,本文通过引入附加的高程约束来改善定标模型的状态,通过将从参考数字高程模型(DEM)中内插的高程值H作为真值引入模型中来优化平差模型,从而保证定标参数解算的精度。由于满足50%重叠的影像对的交会条件非常弱,因此,通常一个公开的粗格网DEM即可满足定标的精度需求,这与高精度的定标场参考数据相比,其成本几乎可忽略不计。
在对模型线性化后,可以得到第k对同名像点的误差方程,如式(7)所示
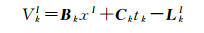 (7)
(7)
式中
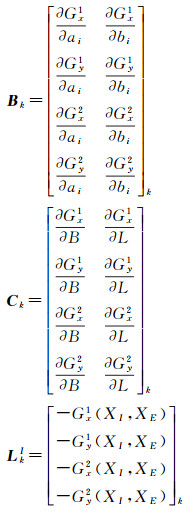
式中,xI是内参数的改正值;tk是第k对同名点对应的物方平面坐标的改正值;(Gx1, Gy1)是同名点中位于第1张影像上的点建立的定标模型;(Gx2, Gy2)是同名点中位于第2张影像上的点建立的定标模型。
最后,采用最小二乘平差的方法逐点构建控制点和同名点的误差方程,进而构建改化法方程,联合解算内参数的改正值。与外参数解算相同,内参数的解算仍是一个迭代过程,每次迭代后需要根据解算的改正数更新内参数,当连续两次解算的结果差值小于一个限差时,解算结束。
3 试验与分析 3.1 试验及数据介绍本文利用两组试验来说明本文方法的有效性。第1组试验对比分析基于3种约束条件情况下的标定结果,第1种情况(Case1)即为本文提出的利用重叠影像同名点相互约束条件和稀少控制点的方法;第2种情况(Case2)为仅使用稀少控制点的标定方法;第3种情况(Case3)为利用从定标场参考数据匹配的密集控制点的传统标定方法[7-8, 21]。第2组试验在标定结果的基础上利用检查点对比验证了基于标定前后的参数构建的成像模型的几何精度。
本文针对我国首颗民用测绘卫星ZY-3号的下视相机进行了定标试验。本文方法利用了我国广西南宁区域的2景重叠的影像(NAD1和NAD2)进行定标试验,参数解算时附加的高程约束来自公开的30 m分辨率的ASTER DEM,立体像对之间的重叠度在50%~60%。基于地面定标场的传统方法使用的影像为覆盖嵩山定标场区域的一景影像NAD3,使用的参考数字正射影像(DOM)和DEM即为嵩山定标场的高精度参考数据,其中DOM的分辨率为0.2 m,平面精度优于1 m;DEM的分辨率为1 m,高程精度优于1 m。表 1列出了所采用的定标景影像的信息。
| 数据 | 采集时间 | 区域 | 中心经纬度 | CCD探元数量 | 分辨率/m |
| NAD 1 | 2014-09-28 | 南宁 | 108.4°E, 22.7°N | 下视:8192×3 前后视:4096×4 |
下视:2.1 前后视:3.5 |
| NAD 2 | 2015-04-13 | 南宁 | 108.6°E, 22.7°N | ||
| NAD 3 | 2012-02-03 | 嵩山 | 113.2°E, 34.4°N |
资源三号卫星下视相机视场中包含了3片TDICCD,但该相机采用了半反半透棱镜的光学拼接方式,将多片CCD器件拼接为一条扫描线,各片CCD之间具有优于0.3个像素的拼接精度[24],因此,本文将多片CCD直接作为一个整片CCD进行几何定标。
影像对的行(沿轨)方向上,布设了4个外业控制点,并在影像上手动进行了量测。此外,由于外方位元素模型拟合误差的随机抖动会给相机内定标结果带来非线性且无规律的畸变误差,为了限制其影响,实现相机内部CCD各探元处几何畸变的最优拟合,本文在待定标影像对的行(沿轨)方向上较短的一段区域内匹配同名点。采用基于SIFT算子的高精度匹配算法对重叠影像对进行自动匹配[25],共获取了29 830个同名点。图 3列出了下视相机定标影像、影像之间的同名点及使用的4个控制点的分布情况。
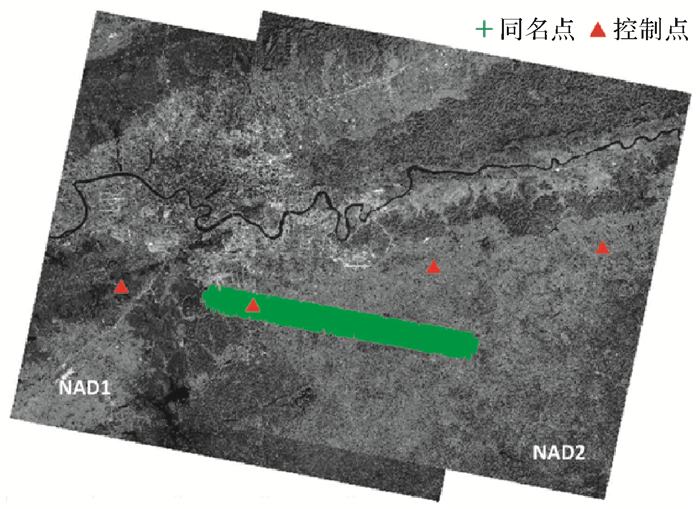
|
| 图 3 ZY-3下视影像及相应点位分布 Fig. 3 Distribution of ZY-3NAD image pair and points |
3.2 定标结果
采用分步解算的方法分别解算外参数和内参数,本文方法在外定标时仅利用稀少控制点确定外参数,然后在此基础上利用稀少控制点和同名点进行内定标,进而恢复每个CCD探元在相机坐标系内的精确指向。然而,由于匹配的同名点数量较多,误匹配难以避免,因此本文从水平方向和高程方向两个角度来剔除粗差。在高程方向,将分布在局部地形起伏过大区域的同名点视为不可靠点,在光线与DEM相交位置的4邻域格网内进行判断,4邻域内高程最大值与最小值之间的差值大于限差即视为需要剔除的不可靠点,本文中的限差设为20 m。在水平方向,在每次迭代解算后计算同名点在像方的相对残差,并将该残差作为观测值来探测粗差,首先计算所有观测值的中误差与均值,然后将观测值与均值之间的偏差大于3倍中误差的同名点视为粗差点并剔除。通过水平方向和高程方向的剔除可保证参与解算的同名点的可靠性与精度。
此外,由于使用的两景影像NDA1和NAD2之间的时间跨度较大,而外参数会随时间变化,为了约束外参数随时间的变化对于内定标的影响,笔者在Case1和Case2中利用稀少控制点对两景影像分别进行外定标,即两景影像各自得到一套外参数。在内定标中,Case1使用了稀少控制点和同名点两种约束条件,而Case2中仍仅使用4个稀少控制点,但Case3在内外标定中均使用了来自定标场参数数据的密集控制点,因此在进行精度评价时可将Case3得到的结果作为基准。
3.2.1 外定标结果对于上述3种情况,分别进行外参数的标定,Case1和Case2在外定标时完全相同,不再分别讨论,最后得到3种情况的外定标结果如表 2所示。其中NAD1和NAD2对应的是Case1和Case2的外定标结果,NAD3对应的是Case3的外定标结果。
| rad | |||
| 外参数 | pitch | roll | yaw |
| 设计值 | 0.0 | 0.0 | 0.0 |
| NAD1 | 0.001 292 035 0 | -0.001 596 842 8 | -0.003 240 301 1 |
| NAD2 | 0.001 399 428 8 | -0.001 230 866 7 | -0.003 120 849 4 |
| NAD3 | 0.001 339 341 8 | -0.001 638 088 9 | -0.003 252 521 7 |
3.2.2 内定标结果
内参数基本不随时间变化,则两个不同时刻的重叠影像可共用一套内参数。在解算的外定标的基础上,对于3种情况的方法和约束条件分别解算相应的内参数,得到相机的内参数见表 3。
| 内参数 | 设计值 | 定标结果 | ||
| Case 1 | Case 2 | Case 3 | ||
| a0 | 0.0 | 5.544 804E-07 | 9.662 450E-06 | -1.110 440E-07 |
| a1 | 0.0 | -2.210 579E-10 | -4.622 201E-09 | -5.070 804E-11 |
| a2 | 0.0 | 1.950 701E-14 | 4.960 980E-13 | 1.333 176E-14 |
| a3 | 0.0 | -7.082 056E-19 | -1.410 958E-17 | -5.610 503E-19 |
| b0 | 5.050 294E-02 | 5.051 685E-02 | 5.048 926E-02 | 5.051 925E-02 |
| b1 | -4.117 647E-06 | -4.117 494E-06 | -4.100 026E-06 | -4.119 179E-06 |
| b2 | 0.0 | -1.244 090E-13 | -2.040 418E-12 | -2.68 5835E-15 |
| b3 | 0.0 | 2.548 508E-18 | 5.575 321E-17 | 1.456 748E-19 |
3.3 定标精度评价与分析
基于上述标定结果评价在轨几何定标的精度,标定后载荷的畸变曲线以及获取的影像的几何定位精度是表征在轨几何定标精度和有效性的重要指标,因此本文从这两个方面对定标方法及结果精度进行验证与分析。试验1对比分析了3种情况下标定后相机的内部畸变;试验2对比验证了在不同系统误差补偿模型下,基于不同方法定标前后影像的几何定位精度。
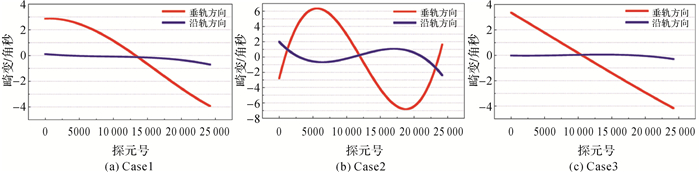
3.3.1 相机的内部畸变对比分析畸变曲线可用于精确刻画标定的内参数相较于内参数设计值的变化。首先,基于标定前后的内参数解算每个CCD探元在相机坐标系中的指向角,然后以标定前的指向角为基础计算标定后每个探元的指向角在沿轨和垂轨两个方向的残差,最后根据该残差值可画出3种情况下的畸变曲线,如图 4所示。
|
| 图 4 下视相机内部畸变曲线 Fig. 4 Internal distortion curves of NAD camera |
采用传统基于密集控制点的方法得到的畸变曲线如图 4(c)所示,可以看出,下视相机在沿轨方向的内部畸变几乎为0,而垂轨方向的几何畸变近似于一个具有固定斜率的线性畸变,说明ZY-3卫星下视相机的内部畸变主要是由卫星在轨运行后相机调焦导致的主距发生变化引起的,内部的高阶光学畸变有限,该结论印证了卫星研制方声称的资源三号卫星三线阵相机具有零畸变设计,同时也说明本文将多片CCD器件视为一个整体来进行标定是合理的。
当仅使用4个稀少控制点进行几何定标时得到的畸变曲线为图 4(b),以Case3的畸变曲线作为标准,则可以发现标定后相机内仍存在较大的非线性畸变,因此,虽然少数的几个控制点的获取成本远低于高精度定标场参考数据制作的成本,但仅使用稀少控制点不足以实现内参数高精度的标定。
采用本文所提出的方法结合使用稀少控制点和重叠影像之间的同名点后,得到的畸变曲线为图 4(a),当以Case3的畸变曲线作为标准评价Case1畸变曲线时,可以发现Case1畸变曲线与Case3大致相同,但仍存在些许的非线性畸变,究其原因主要是由内定标引入的高程约束条件存在的高程误差以及稀少控制点的量测误差引起的。笔者统计Case1曲线中每个CCD探元相较于Case3的偏差,在沿轨方向该偏差的均方差为0.20角秒,在垂轨方向为0.66角秒,且最大偏差均小于1角秒,总体满足优于一个像素的精度需求。
3.3.2 定位精度评价为了进一步分析与评价本方法对ZY-3下视影像几何精度改善的有效性,本文试验比较了定标参数精化前后NAD3影像的几何精度。首先利用SIFT算子从嵩山定标场参考数据匹配了534个均匀分布的高精度控制点作为检查点,验证景影像数据及检查点如图 5所示。

|
| 图 5 验证景影像数据及检查点 Fig. 5 Validation image and check points |
然后,分别利用参数设计值、Case1和Case3的定标结果拟合RPC参数,其中Case1拟合RPC时使用的外参数为基于NAD1影像解算的外参数(NAD1成像时间距NAD3更近)。最后,分别基于相应的RPC参数解算检查点在不同系统误差补偿模型进行校正后的像方残差,并统计残差在X(垂轨)和Y(沿轨)方向的均方差,进而得到不同系统误差补偿模型下,定标前、基于本文方法定标后和基于传统定标场方法定标后影像的几何定位精度,具体如表 4所示。
| 像素 | ||||||||
| 变换模型 | 定标前 | 本文方法标定 | 定标场方法 | |||||
| X | Y | X | Y | X | Y | |||
| 无 | 399.91 | 324.36 | 14.21 | 10.18 | 0.30 | 0.95 | ||
| 刚性平移 | 2.13 | 18.85 | 0.64 | 0.81 | 0.60 | 0.82 | ||
| 相似变换 | 9.53 | 9.12 | 0.66 | 0.67 | 0.63 | 0.72 | ||
| 仿射变换 | 0.61 | 0.60 | 0.63 | 0.61 | 0.59 | 0.67 | ||
| 二次多项式 | 0.56 | 0.60 | 0.55 | 0.61 | 0.58 | 0.67 | ||
| 三次多项式 | 0.56 | 0.56 | 0.55 | 0.59 | 0.57 | 0.63 | ||
从表 4中可以看出,下视相机在标定前在两个方向的初始像方定位误差均大于300像素,即使经过刚性平移变换和相似变换后仍存在较大的定位偏差,说明标定前影像中存在较显著的内部畸变,而经过仿射变换改正后,影像的定位精度提高到一个像素以内,再使用二次多项式等更高阶的改正模型,精度改善的幅度并不显著,再次说明ZY-3卫星下视相机的内部畸变主要是由主距误差引起的,高阶光学畸变有限。
总体来说,基于不同的系统误差补偿模型,从刚性平移到三次多项式模型,无论标定前后影像的定位精度均从显著变化逐渐趋于稳定,但二者趋于稳定的节点不同。对于标定后的影像,在使用刚性平移变换模型改正后精度即趋于稳定,而相较之下,标定前的影像需要在仿射变换模型的修正下才能达到与标定后影像在平移变换模型改正下相当的精度,并在之后精度趋于稳定。这进一步说明了定标前影像存在显著的由主距误差引起的畸变,而标定后这部分误差得到了显著的补偿。
在经过本文方法和定标场方法标定后,影像的初始定位偏差均有显著提高,但本文方法仍存在大于10像素的定位误差,这是由定标景影像与验证景影像之间存在的成像时间差异造成的(外参数发生了变化),而定标场方法使用的定标景影像就是NAD3,与验证景相同,因此初始定位精度已经达到优于1像素的水平。然而,这并不是重点,因为笔者更关注影像的内部畸变。在经过平移变换模型改正后,两种方法在两个方向精度均优于1像素,且几乎相同,经过更高阶的模型改正后,两种方法的精度改善有限,说明这两种方法已经有效地改善了影像的内部畸变,而几乎等同的精度说明本方法在改善ZY-3下视影像几何精度上与定标场方法几乎相同,进而说明了本文方法的有效性。而更低廉的成本和更快速的时效性又说明了本文方法相较于定标场方法的优越性。
4 结论本文提出一种利用重叠影像对和稀少控制点的线阵推扫光学卫星在轨几何定标方法。该方法采用分步解算的方法实现系统误差参数的高精度解算,利用稀少控制点的绝对约束条件实现外参数的标定,同时保证内参数解算的稳健性,利用重叠影像对之间的相互约束条件反演相机内部高阶参数,最终实现定标参数的高精度解算。本文方法使用的数据条件仅为两景重叠影像,几个分布均匀的控制点以及公开的粗格网DEM,无须定标场参数数据即可实现定标参数的高精度解算。从试验验证结果可发现,本文方法在改善卫星影像几何精度上与定标场方法几乎相同,而其成本远低于传统的定标场方法。此外,本文方法所需的影像对在获取时无须考虑天气因素,相较于固定位置的定标场影像在数据采集的时效性上大大提高。然而,本文方法仍然使用了些许控制点数据,并未做到完全的无控制,因此,如何完全摆脱控制点约束条件做内定标甚至外定标是未来一段时间内的重点研究方向。
| [1] | BOUILLON A, BERNARD M, GIGORD P, et al. SPOT5 HRS geometric performances:using block adjustment as a key issue to improve quality of DEM generation[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2006, 60(3): 134–146. |
| [2] | DIAL G. IKONOS satellite mapping accuracy[C]//Proceedings of ASPRS. Washington DC: Springer, 2000. |
| [3] | GRODECKI J, LUTES J. IKONOS geometric calibrations[C]//Proceedings of the ASPRS 2005 Annual Conference. Baltimore, Maryland: Springer, 2005. |
| [4] | FRASER C S, HANLEY H B, YAMAKAWA T. High-precision geopositioning from IKONOS satellite imagery[C]//Proceedings of ASCM-APSRS Annual Convention. Washington DC: Springer, 2002. |
| [5] | GRODECKI J, DIAL G. IKONOS geometric accuracy[C]//Proceedings of Joint Workshop of ISPRS Working Groups Ⅰ/2, Ⅰ/5 and Ⅳ/7 on High Resolution Mapping from Space 2001. Hannover, Germany: University of Hannover: Elsevier, 2001. |
| [6] | MULAWA D. On-orbit geometric calibration of the OrbView-3 high resolution imaging satellite[C]//ISPRS XXth Congress Proceedings. Istanbul: The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences: Elsevier, 2004. |
| [7] |
杨博, 王密.
资源一号02C卫星全色相机在轨几何定标方法[J]. 遥感学报, 2013, 17(5): 1175–1190.
YANG Bo, WANG Mi. On-orbit geometric calibration method of ZY-102C panchromatic camera[J]. Journal of Remote Sensing, 2013, 17(5): 1175–1190. |
| [8] | WANG Mi, YANG Bo, HU Fen, et al. On-orbit geometric calibration model and its applications for high-resolution optical satellite imagery[J]. Remote Sensing, 2014, 6(5): 4391–4408. DOI:10.3390/rs6054391 |
| [9] |
李德仁.
我国第一颗民用三线阵立体测图卫星-资源三号测绘卫星[J]. 测绘学报, 2012, 41(3): 317–322.
LI Deren. China's first civilian three-line-array stereo mapping satellite:ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317–322. |
| [10] |
龚健雅, 王密, 杨博.
高分辨率光学卫星遥感影像高精度无地面控制精确处理的理论与方法[J]. 测绘学报, 2017, 46(10): 1255–1261.
GONG Jianya, WANG Mi, YANG Bo. High-precision geometric processing theory and method of high-resolution optical remote sensing satellite imagery without GCP[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1255–1261. DOI:10.11947/j.AGCS.2017.20170307 |
| [11] |
曹金山, 袁修孝, 龚健雅, 等.
资源三号卫星成像在轨几何定标的探元指向角法[J]. 测绘学报, 2014, 43(10): 1039–1045.
CAO Jinshan, YUAN Xiuxiao, GONG Jianya, et al. The look-angle calibration method for on-orbit geometric calibration of ZY-3 satellite imaging sensors[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1039–1045. DOI:10.13485/j.cnki.11-2089.2014.0147 |
| [12] | CHEN Yifu, XIE Zhong, QIU Zhengge, et al. Calibration and validation of ZY-3 optical sensors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4616–4626. DOI:10.1109/TGRS.2015.2403957 |
| [13] | ZHANG Guo, JIANG Yonghua, LI Deren, et al. In-orbit geometric calibration and validation of ZY-3 linear array sensors[J]. The Photogrammetric Record, 2014, 29(145): 68–88. DOI:10.1111/phor.2014.29.issue-145 |
| [14] | TAKAKU J, TADONO T. PRISM On-orbit geometric calibration and DSM performance[J]. IEEE Transactions on Geoscience & Remote Sensing, 2009, 47(12): 4060–4073. |
| [15] |
孟伟灿, 朱述龙, 曹闻, 等.
线阵推扫式相机高精度在轨几何标定[J]. 武汉大学学报(信息科学版), 2015, 40(10): 1392–1399, 1413.
MENG Weican, ZHU Shulong, CAO Wen, et al. High accuracy on-orbit geometric calibration of linear push-broom cameras[J]. Geomatics & Information Science of Wuhan University, 2015, 40(10): 1392–1399, 1413. |
| [16] | CRESPI M, COLOSIMO G, DE VENDICTIS L, et al. GeoEye-1: Analysis of radiometric and geometric capability[C]//Personal Satellite Services. PSATS 2010. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol. 43. Berlin, Heidelberg: Springer, 2010: 354-369. |
| [17] | GRUEN A, KOCAMAN S, WOLFF K. Calibration and validation of early ALOS/PRISM imagery[J]. Journal of the Japan Society of Photogrammetry & Remote Sensing, 2007(46): 24–38. |
| [18] | RADHADEVI P V, SOLANKI S S. In-flight geometric calibration of different cameras of IRS-P6 using a physical sensor model[J]. The Photogrammetric Record, 2008, 23(121): 69–89. DOI:10.1111/j.1477-9730.2007.00453.x |
| [19] | PI Yingdong, YANG Bo, WANG Mi, et al. On-orbit geometric calibration using a cross-image pair for the linear sensor aboard the agile optical satellite[J]. IEEE Geoscience & Remote Sensing Letters, 2017, 14(7): 1176–1180. |
| [20] | WANG Mi, CHENG Yufeng, CHANG Xueli, et al. On-orbit geometric calibration and geometric quality assessment for the high-resolution geostationary optical satellite GaoFen4[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2017(125): 63–77. |
| [21] | YANG Bo, WANG Mi, XU Wen, et al. Large-scale block adjustment without use of ground control points based on the compensation of geometric calibration for ZY-3 images[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2017(134): 1–14. |
| [22] | YANG Bo, PI Yingdong, LI Xin, et al. Relative geometric refinement of patch images without use of ground control points for the geostationary optical satellite GaoFen4[J]. IEEE Transactions on Geoscience & Remote Sensing, 2018, 56(1): 474–484. |
| [23] |
王密, 杨博, 金淑英.
一种利用物方定位一致性的多光谱卫星影像自动精确配准方法[J]. 武汉大学学报(信息科学版), 2013, 38(7): 765–769.
WANG Mi, YANG Bo, JIN Shuying. A registration method based on object-space positioning consistency for satellite multi-spectral Image[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 765–769. |
| [24] |
曹海翊, 刘希刚, 李少辉, 等.
"资源三号"卫星遥感技术[J]. 航天返回与遥感, 2012, 33(3): 7–16.
CAO Haiyi, LIU Xigang, LI Shaohui, et al. ZY-3 satellite remote sensing technology[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 7–16. DOI:10.3969/j.issn.1009-8518.2012.03.003 |
| [25] | LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |