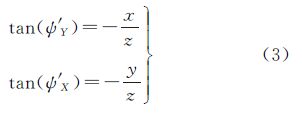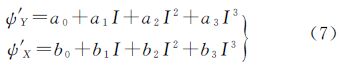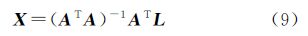2. 武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079;
3. 武汉大学 遥感信息工程学院,湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430049, China;
3. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430049, China
资源三号卫星(ZY-3)是我国自主设计的第一颗民用三线阵立体测绘卫星,主要用于1∶50 000比例尺地形测图、更大比例尺基础地理信息产品更新以及国土资源调查与监测[1, 2]。然而,由于受到安置工艺、卫星发射时加速度过大等因素的影响,根据实验室定标值进行ZY-3影像直接对地目标定位,其正视影像平面定位精度约为±1.1 km,前后视立体像对平面定位精度约为±1.5 km,高程精度约为±270 m[3],无法满足1∶50 000地形测图的精度要求。为此,文献[4]基于虚拟CCD线阵成像技术构建了ZY-3严格几何模型,取得了较高的几何定位精度。文献[3, 4, 5, 6]从ZY-3严格几何模型出发,将待定标参数分为内、外定标参数两类,构建了在轨几何定标模型,并采用分步几何定标方法,实现了ZY-3成像传感器的在轨几何定标。文献[7, 8]提出了基于拼接CCD的分段多项式系统误差模型。将偏置矩阵[9]引入ZY-3严格几何模型时,文献[10]提出了基于偏置矩阵及内方位元素模型的多检校场联合几何检校模型及方案。文献[11, 12, 13]构建了ZY-3影像传感器校正产品几何模型,并对校正影像的定位精度进行了分析。在姿态角常差检校模型[14, 15]的基础上,文献[16]提出了一种卫星影像姿态角系统误差检校方法,并构建了用于ZY-3联合定标的自检校光束法平差模型。
目前,就ZY-3成像传感器在轨几何定标而言,主要采用分步几何定标方法,这需要提供实验室定标值。由于内、外定标参数间存在强相关性,往往采用DOM与待定标影像自动匹配的方式以获取大量的地面控制点。鉴于此,本文从星敏感器坐标系下各CCD探元的指向角出发,研究一种ZY-3成像在轨几何定标的探元指向角法,试图在无须实验室定标参数及少量地面控制点的情况下,实现ZY-3成像传感器的在轨几何定标,以提高ZY-3影像的直接对地目标定位精度。
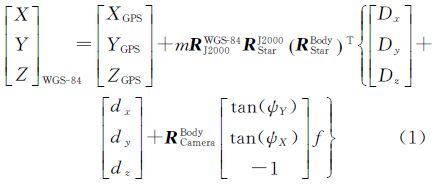
1 严格几何模型的建立根据GPS测定的GPS天线相位中心在WGS-84坐标系下的位置、星敏感器测定的星敏主光轴在J2000坐标系下的指向以及实验室定标值,可建立ZY-3单相机(单线阵影像)的严格几何模型[5, 17, 18]
式中,(X,Y,Z)WGS-84和(XGPS,YGPS,ZGPS)分别为地面点P和GPS天线相位中心在WGS-84坐标系下的三维坐标;m为比例因子;RJ2000WGS-84为J2000坐标系至WGS-84坐标系的旋转矩阵;RStarJ2000为星敏感器坐标系至J2000坐标系的旋转矩阵;RStarBody为星敏感器在卫星本体坐标系下的安置矩阵;(Dx,Dy,Dz)和(dx,dy,dz)分别为GPS天线相位中心和相机节点在卫星本体坐标系下的3个偏移量;RCameraBody为相机在卫星本体坐标系下的安置矩阵;(ψY,ψX)为地面点P所对应的CCD探元在相机坐标系下的指向角;f为相机主距。 2 成像传感器的在轨几何定标 2.1 严格几何定标模型的建立从式(1)可以看出,建立ZY-3影像上某一像点与其对应地面点之间的严格几何关系所涉及的坐标系包括相机坐标系、卫星本体坐标系、星敏感器坐标系、J2000坐标系和WGS-84坐标系。为了便于构建基于探元指向角的ZY-3成像传感器严格几何定标模型,可在式(1)的基础上令
式中,(x,y,z)描述的是CCD线阵各探元在星敏感器坐标系下的坐标。进一步令 式中,(ψ′Y,ψ′X)为CCD线阵各探元在星敏感器坐标系下的指向角。将式(2)中第1、2、3项分别除以-z,得
由式(4)可知,(ψ′Y,ψ′X)可以同时描述外定标参数(Dx,Dy,Dz)、(dx,dy,dz)、RStarBody、RCameraBody以及内定标参数(ψY,ψX)、f对ZY-3影像对地目标定位精度的综合影响。另一方面,ZY-3在轨运行的一段时期内,(Dx,Dy,Dz)、(dx,dy,dz)、RStarBody、RCameraBody以及(ψY,ψX)、f变化都非常小,可以认为是常量。因此,(ψ′Y,ψ′X)也可以认为是常量,这就为在星敏感器坐标系下对各CCD探元指向角进行几何定标提供了可能性。
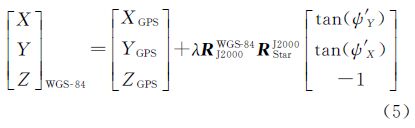
将式(4)代入式(1),可得
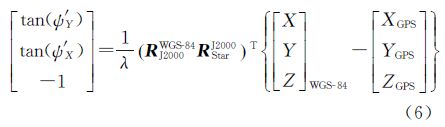
式中,λ=-mz。将式(5)变形,可得
式(6)即为ZY-3成像在轨几何定标探元指向角法的严格模型。ZY-3正视相机、前后视相机拼接后的CCD线阵分别包含有24 530个、16 300个探元。如果直接利用式(6)求解每个探元的指向角,则需要在影像每列方向上至少布设一个地面控制点,这势必要有大量的地面控制点,实际应用中难以操作。为此,本文采用文献[3]的方法,以3次多项式来描述各CCD探元的指向角,即
式中,(a0,a1,a2,a3,b0,b1,b2,b3)为多项式系数;I为CCD探元编号。 2.2 严格几何定标模型的参数求解分析式(6)和式(7)可知,利用本文方法进行ZY-3成像传感器在轨几何定标,只需精确求解出式(7)中的8个多项式系数,而无须分别求解内、外定标参数。因此,当影像覆盖范围内有4个以上地面控制点时,便可采用最小二乘平差原理求解,具体流程如下:
(1)根据各地面控制点,由式(6)的第3项求出比例因子λ。
(2)根据式(6)的第1、2项求解出控制点对应的CCD探元在星敏感器坐标系下的指向角(ψ′Y,ψ′X)。
(3)根据式(7)建立误差方程

(4)根据最小二乘平差原理,求解式(8)中的未知数X
(5)根据式(7)求解每个CCD探元在星敏感器坐标系下的指向角。
综上所述,本文提出的ZY-3成像传感器在轨几何定标方法在求解未知参数时,建立的误差方程为线性方程,无须迭代求解,也无须实验室定标值,而且求解过程非常便捷。
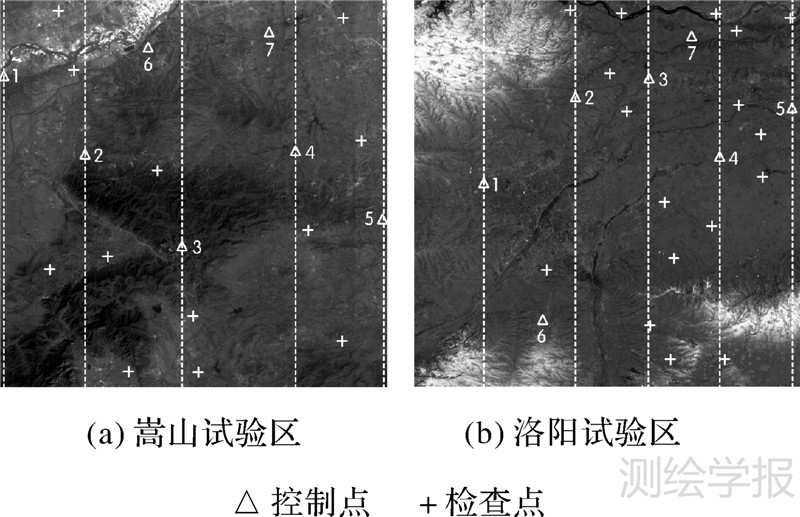
3 试验及其结果分析 3.1 试验设计目前,ZY-3成像传感器在轨几何定标在实际处理时,主要采用文献[3]和文献[5]提出的分步几何定标方法。为了验证本文方法的正确性和有效性,并与分步几何定标方法进行比较分析,本文采用文献[3]和文献[5]中覆盖嵩山和洛阳两个试验区的ZY-3前视、正视和后视影像进行了试验。其中,嵩山ZY-3影像获取于2012年2月3日,覆盖地面高程范围为86.20~1 129.90 m,均匀分布有19个平高地面控制点(如图 1(a)所示);洛阳ZY-3影像获取于2012年1月24日,覆盖地面高程范围为88.52~ 369.90 m,布设了24个平高地面控制点(图 1(b))。两个试验区的地面控制点均采用GPS RTK技术在野外实地测量而获得。
|
| 图 1 试验区中地面控制点的分布 Fig. 1 Distributions of GCPs in empirical areas |
ZY-3配置的前视、正视和后视相机均为线阵CCD传感器,对各CCD探元指向角进行在轨几何定标时,理论上要求地面控制点对应的CCD探元在CCD线阵上均匀分布,即地面控制点应覆盖整个影像幅宽方向,且在影像幅宽方向上均匀分布。基于这一原则,本文选取了不同数量的地面控制点(分布示意如图 1中的△),5个地面控制点为1—5号点(其余同)。
根据2.2节中几何定标的具体流程求解各CCD探元在星敏感器坐标系下的指向角多项式系数列于表 1。受文章篇幅的限制,本节仅以正视相机的在轨几何定标结果为例。
| 试验区 | 控制点个数 | a0 | a1 | a2 | a3 | b0 | b1 | b2 | b3 |
| 嵩山 | 5 | 1.713 9×10-3 | -1.64×10-8 | -2.8×10-14 | 7×10-19 | 4.795 3×10-2 | 4.11×10-6 | 8.0×10-13 | -2×10-17 |
| 6 | 1.714 2×10-3 | -1.68×10-8 | 6.4×10-14 | 8×10-19 | 4.795 2×10-2 | 4.11×10-6 | 8.9×10-13 | -2×10-17 | |
| 7 | 1.714 2×10-3 | -1.69×10-8 | 8.0×10-14 | -1×10-19 | 4.795 2×10-2 | 4.11×10-6 | 7.7×10-13 | -2×10-17 | |
| 洛阳 | 5 | 1.736 8×10-3 | -1.83×10-8 | 1.9×10-13 | -4×10-18 | 4.791 5×10-2 | 4.10×10-6 | 1.3×10-12 | -3×10-17 |
| 6 | 1.738 5×10-3 | -1.89×10-8 | 2.4×10-13 | -5×10-18 | 4.791 9×10-2 | 4.10×10-6 | 1.2×10-12 | -3×10-17 | |
| 7 | 1.738 1×10-3 | -1.88×10-8 | 2.3×10-13 | -5×10-18 | 4.792 0×10-2 | 4.10×10-6 | 1.2×10-12 | -3×10-17 |
分析表 1中的试验结果可以看出:
(1) 利用5个地面控制点即可求解出式(7)中的8个多项式系数,但随着控制点数量的增加,各多项式系数的变化非常小,基本处于同一数量级,这说明地面控制点的数量和分布对本文方法的影响较小。另外,由于受到不同试验区卫星位置观测值(XGPS,YGPS,ZGPS)、星敏感器姿态观测值(RJ2000Star)以及地面控制点坐标观测值中观测误差的影响,嵩山和洛阳两个试验区的多项式系数存在一定的差异,但均属同一数量级,差别较小,这就为本文方法用于ZY-3影像的外推对地目标定位奠定了基础。
(2) 相比于文献[3]和文献[5]中的分步几何定标方法,本文方法建立的误差方程为线性方程,无须实验室定标值(如相机安置矩阵、CCD在相机坐标系下的指向角)作为定标参数求解的初始值,而且各定标参数之间不存在相关性,对地面控制点数量的依赖性较小,仅需利用5个地面控制点求解出式(7)中的8个多项式系数,便可进一步获得各CCD探元在星敏感器坐标系下的指向角。
3.3 直接对地目标定位根据式(5)实施ZY-3正视影像对地目标定位,并统计各地面检查点坐标的最大残差和中误差,列于表 2。其中,地面控制点数为0是指直接利用影像辅助数据根据式(1)进行对地目标定位的试验结果。表 3列出了根据本文方法求解前后视相机各CCD探元在星敏感器坐标系下的指向角后,进行前方交会获得的立体定位结果,前方交会的具体公式可参见文献[19]。
| m | |||||||||
| 试验区 | 控制点个数 | 检查点个数 | 最大残差 | 中误差 | |||||
| X | Y | 平面 | X | Y | 平面 | ||||
| 嵩山 | 0 | 19 | 919.940 | 448.355 | 1 022.636 | 913.346 | 404.672 | 998.980 | |
| 5 | 14 | -4.194 | -3.984 | 4.736 | 2.018 | 1.771 | 2.685 | ||
| 6 | 13 | -3.865 | -4.042 | 4.839 | 2.100 | 1.617 | 2.650 | ||
| 7 | 12 | 2.595 | -3.809 | 4.109 | 1.600 | 1.526 | 2.211 | ||
| 洛阳 | 0 | 24 | 934.527 | 430.075 | 1 028.739 | 927.104 | 389.327 | 1 005.534 | |
| 5 | 19 | -3.487 | -2.992 | 4.190 | 1.797 | 1.227 | 2.176 | ||
| 6 | 18 | -3.292 | -3.016 | 4.077 | 1.798 | 1.236 | 2.182 | ||
| 7 | 17 | 3.485 | -2.775 | 3.973 | 1.634 | 1.125 | 1.984 | ||
| m | |||||||||||
| 试验区 | 控制点个数 | 检查点个数 | 最大残差 | 中误差 | |||||||
| X | Y | 平面 | H | X | Y | 平面 | H | ||||
| 嵩山 | 0 | 19 | 836.211 | 928.757 | 1 211.366 | -210.293 | 809.713 | 833.041 | 1 161.720 | 168.655 | |
| 5 | 14 | -4.438 | -7.402 | 8.487 | -5.866 | 3.105 | 3.020 | 4.332 | 3.117 | ||
| 6 | 13 | -4.961 | -7.397 | 8.493 | -5.631 | 2.547 | 3.127 | 4.033 | 3.118 | ||
| 7 | 12 | 5.744 | -8.057 | 9.895 | -5.789 | 2.704 | 3.492 | 4.417 | 3.173 | ||
| 洛阳 | 0 | 24 | 857.408 | 900.447 | 1 211.309 | -201.344 | 837.597 | 814.107 | 1 168.049 | 152.469 | |
| 5 | 19 | 3.936 | -8.481 | 9.350 | -5.993 | 1.623 | 4.451 | 4.738 | 2.743 | ||
| 6 | 18 | 3.992 | -8.058 | 8.993 | -6.124 | 1.678 | 4.176 | 4.500 | 2.896 | ||
| 7 | 17 | 4.454 | 6.671 | 7.084 | -5.404 | 1.794 | 3.145 | 3.621 | 3.194 | ||
分析表 2和表 3中的试验结果可以看出:
(1)在轨几何定标前,ZY-3正视影像直接对地目标定位的平面精度约为±1 km,前后视立体像对直接对地目标定位的平面与高程精度分别约为±1.1 km、±160 m。此定位精度与文献[3]、文献[5]中的试验结果是一致的,这说明实验室定标获得的参数值与卫星在轨运行时的实际值存在较大的差异。
(2)当在影像覆盖范围内有5个地面控制点时,可利用本文方法求解各CCD探元在星敏感器坐标系下的指向角,有效消除(Dx,Dy,Dz)、(dx,dy,dz)、RStarBody与RCameraBody等参数包含的系统误差,显著提高ZY-3影像对地目标定位精度。就正视影像而言,嵩山和洛阳影像的平面定位精度分别提高至±2.685 m和±2.176 m,接近于±1像素。对于前后视立体像对,定标后的平面与高程精度也接近于±1像素。
(3)随着地面控制点数量的增加,ZY-3影像对地目标定位精度不再有明显的提高。就嵩山试验区的正视影像而言,当地面控制点数量由5个增加至7个时,其平面定位精度仅提升了±0.474 m。
3.4 外推对地目标定位本节试验将在5个地面控制点情况下进行,将嵩山试验区求解的ZY-3正视相机各CCD探元在星敏感器坐标系下的指向角用于洛阳试验区正视影像的对地目标定位(嵩山→洛阳),获得的外推对地目标定位结果如表 4和图 2(a)所示。为了便于比较分析,表 4和图 2(a)中同时列出了文献[3]和文献[5]中外推对地目标定位的结果。

|
| 图 2 ZY-3正视影像外推对地目标定位结果 Fig. 2 Extrapolative object positioning results of ZY-3 nadir images |
分析表 4和图 2(a)中的试验结果可以看出:
(1)相比于定标前的ZY-3影像对地目标定位精度(表 2中地面控制点数为0的情况),将本文方法在嵩山试验区求解获得的正视相机各CCD探元的指向角用于洛阳试验区影像的对地目标定位,其定位精度有显著提高,平面精度由±1 005.534 m提高至±8.509 m。这进一步说明,相机安置误差、星敏感器安置误差等是影响ZY-3影像对地目标定位精度的主要因素,本文方法是行之有效的,能够有效消除这些误差对影像对地目标定位精度的影响。
(2)相比于文献[3]和文献[5]中的分步几何定标方法,本文方法在洛阳试验区获得的外推对地目标定位精度提高了14.389-8.509=5.880 m,达到了约±4 像素的精度水平。究其原因就在于,本文方法以各CCD探元在星敏感器坐标系下的指向误差来综合描述ZY-3相机安置误差、星敏感器安置误差及各CCD探元在相机坐标系下的指向误差,建立的定标模型形式简单,参数易于求解,能够有效消除定标参数之间的强相关性对影像对地目标定位精度的影响。
为充分验证本文方法的有效性,进一步实施了洛阳→嵩山的正视影像外推对地目标定位(表 4和图 2(b))、嵩山→洛阳和洛阳→嵩山的前后视立体像对外推对地目标定位(表 5)。
| m | ||||||||||
| 试验 | 检查点个数 | 最大残差 | 中误差 | |||||||
| X | Y | 平面 | H | X | Y | 平面 | H | |||
| 嵩山→洛阳 | 24 | 9.648 | 21.754 | 22.050 | 7.131 | 6.090 | 16.821 | 17.889 | 3.528 | |
| 洛阳→嵩山 | 19 | -9.564 | -27.823 | 27.935 | -7.368 | 4.999 | 18.253 | 18.925 | 3.968 | |
分析表 4、图 2(b)和表 5中的试验结果可以看出:
(1) 受洛阳试验区地面控制点未能覆盖整个影像幅宽方向的影响,洛阳→嵩山的正视影像外推对地目标定位精度约为±5像素,略低于嵩山→洛阳的定位精度,但这一精度仍明显高于定标前嵩山试验区正视影像的对地目标定位精度。
(2) 对比表 4和表 2中的试验结果可以看出,ZY-3影像外推对地目标定位精度低于在轨几何定标后影像的直接对地目标定位精度。对于嵩山试验区的正视影像,两者精度相差10.729-2.685=8.044 m。究其原因,卫星位置观测误差、星敏感器姿态观测误差和地面控制点坐标观测误差会随着试验区的不同而有所差异,从而导致根据式(6)求解出的各CCD探元指向角也含有误差,降低了ZY-3影像的外推对地目标定位精度。
4 结 论本文方法通过对星敏感器坐标系下各CCD探元指向角的定标,能够有效消除ZY-3相机安置误差、CCD探元指向误差等误差对影像对地目标定位精度的综合影响。相比于分步几何定标方法,本文方法简单易行、定标参数之间不存在相关性,无须实验室定标获得的GPS天线相位中心偏移量、相机节点偏移量、相机和星敏感器安置矩阵等信息,而且对地面控制点数量的依赖性较小,仅需影像幅宽方向上均匀分布的5个控制点即可求解出各CCD探元的指向角,显著提高了ZY-3影像直接对地目标定位精度。将本方法用于ZY-3影像外推对地目标定位的试验结果表明,相比于定标前的定位精度,本文方法获得的外推对地目标定位精度也有大幅提高。
当然,从式(6)可以看出,卫星位置与姿态观测精度、控制点坐标量测精度是影响本文方法的主要因素,其观测精度的高低决定了在轨几何定标结果的优劣。对于ZY-3而言,卫星位置观测精度可以达到厘米级,星敏感器姿态观测精度可以达到角秒级[20],因此本文方法取得了较好的在轨几何定标结果。不过,由于笔者仅拥有获取时间间隔为10 d的两组带有原始姿轨参数的ZY-3影像数据,且影像所覆盖的试验区均位于河南省境内,受试验数据偏少的限制,地形起伏和地域分布对本文方法的影响,本文方法是否适用于获取时间间隔更长影像的外推对地目标定位,仍有待于进一步研究。
| [1] | CRESDA. Introduction to ZY-3 Satellite [EB/OL]. [2012-07-25]. http://www.cresda.com/n16/n1130/n175290/175676.html. (中国资源卫星应用中心. 资源三号卫星介绍[EB/OL]. [2012-07-25]. http://www.cresda.com/n16/n1130/n175290/175676.html.) |
| [2] | SUN C Z,TANG X M. China’a Stereo Surveying and Mapping Satellite ZY-3 and Its Applications [J]. Aerospace China, 2009,10(9): 1-5. |
| [3] | LI Deren,WANG Mi. On-orbit Geometric Calibration and Accuracy Assessment of ZY-3 [J]. Spacecraft Recovery and Remote Sensing, 2012, 33(3): 1-6. (李德仁, 王密.“资源三号”卫星在轨几何定标及精度评估 [J]. 航天返回与遥感, 2012, 33(3): 1-6.) |
| [4] | TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191-198. (唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报, 2012, 41(2): 191-198.) |
| [5] | LI Deren. China’s First Civilian Three-line-array Stereo Mapping Satellite: ZY-3 [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317-322. (李德仁. 我国第一颗民用三线阵立体测图卫星——资源三号测绘卫星[J]. 测绘学报, 2012, 41(3): 317-322.) |
| [6] | XU Wen, LONG Xiaoxiang, YU Wenyong, et al. Geometric Quality Analysis of Three-line Array CCD Imagery of ZY-3 Satellite [J]. Spacecraft Recovery and Remote Sensing, 2012, 33(3): 55-64. (徐文, 龙小祥, 喻文勇, 等. “资源三号”卫星三线阵影像几何质量分析[J]. 航天返回与遥感, 2012, 33(3): 55-64.) |
| [7] | CHEN Yifu, LIU Lu, ZHANG Chunling. Research on the On-orbit Geometric Calibration for ZY-3 [J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 557-560. (谌一夫, 刘璐, 张春玲. ZY-3卫星在轨几何标定方法[J]. 武汉大学学报:信息科学版, 2013, 38(5): 557-560.) |
| [8] | FANG S H,CHEN Y F. Sensor Calibration of Three-line CCD Scanners on ZY-3 [J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2012, 39(B1): 109-114. |
| [9] | ZHANG Guo, YUAN Xiuxiao, LI Deren. Redressing System Error in Satellite Image Based on Bias Matrix [J]. Journal of Liaoning Technical University, 2007, 26(4): 517-519. (张过, 袁修孝, 李德仁. 基于偏置矩阵的卫星遥感影像系统误差补偿[J]. 辽宁工程技术大学学报, 2007, 26(4): 517-519.) |
| [10] | JIANG Yonghua, ZHANG Guo, TANG Xinming, et al. High Accuracy Geometric Calibration of ZY-3 Three-Line Image [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523-529. (蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523-529.) |
| [11] | PAN Hongbo, ZHANG Guo, TANG Xinming, et al. The Geometrical Model of Sensor Corrected Products for ZY-3 Satellite [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 516-522. (潘红播, 张过, 唐新明, 等. 资源三号测绘卫星传感器校正产品几何模型[J]. 测绘学报, 2013, 42(4): 516-522.) |
| [12] | PAN Hongbo, ZHANG Guo, TANG Xinming, et al. Accuracy Analysis and Verification of ZY-3 Products [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 738-751. (潘红播, 张过, 唐新明, 等. 资源三号测绘卫星影像产品精度分析与验证[J].测绘学报, 2013, 42(5): 738-751.) |
| [13] | LIU Bin, SUN Xiliang, DI Kaichang, et al. Accuracy Analysis and Validation of ZY-3’s Sensor Corrected Products [J]. Remote Sensing for Land and Resources, 2012(4): 36-40. (刘斌, 孙喜亮, 邸凯昌, 等. 资源三号卫星传感器校正产品定位精度验证与分析[J]. 国土资源遥感, 2012(4): 36-40.) |
| [14] | YUAN Xiuxiao, YU Junpeng. Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery [J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 36-41. (袁修孝, 余俊鹏. 高分辨率卫星遥感影像的姿态角常差检校[J]. 测绘学报, 2008, 37(1): 36-41.) |
| [15] | YU Junpeng. Accurate Geometric Positioning of High Resolution Satellite Remote Sensing Imagery [D]. Wuhan: Wuhan University, 2009. (余俊鹏. 高分辨率卫星遥感影像的精确几何定位[D]. 武汉: 武汉大学, 2009.) |
| [16] | WANG Tao. Study on Theories and Methods of Linear CCD Sensor Geometric Calibrated Based on Field [D]. Zhengzhou: Information Engineering University, 2012. (王涛. 线阵CCD传感器试验场几何定标的理论与方法研究[D]. 郑州: 信息工程大学, 2012.) |
| [17] | TANG X M, ZHANG G, ZHU X Y, et al. Triple Linear-array Image Geometry Model of ZiYuan-3 Surveying Satellite and Its Validation [J]. International Journal of Image and Data Fusion, 2013, 4(1): 33-51. |
| [18] | GAO X M, TANG X M, ZHANG G, et al. The Geometric Accuracy Validation of the ZY-3 Mapping Satellite [J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013, doi:10.5194/isprsarchives-XL-2-W1-111-2013. |
| [19] | LI Deren,ZHENG Zhaobao. Analytical Photogrammetry [M]. Beijing: Surveying and Mapping Press, 1992. (李德仁, 郑肇葆. 解析摄影测量学[M]. 北京: 测绘出版社, 1992.) |
| [20] | CAO Haiyi, LIU Xigang, LI Shaohui, et al. ZY-3 Satellite Remote Sensing Technology [J]. Spacecraft Recovery and Remote Sensing, 2012, 33(3): 7-16. (曹海翊, 刘希刚, 李少辉,等. “资源三号”卫星遥感技术[J]. 航天返回与遥感, 2012, 33(3): 7-16.) |