当前双排桩支护结构土压力计算模型研究中主要将土压力分为前排桩被动区、后排桩主动土压力区及桩间土压力区3部分。总的计算方法是按平面钢架结构进行，前排桩被动土压力按“m”法计算；后排桩主动土压力按朗肯土压力计算；对于桩间的土压力，各方学者还存有不同的观点，未形成一致的计算理论。研究出合理、可靠的计算方法，不仅能对解决工程实际问题做出理论支撑，更可以为日后相关规范的制定提供参考。

目前，张富军^[1]总结了双排桩支护结构体系目前常用的几种计算方法；杨光华等^[2]提出了一种将基坑面以下的附加压力看作弹性应力，并增加一个等效土柱刚度的新土压力计算模式；赖国梁等^[3]对倾斜双排桩支护结构进行了探讨，并对双排桩的抗倾覆稳定性提出了一种“前斜后直”的计算方法；张玲等^[4]提出并验证了一种考虑排桩与其间成层地基土体的相互作用的计算方法；陈效星等^[5]提出了一种后桩桩后为主动土压力，前桩桩后为静止土压力，被动土压力均采用弹簧来模拟的计算模型，并通过实例验证；罗忠行等^[6]得到了一种可同时考虑非极限土压力理论和支护桩与土相互作用的支护结构水平位移计算方法；陈玉新^[7]在常规双排桩支护结构的基础上提出了在深厚软土地区采用不同刚度及长短组合双排桩支护结构形式；曹净等^[8]通过引入了等效桁架模型， 针对基坑双排桩结构提出了一种等效桁架计算模型；周珩等^[9]提出了双排桩基悬臂式挡土墙结构的承载机理、简化分析模型以及结构内力与变形的解析计算方法，并进行了验证；王杰等^[10]基于《基坑工程手册》中的算例，提出了一种改进的双排桩计算模型。综上所述，大部分研究是基于基坑的双排桩结构来展开，对于双排桩支护结构计算方法的研究较少，尤其是边坡永久双排桩支护结构。

因此，本文结合某地铁停车场工程，参考国内外现有主流的双排桩简化计算模型，提出针对该项目的双排桩简化计算模型，并进行了相应的有限元计算与实测结果对比，验证双排桩简化计算模型的可行性。

1.   基于不同计算方法的现有双排桩简化模型

目前，双排桩支护结构计算方法存在两大问题：土压力分布情况不明确以及桩间土相互作用的模拟不完全。许多学者及科研人员基于现有的双排桩模型计算方法进行改进与简化，提出了一些更便捷的计算模型^[11-12]。

1.1   极限平衡法简化双排桩计算模型

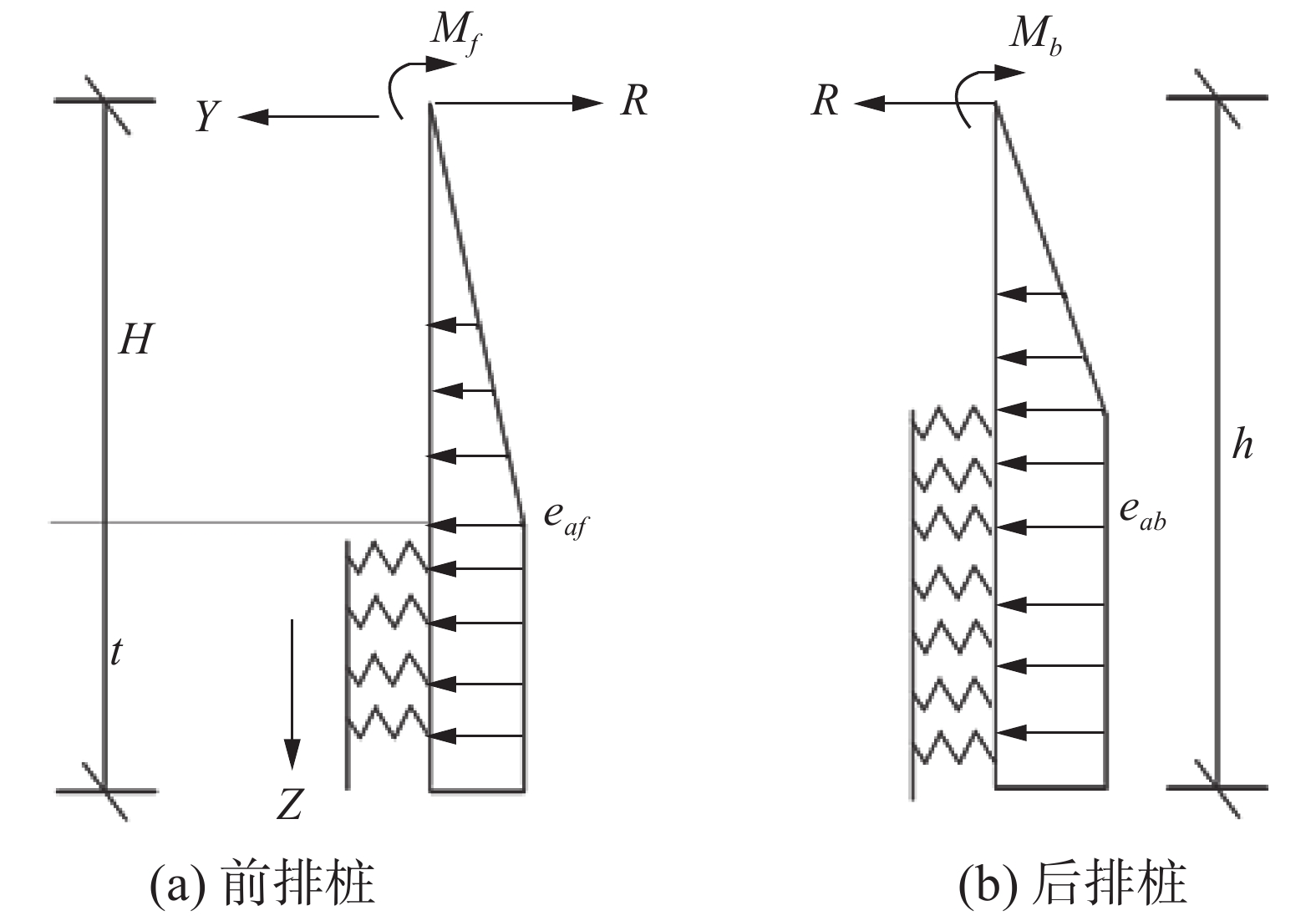
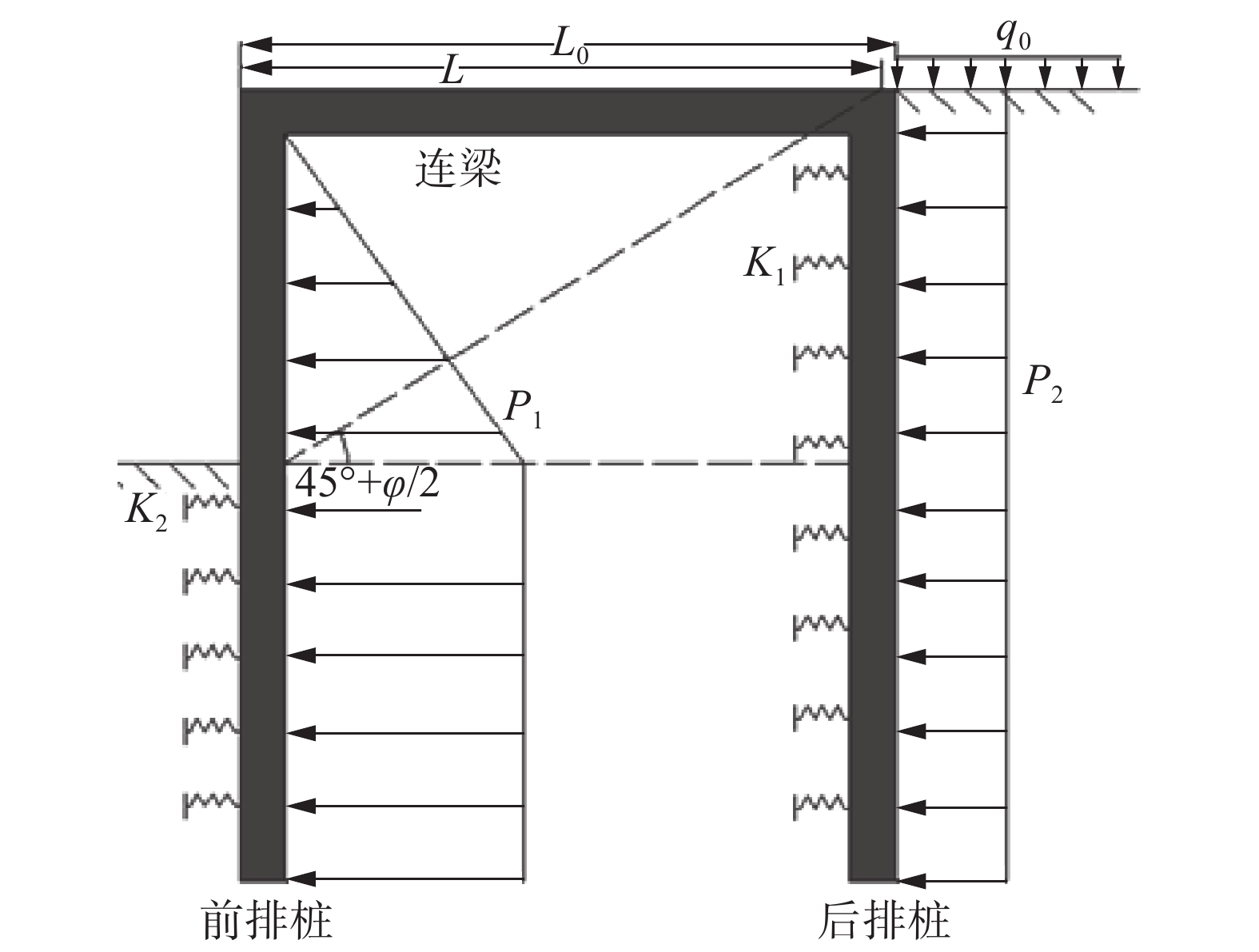
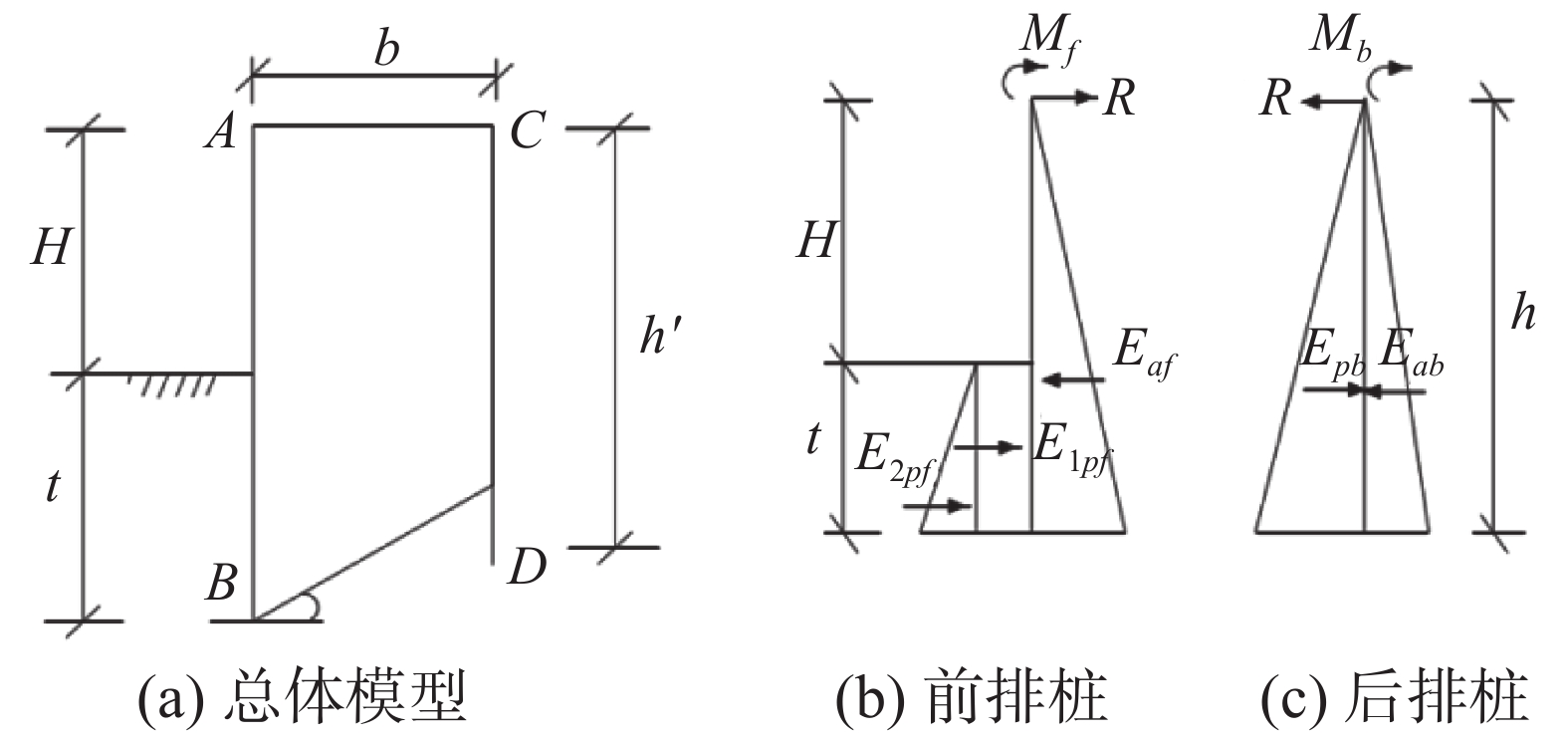
模型根据土体积比例系数法的基本假定，按门式刚架模型对双排桩的内力进行计算和分析。模型将排桩与桩顶盖梁简化为一个门式刚架结构，即排桩底端嵌固、顶端为直角刚结点，且模型中连梁与排桩分离，把连梁的作用用弯矩和反力替代，如图1所示。模型假设盖梁为刚体，在基坑开挖后，前后排桩盖梁标高处只产生相等的水平位移；同时桩底嵌固，即桩底不发生位移和转角。根据双排桩结构水平静力平衡状态和经验方法确定最小入土深度，通过计算简图和极限平衡法计算出前后排桩的内力分布情况，并得出相应挠曲线方程。该方法简化程度高，计算过程较为简便，但土压力计算采用了朗肯土压力理论，未能充分考虑桩土间的作用。

图  1  门架式结构计算模型

下载: 全尺寸图片

图1中，H动基坑深度；t为前排桩入土深度；h为后排桩入土深度；M_f、M_b分别为桩顶盖梁的等效湾距；R为桩顶盖梁的等效反力；E_1pf、E_2pf为前排桩靠基坑一侧被动土压力；E_af为前排桩背离基坑一侧主动土压力；E_pb为后排桩靠基坑一侧被动土压力；Eab为后排桩背离基坑一侧主动土压方。

1.2   弹性抗力法简化双排桩计算模型

根据门式刚架双排桩分解计算的模型以及弹性地基梁的受力特点，建立考虑一定程度的桩−土共同作用的双排桩弹性抗力法计算模型。模型同样将连梁与排桩分离，把连梁的作用用弯矩和反力替代，具体如图2所示。该模型把前、后排桩简化为在桩顶承受剪力和弯矩共同作用的弹性地基梁模型、长桩计算模型，从而根据不同的边界条件和模型假设进行双排桩支护结构的内力、位移和转角等模型参数的求解。可根据桩底入土的深度变化，将桩底端简化为自由端、铰支连接或固定端。然而该模型未充分考虑不同工况的影响，同时，模型土压力为采用经典土压力理论计算得到的已知荷载，最后的计算结果与实际情况可能会有所误差。

图  2  排桩弹性抗力法计算模型

下载: 全尺寸图片

1.3   桩土共同变形理论简化计算方法

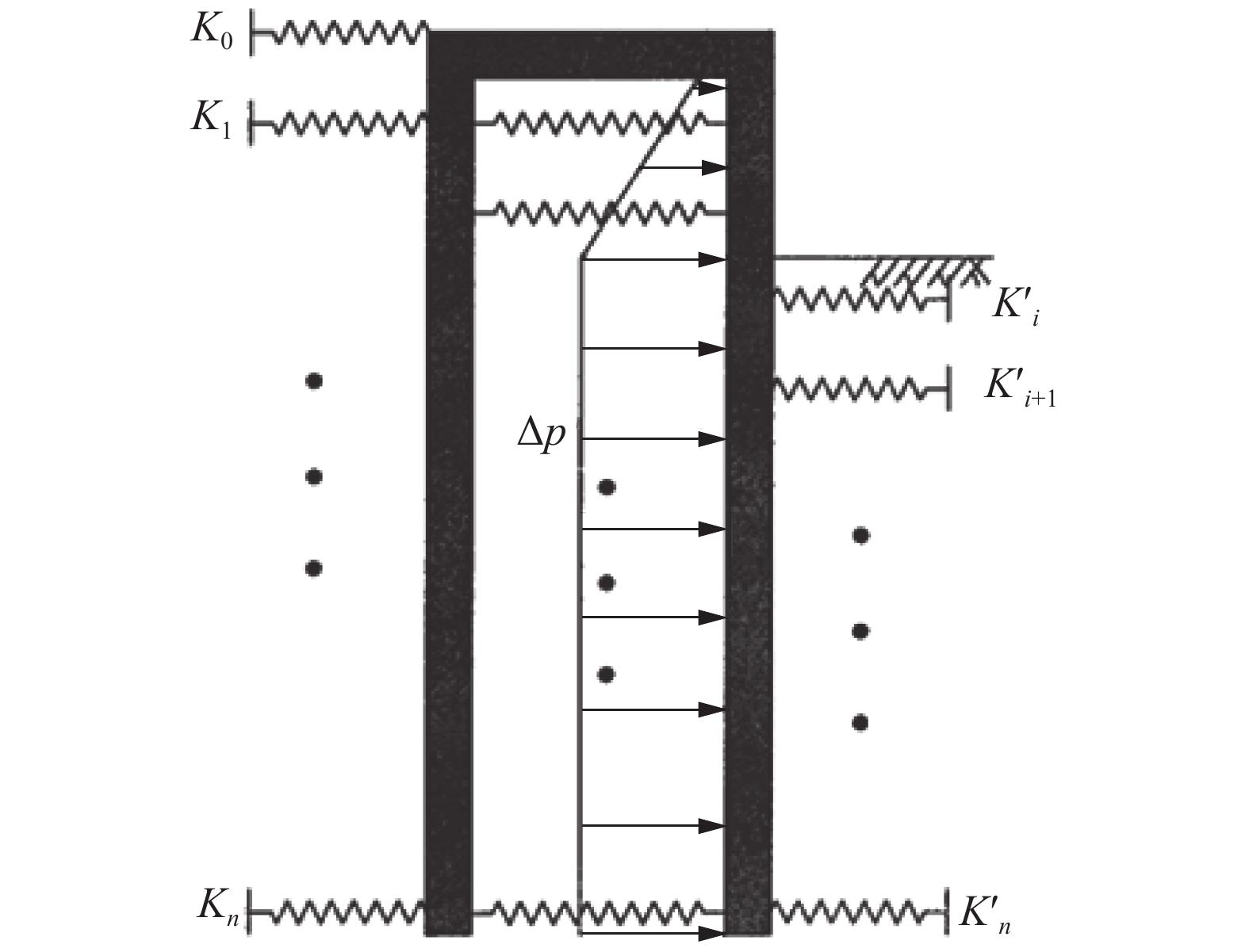
该模型基于Winkle假定的计算方法，如图3所示。模型假定前、后排桩为不考虑桩侧竖向摩阻力的弹性地基梁，视连梁与前、后排桩为刚结点连接，并且开挖释放荷载作用于前排桩。在该假定条件下，采用增量法计算双排桩的土压力分布，将内力、变形增量与上一工况结果相叠加，得到当前工况支护结构的内力和变形，结合变形结果即可求得当前工况的实际有效土压力。同时，桩间土完全采用弹簧来模拟，在后排桩处忽略桩后土体与桩的相互作用，桩后只考虑作用土压力，模型中土弹簧仅设置在前排桩桩前被动土压力区和桩间位置。该法在侧重于模拟实际施工过程的同时忽略了后排桩桩后土体与桩较小的相互作用，使模型计算结果相比实际安全性更高。

图  3  桩土共同效应假定模型

下载: 全尺寸图片

本文双排桩简化计算模型在极限平衡法简化模型上进行修改，得到适用于本项目类型场地的双排桩模型。

2.   双排桩简化计算模型

2.1   双排桩土压力简化计算方法

在双排桩支护结构体系设计中，前排桩嵌固段所受的土反力由弹性抗力组成，可以用一系列水平土弹簧进行等效模拟；后排桩受到的主动土压力作用，可以采用朗肯土压力法进行计算。而在实际设计施工对桩间土压力的考虑中，双排桩桩间土土体的土压力计算规范涉及较少，通常采用郎肯土压力理论，这样对于宽深比较小的设计方案，会出现计算值较实际值偏大的情况。从理论角度出发，考虑前后排桩的相互作用是较符合实际的，但是相关成果体系还不成熟，实际工程项目中应用较少。

桩间土体的土压力计算实际上是有限空间内的土压力计算，目前，规范中关于有限土体的土压力计算较为有限。在北京地方标准《建筑基坑支护技术规程》（DB11/489−2007）中对桩间土的计算采用的是高印立提出的修正系数朗肯土压力计算方法；湖北省地方标准《基坑工程技术规程》（DB42/T159−2012）中推荐采用弹性介质模型，或其他合理的土体本构关系模型来对桩间土体进行计算。

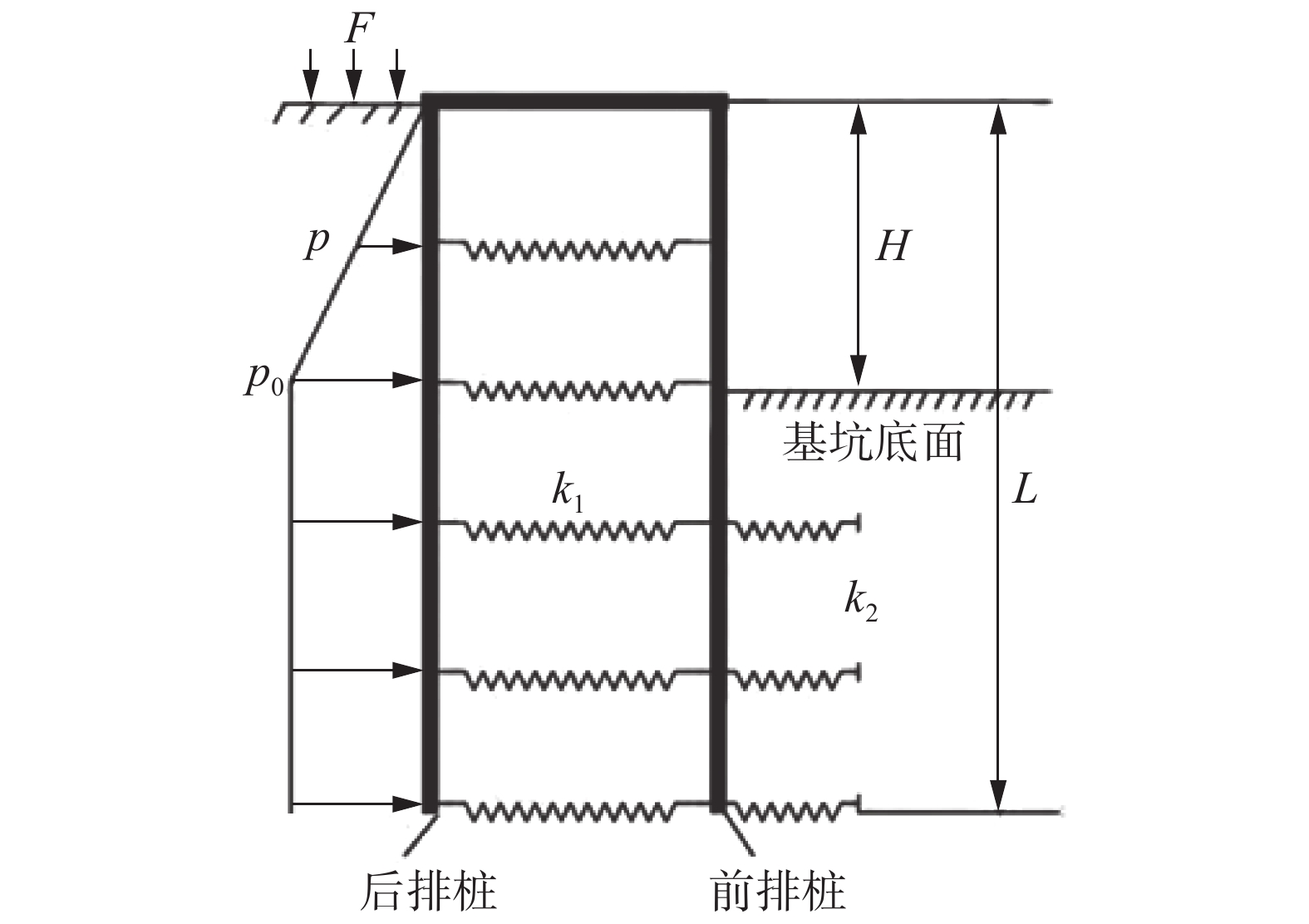
由以上各个行业及地方性规程中可见，各规程中所规定的双排桩桩间土压力计算模型存在差异，但均是基于弹性法的平面刚架计算模型。由于本次研究项目为边坡永久支护结构，安全等级要求较高，为了方便推广，故在进行双排桩支护结构计算模型的简化过程中，对桩间土的土压力计算模型参考朗肯经典土压力计算方法，采用比例系数法进行计算，不考虑前后排桩之间的相互作用，如图4所示。

图  4  考虑桩间土体传递的双排桩计算模型

下载: 全尺寸图片

2.2   双排桩简化计算模型的建立

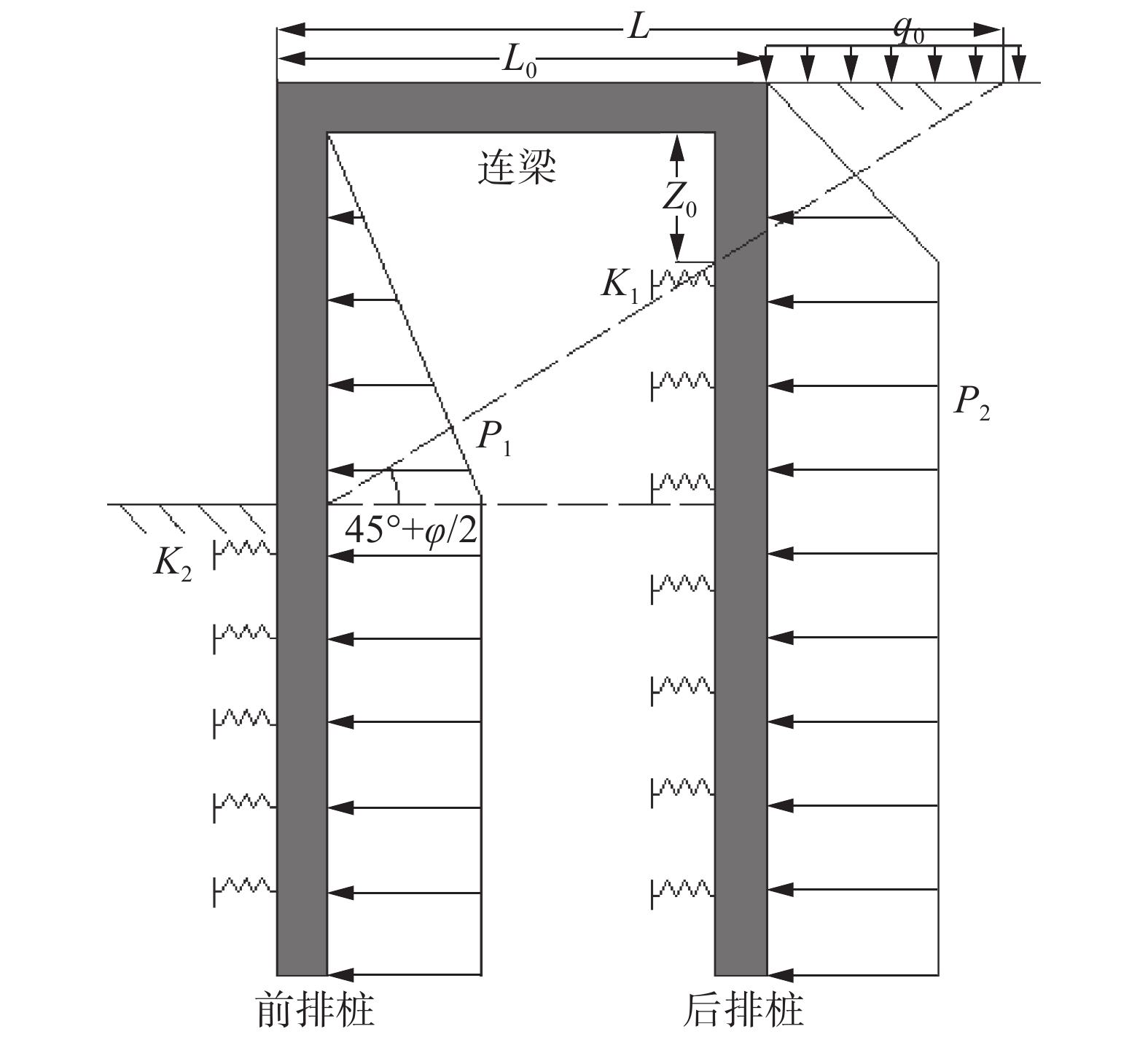
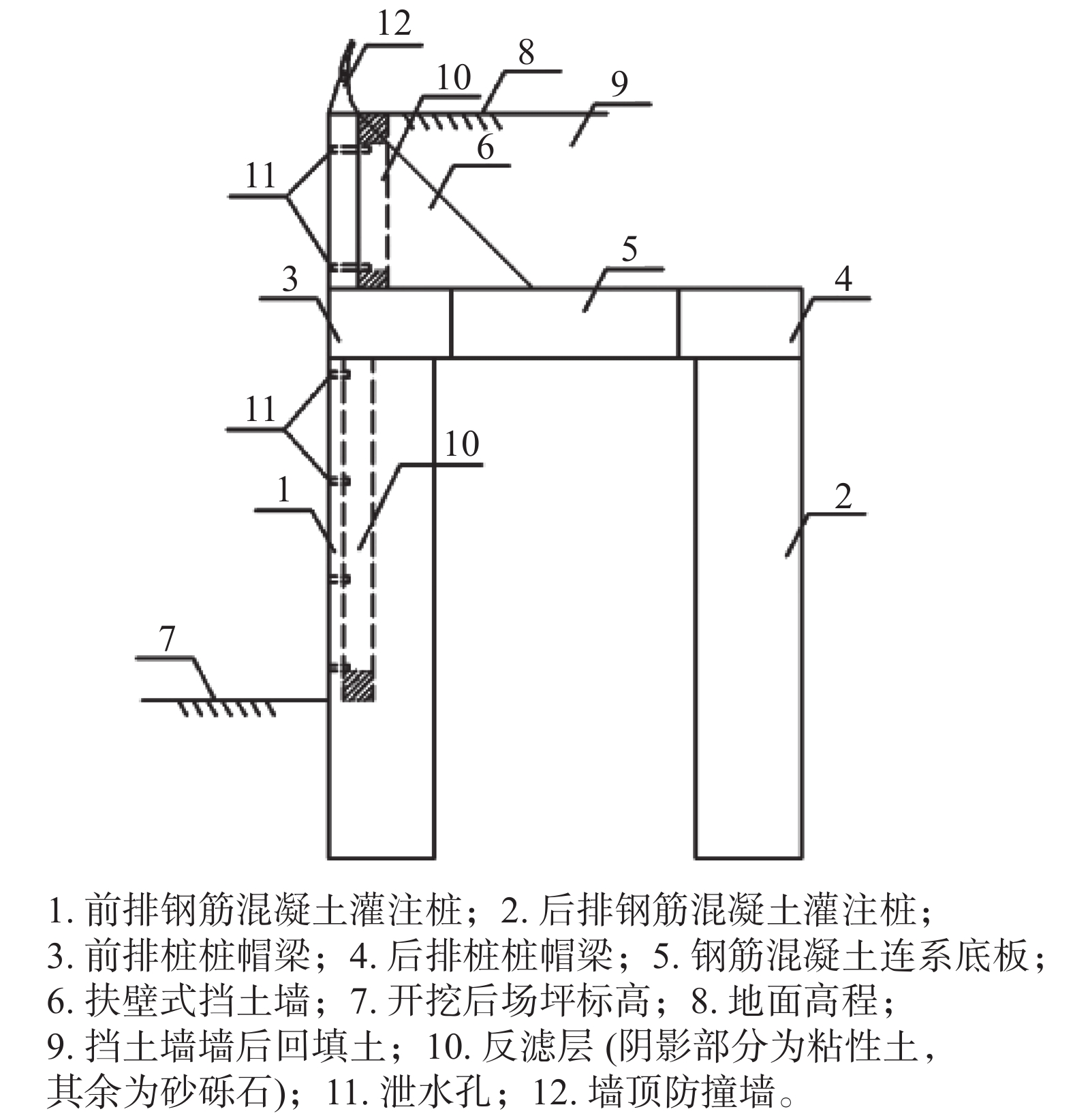
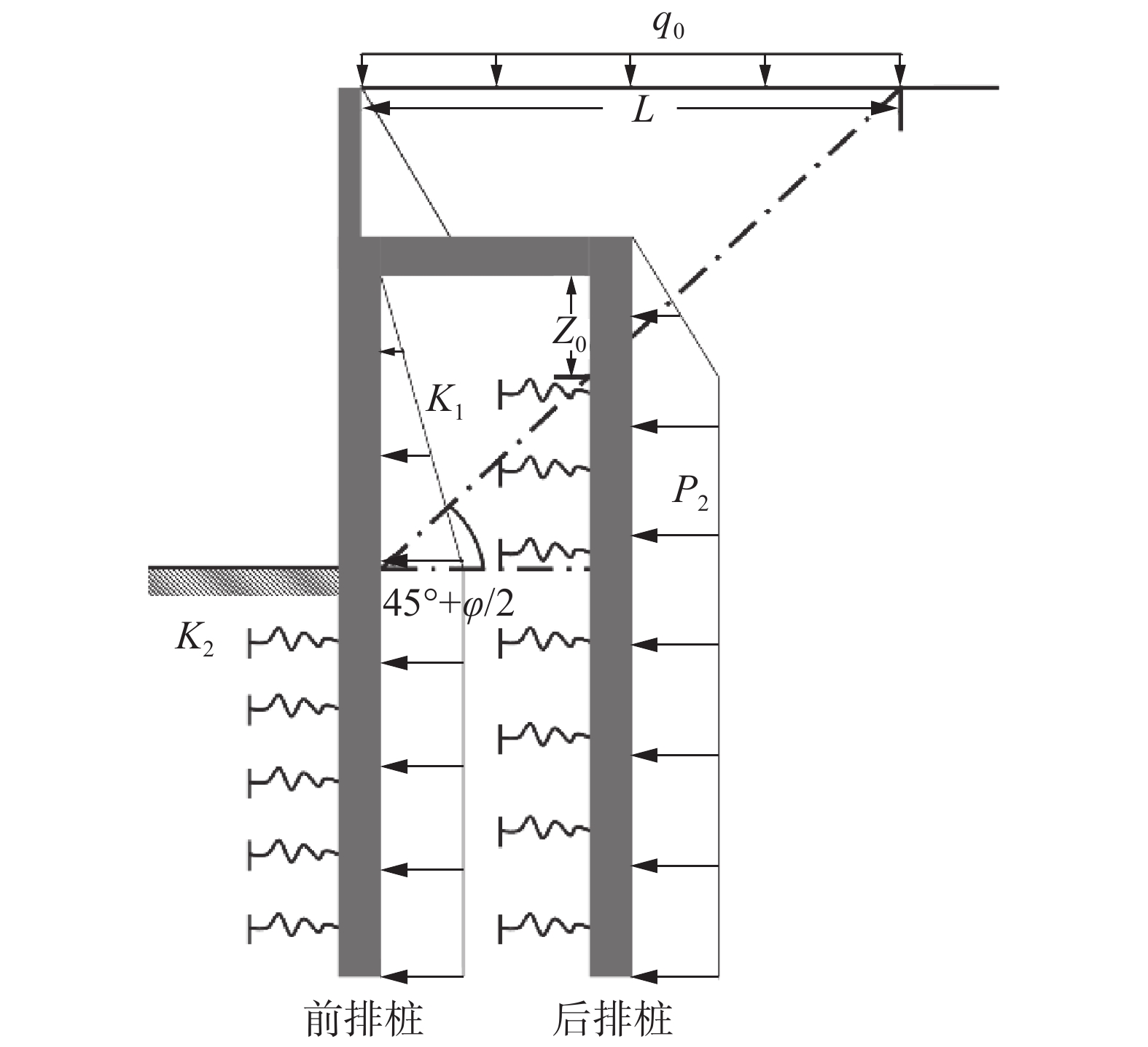
本次简化计算模型（如图5所示）将双排桩支护结构分为前排桩、后排桩和连梁3部分。前、后排桩由于不考虑轴力，这样将会对双排桩支护结构产生一个向土体开挖方向滑移的趋势，在未开挖土体处形成一个剪切滑动面，该滑动面倾角近似取为 $45\text{°}+\varphi/2$ 。开挖对滑动面范围内的土体作用较大，故滑动面以上的土体按照比例系数法进行计算，滑裂面以下的土体为竖直分布。图5中，L为滑动面与前排桩桩顶在地面上的距离， $L{\text{ = }} Z \times {\rm{tan}}\left( {45^\circ - \varphi /2} \right)$ ，Z₀为滑动面与后排桩相交时的土体深度， ${Z_0} = Z\times{L_0}\times\cot \left( {45^\circ - j/2} \right)$ （对于黏性土，内摩擦角应该用等效摩擦角来代替）。前排桩桩前土体用土弹簧模拟，后排桩桩后土体采用朗肯土压力计算，桩间土不考虑前后排桩的荷载传递作用。前排桩桩后主要受到朗肯土压力作用；后排桩桩前用土弹簧模拟其所受被动土压力，不考虑连梁的空间效应；连梁简化为一个只考虑轴力和弯矩作用的梁单元。

图  5  滑动面穿过后排桩时双排桩简化计算模型

下载: 全尺寸图片

根据前人研究^[13-16]，随着排距的增大，前排桩的水平位移和桩身弯矩都相应增大。结合相关资料^[17]调研可知，排距增大时后排桩对土压力存在一定的分担作用，会使前排桩承受的土压力随排距的增加而减小；但是，如果排距增大到一定程度，前排桩所承受的滑动土体作用也会增大，土压力同样上升，这样起挡土作用的主要是前排桩。当双排桩排距L₀>L时，滑移面处于前后桩体之间，双排桩支护结构类似于拉锚结构，此时其主动土压力几乎全部作用于前桩，后排桩不作用土压力荷载，只承担地面荷载，此时简化模型如图6所示，但由于规范要求，在工程实际中不常出现。

图  6  滑动面未穿过后排桩时双排桩简化计算模型

下载: 全尺寸图片

2.3   模型计算公式

根据本次简化模型图5，其计算公式主要如下：

1）总主动土压力计算

总土压力计算按照后排桩桩后的计算点进行计算，按朗肯主动土压力P_ak计算，计算公式为

式中：P_ak为后排桩背离基坑侧主动土压力值，kPa；γ为土体重度，kN·m³；c为土体黏聚力，kPa；K_a为土体主动土压力系数；q₀为地面超载，kPa；Z为计算点的深度，m。

2）前排桩嵌固段的土弹簧计算

前排桩嵌固段采用“m”法进行计算，假定水平地基反力系数在支护深度范围内呈线性分布，具体的计算为

式中：m为前排桩嵌固段土体弹性抗力系数的比例系数，kN/m⁴；h为开挖深度，m。

式(2)中前排桩嵌固段土体弹性抗力系数的比例系数，可按桩的水平荷载实验及地区经验取值。当缺少相关数据时，可按式(3)计算得出，但需特别注意公式的适用范围。

式中：φ为计算点土层的内摩擦角，°；v_b为前排桩在坑底处的水平位移量，mm。

3）桩间的土压力计算

根据简化模型，前排桩主要受到桩间土对桩侧的作用力，考虑采用初始土压力进行计算，后排桩主要受到弹性抗力，采用水平弹簧模拟进行计算。

前排桩桩后土压力为

式中α为比例系数，其计算为

式中：α为计算系数，当计算的α大于１时，取α＝1；P_ak为后排桩外侧计算点处的主动土压力强度，kPa；b为桩间距，m。

后排桩桩内侧土弹簧刚度系数为

式中Z₁为计算点距离等效开挖面的深度。

4）后排桩桩后土压力

按照式(1)~式(7)可以计算出相应的土压力及弹簧的弹性模量值，进而计算桩身水平位移及桩身弯矩值。

5）土压力修正

上述的比例系数分配土压力的计算方法计算的前、后排桩的土压力时，前排桩的土压力分布系数偏小，而实际上当双排桩为前密后疏排列时，主动土压力主要是由前排桩来承担。假设此时前排桩受到的主动土压力由后排桩计算点处的最大土压力与桩间主动土压力组成，即此时前排桩内侧的主动土压力为

后排桩主动土压力不变。

6）后排桩桩内侧土弹簧刚度折减修正

桩间土体本质上是有限空间土体，采用“m”法计算弹簧边界模拟对后排桩的限制作用会造成土抗力过大，与实际不符。因此，对后排桩内侧的土弹簧刚度进行折减，计算出合理的后排桩内侧弹簧刚度折减系数ω。对于桩间土体土质较好的双排桩支护结构，经过资料分析与试算^[18]，可以得出合理的折减系数ω=0.5。

3.   永久边坡双排桩支护工程实例分析

3.1   实例模型计算参数

某地铁停车场项目采用永久双排桩支护作为其边坡支护结构，如图7所示，结构相关参数为桩径1.5 m，前排桩间距1.8 m，后排桩间距3.6 m，连系底板厚度0.6 m，嵌固深度4.0 m，扶壁高1.0 m。场地土性质如表1所示。

图  7  双排桩永久支护结构

下载: 全尺寸图片

3.2   模型计算

由于规范建议桩间距在2~5倍桩径，在如今工程的开挖深度都较深时（即 $H > L \times \cot \left( {45^\circ - \varphi /2} \right)$ ），通常滑动面都在前后排桩之间，即简化模型如图5所示。此地铁停车场项目边坡双排桩永久支护结构也为开挖深度较深、滑动面位于前后排桩之间的情形，因此，本次简化计算模型参照图5所示情况设计，图8为本项目边坡双排桩结构简化计算模型。

图  8  工程实例双排桩简化计算模型

下载: 全尺寸图片

根据式(1)~式(8)和图8所示简化计算模型，计算出相应的土压力及弹簧的弹性模量值，进而得出简化模型计算结果。

有限元模拟使用MIDAS GTS NX大型有限元分析软件建立双排桩三维空间模型，模拟采用地层−结构计算方法来考虑桩土之间的互相作用。

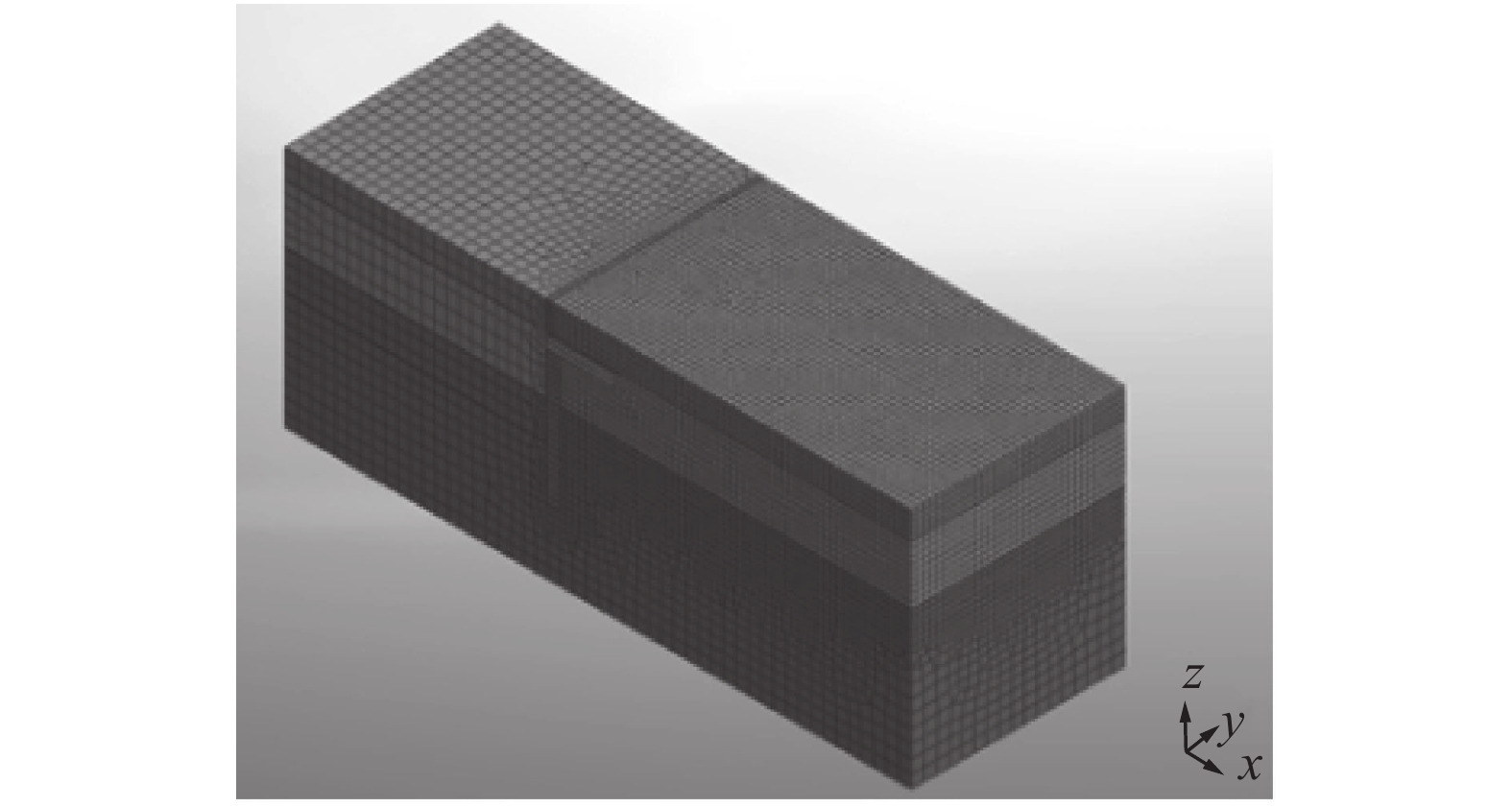
有限元模拟中，将土体设置为莫尔−库伦本构模型，支护桩和顶板设置为各向同性的线弹性本构模型，并且在桩−土之间设置了接触界面。数值模拟的模型尺寸为60 m×20.5 m×23 m，前、后排桩的嵌固深度相同，桩长皆为12.2 m。建立的有限元模型如图9和图10所示。

图  9  三维有限元模型

下载: 全尺寸图片

图  10  双排桩有限元网格划分图

下载: 全尺寸图片

前排桩选取中间第5榀桩，后排桩选取中间第3榀桩，计算双排桩位移与内力情况，并作出水平位移、桩身弯矩图。

3.3   模型计算结果对比分析

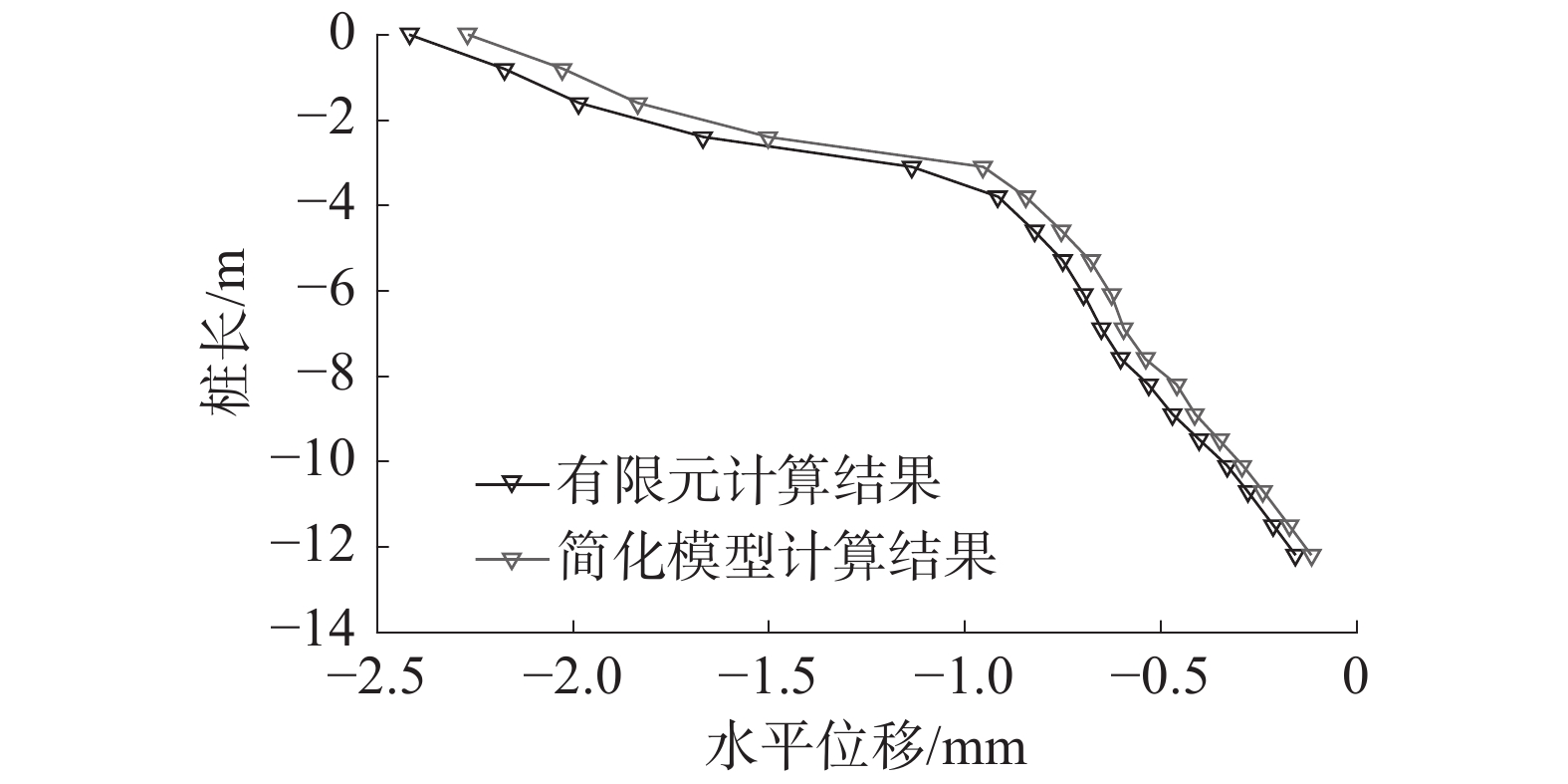
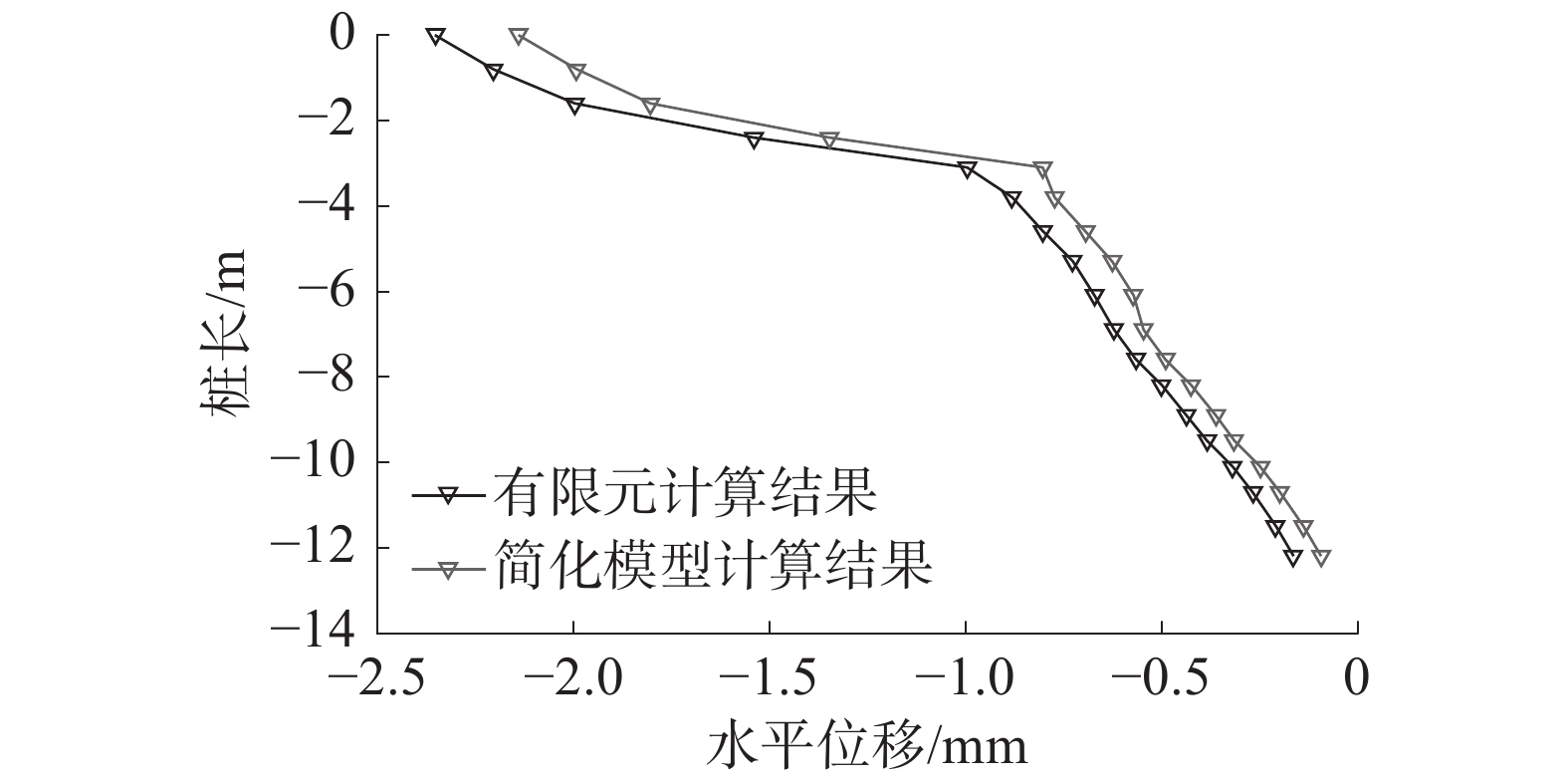
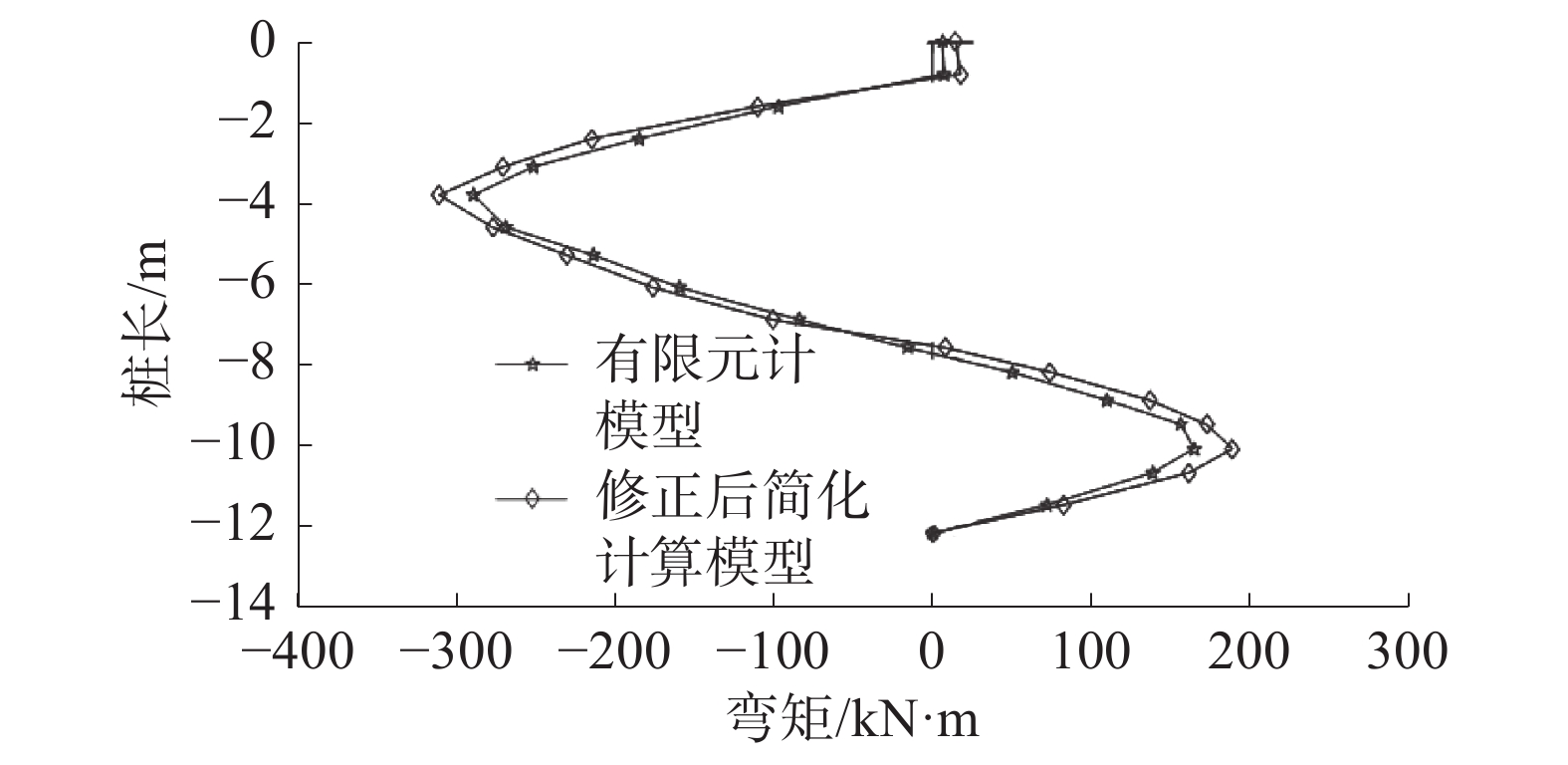
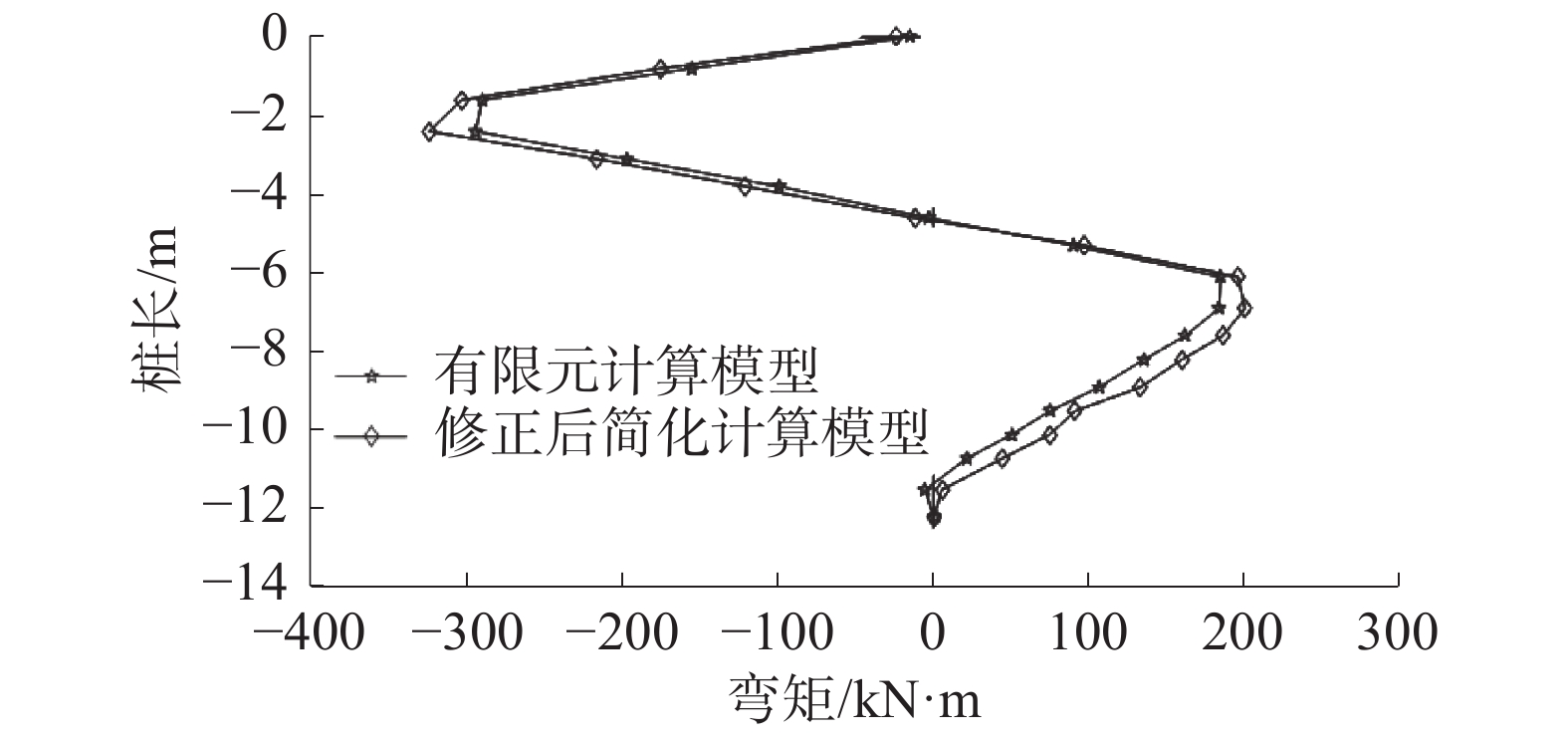
通过简化模型和数值模拟计算，得出双排桩结构的位移及内力变化情况，并作出桩身水平位移与桩身弯矩对比图，将简化计算模型计算结果与有限元三维模型计算结果进行对比，如图11~14所示。

图  11  前排桩水平位移变化对比

下载: 全尺寸图片

图  12  后排桩水平位移变化对比

下载: 全尺寸图片

图  13  按修正公式计算的前排桩桩身弯矩分布对比

下载: 全尺寸图片

图  14  按修正公式计算的后排桩桩身弯矩分布对比

下载: 全尺寸图片

简化模型计算与有限元计算结果都符合桩顶水平位移最大；随深度增加，水平位移减少的特征。两者随桩身深度变化的水平位移曲线走势基本吻合，曲线变化趋势皆呈现先快后慢的特点，且前、后排桩的水平位移大偏差都出现在桩顶和桩身深度约为4 m时。

简化模型计算与有限元计算结果得出的桩身弯矩曲线走势基本相同，呈S型；两曲线弯矩的正负转折深度点处于同一位置，出现峰值的桩体深度一致，前桩位于深度约为4 m处，后桩位于深度约为2 m处；简化模型的桩身弯矩计算结果较有限元模拟大，符合永久支护结构偏安全的设计要求，在弯矩峰值处，简化模型计算结果较有限元模拟结果约大20%。

简化计算方法所得水平位移及弯矩与有限元所得结果相差较小，位移与弯矩的曲线差值在10%~20%，二者计算结果变化规律一致，通过有限元模拟验证了简化模型计算的正确性。

3.4   模型计算结果与实际监测数据对比分析

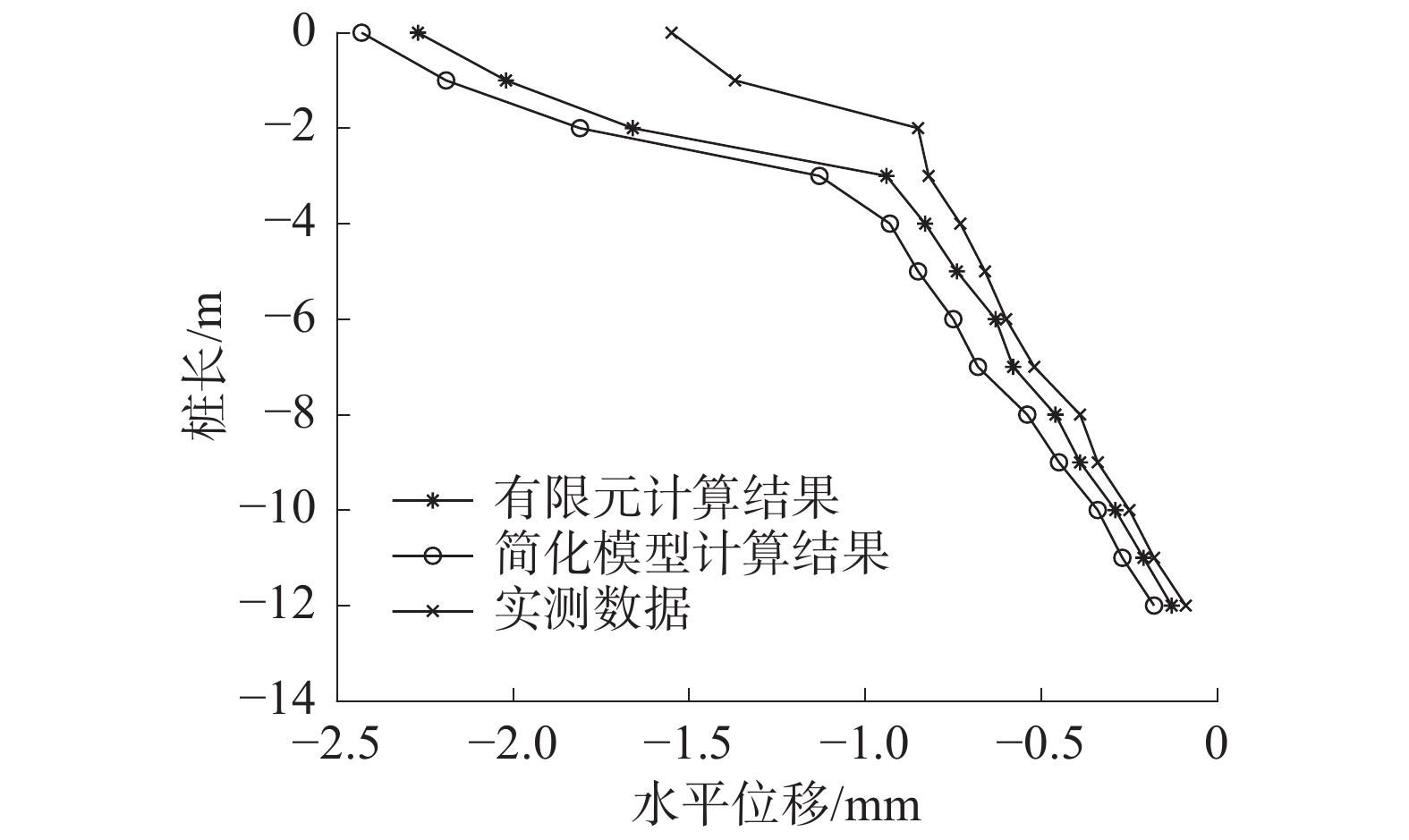
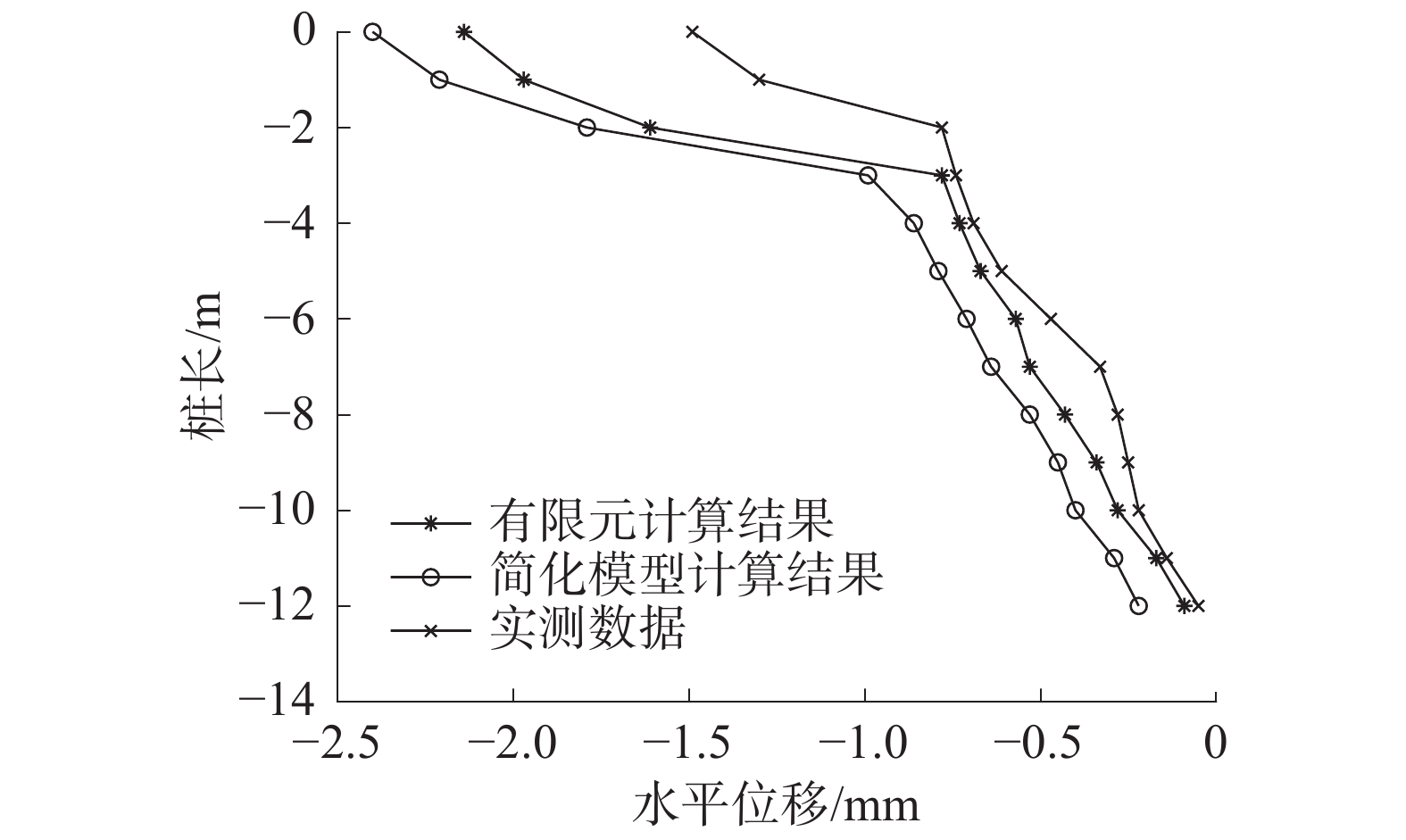
选取某一天的双排桩水平位移值的现场监测数据与模型的计算结果比较分析，如图15和图16所示。

图  15  前排桩水平位移变化计算结果与实测对比

下载: 全尺寸图片

图  16  后排桩水平位移变化计算结果与实测对比

下载: 全尺寸图片

由图15和图16可以看出，监测数据得到的桩身水平位移曲线与两模型计算得到的位移曲线变化趋势相吻合，进一步验证了简化模型和有限元模拟结果的正确性。简化计算模型的计算结果较监测数据更大，满足了永久边坡支护结构安全等级较高的要求，在实际永久双排桩支护工程应用的计算中能得到更为安全的结果，方便推广使用。

4.   结论

本文提出了一种适用于永久边坡支护结构、不考虑前后排桩之间的相互作用的双排桩简化计算方法，通过简化计算与有限元模拟和实测数据的对比，验证了简化计算模型的正确性，得到的结论如下：

1）当前的双排桩支护结构研究大部分是针对基坑双排桩支护来展开的，本文对永久边坡双排桩支护结构的计算进行了研究和分析。

2）基于极限平衡法，提出了一种对桩间土采取简化处理的平面刚架计算模型和对应的结构变形与内力分析的计算方法。

3）双排桩简化计算模型与有限元模拟两者的计算结果得出的水平位移变化曲线与桩身弯矩分布曲线的走势基本吻合。两者结果中弯矩出现峰值处与正负转折处的桩身深度一致，前桩位于深度约为4 m处，后桩位于深度约为2 m处。有限元模拟结果较简化模型计算结果偏差约为10%~20%，所得结果相差较小，二者计算结果变化规律一致，且实测曲线走势与模型计算结果相同。

4）采用前排桩桩前土体用土弹簧模拟、后排桩桩后土体采用朗肯土压力计算、桩间土不考虑荷载传递作用、前排桩桩后受到朗肯土压力作用、后排桩桩前用土弹簧模拟的简化计算方法是适合于永久边坡支护结构，并且可靠和安全的。