长期以来,桨舵干扰都是船舶与海洋工程领域的研究热点之一。螺旋桨决定了船舶的快速性,舵决定了船舶的操纵性,二者之间的水动力干扰对船舶的航行性能具有重要的影响。随着数值技术的高速发展,桨舵干扰作为一个经典课题在新形势下被赋予了更多的研究价值,主要体现在几个方面。1) 不论军用还是民用方面,现代舰船对快速性和操纵性有着更高需求,现代舰船的航速越来越高,螺旋桨和舵的流体分离现象非常严重,有必要进行机理性研究;2) 船桨舵一体化设计是针对传统设计方式的重要改进,针对桨舵干扰的机理分析可以大大促进该领域的研究进展;3) 很多现代节能增效装置,如扭曲舵、舵附推力鳍和反应舵等,十分依赖于桨舵干扰水动力特性的分析和精确预报;4) 计算机和先进数值方法飞速发展,尤其是基于黏性流体的CFD技术在船舶水动力的应用中日趋成熟,验证这些先进技术在桨舵干扰的应用是十分必要的。
早期的研究基本上是以势流理论为基础进行的。1961年日本的高木有男、1965年伊赛采用线性化的升力线理论对桨舵的干扰模型进行了计算,并给出了定性分析。1968年萨利纳斯等[1]采用基于加速度势法的线性升力面理论首次预报了忽略桨舵厚度的桨舵相互干扰非定常水动力性能。1972年萨利纳斯等[2]通过引入压力源的概念来模拟桨叶和舵的厚度效应,做出了一些改进。来自日本的中午名义教授发展了自己的预报螺旋桨和舵相互之间干扰情况的方式。其在预报桨舵相互干扰的水动力性能方法之中是一大发展和创新。后来又有森山文雄基于厚翼理论,即面元法,处理舵的厚度,把奇点分布在舵的表面上,在舵的表面上满足了边界条件。董世汤和朱自理[3]两位教授进行的螺旋桨与舵的相互干扰的非定常工况下的数值模拟计算分析是建立在时域之内协调分析理论基础之上的。武汉交通科技大学的王德恂[4]教授也进行了桨舵干扰系统的模型试验,王德恂教授后又将该方法推广到了桨舵系统的非定常水动力数值模拟计算之中。张建华,王国强等[5]进行对桨舵干扰问题的研究时加入了对于时域的考虑,另外,利用了非定常涡格理论建立了螺旋桨的数值模型,利用非定常的面元方法完成了舵的模型的建立。覃新川[6]博士考虑桨舵之间的相互干扰的方式采用的是迭代计算的方式,基于已有的实验数据进行了单桨双舵的数值模拟计算与分析,得出与德国某内河船研究所所进行实验误差极小的结果。
采用势流理论进行桨舵干扰的研究,其优点在于网格节点少、节省计算资源、容易编程实现。但是其缺点也十分明显。势流理论的一个核心假设是流体的贴体运动,这就决定了其只能针对中等载荷的设计工况得到比较好的结果。在非设计工况、轻载或重载情况,结果误差较大。另外一个问题在于,势流理论忽略了流体黏性。忽略流体黏性的一个重要前提是雷诺数要超过临界值,这对螺旋桨来说是合适的,因为螺旋桨转速很快,雷诺数很大。而舵是静止的,即使处于螺旋桨形成的尾流场中,其相对来流的雷诺数也很难达到可以忽略流体黏性的程度。基于上述原因,本文基于计算流体力学方法[7-10],进行对桨舵干扰流场的数值模拟,并通过试验验证了本文计算结果的准确性,进而研究螺旋桨尾流场对舵的影响,分析了舵对螺旋桨性征曲线、桨后压力分布和涡量分布的影响。
1 理论基础 1.1 控制方程湍流模型流体力学的基本控制方程有3组。因计算中假定流体为不可压缩,所以不涉及到能量守恒,下面介绍质量守恒方程和动量守恒方程。
1.1.1 质量守恒方程质量永远不会凭空产生或消失,质量守恒定律也称作连续性方程,在直角坐标系下表示为
| $\frac{\partial \rho }{\partial t}+\frac{\partial \left( \rho u \right)}{\partial x}+\frac{\partial \rho v}{\partial y}+\frac{\partial \left( \rho w \right)}{\partial z}=0$ | (1) |
写成张量形式为
| $\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial {{x}_{j}}}(\rho {{u}_{j}})=0$ | (2) |
对流体控制体的受力和运动进行分析,可以得到微分形式的动量守恒定律:
| $\left\{ \begin{align} &\frac{\partial \left( \rho u \right)}{\partial t}+\frac{\partial \left( \rho {{u}^{2}} \right)}{\partial x}+\frac{\partial \left( \rho uv \right)}{\partial y}+\frac{\partial \left( \rho uw \right)}{\partial z}= \\ &\quad \rho X+\frac{\partial {{\sigma }_{xx}}}{\partial x}+\frac{\partial {{\tau }_{yx}}}{\partial y}+\frac{\partial {{\tau }_{zx}}}{\partial z} \\ &\frac{\partial \left( \rho v \right)}{\partial t}+\frac{\partial \left( \rho vu \right)}{\partial x}+\frac{\partial \left( \rho {{v}^{2}} \right)}{\partial y}+\frac{\partial \left( \rho vw \right)}{\partial z}= \\ &\quad \rho Y+\frac{\partial {{\tau }_{xy}}}{\partial x}+\frac{\partial {{\sigma }_{yy}}}{\partial y}+\frac{\partial {{\tau }_{zy}}}{\partial z} \\ &\frac{\partial \left( \rho w \right)}{\partial t}+\frac{\partial \left( \rho wu \right)}{\partial x}+\frac{\partial \left( \rho wv \right)}{\partial y}+\frac{\partial \left( \rho {{w}^{2}} \right)}{\partial z}= \\ &\quad \rho Z+\frac{\partial {{\tau }_{xz}}}{\partial x}+\frac{\partial {{\tau }_{yz}}}{\partial y}+\frac{\partial {{\sigma }_{zz}}}{\partial z} \\ \end{align} \right.$ | (3) |
对于不可压缩流体,还可以得到N-S方程。写成张量形式为
| $\frac{\partial {{u}_{i}}}{\partial t}+\frac{\partial }{\partial {{x}_{j}}}\left( {{u}_{i}}{{u}_{j}} \right)={{f}_{i}}-\frac{1}{\rho }\frac{\partial p}{\partial {{x}_{i}}}+\frac{{{\partial }^{2}}{{u}_{i}}}{\partial {{x}_{j}}\partial {{x}_{i}}}$ | (4) |
这就是不可压缩流体的控制方程。
1.2 湍流模型本文所采用的RNG(renormalization group)k-ε模型是由Yakhot和Orzag提出的,RNGk-ε湍流模型和标准k-ε湍流模型有相似的形式:
| $\left\{ \begin{align} &\frac{\partial }{\partial t}\left( \rho k \right)+\frac{\partial }{\partial {{x}_{i}}}\left( \rho k{{u}_{i}} \right)=\frac{\partial }{\partial {{x}_{j}}}\left[ {{\alpha }_{k}}{{\mu }_{\text{eff}}}\frac{\partial k}{\partial {{x}_{j}}} \right]+{{G}_{k}}+\rho \varepsilon \\ &\frac{\partial }{\partial t}\left( \rho \varepsilon \right)+\frac{\partial }{\partial {{x}_{i}}}(\rho \varepsilon {{u}_{i}})= \\ &\quad \quad \frac{\partial }{\partial {{x}_{j}}}\left[ {{\alpha }_{\varepsilon }}{{\mu }_{\text{eff}}}\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right]+C_{1\varepsilon }^{*}\frac{\varepsilon }{k}{{G}_{k}}-{{C}_{2\varepsilon }}\rho \frac{{{\varepsilon }^{2}}}{k} \\ \end{align} \right.$ | (5) |
式中
| ${{\mu }_{\text{eff}}}=\mu +{{\mu }_{t}}$ | (6) |
湍流黏性为
| ${{\mu }_{t}}=\rho {{C}_{\mu }}\frac{{{k}^{2}}}{\varepsilon }$ | (7) |
相比标准k-ε模型,这种模型考虑了平均流动中存在的切向速度;它的产生项不仅取决于流动情况,在同一问题中它还是空间坐标的函数。所以RNG模型不但对充分发展的湍流保持有效性,还可以更好地处理高应变率及流线弯曲程度较大的流动[11]。
2 数值模型建立 2.1 计算模型及网格本文所用桨舵模型如表 1、2所示。螺旋桨为B4-55型螺旋桨,舵为NACA翼型剖面舵,舵位于螺旋桨正后方,展长沿y轴,桨舵间距取0.516倍螺旋桨直径。
|
|
表 1 螺旋桨主要几何参数 |
|
|
表 2 舵主要几何参数 |
如图 1所示,根据螺旋桨绕轴转动的特点,大域被建立成一个圆柱体,其内包含螺旋桨、舵及附近流体。建立如下坐标系:以螺旋桨桨轴中心点为坐标原点,x轴正向为入射水流方向,且与桨轴中心线重合;y轴取为桨叶参考线方向,且与舵的展长方向一致;z轴方向由右手定则确定。一般来讲,黏性流体的数值计算要求在物体附近布置更多网格,距离物体远的位置网格可以适当变疏。为此,本文在大域内建立了2个小域,分别为包含螺旋桨的旋转小域和包含舵的静止小域。在2个小域内布置更多的网格,而其他计算域内布置较少的网格。
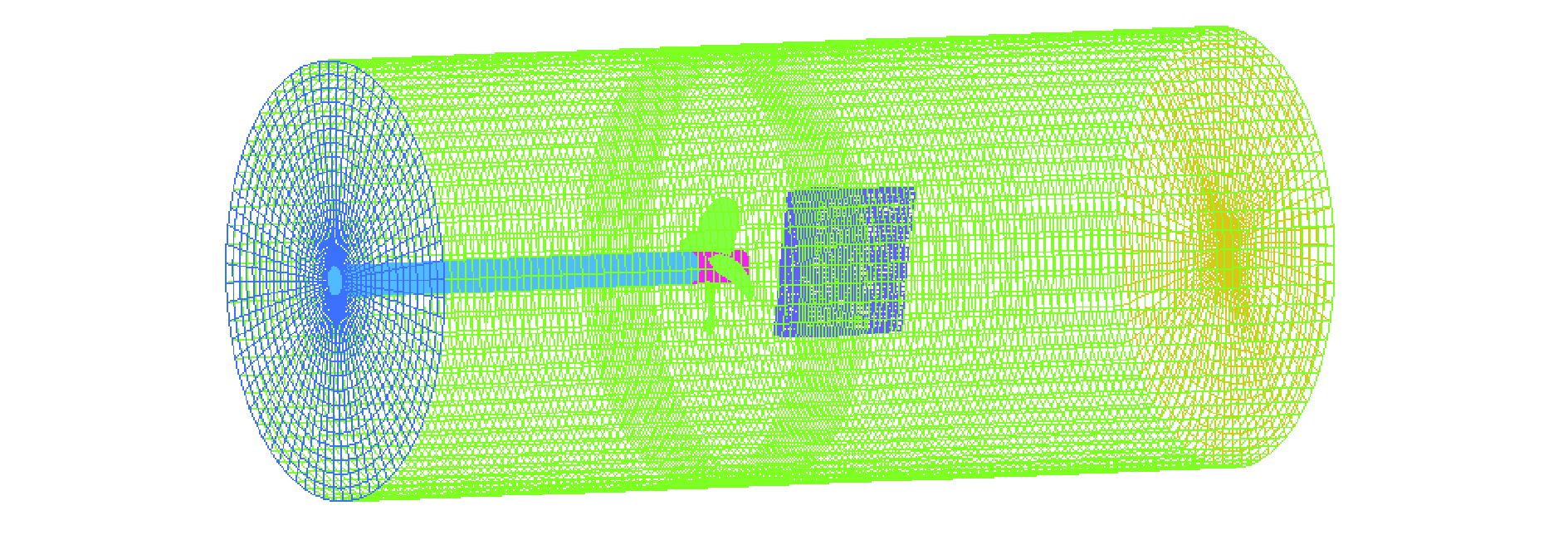
|
图 1 整体计算域和网格示意图 |
本文优化网格质量所采取的另一个方法是采用全结构化网格技术。和非结构化网格技术相比,结构化网格的质量一般较高,在达到同等计算精度的条件下,能够大大节约网格数量,从而缩短了计算时间,螺旋桨网格见图 2(a),舵网格见图 2(b)。
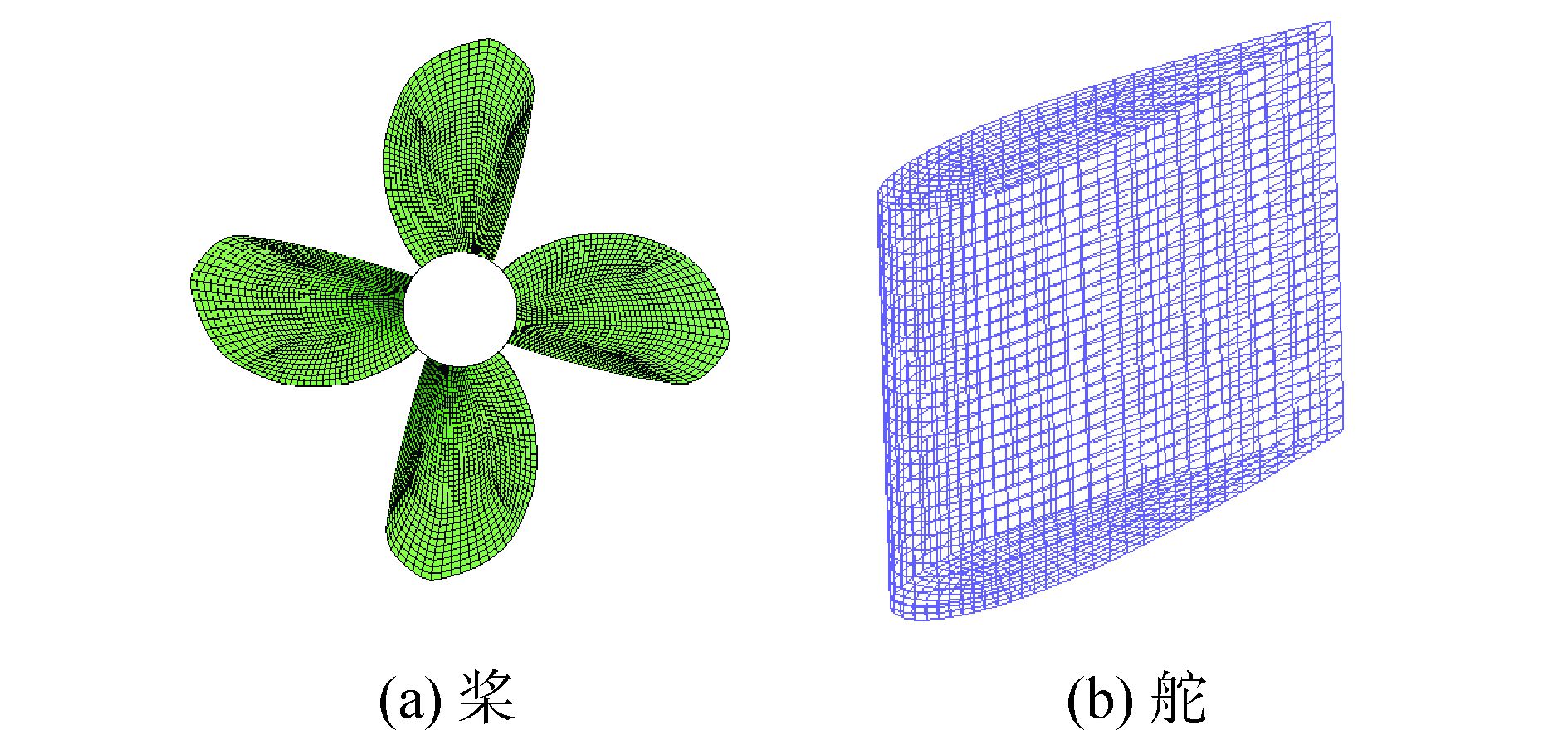
|
图 2 螺旋桨网格、舵表面网格 |
大域与小域的交界面处对网格做适当加密,大域的网格如图 3所示。对于结构化网格,分割的六面体的形状越接近于正方体,其奇异性越好,网格质量也就越好。从图 3可以看出,本文的网格划分方法很好地控制了网格的质量,整体网格十分规则,网格的节点夹角也不存在大锐角。

|
图 3 纵切面网格 |
大域入口处设置为速度入口,出口处设置为自由出口,其余设置为静壁。大域整体不发生运动,螺旋桨小域以一定的转速转动,即桨叶和桨轴发生转动,舵设置为静止不动。叶面、叶背、舵面以及桨轴等真实存在的面均设置为壁面,其他大域和小域连接处的界面设置为交界面,即水流可以自由通过。
求解采用的黏性模型为k-omega SST模型;材料选择water-liquid h2o < l > 液体;界面处的设置如上所述,其中速度入口的湍流强度设置为2%,湍流长度尺寸为1 m;对于压力与速度的耦合,采用压力修正的SIMPLIC算法;N-S方程的离散采用一阶迎风格式;亚松弛因子项保持默认;从大域的入口开始进行标准初始化;非定常计算的时间步长设置为0.002 s。
3 数值结果验证 3.1 系数定义根据进速系数的不同,流速设置为1.14 m/s,改变螺旋桨转速,分别令n=300、375、450、525、600、750来改变进速系数。进速系数J,推力系数Kt和转矩系数Kq分别定义为速度,推力和转矩的无量纲形式:
进速系数:
| $J=\frac{V}{nD}$ | (8) |
推力系数:
| ${{K}_{t}}=\frac{T}{\rho {{n}^{2}}{{D}^{4}}}$ | (9) |
转矩系数:
| ${{K}_{q}}=\frac{Q}{\rho {{n}^{2}}{{D}^{5}}}$ | (10) |
螺旋桨总效率:
| ${\eta _0} = \frac{{{K_t}}}{{{K_q}}} \cdot \frac{J}{{2{\rm{ \mathsf{ π} }}}}$ | (11) |
图 4比较了桨-舵系统螺旋桨推力系数和转矩系数的计算结果和实验结果。其中实验值取自王德恂于1987年发表的《桨舵干扰的实验研究》[12]。
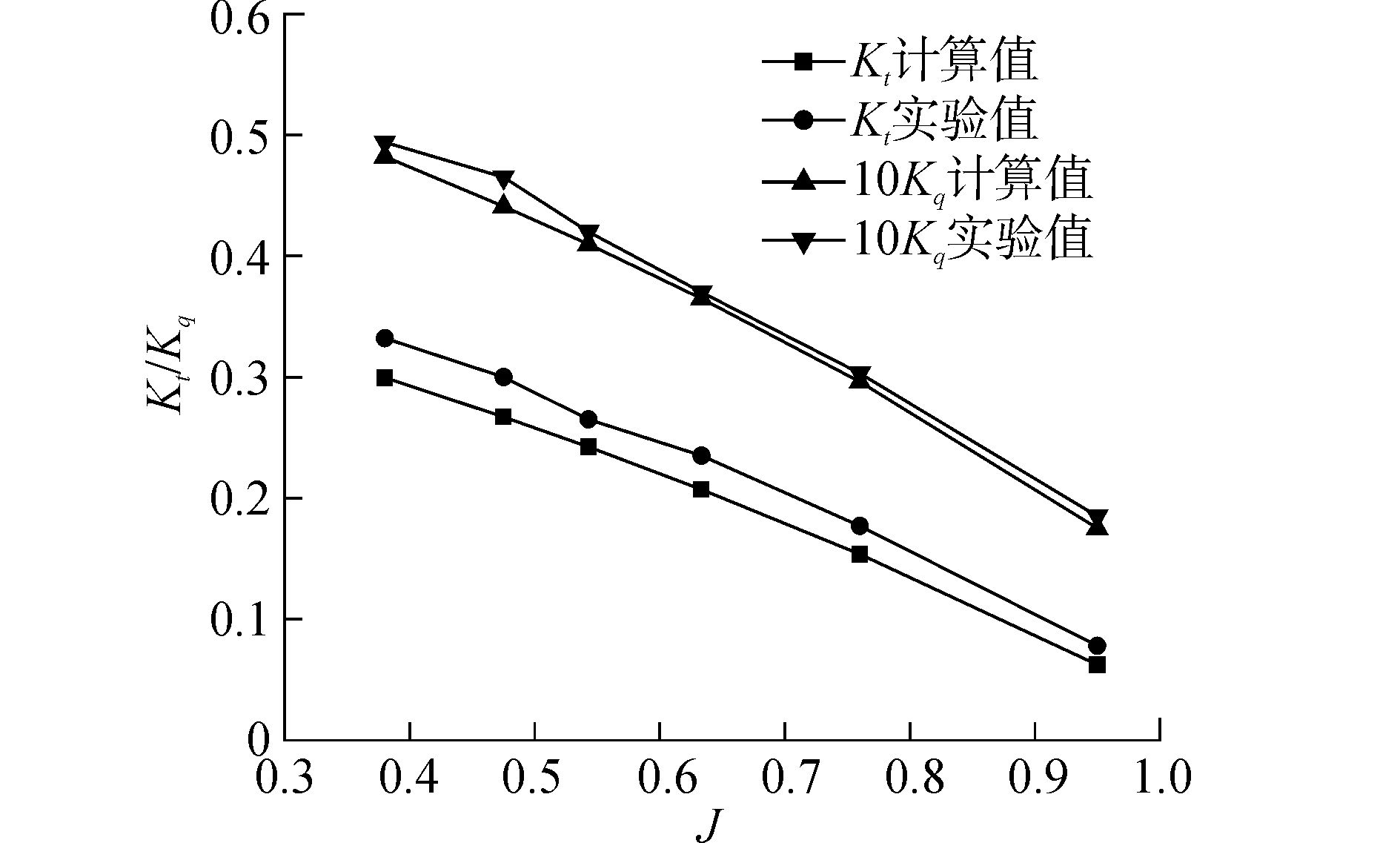
|
图 4 干扰系统的螺旋桨推力、转矩系数曲线 |
王德恂所做循环水槽实验中的模型尺寸如下:螺旋桨为B4-55型,直径为0.24 m,舵剖面形式为NACA0020翼型,展弦比1.0。本文取桨舵间距为0.516D、舵角为0时的实验数据。从中看出,本文计算的推力系数和转矩系数均比实验值略小,但是误差较小。考虑到该问题的复杂性,本文的计算结果是十分准确的。
图 5给出了加装舵前后螺旋桨性能的变化。可以看出舵的存在使得螺旋桨的推力系数和转矩系数均有一定程度的升高,并且这种升高有随着进速系数的增大而逐渐增大的趋势。舵的存在提高了螺旋桨的效率,并且随着进速系数的增大,这种提升越加明显。其根本原因在于舵的存在抑制了螺旋桨为流场的旋转,减小了能量损失。
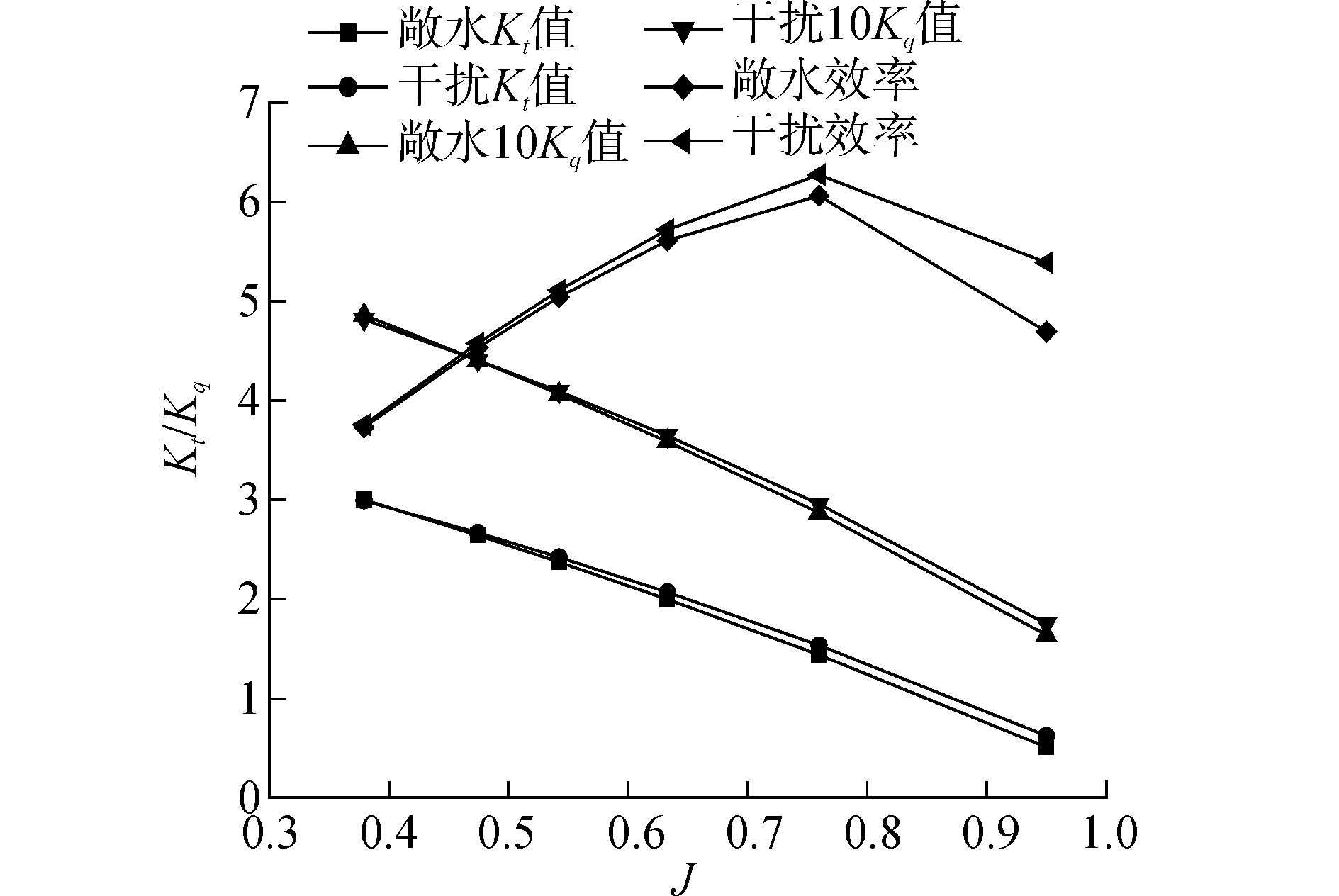
|
图 5 加装桨后舵前后螺旋桨的性征曲线 |
本章以螺旋桨转速n=375 r/min,J=0.76为例比较敞水螺旋桨与桨-舵系统的流场差别,从流场的压力以及速度云图分析舵对螺旋桨性能的影响。
4.1 螺旋桨压力分布螺旋桨叶面及叶背的压力分布如图 6、7。桨叶叶面和叶背的压力差代表了螺旋桨的推力大小,螺旋桨叶面为正压,且高压多分布在导边,叶面推水向后,叶背的压力普遍小于叶面的压力,多为负压,叶背吸水向前。一般来讲螺旋桨叶面压力为正代表其产生推力。从图 6看到的一个特别现象是桨叶内半径位置倒边处出现了负值,证明其在产生阻力。这能够反映传统桨设计理念的一个缺点,那就是过分追求螺旋桨不发生梢空化的临界转速,使桨叶载荷向内半径移动,由此导致的后果是螺旋桨梢空化涡虽然得到了抑制,但是大大增加了毂涡空化的发生概率[13]。
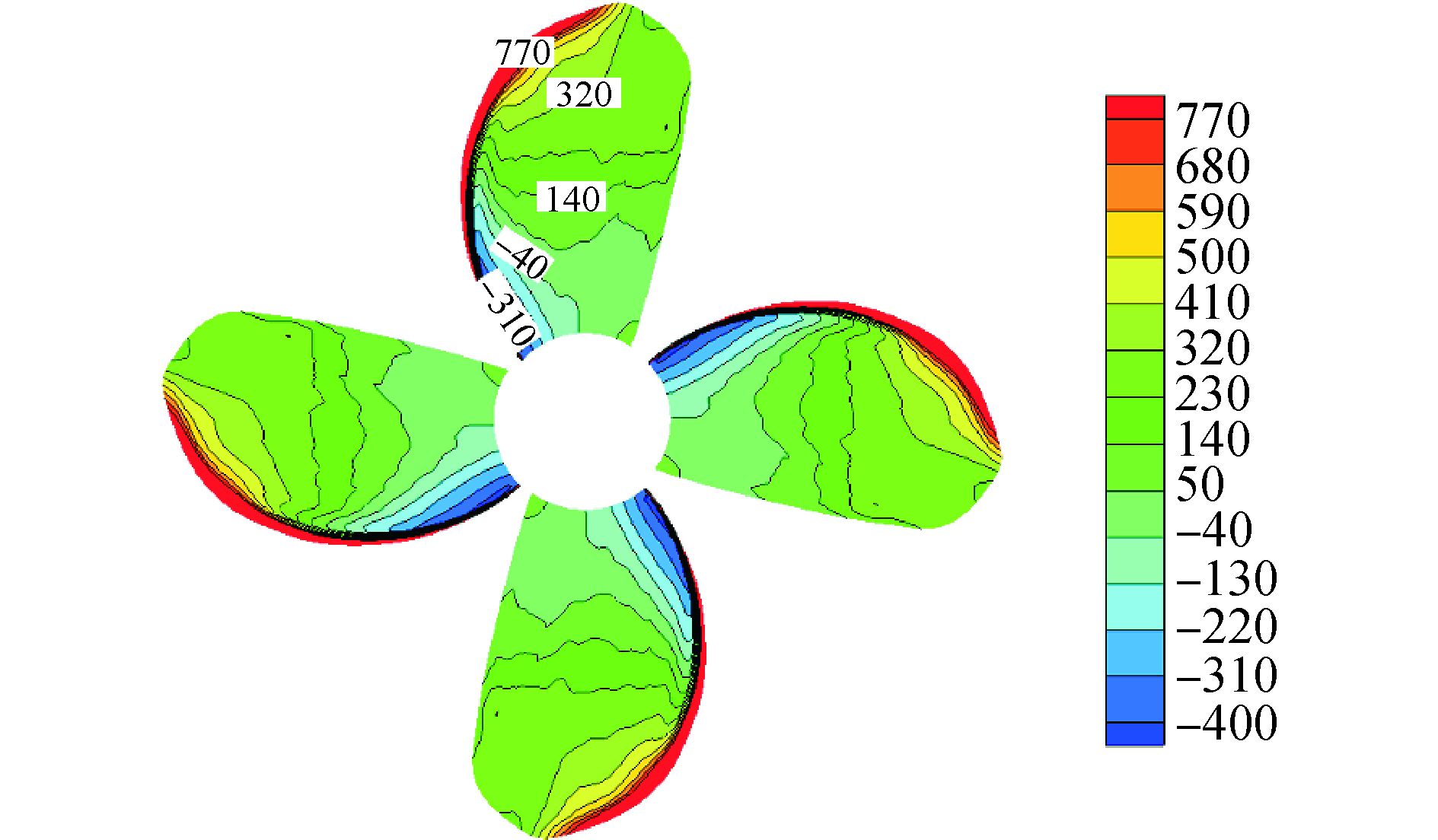
|
图 6 带舵桨桨叶叶面压力分布 |
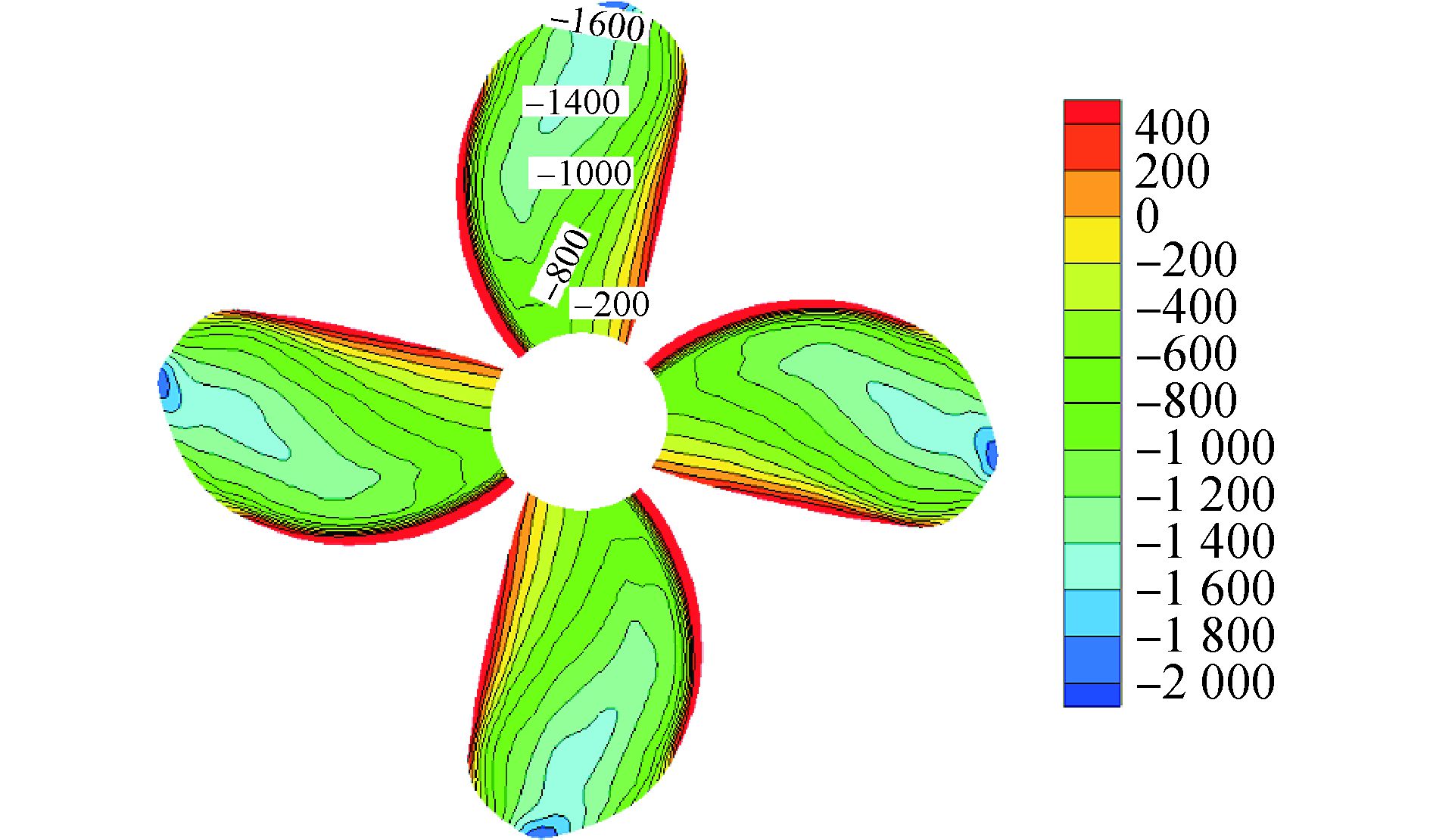
|
图 7 带舵桨桨叶叶背压力分布 |
由于螺旋桨和舵之间的相对运动,螺旋桨的推力和转矩应该随时间周期变化。为了显示这一特征,图 8~11给出了时域中的计算结果。图 8~11中进速系数均为0.475,螺旋桨转速为600 r/min,图中所取为0.5 s,大致为螺旋桨转过五周所用时间。
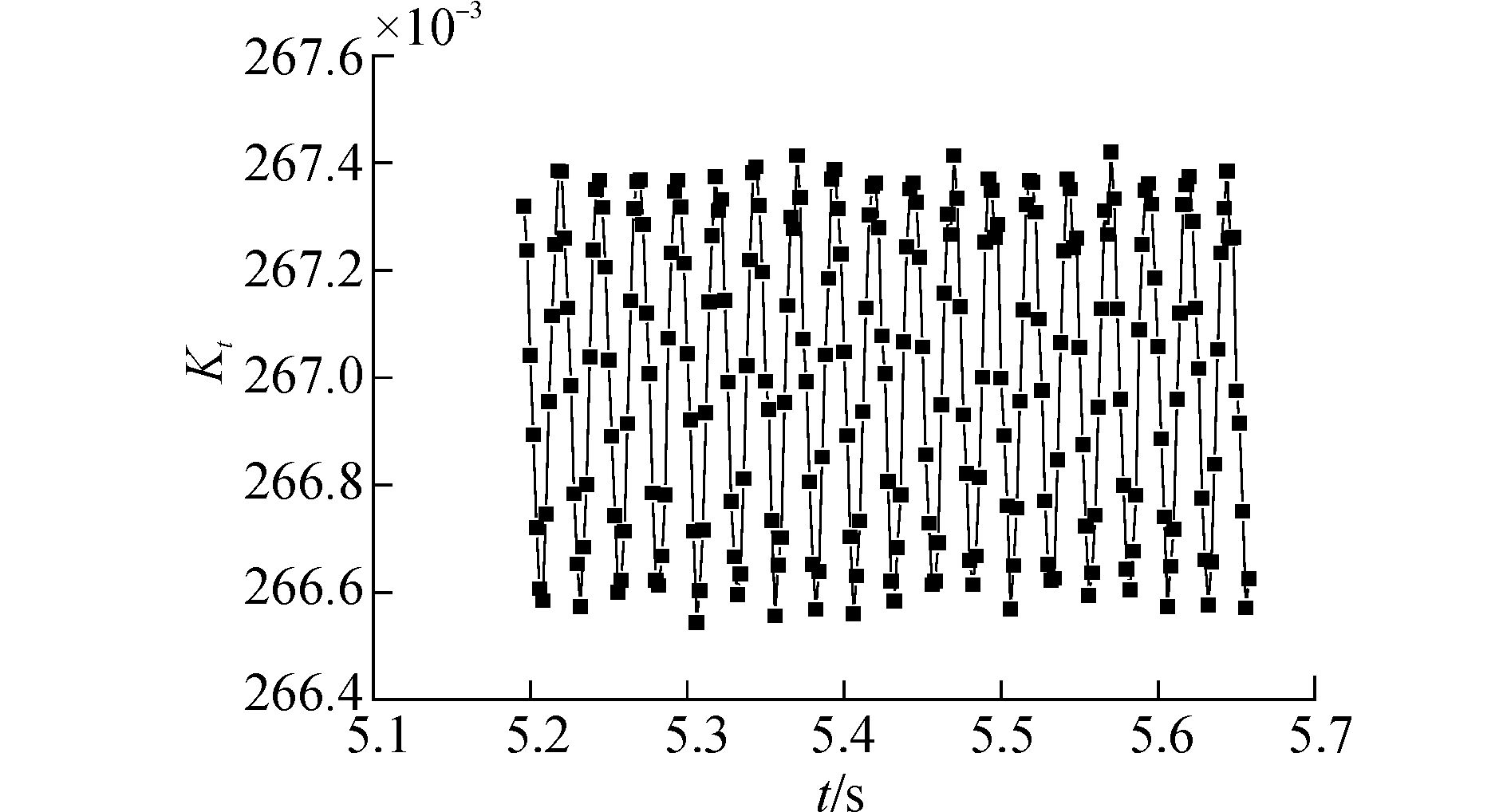
|
图 8 螺旋桨推力系数Kt随时间变化曲线 |
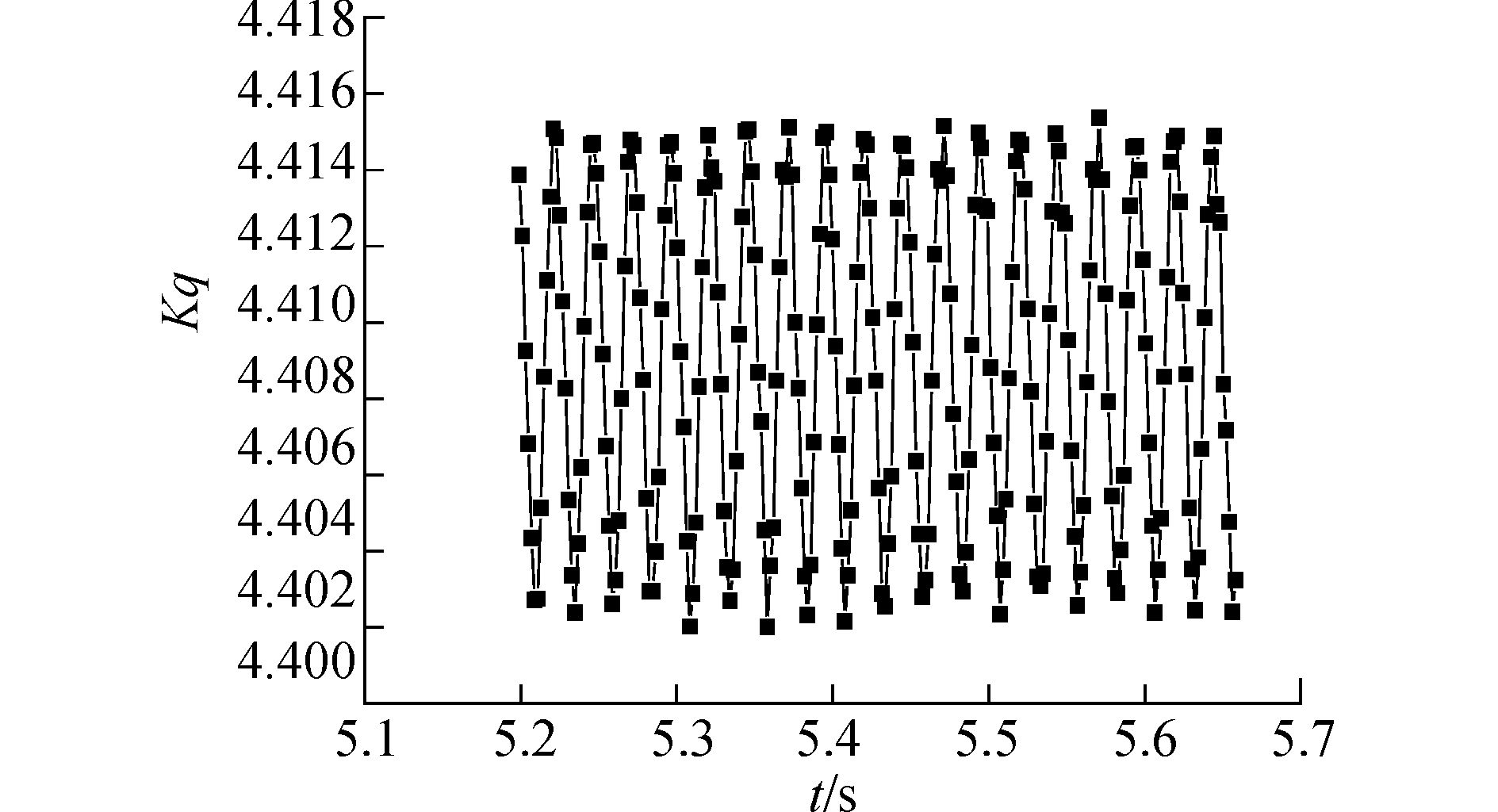
|
图 9 10倍螺旋桨转矩系数Kq随时间变化曲线 |
|
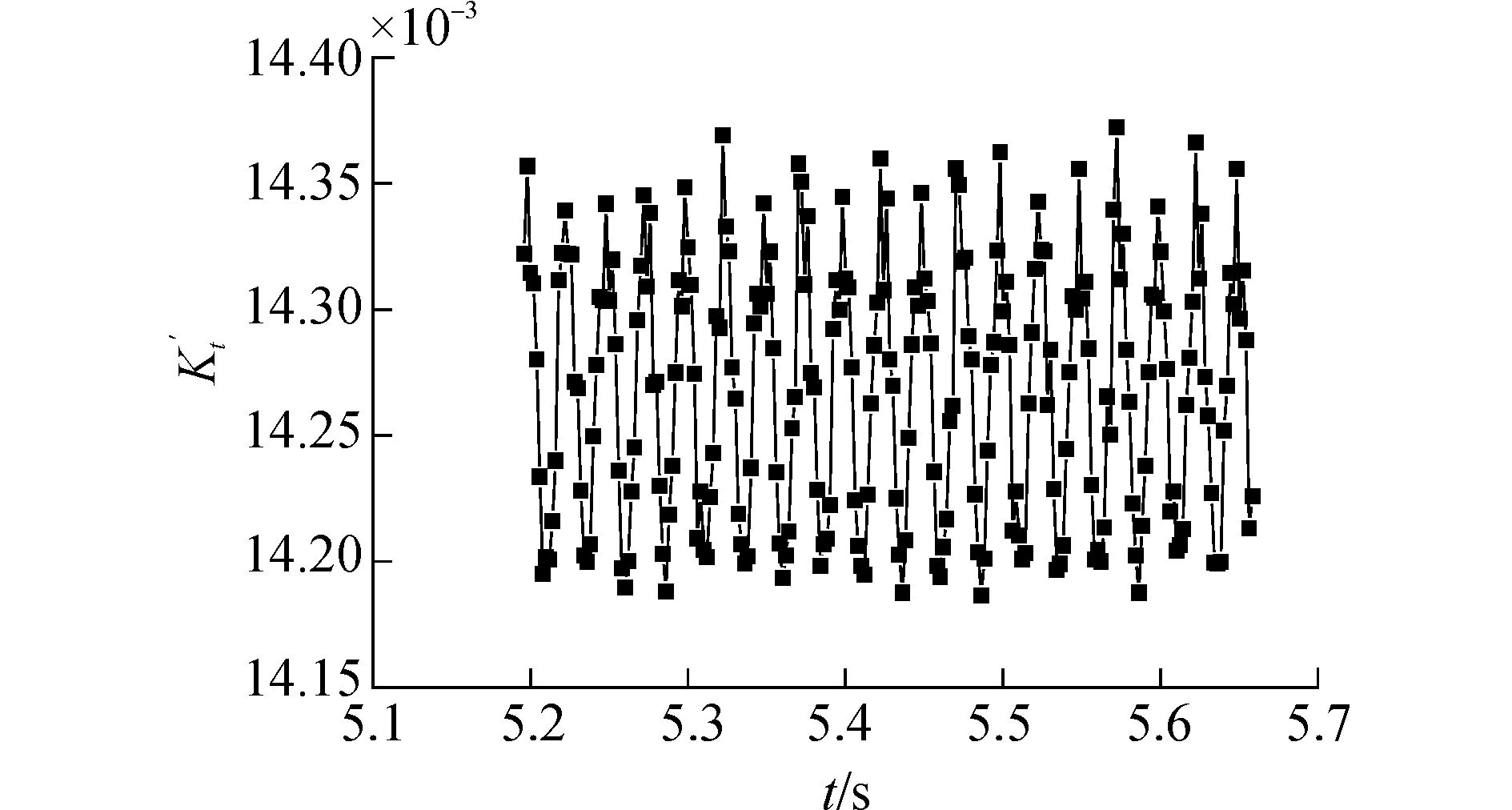
图 10 舵阻力系数Kt′随时间变化曲线 |
|
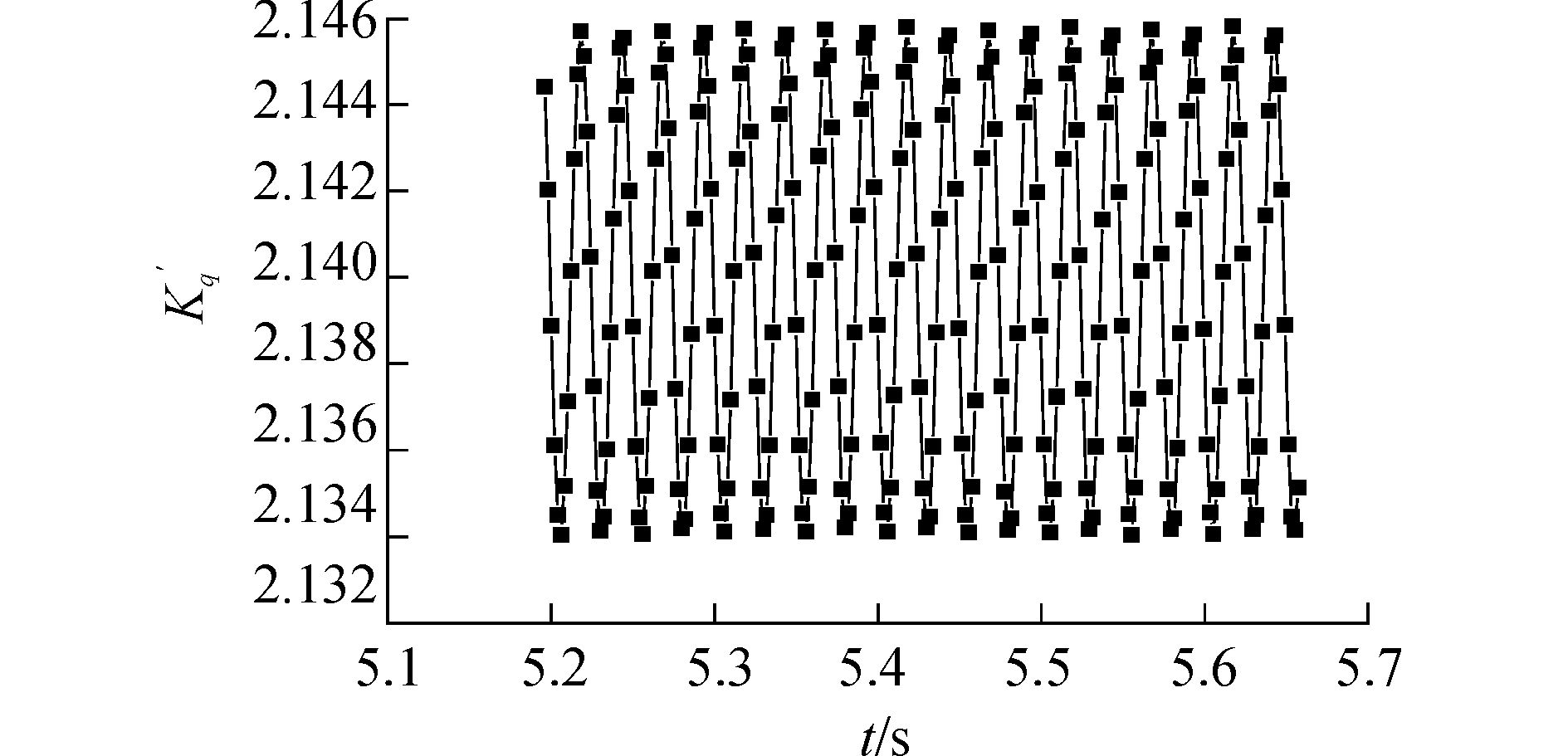
图 11 10倍舵转矩系数Kq′随时间变化曲线 |
从图 8、9可以看出,螺旋桨的推力和转矩是周期性变化的。在360°范围内的周期数等于螺旋桨叶数的2倍。推力的脉动值为0.14,和时均结果的比值为0.16%。从图 10、11可以看出,舵的推力转矩的变化和螺旋桨的推力、转矩变化类似,也具有一定的周期性[14]。不同的是,舵受力的脉动幅值更大。图 8~11具有的一个共同现象是,不同周期的结果并没有绝对相等,这主要是由本文的黏性引起的,也有可能存在网格的原因,即使如此,能在如此小的范围内得到稳定的周期性是非常困难的,这也说明本文网格策略和计算模型选择的合理性。
4.3 敞水舵和桨后舵的压力比较对比敞水舵和进速系数分别为0.76、0.475时的桨后舵打5°舵角时的舵表面压力分布,见图 12~14。
|
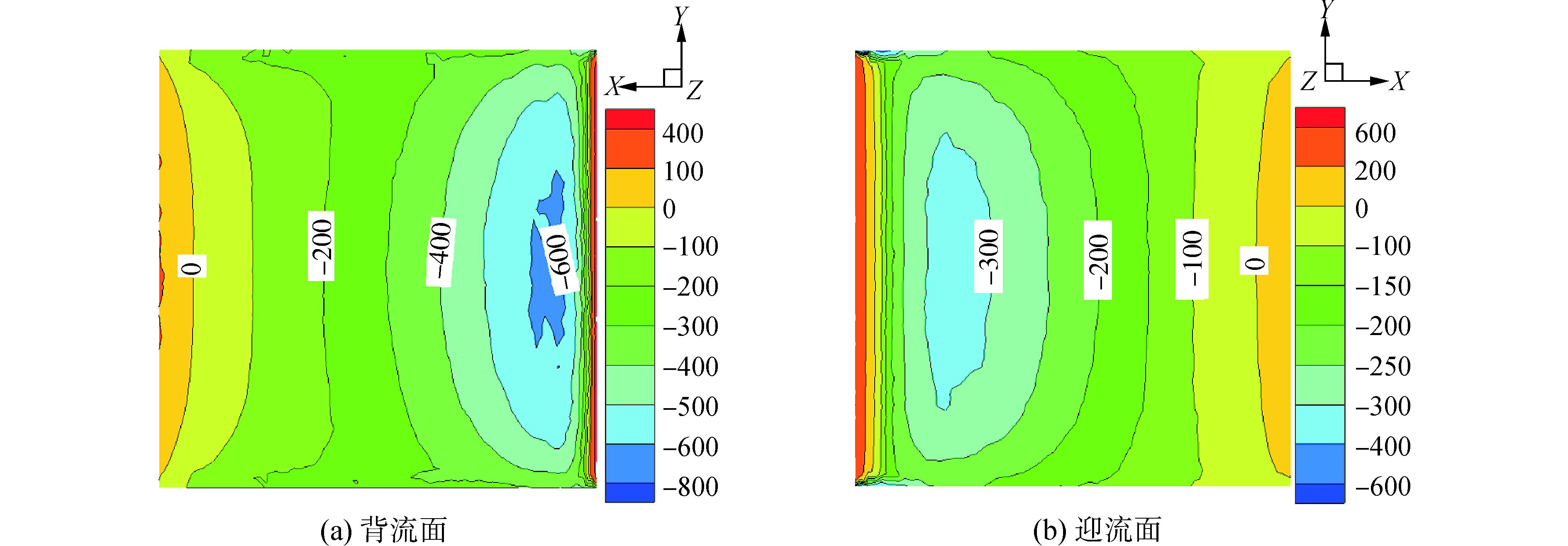
图 12 5°舵角的敞水舵压力分布 |
|
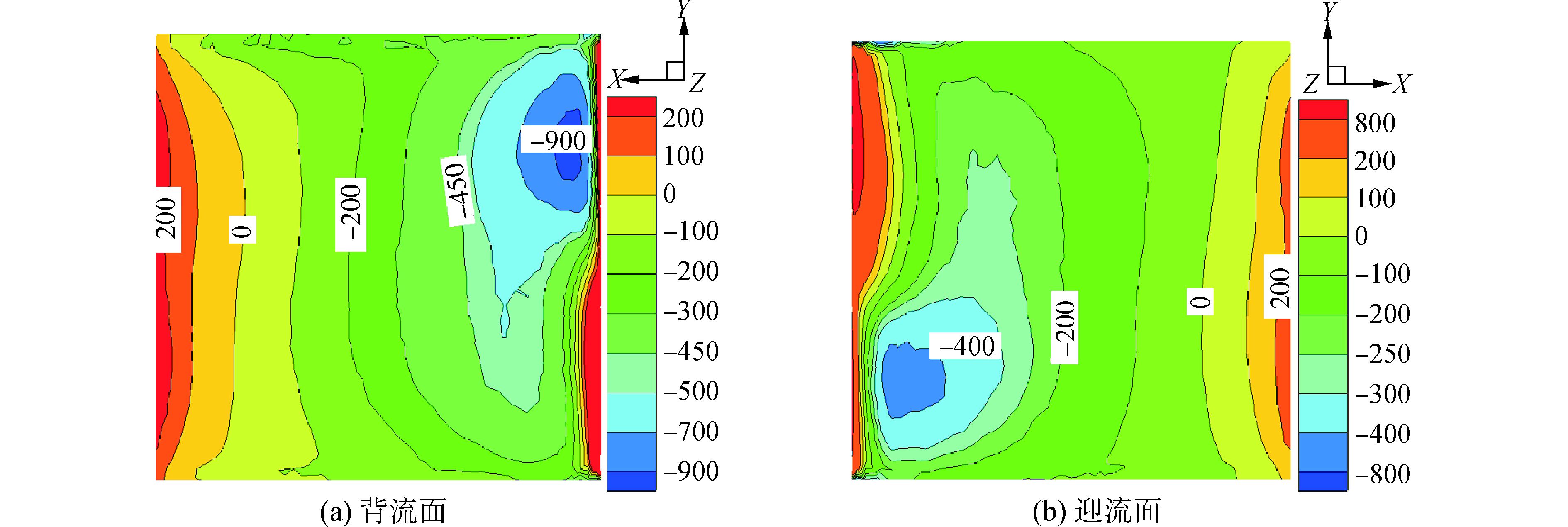
图 13 5°舵角J=0.76干扰系统中舵的压力分布 |
|
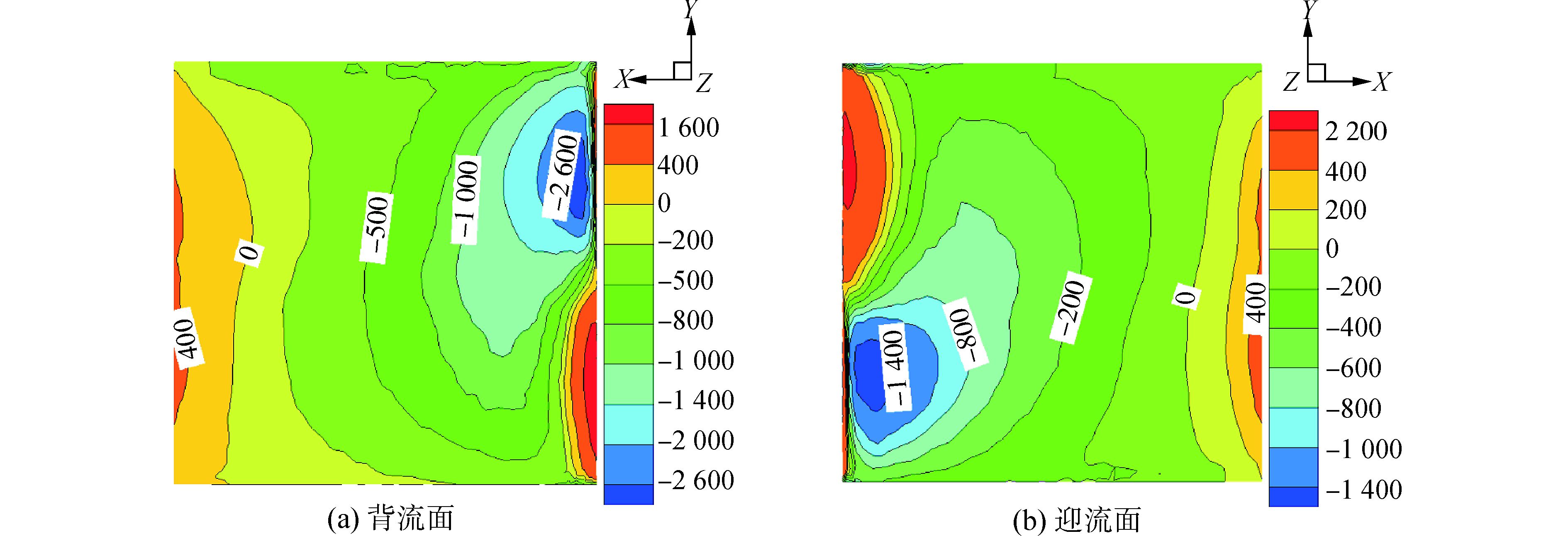
图 14 5°舵角J=0.475干扰系统中舵的压力分布 |
从图 12可以看出,敞水舵的迎流面的压力明显大于背流面的压力,其差值用以产生升力,作用到船舶中心,即为转弯力矩。本文的舵采用NACA0020翼型,这种翼型的厚度比较大,其压力分布的一个明显特征是:在迎流面20%弦长处会产生一个低压区,这和NACA0012等翼型的压力分布是不同的。对于三维敞水舵,压力分布沿展向分布是不均匀的,异端效应十分明显。比较图 12、13,可以看出,由于螺旋桨旋转尾流的作用,舵迎流面前部上半部分和下半部分分别出现了高压区和低压区;而背流面恰恰相反。正因如此,舵在螺旋桨旋转方向上也会受到一个比较大的转矩,这和图 11的结果是一致的。而由于敞水舵背流面和迎流面的压力上下对称,在螺旋桨旋转方向不会产生力矩。比较图 13、14可以看出,随着进速系数从0.76降低到0.475,螺旋桨载荷变大,其流场旋转叶变得更为剧烈,由此导致舵表面受力更不均匀,舵表面高压区压力变得更大,而低压区压力变得更小。由于舵角的存在,这种上下对称分布的高低压并不是完全的对称,正是不对称的高低压的分布使得舵左右侧面存在了压力差,此压力差给予船舶横向的力矩,使得船舶向指定的方向转向,这正是打舵角以改变船舶航向的原理[15]。
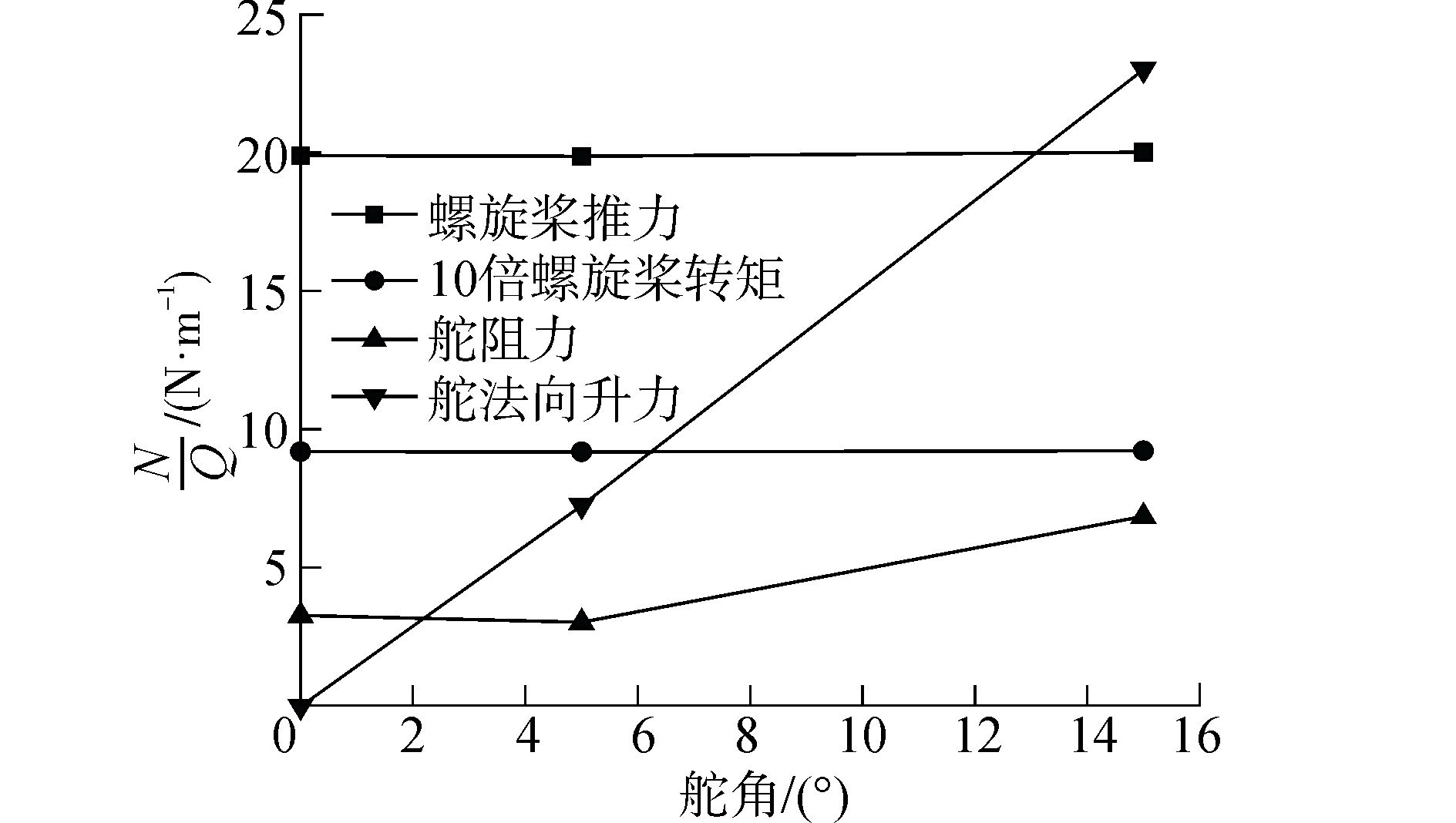
比较在进速系数为0.76时,桨后舵分别打0°、5°、15°舵角时的螺旋桨的推力、螺旋桨转矩、舵阻力、舵升力的变化,见图 15。从中可以看出,舵角增大主要影响了舵的升力和阻力。螺旋桨推力和转矩略有增加,但总体影响较小。舵的升力和阻力随舵角的增大而增大,升力增加尤为明显。
|
图 15 舵角对桨、舵作用力的影响 |
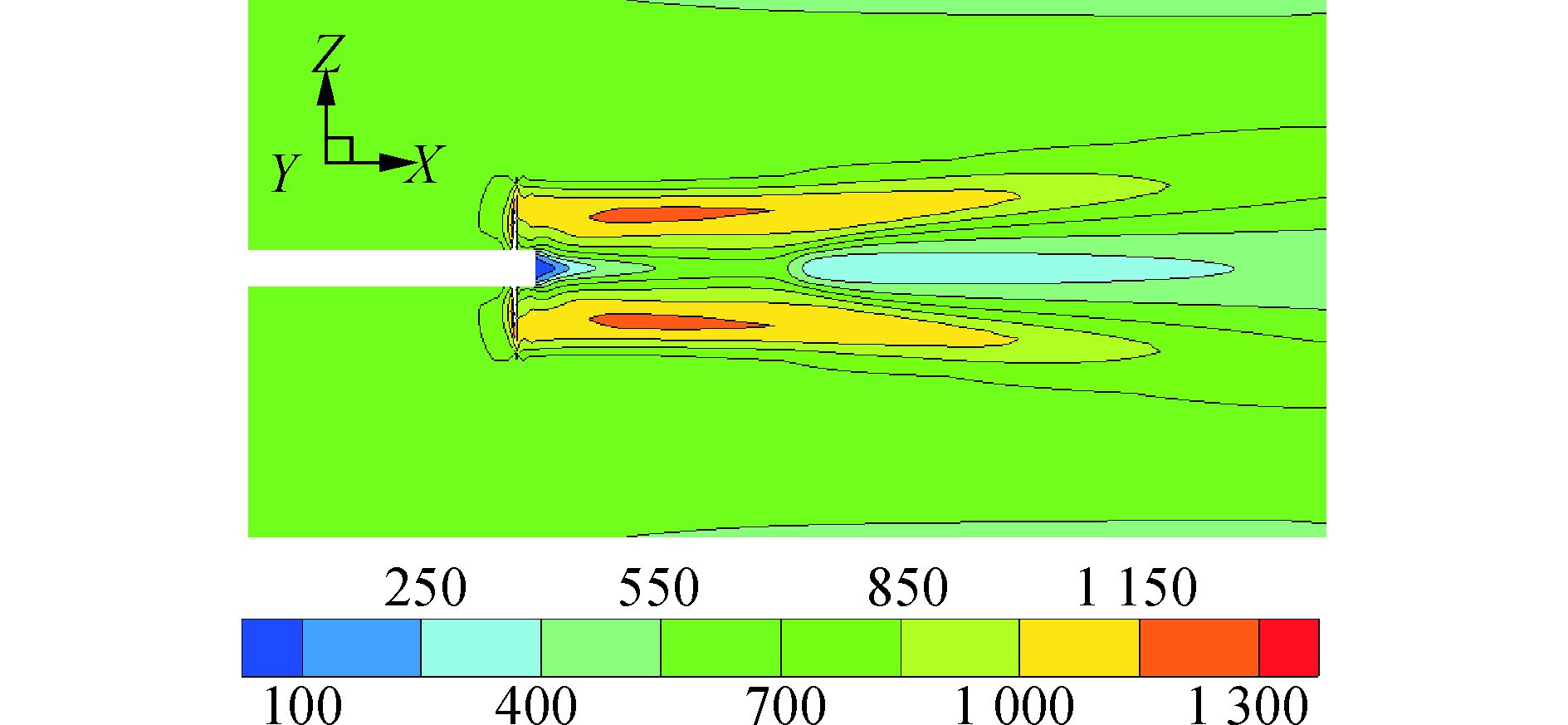
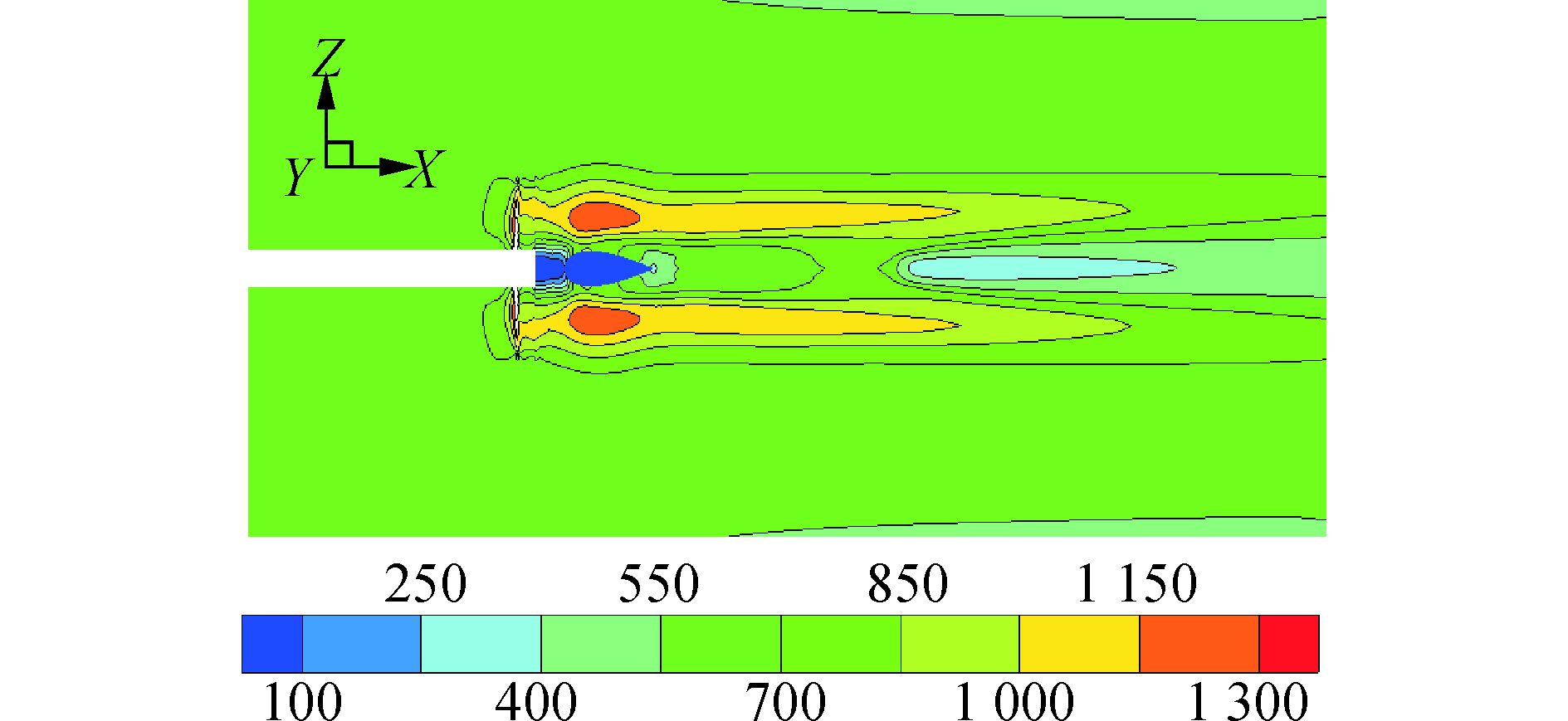
图 16、17以n=375 r/min时J=0.76的流场为例比较了敞水桨和带舵桨后尾流的压力分布。对于敞水桨,桨后尾流开始是呈收缩趋势,在x=0.6D左右处收缩至桨直径的0.8倍左右,此后在螺旋桨的尾流影响区域内一直在扩张,最大可达到螺旋桨直径的1.6倍左右。对比之下,桨后加装舵之后,尾流也经历了收缩的过程,但由于舵的水流的排挤作用,在舵处剖面有明显的“突出”,且最小剖面没有达到敞水桨的水平。流过舵之后,尾流剖面呈平稳趋势,没有出现敞水桨所有的严重的尾流扩张现象,剖面宽度最大处也与螺旋桨直径相差无几[16]。
|
图 16 敞水桨流场纵剖面压力分布 |
|
图 17 桨-舵系统流场纵剖面压力分布 |
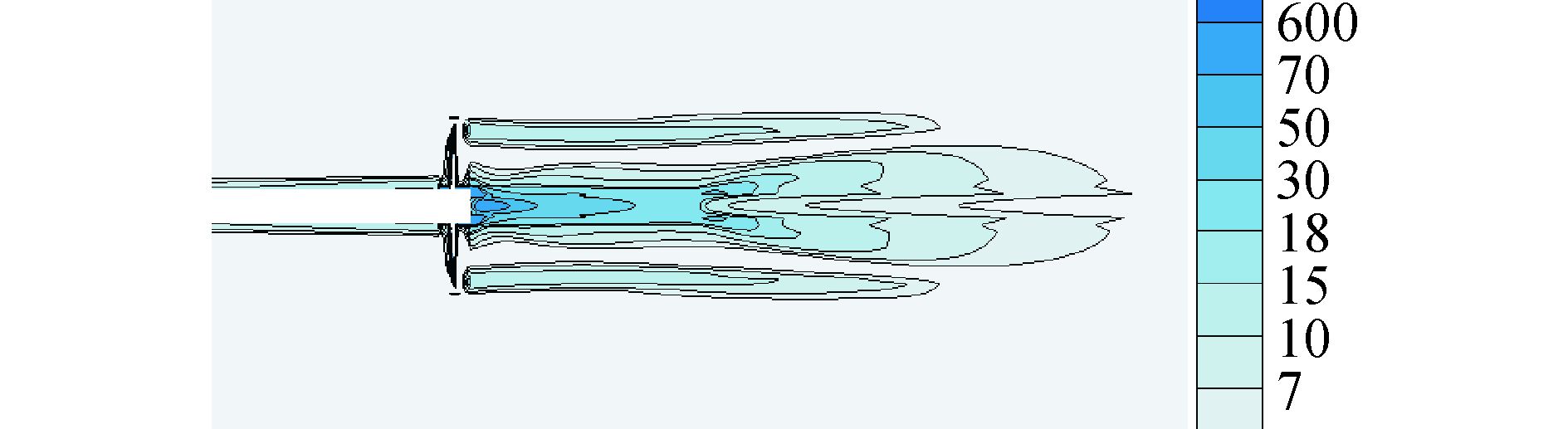
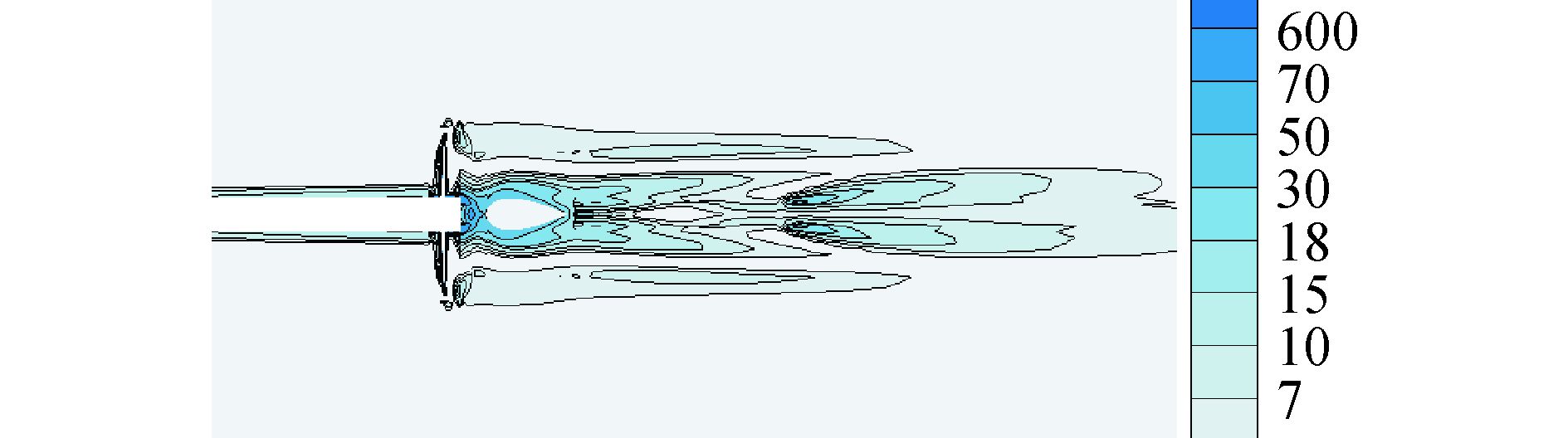
图 18、19比较了敞水桨和带舵桨的尾流涡量。可以看出,敞水桨后方存在强烈的梢涡和毂涡,在桨后加装舵之后,可以明显看到毂涡及其后方和周围的漩涡强度得到了很大的衰减,不仅在强度上,在面积上也有明显的减弱,叶梢向后引发的漩涡也得到了有效的抑制,其强度和影响范围都有了减弱。
|
图 18 敞水桨流场纵剖面涡量分布 |
|
图 19 桨-舵系统流场纵剖面涡量分布 |
本文用计算流体力学方法,分析了桨舵干扰的水动力特性,得出了与理论基础相符合的现象。
1) 桨前呈现为低压区,桨后为高压区,桨叶前后的压力差产生推水向后的效果;
2) 分析桨前后的速度场,发现桨后有水流的切向速度,这是桨后有尾流能量损失的主要原因;
3) 计算结果表明,桨舵干扰属于有利干扰,舵的存在能够提高螺旋桨的效率,螺旋桨所诱导的旋转尾流极大的改变了舵的受力方式;
4) 桨后舵的上下部压力分布不再对称,舵受到一个比较强的旋转力矩。
文章模拟分析了流场中螺旋桨和舵的压力分布,桨后尾流场的速度分布及压力分布,着重分析了舵对桨后尾流场的影响,舵角对螺旋桨和舵的推/阻力和转矩的影响,得到了具有普遍意义的规律。
| [1] |
TSAKONAS S, JACOBS W R, ALI M R. A theory for the propeller-rudder interaction[R]. Hoboken:Stevens Institute of Technology, 1968.
( 0) 0)
|
| [2] |
TSAKONAS S, JACOBS W R, ALI M R. Propeller-rudder interaction[R]. Hoboken:Stevens Institute of Technology, 1972.
( 0) 0)
|
| [3] |
朱自理, 董世汤. 螺旋桨-舵相互干扰水动力性能理论预报方法[C]//第三届船舶推进器及空泡学术讨论会论文集. 北京: 中国造船编辑部, 1983.
( 0) 0)
|
| [4] |
王德恂, 韩久瑞, 谭廷寿, 等. 螺旋桨舵组合体水动力性能计算[J]. 武汉理工大学学报:交通科学与工程版, 1984(4): 4-15. ( 0) 0)
|
| [5] |
ZHANG Jianhua, WANG Guoqiang, JIANG Shaojian. Unsteady hydrodynamic performance of propeller and rudder system[J]. Journal of ship mechanics, 2003, 7: 48-56. ( 0) 0)
|
| [6] |
覃新川. 短翼水动力计算模型与多桨多舵水动力干扰研究[D]. 哈尔滨: 哈尔滨工程大学, 2006: 20-28.
( 0) 0)
|
| [7] |
吴召华. 基于体积力法的船/桨/舵黏性流场的数值模拟[D]. 上海: 上海交通大学, 2013: 14-29.
( 0) 0)
|
| [8] |
杨震, 陈如星, 肖能齐, 等. 一体化桨舵装置造型设计及水动力计算方法研究[J]. 船电技术, 2016, 36(2): 8-12. ( 0) 0)
|
| [9] |
王辉, 李玉胜. 舵前进流的选择对桨舵系统性能的影响[J]. 船舶动力装置, 2014(2): 71-76. ( 0) 0)
|
| [10] |
HOU Lixun, WANG Chao, CHANG Xin. Hydrodynamic performance analysis of propeller-rudder system with the rudder parameters changing[J]. Journal of marine science and application, 2013, 12(4): 406-412. DOI:10.1007/s11804-013-1211-0 ( 0) 0)
|
| [11] |
张德良. 计算流体力学教程[M]. 北京: 高等教育出版社, 2010: 19-22.
( 0) 0)
|
| [12] |
王德恂, 张志军, 张晓敏. 桨舵干扰的试验研究[J]. 武汉理工大学学报:交通科学与工程版, 1987(4): 46-53. ( 0) 0)
|
| [13] |
陈卫, 叶敏. 基于滑移网格法桨-舵相互干扰流场分析[J]. 武汉船舶职业技术学院学报, 2012, 11(3): 36-38. ( 0) 0)
|
| [14] |
季少鹏, 朱爱军, 王文涛. 桨舵相互干扰的水动力特性模型试验研究[C]//第二十五届全国水动力学研讨会暨第十二届全国水动力学学术会议. 无锡, 2015: 497-499.
( 0) 0)
|
| [15] |
侯建军, 石爱国, 吴明, 等. 船-舵-桨的水动力干扰效应研究[J]. 船舶工程, 2014(1): 41-44. ( 0) 0)
|
| [16] |
孙海素, 苏甲, 魏锦芳. 桨舵间距对螺旋桨推进性能影响的研究[J]. 中国造船, 2012, 53(s1): 1-6. ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


