电磁波的极化特征是除信号幅度、相位、频率和波形等信息外,另一个可以利用的重要特征信息。对极化信息的充分挖掘和利用,有利于提高雷达和通信等系统的性能[1-4],因此引起了很多相关领域学者的关注[5-6]。与常规标量阵列相比,极化敏感阵列[7-8]的优势有:能以矢量方式感知入射电磁波在不同方向上的投影分量,可提取更多的有用信息;空域信息辅之以极化域信息,使得空间源信号多维参数估计的性能得到进一步改善;在一些空间受限的实际应用场合,如安装在飞行器上的传感器阵列,电磁矢量传感器更加能够发挥其单天线具有的多分量结构形式,且对共形阵列的信号处理更加灵活。当在实际工程中所使用的接收天线为共形阵列天线时,其不是全向接收的,且各个天线阵元有一定的极化方式。当入射信号的极化方式与接收天线阵元的极化方式不匹配时,各个阵元所接收到的信号可能只是入射信号在某个方向上的分量,也有可能完全无法接收到入射信号,从而导致各个阵元实际所接收到的信号与雷达辐射的信号在幅度以及相位上有较大误差,此时传统MUSIC算法失效。因而针对于此实际情况,便需要在经典MUSIC算法的基础上引入极化修正因子[9-11],形成跟极化相关的极化MUSIC算法。极化MUSIC算法需在空域以及极化域参数范围内进行四维谱峰搜索,相对于经典MUSIC算法,算法的计算复杂度大大增加,而在实际系统中往往要求信号可以进行实时处理,因此需要研究相关的基于极化敏感阵列的参数降维估计算法。
1 数学模型假设空间有D个远场窄带电磁信号入射到如图所示的空间阵元上,天线阵是由8个天线阵元组成的均匀圆阵,各阵元均为与圆周表面相切的极化敏感天线,如图 1所示。
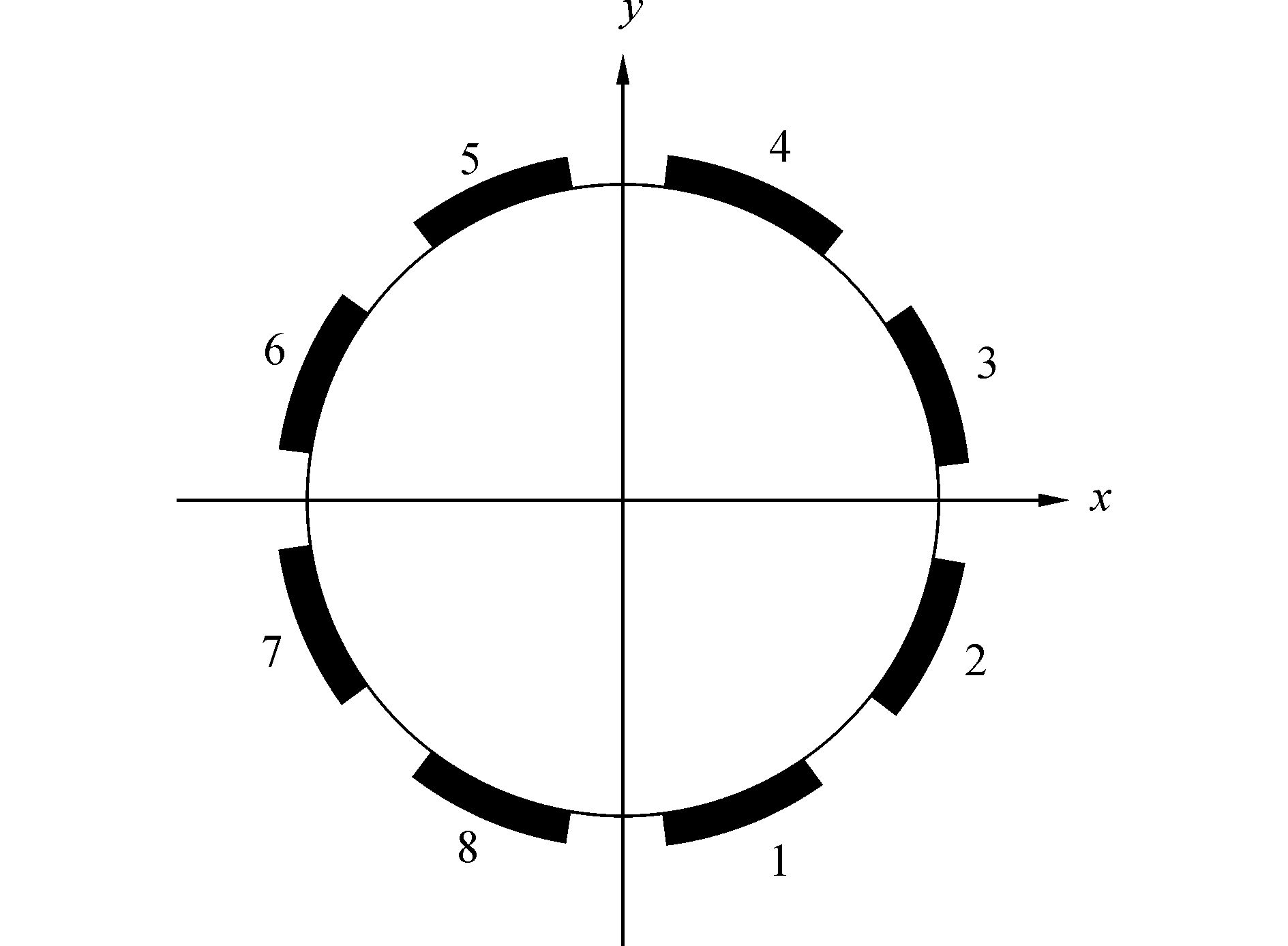
|
图 1 八元均匀圆阵示意图 |
记第m个信号的方位角和仰角分别为θm和φm,极化辅助角和极化相位差分别为γm和ηm。进一步假定阵元噪声为圆空-时-极化白噪声,其方差为σn2;入射信号互不相关,并与噪声统计独立,则有阵列输出信号矢量可表示为
| $\mathit{\boldsymbol{X}}\left( t \right) = \sum\limits_{m = 1}^D {{\mathit{\boldsymbol{a}}_m}{\mathit{\boldsymbol{s}}_m}\left( t \right)} + \mathit{\boldsymbol{N}}\left( t \right) = \mathit{\boldsymbol{AS}}\left( t \right) + \mathit{\boldsymbol{N}}\left( t \right)$ | (1) |
式中:X(t)为阵列的M×1维快拍数据矢量;S(t)为空间信号的D×1维矢量;N(t)为阵列的M×1维噪声数据矢量;A为空间阵列的M×D维阵列流型矩阵(导向矢量阵),其中am为第m个信号的导向矢量。
以坐标系原点即圆阵的圆心为参考点,信号入射到天线阵所在空间直角坐标系上的方向单位矢量为r=(cos φcos θ, cos φsin θ, sin φ),li为各个天线阵元的位置坐标矢量,则信号入射到阵列的空域相移因子为
| ${u_i} = {{\rm{e}}^{^ - {\rm{j}}2{\rm{ \mathsf{ π} }}/\lambda ({\mathit{\boldsymbol{l}}_i}{\mathit{\boldsymbol{r}}^{\rm{T}}})}},{\rm{ }}\left( {i = 1,2, \cdots ,8} \right)$ | (2) |
则该接收信号的导向矢量为
| $\mathit{\boldsymbol{a}} = \mathit{\boldsymbol{r}}\left( {\theta ,\varphi } \right)\mathit{\boldsymbol{B}}\mathit{\boldsymbol{\phi}}\left( {\theta ,{\rm{ }}\varphi } \right)\mathit{\boldsymbol{h}}\left( {\gamma ,\eta } \right)$ | (3) |
式中:r(θ, φ)=diag{u1, u2, u3, u4, u5, u6, u7, u8}为由入射信号在阵列各阵元处的空域相位因子构成的对角阵,ϕ为入射信号波达方向角的函数;B称为极化敏感矩阵,由各阵元的极化敏感矢量构成,B=[g1, g2, g3, g4, g5, g6, g7, g8]T,当天线阵列的阵元摆放位置确定时,该阵列为一个常数矩阵。
| $\mathit{\boldsymbol{\phi}}\left( {\theta ,\varphi } \right) = \left[ {\begin{array}{*{20}{c}} { - {\rm{sin}}\theta } & {{\rm{sin}}\varphi {\rm{cos}}\theta }\\ {{\rm{cos}}\theta } & {{\rm{sin}}\varphi {\rm{sin}}\theta }\\ 0 & { - {\rm{cos}}\varphi }\\ {{\rm{sin}}\varphi {\rm{cos}}\theta } & {{\rm{sin}}\theta }\\ {{\rm{sin}}\varphi {\rm{cos}}\theta } & { - {\rm{cos}}\theta }\\ { - {\rm{cos}}\varphi } & 0 \end{array}} \right]$ | (4) |
| $\mathit{\boldsymbol{h}}\left( {\gamma ,\eta } \right) = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\gamma }\\ {{\rm{sin}}(\gamma {e^{{\rm{j}}\eta }})} \end{array}} \right]$ | (5) |
本文提出的算法主要分为2个部分:首先是利用矩阵的秩亏原理对入射信号进行DOA估计,在得到入射信号的DOA(即方位角和仰角)之后,将入射信号的DOA估计值代入到应用拉格朗日乘子法所得到的计算极化参数的公式中计算得到入射信号的极化参数(即极化辅助角和极化相位差)。
2.1 入射信号DOA估计从导向矢量的表达式中可以看到,导向矢量只跟入射信号的空域参数以及极化参数有关,因而可以将其表示为
| $\mathit{\boldsymbol{a}} = \mathit{\boldsymbol{D}}\left( {\theta ,\varphi } \right)\mathit{\boldsymbol{h}}\left( {\gamma ,\eta } \right)$ | (6) |
极化MUSIC算法的谱函数可表示为
| ${\mathit{\boldsymbol{P}}_{{\rm{MUSIC}}}} = \frac{1}{{{\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {\gamma ,\eta } \right){\mathit{\boldsymbol{D}}^{\rm{H}}}\left( {\theta ,\varphi } \right){\mathit{\boldsymbol{E}}_N}\mathit{\boldsymbol{E}}_N^{\rm{H}}\mathit{\boldsymbol{D}}\left( {\theta ,\varphi } \right)\mathit{\boldsymbol{h}}\left( {\gamma ,\eta } \right)}}$ | (7) |
取式(7) 的倒数,有
| $\begin{align} & {{\mathit{\boldsymbol{P}}}^{'}}={{\mathit{\boldsymbol{h}}}^{\rm{H}}}\left( \gamma ,\eta \right)\left( {{\mathit{\boldsymbol{D}}}^{\rm{H}}}~\left( \theta ,\varphi \right){{\mathit{\boldsymbol{E}}}_{N~}}\mathit{\boldsymbol{E}}_{N}^{\rm{H}}\mathit{\boldsymbol{D}}\left( \theta ,\varphi \right) \right)\mathit{\boldsymbol{h}}\left( \gamma ,\rm{ }\eta \right)= \\ & \quad \quad {{\mathit{\boldsymbol{h}}}^{\rm{H}}}~\left( \gamma ,\eta \right)\mathit{\boldsymbol{H}}\left( \theta ,\varphi \right)\mathit{\boldsymbol{h}}\left( \gamma ,\eta \right) \\ \end{align}$ | (8) |
在极化MUSIC算法中,当利用式(7) 所构造的谱函数进行谱峰搜索得谱峰值时,即相当于解决式(8) 的函数值最小优化问题,也就是在理想情况下应满足式(9):
| ${{\mathit{\boldsymbol{h}}}^{\rm{H}}}\left( \gamma ,\eta \right)\mathit{\boldsymbol{H}}\left( \theta ,\rm{ }\varphi \right)\mathit{\boldsymbol{h}}\left( \gamma ,\eta \right)=0$ | (9) |
而又由于信号特征矢量所张成的子空间与阵列导向矢量所张成的子空间是一致的,再根据信号子空间与噪声子空间的正交性,即可得到结论,噪声子空间中的任意一个噪声特征矢量都和阵列导向矢量矩阵的任意一列向量是正交的。即有
| $\mathit{\boldsymbol{E}}_{N}^{\rm{H}}\mathit{\boldsymbol{a}}\left( \theta ,\varphi ,\gamma ,\eta \right)=\bf{0}$ | (10) |
在式(9) 左端乘EN即有
| ${{\mathit{\boldsymbol{E}}}_{N}}\mathit{\boldsymbol{E}}_{N}^{\rm{H}}\mathit{\boldsymbol{a}}\left( \theta ,\varphi ,\gamma ,\eta \right)=\bf{0}$ | (11) |
在式(10) 左侧左乘DH(θ, φ),则可得到
| $\begin{align} & \left( {{\mathit{\boldsymbol{D}}}^{\rm{H}}}~\left( \theta ,\varphi \right){{\mathit{\boldsymbol{E}}}_{N}}\mathit{\boldsymbol{E}}_{N}^{\rm{H}}\mathit{\boldsymbol{D}}\left( \theta ,\varphi \right) \right)\mathit{\boldsymbol{h}}\left( \gamma ,\eta \right)= \\ & \quad \mathit{\boldsymbol{H}}\left( \theta ,\varphi \right)\mathit{\boldsymbol{h}}\left( \gamma ,\eta \right)=0 \\ \end{align}$ | (12) |
比较式(9) 和式(12) 可知,两式同时成立。将两式均看成是以极化参数(γ, η)未知数的齐次线性方程组。最终极化参数的解为两式解的交集。由式(12) 可以看出,其极化域解的集合即为两式解的交集。因而只需考虑式(12) 所表示的齐次线性方程组的解的情况即可。
由于在本算法中所考虑的极化参数的范围为:极化辅助角γ∈[0, π/2],极化相位差η∈(-π, π],因而对于式(12) 的未知数为(γ, η)的齐次线性方程组,其必定存在非零解。因而此齐次线性方程组的系数矩阵H(θ, φ)必定会发生亏秩现象,其行列式的值为0。即可表示为
| $\left| \mathit{\boldsymbol{H}}\left( \theta ,\varphi \right) \right|=|{{\mathit{\boldsymbol{D}}}^{\rm{H}}}~\left( \theta ,\varphi \right){{\mathit{\boldsymbol{E}}}_{N}}\mathit{\boldsymbol{E}}_{N}^{\rm{H}}\mathit{\boldsymbol{D}}\left( \theta ,\varphi \right)|=0$ | (13) |
由行列式的值为0,对应可求得使系数矩阵H(θ, φ)发生亏秩现象时的方位角θ以及仰角φ,即为入射信号的DOA。将谱峰搜索函数转化为搜索系数矩阵H(θ, φ)行列式的极小值,即为求取行列式倒数的极大值:
| $\left\{ \theta ,\varphi \right\}=\rm{arg}{{\underset{\theta ,\varphi }{\mathop{\rm{maxdet}}}\,}^{-1}}\left\{ \mathit{\boldsymbol{H}}\left( \theta ,\varphi \right) \right\}$ | (14) |
由式(14) 可以看到,在利用了秩亏损方法之后,构造空间谱时无需考虑极化参数,即构造的谱函数与极化参数无关,因而在进行谱峰搜索时依然只是两维搜索,只搜索方位角及仰角的值。将极化MUSIC算法的四维搜索降维成了二维搜索,大大地减少了算法的计算量,能够很大程度地提高算法程序运行的实时性。进行谱峰搜索之后,所得到的谱峰极大值处所对应的方位角θ及仰角φ为入射信号的DOA。
2.2 入射信号极化参数估计根据秩亏MUSIC方法原理,在无噪等理想条件下,矩阵H(θ, φ)在真实信号DOA处发生亏秩现象,由满秩变为奇异,即H(θ, φ)为奇异的厄尔米特矩阵;又D(θ, φ)HD(θ, φ)为厄尔米特正定矩阵,所以{H(θ, φ), D(θ, φ)HD(θ, φ)}的最小广义特征值应为零。而H(θ, φ)h(γ, η)=0,所以h(γ, η)与{H(θ, φ), D(θ, φ)HD(θ, φ)}的零广义特征值所对应的广义特征矢量线性相关,即满足比例关系。
根据上述分析,有下述结论(下标m表示第m个信号):
| $\left\{ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_m}} \right\} = {{\mathit{\boldsymbol{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} { \boldsymbol{\varTheta} } }}}_{{\rm{min}}}}\{ \mathit{\boldsymbol{H}}\left( {{\theta _m},{\varphi _m}} \right),{\rm{ }}\mathit{\boldsymbol{D}}_{{\theta _m},{\varphi _m}}^{\rm{H}}{\mathit{\boldsymbol{D}}_{{\theta _m},{\varphi _m}}}\} \propto {\mathit{\boldsymbol{h}}_{{\gamma _m},{\eta _m}}}$ | (15) |
式中
由信号极化矢量的含义,结合式(15),可以得到下面的信号极化参数确定公式:
| $\left\{ {{\gamma _m}} \right\} = {\text{arctan}}\left\{ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_m}\left( 2 \right)/{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_m}\left( 1 \right)} \right\},{\text{ }}m = 1,{\text{ }}2, \cdots ,{\text{ }}M$ | (16) |
| $\left\{ {{\eta _m}} \right\} = {\text{arg}}\left\{ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_m}\left( 2 \right)/{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_m}\left( 1 \right)} \right\},m = 1,2, \cdots ,M$ | (17) |
1) 根据D个接收信号矢量得到协方差矩阵的估计值。
由阵列输出信号的采样值求协方差矩阵R的估计值
| $\mathit{\boldsymbol{\hat R}} = \frac{1}{N}\sum\limits_{n = 1}^N {\mathit{\boldsymbol{X}}(n){\mathit{\boldsymbol{X}}^{\rm{H}}}(n)} $ | (18) |
2) 对
3) 按照某种准则确定矩阵
| ${\mathit{\boldsymbol{U}}_N} = \left[ {{\mathit{\boldsymbol{v}}_{D + 1}},{\mathit{\boldsymbol{v}}_{D + 2}}, \cdots ,{\mathit{\boldsymbol{v}}_M}} \right]$ | (19) |
4) 按照式(20) 计算谱PRMUSIC(θ, φ),进行谱峰搜索,它的D个极大值所对应的θ、φ就是信号源的方向。
| ${\mathit{\boldsymbol{P}}_{{\rm{RMUSIC}}}}\left( {\theta ,\varphi } \right) = {\rm{de}}{{\rm{t}}^{ - 1}}\left\{ {\mathit{\boldsymbol{H}}\left( {\theta ,\varphi } \right)} \right\}$ | (20) |
1) 将DOA代入H(θ, φ),得到H(θd, φd),对矩阵束{H(θd, φd), DH(θd, φd)D(θd, φd)}进行广义特征值分解,求得对应最小广义特征值的广义特征矢量hd。
2) 根据式(16) 与(17) 计算入射信号的极化辅助角和极化相位差。
3 运算量分析在对于各种MUSIC算法的应用过程中,计算接收数据协方差矩阵部分、特征分解部分、信源数估计部分以及构造信号子空间和噪声子空间部分的计算量在入射信号相同的情况下都是一致的,因而在对各种MUSIC算法的运算量进行分析时,只考虑MUSIC算法的谱峰搜索部分,即重点考虑构造谱函数部分的运算量。由于乘法运算的计算量要远大于加法运算的计算量,因而在进行算法的运算量分析的时候不考虑加、减法运算的计算量。统计计算复杂度时,谱峰搜索部分的各参数的搜索步长均为1°,极化MUSIC算法和秩亏损MUSIC算法的各参数的搜索范围均相同:方位角为0°~360°,仰角为54°~90°。极化MUSIC算法的极化参数搜索范围为极化辅助角为0°~90°,极化相位差为-180°~180°,秩亏损MUSIC算法中计算一个谱函数(矩阵相乘)共需要834次实数乘法,共需要构造361×37≈1.3×104个谱函数,共需要834×361×37≈1.1×107次实数乘法;极化MUSIC算法计算一个谱函数共需要524次实数乘法,共需要构造361×37×91×361≈4.4×108个谱函数,共需要实数乘法524×361×37×91×361≈2.3×1011次,则可得到各算法的计算复杂度如表 1所示。
|
|
表 1 两类MUSIC算法的计算复杂度 |
从表 1中可以看到,极化MUSIC算法的运算量要远远大于秩亏损MUSIC算法的运算量,其运算量为秩亏损MUSIC算法运算量的10 000倍。由此可见,本文所提出的秩亏损MUSIC算法在极化MUSIC算法的基础上大大降低了算法的运算量,具有较好的实时性。
4 仿真分析本文中的接收天线阵列为八元均匀圆阵,天线盘半径为140 mm。仿真分析中用到的误差分析指标为均方根误差,其定义公式为
| $\text{RMSE}=\sqrt{\frac{1}{2m}\sum\limits_{i=1}^{m}{{{({{{\hat{\theta }}}_{i}}-\theta )}^{2}}+{{({{{\hat{\varphi }}}_{i}}-\varphi )}^{2}}}}$ | (21) |
式中:m为测量次数,
仿真条件:入射的2个窄带信号的频率为3 GHz,方位角θ=[35° 40°],仰角为φ=[55° 70°],极化辅助角为γ=[10° 20°],极化相位差为η=[40° 60°],以1通道为基准,6通道加入通道不一致性10°,其余各通道的通道不一致性在0°~10°之间。
1) 秩亏损MUSIC算法DOA估计均方根误差随快拍数的变化。
设置信噪比为20 dB,快拍数在10~250之间以步长40变化,则可得DOA估计均方根误差随快拍数的变化图像如图 2所示。从图 2中可以看到,随着快拍数的增加,DOA估计均方根误差越来越小,最终稳定在0.5°左右。可以看出秩亏损MUSIC算法的DOA估计精度较高,能满足工程中精度要求。
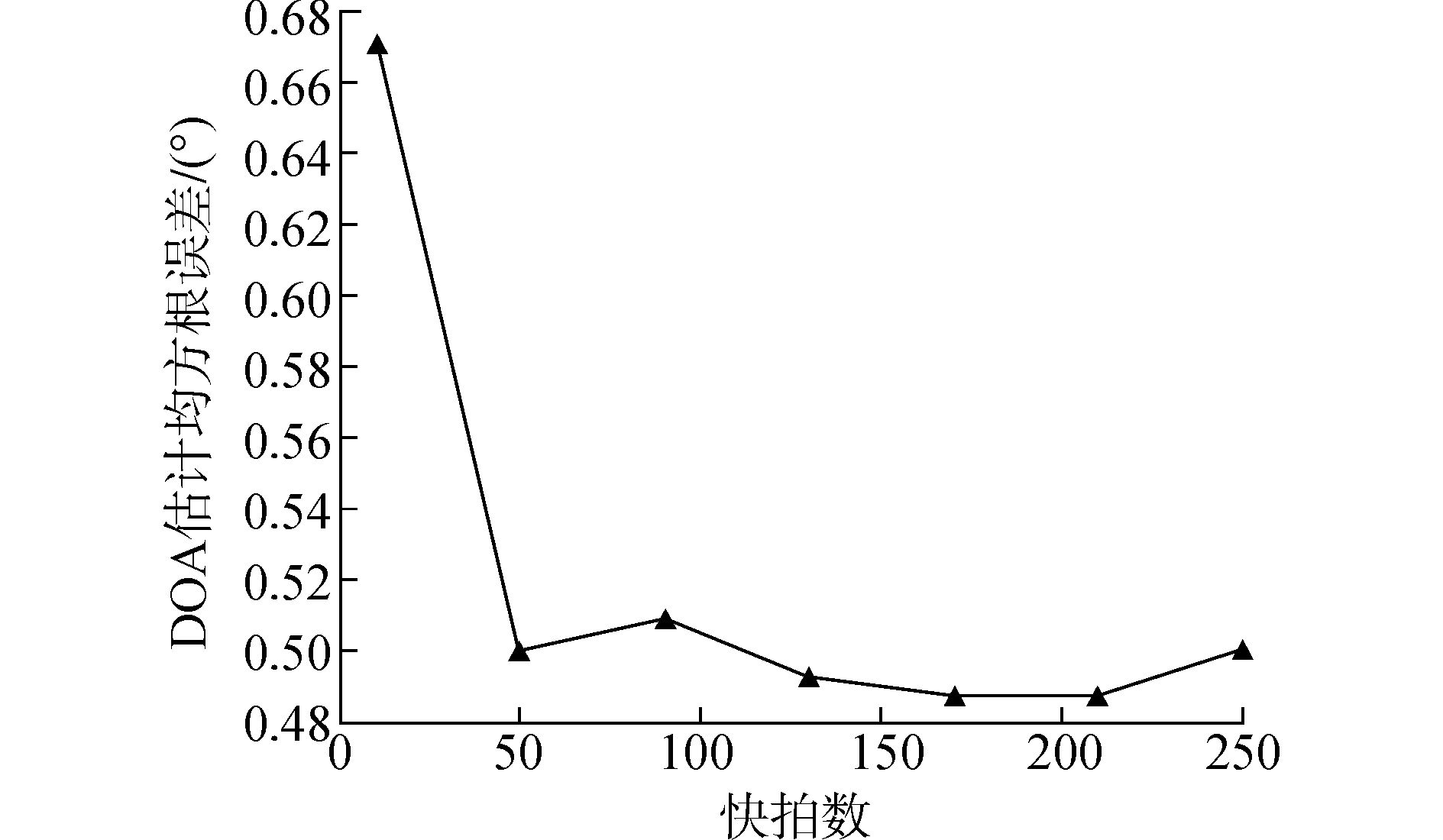
|
图 2 DOA估计均方根误差随快拍数变化图 |
2) 秩亏损MUSIC算法DOA估计均方根误差随信噪比的变化。
设置快拍数为100,信噪比在5~25 dB之间以步长5 dB变化,则可得DOA估计均方根误差随信噪比的变化图像如图 3所示。
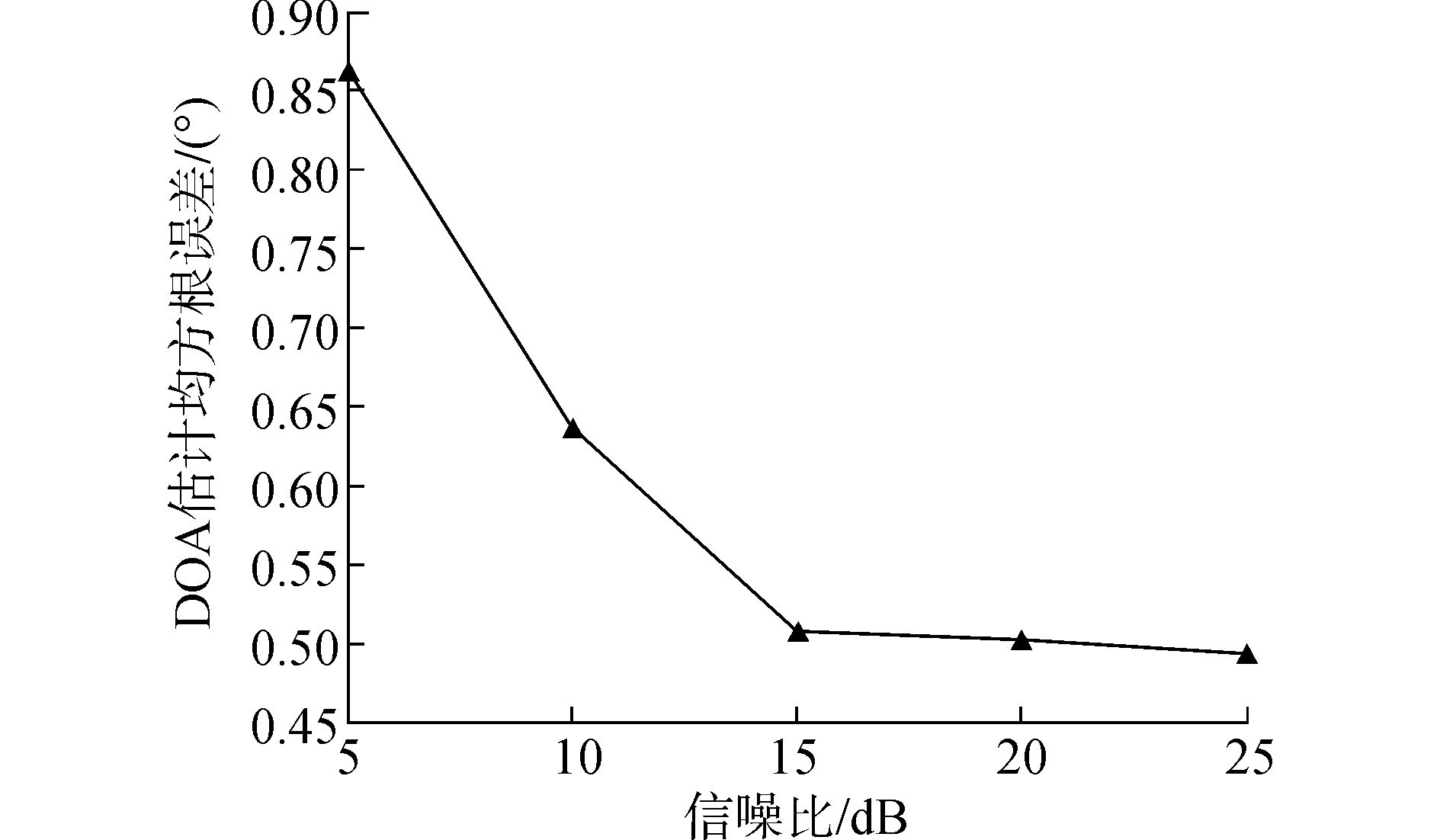
|
图 3 DOA估计均方根误差随信噪比变化图 |
从图 3中可以看到,随着信噪比的增加,DOA估计均方根误差越来越小,最终稳定在0.5°左右。由此可看出秩亏损MUSIC算法的DOA估计精度较高,能够满足工程中的精度要求。
5 结论本文主要介绍了秩亏损MUSIC算法的原理,通过将秩亏损MUSIC算法与极化MUSIC算法的算法原理进行对比可以得到以下结论:
1) 相对于极化MUSIC算法来说,秩亏损MUSIC算法的计算复杂度大大降低,算法运算量降低;
2) 通过计算机仿真实验可以得到秩亏损MUSIC算法在降低算法运算量的同时保证了算法的DOA估计精度。
秩亏损MUSIC算法是极化MUSIC算法的降维算法, 解决了极化MUSIC算法计算复杂度高、无法应用于实际工程的问题。本文算法能够应用于实际工程中, 解决了经典MUSIC算法在接收天线为共形阵列的情况下无法正确测向的问题。
| [1] |
MAO X P, LIU Y T. Null phase-shift polarization filtering for high-frequency radar[J]. IEEE transactions on aerospace and electronic systems, 2007, 43(4): 1397-1408. DOI:10.1109/TAES.2007.4441747 ( 0) 0)
|
| [2] |
PASTINA D, LOMBARDO P, BUCCIARELLI T. Adaptive polarimetric target detection with coherent radar. I. Detection against Gaussian background[J]. IEEE transactions on aerospace and electronic systems, 2001, 37(4): 1194-1206. DOI:10.1109/7.976959 ( 0) 0)
|
| [3] |
肖顺平. 宽带极化雷达目标识别的理论与应用[D]. 长沙: 国防科技大学, 1999: 26-33.
( 0) 0)
|
| [4] |
KIM K T, SEO D K, KIM H T. Efficient radar target recognition using the MUSIC algorithm and invariant features[J]. IEEE transactions on antennas and propagation, 2002, 50(3): 325-337. DOI:10.1109/8.999623 ( 0) 0)
|
| [5] |
NEHORAI A, PALDI E. Vector-sensor array processing for electromagnetic source localization[J]. IEEE transactions on signal processing, 1994, 42(2): 376-398. DOI:10.1109/78.275610 ( 0) 0)
|
| [6] |
MIRON S, YANG S, BRIE D, et al. A multilinear approach of direction finding using a sensor-array with multiple scales of spatial invariance[J]. IEEE transactions on aerospace and electronic systems, 2015: 00. ( 0) 0)
|
| [7] |
庄钊文. 极化敏感阵列信号处理[M]. 北京: 国防工业出版社, 2005: 200-213.
( 0) 0)
|
| [8] |
徐友根, 刘志文, 龚晓峰. 极化敏感阵列信号处理[M]. 北京: 北京理工大学出版社, 2013: 10-21.
( 0) 0)
|
| [9] |
李京书, 陶建武. 信号DOA和极化信息联合估计的降维四元数MUSIC方法[J]. 电子与信息学报, 2011, 33(1): 106-111. ( 0) 0)
|
| [10] |
ZHANG X, CHEN C, LI J, et al. Blind DOA and polarization estimation for polarization-sensitive array using dimension reduction MUSIC[J]. Multidimensional systems and signal processing, 2014, 25(1): 67-82. DOI:10.1007/s11045-012-0186-3 ( 0) 0)
|
| [11] |
司伟建, 朱曈, 张梦莹. 平面极化天线阵列的DOA及极化参数降维估计方法[J]. 通信学报, 2014, 12: 28-35. ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


