2. 南京大学天文与空间科学学院, 江苏 南京 210093
2. School of Astronomy and Space Science, Nanjing University, Nanjing 210093, China
在耀变体观测数据相关性的研究中,有一个值得注意的现象,对于整个样本,单独的平谱射电类星体(Flat-Spectrum Radio Quasars, FSRQ)和单独的蝎虎天体(BL Lac)样本,同步峰峰值频率(νpeaksyn)和同步峰峰值光度(νLpeaksyn(ν))之间相关性是不同的[1-2],而且在若干耀变体的相关性分析中都存在类似的差异性。如文[1]发现康普顿主导(Compton Dominance, CD, 逆康普顿峰峰值光度与同步峰峰值光度之比)和同步峰峰值频率之间的反相关性存在于整个样本和蝎虎天体中,但是不存在于平谱射电类星体中。文[2]研究了一个包含1 425个费米(Fermi)耀变体的样本,他们发现νpeaksyn和αOX, νpeaksyn和Lγ, νpeaksyn和LR之间的反相关性存在于整个样本和单独的蝎虎天体中,但是并不存在于平谱射电类星体中。文[3]发现康普顿主导和同步峰峰值频率之间的反相关性存在于整个样本和单独的蝎虎天体中,但是并不存在于平谱射电类星体中。由于一般会把耀变体当作一个具有连续内在物理性质的整体,所以耀变体整体和子类相关性之间的差异来源值得研究。
另一方面,在通用的单区轻子模型中,对于一定形状的注入电子能谱,由于冷却会导致另一个形状不同的冷却后电子能谱。根据标准的激波加速机制,冷却可以分为快冷却和慢冷却两种。关于耀变体的冷却,有不同的看法。文[4]指出,高功率的平谱射电类星体和蝎虎天体分别位于快冷却和慢冷却区。文[5]在伽马暴和耀变体同步辐射的对比中,得到耀变体整体属于慢冷却。文[6]得到耀变体整体处于快冷却区。所以来自一个同时性较大样本的统计分析对于这个问题是有意义的。
第三方面,观测和理论都指出,耀变体的伽马谱指数和逆康普顿(Inverse Compton scattering, IC)峰峰频之间存在一个线性关系,这个关系被称为“谱指数图”。文[7]使用一个对数抛物线能谱的能均分轻子模型对此进行了解释。这个模型也需要一个同时性的较大样本来进行检验。
1 样本由于耀变体具有快速光变的特点[8-9],为了有效降低峰值频率在估计时不确定的误差[10],需要一个同时或至少准同时性数据的大样本,并且耀变体宽带能谱(Spectral Energy Distribution, SED)的全波段能够很好地拟合。文[11]收集了279个耀变体,其中包括200个平谱射电类星体和79个蝎虎天体。本文的工作基于他们的样本做进一步的研究。
本文选取文[11]样本的3个子样本进行具体研究。子样本A中包含274个可以被拟合出同步峰的耀变体,用于研究同步峰峰值频率(νpeaksyn)和同步峰峰值光度(νLpeaksyn(ν))之间的相关性。子样本B包含143个可以被拟合出逆康普顿峰的耀变体,用于研究逆康普顿峰峰值频率(νpeakIC)分别和逆康普顿峰峰值光度(νLpeakIC(ν))、伽马谱指数(Γγ)之间的相关性。子样本C包含109个可以被拟合出完整宽带能谱的耀变体,用于研究νpeaksyn分别和热光度(Lbol)、康普顿主导之间的相关性。此外,在子样本A,B和C中,分别对整个样本(平谱射电类星体和蝎虎天体)、单独的平谱射电类星体和单独的蝎虎天体进行了5组相关性分析。
2 相关性分析和结果文[11]使用二次函数
| $ \log (\nu {F_\nu }) = \mathit{c}{(log\nu )^2} + b(log\nu ) + \mathit{a} $ | (1) |
分别拟合同步峰和逆康普顿峰。因此可以推导得出峰值光度、峰值频率和康普顿主导。热光度可以通过计算得到:
| $ {\mathit{L}_{{\rm{bol}}}} = 4{\rm{ \mathsf{ π} }}D_{\rm{L}}^{\rm{2}}{F_{{\rm{integrated}}}},$ | (2) |
其中,DL为光度距离;Fintegrated为热流量积分。
在子样本A,B和C中,分别对整个样本、平谱射电类星体和蝎虎天体检验logνpeaksyn和logνLpeaksyn (ν),logνpeakIC和logνLpeakIC (ν),logνpeaksyn和logLbol,logνpeaksyn和logCD以及Γγ和logνpeakIC之间的皮尔逊相关性,分析结果如表 1,相关关系如图 1。
| 关系 | 样本 | 斜率a | 斜率的标准差Δa | 截距b | 截距的标准差Δb | 源的数量N | p值 | 相关系数r |
| logνpeaksyn VS | sub-sample A | -0.81 | 0.05 | 56.87 | 0.71 | 274 | 6.3 × 10-12 | -0.4 |
| logνLpeaksyn(ν) | FSRQs | -1.13 | 0.13 | 60.92 | 1.76 | 179 | 0.07 | -0.137 |
| BL Lacs | -0.86 | 0.10 | 57.72 | 1.47 | 95 | 0.058 | -0.195 | |
| logνpeakIC VS | sub-sample B | -1.10 | 0.11 | 7.094 | 2.53 | 143 | 2.6 × 10-4 | -0.301 |
| logνLpeakIC(ν) | FSRQs | 1.00 | 0.13 | 24.80 | 2.97 | 107 | 0.547 | 0.059 |
| BL Lacs | -1.04 | 0.23 | 69.11 | 5.16 | 36 | 0.173 | -0.232 | |
| Γγ VS | sub-sample B | -0.29 | 0.02 | 8.86 | 0.36 | 143 | < 1.0 × 10-14 | -0.78 |
| logνpeakIC | FSRQs | -0.34 | 0.02 | 9.82 | 0.55 | 107 | < 1.0 × 10-17 | -0.704 |
| BL Lacs | -0.19 | 0.02 | 6.49 | 0.41 | 36 | 6.3 × 10-11 | -0.849 | |
| logνpeaksyn VS | sub-sample C | -0.83 | 0.08 | 11.55 | 1.07 | 109 | 3.1 × 10-7 | -0.465 |
| logCD | FSRQs | 1.04 | 0.18 | -13.07 | 2.41 | 81 | 0.511 | -0.074 |
| BL Lacs | -0.54 | 0.08 | 3.80 | 1.12 | 28 | 0.002 | -0.559 | |
| logνpeaksyn VS | sub-sample C | -1.13 | 0.12 | 62.79 | 1.64 | 109 | 1.1 × 10-5 | -0.405 |
| logLbol | FSRQs | -1.12 | 0.24 | 62.67 | 3.11 | 81 | 0.442 | -0.086 |
| BL Lacs | -0.99 | 0.24 | 60.89 | 3.36 | 28 | 0.214 | -0.242 |

|
| 图 1 (a) logνpeaksyn与logνLpeaksyn (ν)的相关性分析;(b) logνpeakIC与logνLpeakIC (ν)的相关性分析;(c) logνpeaksyn与logLbol的相关性分析;(d) logνpeaksyn与logCD的相关性分析;(e) Γγ与logνpeakIC的相关性分析。黑色空心圆表示平谱射电类星体(图中简写为F);黑色实心正方形表示蝎虎天体(图中简写为B);黑色实心五角星表示平谱射电类星体的质心CF;黑色实心三角形表示蝎虎天体的质心CB;黑色实心三角形;实线是最佳线性拟合 Fig. 1 The correlations between (a) logνpeaksyn and logνLpeaksyn (ν); (b) logνpeakIC and logνLpeakIC (ν); (c) logνpeaksyn and logLbol; (d) logνpeaksyn and logCD; (e) Γγ and logνpeakIC.FSRQ: circles; BL Lac: black solid squares.The centroid of FSRQ: black solid star; The centroid of BL Lac: black solid triangle. The solid line is the best fitting line equation for the whole sample |
分析结果表明,对于整个样本,所有的5组关系存在显著的反相关性。在子样本B中,对于单独的平谱射电类星体和蝎虎天体,Γγ和logνpeakIC之间存在显著的反相关性。在子样本C中,对于单独的蝎虎天体,logνpeaksyn和logCD之间存在显著的反相关性。值得考虑的是,在相关性分析中,样本数据存在一定的弥散度,这可能对分析结果有一定的影响。
3 讨论 3.1 耀变体总体和各子类之间相关性差异的来源分析从图 1 (a), (b), (c), (d)可以明显看到,平谱射电类星体和蝎虎天体的数据点在参数平面上的分布是不同的。相比之下,大多数平谱射电类星体位于参数平面的左上角。然而,蝎虎天体分布在各个部分,从左上角到右下角。在图 1 (e)中,平谱射电类星体和蝎虎天体的数据点在参数平面的分布类似,从左上角到右下角。
为了更清晰地刻画两个子类分布的不同,分别计算了平谱射电类星体和蝎虎天体两个子类的样本数据点坐标在参数平面上的算术平均位置(该位置简称“质心位置”或“质心”)。两个质心如图 1,很明显可以看到,平谱射电类星体和蝎虎天体的质心位置完全不同。相比之下,平谱射电类星体的质心位于参数平面的左上角,而蝎虎天体的质心位于右下角,并且两个质心之间存在明显的距离。
在所有5组相关分析中,存在两个质心分开的情况。为了研究质心分开对整个样本相关性的影响,做了一个数值模拟。
参数平面上,设平谱射电类星体的质心是CF点,蝎虎天体的质心是CB点。首先,将蝎虎天体的所有数据点不动,把平谱射电类星体数据点从原来的位置整体平移,使得移动的平谱射电类星体的质心位置(移动数据点的质心F′)与CB重合。然后从CB出发,使得平谱射电类星体的全部数据点,沿着CF与CB的连线平移。在此过程中计算出由蝎虎天体和F′数据点组成的整个样本的相关显著性参数(即皮尔逊相关系数r,p值)。从图 2可以发现,随着蝎虎天体和F′数据点距离的增大,无论两者的子样本是否存在相关性,蝎虎天体和F′数据点组成的整个样本的反相关性都变得更加显著。由于平谱射电类星体和蝎虎天体两个子类在参数平面上的位置正好位于图中模拟的这样一个线性相关的显著性逐渐增强的过程中,所以在以上5组整个样本的相关性分析中,不能排除平谱射电类星体和蝎虎天体质心的分开而带来的贡献。文[2]和文[3]的分析也给出类似的结果。
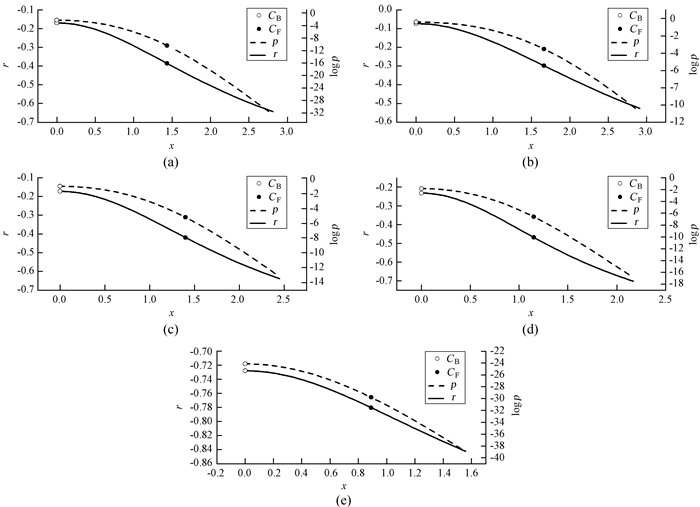
|
| 图 2 整个样本(a) logνpeaksyn与logνLpeaksyn (ν)的相关性数值模拟分析;(b) logνpeakIC与logνLpeakIC (ν)的相关性数值模拟分析;(c) logνpeaksyn与logLbol的相关性数值模拟分析;(d) logνpeaksyn与logCD的相关性数值模拟分析;(e) Γγ与logνpeakIC的相关性数值模拟分析。“logp”是p值的对数形式;“r”是皮尔逊相关系数;“x”是F′与BL Lac的质心之间的距离。虚线表示“logp”与“x”的函数;实线表示“r”与“x”的函数。空心圆和实心圆分别表示平谱射电类星体的起点(即CB点)和质心(即CF点)对应的位置 Fig. 2 The simulations of the correlation for the whole sample between (a) logνpeaksyn and logνLpeaksyn(ν); (b) logνpeakIC and logνLpeakIC(ν); (c) logνpeaksyn and logLbol; (d) logνpeaksyn and logCD; (e) Γγ and logνpeakIC.The 'p' is the p-value; 'r' is the Pearson correlation coefficient; 'x' is the distance between centroids of F′ and BL Lac. The dashed curve denotes the p-value as a function of x and the solid curve denotes the r as a function of x. CB represents the significance of the dataset where the two centroids coincides with each other, and CF represents the significance of the whole sample |
耀变体的统一方案要求沿着高同步峰蝎虎天体-中同步峰蝎虎天体-低同步峰蝎虎天体-平谱射电类星体的耀变体序列存在内在的、物理的、连续的演化趋势。因此可以预期这种趋势自然地分别存在于平谱射电类星体和蝎虎天体中,并进一步存在于耀变体中。然而,在本文的5组相关性中,这种预期并不完全成立。首先,对于logνpeaksyn和logνLpeaksyn (ν),logνpeakIC和logνLpeakIC (ν),logνpeaksyn和logLbol之间的相关性,平谱射电类星体和蝎虎天体都不存在明显的趋势。但是,对于整个样本却存在明显的趋势。其次,logνpeaksyn和logCD之间显著的相关性不存在于单独的平谱射电类星体中,但是对于整个样本和单独的蝎虎天体,又存在这样的趋势。这两种情况下,线性相关的显著性中不能排除平谱射电类星体和蝎虎天体之间质心分开产生的贡献。最后,Γγ和logνpeakIC之间的关系,从3.3节的结果可知,平谱射电类星体和蝎虎天体由于不同的辐射机制而导致不同的斜率。简单地把两个子类合成一个整体,会导致整个样本中得到非物理的相关性。
综上可以认为,至少在某些情况下,把耀变体的两个子类作为一个整体来研究耀变体的统计趋势时,会导致一个虚假的相关性或者非物理的结果。所以,对于耀变体的相关性研究应该对两个子类分别进行。
3.2 耀变体主导冷却机制的研究分析结果表明,对于蝎虎天体,logνpeaksyn和logCD之间存在显著的反相关性。对这组相关性进行如下讨论。对于均匀、单区的轻子模型[1],康普顿主导可以写成:
| $ CD \equiv \frac{{\max \left[ {L_{{\rm{peak}}}^{{\rm{EC}}},L_{{\rm{peak}}}^{{\rm{SSC}}}} \right]}}{{L_{{\rm{peak}}}^{{\rm{syn}}}}} \approx \frac{{\max \left[ {{\mathit{\delta }^2}{u_{{\rm{ext}}}},u{\mathit{'}_{{\rm{syn, peak}}}}} \right]}}{{u{\mathit{'}_{\rm{B}}}}},$ | (3) |
其中,LpeakEC为外康普顿过程的峰值光度;LpeakSSC为同步自康普顿过程的峰值光度;Lpeaksyn为同步峰峰值光度;δ为多普勒因子;
对于蝎虎天体,高能辐射通常是由同步自康普顿过程主导[11-13]。因此,康普顿主导可以改写成:
| $ CD = \frac{{L_{{\rm{peak}}}^{{\rm{SSC}}}}}{{L_{{\rm{peak}}}^{{\rm{syn}}}}} = \frac{{u{\mathit{'}_{{\rm{syn, peak}}}}}}{{u{\mathit{'}_{\rm{B}}}}}. $ | (4) |
同步峰峰值能量密度可以写成
| $ u{\mathit{'}_{{\rm{syn, peak}}}} = \frac{{u{\mathit{'}_{\rm{B}}}{\sigma _{\rm{T}}}}}{{2{\rm{ \mathsf{ π} }}R\mathit{'}_{\rm{b}}^{\rm{2}}}}{Q_0}{t_{{\rm{esc}}}}\left\{ \begin{array}{l} \;\;\gamma _{\rm{c}}^{3 - q}\;\;\;\;{\gamma _1}<{\gamma _{\rm{c}}}\\ {\gamma _{\rm{c}}}\gamma _1^{2 - q}\;\;\;\;{\gamma _{\rm{c}}}<{\gamma _1}\; \end{array} \right., $ | (5) |
其中,R′b为半径;γc为冷却电子的洛伦兹因子;γ1为电子洛伦兹因子的最小值;σT为汤姆逊散射截面;q为注入电子光谱指数;
| $ CD = \frac{{u{\mathit{'}_{{\rm{syn, peak}}}}}}{{u{\mathit{'}_{\rm{B}}}}} = \frac{{{\sigma _{\rm{T}}}}}{{2{\rm{ \mathsf{ π} }}R\mathit{'}_{\rm{b}}^{\rm{2}}}}{Q_0}\frac{{\eta R{\mathit{'}_{\rm{b}}}}}{c}\left\{ \begin{array}{l} \;\;\gamma _{\rm{c}}^{3 - q}\;\;\;\;{\gamma _1}<{\gamma _{\rm{c}}}\\ {\gamma _{\rm{c}}}\gamma _1^{2 - q}\;\;\;\;{\gamma _{\rm{c}}}<{\gamma _1}\; \end{array} \right.. $ | (6) |
| $ V_{{\rm{peak}}}^{{\rm{syn}}} \propto \gamma _{\rm{b}}^2B\delta ,$ | (7) |
其中,γb为电子能谱分布(Electron Energy Distribution)转折处的洛伦兹因子;B为磁场强度。因此,康普顿主导和νpeaksyn之间的相关性可以转换为康普顿主导和γb2之间的相关性。
| $ {Q_{\rm{e}}}(\gamma ) = {Q_0}{\gamma ^{ - q}}H(\gamma ;{\gamma _1},{\gamma _2}),$ | (8) |
其中,H为亥维赛函数。冷却(包含同步冷却和逆康普顿冷却)之后的稳态电子能谱可以用拐折幂律谱描述:
| $ N(\gamma ) = \left\{ \begin{array}{l} {k_1}{\gamma ^{ - {q_1}}}\;\;\;\;{\gamma _1}<\gamma <{\gamma _{\rm{b}}}\\ {k_2}{\gamma ^{ - {q_2}}}\;\;\;\;{\gamma _{\rm{b}}}<\gamma <{\gamma _2}\; \end{array} \right.,$ | (9) |
其中,K2=K1γbq2-q1;q1, q2分别为电子谱在拐折前后的谱指数;γ1为电子的洛伦兹因子的最小值;γ2为其最大值。γc为冷却电子的洛伦兹因子[1]:
| $ {\gamma _{\rm{c}}} = \frac{{3{m_{\rm{e}}}{c^2}}}{{4c{\sigma _{\rm{T}}}(u{\mathit{'}_{\rm{B}}} + u{\mathit{'}_{{\rm{syn, tot}}}} + {\mathit{\Gamma }^2}{\mathit{u}_{{\rm{ext}}}}){\mathit{t}_{{\rm{esc}}}}}},$ | (10) |
其中,u′syn, tot为同步峰总能量密度。γc > γ1的情况对应慢冷却,此时,γb=γc,电子能谱可以近似为
| $ {N_{\rm{e}}}(\gamma ) \approx {Q_0}{\mathit{t}_{{\rm{esc}}}}\gamma _{\rm{c}}^{ - q}\left\{ \begin{array}{l} {(\gamma /{\gamma _{\rm{c}}})^{ - q}}\;\;\;\;{\gamma _1}<\gamma <{\gamma _{\rm{c}}}\\ {(\gamma /{\gamma _{\rm{c}}})^{ - q - 1}}\;\;{\gamma _{\rm{c}}}<\gamma <{\gamma _2}\; \end{array} \right.,$ | (11) |
而γc<γ1的情况对应快冷却,此时,γb=γ1,电子能谱为
| $ {N_{\rm{e}}}(\gamma ) \approx {Q_0}{\mathit{t}_{{\rm{esc}}}}{\gamma _{\rm{c}}}{\gamma _{\rm{1}}^{ - (q + 1)}}\left\{ \begin{array}{l} {(\gamma /{\gamma _{\rm{c}}})^{ - 2}}\;\;\;\;{\gamma _{\rm{c}}}<\gamma <1\\ {(\gamma /{\gamma _{\rm{c}}})^{ - q - 1}}\;\;{\gamma _{\rm{1}}}<\gamma <{\gamma _2}\; \end{array} \right.. $ | (12) |
文[20-23]发现δ和νpeaksyn之间存在反相关关系,这个关系可以具体求出。根据文[24-25],分别可知MBH~δ1.5,νpeaksyn~MBH-1.67。因此有δ~νpeaksyn-0.40。
快冷却机制下,根据(7)式,康普顿主导可以写成:
| $ CD = \frac{{{\sigma _{\rm{T}}}\eta {Q_0}{\gamma _{\rm{c}}}}}{{2{\rm{ \mathsf{ π} }}\mathit{c}R{\mathit{'}_{\rm{b}}}}}{\left( {\left. {\frac{1}{{B\delta }}} \right)} \right.^{1 - \frac{q}{2}}}{(\nu _{{\rm{peak}}}^{{\rm{syn}}})^{^{1 - \frac{q}{2}}}}. $ | (13) |
假设除δ和νpeaksyn外,其他量只贡献离散,那么该结果可以表示为
| $ \log CD = \left( {\left. {1 - \frac{\mathit{q}}{2}} \right)} \right.\log \nu _{{\rm{peak}}}^{{\rm{syn}}} + \left( {\left. {\frac{\mathit{q}}{2} - 1} \right)} \right.\log \delta ,$ | (14) |
有
| $ \log CD = 1.4\left( {\left. {1 - \frac{\mathit{q}}{2}} \right)} \right.\log \nu _{{\rm{peak}}}^{{\rm{syn}}}. $ | (15) |
慢冷却机制下,
| $ CD = \frac{{{\sigma _{\rm{T}}}\eta {Q_0}}}{{2{\rm{ \mathsf{ π} }}\mathit{c}R{\mathit{'}_{\rm{b}}}}}{\left( {\left. {\frac{1}{{B\delta }}} \right)} \right.^{\frac{{3 - q}}{2}}}{(\nu _{{\rm{peak}}}^{{\rm{syn}}})^{\frac{{3 - q}}{2}}},$ | (16) |
类似快冷却的处理,
| $ \log CD = 1.4\left( {\left. {\frac{{{\rm{3}} - \mathit{q}}}{2}} \right)} \right.\log \nu _{{\rm{peak}}}^{{\rm{syn}}}. $ | (17) |
由(15)式和(17)式知,logνpeaksyn和logCD之间存在线性关系,快冷却斜率为
对蝎虎天体有一个显著的反相关关系:logCD=(-0.54±0.09)logνsynpeak+(3.80±1.12) ,(p=0.002, r=-0.559)。假设蝎虎天体是快冷却机制,根据(15)式得到q=2.78;假设蝎虎天体是慢冷却机制,根据(17)式得到q=3.78。考虑到模型研究结果表明q的范围是2~3,例如:文[26-27]给出q~2;文[1]给出q=2.5;文[15]给出q=2.6;文[16]给出q=3;文[17]给出2.4 > q > 3;文[19]给出2.2 > q > 2.3;文[18]给出q~3,所以取q=2.78合理。但是因为该反相关具有一定的弥散,所以这个关系只能解释为蝎虎天体的主导冷却机制为快冷却。与文[1] 图 5中蝎虎天体样本相比,本文样本中高同步峰峰值频率的源较少,也有可能对分析结果有一定影响。
对于平谱射电类星体,高能辐射通常是由外康普顿过程主导[1, 12-13]。根据(3)式,康普顿主导可以得到:
| $ C{D_{{\rm{EC}}}} \propto \delta _{\rm{D}}^2{B^2}.$ | (18) |
考虑到B和δD只在相关关系中贡献离散,结合(7)式,那么logνpeaksyn和logCD之间不存在相关性,这和前述相关分析的结果是一致的。
如果把耀变体当作一个整体进行相关性分析,根据表 1的结果得到q=3.66 (对应快冷却)或者q=4.66(对应慢冷却),q值都与目前研究结果有较大出入,这表明把耀变体当作一个整体进行分析时,有可能导致一些非物理的结果,而按子类分别分析则可以避免这样的情况。
3.3 耀变体的谱指数图分析结果显示,对于整个样本,单独的平谱射电类星体和单独的蝎虎天体,Γγ和logνpeakIC之间存在显著的反相关性。这与前人的研究结果一致[7, 28-30]。
根据均匀的对数抛物线的电子能谱模型,考虑不同的康普顿散射机制,文[7]得到Γγ和logνpeakIC之间的关系:Γγ=d-klogνpeakIC。对于外康普顿过程,
值得注意的是,如果把耀变体看作一个整体,对应的线性回归斜率为k=-0.29 ± 0.02,无法从物理上解释这个斜率。但是容易看出这个斜率来自两个子类质心分开的贡献。这也再次表明,当平谱射电类星体和蝎虎天体在物理机制上不同时,简单地将它们当作一个整体进行相关性分析可能导致一个非物理的结果。
4 结论本文研究了来自费米二期的279个耀变体的准同时性数据,其中包括200个平谱射电类星体和79个蝎虎天体。分析结果表明,logνpeaksyn和logνLpeaksyn (ν)之间显著的反相关性存在于整个样本中,不存在于单独的平谱射电类星体和单独的蝎虎天体中。Γγ和logνpeakIC之间显著的反相关性存在于整个样本、单独的平谱射电类星体和单独的蝎虎天体中。logνpeaksyn和logLbol之间显著的反相关性存在于整个样本中,不存在于单独的平谱射电类星体和单独的蝎虎天体中。logνpeaksyn和logCD之间显著的反相关性存在于整个样本和单独的蝎虎天体中,不存在于单独的平谱射电类星体中。
数值模拟的结果表明,在整个样本的相关性中,平谱射电类星体和蝎虎天体质心的分离对于整个样本相关性的显著性有贡献,这有可能导致一个虚假的相关性。因此,至少在某些情况下,把耀变体的两个子类作为一个整体研究耀变体的统计趋势时,会导致一个虚假的相关性或者非物理的结果。
通过相关性分析认为,蝎虎天体的辐射区的电子冷却机制对应快速冷却机制,分析结果支持光谱指数图,为对数抛物线的电子能谱模型提供了观测上的支持。
| [1] | FINKE J D. Compton dominance and the blazar sequence[J]. The Astrophysical Journal, 2013, 763(2): article id. 134(11pp). |
| [2] | FAN J H, YANG J H, LIU Y, et al. The spectral energy distributions of Fermi blazars[J]. The Astrophysical Journal Supplement Series, 2016, 226(2): article id. 20(18pp). |
| [3] | FAN X L, BAI J M, MAO J R. What determines the observational differences of blazars?[J]. Research in Astronomy and Astrophysics, 2016, 16(11): 61–70. |
| [4] | GHISELLINI G. Extreme blazars[J]. Astroparticle Physics, 1999, 48(5): 375–380. |
| [5] | LYU F, LIANG E W, LIANG Y F, et al. Distributions of gamma-ray bursts and blazars in the L p-E p-plane and possible implications for their radiation physics[J]. The Astrophysical Journal, 2014, 793: article id. 36(8pp). |
| [6] | YAN D H, ZHANG L, ZHANG S N. Formation of very hard electron and gamma-ray spectra of flat spectrum radio quasar in fast-cooling regime[J]. Monthly Notices of the Royal Astronomical Society, 2015, 459(3): 423–426. |
| [7] | DERMER C D, YAN D H, ZHANG L, et al. Near-equipartition jets with log-parabola electron energy distribution and the blazar spectral-index diagrams[J]. The Astrophysical Journal, 2015, 809(2): article id. 174(13pp). |
| [8] | 余莲, 张雄, 张皓晶, 等. 类星体长周期光变分析方法的研究[J]. 天文研究与技术, 2019, 16(2): 139–150 DOI: 10.3969/j.issn.1672-7673.2019.02.003 |
| [9] | 任国伟, 张雄, 张皓晶, 等. Fermi耀变体的辐射特性和演化研究[J]. 天文研究与技术, 2019, 16(3): 253–261 DOI: 10.3969/j.issn.1672-7673.2019.03.001 |
| [10] | DING N, ZHANG X, XIONG D R, et al. The physical properties of Fermi TeV BL Lac objects' jets[J]. Monthly Notices of the Royal Astronomical Society, 2017, 464(1): 599–612. DOI: 10.1093/mnras/stw2347 |
| [11] | XUE R, LUO D, DU L M, et al. Curvature of the spectral energy distribution, the inverse Compton component and the jet in Fermi 2LAC blazars[J]. Monthly Notices of the Royal Astronomical Society, 2016, 463(3): 2038–3050. |
| [12] | NALEWAJKO K, GUPTA M. The sequence of Compton dominance in blazars based on data from WISE andr, Fermir, -LAT[J]. Astronomy & Astrophysics, 2017, 606: article id. A44(8pp). |
| [13] | GHISELLINI G, TAVECCHIO F, FOSCHINI L, et al. General physical properties of bright Fermi blazars[J]. Monthly Notices of the Royal Astronomical Society, 2010, 402(1): 497–518. DOI: 10.1111/j.1365-2966.2009.15898.x |
| [14] | BOULA S, KAZANAS D, MASTICHIADIS A. Accretion disk MHD winds and blazar classification[J]. Monthly Notices of the Royal Astronomical Society, 2018, 482: article id. L80(5pp). |
| [15] | RUEDA-BECERRIL J M, MIMICA P, ALOY M A. The influence of the magnetic field on the spectral properties of blazars[J]. Monthly Notices of the Royal Astronomical Society, 2014, 438(2): 1856–1869. DOI: 10.1093/mnras/stt2335 |
| [16] | DERMER C D. The extragalactic γ ray background[C]//Proceedings of AIP Conference. 2007. http://adsabs.harvard.edu/abs/2007arXiv0704.2888D |
| [17] | BÖTTCHER M, REIMER A. Modeling the multiwavelengthspectra and variability of BL Lacertae in 2000[J]. The Astrophysical Journal, 2004, 609(2): 576–588. DOI: 10.1086/421320 |
| [18] | YANG J P, WANG J C. Mechanism of very high energy radiation in BL Lacertae object 3C 66A[J]. Astronomy & Astrophysics, 2009, 511(1): 197–277. |
| [19] | ACHTERBERG A, GALLANT Y A, KIRK J G, et al. Particle acceleration by ultrarelativistic shocks:theory and simulations[J]. Monthly Notices of the Royal Astronomical Society, 2001, 328(2): 393–408. DOI: 10.1046/j.1365-8711.2001.04851.x |
| [20] | NIEPPOLA E, VALTAOJA E, TORNIKOSKI M, et al. Blazar sequence-an artefact of Doppler boosting[J]. Astronomy & Astrophysics, 2009, 488(3): 867–872. |
| [21] | WU Z, JIANG D R, GU M, et al. VLBI observations of seven BL Lacertae objects, from RGB sample[J]. Astronomy and Astrophysics, 2007, 466(1): 63–73. DOI: 10.1051/0004-6361:20066754 |
| [22] | LISTER M L, HOMAN D C, HOVATTA T, et al. MOJAVE. XVⅡ. jetkinematics and parent population properties of relativistically beamed radio-loud blazars[J]. The Astrophysical Journal, 2019, 874: 43. DOI: 10.3847/1538-4357/ab08ee |
| [23] | VALTAOJA E, LINDFORS E, SALORANTA P M, et al. Hydrodynamics of small-scale jets: observational aspects[C]//Proceedings of ASP Conference Series. 2008. Hydrodynamics of small-scale jets: observational aspects |
| [24] | ARSHAKIAN T G, CHAVUSHYAN V H, ROS E, et al. Radio-optical scrutiny of the central engine in compact AGN[J]. Memorie della Società Astronomica Italiana, 2004, 76: 35–38. |
| [25] | CHEN L, BAI J M. Implications on the blazar sequence and inverse Compton models from Fermi bright blazars[J]. The Astrophysical Journal, 2011, 735(2): 395–402. |
| [26] | YAN D, ZHANG L, ZHANG S N. Formation of very hard electron and gamma-ray spectra of flat spectrum radio quasar in fast-cooling regime[J]. Monthly Notices of the Royal Astronomical Society, 2015, 459(3): 423–426. |
| [27] | QIN L H, WANG J C, YANG C Y, et al. Using the Markov Chain Monte Carlo method to study the physical properties of GeV-TeV BL Lac objects[J]. Publications of the Astronomical Society of Japan, 2018, 70(1): article id. 5. |
| [28] | ABDO A A, ACKERMANN M, AJELLO M, et al. The first catalog of active galactic nuclei detected by the Fermi Large Area Telescope[J]. The Astrophysical Journal, 2010, 715(1): 429–457. |
| [29] | ACKERMANN M, AJELLO M, ALLAFORT A, et al. The second catalog of active galactic nuclei detected by the Fermi Large Area Telescope[J]. The Astrophysical Journal, 2011, 743(2): article id. 171(37pp). |
| [30] | ACKERMANN M, AJELLO M, ATWOOD W B, et al. The third catalog of active galactic nuclei detected by the Fermi Large Area Telescope[J]. The Astrophysical Journal, 2015, 80(1): article id. 14(34pp). |



