在核反应堆屏蔽物理计算中,需要同时考虑对于中子和光子的屏蔽作用。准确的屏蔽计算可以为屏蔽设计提供重要依据,而屏蔽数据库的精度是影响核反应堆屏蔽物理计算的重要因素,因此需要获得高精度的屏蔽数据库用于核反应堆屏蔽物理计算。影响屏蔽数据库精度的因素主要有共振自屏计算方法以及屏蔽数据库能群结构[1]。由于多采用阈能反应的反应率作为探测器响应,所以能群结构的选择应确保可获得准确的快中子注量率,同时又因为热中子对于光子的产生更为重要,因此为保证光子注量率计算结果的准确性,需要在选择能群结构时兼顾热中子注量率的计算精度。
国际常用的屏蔽数据库为BUGLE-B7数据库[2],由美国橡树岭国家实验室基于ENDF/B-Ⅶ.0评价核数据库[3]制作得到。该屏蔽数据库能群结构为47群中子、20群光子,快中子能群(>0.1 MeV) 为26群,可保证计算得到的快中子注量率以及探测器响应的准确性,但热中子能群(< 5.043 5 eV)仅有5群,使计算得到的热中子注量率以及光子注量率存在较大偏差。国内外已针对屏蔽数据库的能群结构优化进行了部分研究,Alpan[4]提出了CPXSD方法对屏蔽数据库能群结构进行优化,对不同能群结构计算结果进行对比;文献[5]在AP1000的1维模型上基于响应贡献理论对中子、光子能群结构进行优化,改进中子、光子注量率计算结果,但并没有将优化后的能群结构应用于辐射屏蔽基准题的计算中。
本文在文献[6]自主研发的核数据处理程序NECP-Atlas的基础上,开发了屏蔽数据库制作功能模块shield_calc,并对其进行了验证。针对验证过程中BUGLE-B7数据库能群结构存在的对热中子注量率以及光子注量率计算不准确等问题,基于响应贡献理论[7]对BUGLE-B7数据库的热群以及超热群能群结构进行了优化,在保证探测器响应计算结果不变的情况下,使计算得到的热中子注量率以及光子注量率更加准确。
1 屏蔽数据库能群结构优化方法 1.1 屏蔽数据库制作理论屏蔽数据库的制作主要包括3部分:细群截面数据库的产生、基于典型问题的共振自屏计算以及问题相关的宽群截面数据库的制作。
1.1.1 细群截面数据库的产生细群截面数据库选用MATXS格式[8],该格式数据库可存储多种类型的数据,例如:不同温度和背景截面下的截面数据、任意阶数的散射矩等,并且MATXS格式数据库具有拓展性强,便于维护等特点,便于扩展用于储存多种粒子的截面数据。
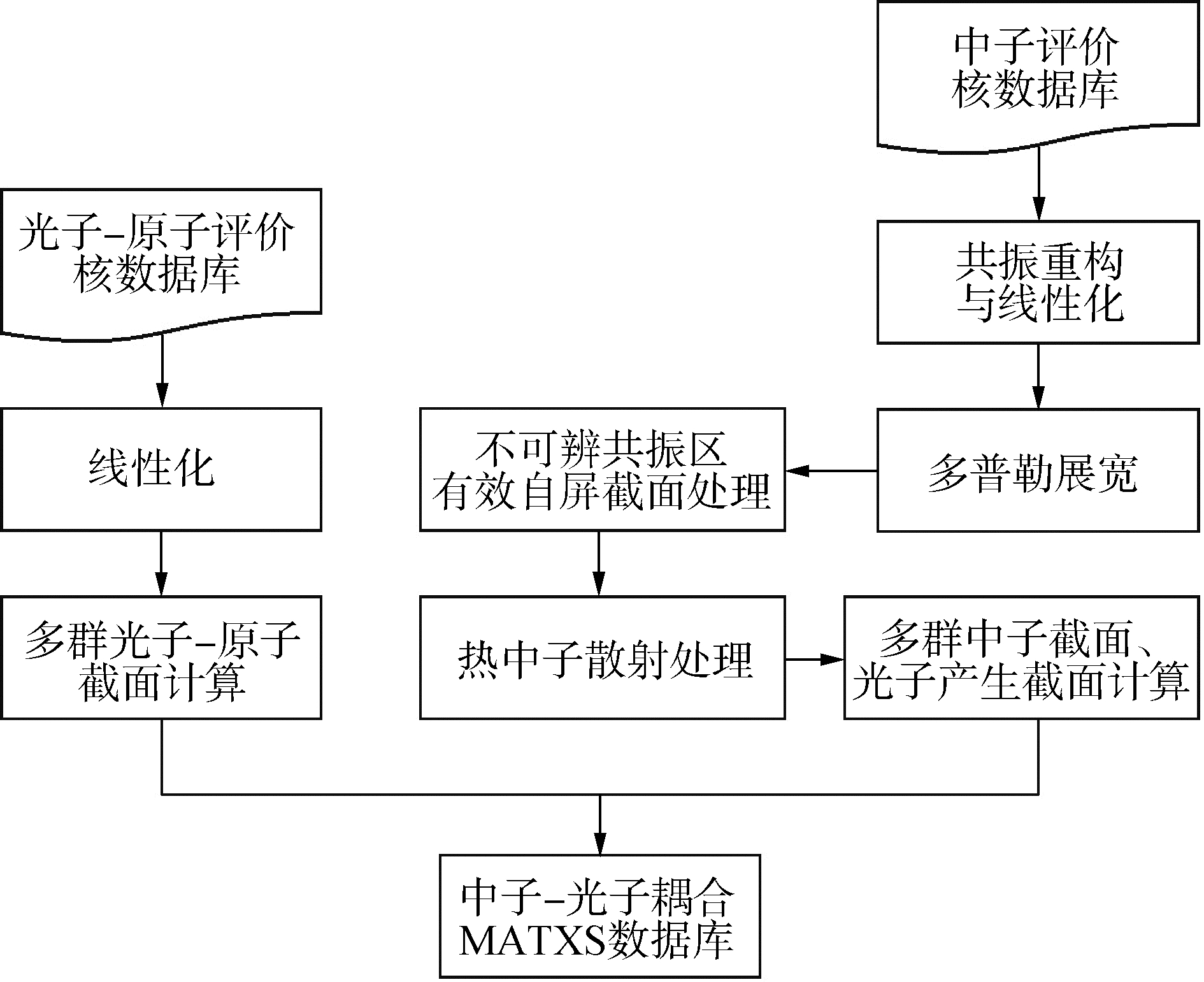
中子、光子耦合截面数据库制作流程如图 1所示。中子截面和中子-光子散射矩阵数据可由评价核数据经过共振重构与线性化、多普勒展宽、不可辨共振区有效自屏截面处理、热中子散射处理以及能群归并获得。对于多群光原子截面的计算,只需要对评价核数据库中给出的截面数据进行线性化以及能群归并即可。图 1为MATXS格式细群截面数据库的制作流程,图中涉及到的NECP-Atlas中各功能模块理论见文献[6]。
|
Download:
|
| 图 1 中子-光子耦合MATXS数据库制作流程 Fig. 1 Procedure for generating coupled neutron-photon MATXS library | |
以上处理过程中,能群结构选用与VITAMIN-B7能群结构相同的199群中子、42群光子;中子权重谱选用fission spectrum+1/e + maxwellian谱;光子权重谱选用1/e+rolloffs谱;勒让德阶数选择为P5;温度点选择为300、600、1 000和2 100 K;数据库中的背景截面选择为1010、106、105、104、1 000、300、100、50、10、1和0.1靶恩。
1.1.2 共振自屏计算获得问题无关的MATXS格式细群截面数据库后,需针对应用堆型开展共振自屏计算,获得问题相关的有效自屏截面。共振计算需处理的典型结构包括压水堆典型燃料栅元、下降水、碳钢、不锈钢以及混凝土等模型。
BUGLE数据库制作时,基于Bondarenko方法进行共振自屏计算,丹可夫因子的计算基于Sauer方法处理燃料栅元的共振自屏。本文为实现对不同反应堆堆型的共振自屏计算,采用超细群方法耦合Bondarenko方法分别处理共振能量段以及非共振能量段的共振自屏效应,可实现对于一维压水堆典型燃料栅元、一维球栅元、一维板栅元以及均匀材料的共振自屏计算。
在共振能量段,采用超细群方法进行共振自屏计算:
| $ {\Sigma _{t, i}}\left( E \right){\phi _i}\left( E \right){V_i} = \sum\limits_j {{P_{j \to i}}\left( E \right){V_j}{S_j}\left( E \right)} $ | (1) |
式中:Σt, i(E)为区域i的宏观总截面;ϕi(E)为注量率;Vi为区域i的体积;Pj→i(E)为区域j到区域i的碰撞概率;Sj(E)为散射源项,可表示为:
| $ {S_j}\left( E \right) = \int_0^\infty {dE\prime {\Sigma _{s, j}}(E\prime \to E){\phi _j}\left( {E\prime } \right)} $ | (2) |
碰撞概率Pj→i(E)针对不同的几何采用Carlvik方法进行计算[9]。对于方程(1)右侧散射源项的计算,采用递推方法提高计算效率,具体方法可见文献[10]。
对于非共振能量段,采用Bondarenko方法计算有效自屏截面,该方法通过背景截面插值细群截面数据库中的共振积分表获得核素的有效自屏截面,区域I中核素r的背景截面可表示为:
| $ \sigma _0^{I, r} = \frac{1}{{N_r^I}}\left( {\sum\limits_{j \ne r} {N_j^I\sigma _t^{I, \mathit{j}} + \Sigma _e^I} } \right) $ | (3) |
式中:NrI、NjI分别为区域I中核素r、j的核子密度;σtI, j为区域I中核素j的微观总截面;ΣeI为区域I的宏观逃脱截面。
对于无限均匀混合物,宏观逃脱截面ΣeI为0;对于非均匀问题,宏观逃脱截面可通过碰撞概率方法求解,区域I到区域J的碰撞概率为:
| $ \sum\limits_{J \ne I} {{P^{I \to J}} = \left( {\frac{{\mathit{\Sigma }_e^I}}{{\mathit{\Sigma }_t^I + \mathit{\Sigma }_e^I}}} \right)} $ | (4) |
由式(4)可知,区域I的碰撞概率可表示为:
| $ \mathit{\Sigma }_e^I = \mathit{\Sigma }_t^I\left( {\frac{{1 - \sum\limits_{J \ne I} {{P^{I \to J}}} }}{{\sum\limits_{J \ne I} {{P^{I \to J}}} }}} \right) $ | (5) |
式中:PI→J为区域I到区域J的碰撞概率;ΣtI为区域I的宏观总截面。
在Bondarenko方法中,式(4)中的碰撞概率计算与区域I的宏观总截面有关,但宏观总截面又是由背景截面插值得到的,因此,需要通过迭代计算求解区域I中核素的有效自屏截面。
利用上述超细群方法以及Bondarenko方法,可根据具体问题模型进行共振自屏计算,获得问题相关的细群有效自屏截面。
1.1.3 能群归并得到问题相关的细群截面库后,为提高计算效率,需要利用典型能谱对细群截面数据库进行能群归并得到宽群截面数据库。为获得精确的并群权重能谱,利用NECP-Hydra[11]基于一维典型压水堆模型进行离散纵标输运计算,获得并群过程中使用的权重能谱,主要包括堆芯、下降水、压力容器1/4厚度以及混凝土位置处的中子注量率,一维典型压水堆模型如图 2所示。基于反应率守恒,对共振自屏后的细群截面库进行能群归并,得到宽群截面数据库,宽群截面数据库可采用BUGLE数据库中的ANISN格式进行输出。

|
Download:
|
| 图 2 一维典型压水堆模型 Fig. 2 1-D typical PWR model | |
由于BUGLE数据库的47群中子能群结构中热群只有5群,导致计算得到的热中子注量率与细群计算结果存在较大偏差,而热中子是光子的重要来源,热中子注量率计算结果不准确会导致光子注量率的计算结果不可信。因此在保证快群能群结构不变的情况下,基于响应贡献理论对热群以及超热群能群结构进行优化,使优化后的能群结构在保证探测器响应计算准确的情况下,可同时获得较为准确的热中子注量率以及光子注量率。
中子对于某一能群的响应贡献C(E)可表示为:
| $ C\left( E \right) = {\smallint _V}{\rm{d}}r{\smallint _\mathit{\Omega }}{\rm{d}}\mathit{\Omega }\psi \left( {r, E, \Omega } \right){\psi ^*}\left( {r, E, \mathit{\Omega }} \right) $ | (6) |
式中:ψ(r, E, Ω)、ψ*(r, E, Ω)分别表示位置r处、能量为E、方向为Ω的前向以及共轭中子角通量。
在实际计算中,对前向以及共轭中子角通量进行球谐函数展开,并且只采用0阶标通量,多群形式的响应贡献可表示为:
| $ {C_g} = \sum\limits_i {{V_i}{\phi _{g, i, 0}}\phi _{g, i, 0}^*} $ | (7) |
式中:Cg表示初始细群第g群的响应贡献;Vi表示材料区i的体积;ϕg, i, 0和ϕg, i, 0*表示细群的前向注量率和共轭注量率。
细群的前向注量率和共轭注量率可基于图 2所示一维典型压水堆模型,通过求解前向以及共轭输运方程获得。共轭输运计算的共轭源项采用探测器响应截面,此时响应贡献表示为探测器响应。
响应贡献理论的基本思想为对响应贡献较小的能群进行归并;对于响应贡献较大的能群,表示其对探测器响应的贡献较为重要,对该能群进行细化,从而使优化后的能群结构更加合理,计算结果更加精确[12]。在能群结构优化过程中,由于探测器响应主要对于能量范围大于0.1 MeV的快中子敏感,且经过了广泛的验证,因此本文在能群结构优化过程中对于能量范围大于0.1 MeV的能群结构采用与BUGLE-B7相同的能群结构,只针对能量范围小于0.1 MeV的能群结构进行优化。由于核反应堆中光子主要由裂变反应和辐射俘获反应产生,且上述2种反应类型主要由热中子主导,因此对于能量范围小于5.043 5 eV的热中子能群进行单独优化。对于某一特定能群,最终得到的宽群第G群的中子贡献CG为:
| $ {C_G} = \sum\limits_{g \in G} {{C_g}} = \frac{{{C_T}}}{H} \approx \frac{{{C_T}}}{H} + \varepsilon $ | (8) |
式中:Cg表示宽群中所包含细群的中子贡献;CG表示该能量段总的中子贡献;H表示该能量段中划分的宽群数目;ε为误差。
基于上述响应贡献理论,选用VITAMIN-B7能群结构作为初始细群能群结构计算中子注量率以及共轭注量率,根据计算得到的热群以及超热群中子响应贡献对热群以及超热群能群结构进行优化,得到优化后的47群中子能群结构如表 1所示。
| 表 1 基于响应贡献理论优化后的能群结构 Table 1 The optimal energy-group structure based on contributon theory |
基于上述屏蔽数据库制作过程,在核数据处理程序NECP-Atlas中开发了屏蔽数据库制作功能模块shield_calc,利用与BUGLE-B7数据库相同的能群结构以及评价核数据库ENDF/B-Ⅶ.0制作了NECL-SHIELD数据库;根据基于响应贡献理论优化得到的能群结构制作了NECL-SHIELD-NEW数据库。利用SN输运程序NECP-Hydra基于上述屏蔽数据库对SINBAD屏蔽基准题库中的PCA基准题[13]、HBR-2基准题[14]以及VENUS-3基准题[15]进行计算。对于快中子计算结果的准确性通过探测器响应进行验证,并与BUGLE-B7验证报告中给出的计算结果进行对比;热中子和光子主要关注利用上述2个数据库计算得到的热中子注量率和光子注量率与细群计算结果的相对偏差。
2.1 探测器响应探测器响应多采用阈能反应的反应率进行量化,因此快中子注量率在进行探测器响应计算时更为重要。以下将对上述3道屏蔽基准题中给出的不同位置处探测器响应进行计算,并与实验结果进行对比验证。
PCA基准题中给出了103Rh(n, n′)、115In(n, n′)以及32S(n, p)探测器反应率。利用NECL-SHIELD以及NECL-SHIELD-NEW数据库对PCA基准题进行计算。图 3给出了利用上述2个屏蔽数据库计算得到的3种探测器的计算结果与实验结果的比值(C/E值)以及BUGLE-B7验证报告中给出的计算结果。由图可以看出,3种探测器反应率的C/E值范围为0.85~1.1,满足美国核学会给定的计算值与实验值偏差小于20%的要求[16]。同时利用NECP-Atlas制作的屏蔽数据库计算结果与BUGLE-B7验证报告中给出的计算结果吻合较好。

|
Download:
|
| 图 3 PCA基准题中不同探测器反应率C/E值 Fig. 3 Different detector reaction rate ratios calculated in PCA benchmark | |
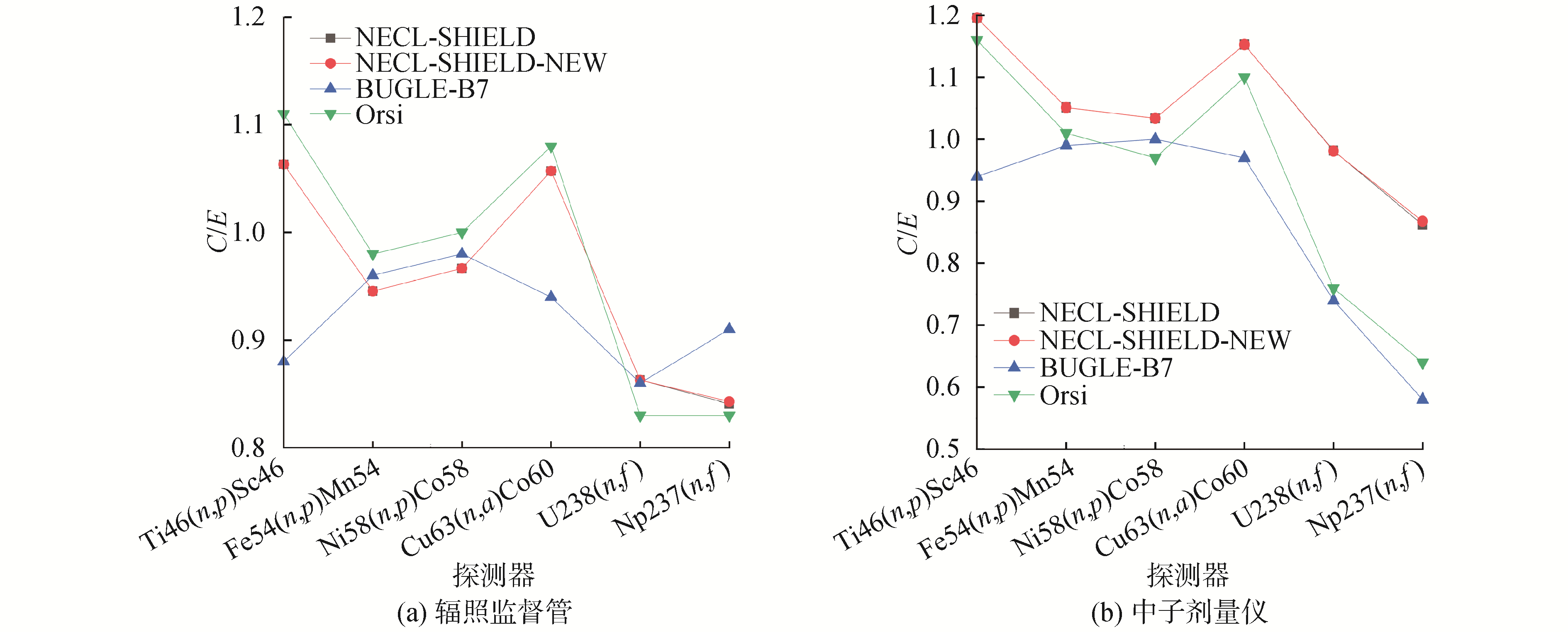
HBR-2基准题中给出了辐照监督管和中子计量仪处的46Ti(n, p)、54Fe(n, p)、58Ni(n, p)、63Cu(n, a)、238U(n, f)以及237Np(n, f)探测器反应率。图 4给出了利用上述2个屏蔽数据库计算得到的辐照监督管和中子计量仪处不同探测器的C/E值。由图 4可以看出,利用上述2个屏蔽数据库计算得到的辐照监督管和中子计量仪处不同探测器的C/E值均在0.8~1.2,与实验结果吻合较好。由于在BUGLE-B7验证过程中,采用DORT程序计算得到一维注量率和二维注量率,重构得到三维注量率,导致计算结果存在一定的偏差,同时在计算过程中模型的网格划分不同也会对结果造成影响。图 4中同时给出了文献[17]中的计算结果,其使用TORT[18]程序建立3维模型进行计算。由图可以看出,NECL-SHIELD数据库计算结果在中子计量仪238U(n, f)和237Np(n, f)探测器处反应率C/E值均优于BUGLE-B7验证报告以及文献[17]中给出的计算结果。
|
Download:
|
| 图 4 HBR-2基准题不同位置探测器反应率C/E值 Fig. 4 Reaction rate ratios calculated for the dosimeters in HBR-2 benchmark | |
VENUS-3基准题中给出了115In(n, n′)、58Ni(n, p)以及27Al(n, a)探测器的等效裂变注量率。图 5给出了利用上述2个屏蔽数据库计算得到的3种反应探测器的等效裂变注量率的C/E值。由图 5可以看出,对于115In(n, n′)探测器,所有位置处探测器C/E值均在0.9~1.15,与实验值吻合较好。对于58Ni(n, p)探测器,除在第153号、167号、174号以及244号探测器处NECL-SHIELD计算结果与BUGLE-B7计算结果存在较大偏差外,其他位置处58Ni(n, p)探测器的等效裂变注量率C/E值均与BUGLE-B7验证报告计算结果吻合较好。对于27Al(n, a)探测器,在前2个探测器处NECL-SHIELD计算结果明显优于BUGLE-B7计算结果,其他位置处27Al(n, a)探测器的等效裂变注量率C/E值与BUGLE-B7验证报告中给出的结果精度相当。

|
Download:
|
| 图 5 VENUS-3基准题不同探测器反应率C/E值 Fig. 5 Different detector reaction rate ratios calculated in VENUS-3 benchmark | |
NECL-SHIELD-NEW数据库基于响应贡献理论对热群以及超热群能群结构进行优化,在保证原有探测器响应计算结果不变的情况下,对热中子注量率以及光子注量率计算结果进行优化。计算基准题选用上述PCA基准题、HBR-2基准题以及VENUS-3基准题,分别统计不同探测器位置处热中子注量率以及光子注量率,并与采用VITAMIN-B7细群能群结构数据库(细群)的计算结果进行对比。
PCA基准题中10个探测器位置处热中子注量率以及光子注量率计算结果及相对偏差如图 6所示,利用BUGLE-B7数据库的能群结构制作的NECL-SHIELD数据库计算得到的热中子注量率和光子注量率与细群计算结果的平均相对偏差分别为108.45%和98.53%,其中第6个探测器位置处热中子注量率相对偏差最大,为164.18%;第10个位置处光子注量率相对偏差最大,为168.98%。基于能群结构优化后的NECL-SHIELD-NEW数据库计算得到的热中子注量率平均相对偏差为14.09%,光子注量率平均相对偏差为18.91%,计算精度均有明显的提高。

|
Download:
|
| 图 6 PCA基准题不同探测器位置处热中子、光子注量率计算结果及相对偏差 Fig. 6 Calculated results and bias of thermal neutron flux and photon flux in different detector positions in PCA benchmark | |
HBR-2基准题中主要关注辐照监督管和中子计量仪位置处的探测器响应,分别统计2个位置处的热中子注量率以及光子注量率,如表 2和表 3所示。计算结果表明,在中子剂量仪位置处,利用NECL-SHIELD-NEW数据库计算得到的热中子注量率相对偏差较NECL-SHIELD数据库计算结果有明显改善,热中子注量率和光子注量率相对偏差减小为NECL-SHIELD数据库计算结果的1/3左右。且在辐照监督管位置处热中子注量率和光子注量率计算结果也均有所改善。
| 表 2 HBR-2基准题不同位置处热中子注量率 Table 2 Thermal neutron flux in different positions in HBR-2 benchmark |
| 表 3 HBR-2基准题不同位置处光子注量率 Table 3 Photon flux in different positions in HBR-2 benchmark |
VENUS-3基准题中3种探测器不同位置处热中子注量率以及光子注量率计算结果及相对偏差如图 7~9所示。对于115In(n, n′)探测器、58Ni(n, p)探测器和27Al(n, a)探测器不同位置处热中子注量率的计算结果相对偏差分别从88.81%、70.15%和82.73%减小为29.49%、18.86%和32.80%;对于上述3种探测器,光子注量率计算结果的相对偏差从60%减小到10%左右。

|
Download:
|
| 图 7 VENUS-3基准题115In(n, n′)探测器位置处热中子、光子注量率计算结果及相对偏差 Fig. 7 Calculated results and bias of thermal neutron flux and photon flux in 115In(n, n′) detector positions in VENUS-3 benchmark | |

|
Download:
|
| 图 8 VENUS-3基准题58Ni(n, p)探测器位置处热中子、光子注量率计算结果及相对偏差 Fig. 8 Calculated results and bias of thermal neutron flux and photon flux in 58Ni(n, p) detector positions in VENUS-3 benchmark | |

|
Download:
|
| 图 9 VENUS-3基准题27Al(n, a)探测器位置处热中子、光子注量率计算结果及相对偏差 Fig. 9 Calculated results and bias of thermal neutron flux and photon flux in 27Al(n, a) detector positions in VENUS-3 benchmark | |
通过以上结果可以发现,当热中子计算结果精度提高后,光子注量率的计算精度也会随之提高。因此,在屏蔽计算中要想获得可信的光子计算结果,需要保证热中子计算结果的准确性。
3 结论1) 在核数据处理程序NECP-Atlas中开发了屏蔽数据库制作功能模块shield_calc,利用与BUGLE-B7数据库相同的能群结构制作得到了NECL-SHIELD屏蔽数据库,并利用PCA基准题、HBR-2基准题和VENUS-3基准题验证了制作得到的屏蔽数据库的正确性。
2) 利用验证后的屏蔽数据库制作流程,针对BUGLE-B7数据库对热中子注量率以及光子注量率计算不准确等问题,基于响应贡献理论对热群以及超热群能群结构进行了优化,制作得到了NECL-SHIELD-NEW数据库,并对上述屏蔽基准题中探测器位置处热中子注量率以及光子注量率进行了计算,使屏蔽数据库计算结果与细群数据库计算结果更加吻合,改善了BUGLE-B7数据库对热中子以及光子计算结果不准确的问题。
| [1] |
ALPAN F A. An advanced methodology for generating multigroup cross sections for shielding calculations[D]. Stetkolich: The Pennsylvania State University, 2003.
(  0) 0)
|
| [2] |
RISNER J M, WIARDA D, DUNN M E, et al. Production and testing of the VITAMIN-B7 fine-group and BUGLE-B7 broad-group coupled neutron/gamma cross-section libraries derived from ENDF/B-Ⅶ. 0 nuclear data (ORNL/TM-2011/12)[R]. Washington: U.S. Nuclear Regulatory Commission, 2011.
(  0) 0)
|
| [3] |
CHADWICK M B, OBLOŽINSKÝ P, HERMAN M, et al. ENDF/B-Ⅶ.0: next generation evaluated nuclear data library for nuclear science and technology[J]. Nuclear data sheet, 2006, 107(12): 2931-3060. DOI:10.1016/j.nds.2006.11.001 (  0) 0)
|
| [4] |
ALPAN A, HAGHIGHAT A. Advanced methodology for selecting group structures for multigroup cross section generation[C]. PHYSOR2000. Pittsburgh, 2000.
(  0) 0)
|
| [5] |
HU Jiaju, ZHANG Bin, DAI Ni, et al. Optimization algorithms based on contribution theory for broad-group energy structures in shielding calculation[J]. Radiation physics and chemistry, 2021, 186: 109547. DOI:10.1016/j.radphyschem.2021.109547 (  0) 0)
|
| [6] |
ZU Tiejun, XU Jialong, TANG Yongqiang, et al. NECP-Atlas: a new nuclear data processing code[J]. Annals of nuclear energy, 2019, 123: 153-161. DOI:10.1016/j.anucene.2018.09.016 (  0) 0)
|
| [7] |
WILLIAMS M L. Generalized contributon response theory[J]. Nuclear science and engineering, 1991, 108(4): 355-383. DOI:10.13182/NSE90-33 (  0) 0)
|
| [8] |
MACFARLANE R, MUIR D W, BOICOURT R M, et al. The NJOY nuclear data processing system. LA-UR-17-20093[R]. Los Alamos: Los Alamos National Laboratory, 2016.
(  0) 0)
|
| [9] |
谢仲生. 压水堆核电厂堆芯燃料管理计算及优化[M]. 北京: 原子能出版社, 2001. XIE Zhongsheng. Calculation and optimization of core fuel management for PWR nuclear power plant[M]. Beijing: Atomic Energy Press, 2001. (  0) 0)
|
| [10] |
ZU Tiejun, YIN Wen, HE Qingming, et al. Application of the hyperfine group self-shielding calculation method to the lattice and whole-core physics calculation[J]. Annals of nuclear energy, 2020, 136: 107045. DOI:10.1016/j.anucene.2019.107045 (  0) 0)
|
| [11] |
XU Longfei, CAO Liangzhi, ZHENG Youqi, et al. Development of a new parallel SN code for neutron-photon transport calculation in 3-D cylindrical geometry[J]. Progress in nuclear energy, 2017, 94: 1-21. DOI:10.1016/j.pnucene.2016.09.005 (  0) 0)
|
| [12] |
YANG Shouhai, XU Jialong, ZU Tiejun, et al. Optimization of energy-group structure for LWR high-fidelity neutronics calculation based on the contributon theory[J]. Journal of nuclear science and technology, 2020, 57(4): 421-432. DOI:10.1080/00223131.2019.1691074 (  0) 0)
|
| [13] |
PESCARINI M, ORSI R. PCA-Replica (H2O/Fe) Neutron Shielding Benchmark Experiment-Deterministic Analysis in Cartesian (X, Y, Z) Geometry Using the TORT-3. 2 3D Transport Code and the BUGJEFF311. BOLIB, BUGENDF70. BOLIB and BUGLE-96 Crosss Section Libraries (UTFISSM-P9H6-009)[R]. ENEA-Bologna Technical Report, 2014.
(  0) 0)
|
| [14] |
REMEC I, KAM F H.B. Robinson-2 pressure vessel benchmark[R]. Washington: Oak Ridge National Lab., 1998.
(  0) 0)
|
| [15] |
LEENDERS L. LWR-PVS benchmark experiment VENUS-3[R]. FCP/VEN/01, 1988.
(  0) 0)
|
| [16] |
ANS 6.1.2, Group-averaged neutron and gamma-ray cross sections for radiation protection and shielding calculations for nuclear power plants[S]. Illinois: American Nuclear Society, 2013.
(  0) 0)
|
| [17] |
ORSI RHB. Robinson-2 pressure vessel dosimetry benchmark: deterministic three-dimensional analysis with the TORT transport code[J]. Nuclear engineering and technology, 2020, 52(2): 448-455. DOI:10.1016/j.net.2019.07.025 (  0) 0)
|
| [18] |
RHOADES W A, SIMPSON D B. The TORT three-dimensional discrete ordinates neutron/photon transport code (TORT Version 3)[R]. Washington: ORNL Report ORNL/TM-13221, 1997.
(  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


