2. 陕西师范大学 应用声学研究所, 陕西 西安 710119
2. Applied Acoustics Institute, Shaanxi Normal University, Xi'an 710119, China
超声波技术应用的关键部件之一是超声换能器,它可将交变的电信号转换成声振动信号或将声振动信号转换为电信号。有电致伸缩和磁致伸缩换能器之分。根据不同的用途,又可设计成多种形状的换能器,如复合棒型[1-3]、弯张型[4-5]、钹型[6-7]、镶拼圆环(圆管)型[8]以及各种模式转换型[9]换能器等。复合棒型换能器结构较简单,又因其具有大强度、机电转换效率高等特性,在工业、农业、医学、军事等领域中有广泛的应用。如将其前盖板做成锥体喇叭形,可用于超声清洗;若将前盖板做成薄喇叭形,可以将振动以声波形式辐射出去;若将前盖板振动聚集成一小半径的柱形,可用作超声乳化;若前端柱形半径小到如钢针般,可用作超声打孔;若将前盖板设计成薄刃刀形,可用作为超声手术刀等。这种复合棒型换能器也可作为单元布阵用。
一般地说,换能器的振动特性与组成部件的材料有关, 如不同的组件材料,换能器的振幅、带宽、阻抗等有可能不一样[10-12], 但当换能器前端面为大面积辐射板向流体中辐射声场时,其辐射声场的分布却与何种材料的辐射板没有直接关系[13]。通常无论是小功率的检测型、接收型换能器,还是大功率的主动声呐水声或功率超声换能器,无论何种类型、何种形状的超声换能器结构中,与有源材料相连接的前后盖板一般均被设计为金属材料,如钢、不锈钢、铝合金、钛合金等。用于变幅或传振的杆件一般也为金属质材料。很少见到用非金属材料作为换能器组件。换能器的组件不为非金属材料主要原因是,非金属材料的机械损耗较高,似乎不适于传播机械振动。
近年来,日本学者的研究表明,一种称为聚苯硫醚的高分子功能材料作为一振动体部件用在了超声马达上,可获得较高的振动振幅[14]。这种换能器的特点是虽有一定的机械损耗,但超声马达的质量较轻。这启发我们可以利用较低损耗因子的非金属材料研制满足高频激振所需用于机械天线的换能器。本文研制了一种压电陶瓷、前盖板为非金属材料的换能器,为了得到较大振幅,谐振频率设计在16 kHz左右,一定加载电压下能实现高振幅度振动。若以前端面振幅与质量比值(输出-质量比)作为评价指标,将高于前盖板为金属材料换能器的比值。
1 PPS材料力学参数测定聚合物的形变性质介于理想弹性体和理想粘性体之间,存在着粘弹性效应,这是聚合物材料的重要特性[15]。衡量粘弹性效应时,弹性模量往往由2个部分组成,称为复数模量:
| $ {E^*} = {E_1} + {\rm{j}}{E_2} $ | (1) |
式中:实数部分称为储能模量,表示应变作用下能量在试样中的储存;虚数部分称为损耗模量,表示能量的损耗。由粘弹性效应导致的能量耗散可以用损耗因子tanδ表示:
| $ {\rm{tan}}\;\delta = \frac{{{E_2}}}{{{E_1}}} $ | (2) |
式中δ为滞后相位角,也称损耗角。
首先比较了PPS、POM、ABS、PBT等几种非金属材料,最终选取了损耗因子较低的PPS高聚物作为换能器的前盖板材料。为能准确设计,对国内生产的PPS材料(密度1 740 kg/m3,泊松比0.36)利用动态热机械分析仪进行了力学参数测试。
聚合物的同一力学松弛现象可以在较高的温度、较短的时间(或较高的作用频率)观察到,也可以在较低的温度下、较长时间内观察到。因此,升高温度与延长观察时间对分子运动是等效的,对聚合物的粘弹性效应也是等效的,称为时温等效原理(time temperature superposition, TTS)[15]。由此可以通过测试材料低温下较低频率的性能参数等效得到高频下的性能参数。
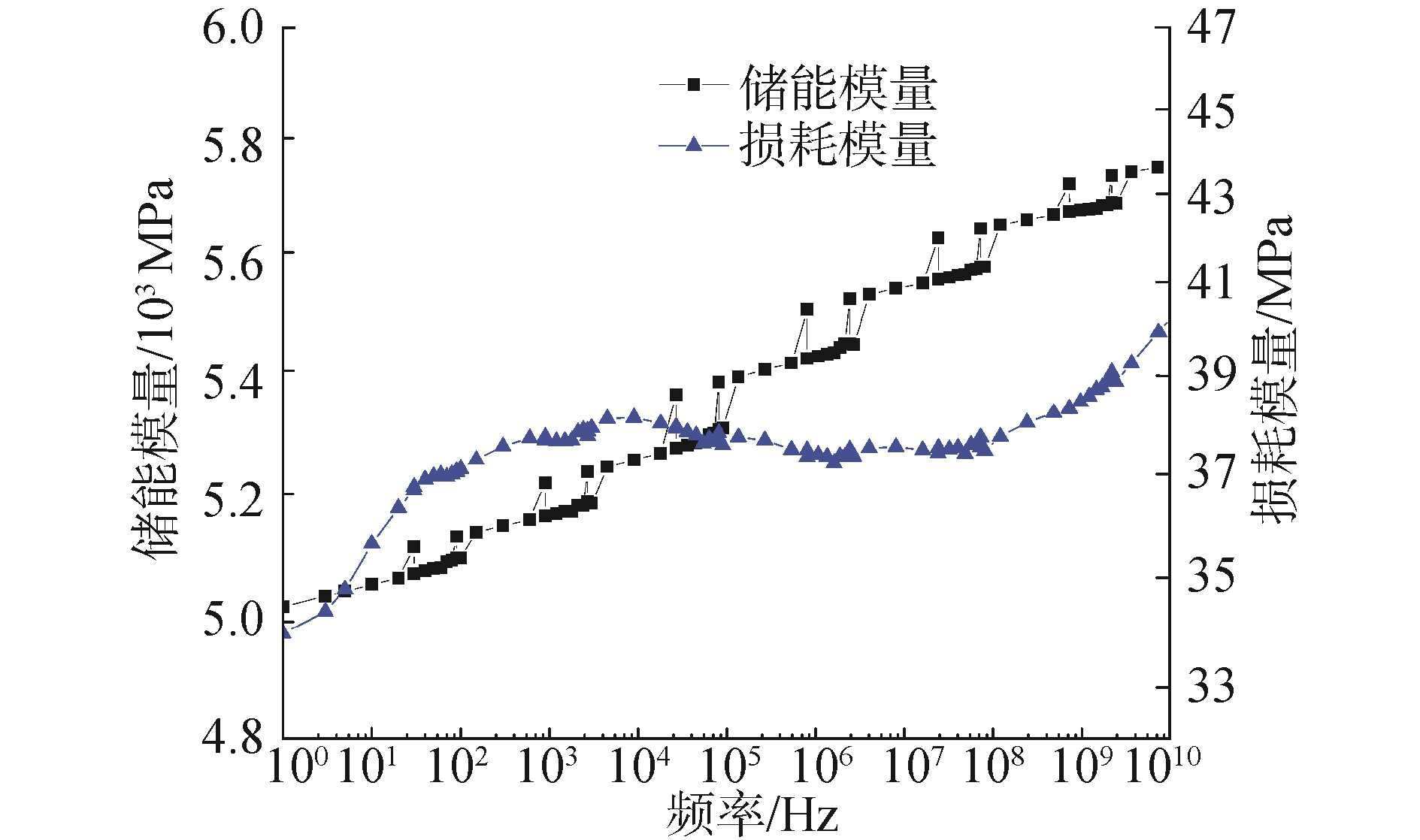
加工了一长50.0 mm、宽12.8 mm和厚3.2 mm的样条,采用动态热机械分析仪DMA Q800(美国TA Instruments公司产),测试了其从-100 ℃~30 ℃的复数弹性模量,通过分析测试软件Rheology Advantage Data Analysis将其等效转换为室温下高频段的复数弹性模量如图 1所示。
|
Download:
|
| 图 1 时温等效平移后的复数模量和损耗因子曲线 Fig. 1 The curves of complex modulus and loss factor after TTS shifting | |
从图 1中知频率为15.5、18.5和20.8 kHz时,PPS的储能模量分别为5.46、5.47和5.48 GPa,损耗模量则分别为37.47、37.30和37.56 MPa。
2 换能器设计对于低损耗的粘弹性材料,其相位速度为[16]:
| $ c = \frac{{\left| {{E^*}} \right|}}{{\sqrt \rho {E^{Ⅲ}}}} $ | (3) |
式中:
| $ \sqrt {{E_1} - {\rm{j}}{E_2}} = {E^Ⅲ} - {\rm{j}}{E^Ⅳ} $ | (4) |
将PPS材料储能模量和损耗模量代入式(3)和式(4)得:
| $ c = \frac{{\left| {{E^*}} \right|}}{{\sqrt \rho {E^{Ⅲ}}}} = 1771\;{\rm{m/s}} $ | (5) |
此即PPS材料在一维理论下的纵波传播速度。
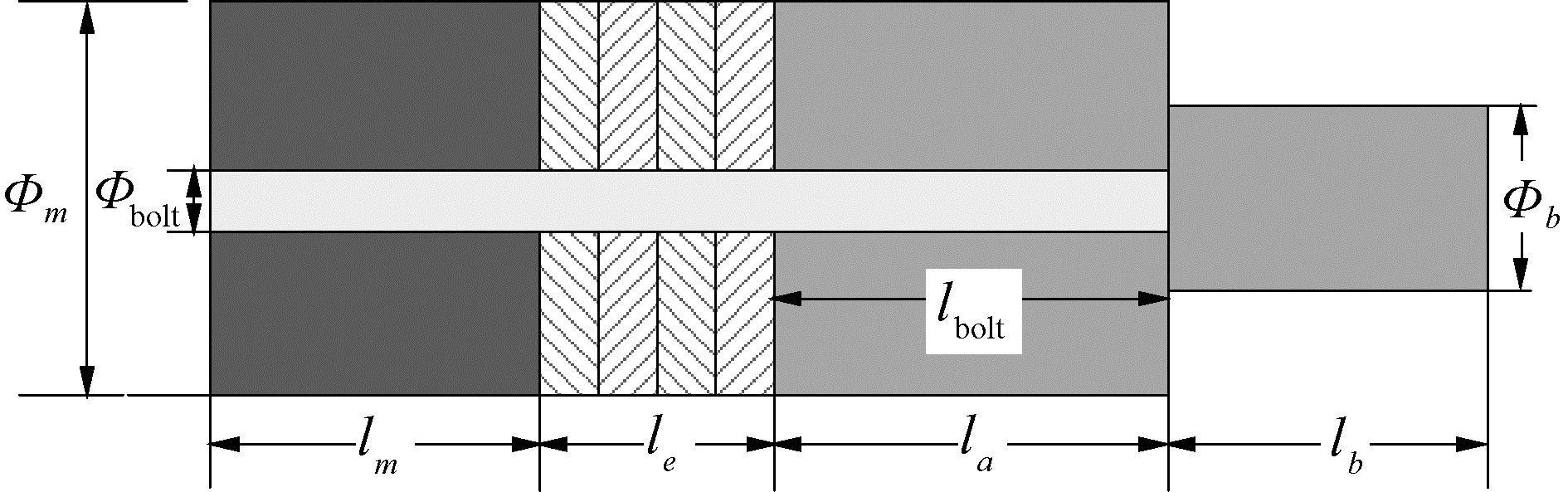
为了输出端得到高振幅,换能器后盖板采用钢材,前盖板采用PPS材料,并将其设计成阶梯状。换能器的结构如图 2所示,其中,Φm=30mm、Φbolt=8mm、lm=20mm、le=12mm、la=lb=lbolt=25 mm、Φb=8mm。
|
Download:
|
| 图 2 换能器结构 Fig. 2 Structure of the transducer | |
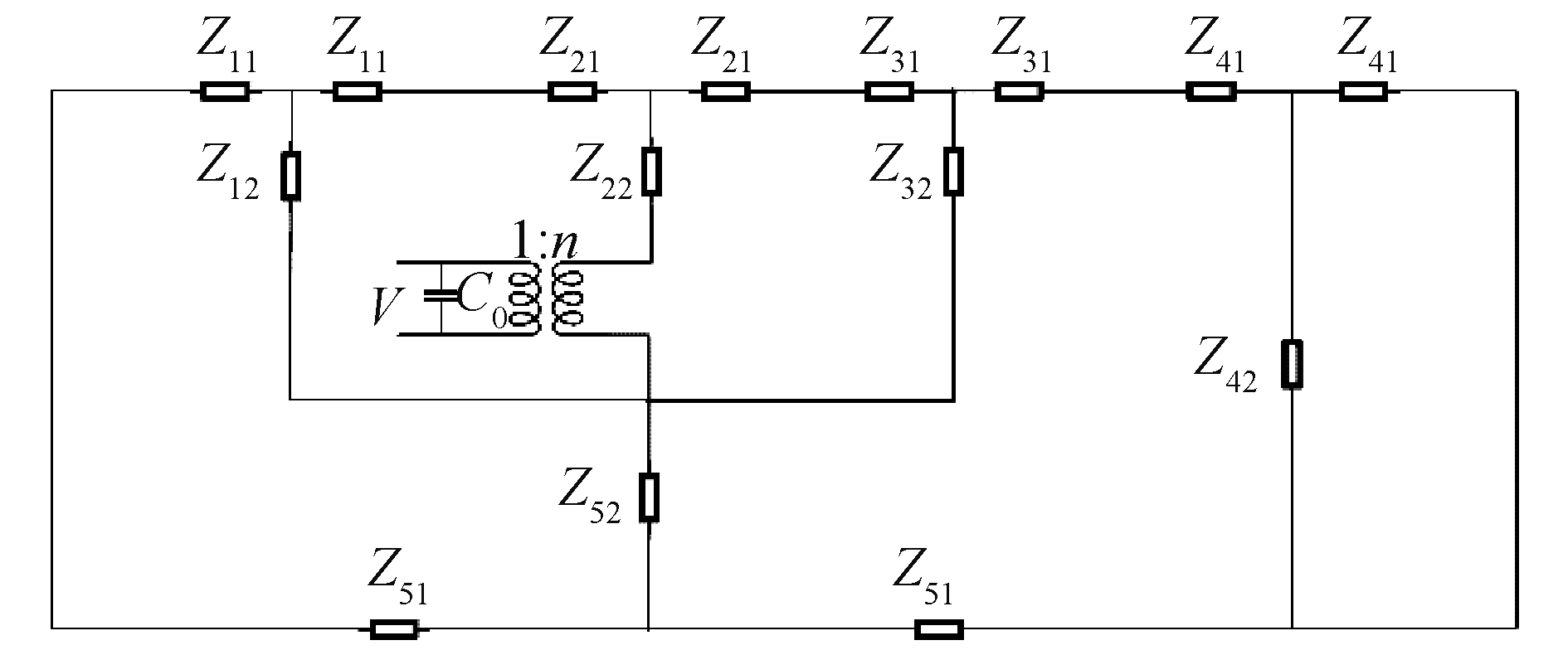
图 3为考虑螺栓后换能器的Mason等效电路,此时换能器的前后端面均为空载。图 3中:
| $ \begin{array}{*{20}{c}} {{Z_{n1}} = {\rm{j}}{Z_{0n}}{\rm{tan}}\left( {\frac{{{k_n}{l_n}}}{2}} \right)}\\ {{Z_{n2}} = \frac{{{Z_{0n}}}}{{{\rm{jsin}}({k_n}{l_n})}}}\\ {{Z_{0i}} = {\rho _i}{c_i}{S_i}, {\rm{ }}i = 1, 2, 3, 4, 5} \end{array} $ |
|
Download:
|
| 图 3 换能器的等效电路 Fig. 3 The equivalent circuit of the transducer | |
式中:ln、ρn、cn、Sn、kn分别为换能器第n段的长度、密度、声速、横截面积、波数。对于如图 2所示的换能器,第1段为后盖板,第2段为压电晶堆,第3段为阶梯状前盖板较宽段,第4段为阶梯状前盖板较窄段,第5段为金属螺栓。
当回路总电抗为零时,得到换能器的谐振频率为16.18 kHz。
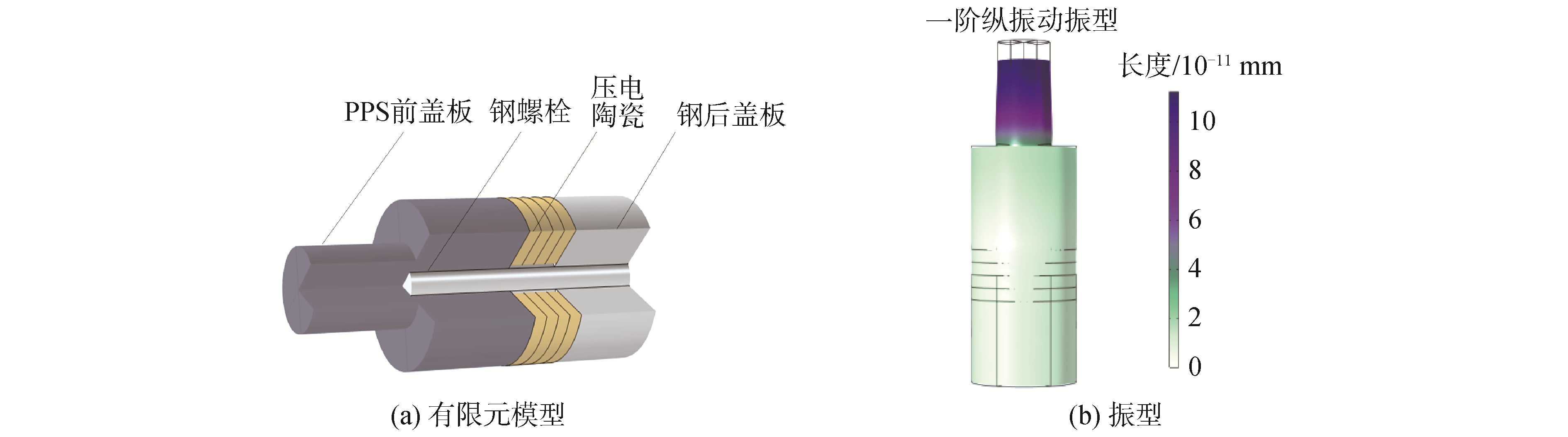
在有限元软件COMSOL中,按照图 2给出的几何尺寸建立模型,如图 4(a)所示,计算得到换能器的一阶纵振动谐振频率为15.69 kHz,对应的振型如图 4(b)所示。
|
Download:
|
| 图 4 有限元模型和振型 Fig. 4 Model and vibration shape mode of FEM | |
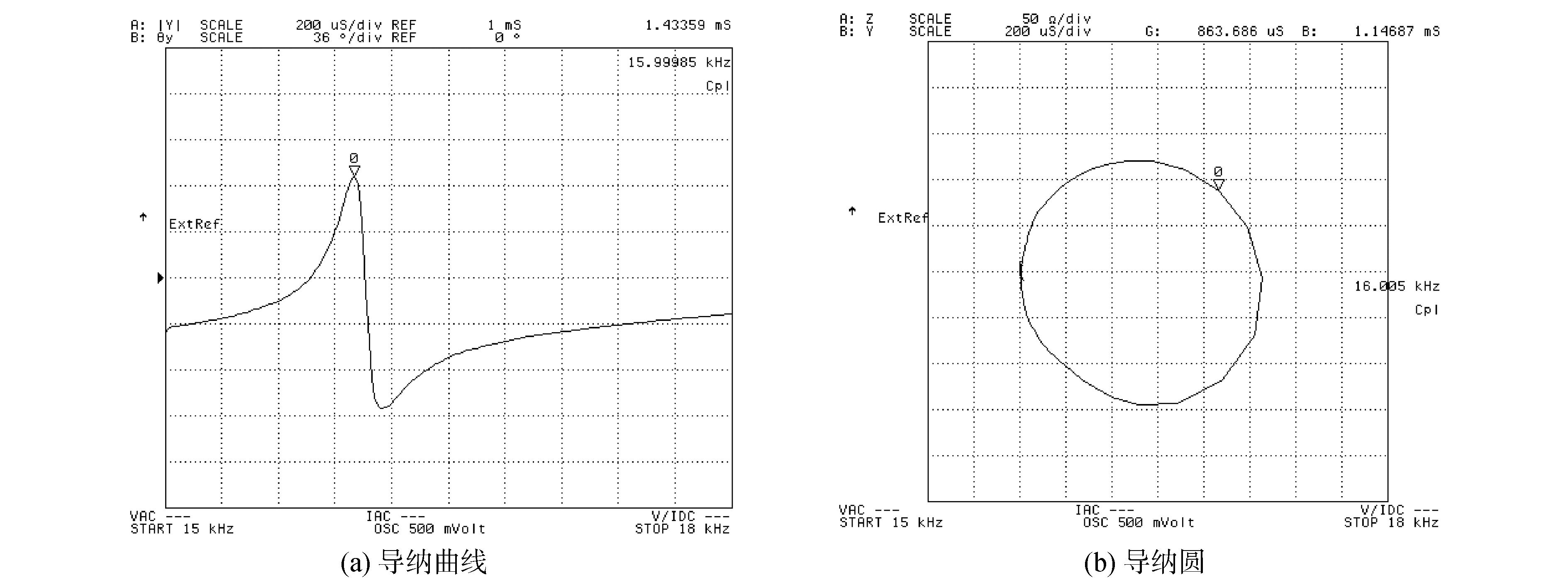
图 5为PPS换能器的实物图。图 6(a)和6(b)分别是用HP4294A阻抗分析仪测定换能器的谐振频率和导纳圆,可以看出换能器的谐振频率约为16 kHz,半功率带宽约为127 Hz。

|
Download:
|
| 图 5 换能器的实物 Fig. 5 Picture of transducer | |
|
Download:
|
| 图 6 阻抗分析仪测定的换能器导纳曲线及导纳圆 Fig. 6 Admittance curve and admittance chart of the transducer measured by impedance analyzer | |
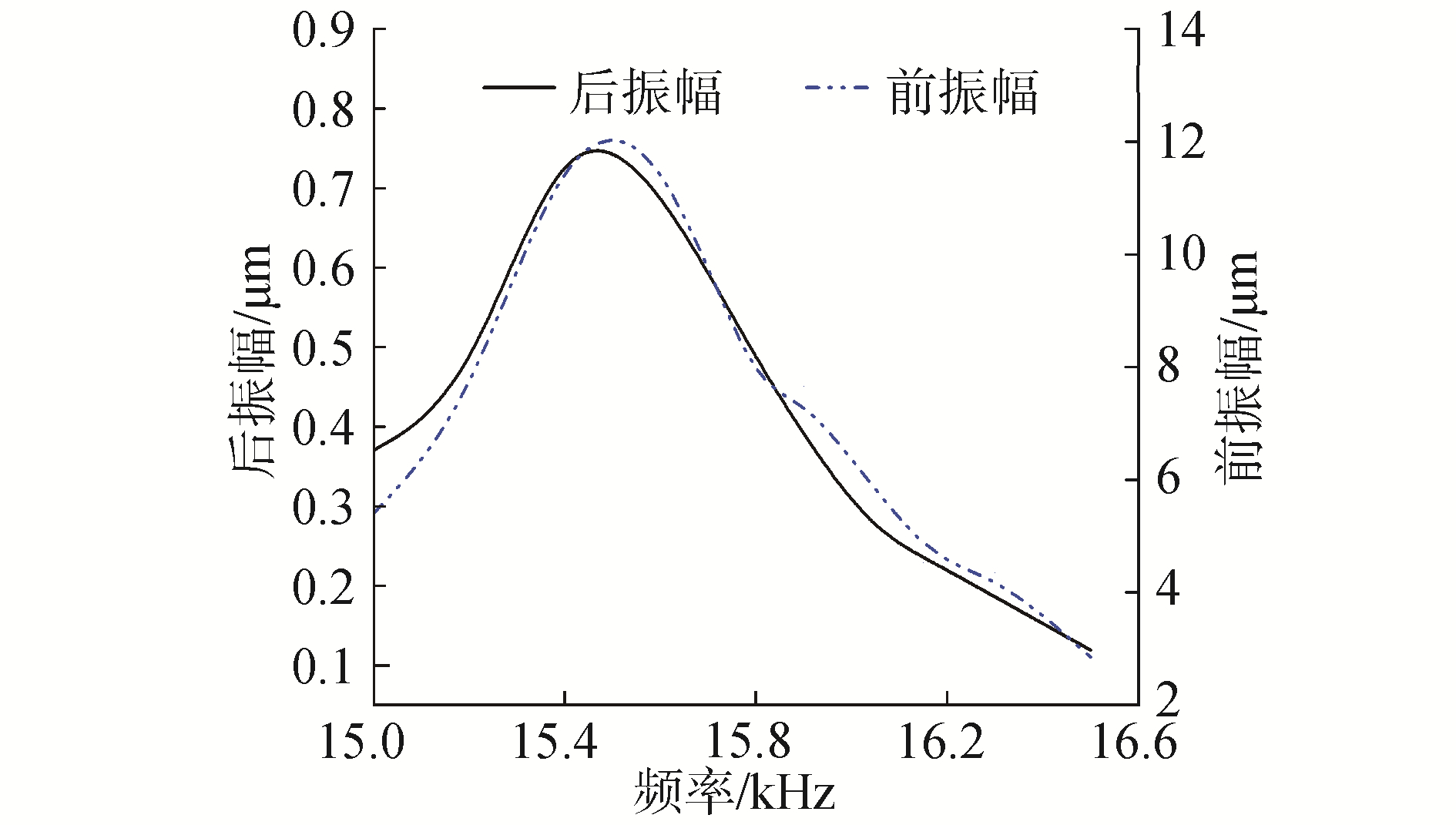
利用激光测振仪OFV-505(德国Polytec公司产)测试了其在谐振频率附近的前后振幅,施加到换能器上的电压与前端面振幅的关系结果如图 7和8所示。还测试了在谐振频率处施加电压为170 V时,换能器PPS部件前盖板前端面处以及前盖板变截面处(小端和大端面交界处)的升温情况,如图 9所示。另外,对换能器前端面进行了雾化效果测试,结果如图 10所示。
|
Download:
|
| 图 7 谐振频率附近的前后振幅 Fig. 7 The front head & rear end vibration amplitude near resonant frequency | |
|
Download:
|
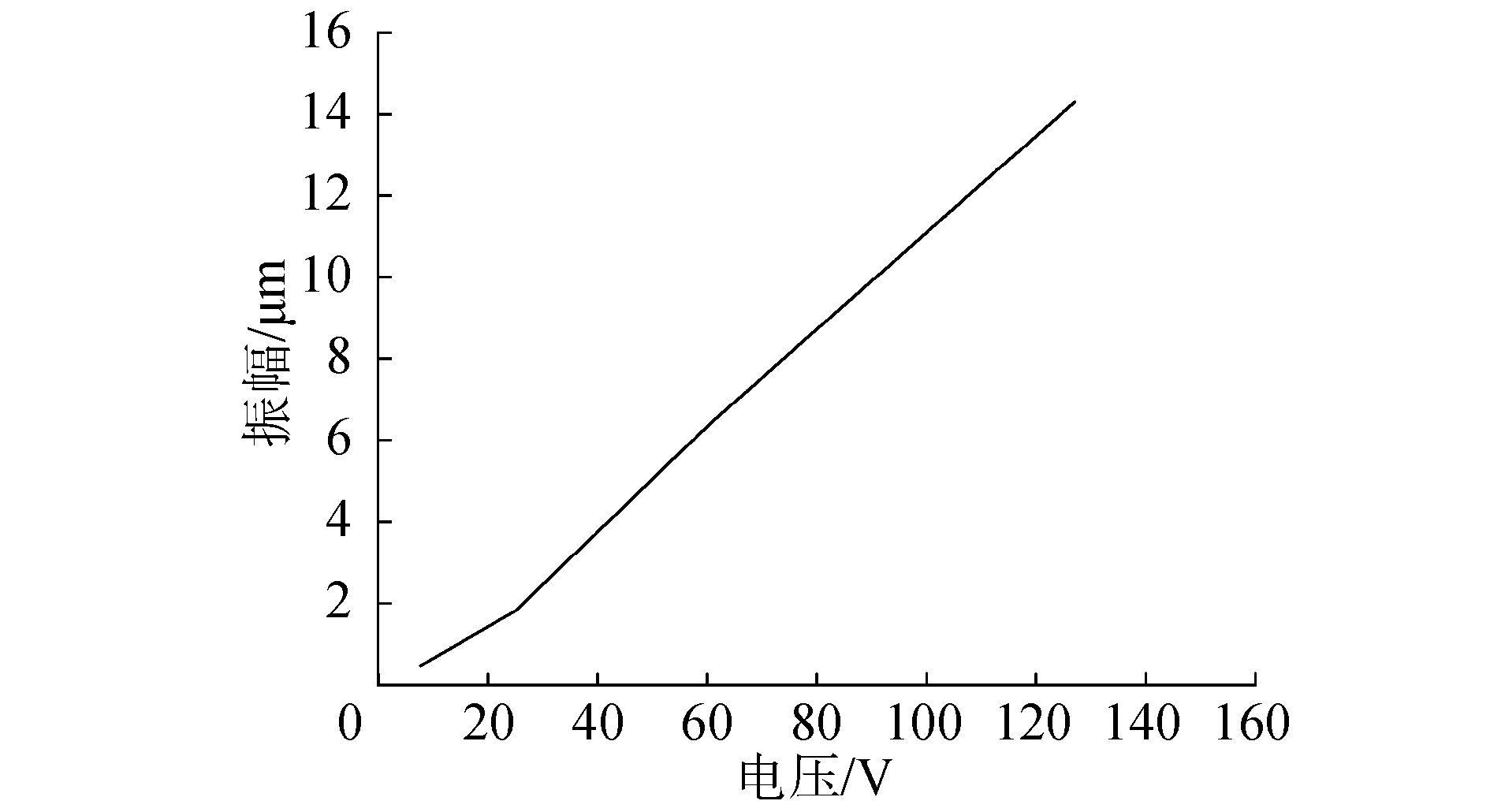
| 图 8 谐振频率处电压与前端面振幅之间的关系 Fig. 8 The relationship between the voltage and the vibration amplitude of the front head at the resonant frequency | |
|
Download:
|
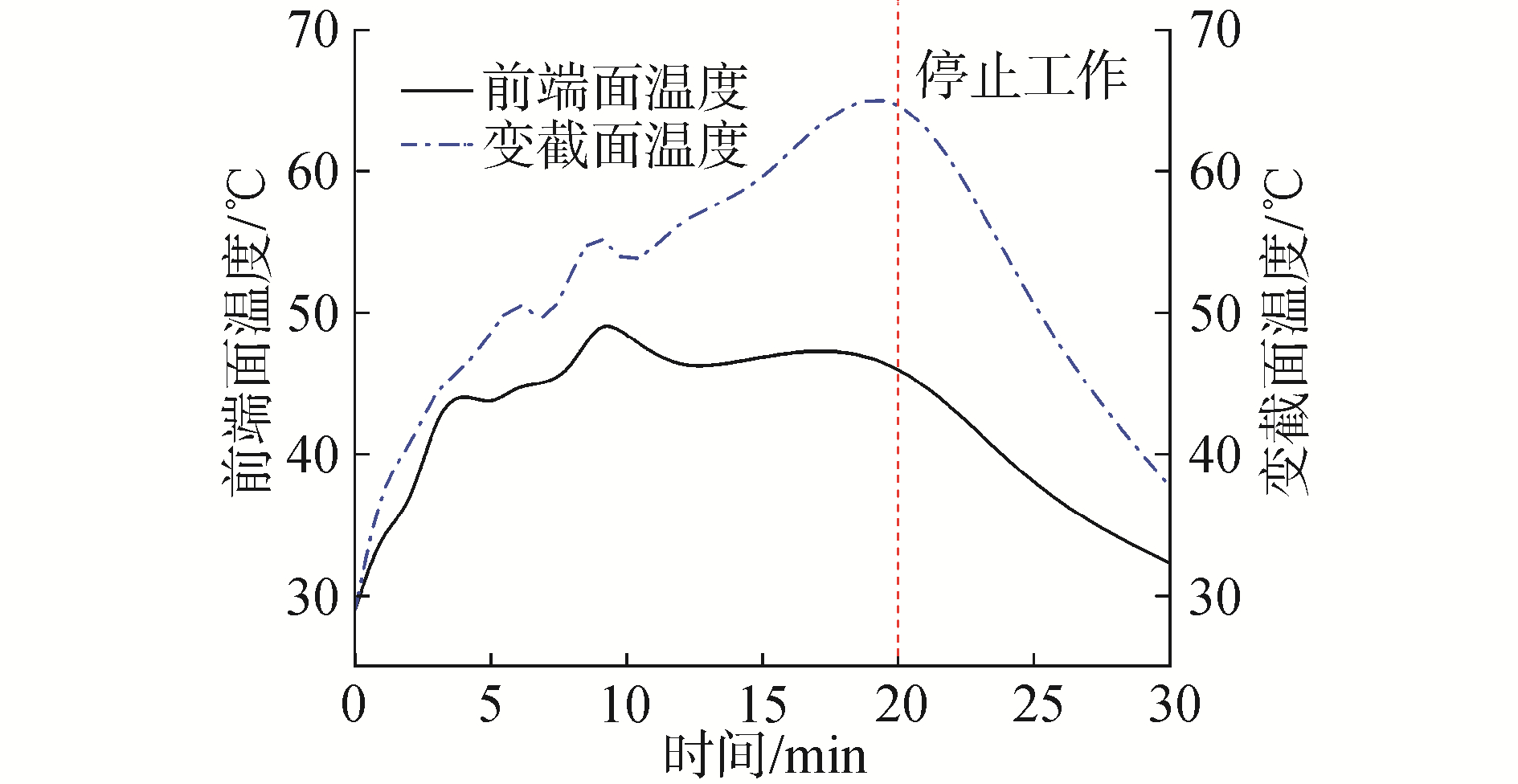
| 图 9 恒定电压下的换能器前端面变截面处的温度 Fig. 9 The temperature of the front cross section end at fixed voltage | |

|
Download:
|
| 图 10 雾化实验 Fig. 10 Atomization test | |
本文利用了Mason等效电路、有限元2种方法设计了换能器。前者计算得到的谐振频率为16.18 kHz,后者为15.69 kHz,与阻抗分析仪HP4294测试得的频率16 kHz相比较,Mason等效电路方法的相对误差为1.1%,有限元方法的相对误差为1.9%。测试表明,PPS换能器的半功率带宽为127 Hz,机械品质因数约为126,后者比一般金属压电陶瓷的换能器的略低些。
从图 7可以看出,换能器前端面振幅高于后端面振幅约一个数量级,谐振频率处两者的振幅比达到15.4左右。实验中发现,随着工作时间的延长,导致PPS部件温度升高,谐振频率会向低端漂移。
图 8表明,谐振频率处前端面振幅与施加到换能器上的电压近似为正比线性关系。可以看出,换能器两端电压为140 V时,前端面振幅达到14.4 μm。图 9表明,谐振频率附近处施加电压为170 V时,换能器PPS部件前盖板变截面处的温升要高于其前端面处的温升。如工作时间为20 min时,前者温升为36 ℃,后者则为13.3 ℃左右。停止工作10 min后,基本下降到室温。
雾化实验表明,换能器两端电压为26.3 V时,此时对应的振幅约为1.8 μm,换能器前端面开始产生较为明显的雾化现象。
计算了本文设计的换能器在相同电压下前端面的振幅与其质量之比,与同频率下前端面换为钢材料时的振幅与质量比值。若将其定义为输出-质量比,比较两者发现,前者的输出-质量比是后者的7.8倍,这也是PPS换能器的优点。
4 结论1)PPS换能器谐振频率处半功率带宽较金属换能器稍大,其机械品质因数比一般金属压电陶瓷的换能器的略低;
2) PPS换能器工作时,随着工作时间的延长,有温升,并导致其谐振频率会向低端漂移;
3) 谐振频率处前端面振幅与施加到换能器上的电压近似呈正比线性关系,因后盖板为金属材料,其前后振幅比值较大。计算表明,相同激励电压下,同频率的PPS换能器的输出-质量比为金属材料换能器的数倍。
| [1] |
周天放, 蓝宇, 桑永杰. 空腔式前盖板宽带纵向换能器研究[J]. 哈尔滨工程大学学报, 2016, 37(9): 1215-1219, 1226. ZHOU Tianfang, LAN Yu, SANG Yongjie. Research on longitudinal broadband transducer with cavity-type front cover[J]. Journal of Harbin Engineering University, 2016, 37(9): 1215-1219, 1226. (  0) 0)
|
| [2] |
胡静, 贺西平. 穿孔宽带换能器等效质量与孔尺寸关系研究[J]. 陕西师范大学学报(自然科学版), 2011, 39(2): 23-26. HU Jing, HE Xiping. The relation between equivalent mass of the perforation wide-band transducer and the dimension of the hole[J]. Journal of Shaanxi Normal University (natural science edition), 2011, 39(2): 23-26. (  0) 0)
|
| [3] |
BUTLER S C. Triple-resonant transducers[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2012, 59(6): 1292-1300. DOI:10.1109/TUFFC.2012.2320 (  0) 0)
|
| [4] |
JONES D F, CHRISTOPHER D A. A broadband omnidirectional barrel-stave flextensional transducer[J]. The journal of the acoustical society of America, 1999, 106(2): L13-L17. DOI:10.1121/1.427032 (  0) 0)
|
| [5] |
李志强, 莫喜平, 张运强, 等. 双椭圆壳串联宽带弯张换能器[J]. 声学学报, 2016, 41(4): 494-498. LI Zhiqiang, MO Xiping, ZHANG Yunqiang, et al. Dual elliptical shells serially connected broadband flextensional transducer[J]. Acta acustica, 2016, 41(4): 494-498. (  0) 0)
|
| [6] |
OCHOA P, VILLEGAS M, PONS J L, et al. Tunability of cymbals as piezocomposite transducers[J]. Journal of electroceramics, 2005, 14(3): 221-229. DOI:10.1007/s10832-005-0961-8 (  0) 0)
|
| [7] |
GOH P H, LI M J, TSOU N T. The design and analysis for low-frequency piezoelectric cymbal transducers[J]. Ceramics international, 2017, 43(Suppl 1): S49-S54. (  0) 0)
|
| [8] |
宋哲, 严由嵘. 一种镶拼圆环换能器宽频带应用研究[J]. 水下无人系统学报, 2018, 26(5): 498-502. SONG Zhe, YAN Yourong. Application of broad bandwidth to Mosaic transducer[J]. Journal of unmanned undersea systems, 2018, 26(5): 498-502. (  0) 0)
|
| [9] |
GALLEGO-JUÁREZ J A, RODRIGUEZ G, ACOSTA V, et al. Power ultrasonic transducers with extensive radiators for industrial processing[J]. Ultrasonics sonochemistry, 2010, 17(6): 953-964. DOI:10.1016/j.ultsonch.2009.11.006 (  0) 0)
|
| [10] |
于文鑫, 郑凯, 王丽慧, 等. 换能器辐射板材料对辐射声场分布的影响[J]. 吉林化工学院学报, 2018, 35(9): 36-40. YU Wenxin, ZHENG Kai, WANG Lihui, et al. The influence of magnetostrictive transducer radiation plate material on radiation sound field distribution[J]. Journal of Jilin institute of chemical technology, 2018, 35(9): 36-40. (  0) 0)
|
| [11] |
付琳, 高永康, 高晶敏. 背衬参数对厚度模压电换能器特性的影响[J]. 声学学报, 2019, 44(2): 251-257. FU Lin, GAO Yongkang, GAO Jingmin. Influence of the backing parameters on the performance of thickness mode piezoelectric transducer[J]. Acta acustica, 2019, 44(2): 251-257. (  0) 0)
|
| [12] |
宋希阳.结构尺寸和材料组成对换能器频带宽度的影响[D].西安: 陕西师范大学, 2010: 5. SONG Xiyang, Effect of structure size and material composition on the frequency bandwidth of transducer[D]. Xi'an: Shaanxi Normal University, 2010: 5. (  0) 0)
|
| [13] |
HE Xiping, YAN Xiuli, LI Na. Directivity pattern of the sound radiated from axisymmetric stepped plates[J]. The journal of the acoustical society of America, 2016, 140(2): 1387-1396. DOI:10.1121/1.4961363 (  0) 0)
|
| [14] |
WU Jiang, MIZUNO Y, TABARU M, et al. Ultrasonic motors with polymer-based vibrators[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2015, 62(12): 2169-2178. DOI:10.1109/TUFFC.2015.007122 (  0) 0)
|
| [15] |
何曼君, 陈维孝, 董西侠. 高分子物理(修订版)[M]. 上海: 复旦大学出版社, 2000. HE Manjun, CHEN Weixiao, DONG Xixia. Polymer physics (revised edition)[M]. Shanghai: Fudan University Press, 2000. (  0) 0)
|
| [16] |
HE Xiping, BENATAR A. Determination of complex Young's modulus of viscoelastic bars using forced longitudinal vibration of slender rods[J]. Chinese journal of acoustics, 2013, 32(1): 63-70. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


