2. 兰州交通大学 甘肃省道路桥梁与地下工程重点实验室, 甘肃 兰州 730070
2. Key Laboratory of Road and Bridge and Underground Engineering of Gansu Province, Lanzhou Jiaotong University, Lanzhou 730070, China
青藏铁路是我国“一带一路”战略的重要内容,同时也是世界上海拔最高、在冻土区里程最长的高原铁路。混凝土材料由于性价比高、使用寿命长等优点在我国铁路建设中得到了广泛的应用[1]。青藏地区存在大量的多年冻土,因此在该地区施工的混凝土结构物,尤其是桩基等深埋地下的混凝土,浇筑后即处于负温条件下养护。在持续负温环境下,混凝土水化反应不充分,孔结构劣化,使混凝土结构耐久性降低。而该地区的冻土又普遍含有较多的腐蚀性盐类,因此对该地区混凝土的抗渗性要求较高。孔结构对其抗渗性等宏观性能起到决定性的作用[2-5],早龄期混凝土性能的快速发展变化,根本上来源于混凝土剧烈的水化反应,但目前对于混凝土抗渗性的研究,多集中在孔结构与抗渗性两者之间的关系上[6-10],对孔结构如何随水化的进程而变化,进而影响抗渗性发展的研究较少,同时,众多关于混凝土抗渗性的研究多为常温养护环境下进行,对负温养护环境下该问题的研究还鲜有报道,但负温环境会明显减缓水泥的水化速率[11],故在负温养护条件下,水泥水化情况与常温条件下必定不同,这将导致混凝土的孔结构产生变化,进而对其抗渗性产生较大影响。因此,本文以青藏高原冻土区混凝土结构物为研究对象,从水泥的水化入手,并与其微观孔结构相结合,对混凝土的抗渗性进行研究,从根本上解释在负温环境下其抗渗性随微观孔结构的发展机理。
1 实验材料及方法 1.1 试验原材料试验中水泥采用兰州甘草水泥有限集团生产的P ·O 42.5水泥,氯离子含量为0.012%,碱含量为0.58%;细骨料为河砂,细度模数2.2,表观密度2 620 kg/m3,堆积密度1 520 kg/m3;粗骨料为5~31.5 mm的连续级配碎石,压碎指标为7.0%,表观密度2 790 kg/m3;减水剂为萘系高效减水剂,减水率为24%;水为自来水。
1.2 试验用配合比配制3种不同水灰比的混凝土C1、C2、C3进行试验研究,如表 1所示;同时对应于C1、C2、C3配制与其水灰比相同的水泥净浆F1、F2、F3,用于水泥水化试验研究。
| 表 1 混凝土配合比 Table 1 The mix proportions of concrete |
试验仪器主要有:AutoPore IV9500全自动压汞仪、人工气候模拟试验箱、温度自动巡检仪、恒温瓶、温度传感器、氯离子扩散系数测定仪等。
1.3.2 测试方法混凝土入模后,一部分直接放入(-3±0.2)℃,湿度的大气模拟箱内带模养护,5 d后脱模;另一部分1 d后脱模放入(20±2)℃的标准养护室内养护,达到指定龄期后对孔结构及抗渗性进行测定。孔结构采用压汞法进行测定,测试试样为混凝土浇筑过程中筛得的浆体,如图 1所示, 其体积约为2.5 cm3左右;抗氯离子渗透性的测试参照GB/T 50082-2009《普通混凝土长期性能和耐久性能试验方法标准》,采用RCM法进行测定。

|
Download:
|
| 图 1 孔结构测试试样 Fig. 1 Test specimen of pore structure | |
水泥的水化程度按照文献[12]中提出的方法,通过测定不同龄期下的水化放热量,对其水化程度进行计算。水泥净浆的放热量采用《水泥水化热测定方法》(GB/T 12959-2008)中的直接法进行测定。温控装置通过恒温瓶内冷冻过的氯化钠溶液及放置恒温瓶的大气环境模拟箱对水泥净浆的水化环境温度进行控制,使其保持在-3 ℃左右,并通过温度巡检仪进行实时监测,直至试验结束。水泥净浆的水化放热试验装置如图 2所示。

|
Download:
|
| 图 2 水化热实验装置示意 Fig. 2 Schematic diagram of experimental device for hydration heat | |
图 3为不同养护方式下水泥净浆的水化程度,由图 3分析可知,在标准养护条件及负温(-3 ℃)养护条件下,水泥水化程度均随时间呈增长的趋势,但2种不同养护方式下,水化程度增长的速率不同,标准养护条件下,从水化开始直至14 d,水化程度均呈快速增长的趋势,到14 d时F1、F2、F3的水化程度达到了63.9%、68%和74.6%;负温(-3 ℃)养护条件下,水泥水化有个短暂的快速发展期,之后其水化速率便开始减缓,14 d时,F1、F2、F3的水化程度分别为34.8%、37.1%和35.7%,仅为标准养护条件下的47%~56%,而28 d时,负温(-3 ℃)养护条件下的水化程度为39.4%、42.4%和40%,仅为标准养护条件下的51%~57%,可见养护温度对水泥水化有较大的影响,而且负温(-3 ℃)养护条件下,28 d龄期时,水灰比为0.31的F2水泥净浆水化程度最高,而标准养护条件下水灰比为0.38的F3水泥净浆水化程度最高,两者情况不同。

|
Download:
|
| 图 3 不同养护条件下水泥净浆水化程度 Fig. 3 The cement hydration degree under different curing conditions | |
水泥的水化作用是其主要的矿物成分(C3A、C3S、C2S、C4AF等)与水以及掺入的石膏之间发生的一系列化学反应,而该过程受到温度、水灰比、水泥细度等多种因素的影响,当原材料确定之后,其反应过程主要由温度及水灰比决定。文献[13]指出,分子平均动能与热力学温度成正比,因此,当养护温度降低时,水分子运动能力减弱,同水泥颗粒碰撞的频率下降,减缓了水化反应的进行。且在负温下养护时,部分孔隙中的水会冻结成冰,水化单元孔隙中水含量对水化反应具有较大的影响[14],部分水结冰,导致实际参与水化反应的水分减少,水化单元中的水含量显著降低,严重影响了水化反应的进程。
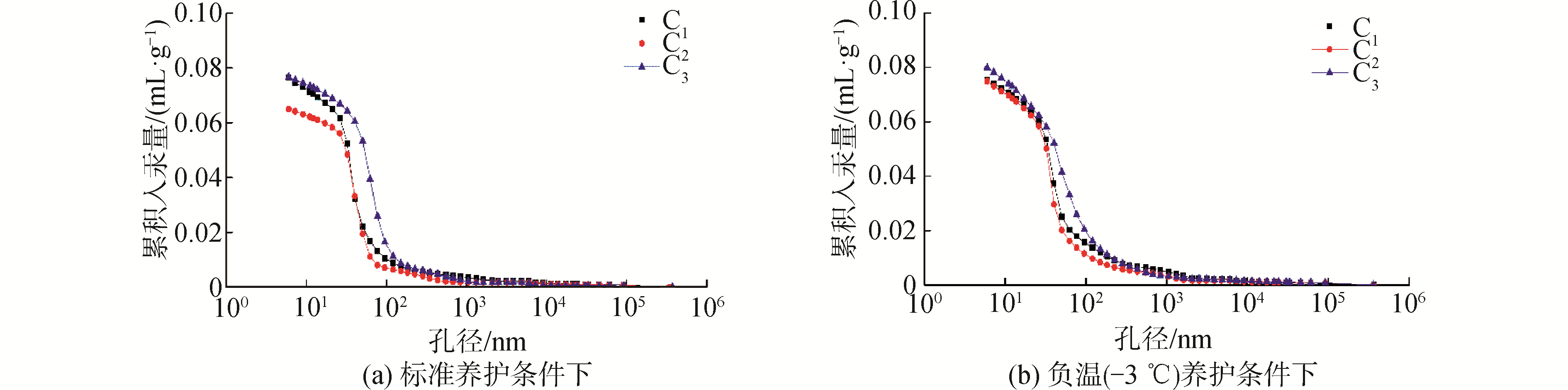
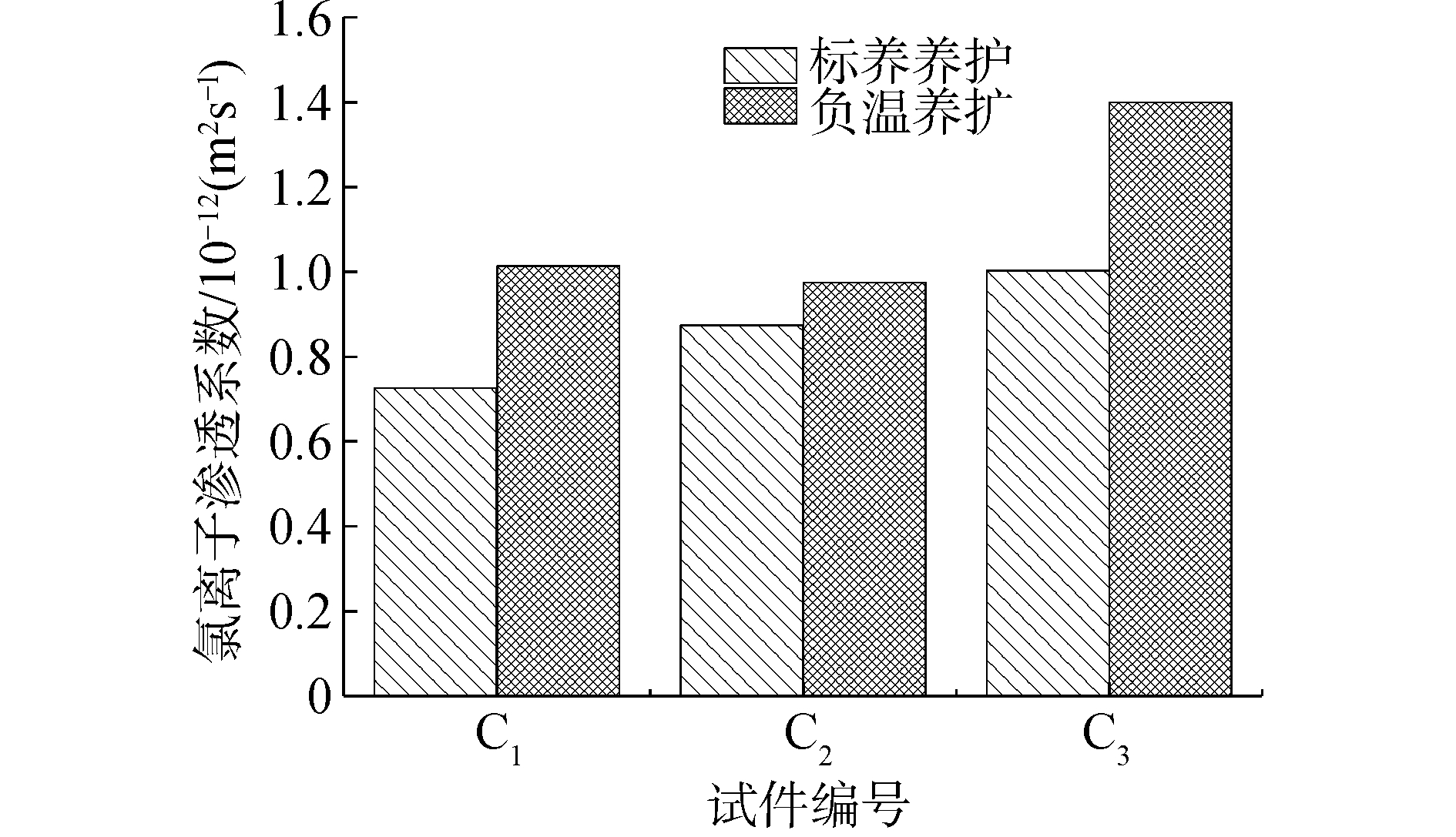
水化反应的程度直接影响其孔结构发育情况,同时,由于氢键键能小于分子间的范德华力,因而水结冰膨胀后产生巨大的膨胀应力,对形成的混凝土结构产生破坏,使其孔结构劣化,孔径粗化,从表 2可以看出,负温养护28 d时,C1、C2、C3混凝土的平均孔径为标养条件下的1.06~1.22倍;而临界孔径表征孔结构的连通性,对混凝土抗渗性的影响最大,从图 4及表 2可以看出,负温养护条件下混凝土的临界孔径为标养条件下的1.05~1.53倍。因此,负温下混凝土的抗渗性降低,而图 6直观反映出:标养下混凝土的氯离子渗透系数仅为负温养护条件下的71.6%~89.6%。
| 表 2 不同水灰比混凝土28 d孔结构试验结果 Table 2 Test results of 28 d pore structure of concrete with different water cement ratio |
|
Download:
|
| 图 4 测试试样累计压入汞量与孔径关系 Fig. 4 Relationships between cumulative mercury and pore diamante of test specimen | |
|
Download:
|
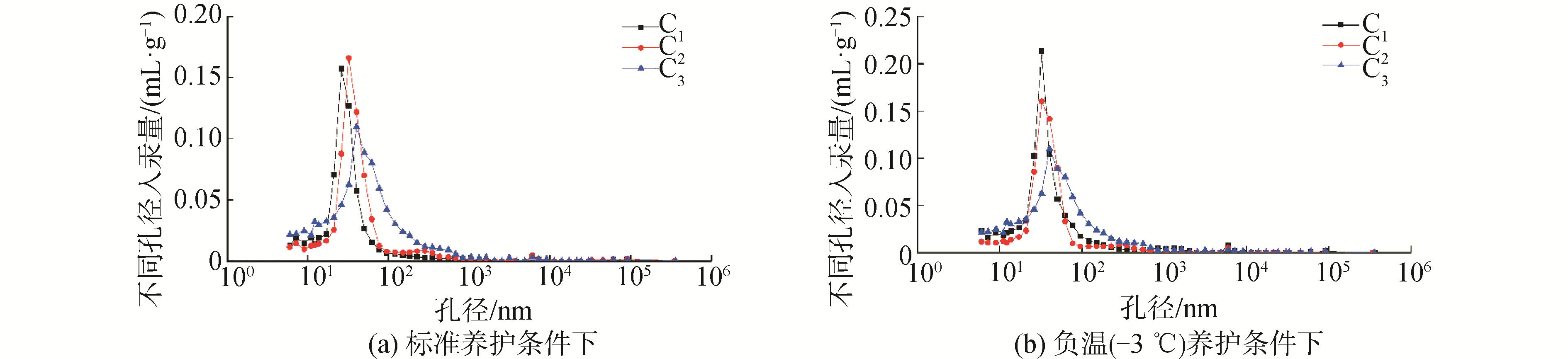
| 图 5 测试试样孔径分布微分曲线 Fig. 5 Differential curves of pore size distribution of test specimen | |
|
Download:
|
| 图 6 不同养护条件下混凝土氯离子渗透系数 Fig. 6 The chloride ion permeability coefficient of concrete under different curing conditions | |
由以上研究可发现,在标准养护条件及负温(-3 ℃)养护条件下,两者的水化程度差异巨大,从而直接影响了孔结构的发育及抗渗性能的优劣。上述2种养护条件下,对混凝土所造成影响的最大原因可能是,在标准养护条件下,早龄期混凝土中的水分均为液相水,但在负温(-3 ℃)养护条件下,早龄期混凝土中部分水冻结成冰,液相水含量明显减少,而在水化单元孔隙中,液相水含量对水化反应影响巨大[13],因此,为了论证负温(-3 ℃)养护条件下水化程度、孔结构发育及抗渗性的差异,本文基于热力学原理,建立了不同孔隙中,水的冰点计算模型,探究早龄期负温养护条件下混凝土中水泥水化、孔结构发育及抗渗性发展的规律和机理。
2.2 水的冰点与孔径之间计算模型由于水在结冰时会膨胀,所以当压强增大时,膨胀受到阻碍,水的冰点就会降低,标准大气压下水的冰点为0 ℃,而在微小孔隙中,曲面液体所承受的压力为气压以及由于液面弯曲而产生的附加压力的总和[15],此时压强大于标准大气压,压强增大保证了负温下液相水的存在。根据Young-Laplace公式[16],混凝土中孔径大小不同的孔结构对气压的改变不同,因而对水的冰点降低的程度也不同,但是孔径的大小与水的冰点之间的关系,大多数学者只进行了定性的分析,并无定量的研究[17-19],而本文从热力学角度出发,对两者的定量关系进行了推导。
Clausius-Clapeyron方程[20]指出了纯物质两相平衡时,压力与温度之间的关系,水在三相平衡时[21],亦满足此方程:
| $ \frac{{{\rm{d}}P}}{{{\rm{d}}T}} = \frac{{\Delta {H_{\rm{m}}}}}{{T{V_{\rm{g}}}}} $ | (1) |
将
| $ \frac{{{\rm{d}}P}}{{{\rm{d}}T}} = \frac{{\Delta {H_{\rm{m}}}P}}{{R{T^2}}} $ | (2) |
化简并对两边积分可得:
| $ {\mathop{\rm In}\nolimits} P = \frac{{\Delta {H_{\rm{m}}}}}{R}\left( { - \frac{1}{T}} \right) $ | (3) |
| $ T = \frac{{ - \Delta {H_{\rm{m}}}}}{{R{\mathop{\rm In}\nolimits} P}} $ | (4) |
式中:T为热力学温度,单位为K,设T0为标准大气压(P0)下水的凝固点,即水的冰点,此时,冰点T0=273.15 K=0℃;T1为液体所受压强为P1时的冰点,故在2种压强下,液体冰点的变量为:θ=T0-T1,将式(4)代入可得:
| $ \begin{array}{l} \theta = {T_0} - {T_1} = \frac{{ - \Delta {H_{\rm{m}}}}}{{R{\mathop{\rm In}\nolimits} {P_0}}} - \frac{{ - \Delta {H_{\rm{m}}}}}{{R{\mathop{\rm In}\nolimits} {P_1}}} = \frac{{\Delta {H_{\rm{m}}}}}{R}\left( {\frac{1}{{{\mathop{\rm In}\nolimits} {P_1}}} - \frac{1}{{{\mathop{\rm In}\nolimits} {P_0}}}} \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\Delta {H_{\rm{m}}}}}{R} \cdot \frac{{{\mathop{\rm In}\nolimits} {P_0} - {\mathop{\rm In}\nolimits} {P_1}}}{{{\mathop{\rm In}\nolimits} {P_0}{\mathop{\rm In}\nolimits} {P_1}}} \end{array} $ | (5) |
| $ \frac{\theta }{{{T_0}}} = \frac{{\frac{{{\mathop{\rm In}\nolimits} {P_0} - {\mathop{\rm In}\nolimits} {P_1}}}{{{\mathop{\rm In}\nolimits} {P_0}{\mathop{\rm In}\nolimits} {P_1}}}}}{{ - \frac{1}{{{\mathop{\rm In}\nolimits} {P_0}}}}} = \frac{{{\mathop{\rm In}\nolimits} \frac{{{P_1}}}{{{P_0}}}}}{{{\mathop{\rm In}\nolimits} {P_1}}} $ | (6) |
引入Kelvin方程[22]
| $ \frac{\theta }{{{T_0}}} = \frac{{{\mathop{\rm In}\nolimits} \frac{{{P_1}}}{{{P_0}}}}}{{{\mathop{\rm In}\nolimits} {P_1}}} = \frac{{\frac{{2\sigma {V_{\rm{L}}}}}{{R{T_1}r}}}}{{\left( { - \frac{{\Delta {H_{\rm{m}}}}}{{R{T_1}}}} \right)}} = - \frac{{2\sigma {V_{\rm{L}}}}}{{\Delta {H_{\rm{m}}}r}} $ | (7) |
| $ \theta = - \frac{{2\sigma {V_{\rm{L}}}{T_0}}}{{\Delta {H_{\rm{m}}}r}} $ | (8) |
其中冰点的绝对改变量为:
| $ \Delta T = \left| { - \frac{{2\sigma {V_{\rm{L}}}{T_0}}}{{\Delta {H_{\rm{m}}}r}}} \right| = \frac{{2\sigma {V_{\rm{L}}}{T_0}}}{{\Delta {H_{\rm{m}}}r}} $ | (9) |
负号代表冰点向比T0温度更低的方向改变,故可得:
| $ {T_1} = {T_0} - \Delta T = {T_0} - \frac{{2\sigma {V_{\rm{L}}}{T_0}}}{{\Delta {H_{\rm{m}}}r}} = 273.15\left( {1 - \frac{{2\sigma {V_{\rm{L}}}}}{{\Delta {H_{\rm{m}}}r}}} \right) $ | (10) |
式(10)是以热力学温度(单位为K)计量,当以摄氏温度(单位为℃)计时,式(10)可以转变为:
| $ {t_1} = {T_1} - 273.15 = - \frac{{2\sigma {V_{\rm{L}}}{T_0}}}{{\Delta {H_{\rm{m}}}r}} $ | (11) |
从式(9)可以看出,孔径越小,水的冰点降低越多,这是因为,曲面液体的附加压力与曲率半径为反比[16],r越小,曲面液体所受压力越大,则水在结冰膨胀时所受的阻力越大,所以压强越大时,液体越不容易凝结,则冰点降低的越多,这与式(11)中的变化趋势亦相同。而当r→∞时,此时的液体为平液面液体,根据Young-Laplace公式,此时的附加压力为0,仅受大气压强,若此时的大气压强为标准大气压,则ΔT=0,水的冰点为0 ℃,与式(11)计算所得相同。
文献[23]中指出,每增大(或下降)一个大气压,水的冰点(或冰的融点)将会降低(或升高)0.007 5 ℃。故令弯曲液面产生的附加压力为1个标准大气压,将该值代入Young-Laplace方程[20]及式(9)进行计算,可得ΔT=0.008 2 ℃,即本模型计算可得,增加一个大气压,冰点下降0.008 2 ℃,与0.007 5 ℃相差9.3%,因此式(9)~(11)可较为准确的反应混凝土孔隙中水的冰点与孔径之间的关系。
2.4 模型计算及分析利用式(11)反算,求得当水的冰点为-3 ℃时孔径的大小,具体计算过程如下:
液体的表面张力对温度的变化较为敏感,表面张力与温度呈负相关性,根据文献[24]中所给出的热力学温度与水的表面张力之间的计算模型可得,270.15 K(即-3 ℃)时,其表面张力σ=75.83×10-3 N/m,VL及ΔHm由文献[22]及文献[25]查得,具体如表 3。
| 表 3 计算参数 Table 3 Calculation parameters |
将表 3中参数代入式(11),并令t1=-3 ℃可得r=41.4 nm,即孔半径为41.4 nm(直径d=82.8 nm)的孔隙中,水的冰点为-3 ℃,因此在-3 ℃养护条件下,当孔径d≤82.8 nm时,孔隙中的水为液相水,这个孔径按照吴中伟[26]的孔径分类,属于少害孔的范围。
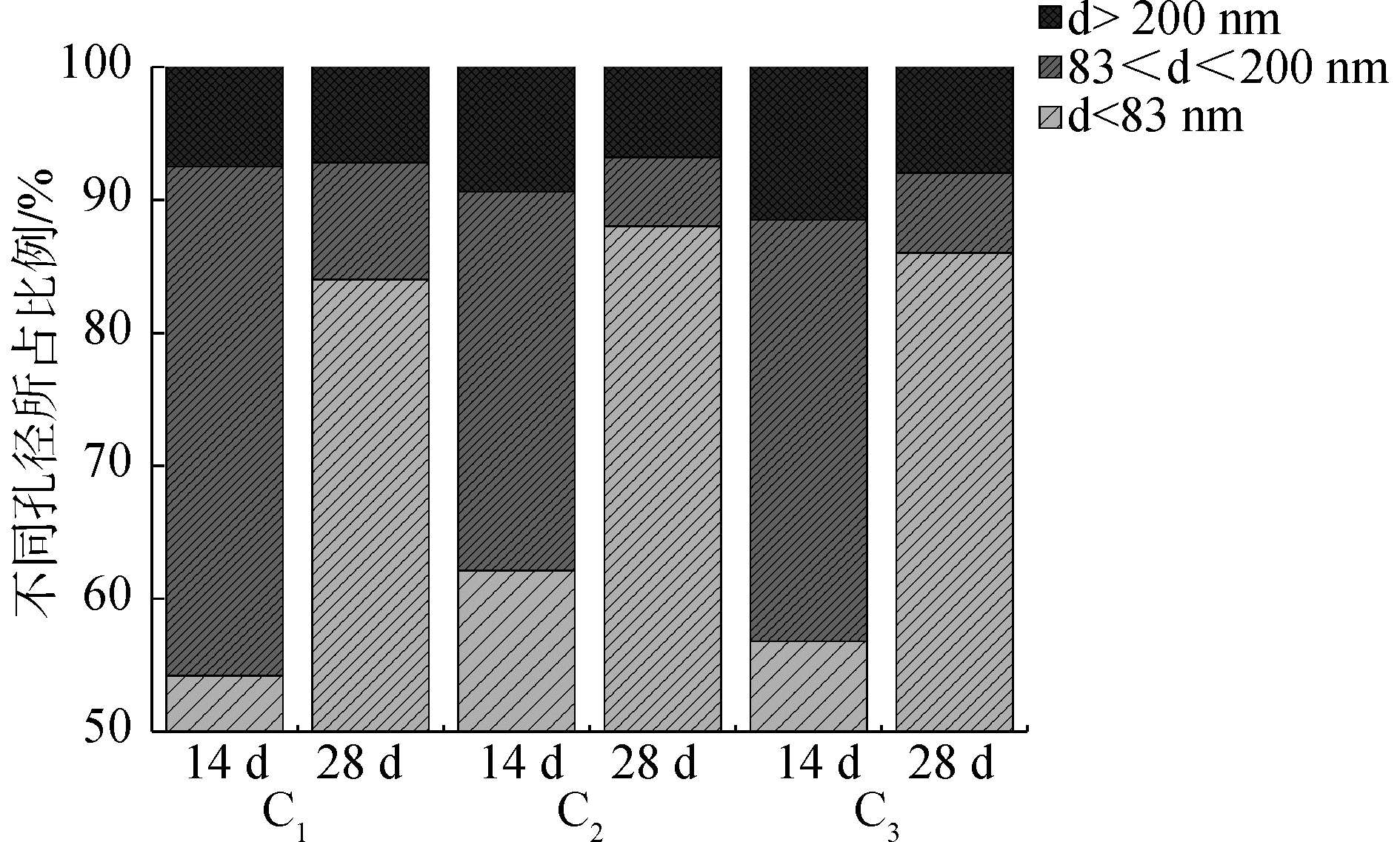
从图 3可以看出,负温养护条件下,当水泥水化至14 d时,F2水化程度最大,F3次之,F1最小,这与标养条件下有所不同,直至28 d,该趋势依旧如此,究其原因,由图 7分析可以看出,14 d时,与F2对应的C2混凝土的微观孔隙中,小于83 nm的孔径占总孔体积比例的62.1%,C3的为56.8%,C1的为54.2%,因此,其孔隙中液相水的含量C2混凝土最多,C3次之,C1最少,故水化至28 d时,C2混凝土的水化程度最高,孔隙结构最佳,其抗渗性亦最优;C1及C3混凝土的孔结构水化程度分别为39.4%和40%,两者基本相同,其中C3略高,但就其临界孔径来说,C3混凝土要大于C1混凝土,这是因为,本文中负温环境为模拟冻土区灌注桩养护环境,即负温和无外界水分补给环境,这种环境状态下的混凝土即为干燥状态,存在水气扩散[27],环境湿度对混凝土的影响亦与其水灰比有关,环境湿度相同时,水灰比越大,水分散失趋势越强[28],这种定向的水分迁移会提高孔隙的连通性,C3的水分扩散程度高于C1,故其连通性亦较大,进而使其抗渗性降低,从图 6可以看出,C3混凝土的氯离子渗透系数高于C1混凝土。
|
Download:
|
| 图 7 负温养护条件下混凝土孔径分布情况 Fig. 7 The distribution of the pore of concrete under negative temperature curing conditions | |
1) 负温养护条件会对混凝土的水化程度、孔结构的变化趋势及抗渗性的发展情况造成较大的影响,该养护条件下,水灰比对上述三者的影响情况与标养条件下有所不同,28 d龄期时,0.31水灰比的抗渗性最优,0.24水灰比次之,0.38水灰比最差,这与负温下混凝土中水的存在状态有较大的关系。
2) 基于热力学原理,考虑弯曲液面附加压力的影响,推导出了孔隙结构中液体冰点与孔径之间的关系,并通过相关文献进行了验证,结果表明,该计算模型能较为准确的反映出不同孔径中水的冰点变化情况。
3) 水泥基材料的水化反应决定其微观孔结构的发育情况,而孔隙结构又会反过来影响水化的进程,因此两者为相互作用的关系,水化过程中液相水的含量是影响其水化及孔结构发展的重要因素,最终的影响结果将会表现在混凝土的抗渗性上。
| [1] |
王月, 安明喆, 余自若, 等. 氯盐侵蚀与冻融循环耦合作用下C50高性能混凝土的耐久性研究[J]. 中国铁道科学, 2014, 35(3): 41-46. WANG Yue, AN Mingzhe, YU Ziruo, et al. Durability of C50 High performance concrete under the coupled action of chloride salt erosion and freeze-thaw cycle[J]. China railway science, 2014, 35(3): 41-46. DOI:10.3969/j.issn.1001-4632.2014.03.07 (  0) 0)
|
| [2] |
高矗, 申向东, 王萧萧, 等. 石灰石粉对浮石混凝土力学性能和微观结构的影响[J]. 硅酸盐通报, 2014, 33(7): 1583-1588. GAO Chu, SHEN Xiangdong, WANG Xiaoxiao, et al. Influence of limestone powder on mechanical property and microstructure of pumice concrete[J]. Bulletin of the Chinese ceramic society, 2014, 33(7): 1583-1588. (  0) 0)
|
| [3] |
刘军, 邢锋, 董必钦, 等. 混凝土的微观孔结构及对渗透性能的影响[J]. 混凝土, 2009(2): 32-34. LIU Jun, XING Feng, DONG Biqin, et al. Influence of micro-pore structure on the permeability of concrete[J]. Concrete, 2009(2): 32-34. (  0) 0)
|
| [4] |
何锐, 王铜, 陈华鑫, 等. 青藏高原气候环境对混凝土强度和抗渗性的影响[J]. 中国公路学报, 2020, 33(7): 29-41. HE Rui, WANG Tong, CHEN Huaxin, et al. Impact of Qinghai-Tibet Plateau's climate on strength and permeability of concrete[J]. China journal of highway and transport, 2020, 33(7): 29-41. (  0) 0)
|
| [5] |
王申, 李保亮, 潘子云, 等. 掺磨细镍铁渣混凝土的耐久性及其与孔结构和水化程度的关系[J]. 中南大学学报(自然科学版), 2020, 51(5): 1189-1199. WANG Shen, LI Baoliang, PAN Ziyun, et al. Durability and its relation with pore structure and hydration degree of concrete with ferronickel slag powder[J]. Journal of Central South University (Science and Technology), 2020, 51(5): 1189-1199. (  0) 0)
|
| [6] |
MEHTA P K, MONTEIRO P J M. Concrete:microstructure, properties, and materials[M]. 2nd ed. New York: McGraw-Hill, 1993.
(  0) 0)
|
| [7] |
陈立军, 王永平, 尹新生, 等. 混凝土孔径尺寸对其抗渗性的影响[J]. 硅酸盐学报, 2005, 33(4): 500-505. CHEN Lijun, WANG Yongping, YIN Xinshen, et al. Effect of aperture size on impermeability of concrete[J]. Journal of the Chinese ceramic society, 2005, 33(4): 500-505. DOI:10.3321/j.issn:0454-5648.2005.04.017 (  0) 0)
|
| [8] |
GALLÉ C, PEYCELON H, LE BESCOP P. Effect of an accelerated chemical degradation on water permeability and pore structure of cementbased materials[J]. Advances in cement research, 2004, 16(3): 105-114. (  0) 0)
|
| [9] |
MA Xianwei, LIU Jianhui, WU Zemei, et al. Effects of SAP on the properties and pore structure of high performance cement-based materials[J]. Construction and building materials, 2017, 131: 476-484. (  0) 0)
|
| [10] |
LEE C, CHI M, HUANG Ran. Quantitative evaluation of mineral admixtures on the properties, pore structure, and durability of cement-based composites[J]. Science and engineering of composite materials, 2012, 19(2): 199-207. (  0) 0)
|
| [11] |
王甲春, 阎培渝, 韩建国. 混凝土绝热温升的实验测试与分析[J]. 建筑材料学报, 2005, 8(4): 446-451. WANG Jiachun, YAN Peiyu, HAN Jianguo. Experiment and analysis of concrete adiabatic temperature rise[J]. Journal of building materials, 2005, 8(4): 446-451. DOI:10.3969/j.issn.1007-9629.2005.04.018 (  0) 0)
|
| [12] |
王起才, 陈川, 张戎令, 等. 考虑持续低温影响的水泥水化放热计算模型[J]. 建筑材料学报, 2015, 18(2): 249-254. WANG Qicai, CHEN Chuan, ZHANG Rongling, et al. Computing model for the hydration heat of cement paste considering the effect of sustained low temperature[J]. Journal of building materials, 2015, 18(2): 249-254. DOI:10.3969/j.issn.1007-9629.2015.02.011 (  0) 0)
|
| [13] |
李椿, 章立源, 钱尚武. 热学[M]. 2版. 北京: 高等教育出版社, 2008. LI Chun, ZHANG Liyuan, QIAN Shangwu. Thermology[M]. 2nd ed. Beijing: Higher Education Press, 2008. (  0) 0)
|
| [14] |
金贤玉, 王宇纬, 田野, 等. 基于微观信息的水泥水化动力学模型研究[J]. 建筑材料学报, 2014, 17(5): 862-867. JIN Xianyu, WANG Yuwei, TIAN Ye, et al. Research on kinetics model of cement hydration based on microstructure information[J]. Journal of building materials, 2014, 17(5): 862-867. DOI:10.3969/j.issn.1007-9629.2014.05.018 (  0) 0)
|
| [15] |
傅鹰. 化学热力学导论[M]. 北京: 科学出版社, 1963: 114. FU Ying. Introduction to chemical thermodynamics[M]. Beijing: Science Press, 1963: 114. (  0) 0)
|
| [16] |
A. W.亚当森.表面的物理化学[M].顾惕人, 译.北京: 科学出版社, 1984: 114. ADAMSON A W. Physical chemistry of surfaces[M]. GU Tiren, trans. Beijing: Science Press, 1963: 114. (  0) 0)
|
| [17] |
戴长印. 水的冰点和三相点相同吗?[J]. 化学教学, 1990(2): 38-39. DAI Changyin. Is the freezing point of water the same as the triple point?[J]. Education in chemistry, 1990(2): 38-39. (  0) 0)
|
| [18] |
陈树人, 刘棱哲, 王久良. 混凝土孔结构对冰点的影响[J]. 低温建筑技术, 2000(1): 9, 17. CHEN Shuren, LIU Lengzhe, WANG Jiuliang. Effect of concrete hole structure on freezing temperature[J]. Low temperature architecture technology, 2000(1): 9, 17. (  0) 0)
|
| [19] |
杨文萃.无机盐对混凝土孔结构和抗冻性影响的研究[D].哈尔滨: 哈尔滨工业大学, 2009. YANG Wencui. Effect of inorganic salts on pore structure and frost resistance of concrete[D]. Harbin: Harbin Institute of Technology, 2009. (  0) 0)
|
| [20] |
杨永华. 物理化学[M]. 北京: 高等教育出版社, 2012. YANG Yonghua. Physical chemistry[M]. Beijing: Higher Education Press, 2012. (  0) 0)
|
| [21] |
何忠茂, 巴恒静, 王岩. 负温下水泥水化热力学模型的研究与论证[J]. 材料科学与工艺, 2005, 13(4): 435-437, 441. HE Zhongmao, BA Hengjing, WANG Yan. Research and argument on the thermodynamic model of cement hydration at minus temperature[J]. Materials science & technology, 2005, 13(4): 435-437, 441. DOI:10.3969/j.issn.1005-0299.2005.04.027 (  0) 0)
|
| [22] |
王竹溪. 热力学简明教程[M]. 北京: 商务印书馆, 1975: 160. WANG Zhuxi. Brief course on thermodynamics[M]. Beijing: The Commercial Press, 1975: 160. (  0) 0)
|
| [23] |
屈永平, 唐川, 刘洋, 等. 西藏林芝地区冰川降雨型泥石流调查分析[J]. 岩石力学与工程学报, 2015, 34(S2): 4013-4022. QU Yongping, TANG Chuan, LIU Yang, et al. Investigation and analysis of glacier debris flow in Nyingchi area, Tibet[J]. Chinese journal of rock mechanics and engineering, 2015, 34(S2): 4013-4022. (  0) 0)
|
| [24] |
吴义彬. 定量计算水表面张力系数及其温度变化率[J]. 物理通报, 2015(1): 103-106. WU Yibin. Quantitative calculation on water surface tension coefficient and its temperature variation percentage[J]. Physics bulletin, 2015(1): 103-106. (  0) 0)
|
| [25] |
郭天同.冰水固流转化理论研究[D].青岛: 青岛科技大学, 2011. GUO Tiantong. The theoretical research on transformation between solid and liquid of water and ice[D]. Qingdao: Qingdao University of Science and Technology, 2011. (  0) 0)
|
| [26] |
吴中伟, 廉慧珍. 高性能混凝土[M]. 北京: 中国铁道出版社, 1999. WU Zhongwei, LIAN Huizhen. High performance concrete[M]. Beijing: China Railway Publishing House, 1999. (  0) 0)
|
| [27] |
王新友, 蒋正武, 高相东, 等. 混凝土中水分迁移机理与模型研究评述[J]. 建筑材料学报, 2002, 5(1): 66-71. WANG Xinyou, JIANG Zhengwu, GAO Xiangdong, et al. Review on the mechanism and model of moisture transfer in concrete[J]. Journal of building materials, 2002, 5(1): 66-71. (  0) 0)
|
| [28] |
苏卿, 万小梅, 赵铁军, 等. 环境湿度对水泥基材料中水分迁移的影响[J]. 建筑结构学报, 2009, 30(S2): 319-322. SU Qing, WANG Xiaomei, ZHAO Tiejun, et al. Experimental research on influence of humidity on moisture diffusion in cementitious composites[J]. Journal of building structures, 2009, 30(S2): 319-322. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


