2. 西安工程大学 环境与化学工程学院, 陕西 西安 710048
2. School of Environmental and Chemical Engineering, Xi'an Polytechnic University, Xi'an 710048, China
砌体结构是我国现存古建筑的主要结构形式之一,有着几千年的悠久历史,一砖一石之间无不凝结着我国文明的发展轨迹。由于大多数砌体古建筑建造之初主要为满足竖向承载力的要求,而忽略了水平荷载(如地震)对其的影响[1]。同时由于年限久远,砌筑灰浆性能由于各种原因往往显著退化[2],结构整体一旦遇到较强地震通常发生严重破坏甚至倒塌。通过汶川地震震害调查[3]中砖石砌体古塔的破坏即可印证上述观点。因此,针对砌体古建筑保护特点对砌筑灰浆进行加固,同时对加固后构件的抗震性能进行分析,显得尤为必要。
对于古建筑修缮,要求从风貌、结构等方面做到“修旧如旧”[4]。在目前诸多历史砌体加固的方法中,诸如外加装置加固法[5]、FRP贴面加固法[6]等虽提高了砌体承载力,但对其外观影响较大,与“修旧如旧”原则违背。而注浆加固则是将注浆液注入砌体孔洞或裂隙中,通过浆液渗透来提高砌体强度的一种方法,很大程度上保留历史建筑的原有外观。近年来已有诸多学者通过注浆法,采用天然石灰基或水泥基浆液对历史砌体建筑进行了修复加固[7-9],然而却很少采用高分子聚合物浆液对古砌体进行注浆加固。人工神经网络可以通过学习来最佳逼近非线性映射,在近几年的土木工程领域有着广泛应用,如混凝土强度的预测[10]、结构损伤裂缝探测[11]、火荷载下木构件的温度计算[12]、结构整体动力反应模型识别[13]等方面均表现出优异性能。
本文针对历史青砖墙,将环氧树脂浆液作为注浆液,通过其在砌筑灰缝微孔道中渗透来提高砌筑灰浆的强度和粘结力,从而提升整个砖砌体的力学性能。同时通过注浆加固前后古砖墙的静力与拟静力试验对比,说明了环氧树脂浆液注浆法可以明显提高古砖墙的受压、受剪与抗震性能。最后使用遗传优化神经网络算法,建立古砖墙在水平反复荷载下的滞回模型,并通过对比分析验证了模型正确性。
1 试件制作与注浆加固 1.1 试验试件制作为尽量模拟还原我国古代糯米灰浆青砖墙,并兼顾试验可行性,采用青砖作为砌块,青砖收集自具有100年以上历史的拆除民居建筑,糯米灰浆参考清代《工程做法则例》记载的插灰泥糯米灰浆制作,采用生石灰、黄土和糯米浆配制:原状黄土经晾晒筛分祛除杂质得到备用黄土;糯米粉按5%浓度与水混合,加热煮沸过滤得到备用糯米浆;将生石灰粉按水灰比0.8制作得到备用石灰浆;备用石灰浆与备用黄土按体积比1:1拌合并焖制8 h,再掺入备用糯米浆并拌合形成砌筑用糯米灰浆。采用上述灰浆与和青砖对古砖墙试件进行了模拟制作。注浆加固用环氧树脂浆液为一种由A和B 2组份按质量比2:1混合而成的改性环氧树脂胶液,试件制作原材料如图 1所示。

|
Download:
|
| 图 1 试件材料 Fig. 1 Specimen materials | |
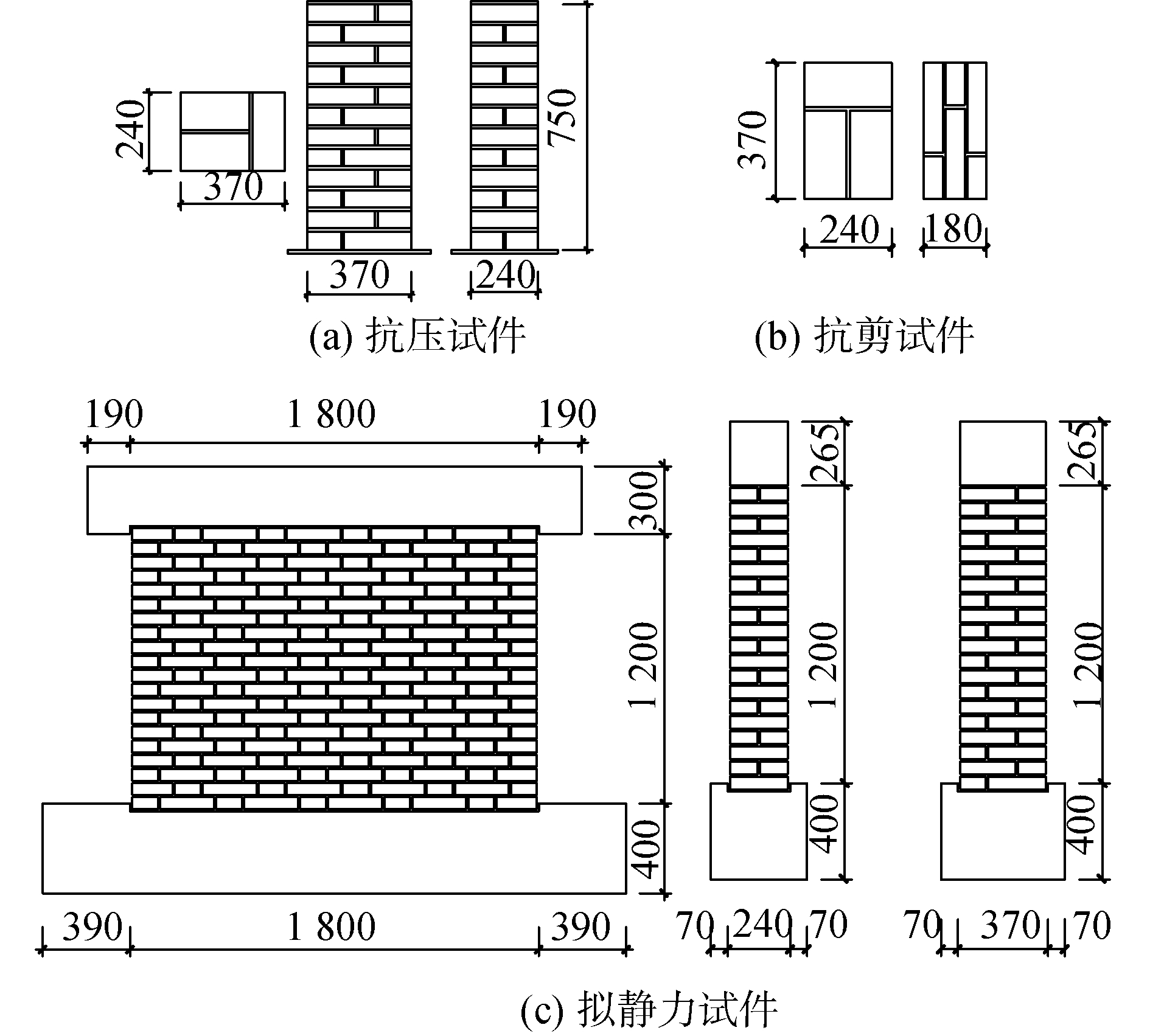
采用同样材料与砌筑工艺同一砌筑所有试件,砌体强度试件共分为CN、CY、VN、VY 4组,分别表示轴心抗压未加固、注浆加固,抗剪未加固、注浆加固,每组3个试件。抗压试件如图 2(a)所示,抗剪试件如图 2(b)所示。拟静力试件砌筑2组共4片墙体,第1组W11和W12墙体截面尺寸为1 800 mm×240 mm,第2组W21和W22墙体截面尺寸为1 800 mm×370 mm,其中W12和W22为加固试件,墙体高度均为1 200 mm,所有试件砌筑灰缝厚度为10 mm,试件尺寸如图 2(c)所示。墙体砌筑于底梁之上,顶部设置加载顶梁。
|
Download:
|
| 图 2 试件尺寸 Fig. 2 Specimens dimensions | |
试件砌筑完毕后均养护至28 d,再对相应试件进行注浆加固,具体操作步骤以拟静力试件加固为例叙述,如图 3所示。

|
Download:
|
| 图 3 注浆加固步骤 Fig. 3 Grouting reinforcement steps | |
图(a)注浆孔设置:试件两侧沿水平灰缝每隔400~600 mm钻凿直径为8 mm的圆形孔,孔深为砌体试件1/3的厚度。图(b)安装注浆嘴:使用清水冲洗孔眼以湿润灰浆并用少量糯米灰浆将灌浆嘴固定。图(c)人工注浆:用注射器将高分子浆液由下向上逐缝注入注浆孔至注浆嘴溢出注浆料,待注入浆液充分渗入灰缝后重复注浆5次。图(d)填封处理:用拌和了注浆液的糯米灰浆对注浆孔洞填实密封,并在自然条件下养护48 h。
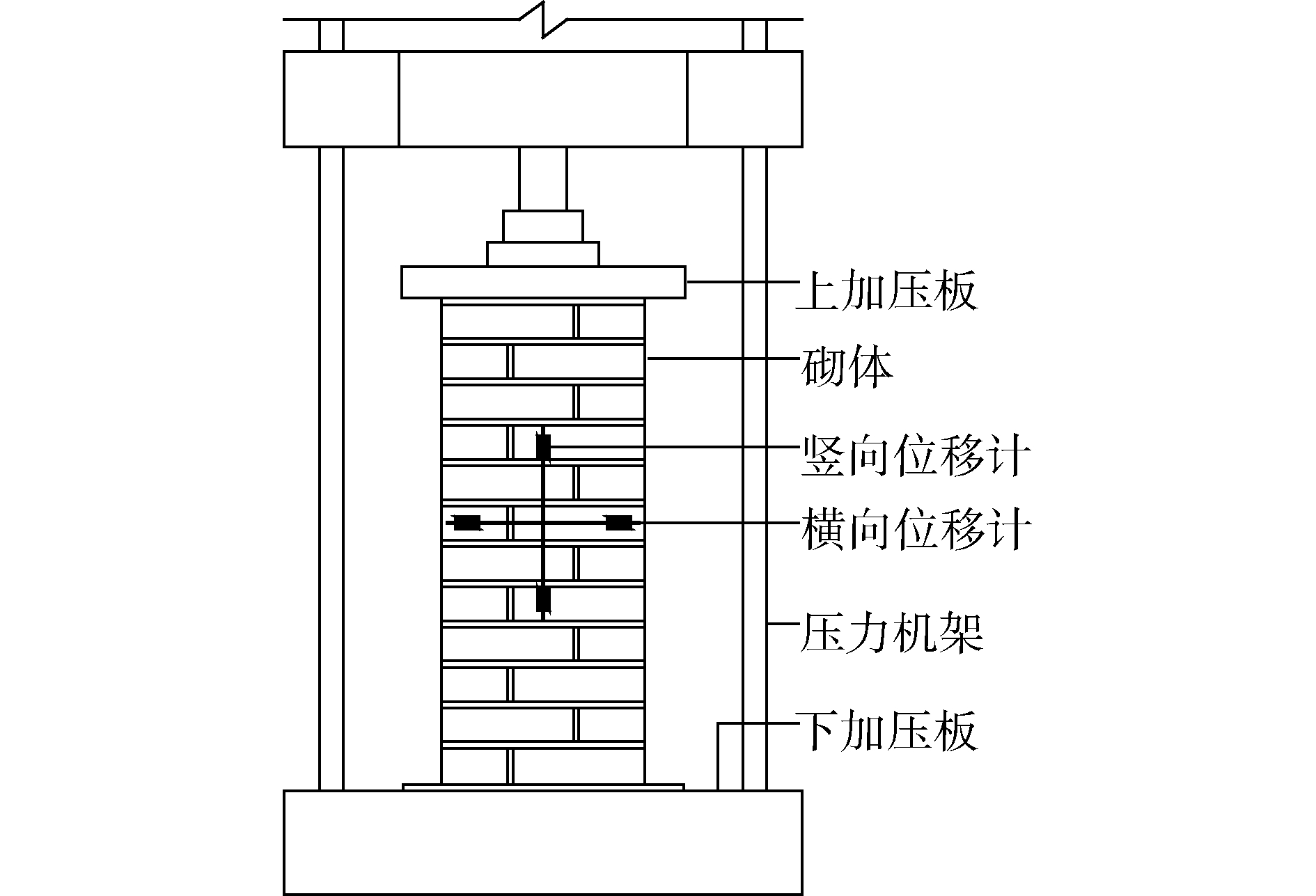
2 试验概况 2.1 抗压与抗剪试验轴心抗压与抗剪试验根据规范GB/T 50129-2011[14]的相关要求进行。对于抗压试验,采用分级加载制度,首先施加5%预估极限荷载,以检查试验设备的工作性,之后每次在1 min之内匀速施加10%预估极限荷载且保持1 min,当压力试验机读数出现明显回弹时,即宣告砌体破坏,此时压力值为极限荷载。对于抗剪试验,试件中心与试验机上、下压板中线重合且压板与试件接触面紧密贴合,采用匀速加载方法,加载速率为0.05 kN/s。在加载过程中若一个剪切面发生破坏即认为试件破坏,此时荷载即为极限荷载。抗压与抗剪试验加载如图 4所示,砌体的测点布置如图 5所示。

|
Download:
|
| 图 4 试验加载图 Fig. 4 Test loading photos | |
|
Download:
|
| 图 5 试验装置简图 Fig. 5 Test setup diagram | |
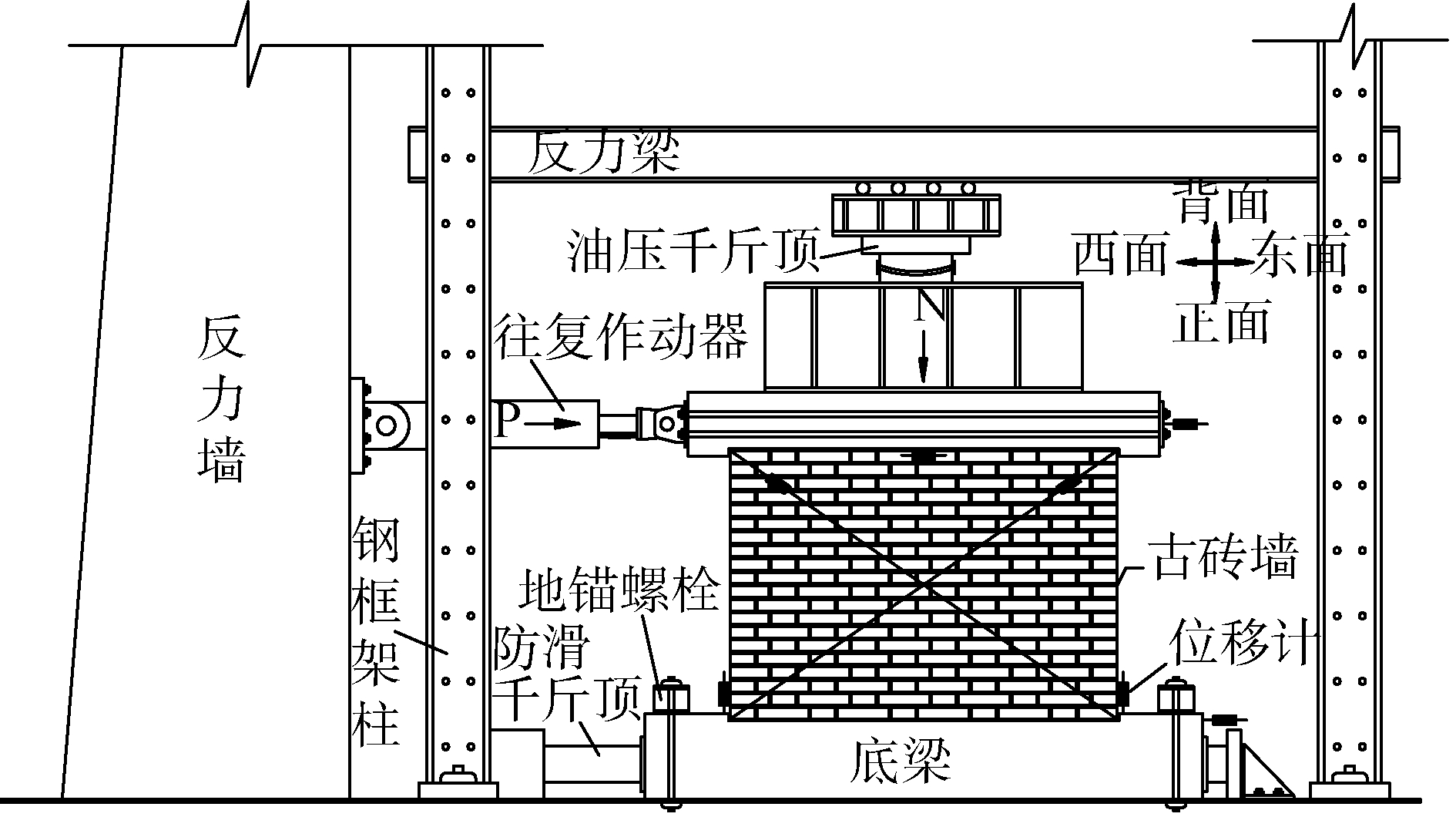
该试验采用电液伺服装置加载,试验装置及位移计布置如图 6。竖向加载对墙体(顶梁)一次加足,第1组施加80 kN,第2组施加135 kN,并在后续试验过程中保证竖向荷载恒定。水平加载采用荷载-位移双控加载方式[15]。试件开裂前按荷载控制,按每10 kN一级逐级递增,每级循环一次。试件开裂后,水平加载按位移控制,按每1 dc(墙体开裂位移)一级逐级递增。达到极限荷载后,继续按位移控制加载,直至墙体破坏或反力荷载下降到极限荷载的80%,停止加载。
|
Download:
|
| 图 6 墙片拟静力试验简图 Fig. 6 Wall pseudo static facilities diagram | |
注浆加固轴心受压过程与未加固试件相似,从开始加载,砌体基本处于弹性状态,直至首条裂缝均出现在短面底部中心位置的灰缝处;随着荷载增加,裂缝不断发展向上延伸贯通若干皮砖,灰缝出现明显剥落,同时在宽面出现数条竖向裂缝;荷载继续增加,表面出现贯通竖向裂缝,CN砌体下部砖块发生破裂并向外鼓胀,压力试验机指针明显回弹,试件出现劈裂破坏,呈现明显脆性破坏特征;相较于基材试件,CY砌体裂缝分布较少,灰浆剥落较少,没有出现砖块的压碎与鼓胀现象,试件典型破坏形态如图 7所示。

|
Download:
|
| 图 7 抗压试件破坏形态 Fig. 7 Failure patterns of compressive specimens | |
注浆加固抗剪试件受剪过程与未加固试件基本相同,在加载初期砖块与灰浆的连接面没有开裂迹象,随着荷载增加,一侧连接界面出现细裂缝并向沿灰缝向试件中部发展变宽,最终成为贯通裂缝,发生单侧剪切破坏,如图 8所示。

|
Download:
|
| 图 8 抗剪试件破坏形态 Fig. 8 Failure pattern of shear specimen | |
试验强度结果如表 1所示,试件C、CE的抗压强度平均值分别为:2.27 MPa,3.19 MPa;试件V、VE、VM的抗剪强度平均值分别为:0.045 MPa、0.050 MPa。试件CE抗压强度与试件VE抗剪强度的提高率分别为40.5%、11.1%。可以看出改性环氧树脂注浆加固可以提高古砖墙试件的抗压与抗剪强度,且对抗压强度提高幅度较大。
| 表 1 抗压与抗剪强度 Table 1 Compressive strength and shear strength |
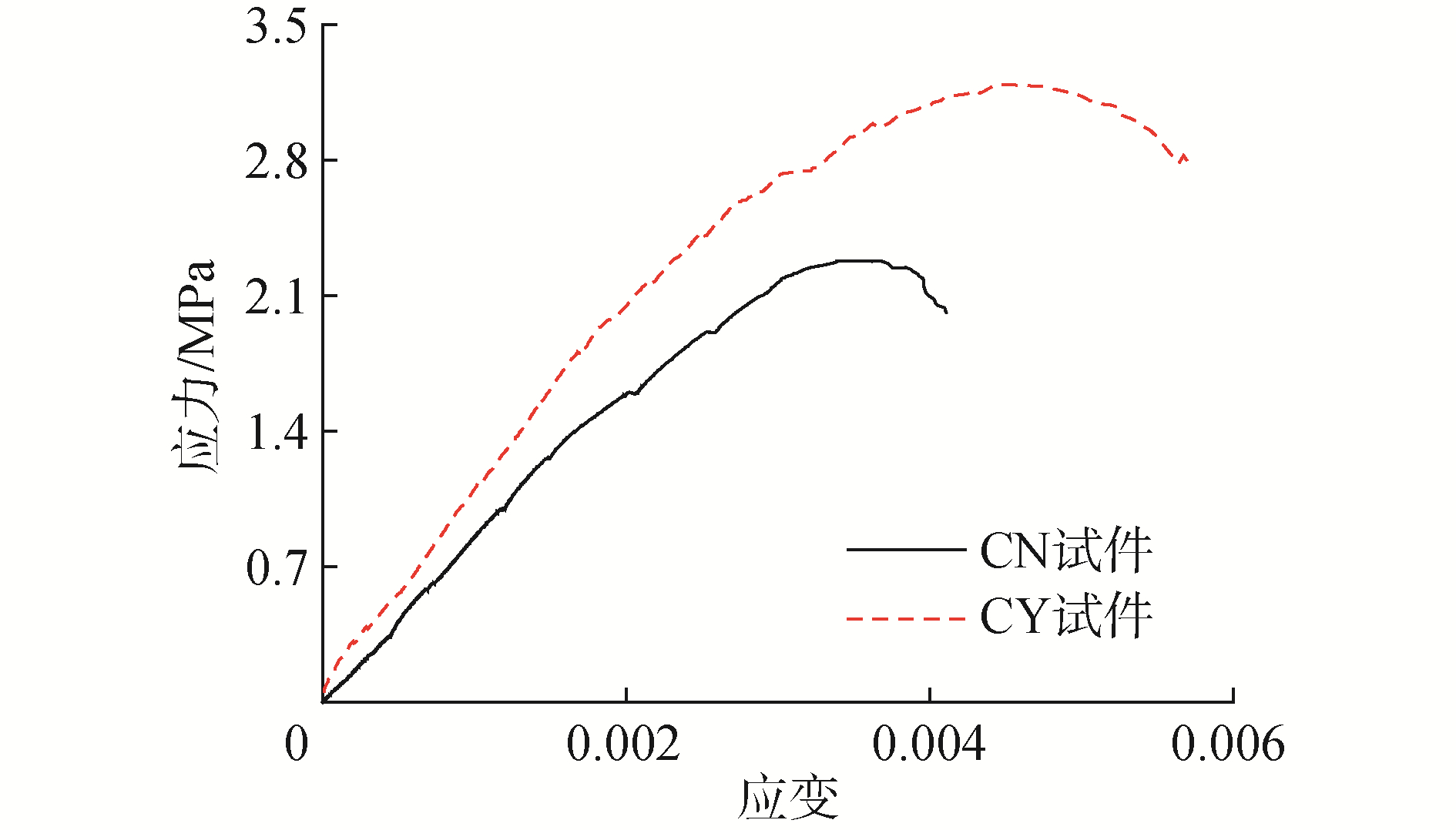
轴心受压试件应力-应变曲线如图 9,砖墙试件弹性模量E按式(1)[14]计算,式中ε0.4为对应应力为0.4fc, i时的应变值。得出试件C、CE弹性模量平均值分别为852、1 080 MPa,试件CE弹性模量提高率为26.8%。且从图中可以看出,相对与基材试件C,试件CE的峰值应力、峰值应变、极限应变均有所提高。
|
Download:
|
| 图 9 轴心抗压应力应变曲线 Fig. 9 Compressive stress-strain curves | |
| $E=\frac{0.4 f_{c, i}}{\varepsilon_{0.4}} $ | (1) |
注浆加固可以提高部分灰浆强度, 各墙体试件破坏机理相同,均为对角剪切破坏。各试件试验现象基本一致,现以W11为例进行描述,其主要破坏过程如下:水平加载至+30 kN前(以作动器推为正,拉为负),整体试件没有肉眼可见裂缝出现,且卸载无残余变形,可归于弹性阶段;当水平荷载加至+30 kN时,墙体东侧(正面)底部1、2皮砖之间(即第1层灰缝)出现水平裂缝,水平裂缝由东向西不断延展,此时水平位移为+0.81 mm,卸载时荷载-位移曲线出现弯曲,开始进入塑性段;当水平荷载加至-40 kN时,墙体西侧(正面)底部第3、4皮砖之间(即第3层灰缝)出现水平裂缝,墙正面裂缝由西向东呈阶梯状向第1层灰缝延伸,此时水平位移为-0.64 mm;上述裂缝的发展在墙体背面基本与正面对应一致。当加载至48 kN时,荷载-位移曲线发生明显弯曲,此时以开裂位移dcr=1.4 mm控制分级加载。当循环加载至2dcr后,墙正面中部出现跨越5皮砖的由东(背面)向西(正面)发展的斜裂缝(记为“拉向斜裂缝”),背面墙同时在东侧出现跨越5、6层灰缝的阶梯状斜裂缝;当循环加载4dcr后,墙正面拉向斜裂缝自东向西贯通且与墙背面裂缝基本对应,同时墙面还出现由西向东、自上至下发展的斜向阶梯形裂缝(记为“推向斜裂缝”)。在裂缝不断发展过程中伴随有砖崩裂声响。拉向斜裂缝与推向斜裂缝在墙中部附近相交,形成X向阶梯形交叉斜裂缝;当循环加载5dcr后,推、拉向斜裂缝变宽,灰缝起皮掉渣严重,在墙中部出现少量短小的斜向裂缝;历经6dcr循环加载后,荷载下降到峰值荷载的85%以下,完成7dcr的循环加载后终止加载,各试件最终破坏形态见图 10。

|
Download:
|
| 图 10 W11墙体破坏形态 Fig. 10 Brick wall failure pattern W11 | |
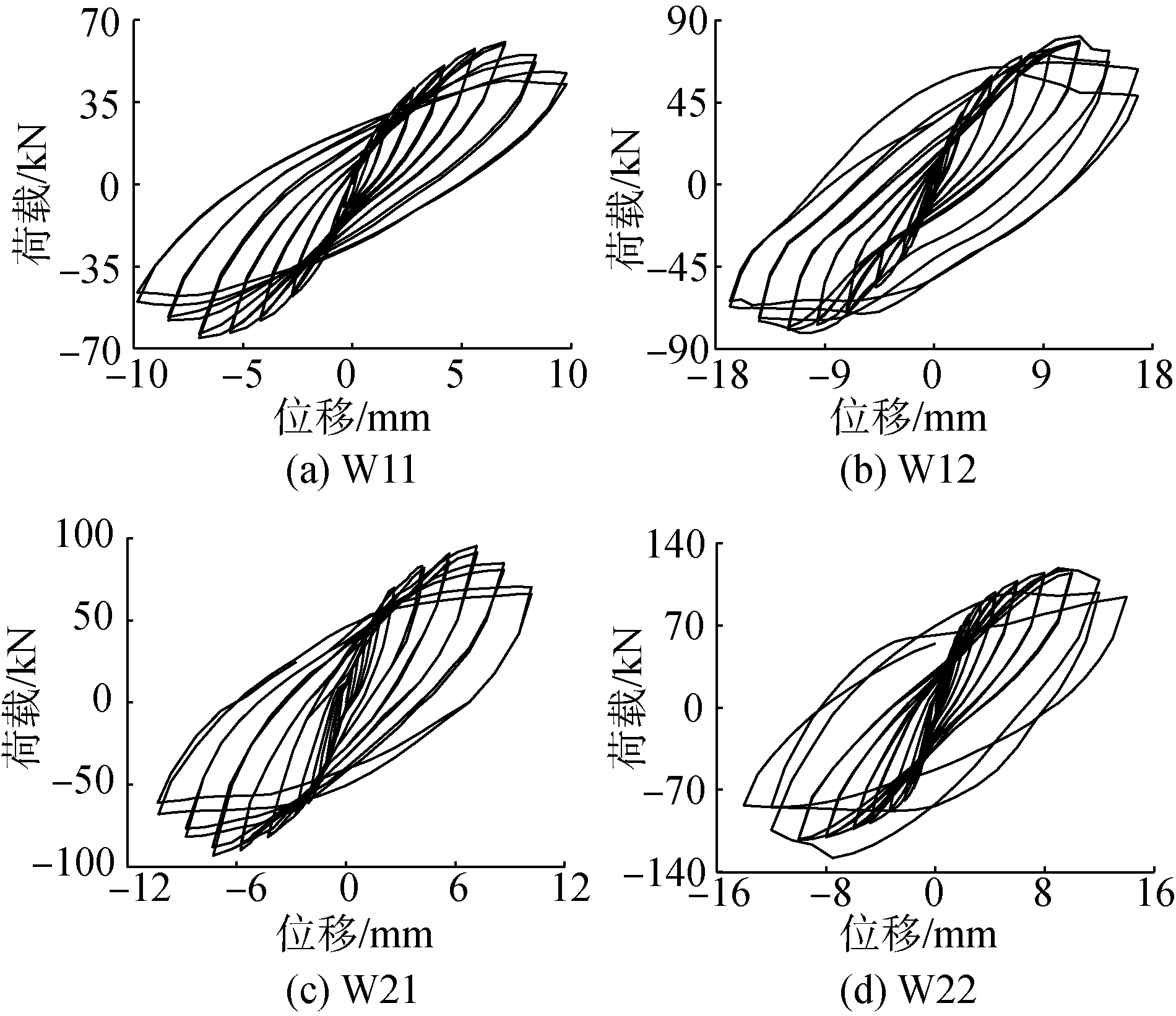
拟静力试验试件荷载-位移滞回曲线所包围面积表征了其地震荷载下的耗能能力,各试件的滞回曲线如图 11所示。通过计算得出各试件在屈服、峰值和极限荷载下对应的滞回耗能,列于表 2。可知试件W12(W22)与W11(W21)相比, 滞回环包围面积更大,各阶段耗能均增大,注浆加固可以提高试件的耗能能力;且随试件厚度增加,试件耗能能力越来越强。试件的延性系数μ按照式(2)计算列于表格2中,可知试件W12和W22分别提高了28.0%和27.5%,可知注浆加固提高了砖墙试件的延性。
| 表 2 滞回耗能与延性系数 Table 2 Hysteretic energy dissipation and ductility coefficient |
|
Download:
|
| 图 11 试件滞回曲线 Fig. 11 Hysteresis curves of specimens | |
| $\mu=\frac{\Delta_{u}}{\Delta_{y}} $ | (2) |
式中:Δu为极限位移;Δy为屈服位移。
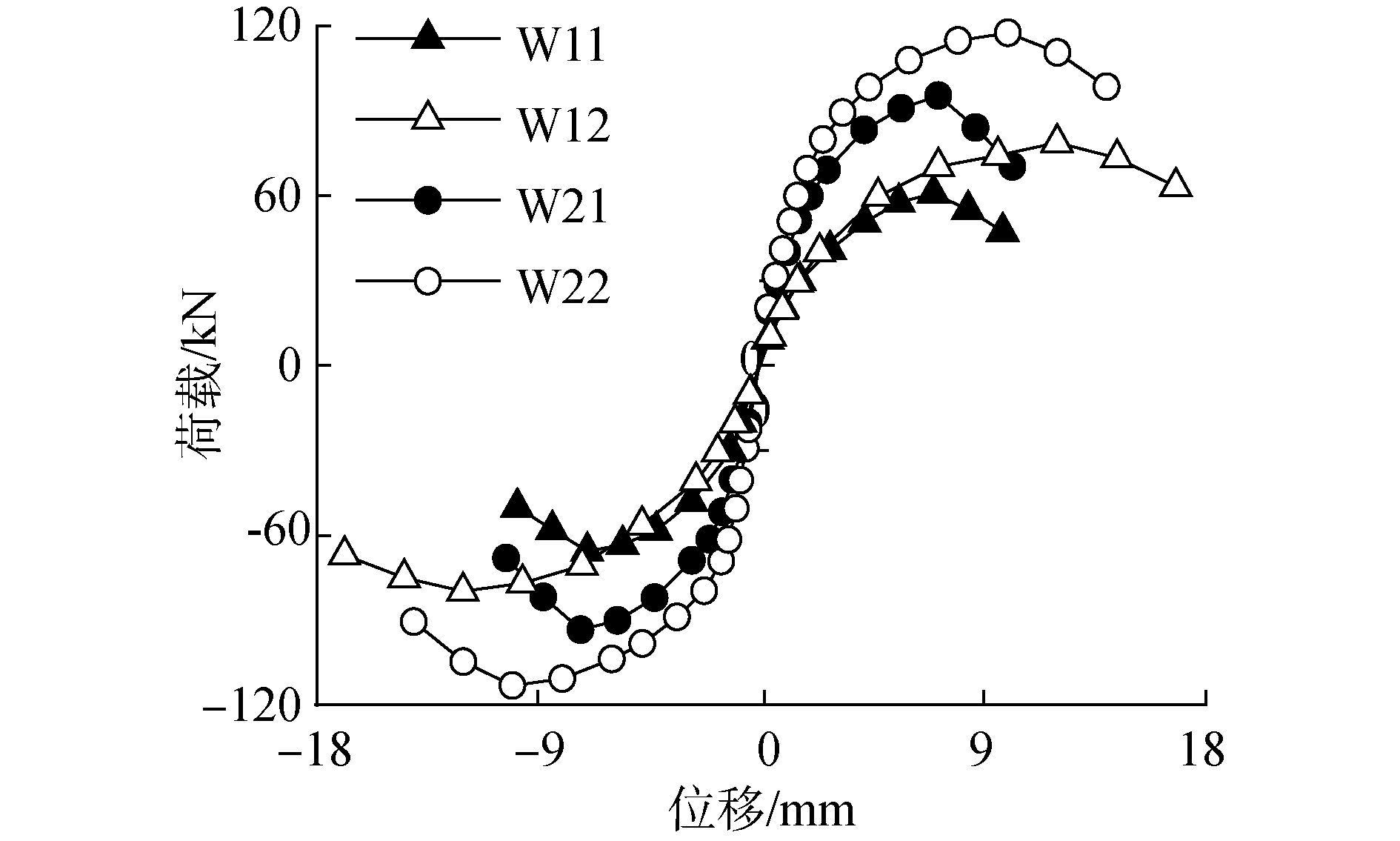
试件骨架曲线如图 12所示,加载初期近似呈直线,加固前后斜率相差不大,加固后直线段更长;达到峰值荷载后,各试件刚度均开始减小,但未加固曲线下降段斜率较大,水平承载力下降快,刚度退化较快,加固后平面内侧向变形发展更为充分,极限位移增大。砌体墙平面内刚度表征了其平面内抗侧移能力。取试件每级加载循环正、反两方向荷载峰值绝对值之和与位移峰值绝对值之和的比值来确定割线刚度[16]:
|
Download:
|
| 图 12 骨架曲线 Fig. 12 Skeleton curve | |
| $K_{i}=\frac{\left|F_{i}\right|+\left|-F_{i}\right|}{\left|d_{i}\right|+\left|-d_{i}\right|} $ | (3) |
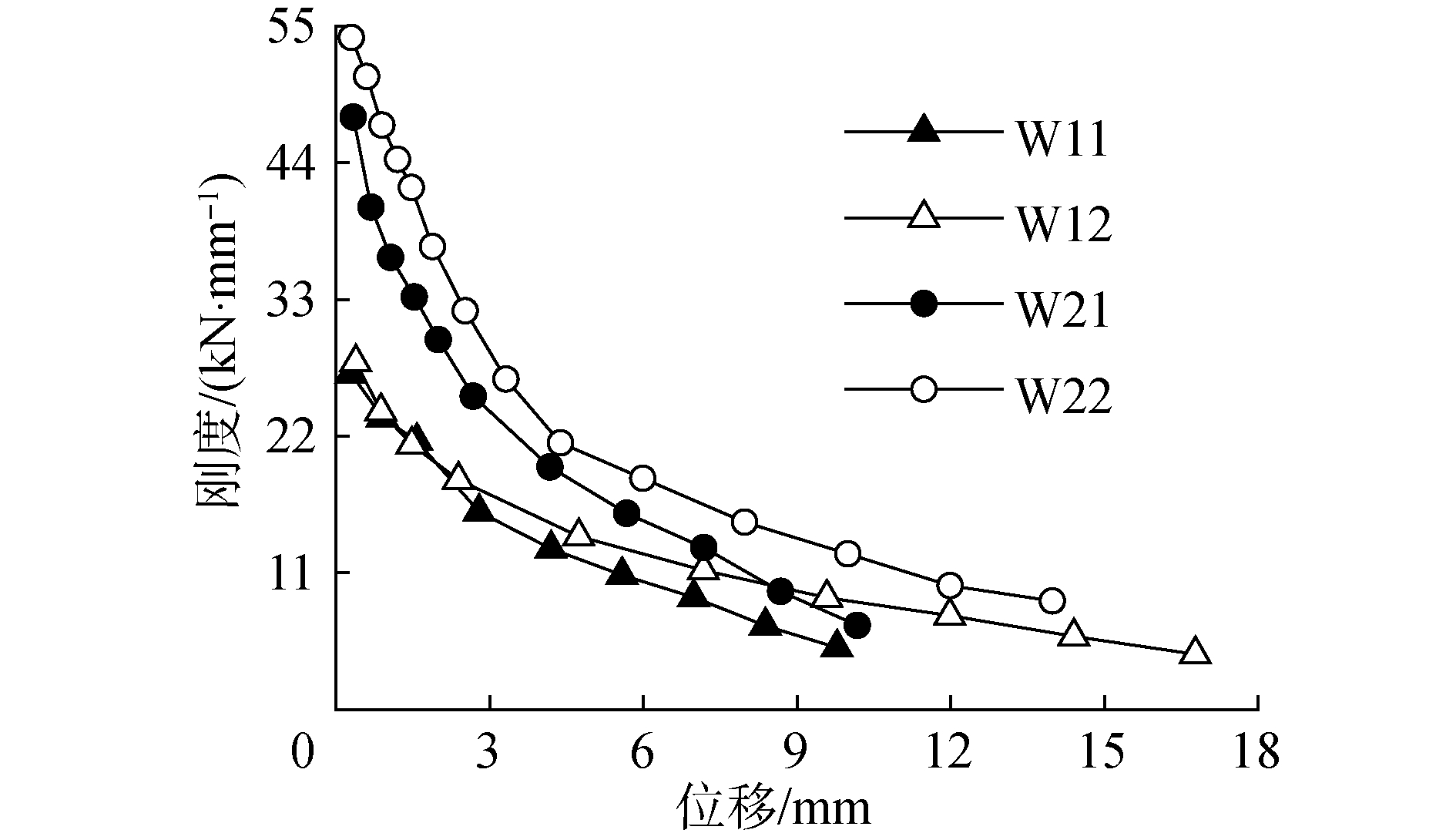
式中:Ki为第i次加载循环刚度;Fi、-Fi为第i次加载循环荷载值;di、-di为第i次加载循环峰点位移值。试件刚度退化曲线如图 13,各试件刚度退化规律一致,随位移增加而逐渐减小,由W11与W12曲线,未加固试件曲线斜率较大,刚度退化较快,注浆加固试件刚度退化曲线斜率增大,刚度退化减慢,提高了墙体延性;由W21与W22曲线,加固前后试件刚度退化速率相差不大,但加固墙体刚度较大;随墙厚增加,试件刚度增大,但加固前后刚度退化减缓效果降低。
|
Download:
|
| 图 13 刚度退化曲线 Fig. 13 Stiffness degradation | |
人工神经网络是一种模拟生物神经元系统的一种智能计算与预测模型。其中BP神经网络(Back propagation neural network,BPNN)是典型的前向性神经网络,通常由一层输入层神经单元,一层输出层神经单元,一层或多层隐含层神经单元组成,是广泛应用的高效神经网络之一。本文采用Levenberg-Marquardt BPNN算法[17]来建立滞回模型,通过输出误差反向传递来降低网络预测输出与期望输出之间的误差,进而调整网络连接权值和阀值。训练过程主要包含2个阶段:1)输入信号前向传递;2)输出误差反向传播。在第1阶段,输入信号从输入层传向隐含层,隐含层神经单元将输入信号通过激活函数处理得到输出信号并传递给输出层神经单元,输出层神经单元同样通过激活函数处理最终得到BPNN的训练与预测输出。隐含层激活函数选择为logsig,考虑到sigmoid型激活函数的饱和性影响网络收敛,输出层激活函数选择为purelin线性函数。
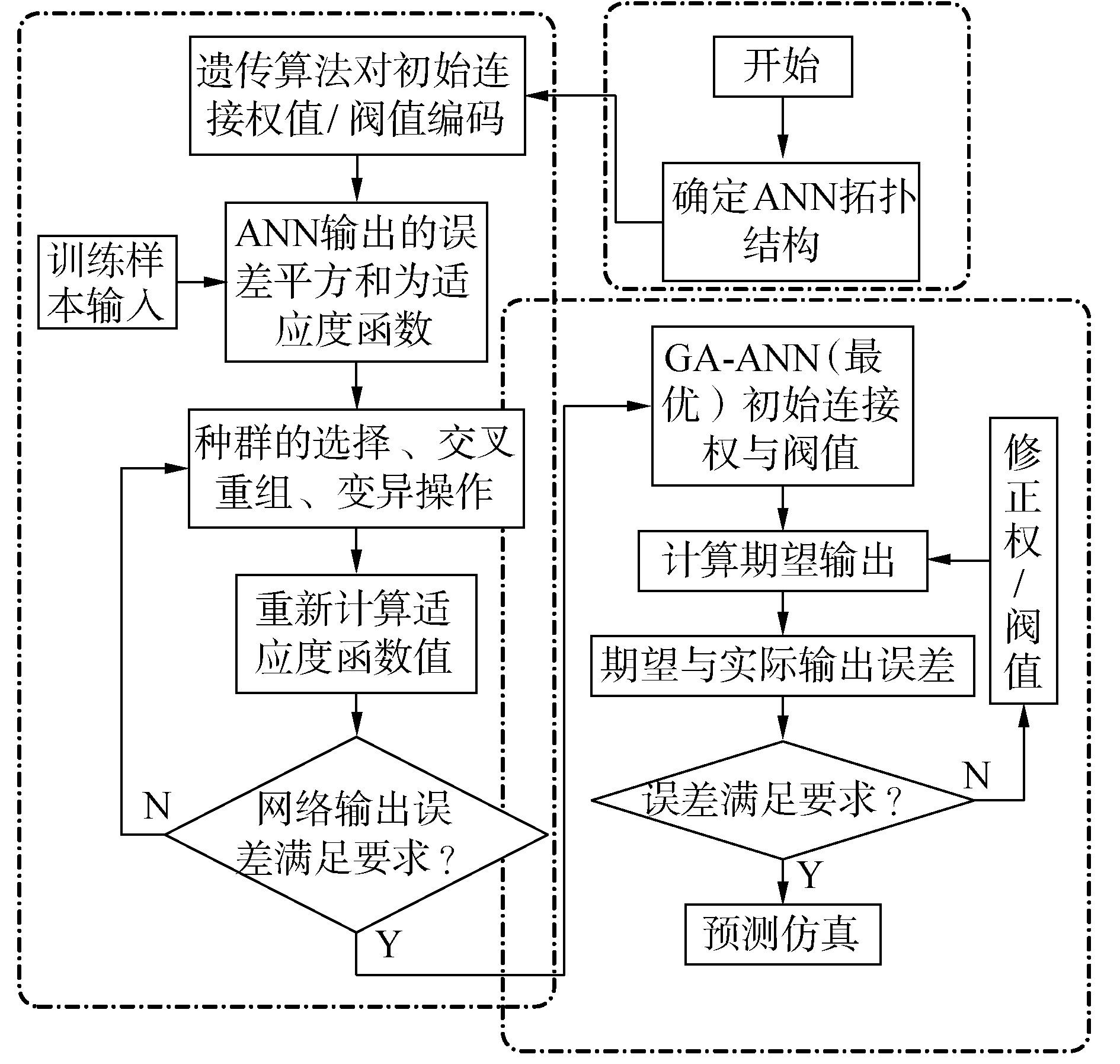
神经单元的初始连接权/阀值初值对网络训练效果影响较大,默认每次循环前连接权/阀值取值由系统随机指定,因此每次训练后得到的网络模型会存在较大差异,使得网络不易推广与泛化。遗传算法(genetic algorithm,GA)基于生物进化论,具有较强的全局寻优能力,可以通过其确定连接权/阀值初始最优值,形成遗传优化神经网络算法(genetic algorithm optimizing artificial neural network,GA-ANN),使得网络在初始最优值基础上迭代循环,避免由于初始连接权/阀值不同造成的训练后网络差异性。GA-ANN模型建立分为ANN拓扑结构确定、遗传算法优化初始连接权/阀值和GA-ANN训练与预测3个部分,遗传优化种群个体包括了BPNN所有的连接权/阀值,GA-ANN仿真流程如图 14所示。
|
Download:
|
| 图 14 GA-ANN流程 Fig. 14 GA-ANN flowchart | |
根据Kolmogolov定理[18], 由输入层、隐含层和输出层组成的3层BPNN可实现对任何输入与输出间的非线性映射的逼近与预测。采用MATLAB2014b®建立3层Levenberg-Marquardt BPNN,认为影响砖墙抗震性能的主要因素可以归结为3个方面,既是砖墙的砌筑组成、砖墙尺寸与受荷加载历史。依据上述试验数据,在此将以下11个参数变量作为输入单元:X1=σc,X2=σv,X3=E,X4=h/t,X5=b/t,X6=n,X7=Ri-2,X8=di-2,X9=Ri-1,X10=di-1,X11=di。
σc和σv为古砖砌体抗压和抗剪强度,E为砌体弹性模量,h/t为砖墙的高厚比,b/t为宽厚比,n=N/(σcbt)为轴压比,加载历史取为当前加载状态的前2个阶段,di为i时刻的位移,根据研究目标将输出层取为一个输出单元Y=Ri,即为i时刻的恢复力。隐含层神经单元数目确定是神经网络中的一个复杂问题,本文采用估算方法(4)[18]确定隐含层数目:
| $h \geqslant \max \{m \times(n+1), m \times 3\} $ | (4) |
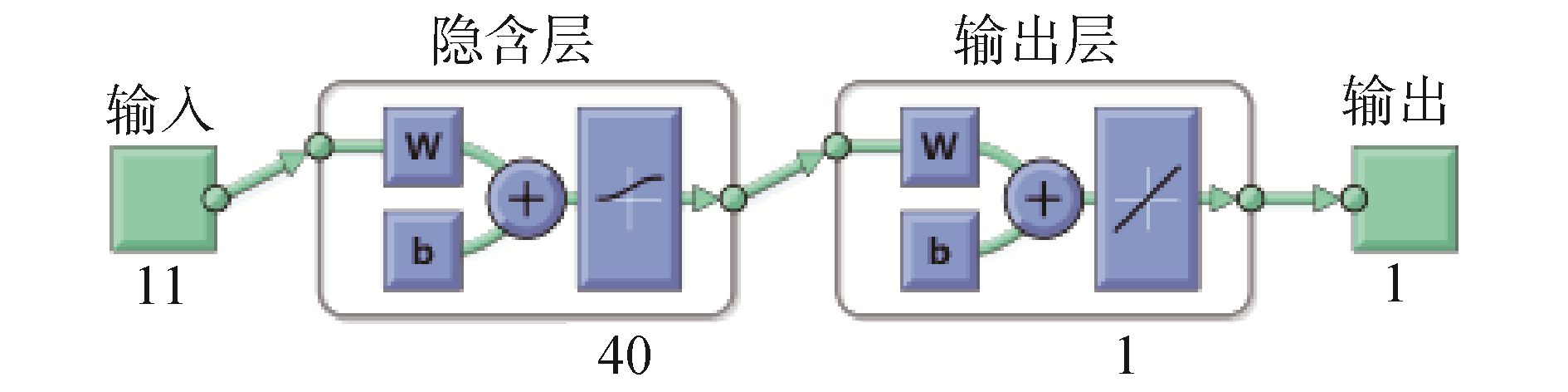
式中:h、m、n分别为隐含层神经元个数、输入层神经元个数和输出层神经元个数。据此将BP网络的隐含层神经元个数h取为40。可以得出本文的ANN的拓扑结构为11-40-1,如图 15。
|
Download:
|
| 图 15 ANN拓扑图 Fig. 15 ANN topology | |
采用注浆加固墙体W12和W22奇数圈滞回曲线数据训练网络,预测W12和W22偶数圈滞回曲线;未加固墙体W11和W21奇数圈滞回曲线数据训练网络,预测W11和W21偶数圈滞回曲线。最终分别得出加固与未加固古砖墙GA-ANN滞回模型。形成训练与预测样本时对数据进行了归一化处理。BPNN待确定连接权/阀值总数为11×40+40×1+40+1=521个,遗传算法采用实值编码,则染色体总长度为521,适应度函数为由训练样本输入所得BPNN输出与实际输出的误差平方和。利用MATLAB神经网络工具箱及Sheffield大学gatbx工具箱,编写GA-ANN代码程序。网络最大训练次数设置为1 000次,目标训练误差设置为10-4,学习率为0.08。遗传算法其他参数设置:初始种群数目50,采用随机遍历采样选择函数,代沟0.9,选择中间重组交叉算子与实值变异算子,变异概率0.01,最大遗传代数200代。
4.3 遗传优化神经网络滞回模型评价为充分说明GA-ANN的稳定性与适用性,在此选择未优化BP网络作为对比,采用上述同样训练与预测样本,同样网络参数,将二者的训练与预测结果进行对比,经过反复运行程序,选择理想结果列于图 16。2种网络的预测误差为OAi-Oi与OGAi-Oi,误差结果如图 16(a)~(d)所示,网络预测平均绝对误差按式(5)、(6)计算。

|
Download:
|
| 图 16 试验与仿真结果对比 Fig. 16 Comparison of test and simulation results | |
| $E_{A}^{\mathrm{avg}}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|O_{A i}-O_{i}\right| $ | (5) |
| $E_{\mathrm{GA}}^{\mathrm{avg}}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|O_{G A i}-O_{i}\right| $ | (6) |
式中:OAi和OGAi分别为ANN和GA-ANN网络的预测输出; Oi为试验输出; i代表第i个预测样本; n为预测样本总量; 计算得出W11、W21、W12、W22的预测平均绝对误差EAavg/EGAavg,分别为:1.899 kN/0.94 kN、2.904 kN/1.970 kN、3.335 kN/1.322 kN、4.827 kN/2.194 kN。可知ANN预测误差分布相对较为分散,GA-ANN预测误差分布较为集中,且大体分布于ANN误差范围以内,预测平均绝对误差大幅减小,预测精度明显提高。
从图 16(e)~(h)加固与未加固滞回曲线的拟合效果来看,GA-ANN滞回模型能够较好反映出古砖墙的滞回特征,加载初期与试验曲线吻合最好,后续在每次加载平稳段与卸载平稳段同样有较好的拟合效果,在每次循环峰值位移点附近,既加载段与卸载段转折点附近的偏差加大,可以通过增加转折点附近训练样本以增加训练次数来对网络模型作进一步改善。对比2种网络预测效果,可知GA-ANN滞回曲线与实际曲线拟合程度明显高于ANN。GA-ANN滞回模型可以较好地反映出古砖墙及其注浆加固后的抗震性能,具有较好稳定性和适用性。
5 结论1) 采用了糯米灰浆和古青砖以尽量还原我国传统糯米灰浆砌筑砖墙,并提出古砖墙高分子浆液注浆加固法,并通过试验证明了环氧树脂浆液注浆加固可以提高古砖墙抗压、抗剪强度和弹性模量。
2) 水平荷载下,注浆加固与未加固砖墙的破坏机理相同,各砖墙的破坏过程基本一致,均为首先在墙角出现水平裂缝,之后伴随荷载加大,形成“拉向斜裂缝”和“推向斜裂缝”,二者进一步在墙体中部附近相交,形成“X”型阶梯形交叉斜裂缝,呈“X”型剪切破坏形态。
3) 同尺寸古砖墙,加固后加载循环次数增加,滞回环更加饱满,滞回耗能增大,滞回加载极限位移增大,墙体延性及平面内刚度增大,刚度退化减缓,环氧树脂浆液注浆加固可以明显提高古砖墙的抗震性能。
4) 使用GA-ANN建立砖墙滞回模型,避免了从复杂滞回关系中寻找显式表达式,通过对注浆加固与未加固GA-ANN滞回模型仿真结果比较,表明了GA-ANN较强的泛化性,在选择适合的网络结构与训练样本后,GA-ANN滞回模型可以较好地拟合试验滞回曲线。可以将该方法进一步推广至整体结构宏观地震反应的建模与预测,为古建筑砌体抗震研究提供新思路。
| [1] |
D'AMBRISI A, MARIANI V, MEZZI M. Seismic assessment of a historical masonry tower with nonlinear static and dynamic analyses tuned on ambient vibration tests[J]. Engineering structures, 2012, 36: 210-219. DOI:10.1016/j.engstruct.2011.12.009 (  0) 0)
|
| [2] |
APOSTOLOPOULOU M, AGGELAKOPOULOU E, SIOUTA L, et al. A methodological approach for the selection of compatible and performable restoration mortars in seismic hazard areas[J]. Construction and building materials, 2017, 155: 1-14. DOI:10.1016/j.conbuildmat.2017.07.210 (  0) 0)
|
| [3] |
谢启芳, 薛建阳, 赵鸿铁. 汶川地震中古建筑的震害调查与启示[J]. 建筑结构学报, 2010, 31(S2): 18-23. XIE Qifang, XUE Jianyang, ZHAO Hongtie. Seismic damage investigation and analysis of ancient buildings in Wenchuan earthquake[J]. Journal of building structures, 2010, 31(S2): 18-23. (  0) 0)
|
| [4] |
雷宏刚, 李铁英, 魏剑伟. 典型古建筑保护中的基础性问题研究[J]. 工程力学, 2007, 24(S2): 99-109. LEI Honggang, LI Tieying, WEI Jianwei. Research on the basic problems in old building protection[J]. Engineering mechanics, 2007, 24(S2): 99-109. (  0) 0)
|
| [5] |
QUIROZ A P, SPERBECK S T, BUDELMANN H, et al. Seismic risk mitigation of historical masonry towers by means of prestressing devices[J]. Advanced materials research, 2010, 133. (  0) 0)
|
| [6] |
CAPOZUCCA R, RICCI V. Bond of GFRP strips on modern and historic brickwork masonry[J]. Composite structures, 2016, 140: 540-555. DOI:10.1016/j.compstruct.2015.12.047 (  0) 0)
|
| [7] |
URANJEK M, BOSILJKOV V, ARNI R, et al. Lime based grouts for strengthening of historical masonry buildings in Slovenia[M]//V LEK J, HUGHES J J, GROOT C J W P. Historic Mortars: Characterisation, Assessment and Repair. Dordrecht: Springer, 2012: 393-409.
(  0) 0)
|
| [8] |
PINEDA P, GARCÍA-MARTÍNEZ A, CASTIZO-MORALES D. Environmental and structural analysis of cement-based vs. natural material-based grouting mortars. Results from the assessment of strengthening works[J]. Construction and building materials, 2017, 138: 528-547. DOI:10.1016/j.conbuildmat.2017.02.013 (  0) 0)
|
| [9] |
XU Shuqiang, MA Qinglin, WANG Julin, et al. Grouting performance improvement for natural hydraulic lime-based grout via incorporating silica fume and silicon-acrylic latex[J]. Construction and building materials, 2018, 186: 652-659. DOI:10.1016/j.conbuildmat.2018.07.056 (  0) 0)
|
| [10] |
KHADEMI F, AKBARI M, JAMAL S M, et al. Multiple linear regression, artificial neural network, and fuzzy logic prediction of 28 days compressive strength of concrete[J]. Frontiers of structural and civil engineering, 2017, 11(1): 90-99. DOI:10.1007/s11709-016-0363-9 (  0) 0)
|
| [11] |
GETAHUN M A, SHITOTE S M, GARIY Z C A. Artificial neural network based modelling approach for strength prediction of concrete incorporating agricultural and construction wastes[J]. Construction and building materials, 2018, 190: 517-525. DOI:10.1016/j.conbuildmat.2018.09.097 (  0) 0)
|
| [12] |
CACHIM P B. Using artificial neural networks for calculation of temperatures in timber under re loading[J]. Construction and building materials, 2011, 25(11): 4175-4180. DOI:10.1016/j.conbuildmat.2011.04.054 (  0) 0)
|
| [13] |
CHAKRAVERTY S, GUPTA P, SHARMA S. Neural network-based simulation for response identification of two-storey shear building subject to earthquake motion[J]. Neural computing and applications, 2010, 19(3): 367-375. DOI:10.1007/s00521-009-0279-6 (  0) 0)
|
| [14] |
中华人民共和国住房和城乡建设部. GB/T 50129-2011, 砌体基本力学性能试验方法标准[S].北京: 中国计划出版社, 2012. Ministry of Housing and Urban-Rural Construction of the People's Republic of China. GB/T 50129-2011, Standard for test method of basic mechanics properties of masonry[S]. Beijing: China Planning Press, 2012. (  0) 0)
|
| [15] |
中华人民共和国住房和城乡建设部. JGJ/T 101-2015, 建筑抗震试验规程[S].北京: 中国建筑工业出版社, 2015. Ministry of Housing and Urban-Rural Construction of the People's Republic of China. JGJ/T 101-2015, Specification for seismic test of buildings[S]. Beijing: China Building Industry Press, 2015. (  0) 0)
|
| [16] |
顾祥林, 陈贡联, 马俊元, 等. 反复荷载作用下混凝土多孔砖墙体受力性能试验研究[J]. 建筑结构学报, 2010, 31(12): 123-131. GU Xianglin, CHEN Gonglian, MA Junyuan, et al. Experimental study on mechanical behavior of concrete perforated brick walls under cyclic loading[J]. Journal of building structures, 2010, 31(12): 123-131. (  0) 0)
|
| [17] |
ZHOU Qiang, WANG Fenglai, ZHU Fei. Estimation of compressive strength of hollow concrete masonry prisms using artificial neural networks and adaptive neuro-fuzzy inference systems[J]. Construction and building materials, 2016, 125: 417-426. DOI:10.1016/j.conbuildmat.2016.08.064 (  0) 0)
|
| [18] |
白建方, 白国良, 史冠卿. 基于人工神经网络的钢筋混凝土异型节点滞回模型[J]. 世界地震工程, 2004, 20(2): 50-54. BAI Jianfang, BAI Guoliang, SHI Guanqing. Artificial neural networks-based modeling of hysteretic behavior for RC abnormal joints[J]. World earthquake engineering, 2004, 20(2): 50-54. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


