2. 复杂系统控制与智能协同技术重点实验室, 北京 100074;
3. 哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨 150001;
4. 哈尔滨工程大学 航天与建筑工程学院, 黑龙江 哈尔滨 150001
2. Science and Technology on Complex System Control and Intelligent Agent Cooperation Laboratory, Beijing 100074, China;
3. College of Automation, Harbin Engineering University, Harbin 150001, China;
4. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China
近年来无人机作为侦察、救援、观测等任务的空中平台在军用、民用领域受到广泛应用。得益于无人机编队的高效率、高可靠性的任务执行能力,无人机拥有着更广阔的应用前景。而更广泛的应用和更复杂的任务对无人机编队的相关技术、性能也提出了更高的要求。路径规划作为保障无人机安全、高效完成既定任务的基础,是无人机研究的一个重点。特别是在无人机编队飞行过程中,针对突发威胁的规避路径规划,具有重要的研究意义。
针对无人机路径规划问题提出了基于部分可观测马尔可夫决策过程理论[1]、遗传算法和粒子群算法[2]、最优控制方法[3]、生物应激条件反射理论[4]的无人机路径规划方法。这些研究重点解决了无人机实时路径规划问题,但是对突发威胁规避问题、无人机机载计算机性能考虑不多。针对无人机对突发威胁规避问题提出了基于粒子群算法[5]、切向量场导引和李雅普诺夫矢量场导引算法[6]、动态域快速搜索随机树与线性二次高斯运动[7]的路径规划算法。这些研究重点解决了无人机飞行过程中突发威胁、动态威胁规避问题,但是针对无人机编队之间的协同作用考虑较少。针对无人机编队路径规划问题提出了基于动态混合整数线性规划和路径平滑器方法[8]、图形处理单元加速势场方法[9]、最优控制方法和人工势场法[10]、改进人工势场方法[11]的防碰撞规划算法。这些研究重点解决了无人机编队之间的碰撞避免,路径中的障碍规避问题,但是所设计算法多采用智能算法,由于运算量大、运算效率低,不适用于突发威胁实时规避的情况。
针对上述问题,设计了基于凸优化算法的多无人机编队突发威胁规避路径规划算法,首先,基于突发威胁模型、无人机飞行模型将突发威胁规避问题建模成一个受约束的最优化问题;其次,基于等效约束将原始最优化问题转化成一系列待求解的凸优化问题;然后,运用凸优化算法进行迭代求解。
1 路径规划问题的建模 1.1 规划问题描述设由n架无人机组成的多无人机编队在复杂环境中跟踪全局规划路径飞行。在飞行过程中探测到突发威胁,此时需要编队中的无人机进行突发威胁的规避,并在越过所有威胁后组成原编队继续按照全局路径进行任务。基于此任务背景,本文进行突发威胁规避路径规划算法研究。
路径规划问题就是选择一条最佳路径保证无人机从起点到终点安全、高效的飞行。因此在规划过程中首先需要考虑无人机机动性能,本文主要针对最大航程、最小转弯半径2个方面考虑无人机机动性能。此外,还需考虑多无人机编队之间的相对距离,避免无人机相互碰撞。
1.2 无人机飞行模型在本文的研究中,无人机飞行的非线性动力学方程表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot x = V\cos \theta }\\ {\dot y = V\sin \theta }\\ {\dot \theta = u} \end{array}} \right. $ | (1) |
式中:(x, y)为无人机状态量,表示无人机位置;θ为无人机状态量,表示无人机的方向角;V为无人机的飞行速度;u为无人机的控制量,控制无人机的方向角。
基于无人机动力学模型,可以针对无人机机动性能和多无人机编队之间的相对距离进行定义。并分别针对最大航程、最小转弯半径、最小相对距离进行建模。
1.3 突发威胁模型定义突发威胁,假设存在2种类型的突发威胁:探测威胁和打击威胁。探测威胁即为在该范围内敌对方能够探测到无人机,对这类威胁尽量避免无人机在其覆盖范围内飞行,不可避免的情况下尽量减少在其覆盖范围内飞行时间。打击威胁即为在该范围内无人机会受到敌对方打击,对于这类威胁需要保证无人机不在其覆盖范围内飞行。
本文将突发威胁看成是二维平面内的圆形区域。假设突发威胁中心点坐标为(xpoi, ypoi),作用半径为rpoi,则突发威胁模型可以描述为:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{{\rm{pop}}}} \le {r_{{\rm{poi}}}}\cos \theta }\\ {{y_{{\rm{pop}}}} \le {r_{{\rm{poi}}}}\sin \theta } \end{array}\quad 0 \le \theta \le 2{\rm{ \mathsf{ π} }}} \right. $ | (2) |
本文针对多无人机编队在复杂环境中突发威胁规避问题进行突发威胁规避路径规划研究。由上一小节规划问题可知,需要针对每一架无人机进行路径规划,且规划过程中需要考虑多无人机编队之间的协同。为了便于区分,这里定义变量上标s、f分别代表初始、最终,例xis表示无人机i初始时刻位置的x轴坐标。
对于无人机i复杂环境中突发威胁规避就是搜索一条路径(xi(t), yi(t))在规定初始、最终位置以及满足相关约束的情况下规避突发威胁,可以写为:
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {{x_i}(0),{y_i}(0)} \right) = \left( {x_i^s,y_i^s} \right)}\\ {\left( {{x_i}(T),{y_i}(T)} \right) = \left( {x_i^f,y_i^f} \right)}\\ {{L_i} \le {L_{{\rm{max}}}},{r_i} \ge {r_{{\rm{min}}}},{d_{ij}} \ge {d_{{\rm{min}}}}} \end{array}\quad i,j = 1,2, \cdots ,N,i \ne j} \right. $ | (3) |
为了实现所规划路径的评价,需要针对路径规划任务建立代价函数。本文综合路径最短、探测威胁规避、打击威胁规避3个方面进行代价函数的建立。
1) 飞行路径最短。
考虑无人机携带燃料,需要规划出的路径较短。设计飞行路径最短代价函数为:
| $ {f_{i1}} = {L_i} = \int_0^T {\sqrt {{{\left( {\frac{{{\rm{d}}{x_i}(t)}}{{{\rm{d}}t}}} \right)}^2} + {{\left( {\frac{{{\rm{d}}{y_i}(t)}}{{{\rm{d}}t}}} \right)}^2}} {\rm{d}}t} $ | (4) |
2) 探测威胁规避。
由于无人机在突发探测区域内可能会被敌方雷达等探测设施发现,导致飞行任务的失败,所以规划出的路径尽量避开探测区域,如无法规避也应尽量缩短在探测区域内的飞行距离。设计探测威胁规避代价函数为:
| $ {f_{i2}} = {L_{{\rm{iequ}}}} = \int_0^T {\sqrt {{{\left( {\frac{{{\rm{d}}{x_{{\rm{iequ}}}}(t)}}{{{\rm{d}}t}}} \right)}^2} + {{\left( {\frac{{{\rm{d}}{y_{{\rm{iequ}}}}(t)}}{{{\rm{d}}t}}} \right)}^2}} {\rm{d}}t} $ | (5) |
3) 打击威胁规避。
由于无人机在突发打击区域内会被敌方击毁,所以无人机需要规避打击威胁区域,不能在该区域飞行。设计打击威胁规避代价函数为:
| $ {f_{i3}} = \left\{ \begin{array}{l} 0,\;\;\;\;\;{x_i} \le {r_{{\rm{EQU}}}}\cos \theta \;\& \;{y_i} \le {r_{{\rm{EQU}}}}\sin \theta \\ 1,\;\;\;\;\;\;其他 \end{array} \right. $ | (6) |
综合路径最短、探测威胁规避、打击威胁规避得到综合代价函数为:
| $ {f_i} = {f_{i3}}\left[ {\eta {f_{i1}} + \left( {1 - \eta } \right){f_{i2}}} \right] $ | (7) |
式中η为权重系数。
结合突发威胁规避路径规划问题和代价函数,可以将突发威胁规避问题描述为带约束的优化问题:
| $ \left\{ \begin{array}{l} \min {f_i} = {f_{i3}}\left[ {\eta {f_{i1}} + (1 - \eta ){f_{i2}}} \right]\\ {\rm{s}}.{\rm{t}}.\quad \left( {{x_i}(0),{y_i}(0)} \right) = \left( {x_i^s,y_i^s} \right)\\ \;\;\;\;\;\;\;\left( {{x_i}(T),{y_i}(T)} \right) = \left( {x_i^f,y_i^f} \right)\\ \;\;\;\;\;\;\;{L_i} \le {L_{\max }},{r_i} \ge {r_{\min }},{d_{ij}} \ge {d_\min} \end{array} \right. $ | (8) |
针对上述所建立的带约束的优化问题在本节中通过等效变换将上述带约束的优化问题转换为一系列的凸优化问题,通过凸优化解的迭代实现优化问题的求解[12-13]。
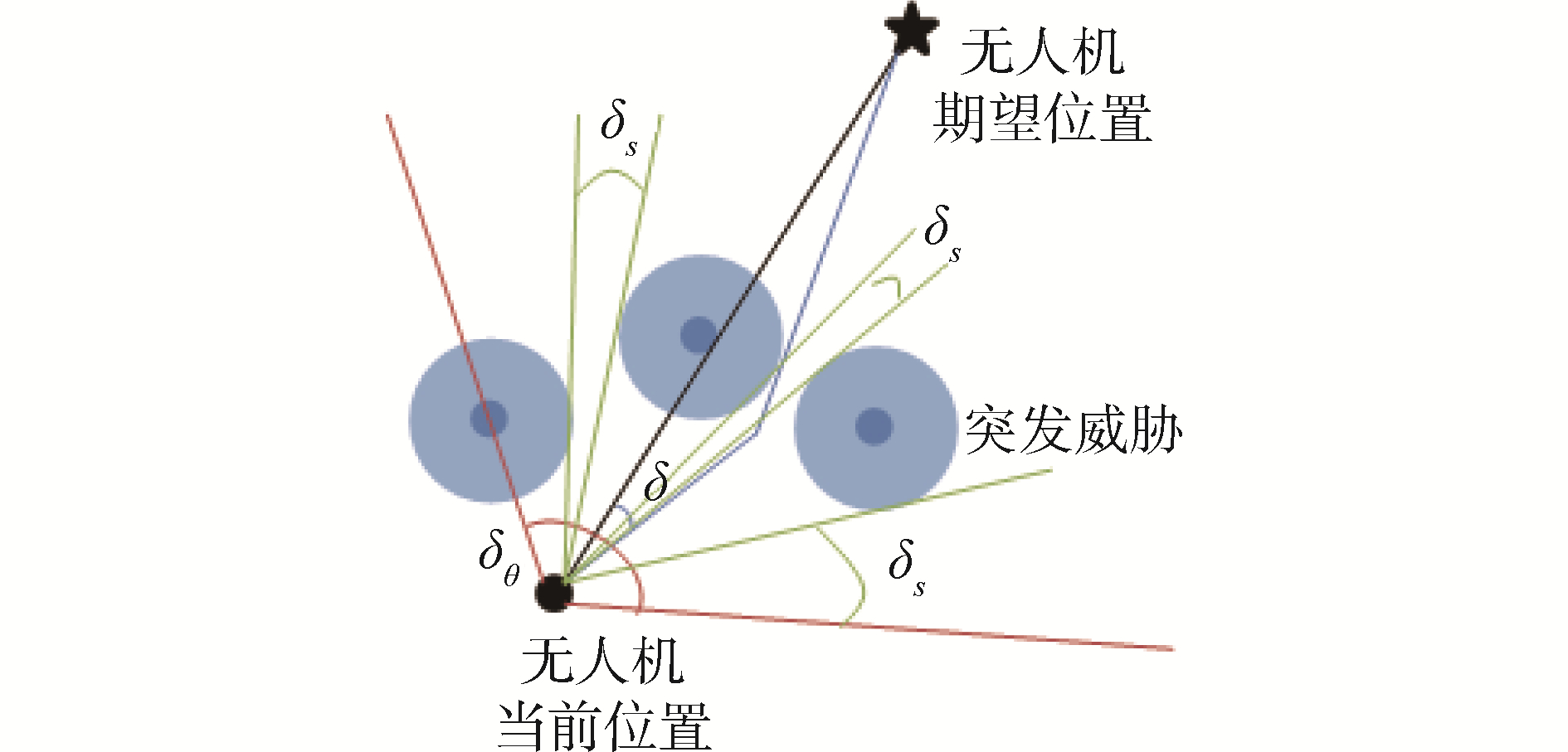
由于2个点之间直线最短,所以在无人机当前位置和目标位置之间最短路径为2个点之间的连线。但是由于突发威胁的影响,如果无人机朝着目标直线飞行可能会被发现甚至击毁。基于此,本文采用当前位置和目标位置之间的连线为基准线调整飞行路径,调整后的路径与基准线之间的夹角为δ,如图 1所示。由此可知,δ越小,到达目标飞行的路径越短。因此,飞行路径最短的代价函数可以采用关于δ的函数进行等效。
|
Download:
|
| 图 1 规划路径示意 Fig. 1 Planning path diagram | |
为了采用δ评价飞行路径,这里将无人机飞行路径离散化,通过路径上的m个节点描述飞行路径。针对无人机i在第k个路径节点上的位置(xi(k), yi(k))和期望位置(xif, yif),当前位置和期望位置的连线为:
| $ r = \left( {x_i^f - {x_i}(k),y_i^f - {y_i}(k)} \right) $ | (9) |
为了规避突发威胁调整路径角度为δi(k),则对于无人机编队在t时刻则有代价函数:
| $ \mathit{\boldsymbol{F}} = {\mathit{\boldsymbol{\delta }}^{\rm{T}}}\mathit{\boldsymbol{E\delta }} $ | (10) |
式中:
针对最小转弯半径约束,通过路径点之间的夹角进行等效,即在第k个路径节点上只能在δθi(k)夹角区域内选择要调整的角度δi(k)。
为了便于优化问题的转化,这里假设无人机进入探测威胁范围后即被发现,即所规划的路径不能穿过探测威胁范围。并且为了保证无人机最优路径的选择,在第k个路径节点上只考虑以ri(k)为半径δθi(k)夹角区域内的威胁。通过无人机当前位置和该区域威胁的切线可以确定无人机i在第k个节点的路径调整夹角的搜索区域δsi(k)。确定路径调整夹角后无人机按照该方向飞行li(k),然后进行下一个节点的搜索,直到当前节点和目标位置之间的连线与威胁区域无交叉为止。这里,考虑无人机编队之间的相互作用,避免无人机之间的碰撞,在迭代运算过程中无人机飞行距离li(k)为在某一范围内的随机数,这样就能够调整无人机在路径上不同时间的位置,从而避免无人机之间的碰撞。
对比δθi(k),δsi(k),选择边界值较小的作为该点的搜索区域。假设无人机i在第k个节点的搜索区域为
| $ \begin{array}{*{20}{c}} {{a_i}(k) \le {\varepsilon _i}(k) \le {b_i}(k),{a_i}(k) = \sin \left( {{\delta _{\theta sia}}(k)} \right)}\\ {{b_i}(k) = \sin \left( {{\delta _{\theta sib}}(k)} \right)} \end{array} $ |
令
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\varepsilon }}_k} = {{\left[ {\begin{array}{*{20}{l}} {{\mathit{\varepsilon }_1}(k)}&{{\mathit{\varepsilon }_2}(k)}& \cdots &{{\mathit{\varepsilon }_n}(k)} \end{array}} \right]}^{\rm{T}}} = }\\ {{{\left[ {\begin{array}{*{20}{c}} {\sin \left( {{\delta _1}(k)} \right)}& \cdots &{\sin \left( {{\delta _n}(k)} \right)} \end{array}} \right]}^{\rm{T}}}} \end{array} $ |
即针对多无人机编队在第k个路径上的路径规划可以转化为如下凸优化问题:
| $ \left\{ {\begin{array}{*{20}{l}} {\min \left\{ {\frac{1}{2}\mathit{\boldsymbol{\varepsilon }}_k^{\rm{T}}P{\mathit{\boldsymbol{\varepsilon }}_k}} \right\}}\\ {{\rm{s}}.{\rm{t}}.\;\;\;\mathit{\boldsymbol{G\varepsilon }} \le h} \end{array}} \right. $ | (11) |
式中:
| $ \mathit{\boldsymbol{P}} = 2\mathit{\boldsymbol{E}} $ |
| $ \mathit{\boldsymbol{h}} = {\left[ {{b_1}(k) - {a_1}(k){b_2}(k) - {a_2}(k) \cdots {b_n}(k) - {a_n}(k)} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} 1&0& \cdots &0&0\\ { - 1}&0& \cdots &0&0\\ 0&1&0& \cdots &0\\ 0&{ - 1}&0& \cdots &0\\ \vdots & \vdots &{}& \vdots & \vdots \\ 0&0& \cdots &0&1\\ 0&0& \cdots &0&{ - 1} \end{array}} \right] $ |
至此,通过多次等效变换和迭代、凸优化问题求解,可以完成无人机突发威胁规避路径的规划。考虑多无人机编队在飞行过程中的协同,这里对规划出的路径引入时间变量,对规划出的路径进行拟合。通过调整无人机通过路径交叉点的时间避免无人机碰撞。
将无人机从开始规避突发威胁到越过威胁重新组成编队的时间T分为m-1个时间段,每个时间节点对应规划出的路径的节点。然后利用三次函数法插值实现路径函数的建立。
通过对拟合后的路径函数可以判断无人机编队之间的距离,当某段时间内无人机间相对距离小于最小相对距离dmin时,调整两条路径之间的时间分割重新进行曲线拟合保证无人机之间的安全相对距离。
通过等效变换、凸优化问题求解、突发威胁规避路径迭代、路径点函数建立等实现多无人机编队突发威胁规避路径的规划。算法步骤如下:
1) 初始化参数,无人机编队当前位(xis, yis)、期望位置(xif, yif),突发威胁位置(xpoi, ypoi),威胁作用范围rpoi,无人机最小转弯半径rmin,无人机间最小相对距离dmin;
2) 迭代开始;
3) 计算无人机当前位置和期望位置之间的连线ri(k),确定ri(k)范围内的威胁;
4) 计算无人机当前位置搜索范围δθsia(k)≤δi(k)≤δθsib(k);
5) 建立如式(11)所示的凸优化问题;
6) 求解凸优化问题(11)得到路径调整角度δi(k);
7) 设定在[0.3ri(k), 0.5ri(k)]内随机选择li(k);
8) 确定无人机按照路径调整角度后的位置;
9) 返回3),直到所有无人机当前节点和目标位置之间的连线与威胁区域无交叉为止;
10) 分别对无人机在T时间内进行节点划分;
11) 根据得到的路径点建立路径函数(xi(t), yi(t));
12) 判定无人机是否小于最小相对距离,如有返回10);
13) 输出路径函数(xi(t), yi(t))。
4 仿真分析为了验证本文所提出的基于凸优化算法的多无人机编队突发威胁规避路径规划算法,本节利用Matlab提供的CVX工具包对所设计算法进行仿真验证。
本文假设无人机在2 000 m×2 000 m的范围内进行飞行仿真,编队中无人机数量为n=4,初始位置和最终期望位置设置为:
| $ \left( {x_1^s,y_1^2} \right) = (150,100){\rm{m}},\left( {x_1^f,y_1^f} \right) = (1600,1850){\rm{m}} $ |
| $ \left( {x_2^s,y_2^s} \right) = (250,100){\rm{m}},\left( {x_2^f,y_2^f} \right) = (1600,1750){\rm{m}} $ |
| $ \left( {x_3^s,y_3^s} \right) = (100,150){\rm{m}},\left( {x_3^f,y_3^f} \right) = (1550,1900){\rm{m}} $ |
| $ \left( {x_4^s,y_4^s} \right) = (100,250){\rm{m}},\left( {x_4^f,y_4^f} \right) = (1450,1900){\rm{m}} $ |
最小转弯半径的等效角度假设为:
| $ {\theta _r} = {\rm{ \mathsf{ π} }}/3 $ |
编队中无人机相对距离最小为:
| $ {d_{\min }} = 10\;{\rm{m}} $ |
设置突发威胁数量npop=8,这里在[100,150]m范围内随机生成威胁半径,在[400, 1 600]m范围内随机生成威胁中心坐标。本文仿真结果生成的突发威胁数据如表 1所示。
| 表 1 突发威胁位置、作用半径表 Table 1 Unexpected threats location, action radius |
假设无人机从开始规避突发威胁到越过威胁重新组成编队的时间T=150 s。
按照本文所设计的算法进行突发威胁规避路径规划算法仿真。仿真结果如图 2~5所示,图 2(a)为经过凸优化求解得到的无人机突发威胁规避路径点,可以看出,无人机在探测到威胁后开始调整原本路径,且在规避威胁时沿着威胁圆的切线飞行,此时无人机在规避威胁的同时保持了路径最短。

|
Download:
|
| 图 2 凸优化迭代得到的无人机突发威胁规避路径 Fig. 2 UAV unexpected threats convex optimization iterations to get circumvention path | |

|
Download:
|
| 图 3 无人机1相对于无人机2、3、4的相对距离 Fig. 3 Relative distance of drone 1 relative to drones 2, 3, 4 | |

|
Download:
|
| 图 4 无人机2相对于无人机3、4的相对距离 Fig. 4 Relative distance of drone 2 relative to drones 3, 4 | |

|
Download:
|
| 图 5 无人机3相对于为人机4的相对距离 Fig. 5 The relative distance of the drone 3 relative to the human machine 4 | |
由图 2(b)经过三次函数插值得到的无人机突发威胁规避轨迹可以看出,无人机在飞行过程中没有超出无人机机动性能的路径,飞行路径较平滑。
由图 3~5多无人机编队飞行过程中相对距离变化曲线可以看出,无人机飞行过程中虽然飞行路径有距离较近,甚至交叉的地方,但是通过引入时间,拟合飞行轨迹,保证了编队之间的安全距离。
由仿真结果可以看出,本文所设计的基于凸优化算法的多无人机编队突发威胁规避路径规划算法能够在无人机机动性能允许的条件下实现突发威胁的规避,并且所规划的路径满足编队飞行安全距离。
以上对无人机编队遭遇突发威胁后规避路径规划进行了仿真,结果验证了本文所设计算法的有效性。为了更进一步验证所设计算法的性能,假设无人机从不同位置开始飞向目标点并组成编队。在飞行过程中由于探测器探测范围有限,在较小范围内遭遇突发威胁,即无人机目标点、突发威胁等条件不变,无人机初始位置调整为:
| $ \left( {x_1^s,y_1^2} \right) = (600,500){\rm{m}},\left( {x_2^s,y_2^s} \right) = (750,800){\rm{m}} $ |
| $ \left( {x_3^s,y_3^s} \right) = (300,1250){\rm{m}},\left( {x_4^s,y_4^s} \right) = (1150,250){\rm{m}} $ |
按照本文所设计的算法进行突发威胁规避路径规划算法仿真。仿真结果如图 6~9所示。

|
Download:
|
| 图 6 凸优化迭代得到的无人机突发威胁规避路径 Fig. 6 UAV unexpected threats convex optimization iterations to get circumvention path | |

|
Download:
|
| 图 7 无人机1相对于无人机2、3、4的相对距离 Fig. 7 Relative distance of drone 1 relative to drones 2, 3, 4 | |
|
Download:
|
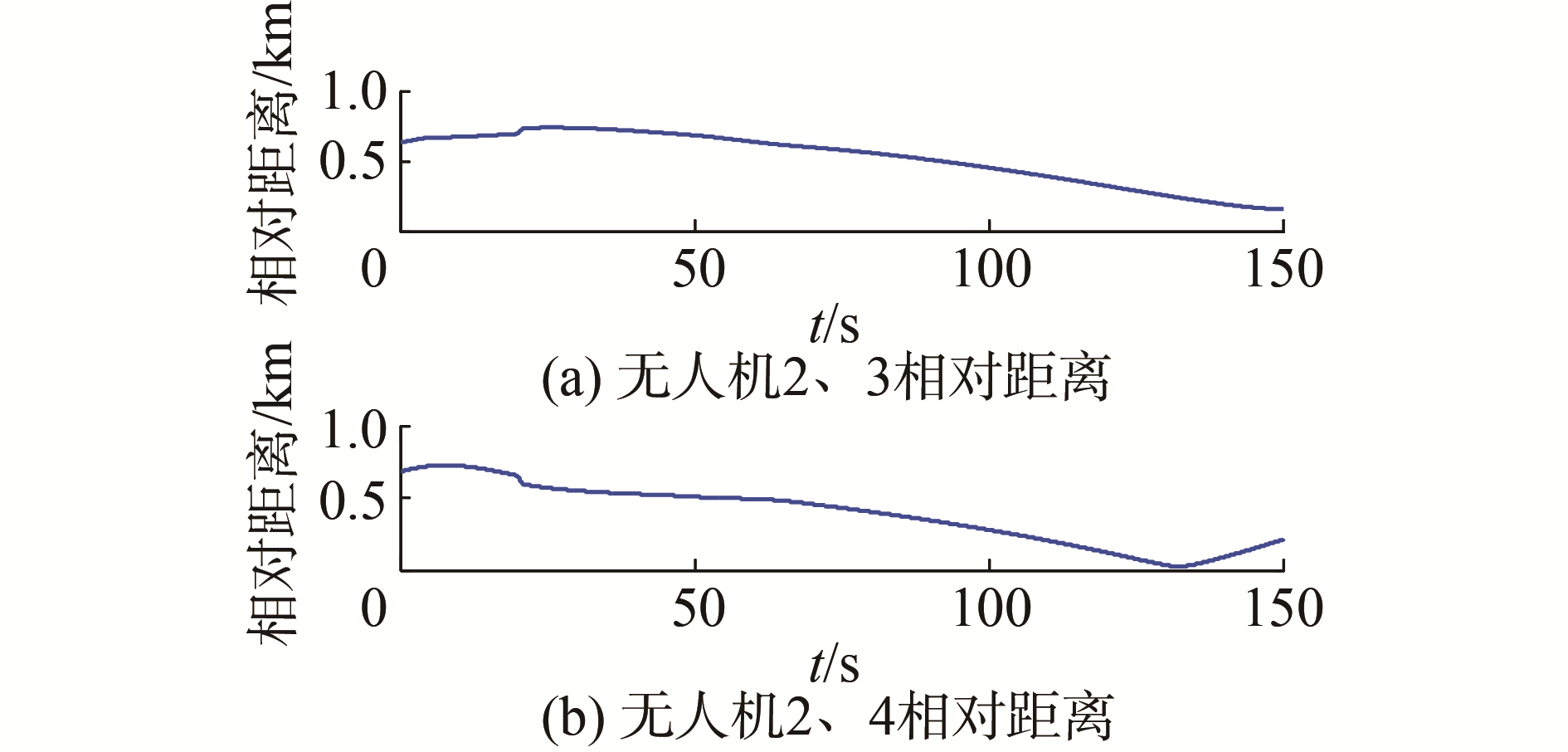
| 图 8 无人机2相对于无人机3、4的相对距离 Fig. 8 Relative distance of drone 2 relative to drones 3, 4 | |

|
Download:
|
| 图 9 无人机3相对于为人机4的相对距离 Fig. 9 The relative distance of the drone 3 relative to the human machine 4 | |
图 6(a)为经过凸优化求解得到的无人机突发威胁规避路径点,可以看出,无人机在正前方较小距离突发威胁后能够迅速调整原本路径,实现突发威胁的规避。以及在当前位置和目标位置中间无威胁时,无人机会采取最短路径(直线)飞向目标。由图 6(b)经过曲线拟合后的无人机飞行路径可以看出,由于转弯半径的约束,无人机避过威胁后不能直线向着目标飞去,需要经过调整航向继续飞向目标。图 7、图 8、图 9多无人机编队飞行过程中距离变化曲线可以看出无人机在接近目标并组成编队前相对距离较小,这是由于无人机同时到达目标点附近导致,此时需要注意无人机之间的碰撞。
对比2个工况,可以看出本文所设计的突发威胁规避路径规划算法不仅能够实现编队飞行过程中的突发威胁规避,并且能够实现不同位置的无人机组成编队的路径规划,而且在飞行过程中对较小范围内突发威胁能够进行敏捷反应,实现快速规避。
为了进一步验证所设计基于凸优化算法的多无人机编队突发威胁规避路径规划算法的性能,调整突发威胁覆盖范围和无人机飞行速度,对无人机路径规划的成功率进行分析。这里针对不同突发威胁覆盖范围和不同无人机飞行速度情况下,执行100次算法,计算无人机编队路径规划成功的概率。
首先针对突发威胁覆盖范围对算法成功率的影响进行分析,这里假定威胁区域固定,通过调整威胁个数来调整威胁覆盖范围,但由于随机生成的威胁可以相互重叠,所以相同威胁个数下突发威胁的聚散程度对规划结果也有影响。
设置突发威胁半径为150 m,在[400, 1 600]m范围内随机生成威胁中心坐标。其他参数采用工况1的设置。
表 2表示在上述参数设置情况下,对突发威胁的聚散程度不做要求进行规划的结果。
| 表 2 不同威胁个数时规划成功次数对比 Table 2 Comparison of the number of different threats |
由表 2可以看出,在不考虑突发威胁聚散程度的情况下,突发威胁个数越多规划成功的成功率越低。由于没有考虑聚散程度,相同威胁个数时突发威胁对飞行区域的覆盖了也不一样,所以有不符合总体成功率随突发威胁个数增加而降低的整体趋势(如表突发威胁个数为18时成功率比突发威胁个数为16时要高)。
考虑突发威胁聚散程度的影响,这里以威胁中心最小距离作为聚散程度的评价,即突发威胁中两两威胁中心之间的距离大于等于dcent。图 10给出不同威胁个数,不同聚散程度下规划算法的规划成功率变化曲线。

|
Download:
|
| 图 10 成功率随聚散程度、威胁个数变化 Fig. 10 The success rate varies with the degree of convergence and the number of threats | |
由图 10可以看出,当威胁个数小于等于4个时,规划成功率都为1,而且当威胁中心最小距离大于威胁直径时,规划成功率也为1。除此之外,规划成功率是随着威胁个数增加而减小,随着威胁中心最小距离减小而增大的。
由于本文路径规划算法是在无人机飞行路径规划完成后进行飞行轨迹的拟合,所以在路径规划过程中无人机的速度相关的约束是无人机的最小转弯半径,本文通过角度对转弯半径进行等效。所以无人机飞行速度与规划成功率的关系可以等效为最小转弯半径的等效角度θr与成功率之间的关系。按照工况1中的设置,改变最小转弯半径等效角度进行路径规划成功率分析。图 11给出成功率随最小转弯半径等效角度变化曲线。

|
Download:
|
| 图 11 成功率随最小转弯半径等效角度变化 Fig. 11 Equivalent angle of success rate with minimum turning radius | |
由图 11可以看出,成功率总体趋势是随着等效角度的增加而增大的。这是因为当等效角度增大时,说明此时最小转弯半径变小,也就是说无人机下一节点位置的搜索区域变大,因此成功率变大。但是当等效角度增大到一定值后,此时等效角度的变化对成功率的影响降低。
针对算法的运算效率进行分析,验证所设计算法能够实时实现规避路径的规划,这里针对不同突发威胁个数分别执行100次算法进行无人机编队的路径规划,计算算法平均运行时间。采用对突发威胁覆盖范围对算法成功率影响分析的参数设置,假定威胁区域固定,通过调整威胁个数来调整威胁覆盖范围。在Intel(R) Core(TM) i7-4510U CPU处理器的PC机平台上采用Matlab 2010b软件进行算法仿真。仿真结果为:在威胁个数为2、4、6、8、10时,平均执行时间分别为0.011 7、0.015 9、0.020 8、0.038、0.043 6 s。表 3给出在不同威胁个数下,算法执行100次的平均运行时间。由不同威胁个数下算法平均运行时间可以看出,算法运行时间随着威胁个数的增加而增加,这是因为威胁个数的增加导致搜索区域变的复杂,算法搜索次数增加。总体上针对不同数目的威胁,算法都能够在0.05 s内完成路径规划,表明算法具有较高的运算效率,满足无人机规避突发威胁的路径的实时规划需求。
由仿真可知,所设计的基于凸优化算法的多无人机编队突发威胁规避路径规划算法能够实现无人机对突发威胁的规避,并且在不同影响因素下具有较高的成功率,且运算效率较高,算法具有良好的性能。
5 结论1) 所设计的突发威胁规避路径规划算法能够实现无人机编队飞行过程中的突发威胁的实时规避,并且能够对正前方较小距离突发威胁进行敏捷反映,实现敏捷规避。
2) 所设计算法还能够实现无人机组成编队路径的规划。与传统的路径规划和突发威胁规避方法相比,基于凸优化算法的实时路径规划运算简洁,计算量小,能够在机载计算机运算性能较低的情况下保证路径的实时规划,实现突发威胁规避,在实际应用中具有很好的前景。
| [1] |
RAGI S, CHONG E K P. UAV path planning in a dynamic environment via partially observable Markov decision process[J]. IEEE transactions on aerospace and electronic systems, 2013, 49(4): 2397-2412. DOI:10.1109/TAES.2013.6621824 (  0) 0)
|
| [2] |
ROBERGE V, TARBOUCHI M, LABONTE G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning[J]. IEEE transactions on industrial informatics, 2013, 9(1): 132-141. DOI:10.1109/TII.2012.2198665 (  0) 0)
|
| [3] |
CHEN Yongbo, LUO Guanchen, MEI Yuesong, et al. UAV path planning using artificial potential field method updated by optimal control theory[J]. International journal of systems science, 2016, 47(6): 1407-1420. DOI:10.1080/00207721.2014.929191 (  0) 0)
|
| [4] |
刘鑫, 杨霄鹏, 刘雨帆, 等. 基于GA-OCPA学习系统的无人机路径规划方法[J]. 航空学报, 2017, 38(11): 287-297. LIU Xin, YANG Xiaopeng, LIU Yufan, et al. UAV path planning based on GA-OCPA learning system[J]. Acta aeronauticaet astronautica sinica, 2017, 38(11): 287-297. (  0) 0)
|
| [5] |
SUJIT P B, BEARD R. Multiple UAV path planning using anytime algorithms[C]//Proceedings of 2009 American Control Conference. St. Louis, MO, USA, 2009: 2978-2983.
(  0) 0)
|
| [6] |
CHEN Hongda, CHANG Kuochu, AGATE C S. UAV path planning with tangent-plus-Lyapunov vector field guidance and obstacle avoidance[J]. IEEE transactions on aerospace and electronic systems, 2013, 49(2): 840-856. DOI:10.1109/TAES.2013.6494384 (  0) 0)
|
| [7] |
WEN Naifeng, SU Xiaohong, MA Peijun, et al. Online UAV path planning in uncertain and hostile environments[J]. International journal of machine learning and cybernetics, 2017, 8(2): 469-487. DOI:10.1007/s13042-015-0339-4 (  0) 0)
|
| [8] |
RADMANESH M, KUMAR M. Flight formation of UAVs in presence of moving obstacles using fast-dynamic mixed integer linear programming[J]. Aerospace science and technology, 2016, 50: 149-160. DOI:10.1016/j.ast.2015.12.021 (  0) 0)
|
| [9] |
CETIN O, YILMAZ G. Real-time autonomous UAV formation flight with collision and obstacle avoidance in unknown environment[J]. Journal of intelligent & robotic systems, 2016, 84(1/2/3/4): 415-433. (  0) 0)
|
| [10] |
CHEN Yongbo, YU Jianqiao, SU Xiaolong, et al. Path planning for multi-UAV formation[J]. Journal of intelligent & robotic systems, 2015, 77(1): 229-246. (  0) 0)
|
| [11] |
朱旭, 闫茂德, 张昌利, 等. 基于改进人工势场的无人机编队防碰撞控制方法[J]. 哈尔滨工程大学学报, 2017, 38(6): 961-968. ZHU Xu, YAN Maode, ZHANG Changli, et al. UAV formation collision avoidance control method based on improved artificial potential field[J]. Journal of Harbin Engineering University, 2017, 38(6): 961-968. (  0) 0)
|
| [12] |
DINH Q T, DIEHL M. Local convergence of sequential convex programming for nonconvex optimization[M]//DIEHL M, GLINEUR F, JARLEBRING E, et al. Recent Advances in Optimization and its Applications in Engineering. Berlin, Heidelberg: Springer, 2010: 93-102.
(  0) 0)
|
| [13] |
SCHULMAN J, HO J, LEE A X, et al. Finding locally optimal, collision-free trajectories with sequential convex optimization[C]//Proceedings of Robotics: Science and Systems. Berlin, Germany, 2013: 1-10.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


