钝体结构在工业领域中广泛应用，如飞机起落架、飞机机体、水下航行器、汽车后视镜、输电线缆及建筑等。流体流过钝体时，由刚性壁面作用产生额外的气动噪声。随着对噪声问题的关注，对钝体绕流噪声有效控制的需求日益提高，此时评估近场或远场噪声水平极为重要。钝体气动噪声预测方法主要有3种：直接数值模拟(direct numerical simulation，DNS)、基于声类比理论^[1-3]的远场噪声预测方法和基于LEE^[4]或流声分解法^[5]的混合计算气动声学(hybrid computational aero-acoustics，HCAA)。DNS采用极高分辨率网格和高精度数值算法直接求解Navier-Stokes (N-S)方程组，在计算流场结构的同时，直接获得声场解，因此对研究噪声的产生机理和传播过程极为有利。但其计算量巨大，尤其是预测远场噪声时，计算代价对工业应用来说不可接受，目前DNS仅应用于简单结构、低雷诺数的气动噪声问题。Inoue等^[6]采用DNS计算了均匀流场中的二维圆柱噪声，仿真局限于低马赫数(Ma =0.05~0.3)、低雷诺数(Re=150)条件，并假设分子粘度和热对流均是常数。声类比法预测远场噪声的过程包括2步：1)采用非稳态雷诺平均(unsteady reynolds averaged navier-stokes，URANS)方法、LES、DNS等求解流场，获得近场的压力、速度等变量信息作为声源；2)采用Lighthill^[1]、Curle^[2]或FW-H^[3]等声类比方法在声源面/体上对声源变量积分计算远场的声压。流场仅需要计算近场，对网格尺度、计算域大小和算法精度的要求大大降低，极大提高了远场噪声预测效率。针对圆柱绕流噪声，Cox等^[7]采用有限体积法求解Ma=0.2的二维可压缩URANS方程，采用FW-H方程计算远场噪声，重点分析了二维流场仿真对不同雷诺数(100≤Re≤5×10⁶)的适用性；Pérot^[8]、Gloerfelt^[9]在Ma≈0.1的流动中，对二维圆柱近场求解不可压缩URANS，远场噪声预测采用Curle公式；Guo^[10]采用LES计算声源信息，结合Curle公式计算了Ma=0.1的三维圆柱的远场噪声。声类比方法也存在较大的局限性，如仅能对简单结构获得解析的格林函数、对传播路径上障碍物对声波的影响难以考虑等。流声分解法^[5]认为低速流动由不可压流动和声扰动组成，基于此思想将可压缩N-S方程组分解为不可压方程组和声扰动方程组，分别求解获得流动参数和声学量。基于流声分解法，倪大明等^[11]模拟了Ma=0.2低速流场中单圆柱的声传播，杜炳鑫等^[12]计算了Ma=0.1并列双圆柱的噪声辐射。LEE法^[4]基于声学量的传播过程是小幅无黏的条件，采用线性化欧拉方程求解声学量。Cheong等^[13]对低马赫数下的圆柱绕流噪声，采用不可压RANS方程计算近场的粘性流动，获得基于Lighthill应力张量形式的声源模型，在此基础上，采用LEE求解声场，计算的声学结果与Curle理论符合很好，但其马赫数很低，对流效应对声传播的影响可以忽略。

与DNS方法相比，LEE能兼顾声场模拟的计算效率和预测精度。同时，与声类比理论相比，LEE能考虑声波传播路径上包含散射体等更加复杂的声辐射情况。然而对于高速流动条件下的声场的数值模拟，LEE法易产生时间推进数值不稳定问题，因此采用具有自阻尼特性的迎风差分格式有利于增强LEE方程求解的数值稳定性。文献[14]通过理想模型验证了采用迎风差分算法求解拟特征方程(pesudo-characteristic formulation, PCF)形式的LEE方程在气动噪声时间反演方面具有稳定性高的优点。然而，在真实物体气动噪声辐射的正模拟问题中，PCF方程结合迎风差分求解的计算方法尚无应用，其可靠性和稳定性亦需要验证。

本文以Ma=0.4的钝体-圆柱体为研究对象，将PCF方程用于圆柱绕流噪声辐射特性仿真，采用迎风差分对PCF方程进行空间离散。建立均匀流条件下声波动LEE控制方程，并基于紧致声源假设建立集中力点声源模型，验证这种声源模拟方法的准确性，分别分析介质静止和对流条件下的声传播和衰减规律，并与LES直接计算结果进行对比。

1 LEE控制方程与数值算法 1.1 控制方程

远场流体密度为常数ρ₀，速度U₀是沿x正方向的均匀流。此时，文献[4, 15]中的非齐次LEE声波动连续性方程和动量方程可简化为：

$\frac{\partial p^{\prime}}{\partial t}+U_{0} \frac{\partial \rho^{\prime}}{\partial x}+\rho_{0}\left(\frac{\partial u^{\prime}}{\partial x}+\frac{\partial v^{\prime}}{\partial y}\right)=S_{1} $

(1)

$\rho_{0} \frac{\partial u^{\prime}}{\partial t}+\rho_{0} U_{0} \frac{\partial u^{\prime}}{\partial x}+\frac{\partial p^{\prime}}{\partial x}=S_{2} $

(2)

$\rho_{0} \frac{v^{\prime}}{\partial t}+\rho_{0} U_{0} \frac{\partial v^{\prime}}{\partial x}+\frac{\partial p^{\prime}}{\partial y}=S_{3} $

(3)

式中：p′(x, y, t)、ρ′(x, y, t)，u′(x, y, t)和v′(x, y, t)分别为声压、声密度和x、y方向的声质点振速。(S₁, S₂, S₃)表示源项，用于模拟单极子、偶极子或四极子声源。当圆柱直径D_cyl远小于声波波长λ时(D_cyl≪λ)，认为声源是紧致的。实际上对于圆柱绕流噪声，根据无量纲频率-斯特劳哈尔数的计算公式S_t=(f·D_cyl)/U₀，及波长λ与频率f的关系λ=c₀/f(c₀为声速)，可得声波波长与圆柱直径之比为：

$\frac{\lambda}{D_{\mathrm{cyl}}}=\frac{1}{S t \cdot M a} $

(4)

式(4)说明，声源的紧致性仅与来流马赫数和关注频率对应的S_t数有关。本文来流条件下，涡脱落频率处S_t≈0.21，将Ma=0.4代入可得λ/D_cyl≈11.9，近似满足紧致声源条件。

对于本文均匀流动中静止的刚性圆柱，以圆柱对流体的脉动集中力作为点声源模型，表示为：

$S_{1}(x, y)=0 $

(5)

$S_{2}(x, y)=-\left(F_{d}(t)-\bar{F}_{d}\right) \delta\left(x-x_{0}\right) \delta\left(y-y_{0}\right) $

(6)

$S_{3}(x, y)=-F_{l}(t) \delta\left(x-x_{0}\right) \delta\left(y-y_{0}\right) $

(7)

式中：F_d(t)、F_l(t)分别是LES计算的圆柱受到的瞬态阻力和升力；F_d表示阻力的平均值；(x₀, y₀)表示力在LEE中的作用节点坐标(文中x₀=y₀=0)；δ是Dirac-Delta函数。

1.2 数值算法

LEE矩形计算域为|x|≤40D_cyl, |y|≤40D_cyl，网格划分为等间距网格Δx=Δy=Δn=D_cyl/8，总节点数为641×641。为了利用迎风差分格式对高频波的非零阻尼特性来增强数值时间稳定性，将式(1)~(3)转换为PCF (Pesudo-characteristic formulation)形式^[15]，其中声压、密度和质点振速的空间偏导数总体上采用迎风格式有限差分法计算，对于计算域内部节点和最邻近边界节点，采用四阶精度7节点优化迎风差分，对边界附近的节点采用五阶标准迎风差分格式，边界节点采用7节点优化三阶向后差分格式。时间项采用三阶龙格-库塔法(Total Variation Diminishing，TVD)求解。根据CFL (Courant-Friedrich-Lewy)稳定性条件计算仿真中的时间步长：

$C_{F L}=\frac{\left(c_{0}+U_{0}\right) \Delta t_{\mathrm{LEE}}}{\Delta n} \leqslant 1 $

(8)

取C_FL=0.4，则时间步长Δt_LEE=5.714 3 × 10^-4 s。为了模拟自由辐射边界，计算域外边界采用一阶CEM (Clayton-Engquist-Majda)辐射边界条件^[16]，并对矩形计算域的4个角节点作特殊的角吸声处理。在文献[16]静止介质辐射边界条件的基础上，本文在边界x=±40D_cyl处的CEM和角吸声边界条件隐式地包含了流体的对流效应。

2 LES仿真模型和数值算法 2.1 仿真模型

以圆柱直径为特征长度的雷诺数Re=3 000，圆柱后的流动处于亚临界状态，为了获得尾迹中的湍流脉动声源，采用LES方法计算流动，计算域和边界条件如图 1所示。为了单纯模拟圆柱的发声，来流条件中未引入扰动。计算域出口采用Poinsot^[17]基于特征分析的无反射边界条件(characteristic boundary condition, CBC)。为进一步增强外边界对声波的吸收以避免虚假反射，将计算域划分为等尺寸(25D_cyl)的声学计算域和声学阻尼层。在声学计算域内计算近场流动的同时，获得辐射声波，圆柱近壁面第一层网格厚度为Δr_min =D_cyl/200，对应的无量纲Y⁺值为y_max⁺=0.9，最外层网格厚度Δr_max=D_cyl/4，网格总数为N_θ×N_r=266×170。声学阻尼层采用拉伸网格降低对声波的分辨率，同时增强对流动尾迹的耗散，最内层、最外层网格厚度分别为Δr′_min=D_cyl/3、Δr′_max=4.9D_cyl。

2.2 数值算法

基于Ansys 16.2-Fluent软件对流场进行数值仿真，控制方程为二维可压缩粘性流动连续性方程、N-S方程及能量方程组。考虑到马赫数较高，能量方程中采用Surtherland定律定义理想气体随温度变化的粘度，气体普朗特数P_r=0.72。采用密度基隐式算法求解流动变量，湍流亚格子模型是具有粘性耗散修正的动态Smagrinsky模型，空间离散对流项采用Roe-FDS通量差分格式和三阶MUSCL格式，时间项采用二阶中心差分离散格式。计算的时间步长为Δt_LES=2×10^-4 s，对应于CFL=(U₀Δt_LES)/Δx_min=0.67。因Δt_LES≠Δt_LEE，在LEE中对升力和阻力数据进行样条插值。

流场在约25个涡脱落周期后基本达到准稳定，图 2给出了LES仿真的圆柱升力系数C_l和阻力系数C_d随时间变化的曲线，其中横坐标是以涡脱落周期为参考的无量纲流动时间$\tilde{t}=t / T$，即涡脱落周期数。由结果可知，升力系数对应于S_t=0.21，与文献[18]中的DNS结果St=0.203及文献[19]的实验结果S_t=0.215±0.005基本一致。阻力系数和升力系数分别在平均值C_d=1.26及C_l=0上下周期性波动，阻力系数脉动频率是升力系数的2倍，且其脉动幅值与升力系数脉动幅值相比很小。

3 结果与分析 3.1 忽略对流效应

当忽略流体介质的流动对噪声传播的影响时，式(1)~(3)中关于U₀的项均为零，即:

$U_{0} \frac{\partial \rho}{\partial x} \rightarrow 0, \rho_{0} U_{0} \frac{\partial u}{\partial x} \rightarrow 0, \rho_{0} U_{0} \frac{\partial v}{\partial x} \rightarrow 0 $

(9)

该条件下，文献[13]给出了均匀流中二维紧致脉动力声源的远场声压解析解：

$p_{\mathrm{rms}}^{\prime}(r, \theta)=\frac{1}{2} \sqrt{\frac{\omega}{2 \pi r c_{0}}} F_{\mathrm{rms}}^{\prime} \sin \theta $

(10)

式中：F′_rms是集中脉动力的均方根值(root mean square, rms)；c₀表示静止介质中的声传播速度；θ是传播方向与x轴正方向的夹角，如图 1所示；ω代表圆柱涡脱落角频率。式(10)假设噪声频率满足k₀·D_cyl≪1，其中k₀表示声波数，在本文中，升力和阻力脉动引起的噪声分别对应于k_{0, Cd}·D_cyl=0.52、k_{0, Cl}·D_cyl=1.04。可见，阻力噪声远不能满足解析解的适用条件。因此，后续仅将LEE计算的升力脉动噪声与式(10)的解析解进行了对比，即F′=F′_l=1/(2C′_lρ₀U₀D_cyl)。

图 3给出了第262个涡脱落周期时，LEE模拟的升力、阻力以及合力脉动产生的瞬态声压辐射云图。图 3(a)表明圆柱升力脉动产生的声压波呈规则的偶极子辐射特征，以正“8”字形向远处传播，上下声瓣对称分布，但相位相差180°。图 3(b)对比了在r=40D_cyl处LEE仿真与式(9)得到的升力脉动辐射声压rms值的空间指向性，结果表明仿真值与解析值相差很小，在90°和270°差值约0.11 dB，说明当忽略对流效应时，LEE能够准确地模拟压力波由近场向远场的传播。

图 3(c)给出了阻力脉动产生的声压辐射云图。阻力脉动在水平方向上交替产生正、负压力波，以倒“8”字形对称地向远场辐射，左右声瓣相位相反。图 3(d)表示合力作用下的瞬态声压分布云图。圆柱升力脉动在声波产生中起主导作用，表现为声波主要在升力的方向上传播，但与单纯的升力作用下的声辐射相比，对称性减弱而具有一定的旋流特征，文献[12]在双圆柱绕流噪声的流声分解模拟中也观察到了这种旋流形式的声波，这种旋流特征是升力和阻力各自产生的声波相互干涉的结果。

图 4给出了在声学监测点(0, 40D_cyl)处由圆柱合力脉动产生的总声压$\tilde{p}^{\prime}$、圆柱压差力脉动产生的声压$\tilde{p}^{\prime}_p$以及圆柱壁面摩擦力脉动产生的声压$\tilde{p}^{\prime}_ν$的时间历程图。可以看出，流体绕圆柱流动产生的压差力噪声与粘性摩擦力噪声的脉动周期相同，但前者的幅值远大于后者幅值。压差力噪声声压与总声压峰峰值对比为:

$\frac{\left|\tilde{p}_{p}^{\prime}\right|_{\text {peak }}}{\left|\tilde{p}^{\prime}\right|_{\text {peak }}} \approx 97.8 \% $

可见，圆柱的压差力脉动是噪声的主要来源，而圆柱表面的粘性摩擦力对噪声的贡献很小，可以忽略。

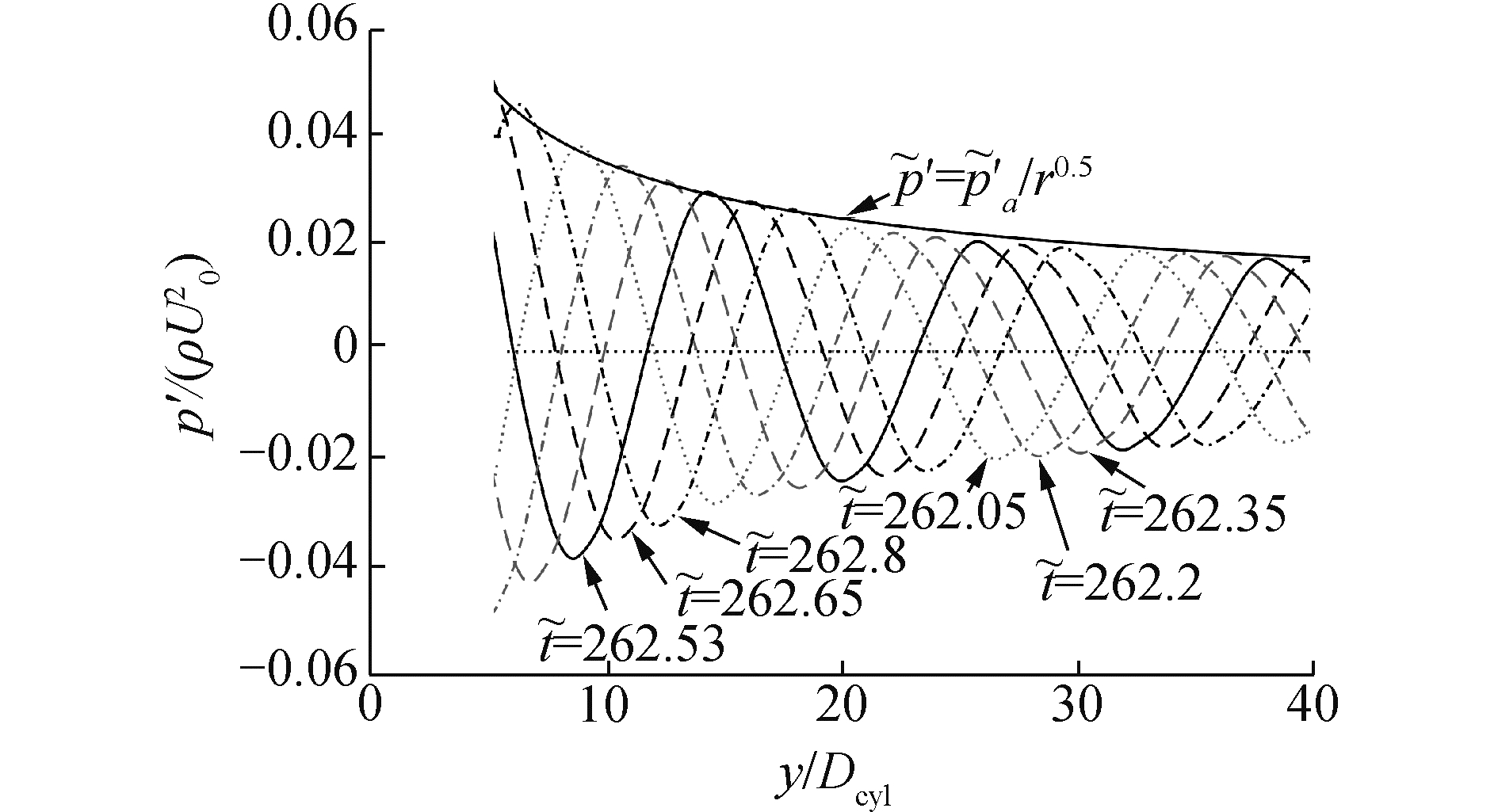
声波在θ=90°方向上的传播和衰减曲线如图 5所示，并在图中给出了声波峰值随距离衰减的拟合曲线，不同曲线代表不同时刻y坐标在5D_cyl≤y≤40D_cyl范围内的瞬态声压分布。由图可知，涡脱落频率对应的波长约为圆柱直径的11.5倍，即λ_vortex≈11.5D_cyl；在y>10D_cyl时，声压基本随距离衰减:

$\tilde{p}^{\prime}=\tilde{p}_{a}^{\prime} / r^{0.5} $

(11)

式中$\tilde{p}^{\prime}_a$=0.021 8是y=22.13D_cyl位置在$\tilde{t}$=262.2时刻的无量纲声压值。Inoue等^[6]通过量纲分析得到，紧致偶极子声源的远场声压与马赫数、距离的关系近似满足p′∝Ma^5/2/r^1/2，可见，LEE仿真出的圆柱气动噪声声压的衰减规律与理论一致。

3.2 对流的影响

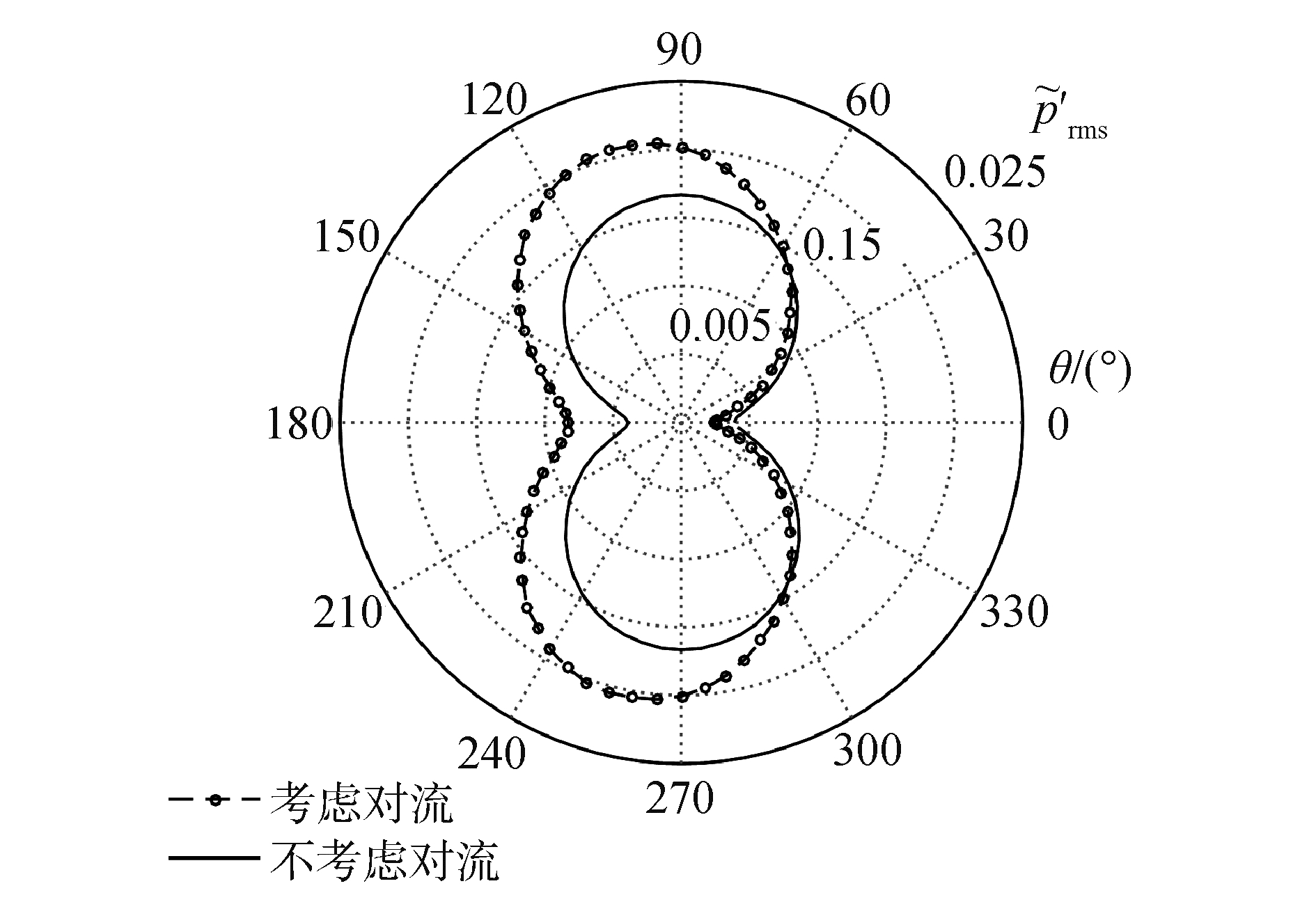
考虑介质流动对声波传播的影响，图 6给出了声压均方根值的指向性曲线，声监测点位于对流修正半径$r^{\prime}=r\left(\sqrt{1-M a^{2} \sin ^{2} \theta^{\prime}}-M a \cos \theta^{\prime}\right)$处，其中r=20D_cyl，因子$\sqrt{1-M a^{2} \sin ^{2} \theta^{\prime}}-M a \cos \theta^{\prime}$是因多普勒效应引入的修正因子^[6]，θ′为监测点方向与x轴负方向的夹角，且-180°≤θ′≤180°。由图中可知，在对流作用下，声压保持偶极子辐射特征，但传播角度由θ′≈±90°(对应于θ≈90°、θ≈270°)方向偏转到θ′≈±69°(对应于θ≈111°、θ≈249°)方向，声瓣向上游倾斜了约21°。

图 7分别表示LEE、LES仿真的在$\tilde{t}$=262时刻的瞬态声压、脉动压力分布。可以看出，图 7(a)与图 7(b)在远场的声波分布云图吻合较好，在近场也均捕捉到了相似的波的旋流特征。与图 7(a)中LEE模拟的单纯声波传播相比，观察到图 7(d)中圆柱下游的压力脉动特征比较复杂：一方面，近场流体剧烈的压力扰动随流动向下游运动，形成尾迹中的压力脉动波带，即“拟声现象”；另一方面，在圆柱下游，流体压力波与声波相互融合，影响了声波的偶极子辐射特征，在下游形成了“压力波-声波混合区”。

介质流动对声波传播产生的多普勒效应使声瓣出现偏转，图 7中的“⊕”、“ ⊖”符号分别表示一个声波中压力的正最大值和负最小值的位置。可以看到，LEE和LES模拟得到的声波传播方向相同，均约为θ′≈±69°。声压极值理论传播方向的计算公式为θ′_p≈arccos Ma^[6]，当Ma=0.4时，可得θ′_p≈±66.4°，与仿真值相差约3.7%，该差值来源于θ′_p≈arccos Ma是基于马赫数很小的简化条件。

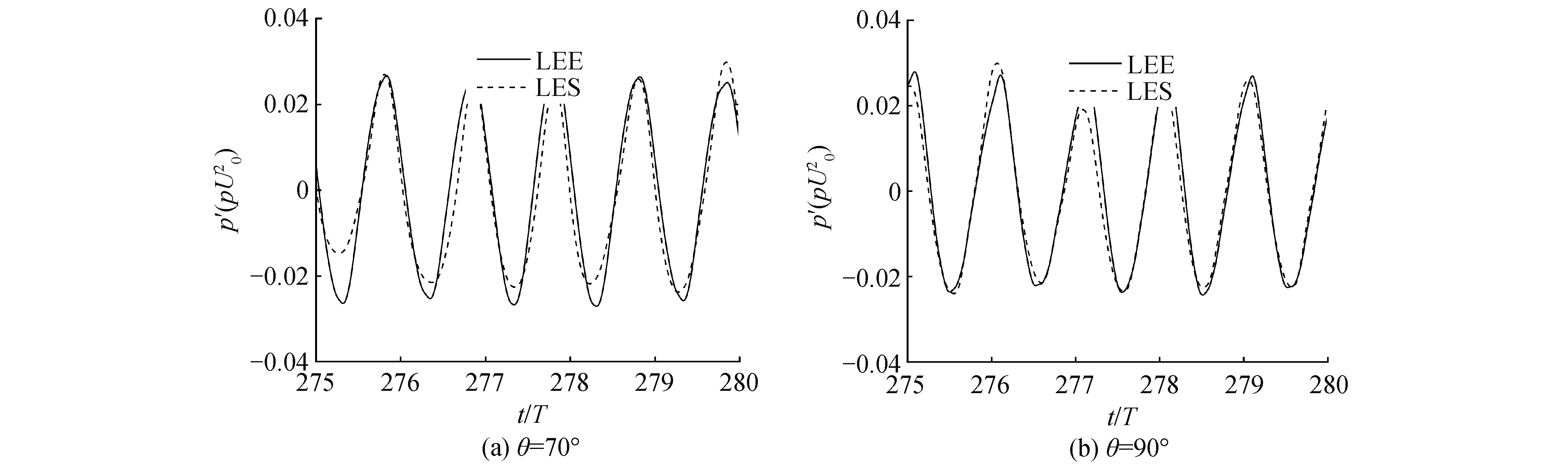
图 8对比了LEE和LES计算的r=20D_cyl处监测点声压随时间变化的曲线，其中图 8(a)、图 8(b)分别表示θ=70°和θ=90°监测点处的声压对比。结果表明，2种方法计算的声波相位和幅值基本一致，进一步验证了LEE在Ma=0.4的介质流动条件下计算声波传播特性的准确性。

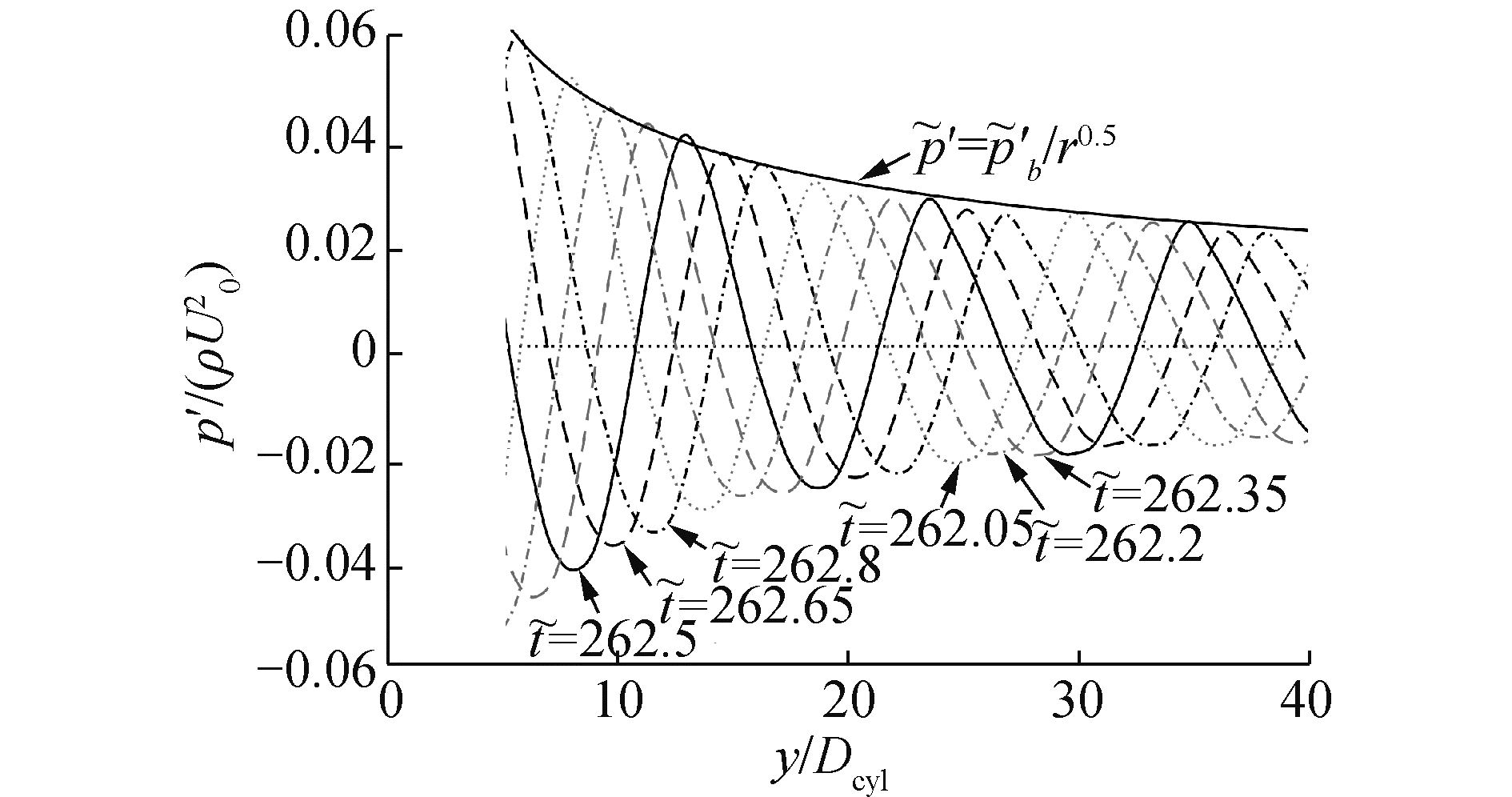
图 9给出了考虑Ma=0.4的介质流动后，LEE计算的在θ=90°方向不同时刻声压分布及衰减曲线。在y>10D_cyl时，声压峰值拟合公式为:

$\tilde{p}^{\prime}=\tilde{p}_{b}^{\prime} / r^{0.5} $

(12)

式中$\tilde{p}_{b}^{\prime}$=0.027 6是y=22D_cyl位置在$\tilde{t}$=262.35时刻的无量纲声压值。采用多普勒因子对距离r修正，即$r^{\prime}=r\left(\sqrt{1-M a^{2} \sin ^{2} \theta^{\prime}}-M a \cos \theta^{\prime}\right)$^[6]，当θ′=90°时:

$\tilde{p}^{\prime}=\tilde{p}_{b, r^{\prime}}^{\prime} / r^{\prime 0.5} $

(13)

式中$\tilde{p}_{b, r^{\prime}}^{\prime}=\tilde{p}_{b}^{\prime} \cdot\left(1-M a^{2}\right)^{1 / 4}$。与不考虑对流时的声压衰减关系式(11)及图 6给出的在r=20D_cyl处的仿真结果相比，代入Ma=0.4:

$\frac{{\tilde p_{b, {r^\prime }}^\prime }}{{\tilde p_a^\prime }} = 1.21 = {\left( {\frac{{\tilde p_{{\rm{rms}}, {r^\prime }}^\prime }}{{\tilde p_{{\rm{rms}}, r}^\prime }}} \right)_{20{D_{{\rm{cyl}}}}}} $

(14)

可见，考虑Ma=0.4的介质流动对声波传播的影响后，LEE计算的圆柱绕流噪声声压仍按照$\tilde{p}^{\prime}$~1/r′^0.5的关系衰减。

4 结论

1) LEE计算的声压分布与静止介质中的声场解析解、介质流动状态下的LES直接数值解吻合较好，验证了本文采用圆柱的集中脉动力模拟声学LEE控制方程的紧致声源项是恰当的，计算结果揭示了圆柱的升力脉动和压差力脉动是主要的声源。

2) Ma=0.4的介质流动对声波传播有显著的影响，声波辐射方向与来流的负方向夹角约为69°，声瓣总体上向上游偏转了约21°。

3) 考虑对流效应，声压与经多普勒因子修正的传播半径依然满足$\tilde{p}^{\prime} \sim 1 / r^{\prime 0.5}$的衰减关系。