整体穿刺是制造立体织物的一种工艺技术,采用碳纤维叠层机织布与Z向钢针阵列整体穿刺,再由连续碳纤维逐一替代Z向钢针形成碳纤维穿刺织物,最早由有美国AVCO公司研究成功[1]。该织物是一种结构特殊的碳纤维立体织物,具有良好的整体结构和较高的纤维体积含量,是制作高性能防热隔热炭/炭复合材料的优良基材[2]。我国整体穿刺技术最先由南京玻璃纤维研究院实现重大技术突破,该院生产的整体穿刺立体织物经炭/炭复合制造的先进炭/炭复合材料,已成功用作高性能防热材料,如固体火箭发动机喉衬、喷管等,使我国在该领域跻身于世界先进水平[3-6]。
董九志等[7]对整体穿刺织物成型技术进行研究并研制了立体织物整体穿刺钢针阵列布放装置。平面叠层机织碳布在Z向钢针穿刺过程中,机织碳布平面面积被钢针挤占,经纬向纤维被排挤、推移、充填到钢针周围的空隙中,增加了织物的纤维含量,有利于复合材料性能的提高[8]。为使整体穿刺过程顺利进行,朱建勋等[9-10]在钢针针尖形态优化方面进行了大量的研究工作。在整体穿刺机织布顶弯模式下的钢针针尖形态优化方面, 建立了机织布顶弯模式下钢针针尖的力学模型, 提出了针尖压弯微分方程和边界条件, 得出了不同曲线形状针尖临界压力的方程, 并用MathCAD软件求出了临界压力的数值解, 为确定合理的针尖形态提供了理论依据;对于基于纤维弯曲伸长模式的Z向钢针针尖形态优化工作,分析了整体穿刺过程中纤维弯曲伸长机理, 建立了钢针的力学模型, 分别讨论了作用在针尖上的最大弯曲正应力、最大剪切应力以及穿刺阻力与针尖半径和针尖长度之间的关系, 然后根据获得的结果对钢针针尖的形状进行了优化。然而在纤维的绕针弯曲阶段对穿刺钢针在压缩与弯曲的组合变形条件下进行强度校核以及运用叠加法求弯曲变形、计算穿刺钢针的位移、优化钢针针尖形态的工作还有待开展。
1 整体穿刺过程分析及穿刺钢针模型 1.1 整体穿刺过程分析整体穿刺过程中正交叠层机织碳布放置在穿刺钢针阵列上,穿刺模板向下移动碳布中纱线变形伸长,钢针针尖顶压碳布;随着穿刺模板下移在其作用下纱线绕过钢针针尖,在此过程中纤维发生绕针弯曲;穿刺模板进一步向下移动,碳布被推至针杆部分,纤维被推压至针杆段,如图 1所示。

|
Download:
|
| 图 1 整体过程示意 Fig. 1 Schematic diagram of whole process | |
通过分析,整体穿刺过程可细分为:顶压碳布阶段、绕针弯曲阶段、压至针杆段。
在纤维绕针弯曲阶段随着穿刺模板下移,纱线与穿刺钢针接触处钢针半径随之增加大,纱线张力也随之增大,而在顶压碳布阶段和纤维被压至针杆段穿刺钢针与纱线接触处钢针半径无变化,因此在纤维绕针弯曲阶段有必要研究纱线张力对穿刺钢针针尖位移的作用、对针杆强度的影响进行分析。
1.2 穿刺钢针针尖模型以针尖的顶点为坐标原点,通过坐标原点垂直向下为Y轴,垂直于Y轴且通过坐标原点,方向向右建立X轴,L1为钢针针尖的长度,如图 2所示。

|
Download:
|
| 图 2 穿刺钢针示意 Fig. 2 Schematic drawing of needle steel needle | |
在给定坐标系下设钢针针尖的曲线方程为:
| $ y = {a_1}{x^m} $ | (1) |
式中:a1为针尖曲线系数;m为钢针针尖曲线次数。
用针尖的长度和针尖直径的对应关系,并对式(1)进行化简可得:
| $ y = \frac{{{2^m}{L_1}}}{{d_n^m}}{x^m} $ | (2) |
式中:L1为钢针针尖的长度;dn为钢针针杆的直径。
对式(2)进行化简可得针尖在任意位置处的钢针针尖的半径为:
| $ x = \frac{{{d_n}}}{2}\left( {\frac{y}{{{L_1}}}} \right)\frac{1}{m} $ | (3) |
钢针针尖对Y轴的极惯性矩为:
| $ {I_1} = \frac{{{\rm{ \mathsf{ π} }}{{\left( {2x} \right)}^4}}}{{64}} $ | (4) |
穿刺针杆对Y轴的极惯性矩为:
| $ {I_2} = \frac{{{\rm{ \mathsf{ π} }}d_n^4}}{{64}} $ | (5) |
在纤维绕针弯曲阶段,若忽略由于碳布相对于钢针针尖的相对位移产生摩擦力的影响,并假设正交叠层机织碳布的经纱和纬纱的纤维面积相等,则纱线的最大张力为[5]:
| $ {F_{\max }} = \sqrt 2 \left[ {\frac{{2x\arcsin \left( {\frac{{2x}}{{{d_z}}}} \right) + \sqrt {d_Z^2 - 2{x^2}} - {d_z}}}{{\left( {{n_2} - 1} \right){d_z}}}} \right]{E_1}{A_Z} $ | (6) |
式中:dz为相邻两钢针之中心间距;AZ为纤维的截面积;n2为等距密排单排钢针数;E1为纤维的杨氏模量。
2 穿刺钢针强度校核位移计算及分析 2.1 穿刺钢针危险截面强度校核 2.1.1 穿刺钢针张力分解整体穿刺过程中在纤维绕针弯曲阶段,由于穿刺模板的作用,正交叠层机织碳布在针尖段随着穿刺过程的进行处于不同的位置。钢针针尖在某一瞬间受到的最大力的方向与水平面的夹角设为θ1,纱线张力在给定的坐标系下,将纱线的张力分解为水平的分力F1和竖直方向的分力即:F1=Fmaxsinθ1,F2=Fmaxcosθ1,如图 3所示。

|
Download:
|
| 图 3 纱线张力分解示意 Fig. 3 Schematic diagram of tension decomposition | |
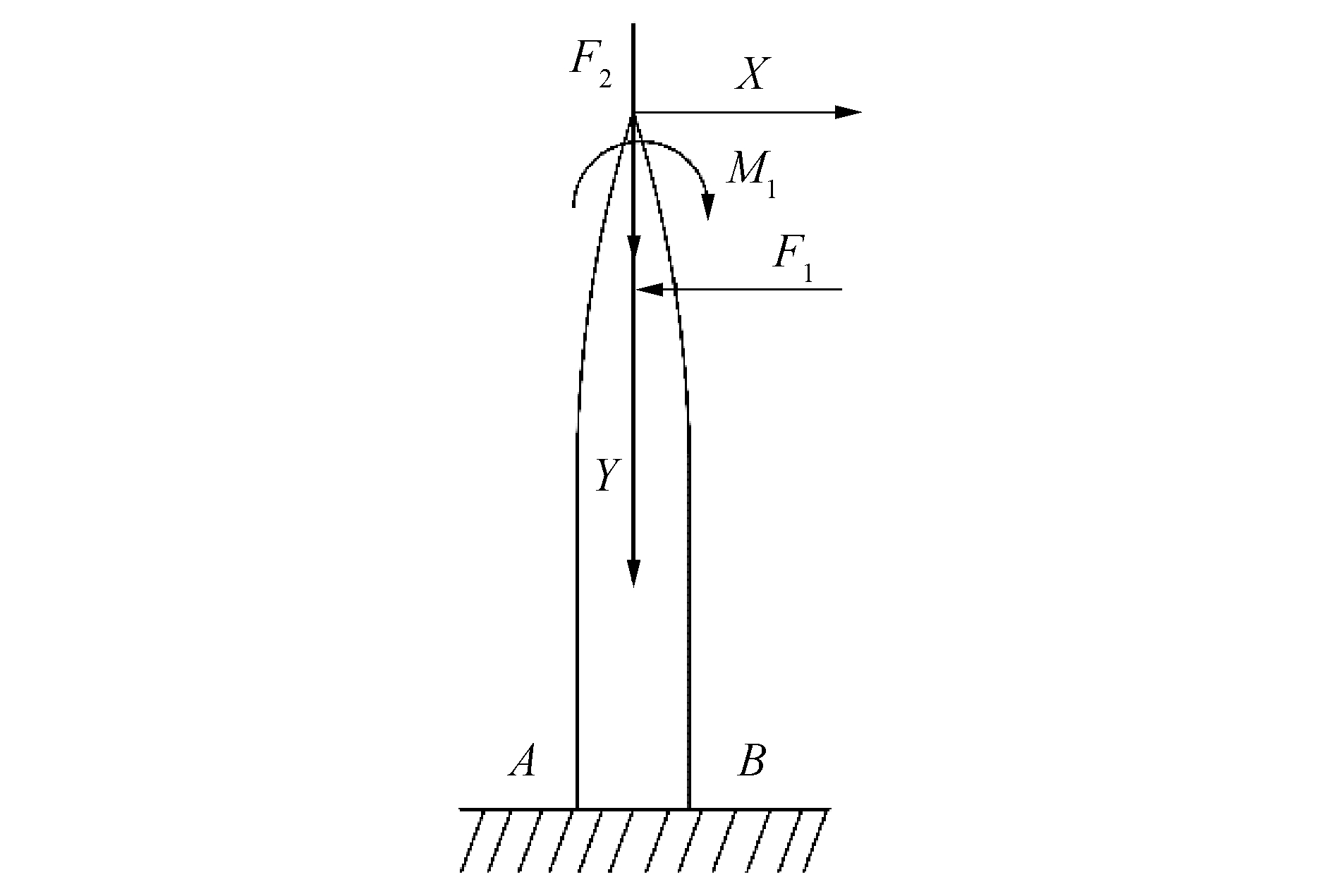
将竖直分力F1平移到针尖的轴线的位置,由力的平移原理可得竖直向下的压力F1和顺时针的附加力矩M1,其中:M1=F1x,对钢针针尖进行受力分析得钢针受到轴向力F2压缩、水平力F1的以及顺时针的力偶矩M1组合变形,如图 4所示。
|
Download:
|
| 图 4 钢针受力平移 Fig. 4 Stress translation diagram of steel needle | |
根据穿刺钢针的受力情况可知,显然AB截面为穿刺钢针的危险截面。为确定穿刺钢针AB截面危险点的位置,分别画出水平应、附加力偶矩、轴向力在AB截面应力分布图,如图 5所示。

|
Download:
|
| 图 5 钢针应力分布 Fig. 5 Stress distribution map | |
从应力分布图可以看出,A、B两点都为穿刺钢针的危险点。由于A点处于单项拉伸、压缩应力状态,为使A点满足强度要求,应使A点的最大正应力满足的条件为:
| $ {\sigma _{\max }} = \frac{{{M_1}}}{{{W_1}}} - \frac{{{F_1}}}{A} - \frac{{{M_2}}}{{{W_2}}} \le \left[ \sigma \right] $ | (7) |
式中:W1为针尖截面的抗弯截面系数;W2为针杆截面的抗弯截面系数;[σ]为钢针材料的许用应力;A为正交叠层机织碳布钢针针尖体锥段钢针针尖的截面积。
因M1为水平分力平移产生的附加力偶矩,因其位置在针尖位置随机变化,为让钢针危险点满足强度的要求,取最大的弯矩,即水平分力在针尖顶点处,故最大的弯矩为:M2=F2(L1+L2),其中L2为针杆的长度。
将以上相关的变量代入式(7)并化简得:
| $ \frac{{124{F_1}{W_2}}}{{{\rm{ \mathsf{ π} }}d_{\rm{n}}^2\left( {{M_2} + \left[ \sigma \right]{W_2}} \right)}} \le {\left( {\frac{y}{{{L_1}}}} \right)^{\frac{2}{m}}} $ | (8) |
为使B点满足强度要求,应使B点的最大正应力满足的条件为:
| $ {\sigma _{\max }} = - \frac{{{M_1}}}{{{W_1}}} - \frac{{{F_1}}}{A} + \frac{{{M_2}}}{{{W_2}}} \le \left[ \sigma \right] $ | (9) |
将以上相关的变量代入式(9)并化简得:
| $ \frac{{33{F_1}{W_2}}}{{{\rm{ \mathsf{ π} }}{{\rm{x}}^2}}} \ge \frac{{{M_2} - \left[ \sigma \right]{W_2}}}{{{W_2}}} $ | (10) |
当M2-[σ]W2>0时,将式(10)进一步化简得:
| $ \frac{{132{F_1}{W_2}}}{{{\rm{ \mathsf{ π} }}d_n^2\left( {{M_2} - \left[ \sigma \right]{W_2}} \right)}} \ge {\left( {\frac{y}{{{L_1}}}} \right)^{\frac{2}{m}}} $ | (11) |
当M2-[σ]W2<0时,将式(10)进一步化简得:
| $ \frac{{132{F_1}{W_2}}}{{{\rm{ \mathsf{ π} }}d_n^2\left( {{M_2} - \left[ \sigma \right]{W_2}} \right)}} \le {\left( {\frac{y}{{{L_1}}}} \right)^{\frac{2}{m}}} $ | (12) |
在整体穿刺的过程中随着穿刺模板的相对于穿刺钢针产生竖直向下的位移穿刺钢针在纱线张力的作用下产生水平位移,该位移导致穿刺钢针与穿刺模板孔壁接触,破坏钢针针尖形态, 图 6所示为穿刺模板和穿刺钢针接触示意图,钢针针尖破坏实物图。

|
Download:
|
| 图 6 穿刺钢针破坏 Fig. 6 Sketch map of steel needle tip interaction | |
为避免上述问题的发生应使穿刺钢针在绕针弯曲阶段的位移,小于穿刺模板直径的一半,即:
| $ {f_s} \le {d_m}/2 $ | (13) |
式中:fs为穿刺钢针针尖的总位移;dm为穿刺模板直径。
为求穿刺钢针针尖在等距密排系统中在纱线张力的作用下产生的位移,因穿刺钢针的针尖、针杆截面的抗弯刚度不同,可采用叠加计算穿刺钢针的位移,即分别钢化穿刺钢针针尖段,穿刺钢针针杆段为求位移应钢化针杆,穿刺钢针分段钢化示意图,如图 7所示。

|
Download:
|
| 图 7 针尖针杆分段钢化 Fig. 7 Sectional drawing of steel needle tip | |
首先钢化针杆BC段,可求得钢针针尖在A点水平向左的位移为:
| $ {f_1} = - \frac{{{F_1}L_1^3}}{{3E{I_1}}} $ | (14) |
式中E为穿刺钢针的弹性模量。
穿刺钢针针尖截面产生端界面转角为:
| $ {\theta _1} = - \frac{{{F_1}L_1^2}}{{2E{I_1}}} $ | (15) |
然后在钢化针尖AB段将水平力平移到针杆段B点,由力的平移原理可得水平的分力和附加力偶矩。
由水平力F1在B处产生的水平向左的位移为:
| $ {f_2} = - \frac{{{F_1}L_2^2\left( {2{L_2} + 3{L_1}} \right)}}{{6E{I_2}}} $ | (16) |
在B截面处产生端界面转角为:
| $ {\theta _2} = - \frac{{{F_1}L_2^2}}{{2E{I_2}}} $ | (17) |
由附加力偶矩产生水平向左的位移和转角,F1在B截面处产生端截面转角为:
| $ {\theta _3} = - \frac{{{F_1}{L_1}{L_2}}}{{E{I_2}}} $ | (18) |
在B处产生的水平向左的位移为:
| $ {f_3} = - \frac{{{F_1}{L_1}{L_2}\left( {{L_1} + {L_2}} \right)}}{{2E{I_2}}} $ | (19) |
由叠加法,可得水平力F1在自由端A处产生水平向左的总位移为:
| $ {f_s} = - \frac{{{F_1}L_1^3}}{{3E{I_1}}} - \frac{{{F_1}{L_2}\left( {L_1^3 + 6{L_1}{L_2} + 2L_2^2} \right)}}{{6E{I_2}}} $ | (20) |
将式(20)代入式(13)并化简得:
| $ \frac{{2{F_1}L_1^3}}{{3E{I_2}{d_m} - {F_1}{L_2}\left( {L_1^3 + 6{L_1}{L_2} + 2L_2^2} \right)}} \le {\left( {\frac{y}{{{L_1}}}} \right)^{\frac{4}{m}}} $ | (21) |
为计算穿刺钢针在纤维绕针弯曲阶段纱线张力,给定参数:dn=1.2×10-3 m、dz=2.3×10-3 m,以规格230 mm×230 mm的碳布为例,即:n2=1 001、E1=2.3×1011 Pa。选用3K机织碳布,并给定碳纤维的单丝直径为:dt=9×10-6 m。将以上相关参数代入式(6)并计算得当穿刺钢针半径在0~6×10-4 m取值时,纱线张力在0~15 N变化,如图 8所示。

|
Download:
|
| 图 8 纱线张力和穿刺钢针半径 Fig. 8 Yarn tension and puncture needle radius | |
为进行穿刺钢针危险截面强度校核,以危险点A点为例,给定参数:L1=5×10-3 m、L2=7×10-3 m,[σ]=120×106 Pa,并假设纱线位于钢针针尖的中点位置处,将以上相关参数代入式(8)并计算可得当纱线张力在0~15 N取值时,钢针针尖曲线次数与纱线张力的关系如图 9所示。

|
Download:
|
| 图 9 曲线次数与危险点受力 Fig. 9 Curve times and stress points | |
为进行穿刺钢针针尖在纱线张力的作用下,穿刺钢针针尖在等距密排系统中产生的位移给定参数:dm=2.0×10-3 m、E=200×109 Pa,将以上相关参数并代入式(21)并计算可得当纱线张力在0~15 N取值时,钢针针尖曲线次数与纱线张力的关系如图 10所示。

|
Download:
|
| 图 10 纱线张力与曲线次数 Fig. 10 Yarn tension and curve times | |
综上,在给定的参数下通过计算可得纱线张力随着穿刺半径的增大而增大;为满足在整体穿刺过程中穿刺钢针针杆在压缩与弯曲组合变形的条件下满足强度要求,在给定的参数下钢针针尖次数随着纱线长的增加而增加,考虑整体穿刺钢针针尖加工实际及增加整体穿刺工艺过程的安全系数,当纱线张力为15 N时,钢针针尖曲线次数应为m>1.5;为满足穿刺钢针不与穿刺孔板孔壁接触的位移要求,在给定的参数下钢针针尖次数随着纱线张力长的增加而增加,当纱线张力为15 N时,钢针针尖曲线次数应为m>1.0。为同时满足以上要求的条件且考虑到钢针针尖加工的难度及成本,在当前穿刺系统下钢针针尖曲线为二次曲线即满足要求。
根据算例结果加工后的穿刺钢针进行了经正交叠层机织碳布整体穿刺实验,选择制成含Z向钢针阵列立体织物1件,织物高度100 mm,如图 11所示,钢针针尖形态特写见图右上角。

|
Download:
|
| 图 11 优化后的钢针整体穿刺实验及钢针针尖特写 Fig. 11 Optimized steel needle puncture experiment and needle tip close-up | |
1) 针对穿刺钢针针杆在纱线张力的作用下出现压缩与弯曲组合变形的情况,通过危险截面进行了应力分析并对其进行了强度校核。穿刺钢针曲线次数取1.5即可满足穿刺钢针针杆危险截面的强度要求。
2) 为保证整体穿刺过程顺利进行,满足穿刺钢针针尖不与穿刺模板孔壁接触对位移的要求,运用叠加法求解出穿刺钢针在纱线张力的作用下针尖的位移。在满足总位移条件限制下,当穿刺钢针曲线次数取1.0即可满足穿刺系统对其位移的要求。
3) 针对化简求解出纱线张力与穿刺钢针在组合变形条件下以及穿刺钢针针尖在总位移限制条件下的函数关系。穿刺钢针针尖曲线次数与纱线杨氏模量、穿刺钢针结构尺寸、穿刺钢针弹性模量等参数相关。
4) 为验证所计算理论的正确性,依据优化后的结果,进行了正交叠层机织碳布的整体穿刺实验,实验结果表明优化后的穿刺钢针能够确保整体穿刺工艺过程顺利进行,满足使用要求。
| [1] |
Rolincik P G. Properties and application of mod 3 pierced fabric composites[C]//In: 17th National Symposium of SAMPE. Calif, USA: 1972.
(  0) 0)
|
| [2] |
朱建勋. 细编穿刺织物的结构特点及性能[J]. 宇航材料工艺, 1998(1): 41-43. ZHU Jianxun. The structural characteristics and properties of fine weave pierced fabric[J]. Journal of Aerospace Materials and Technology, 1998(1): 41-43. (  0) 0)
|
| [3] |
朱建勋, 何建敏, 王海燕. 正交叠层机织布整体穿刺工艺的纤维弯曲伸长机理[J]. 中国工程科学, 2003, 5(5): 59-62, 69. ZHU Jianxun, HE Jianmin, WANG Haiyan. The mechanism of fiber bending and elongation in the integrated piercing process of orthogonal laminated woven fabrics[J]. Engineering Science, 2003, 5(5): 59-62, 69. DOI:10.3969/j.issn.1009-1742.2003.05.010 (  0) 0)
|
| [4] |
朱建勋, 何建敏, 周之刚, 等. 整体穿刺机织布顶弯模式下的钢针针尖形态优化[J]. 天津大学学报, 2004, 37(8): 690-694. ZHU Jianxun, HE Jianmin, ZHOU Zhigang, et al. Optimizing of the form of steel needlepoint based on bending of woven in the integrated piercing process[J]. Journal of Tianjin University, 2004, 37(8): 690-694. DOI:10.3969/j.issn.0493-2137.2004.08.009 (  0) 0)
|
| [5] |
朱建勋.碳布整体穿刺织物编织工艺与结构参数优化[D].南京: 东南大学, 2004: 10-24. ZHU Jianxun. Carbon fiber integrated piercing fabrics braiding technology and parameter optimization[D]. Nanjing: Southeast University, 2004: 10-24. (  0) 0)
|
| [6] |
乔志炜, 胡方田. 细编穿刺织物矩阵刚度优化设计的研究[J]. 玻璃纤维, 2014(3): 22-25. QIAO Zhiwei, HU Fangtian. Study on the optimum design of matrix stiffness for fine woven fabric[J]. fiber, 2014(3): 22-25. DOI:10.3969/j.issn.1005-6262.2014.03.006 (  0) 0)
|
| [7] |
董九志, 蒋秀明, 杨建成, 等. 立体织物整体穿刺钢针阵列布放装置研制及实验验证[J]. 纺织学报, 2015, 36(3): 115-120. DONG Jiuzhi, JIANG Xiuming, YANG Jiancheng, et al. Development and experimental verification of steel needle array placement device for solid fabric puncture[J]. Journal of textile, 2015, 36(3): 115-120. (  0) 0)
|
| [8] |
周钰博, 李艳霞, 李敏, 等. 细编穿刺织物的数建模理论与实例[J]. 材料工程, 2017, 45(4): 102-107. ZHOU Yubo, LI Yanxia, LI Min, et al. Mathematical modeling theory and example of fine woven fabric[J]. material engineering, 2017, 45(4): 102-107. (  0) 0)
|
| [9] |
朱建勋, 何建敏, 周之刚, 等.整体穿刺机织布顶弯模式下的钢针针尖形态优化[J].天津大学学报(自然科学与工程技术版), 2004, 37(8):690-694. ZHU Jianxun, HE Jianmin, WANG Haiyan, et al. Optimization of Z oriented needle tip shape based on fiber bending elongation model[J]. China Engineering Science, 2003, 5(9):18-21. http://www.cnki.com.cn/Article/CJFDTotal-GCKX200309003.htm (  0) 0)
|
| [10] |
朱建勋, 何建敏, 王海燕, 等.基于纤维弯曲模式Z向钢针针尖形态优化[J].中国工程科学, 2003, 5(9):18-21. HU Jianming, HU Gang. Study on puncture damage and tip morphology of carbon cloth containing metal powder[J]. Glass fiber, 2012(3):29-32. http://www.cnki.com.cn/Article/CJFDTotal-GCKX200309003.htm (  0) 0)
|
| [11] |
孙乐, 王成, 李晓飞, 等. C/C复合材料预制体的研究进展[J]. 航空材料学报, 2018, 38(2): 86-95. SUN Le, WANG Cheng, LI Xiaofei, et al. Research progress of C/C composite prefabricated bodies[J]. Journal of aeronauticl materials, 2018, 38(2): 86-95. (  0) 0)
|
| [12] |
梁珩, 童明波, 王玉青, 等. 细编穿刺C/C复合材料热导率数值模拟[J]. 固体火箭技术, 2017, 40(3): 364-371. LIANG Wei, TONG Mingbo, WANG Yuqing, et al. Numerical simulation of thermal conductivity of fine-puncture C/C composites[J]. Solid state rocket technology, 2017, 40(3): 364-371. (  0) 0)
|
| [13] |
吴小军, 程文, 周绍建, 等. 电耦合CVI制备穿刺C/C喉衬材料的微结构及性能[J]. 复合材料学报, 2018, 35(2): 391-396. WU Xiaojun, CHENG Wen, ZHOU Shaojian, et al. Microstructure and properties of C/C laryngeal lining materials prepared by electro-coupled CVI[J]. Journal of composite Materials, 2018, 35(2): 391-396. (  0) 0)
|
| [14] |
解惠贞, 崔红, 李瑞珍, 等. 穿刺结构参数对C/C复合材料拉伸性能的影响[J]. 固体火箭技术, 2015(1): 107-110. XIE Huizhen, CUI Hong, LI Ruizhen, et al. Effect of puncture structure parameters on tensile properties of C/C composites[J]. Solid state rocket technology, 2015(1): 107-110. (  0) 0)
|
| [15] |
胡健明, 胡方田. 含金属粉体碳布穿刺损伤与针尖形态研究[J]. 玻璃纤维, 2012(3): 29-32. HU Jianming, HU Fangtian. Puncture damage and tip shape of metallic powder carbon sheet[J]. Fiberglass, 2012(3): 29-32. DOI:10.3969/j.issn.1005-6262.2012.03.007 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


