2. 黑龙江工程学院 经济管理学院, 黑龙江 哈尔滨 150050;
3. 清华大学 公共管理学院, 北京 100084
2. College of Economics and Management, Heilongjiang Institute of Technology, Harbin 150050, China;
3. School of Public Policy & Management, Tsinghua University, Beijing 100084, China
市场竞争的日益变化导致企业外部环境的不确定性不断增强, 处于技术快速变革环境中的企业, 只有不断地进行创新才能获得持续竞争优势。然而, 由于知识资源分布不均以及自身创新能力的限制[1], 我国现阶段技术市场的发展趋势已超过了单个企业、高校以及科研院所的承受能力。因此, 企业和学研机构之间进行协同创新, 整合内外部资源、提高创新资源配置, 已逐步成为提高国家自主创新能力的重要引擎。协同创新主要表现为创新合作伙伴之间的共同协作与研发, 因此, 合作伙伴的选择作为创新合作的始点与根基, 受到越来越多决策者的重视。如何选择切合度与满意度最高的合作伙伴已成为推动各主体之间协同创新顺利发展的关键。
国内外学者对创新合作伙伴选择的研究主要集中于合作伙伴选择的影响因素、合作关系的管理以及合作伙伴选择方法三个方面。针对合作伙伴选择的影响因素研究, 学者普遍认为合作成员之间的公平性[2]、网络嵌入性[3]、成员之间的信任度[4-5]以及相容性[6-7]等将影响创新合作伙伴的选择及创新绩效。在影响因素的研究基础上, 学者们多从缩小文化差异增强双方信任[8]、增加价值链互补性[9]以及技术相容性[10]等角度对于创新合作伙伴关系的管理进行研究, 并结合实证分析提出改善合作伙伴关系管理的相关建议。随着协同创新的逐步深化, 针对合作伙伴选择方法的研究成为近年来的热点。Sheu等[11]提出了基于语言变量选择的层次分析(AHP)模型, 以解决研发战略联盟的合作伙伴选择问题;曹霞等[12]提出了利用直觉模糊多属性决策理论与相对熵理论相结合的方法, 以解决具有多阶段、多属性、信息不对称、带有偏好选择的相关决策问题, 并在产学研合作伙伴的选择中进行了实证研究;郑登攀等[13]利用QAP回归法分析了网络嵌入性对以多方合作为特点的技术创新企业合作伙伴选择问题;针对合作伙伴选择中专家对各种指标评价的主观性和指标权重的非线性规划问题, 韩国元等[14]构建了利用微粒群算法(PSO)定权和基于联系度改进的TOPSIS模型, 保证了企业创新合作伙伴选择过程中的客观性及大规模数学优化的效率和全局优化能力;此外, 学者多应用模糊综合分析法、网络层次分析法、层次分析法[15-17]对创新合作伙伴的选择方法进行研究。
综合以上, 发现现有研究仍存在一些问题:第一, 模糊综合评价、层次分析以专家的判断为基础给出唯一确定分数, 因此主观性较强;第二, 多属性群决策法在候选合作伙伴数量巨大时, 存在可操作性差、筛选效率低等问题;第三, 现有文献大多忽略了创新合作伙伴初选阶段的数据量大等问题, 而直接对少量候选者进行评价, 欠缺对创新合作伙伴选择的宏观把握。
创新合作伙伴的选择是一个复杂的过程[12]。目前技术创新企业合作伙伴选择问题具有多属性特点, 且由于合作方式更加多元化, 选择目标企业数量巨大, 这给传统方法的数学计算和优化带来巨大压力。基于以上分析, 本文以合作伙伴选择不同阶段的诉求为基础, 构建创新合作伙伴的阶段性选择指标, 引入支持向量机(SVM)方法在初选阶段对广泛获得的潜在合作伙伴进行分类筛选, 以解决数量巨大、筛选效率较低的问题;利用直觉模糊集对初选获得的创新合作伙伴的判别属性进行评价, 降低单一数值引起的强主观性, 以解决社会资本的涌入对创新合作伙伴选择的偏好误导[18], 并利用TOPSIS法从候选合作伙伴中评价最优理想决策[37-38]。
1 创新合作伙伴优选决策分析 1.1 创新合作伙伴优选决策过程协同创新涉及多阶段过程[19], 因此创新合作伙伴的选择应综合考虑协同创新过程中不同阶段的诉求。通常情况, 创新企业作为技术需求方, 首先会根据合作项目的多属性需求从备选数据库中筛选合作伙伴以缩小搜索范围;其次, 创新企业通过邀请相关领域专家评审, 以实现对候选合作伙伴的综合评价, 并最终确定优选合作伙伴, 进行共同研发[20]。综上所述, 本文将创新合作伙伴优选决策过程划分为“初选-精选与优化”两个阶段。
近年来, 由于国家大幅推进协同创新工作, 因此参与创新合作的机构与日俱增。在初选阶段, 协同创新伙伴主要呈现候选伙伴数量大、伙伴选择属性参考多的情况[21], 若仅考虑个别伙伴的能力而进行选择, 很大可能会出现错选、漏选的情况, 导致合作效率低下等情况。此外, 初选阶段的基本指标多以候选伙伴的研发背景、所处地域、科研设施等硬约束条件为主, 且为已公开的对称信息。因此, 通过传统的方式进行筛选, 既增加了专家劳动量及不必要的成本, 又降低了工作效率。为了避免盲目筛选造成高切合度合作伙伴的流失及效率的低下, 本文引入支持向量机, 其作用是从海量数据中, 选择具有高度匹配性的伙伴, 缩小精选范围以提高后续选择阶段的效率, 解决了初选阶段专家评价大量合作方所引起的合作伙伴流失量大、评判效率低等问题[22]。
处于精选与优化阶段的决策者, 需要针对少数已筛选出的合作伙伴进行信息甄别以防止逆向选择风险[23]。该阶段协同创新伙伴具有一定的针对性, 但是合作伙伴的选择不仅仅考虑单一指标, 同时, 指标的选择具有多属性特征, 既包括可以用数字衡量的财务、销售、研发等情况, 又包括了一些定性指标。该阶段协同创新的决策者会通过对不同合作伙伴的各类细节属性进行评判, 利用专家评审对合作伙伴进行进一步选择, 优化自身心理预期选择最终的协同创新伙伴, 以确定最优决策。因此, 该阶段将会面临选择多属性、主、客观数据相容的问题。基于此, 在精选与优化阶段引入直觉模糊集多属性群体决策TOPSIS法, 在客观数据基础上, 利用专家的实践经验, 对候选合作伙伴的满意度给出区间范围, 从隶属度与正理想解最优化两个角度, 选择创新合作伙伴。
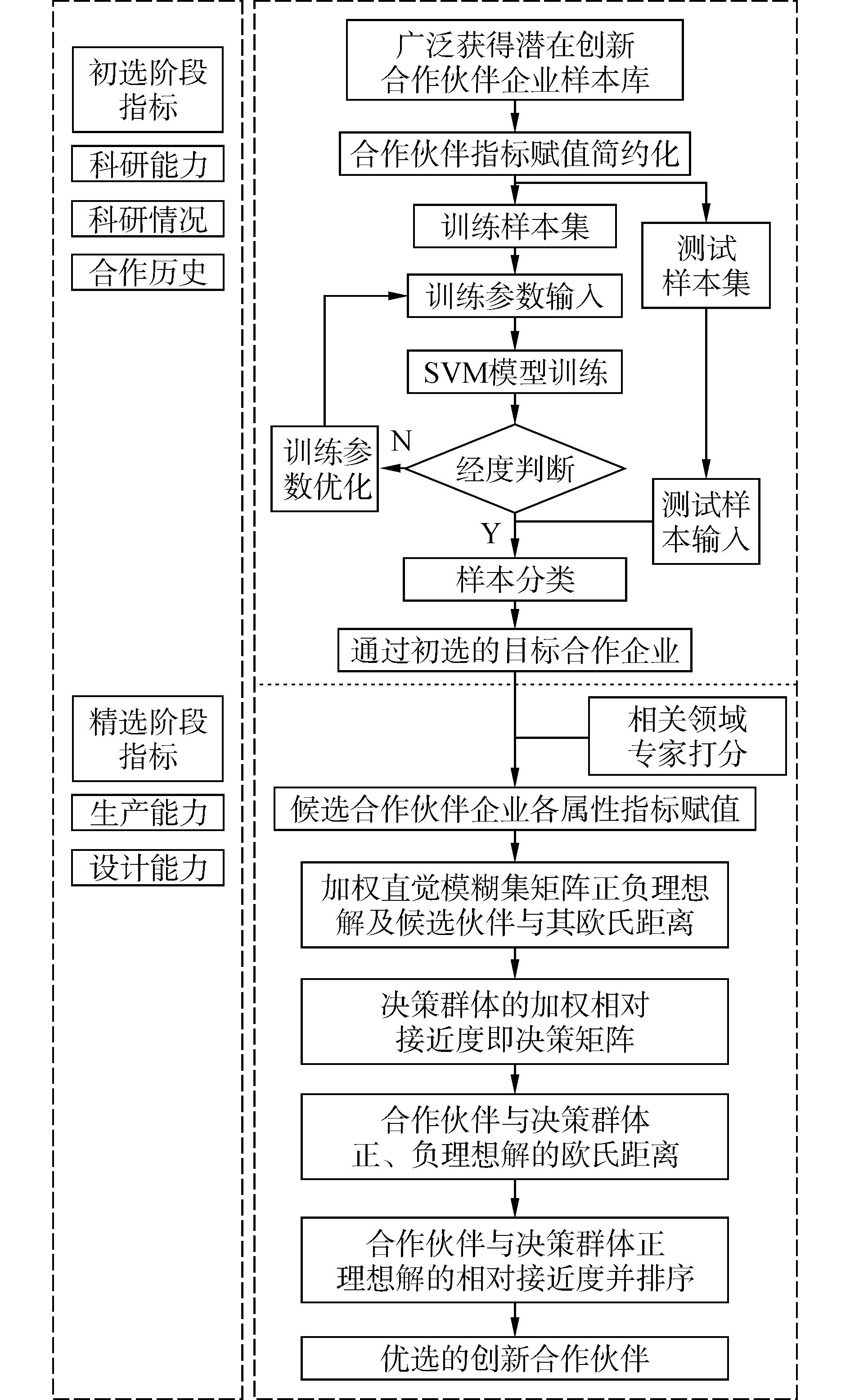
1.2 创新合作伙伴优选指标体系构建创新合作伙伴的选择是一个复杂的过程, 涉及产品研发、试验以及产业化多个阶段[12], 因此, 应兼顾定量与定性双特征指标, 才能使创新合作伙伴的选择更加科学准确。综合考虑创新合作伙伴选择的三阶段特点, 初选阶段决策者从数据库中筛选合作伙伴, 因此, 从科研环境、科研能力、历史合作三个宏观角度考察大量合作伙伴的基本情况;精选阶段从研发效果与产品的设计能力[24]等特定角度考察合作伙伴的产业化情况。在梳理了大量国内外文献、公开的企业数据库及创新合作项目书的基础上[12, 24, 32-36], 结合相关领域的专家意见, 构建了由目标层、准则层、指标层组成的协同创新合作伙伴选择指标体系考察候选合作伙伴的情况(见表 1)。优选过程流程如图 1所示。
| 表 1 创新合作伙伴选择指标体系 Tab.1 Index System of innovation partner |
|
图 1 创新合作伙伴优选决策模型 Fig.1 The optimization decision-making model of partners in collaborative innovation |
SVM是基于统计学习理论和结构风险最小化原理提出的一种新型数据挖掘方法, 其算法的精确度已经远远超过了传统的学习[25], 目前SVM算法已广泛应用于模式识别、回归估计、概率密度函数估计等方面[26]。支持向量机多级分类算法在解决数据分类方面具有良好的预测性能, 可帮助企业从海量的数据中发现潜在的、理想的创新合作伙伴, 从而为企业的决策提供有力的支持[27]。鉴于此, 构建支持向量机的创新合作伙伴初选决策模型, 以提高精选与优化阶段的效率。
假设xij∈Rn为训练样本集, j=1, 2, …, s为样本所属分类,
| $ \begin{array}{*{20}{c}} {\min \frac{1}{2}\left( {w \cdot w} \right) + A\sum\limits_i {\sum\limits_j {\left( {\varepsilon _i^j + \varepsilon _i^{j + 1}} \right)} } }\\ {{\rm{s}}.\;{\rm{t}}.\left\{ \begin{array}{l} wx_i^j - {b_j} \le \varepsilon _i^j - 1\\ wx_i^{j + 1} - {b_j} \le 1 - \varepsilon _i^{j + 1}\\ {b_j} \le {b_{j + 1}}\\ \varepsilon _i^j \le 0\\ \varepsilon _i^{j + 1} \ge 0 \end{array} \right.} \end{array} $ | (1) |
构造拉格朗日函数求解(1) 式二次优化问题:
| $ \begin{array}{*{20}{c}} {L\left( \cdot \right) = \frac{1}{2}\left( {w \cdot w} \right) +A \sum\limits_{i,j} {\left( {\varepsilon _i^j + \varepsilon _i^{j + 1}} \right)} + }\\ {\sum\limits_{i,j} {\lambda _i^j\left( {wx_i^i - {b_j} + 1 - \varepsilon _i^i} \right)} + }\\ {\sum\limits_{i,j} {\gamma _i^j\left( {1 - \varepsilon _i^{j + 1} + {b_j} - wx_i^{j + 1}} \right)} - \sum\limits_{i,j} {\varepsilon _i^j\xi _i^j} - \sum\limits_{i,j} {\varepsilon _i^{j + 1}\xi _i^{j + 1}} } \end{array} $ | (2) |
式中λij、γij、ξij与ξij+1为非负拉格朗日乘子, 由于原问题为凸, 强对偶定理成立, 因此分别对w、bj、εij、εij+1求最小值, 得到以拉格朗日乘子为变量的对偶问题的目标函数, 对w、bj、εij、εij+1分别求偏导数得到μ, 同时得到超平面的方向w以及bj的值, 从而基于合作伙伴的多属性要求, 从大量候选伙伴中筛选出符合基本要求的伙伴进行精选及优化。
2.2 基于直觉模糊集TOPSIS的创新合作伙伴优选决策模型模糊集理论是1965年扎德教授提出的一种处理模糊性的有效方法, 随后为了更加精确的描述模糊性问题, Atanassov于1983年提出了直觉模糊集的概念[28]。随着直觉模糊集在理论与应用研究中取得的巨大成功, 现已被用于经济管理决策、社会、环境、军事等众多领域[29]。由于有多个决策者参与创新合作伙伴的精选与优化, 而决策者的经验有时并不能用某一准确数字衡量, 因此引入直觉模糊集多属性群体决策TOPSIS, 基于以下定义构建基直觉模糊集TOPSIS的创新合作伙伴优选模型[30]。
定义1 设X是个论域。若X上两个映射μA:X→[0, 1]和νA:X→[0, 1], 使得x∈X→μA(x)∈[0, 1]和x∈X→νA(x)∈[0, 1]并满足条件0≤μA(x)+νA(x)≤1, 则称μA和νA确定了论域X上的一个直觉模糊集, 记为A={<x, μA(x), νA(x)>|x∈X}。
假设初选阶段后, 剩余n个有效创新合作伙伴xj(j=1, 2, …, n)组成的精选方案集X={x1, x2, …, xn}, K个决策者Pk(k=1, 2, …, K)组成一个决策群体对每个创新伙伴关于m个属性oi (i=1, 2, …, m)进行评价, 记属性集合为O={o1, o2, …, om}。假设决策者Pk对创新合作伙伴xj∈X关于属性oi∈O的评价值表示为直觉模糊集Fijk= < μijk, νijk>(i=1, 2, …, m; j=1, 2, …, n), 其中μijk和νijk分别表示决策者Pk对于创新合作伙伴关于某一属性oi所给定的满意度(或不满意度), 且0≤μijk≤1、0≤νijk≤1和0≤νijk+μijk≤1, 则决策者对创新合作伙伴关于所有m个属性的评价结果用向量表示为Fjk=(F1jk, F2jk, …, Fmjk)T, 用矩阵简记为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}^k} = \left( {F_{ij}^k} \right) = {{\left( {\left\langle {\mu _{ij}^k,\mathit{\boldsymbol{v}}_{ij}^k} \right\rangle } \right)}_{m * n}} = }\\ {\left[ {\begin{array}{*{20}{c}} {\left\langle {\mu _{11}^k,\mathit{\boldsymbol{\nu }}_{11}^k} \right\rangle }&{\left\langle {\mu _{12}^k,\mathit{\boldsymbol{\nu }}_{12}^k} \right\rangle }& \cdots &{\left\langle {\mu _{1n}^k,\mathit{\boldsymbol{\nu }}_{1n}^k} \right\rangle }\\ {\left\langle {\mu _{21}^k,\mathit{\boldsymbol{\nu }}_{21}^k} \right\rangle }&{\left\langle {\mu _{22}^k,\mathit{\boldsymbol{\nu }}_{22}^k} \right\rangle }& \cdots &{\left\langle {\mu _{2n}^k,\mathit{\boldsymbol{\nu }}_{2n}^k} \right\rangle }\\ \vdots&\vdots&\ddots&\vdots \\ {\left\langle {\mu _{m1}^k,\mathit{\boldsymbol{\nu }}_{m1}^k} \right\rangle }&{\left\langle {\mu _{m2}^k,\mathit{\boldsymbol{\nu }}_{m2}^k} \right\rangle }& \cdots &{\left\langle {\mu _{mn}^k,\mathit{\boldsymbol{\nu }}_{mn}^k} \right\rangle } \end{array}} \right]} \end{array} $ | (3) |
同理, 决策者Pk给定属性oi∈O(i=1, 2, …, m)的权重表示为直觉模糊集ωik= < ηik, τik> (i=1, 2, …, m; k=1, 2, …, K), 其中ηik和τik分别表示决策者Pk对于属性oi∈O给出的重要性程度(或隶属度)、不重要性程度(或非隶属度), 且0≤ηik≤1、0≤τik≤1和0≤ηik+τik≤1, 则决策者给定的所有m个属性的权重可表示为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\omega }}^k} = {{\left( {\mathit{\boldsymbol{\omega }}_i^k} \right)}_{m * 1}} = \left( {\left\langle {\eta _1^k,\tau _1^k} \right\rangle ,\left\langle {\eta _2^k,\tau _2^k} \right\rangle , \cdots ,} \right.}\\ {{{\left. {\left\langle {\eta _m^k,\tau _m^k} \right\rangle } \right)}^{\rm{T}}}\left( {k = 1,2, \cdots ,K} \right)} \end{array} $ |
定义2 设A和B是论域X上的任意两个直觉模糊集, λ>0是任意实数。则直觉模糊集的积为AB={<x, μA(x)μB(x), νA(x)+νB(x)-νA(x)νB(x)>|x∈X}。
利用直觉模糊集决策矩阵及权重向量, 求得加权直觉模糊集决策矩阵为
| $ {{\mathit{\boldsymbol{\bar F}}}^k} = {\left( {\omega _i^k\mathit{\boldsymbol{F}}_{ij}^k} \right)_{m * n}} = \left[ {\begin{array}{*{20}{c}} {\left\langle {\eta _1^k\mu _{11}^k,\tau _1^k + \mathit{\boldsymbol{v}}_{11}^k - \tau _1^k\mathit{\boldsymbol{v}}_{11}^k} \right\rangle }& \cdots &{\left\langle {\eta _1^k\mu _{1n}^k,\tau _1^k + \mathit{\boldsymbol{v}}_{1n}^k - \tau _1^k\mathit{\boldsymbol{v}}_{1n}^k} \right\rangle }\\ \vdots&\vdots&\vdots \\ {\left\langle {\eta _m^k\mu _{m1}^k,\tau _m^k + \mathit{\boldsymbol{v}}_{m1}^k - \tau _m^k\mathit{\boldsymbol{v}}_{m1}^k} \right\rangle }& \cdots &{\left\langle {\eta _m^k\mu _{mn}^k,\tau _m^k + \mathit{\boldsymbol{v}}_{mn}^k - \tau _m^k\mathit{\boldsymbol{v}}_{mn}^k} \right\rangle } \end{array}} \right] $ | (4) |
定义3 决策者Pk的直觉模糊集正理想解xk+和直觉模糊集负理想解xk-分别记为
| $ {\mathit{\boldsymbol{F}}^{k + }} = {\left( {\left\langle {\mu _1^{k + },v_1^{k + }} \right\rangle , \cdots ,\left\langle {\mu _m^{k + },v_m^{k + }} \right\rangle } \right)^{\rm{T}}} $ | (5) |
| $ {\mathit{\boldsymbol{F}}^{k - }} = {\left( {\left\langle {\mu _1^{k - },v_1^{k - }} \right\rangle , \cdots ,\left\langle {\mu _m^{k - },v_m^{k - }} \right\rangle } \right)^{\rm{T}}} $ | (6) |
其中
| $ \left\{ \begin{array}{l} \mu _i^{k + } = \mathop {\max }\limits_{1 \le j \le n} \left\{ {\bar \mu _{ij}^k} \right\}\\ \mathit{\boldsymbol{v}}_i^{k + } = \mathop {\min }\limits_{1 \le j \le n} \left\{ {\mathit{\boldsymbol{\bar v}}_{ij}^k} \right\} \end{array} \right.和\left\{ \begin{array}{l} \mu _i^{k - } = \mathop {\min }\limits_{1 \le j \le n} \left\{ {\bar \mu _{ij}^k} \right\}\\ \mathit{\boldsymbol{v}}_i^{k - } = \mathop {\max }\limits_{1 \le j \le n} \left\{ {\mathit{\boldsymbol{\bar v}}_{ij}^k} \right\} \end{array} \right. $ |
定义4 决策者Pk关于创新合作伙伴xj∈X与直觉模糊集正、负理想解的欧式距离定义为
| $ \begin{array}{*{20}{c}} {D_2^k\left( {{x_j},{x^{k + }}} \right) = }\\ {\sqrt {\frac{1}{2}\sum\limits_{i = 1}^m {\left[ {{{\left( {\bar \mu _{ij}^k - \mu _i^{k + }} \right)}^2} + {{\left( {\bar v_{ij}^k - v_i^{k + }} \right)}^2} + {{\left( {\bar \pi _{ij}^k - \pi _i^{k + }} \right)}^2}} \right]} } } \end{array} $ | (7) |
| $ \begin{array}{*{20}{c}} {D_2^k\left( {{x_j},{x^{k - }}} \right) = }\\ {\sqrt {\frac{1}{2}\sum\limits_{i = 1}^m {\left[ {{{\left( {\bar \mu _{ij}^k - \mu _i^{k - }} \right)}^2} + {{\left( {\bar v_{ij}^k - v_i^{k - }} \right)}^2} + {{\left( {\bar \pi _{ij}^k - \pi _i^{k - }} \right)}^2}} \right]} } } \end{array} $ | (8) |
其中
| $ \left\{ \begin{array}{l} {\rm{ \mathsf{\bar π} }}_{ij}^k = 1 - \bar \mu _{ij}^k - \mathit{\boldsymbol{\bar v}}_{ij}^k\\ {\rm{ \mathsf{ π} }}_i^{k + } = 1 - \mu _i^{k + } - \mathit{\boldsymbol{v}}_i^{k + }\\ {\rm{ \mathsf{ π} }}_i^{k - } = 1 - \mu _i^{k - } - \mathit{\boldsymbol{v}}_i^{k - } \end{array} \right. $ | (9) |
定义5 就决策者Pk而言, 定义xj∈X与直觉模糊集正理想解xk+的相对接近度为ρjk, 可知ρjk越大, 相应的方案越优。
| $ \rho _j^k = \frac{{D_2^k\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{x}}^{k - }}} \right)}}{{D_2^k\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{x}}^{k + }}} \right) + D_2^k\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{x}}^{k - }}} \right)}} $ | (10) |
定义6 创新合作伙伴与决策群体正、负理想解x+和x-的欧式距离分别为
| $ D_j^ + = \sqrt {\sum\limits_{k = 1}^K {{{\left( {\bar \rho _j^k - \rho _k^ + } \right)}^2}} } $ | (11) |
| $ D_j^ - = \sqrt {\sum\limits_{k = 1}^K {{{\left( {\bar \rho _j^k - \rho _k^ - } \right)}^2}} } $ | (12) |
定义7 xj∈X与决策群体正理想解的相对贴近度为
| $ {C_j} = \frac{{D_j^ - }}{{D_j^ + - D_j^ - }} $ | (13) |
由式(13) 可知, Cj∈[0, 1]且越大, 创新合作伙伴越优。因此, 根据相对贴近度的排序, 可确定创新合作伙伴集X={x1, x2, …, xm}的优劣程度, 从而确定最优方案。
2.3 创新合作伙伴的优选决策步骤创新合作伙伴的具体优选决策步骤如下:
1) 利用Matlab软件进行SVM程序设计, 通过初选指标体系, 对数据库中的候选合作伙伴进行初步筛选, 确定需要专家评定的候选合作伙伴方案集;
2) 根据“精选与优化”阶段的指标体系, 确定相应领域专家并对全部方案集之中候选合作伙伴的各类属性数值进行赋权;
3) 利用式(4), 计算专家的加权直觉模糊集决策矩阵;
4) 利用式(5)、(6), 确定专家的直觉模糊集正、负理想解;
5) 利用式(7)、(8)、(9), 计算每个专家对于候选合作伙伴与直觉模糊集正、负理想解的欧式距离;
6) 利用式(10) 计算合作伙伴与直觉模糊集正理想解的相对接近度及决策群体的加权相对接近度决策矩阵;
7) 利用式(11)、(12) 确定专家决策群体的正、负理想解及合作伙伴与正、负理想解的欧式距离;
8) 利用式(13) 计算合作伙伴候选方案与决策群体正理想解的相对接近度, 并确定方案的优劣排序, 最终选出创新合作伙伴。
3 算例分析Y集团公司是一家融医药制造、贸易、科研于一体的中外合资企业, 为了提高公司的抗生素研发质量, 研发部门欲寻找合作伙伴进行协同创新, 共同完成新型抗生素的研发与生产。
初选阶段, Y公司在合作数据库中筛选互补性、切合度较高的创新合作伙伴, 以表 1中初选阶段指标体系为属性值, 从科研能力、科研环境以及历史合作情况三方面利用SVM进行创新合作伙伴的初选。
首先, 利用Matlab支持向量机工具箱, 从Y公司提供的173家创新合作伙伴数据库中筛选符合初选阶段指标合作伙伴, 并按照表 2所示专家评价等级及标准进行筛选。
| 表 2 专家评价等级及标准 Tab.2 Standards and grades of expert evaluation |
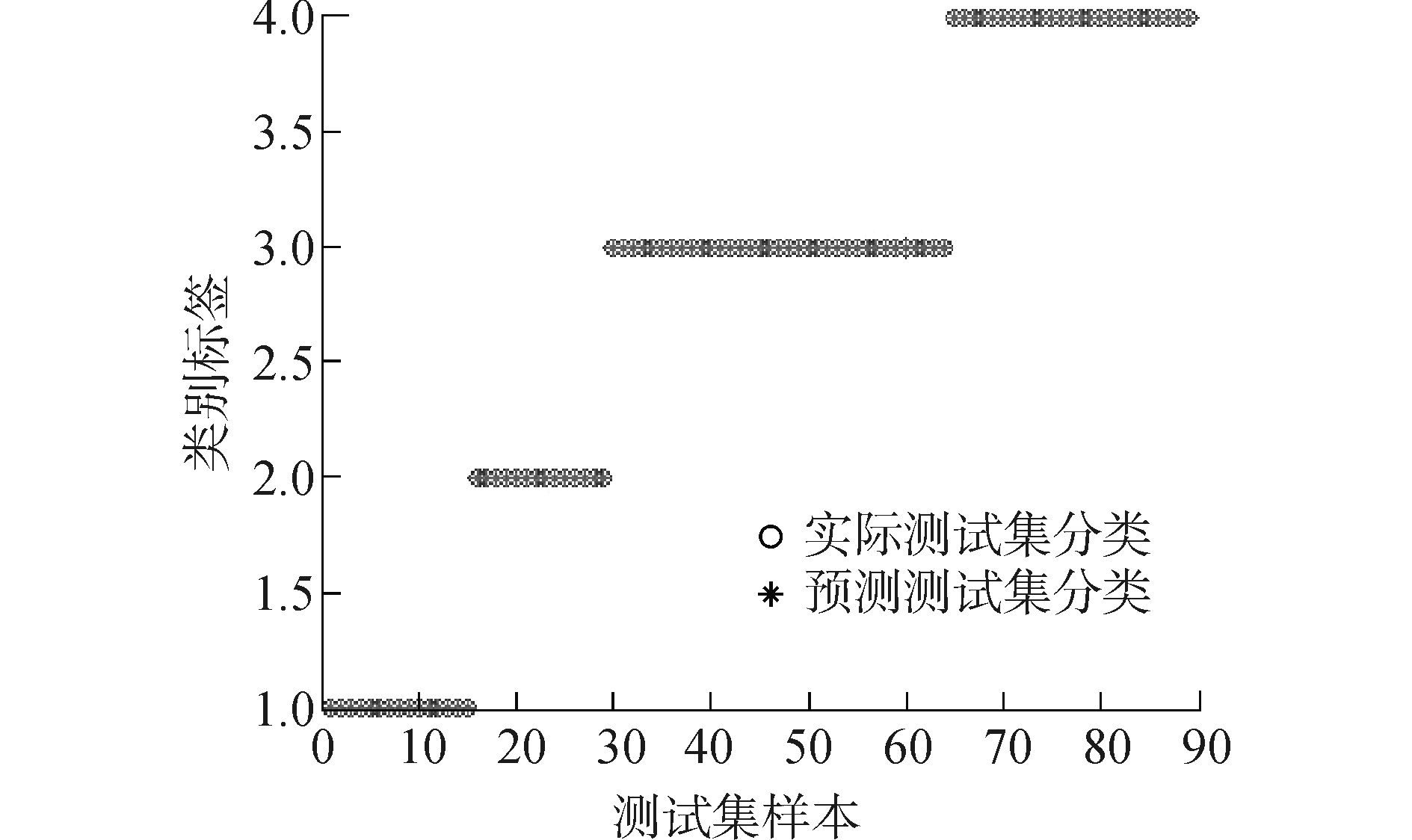
相比于其他核参数, 径向基函数的数值限制较少, 可以将样本非线性映射到更高维的空间, 解决类别和属性间非线性关系[31], 因此, 本文选用径向基函数作为核参数进行合作伙伴的筛选(由于数据库候选伙伴较多在此不详细列出)。通过Matlab, 对已有合作历史的90家合作方进行测试, 结果表明SVM预测准确率为100%。基于此, 从企业已获取数据库中最终筛选出6家适合与Y公司进行协同创新的合作伙伴。
Y集团公司聘请5位相关领域专家针对初选后的6家合作伙伴进行评价, 按照表 1所示精选与优化指标, 给出评价数据。
依据表 1与专家打分情况, 根据式(4) 计算加权直觉模糊集矩阵, 并判断各个候选伙伴与直觉模糊集正、负理想解的欧式距离及正理想解的相对接近度如表 4、5所示。
| 表 3 精选优化阶段指标的专家评价 Tab.3 The experts evaluation in optimization phase |
| 表 4 候选合作伙伴与直觉模糊集正、负理想解的欧式距离 Tab.4 Euclidean distance of candidate partner |
| 表 5 候选合作伙伴与直觉模糊集正理想解的相对接近度 Tab.5 Relatively close to degree of candidate partner |
|
图 2 测试集的实际分类与预测分类 Fig.2 The actual and prediction classification of test |
利用式(11)、(12) 求得合作伙伴与决策群体正、负理想解的欧式距离, 并根据式(13) 计算决策群体对于6家候选合作伙伴的正理想解相对贴进度分别为:0.404、0.697、0.203、0.262、0.228、0.820, 可知优劣排序为
X6>X2>X1>X4>X5>X3
通过以上分析, Y集团应该与合作伙伴X6协同创新, 完成新产品的研发与推广工作。
4 结论1) 随着协同创新的推进, 大量的创新合作伙伴不断涌现, 引入SVM进行合作伙伴的初步筛选, 解决了初选合作伙伴众多的问题, 从而降低专家在精选阶段的工作量, 提高决策分析的效率, 避免专家对大量的合作伙伴进行重复打分带来的工作冗余及成本消耗;初选阶段的方案属性多为硬约束条件, 采用支持向量机可以准确地对合作伙伴进行分类筛选, 避免了合作伙伴的初选遗漏问题。
2) 利用直觉模糊数进行评价, 解决了社会资本的大量涌入对专家评价的误导, 从隶属度及非隶属度两个方面, 考察每一个候选合作伙伴的属性特点后进行评价, 从一定程度上克服了专家打分的偏好性。引入TOPSIS法, 求解专家群决策下不同方案与理想方案的差距, 综合多位专家意见, 得出不同方案的优劣排序, 为决策者提供更为客观的指导。
3) 从协同创新的宏观角度出发, 构建了创新合作伙伴选择“初选——精选与优化”阶段的指标体系, 使各个阶段的评价更有针对性, 解决了大众化评价指标的评判对创新合作伙伴选择的盲目性。
| [1] |
孙笑明, 崔文田, 董劲威. 创新合作伙伴选择与创新绩效之间的关系[J]. 科学学与科学技术管理, 2011, 32(11): 173-179. SUN Xiaoming, CUI Wentian, DONG Jinwei. Relationship between the selection of collaborative innovation partners and innovation performance[J]. Science of science and management of S. & T, 2011, 32(11): 173-179. (  0) 0)
|
| [2] |
DAELLENBACH U S, DAVENPORT S J. Establishing trust during the formation of technology alliances[J]. Journal of technology transfer, 2004, 29(2): 187-202. DOI:10.1023/B:JOTT.0000019537.61121.c3 (  0) 0)
|
| [3] |
CANTNER W, HOLGER G. The network of innovators in Jena:an application of social network analysis[J]. Research policy, 2006, 35(4): 463-480. DOI:10.1016/j.respol.2006.01.002 (  0) 0)
|
| [4] |
BUNDUCHI R. Trust partner selection and innovation outcome in collaborative new product development[J]. Production planning & control, 2013, 24(2): 145-157. (  0) 0)
|
| [5] |
D'ESTE P, PATEL P. University-industry linkages in the UK:what are the factors underlying the variety of interactions with Industry[J]. Research policy, 2007, 36: 1295-1313. DOI:10.1016/j.respol.2007.05.002 (  0) 0)
|
| [6] |
DODOUROVA M. Alliances as strategic tools:a cross industry study of partnership planning, formation and success[J]. Management decision, 2009, 47(5): 831-844. DOI:10.1108/00251740910960150 (  0) 0)
|
| [7] |
HOLMBERG S R, CUMMINGS J L. Building successful strategic alliances:strategic process and analytical tool for selecting partner industries and firms[J]. Long range planning, 2009, 42(2): 164-193. DOI:10.1016/j.lrp.2009.01.004 (  0) 0)
|
| [8] |
SHEHRI A l, EBRAHIM M A B. Bridging the gap between university and industry:efforts made at faculty of engineering-rabigh-saudi arabia[M]. Advances in Intelligent Systems Research, 2013: 448-456.
(  0) 0)
|
| [9] |
Von RAESFELD A. Influence of partner diversity on collaborative public R & D project outcomes:a study of application and commercialization of nanotechnologies in the Netherlands[J]. Technovation, 2012, 32(3/4): 227-233. (  0) 0)
|
| [10] |
PETRUZZELLI A M. The impact of technological relatedness, prior ties, and geographical distance on university-industry collaborations:a joint-patent analysis[J]. Technovation, 2011, 31(7): 309-319. DOI:10.1016/j.technovation.2011.01.008 (  0) 0)
|
| [11] |
韩国元, 陈伟, 冯志军. 企业合作创新伙伴的选择研究-基于微粒群算法定权的改进TOPSIS法[J]. 科研管理, 2014, 35(2): 119-126. HAN Guoyuan, CHEN Wei, FENG Zhijun. Selection of enterprise's cooperative innovationpartners-based on PSO fixed weight and ameliorated TOPSIS method[J]. Science research management, 2014, 35(2): 119-126. (  0) 0)
|
| [12] |
曹霞, 刘国巍, 付向梅. 基于偏好和动态直觉的产学研合作伙伴选择群决策分析[J]. 运筹与管理, 2013, 22(4): 33-41. CAO Xia, LIU Guowei, FU Xiangmei. Analysis on group decision making of industry-university-research partners choice based on preferences and dynamic intuition[J]. Operations research and management science, 2013, 22(4): 33-41. (  0) 0)
|
| [13] |
郑登攀, 党兴华. 网络嵌入性对企业选择合作技术创新伙伴的影响[J]. 科研管理, 2012, 32(1): 154-160. ZHENG Dengpan, DANG Xinghua. The impact of network embeddedness on the partner selection of Cooperative technological innovation[J]. Science research management, 2012, 32(1): 154-160. (  0) 0)
|
| [14] |
SHEU Huachen, PEI Wenwang, CHIEN Minchen, et al. An analytic hierarchy process approach with linguistic variables for selection of an R & D strategic alliance partner[J]. Computers & industrial engineering, 2010, 58(2): 278-287. (  0) 0)
|
| [15] |
阮国祥, 毛荐其. 合作创新伙伴选择的ANP方法研究[J]. 科技进步与对策, 2007, 4(11): 31-33. RUAN Guoxiang, MAO Jianqi. Research on selection of joint innovation partners with ANP method[J]. Science & technology progress and policy, 2007, 4(11): 31-33. DOI:10.3969/j.issn.1001-7348.2007.11.008 (  0) 0)
|
| [16] |
桂黄宝, 赵付民. 基于模糊层次分析法的合作技术创新伙伴选择研究[J]. 科学学与科学技术管理, 2007(9): 50-54. GUI Huangbao, ZHAO Fumin. Research on cooperative innovation partner selection based on fuzzy analytic hierarchy process[J]. Science of science and management of S & T, 2007(9): 50-54. (  0) 0)
|
| [17] |
曾德明, 华金科, 孙耀吾. 基于技术标准的企业协作研发伙伴选择研究[J]. 科学学与科学技术管理, 2005(11): 39-43. ZENG Deming, HUA Jinke, SUN Yaowu. Research on partners selection in enterprise' cooperative r & d based on technical standard[J]. Science of science and management of S & T, 2005(11): 39-43. DOI:10.3969/j.issn.1002-0241.2005.11.007 (  0) 0)
|
| [18] |
周小虎, 马莉. 企业社会资本、文化取向与离职意愿——基于本土化心理学视角的实证研究[J]. 管理世界, 2008(6): 109-117. (  0) 0)
|
| [19] |
冯蔚东, 陈剑, 赵纯均. 基于遗传算法的虚拟企业伙伴选择过程及优化模型[J]. 清华大学学报(自然科学版), 2000, 40(10): 120-124. FENG Weidong, CHEN Jian, ZHAO Chunjun. Partners selection process and optimization model for virtual corporations based on genetic algorithms[J]. Journal of Tsinghua University (science and technology), 2000, 40(10): 120-124. DOI:10.3321/j.issn:1000-0054.2000.10.032 (  0) 0)
|
| [20] |
陈菊红, 汪兴洛, 孙林岩. 虚拟企业伙伴选择过程及方法研究[J]. 系统工程理论与实践, 2001(7): 48-52. CHEN Juhong, WANG Xingluo, SUN Linyan. Study on the processes and methods of partner selection in virtual organization[J]. System engineering theory and practice, 2001(7): 48-52. (  0) 0)
|
| [21] |
张成考, 聂茂林, 吴价宝. 基于改进型灰色评价的虚拟企业合作伙伴选择[J]. 系统工程理论与实践, 2007(11): 54-60. ZHANG Chengkao, NIE Maolin, WU Jiabao. Selection of cooperative partners for virtual enterprises based on modified grey evaluation method[J]. Systems engineering——theory & practice, 2007(11): 54-60. DOI:10.3321/j.issn:1000-6788.2007.11.008 (  0) 0)
|
| [22] |
SHAFIEIAN M A, JAMSHIDI A. Power allocation and partner selection in energy efficient cooperative WSN[J]. Arabian journal for science and engineering, 2014, 39(3): 2071-2081. DOI:10.1007/s13369-013-0781-0 (  0) 0)
|
| [23] |
曹兴, 龙凤珍, 秦耀华. 基于知识转移的技术联盟合作伙伴选择机制[J]. 系统工程, 2011, 29(8): 79-85. CAO Xing, LONG Fengzhen, QIN Yaohua. The mechanism of partner selection within technology alliance based on knowledge transfer[J]. Systems engineering, 2011, 29(8): 79-85. (  0) 0)
|
| [24] |
AGUSTÍ S B, JOSEPMARIA A C. Sources of innovation and industry-university interaction:evidence from Spanish firms[J]. Reasearch policy, 2008, 37(8): 1283-1295. DOI:10.1016/j.respol.2008.05.003 (  0) 0)
|
| [25] |
AMARI S, WU S. Improving support vector machine classifiers by modifying kernel functions[J]. Neural netw, 1999(12): 783-789. (  0) 0)
|
| [26] |
YANG Y T, FISHBAIN B, HOCHBAUM D S. The supervised normalized cut method for detecting, classifying and identifying special nuclear materials[J]. Informs journal on computing, 2014, 26(1): 45-58. DOI:10.1287/ijoc.1120.0546 (  0) 0)
|
| [27] |
YAO Zhenjie, YI Weidong. License plate detection based on multistage information fusion[J]. Information fusion, 2014(18): 78-85. (  0) 0)
|
| [28] |
ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy sets and systems, 1986, 20(1): 87-96. DOI:10.1016/S0165-0114(86)80034-3 (  0) 0)
|
| [29] |
LI Dengfeng. Extension principles for interval-valued intuitionistic fuzzy sets and algebraic operations[J]. Fuzzy optimization and decision making, 2011, 10(1): 45-58. DOI:10.1007/s10700-010-9095-9 (  0) 0)
|
| [30] |
李登峰. 直觉模糊集决策与对策分析方法[M]. 北京: 国防工业出版社, 2012. LI Dengfeng. Intuitionistic fuzzy set decision and game analysis methodologies[M]. Beijing: National Defense Industry Press, 2012. (  0) 0)
|
| [31] |
李斐, 杨育. 协同产品创新中的创新客户流失预测模型[J]. 计算机集成制造系统, 2015, 21(1): 40-47. LI Fei, YANG Yu. Innovative customer churn prediction in collaborative products innovation[J]. Computer integrated manufacturing systems, 2015, 21(1): 40-47. (  0) 0)
|
| [32] |
林向义, 张庆普, 罗洪云. 知识创新联盟合作伙伴选择研究[J]. 中国管理科学, 2008(1): 404-408. LIN Xiangyi, ZHANG Qingpu, LUO Hongyun. Partners' selection of knowledge innovation alliances[J]. Chinese journal of management science, 2008(1): 404-408. (  0) 0)
|
| [33] |
IBRAHIM A B. Interactive TOPSIS algorithms for solving multi-level non-linear multi-objective decision-making problems[J]. Applied mathematical modelling, 2014, 38(4): 1417-1433. DOI:10.1016/j.apm.2013.08.016 (  0) 0)
|
| [34] |
游达明, 黄曦子. 突破性技术创新合作伙伴选择及其评价[J]. 系统工程, 2014, 32(3): 99-103. YOU Daming, HUANG Xizi. Partner selection and evaluation of radical technological innovation[J]. Systems engineering, 2014, 32(3): 99-103. (  0) 0)
|
| [35] |
喻金田, 胡春华. 技术联盟协同创新的合作伙伴选择研究[J]. 科学管理研究, 2015, 33(1): 13-16. YU Iintian, HU Chunhua. Study on partner selection of synergy innovatison in technology alliance[J]. Scientific management research, 2015, 33(1): 13-16. (  0) 0)
|
| [36] |
张敬文, 江晓珊, 周海燕. 战略性新兴产业技术联盟合作伙伴选择研究[J]. 宏观经济研究, 2016(5): 79-86. ZHANG Jingwen, JIANG Xiaoshan, ZHOU Haiyan. Strategic emerging industry technology innovation alliance partner choice research[J]. Macroeconomics, 2016(5): 79-86. (  0) 0)
|
| [37] |
WANG Chengyi, CHEN Shiming. Multiple attribute decision making based on interval-valued intuitionistic fuzzy sets, linear programming methodology, and the extended TOPSIS method[J]. Information sciences, 2017(397/398): 155-167. (  0) 0)
|
| [38] |
DEEPA J, SANJAY K. Interval-valued intuitionistic hesitant fuzzy choquet integral based TOPSIS method for multi-criteria group decision making[J]. European journal of operational research, 2016, 248(1): 183-191. DOI:10.1016/j.ejor.2015.06.047 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


