哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001
收稿日期:2016-09-10;网络出版日期:2017-04-27
基金项目:国家自然科学基金项目(11272097)
作者简介:黄山(1992-), 男, 硕士研究生;
段文洋(1967-), 男, 教授, 博士生导师.
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
格林函数法以其鲜明的物理意义、简单的表达形式而被广泛地用于船舶与海洋结构物航行及其与波浪相互作用时的水动力载荷与运动的计算[1]。自由面格林函数是船舶与海洋工程水动力学中最重要的术语之一,是船舶与海洋工程结构物性能计算的关键基础[2-3]。对于船舶与海洋结构物,常用自由面格林函数面元法解决有关附加质量、阻尼系数以及波浪力和力矩的波浪辐射绕射问题[4]。这种势流方法是建立在由满足线性自由表面条件的格林函数构成的边界积分方程的数值解的基础上[5-6]。基于无航速船舶辐射绕射问题的自由面格林函数在许多软件中已得到广泛应用,如AQWA等。但对有航速问题,有航速自由面格林函数计算复杂是导致这些方法实用性不足的主要困难[7-8]。为此,2004年Noblesse[9]提出了一种简化格林函数处理有航速下的波浪辐射绕射问题,但该方法尚未得到广泛应用,其中简化格林函数的实用算法是必须解决的第一个问题。
1 定常兴波简化格林函数
对于有航速船舶在简谐波中的辐射绕射问题,格林函数G(ξ; x)表示点x=(x, y, z)的移动脉动源在场点ξ=(ξ, η, ζ)产生的流动的速度势[10],在远方趋于零,满足泊松方程(1) 和Michell线性自由表面条件(2):
|
$
{G_{\xi \xi }} + {G_{\eta \eta }} + {G_{\zeta \zeta }} = \delta \left( {\xi - x} \right)\delta \left( {\eta - y} \right)\delta \left( {\zeta - z} \right)
$
|
(1) |
|
$
{G_\zeta } + F_n^2{G_{\xi \xi }} - {f^2}G + {\rm{i}}2\tau {G_\xi } - \varepsilon \left( {{F_n}{G_\xi } + {\rm{i}}fG} \right) = 0
$
|
(2) |
其中,
|
$
{F_n} = u/\sqrt {gL} ,f = \omega = \sqrt {L/g} ,\tau = {F_n}f = u\omega /g
$
|
式中:g为重力加速度,u为船速,L为参考长度(一般为船长),ω为船舶的遭遇频率。
根据参考长度L对ξ和x进行无因次化。X轴沿船长方向指向船艏,Z轴竖直向上,平面z=0即为自由表面。相关参数有如下定义:
|
$
\left\{ \begin{array}{l}
X = \xi - x\\
Y = \eta - y\\
Z = \zeta - z\\
{Z_ * } = \zeta + z
\end{array} \right.
$
|
(3) |
|
$
\left\{ \begin{array}{l}
h = \sqrt {{X^2} + {Y^2}} \\
r = \sqrt {{h^2} + {Z^2}} \\
{r_ * } = \sqrt {{h^2} + {{\left( {{Z_ * }} \right)}^2}} \\
{r_F} = \sqrt {{h^2} + {{\left( {{Z_ * } - F_n^2} \right)}^2}}
\end{array} \right.
$
|
(4) |
Noblesse在此基础上提出了船舶定常兴波简化格林函数:
|
$
4{\rm{ \mathsf{ π} }}G = - \frac{1}{r} + \frac{1}{{{r_ * }}} - \frac{2}{{{r_F}}} + {W^0}
$
|
(5) |
该格林函数满足泊松方程(1) 和辐射条件,并在远场满足Michell线性自由表面条件(2)。不同于一般的自由面格林函数能在整个域内满足自由表面条件,该格林函数在近场只能近似满足式(2)。式(5) 中W0为当τ=0时的波浪组分:
|
$
\begin{array}{*{20}{c}}
{{W^0} = \frac{1}{{F_n^2}}\int_{ - \infty }^\infty {{\rm{d}}t \cdot \frac{{\sqrt {T + 1} }}{T} \cdot A \cdot {{\rm{e}}^{Zk}} \cdot {\mathop{\rm Im}\nolimits} \left( {1 - \mathit{\bar \Theta }} \right){{\rm{e}}^{{\rm{i}}\phi }}} = }\\
{\frac{1}{{F_n^2}}\int_{ - \infty }^{ + \infty } {f\left( t \right){\rm{d}}t} }
\end{array}
$
|
其中:
|
$
\begin{array}{*{20}{c}}
{波数\;k = \frac{T}{{F_n^2}}}\\
{T = \sqrt {1 + {t^2}} }\\
{\phi = \left( {X + {\mathop{\rm sign}\nolimits} \left( t \right)Y\;R\sqrt {T - 1} } \right)\sqrt T /F_n^2}
\end{array}
$
|
误差函数由双曲函数tanh表示:
|
$
\begin{array}{*{20}{c}}
{\mathit{\Theta = }{\rm{tanh}}\left( {\frac{{\phi + {\rm{i}}V}}{\sigma }} \right) = }\\
{\frac{{\tanh \left( {2\phi /\sigma } \right) + {\rm{isin}}\left( {2V/\sigma } \right)/cos\left( {2\phi /\sigma } \right)}}{{1 + \cos \left( {2V/\sigma } \right)/cosh\left( {2\phi /\sigma } \right)}}}
\end{array}
$
|
(6) |
若1=N≤|2φ/σ|,则Θ≈sign(φ),当N≈10时,这种近似方式成立。
若φ=0,则Θ=-itanλ
其中
|
$
\begin{array}{*{20}{c}}
{\lambda = - {Z_ * }k/\sigma }\\
{V = \frac{{{Z_ * }k}}{{1 + {{\left( {{Z_ * }k} \right)}^4}/{{\left( {C\sigma } \right)}^4}}}}\\
{C = 2,\sigma = 2.5}
\end{array}
$
|
2 实用算法
将W0表示为式(7) 所示的积分形式,
|
$
\begin{array}{*{20}{c}}
{{W^0} = \frac{1}{{F_n^2}}\int_{ - A{\rm{\pi }}}^{A{\rm{\pi }}} {f\left( t \right){\rm{d}}t} = }\\
{\frac{1}{{F_n^2}}\sum\limits_{n = - A{\rm{\pi }}}^{A{\rm{\pi }} - 2A{\rm{\pi /}}M} {\frac{{A{\rm{\pi }}}}{M}\left[ {f\left( n \right) + f\left( {n + \frac{{2A{\rm{\pi }}}}{M}} \right)} \right]} = }\\
{I\left( {A,M} \right)}
\end{array}
$
|
(7) |
使用梯形法,在区间[-Aπ, Aπ]内,划分为M份,研究积分精度到达10-6时所需的积分限与积分区间的划分规律。因此W0可以表示为由参数A和M构成的函数I。
定义误差函数E1和E2,分别表示单一参数变化对积分精度的影响:
|
$
\begin{array}{l}
{E_1} = I\left( {{A_1},M} \right) - I\left( {{A_2},M} \right)\\
{E_2} = I\left( {A,{M_1}} \right) - I\left( {A,{M_2}} \right)
\end{array}
$
|
以点(x, y, z)=(0, 0, -0.02) 处的点源兴波为例,取Fn=0.3,在计算域ξ∈[-4, 1], η∈[-2, 2]内做收敛性分析,计算步长取0.05,区域内共8 000个计算点。令M0=100 A,分别计算当A依次递增时的E1,并取其绝对值按降序排列;当A<15时,误差较大,当A≥15时,结果如图 1所示。
由图 1可知,当积分区间为±25π时,计算域内每一点的精度都达到10-6。当区间划分个数依次递增时,分别计算每两种不同划分方式之间的相对误差并按与图 1相同的方式排列,结果如图 2所示。
由图 2可知,随着积分区间划分密度的增加,区域内达到计算精度的点的个数也逐渐增加,当积分区间被划分为6 000份时,计算域内每一点的精度都达到10-6。据此选择积分限为±25π,区间划分为6 000份,得到点源(0, 0, -0.02) 在自由表面z=0产生的稳定流动的速度势,如图 3所示。
另外,通过分析图 2中不满足精度要求的计算点在计算域中的分布状况,并与图 3进行对比知,误差点主要分布在计算域内无波的区域。由此推断对积分精度的影响因素中,积分限的选择占主导地位。
令ZS=|ζ+z|,当源点分布在不同水深时,积分限A为ZS的函数。由于当源点分布在自由表面上时,格林函数(5) 无法准确得到自由表面上与源点y坐标相同的场点的函数值。但在船舶兴波计算中,通常把源汇分布在物体水下的全部表面上,避免了该问题的存在。因此,对源点x∈[0.005, 0.05],场点ξ∈[0, 0.25],计算满足精度要求10-6的条件下W0以及W0的偏导数所需的积分限A与ZS的关系,结果如图 4所示。
由图 4可知,积分限A随Zs的变化规律可以表示为由幂指函数y=axb和常数函数y=C构成的分段函数。图 5~8分别表示W0、Wx0、Wy0、Wz0的积分参数函数拟合结果。其中标准差表示了所有数据与平均值的平均距离,其值越小表示数据集中在平局值附近。残差平方和与相关系数代表现有数据和方程式的拟合度,残差平方和越小、R2越接近1,说明拟合度越好。
由图 5得,格林函数G的积分规律如下:
|
$
{A_G}\left( {{Z_S}} \right) = \left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
0.463\;19 \times Z_S^{ - 0.965\;03}\\
4\\
3\\
2
\end{array}&\begin{array}{l}
0 < {Z_S} < 0.1\\
0.1 \le {Z_S} < 0.13\\
0.13 \le {Z_S} < 0.19\\
0.19 \le {Z_S} \le 0.25
\end{array}
\end{array}} \right.
$
|
(8) |
由图 6得,W0的x方向偏导数Wx0的积分规律如式(9) 所示:
|
$
{A_{{W_x}}}\left( {{Z_S}} \right) = \left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
0.541\;15 \times Z_S^{ - 0.998\;67}\\
4\\
3\\
2
\end{array}&\begin{array}{l}
0 < {Z_S} \le 0.12\\
0.12 < {Z_S} \le 0.16\\
0.16 < {Z_S} < 0.24\\
0.24 \le {Z_S} \le 0.25
\end{array}
\end{array}} \right.
$
|
(9) |
由图 7得,W0的y方向偏导数Wy0的积分规律如下:
|
$
{A_{{W_y}}}\left( {{Z_S}} \right) = \left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
0.537\;24 \times Z_S^{ - 1.023\;43}\\
4\\
3
\end{array}&\begin{array}{l}
0 < {Z_S} \le 0.13\\
0.13 < {Z_S} < 0.17\\
0.17 \le {Z_S} \le 0.25
\end{array}
\end{array}} \right.
$
|
(10) |
由图 8得,W0的z方向偏导数Wx0的积分规律如式(11) 所示:
|
$
{A_{{W_z}}}\left( {{Z_S}} \right) = \left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
0.726\;41 \times Z_S^{ - 1.032\;43}\\
5\\
4\\
3
\end{array}&\begin{array}{l}
0 < {Z_S} < 0.14\\
0.14 \le {Z_S} \le 0.17\\
0.17 < {Z_S} \le 0.22\\
0.22 < {Z_S} \le 0.25
\end{array}
\end{array}} \right.
$
|
(11) |
另外,考虑傅汝德数对积分参数的影响,使用二次多项式拟合,积分参数的变化规律可以表示为:
|
$
\begin{array}{l}
A\left( {{Z_S}} \right) = aZ_S^b = f\left( {{F_n}} \right) \cdot Z_S^b\\
\;\;\;\;\;\;\;\;\;\; = \left( {pF_n^2 + q{F_n} + r} \right) \cdot Z_S^b
\end{array}
$
|
(12) |
对W0、Wx0、Wy0、Wz0、f(Fn)分别表示为
|
$
{f_{{W^0}}}\left( {{F_n}} \right) = 3.839\;1F_n^2 + 0.338\;2{F_n} + 0.040\;6
$
|
|
$
{f_{W_x^0}}\left( {{F_n}} \right) = 4.872\;7F_n^2 + 0.398\;5{F_n} + 0.002\;4
$
|
|
$
{f_{W_y^0}}\left( {{F_n}} \right) = 6.165\;3F_n^2 + 0.197\;8{F_n} + 0.056\;8
$
|
|
$
{f_{W_z^0}}\left( {{F_n}} \right) = 7.684\;9F_n^2 + 0.093\;2{F_n} + 0.012\;8
$
|
不同傅汝德数下b的取值见表 1所示。
表 1(Tab. 1

表 1 不同傅汝德数下b的取值
Tab. 1 b for different Froude number
| Fn | W0 | Wx | Wy | Wz |
| 0.4 | -0.959 7 | -0.999 7 | -1.017 1 | -1.031 1 |
| 0.5 | -0.963 1 | -0.999 4 | -1.019 5 | -1.032 1 |
| 0.6 | -0.959 5 | -1.000 0 | -1.014 0 | -1.031 8 |
| 0.7 | -0.957 5 | -1.000 0 | -1.015 1 | -1.032 0 |
|
表 1 不同傅汝德数下b的取值
Tab.1 b for different Froude number |
3 与其他格林函数的对比
对于船舶在静水中匀速航行的问题,Noblesse(1981) 提出了如下所示的格林函数,它在整个流域内都满足Michell线性自由表面条件:
|
$
\begin{array}{*{20}{c}}
{4{\rm{ \mathsf{ π} }}F_n^2G = - \frac{{F_n^2}}{r} + \frac{{F_n^2}}{{{r_ * }}} + 2\left( {1 - {\rm{sign}}\left( X \right)} \right)\int\limits_{ - \infty }^\infty {{{\rm{e}}^{{Z_ * }k}}{\rm{Im}}{{\rm{e}}^{{\rm{i}}\mathit{\Phi }}}{\rm{d}}t} + }\\
{\frac{2}{{\rm{ \mathsf{ π} }}}\int\limits_{ - 1}^1 {{\rm{Im}}{{\rm{e}}^Z}{E_1}\left( Z \right)} }
\end{array}
$
|
根据该格林函数及上文得出的定常兴波简化格林函数的实用算法,考虑一个由一个点源和一个点汇在静水中匀速前进所产生的稳定流动。点源坐标为(0.5, 0, -0.02),点汇坐标为(-0.5, 0, -0.02)。源汇的强度q=Q/(uL2)取0.001。傅汝德数取0.3。计算域为ξ∈[-4, 1], η∈[-2, 2],计算步长为0.01。得到其在z=0平面产生的稳定流动的速度势如图 9所示。
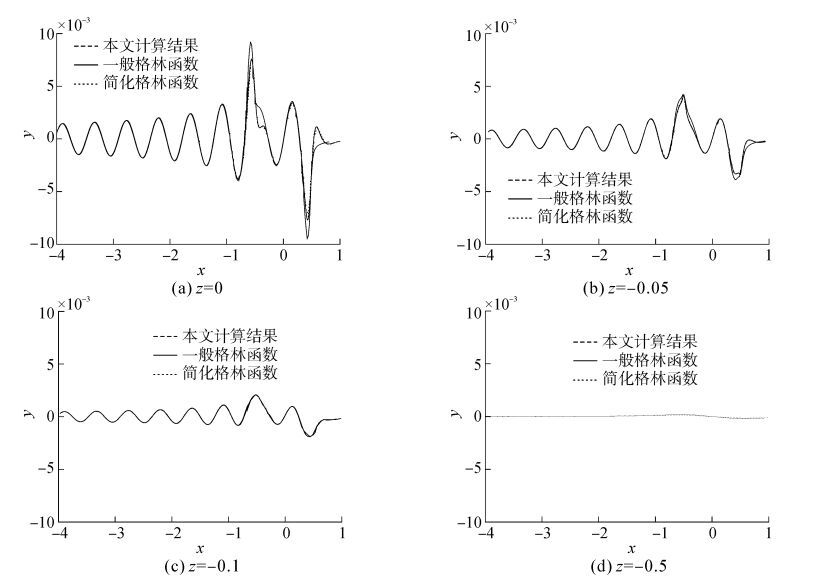
图 10、图 11表示在-4≤x≤1的范围内,源-汇所产生的流动的速度势分别沿y=0及z=0(自由表面)2个平面内的4条水平线的分布情况。并与文献[11]的结果进行对比。
4 结束语
1) 该算法保证了格林函数的计算精度达到10-6,并提高了计算效率,文中的算例共20万个计算点在个人计算机上(处理区core i5,主频3.20 GHz)耗时290 s,进一步凸显了该方法的准确性与快速性。2) 由于该方法在近场不完全满足自由表面条件,在进行船舶定常兴波计算时,需结合Rankine源进行流场区域划分来进行,通过控制面将流域分割为内域和外域,内外域分别采用Rankine源和自由面格林函数,进行耦合求解。










 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2017, Vol. 38
2017, Vol. 38


