2. 渤海造船厂集团有限公司 规划建设处, 辽宁 葫芦岛 125000
2. Planning And Construction Office, Bohai Shipyard Group Company Ltd., Huludao 125000, China
超空泡航行体是一种利用超空泡技术在水下大幅降低航行体和流体之间的阻力,从而提高航行速度的水下航行体[1]。其已成为目前可知的能够大幅提高水下或水面航行体速度的重要技术手段[2]。
超空泡航行体由于空泡自身特性的限制,使得其控制机构少、无法对空泡形态进行准确控制,因此超空泡航行体的控制技术一直是制约其发展的重要原因。
目前在超空泡航行体控制问题的研究方面,国内外学者具有代表性的成果如下:
Dzielski[3]和乌克兰流体科学院的Semennenko和Savchenko[4-6]等都给出了数学模型,其区别主要在受力分析的坐标系选取和某些参数的简略处理。其中Dzielski提出了一个垂直平面内的4状态2自由度模型,由于其形式规范、参数描述简洁,目前被众多文献引用,已经成为研究超空化航行体控制问题的基准模型。在超空泡航行体的控制器设计方面,Bálint Vanek、Gary Balas[7]等运用低数量级纵轴模型进行了相关研究,使用动力可逆原理设计了控制器,并进行了验证。特别值得强调的是DAVID、Gary Balas、ROGER[8]在水洞中建立了控制测试系统,针对超空泡航行体的缩比模型进行了空化器可控的试验研究。此外,Dzielski[9]介绍了超空泡航行体的纵向稳定控制问题,Xiaofeng Mao[10]采用LPV结合H∞对超空泡航行体的控制进行了研究。
国内方面,哈尔滨工业大学的于开平、魏英杰、王聪、邹望[11-13]等根据超空泡航行体的静态水洞试验数据和仿真分析,对超空泡航行体及超空泡进行了分析,并使用鲁棒控制等方法对其进行了控制研究。西北工业大学的范辉、张宇文[14]等采用圆判据切换方法设计了控制器。哈尔滨工程大学的张晓宇、韩云涛、赵新华、白涛[15-18]等采用突变控制、鲁棒控制、滑模控制、BTT、LPV等控制等方法对超空泡航行体的纵向运动控制进行了研究。
由上述资料可知,由于超空泡航行体实际测试费用太大,一般在实验室中多采用水洞试验对其进行研究。水洞试验最初只用于对超空泡的流体特性的研究,多为使用固定模型,研究多种环境下的空泡的流体力学特性,国外方面原苏联、美国等在此方面做了大量工作[1-2],国内哈尔滨工业大学[11]和西北工业大学[19]都使用水洞对静态超空泡缩比模型进行了试验,并取得了大量数据。这些研究在力学方面有着重要的意义,但在控制研究方面,更加关心的是在控制器的控制过程中的相关参数的变化及外部干扰的消除等问题,目前的成果均无法对控制规律进行精确验证。
本文针对这一问题,将空化器可控的超空泡航行体的缩比模型的水洞实验数据带入超空泡航行体的纵向运动控制研究中,使研究结果更加贴近于实际运动环境。
1 超空泡航行体的数学模型对超空泡航行体数学模型的推导,特别是纵向运动模型的推导,许多研究者从不同角度给出了其研究成果,目前使用较多的是Dzielski[3]给出的二自由度数学模型。
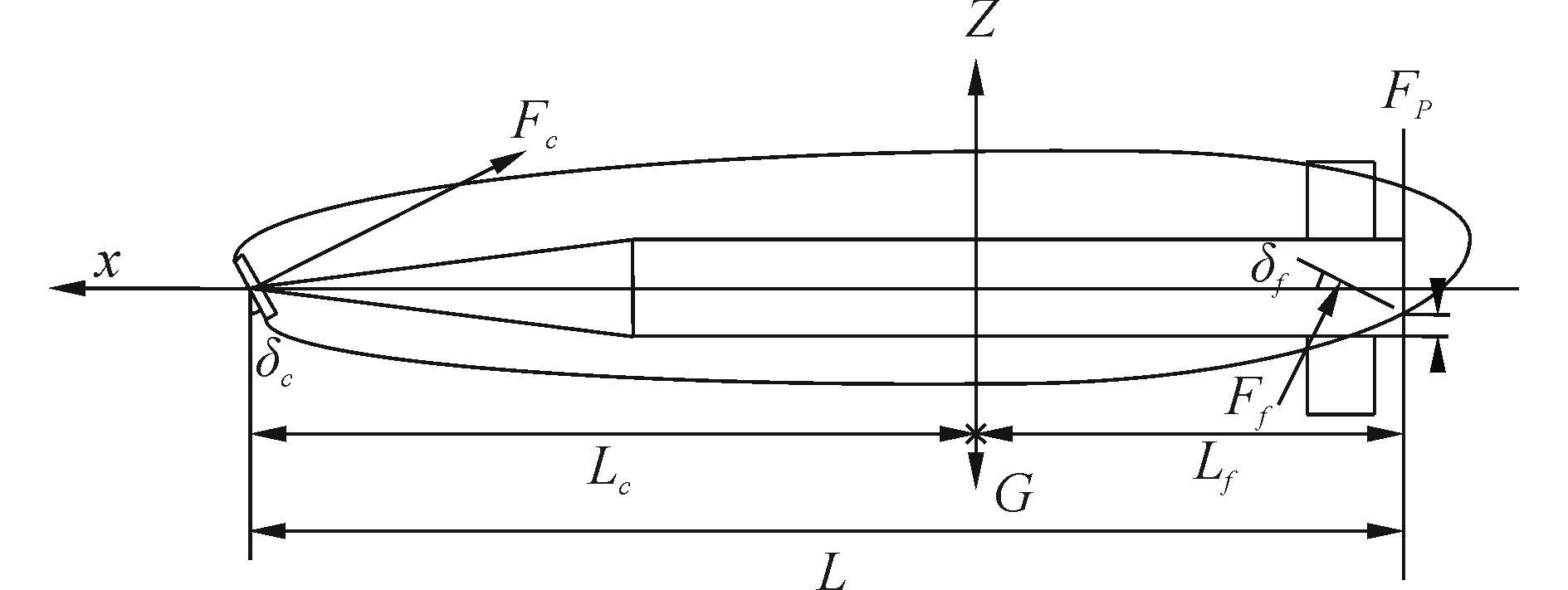
在Dzielski的数学模型中,将航行体在航行过程中的尾部探出空泡的状态做为稳定状态,其模型的外形和基本描述如图 1所示。模型前端为圆锥体,后为圆柱体,其长度比是1:2。运动体全长为Lh,Lc是空化器中心到模型重心的距离,h为航行体艉部探出空泡的长度。模型的控制机构为前端的圆盘形空化器和艉部的艉舵。
|
图 1 超空泡航行体示意图 Fig.1 Configuration of supercavitating vehicles |
在航行过程中,超空泡航行体大部分被空泡包裹, 仅头部空化器、艉舵和艉部一部分沾湿, Fc, G, Ff和Fp分别为空化器流体动力、重力、艉舵流体动力和滑行力,其受力分析见文献[3]。
根据超空泡航行体的受力及力学定律得到航行体的数学模型如下
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot z}} = \mathit{\boldsymbol{w}} - \mathit{\boldsymbol{V\theta }}\\ \mathit{\boldsymbol{\dot \theta }} = \mathit{\boldsymbol{q}}\\ \mathit{\boldsymbol{M}}\left[ \begin{array}{l} {\mathit{\boldsymbol{\dot w}}}\\ {\mathit{\boldsymbol{\dot q}}} \end{array} \right] = \mathit{\boldsymbol{A}}\left[ \begin{array}{l} \mathit{\boldsymbol{w}}\\ \mathit{\boldsymbol{q}} \end{array} \right] + \mathit{\boldsymbol{B}}\left[ \begin{array}{l} {\mathit{\boldsymbol{\delta }}_f}\\ {\mathit{\boldsymbol{\delta }}_{\rm{c}}} \end{array} \right] + {\mathit{\boldsymbol{F}}_g} + \left[ \begin{array}{l} 1/\left( {{m_l}L} \right)\\ 1/{m_l} \end{array} \right]{\mathit{\boldsymbol{F}}_p} \end{array} \right. $ | (1) |
| $ \begin{array}{*{20}{c}} {h = }\\ {\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0,\\ \left( {L/R} \right)\left| {hw/\mathit{\boldsymbol{V}}} \right|, \end{array}&\begin{array}{l} \left( {{R_c} - R} \right)/R > \left( {L/R} \right)\left| {kw/\mathit{\boldsymbol{V}}} \right|\\ 其他 \end{array} \end{array}} \right.} \end{array} $ | (2) |
| $ {\mathit{\boldsymbol{a}}_p} = \left\{ \begin{array}{l} {\tan ^{ - 1}}\left( {\frac{\mathit{\boldsymbol{w}}}{\mathit{\boldsymbol{V}}}} \right) - {\tan ^{ - 1}}\left( {\frac{{{{\mathit{\boldsymbol{\dot R}}}_c}}}{\mathit{\boldsymbol{V}}}} \right),\;\;\;\;\frac{\mathit{\boldsymbol{w}}}{\mathit{\boldsymbol{V}}} > 0\\ {\tan ^{ - 1}}\left( {\frac{\mathit{\boldsymbol{w}}}{\mathit{\boldsymbol{V}}}} \right) + {\tan ^{ - 1}}\left( {\frac{{{{\mathit{\boldsymbol{\dot R}}}_c}}}{\mathit{\boldsymbol{V}}}} \right),\;\;\;\;其他 \end{array} \right. $ | (3) |
| $ {\mathit{\boldsymbol{F}}_p} = {\rm{ \mathsf{ π} \mathsf{ ρ} }}\mathit{\boldsymbol{R}}_c^2{\mathit{\boldsymbol{V}}^2}\left( {\frac{{1 + h}}{{1 + 2h}}} \right)\left( {1 - {{\left( {\frac{{{R_c} - R}}{{hR + {R_c} - R}}} \right)}^2}} \right){a_p} $ | (4) |
式中:模型的状态变量与控制变量分别为z(航行体纵向位移), w(航行体垂直方向速度), θ(航行体俯仰角), q(航行体俯仰角速度);系统输入为空化器转角δc和艉舵偏转角δf。其中,V是航行体水平方向速度,假定其为恒定;M、A、B为受力平衡方程的相应系数矩阵,Fg为重力矩阵,L为航行体长度,m1为航行体的质量,R为航行体半径,Rc为航行体艉部的空泡半径,
经处理,令x=[z w θ q]T,u=[δf δc]T得到状态空间描述模型如下
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}} + \mathit{\boldsymbol{G}} + \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{F}}_p}\\ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Cx}} + \mathit{\boldsymbol{Du}} \end{array} \right. $ | (5) |
目前的水洞实验多用于测试固定模型(模型本身固定且空化器的角度也固定)的流体动力学参数,但在控制中,更加关心的是控制机构(空化器和艉翼)运动时,各种因素是否会对航行体的状态产生不可预期的改变进而影响航行体的稳定。由于空化器作为超空泡航行体的主要控制机构,所以空化器在运动时的空泡形态变化对超空泡航行体的控制来说更为重要,特别是随空化器转动而产生的空泡形态的变化更是超空泡航行体运动控制中必须取得的要素。
本文使用空化器可控的超空泡航行体的缩比模型进行水洞试验,得到在空化器的在约±30°内的空化数和空泡形态变化数据,通过录像采集空化器在不同时刻的偏转角和空泡形态的对应值,以这些数据为基础,修正超空泡航行体在运动过程中的对应空化器偏转时的空泡形态,进而修正滑行力(默认航行体艉部探出空泡时不影响空泡形态)的模型,得到的模型较理想模型在某一类环境中更为贴近实际环境,更为有指导意义。
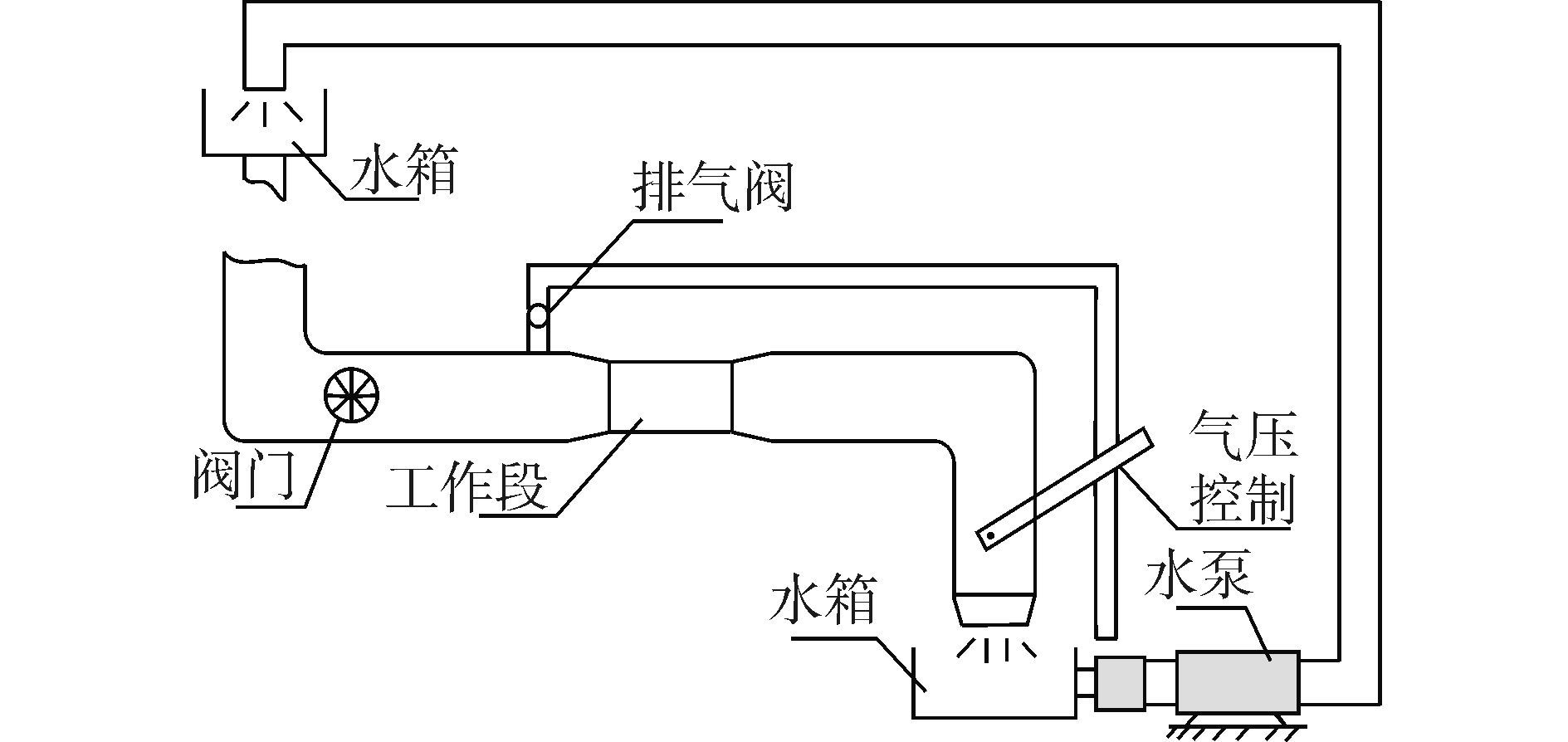
本次实验采用重力式水洞,重力式水洞的优点是其结构简单,能够提供速度较为稳定的水流,受其他设备的影响小,缺点是其有效工作时间少,两次试验间隔时间长。本次实验所用重力式水洞的结构图如图 2所示。
|
图 2 重力水洞结构 Fig.2 The assumption diagram of gravity water tunnel |
整个水洞结构图如图 3所示。包括重力式水洞平台、超空泡航行体模型、伺服电机控制系统、充气系统、流量检测控制系统、压力检测系统、高速摄像机记录系统。本次试验的缩比模型的空化器为圆盘空化器,直径20 mm,模型长度为220 mm;设定稳定时的水流速度为9.69 m/s,设定充气空化数为0.1(由外部充气系统根据设定充气率进行充气,得到预设充气空化数)。试验中,空化器上端和底端分别引出两根钢丝缆线,穿过其自身基座后与伺服电机轴相连,由伺服控制系统上位机发送指令,对空化器舵机的偏转角进行控制。试验中测量两个压力数值,一个由固定在水洞盖板上的压力传感器采集的水洞内压力;一个由连接在模型表面的软管引出到模型艉部,由模型艉部的小型压力传感器采集模型表面的压力,其在超空泡形成时实际是泡内压力;这2个压力传感器的值由动态压力数据采集系统采集。

|
图 3 实验环境示意图 Fig.3 Scheme of experimental environment |
本次实验采用伺服电机对水流状态下的空化器进行控制,使空化器以一个固定频率和振幅摆动,实时采集超空泡的泡内、外压力并对试验现象进行录像分析。实验首先在水流静止时开始充气,同时启动压力测试系统和录像系统,当气量稳定时启动水流(打开阀门),水流速度稳定后,开始启动电机驱动空化器转动,并同时开始计算试验时间,实验持续时间一般为30 s,之后水流速度减缓直至停止,所有设备停止,并提取实验数据。
试验中模型被完整空泡包裹如图 4所示。

|
图 4 水洞实验示意图 Fig.4 Scheme of water tunnel experiment |
图 5为空泡偏移与空化器偏角之间的录像记录。

|
图 5 空泡形态与空化器偏转角 Fig.5 Supercavity shape and cavitator angle |
由于钢丝弹性导致的机械误差原因,上表的图中显示角度为图片测量值,之后的空化器角度和空泡形态值均由图片进行测量给出。
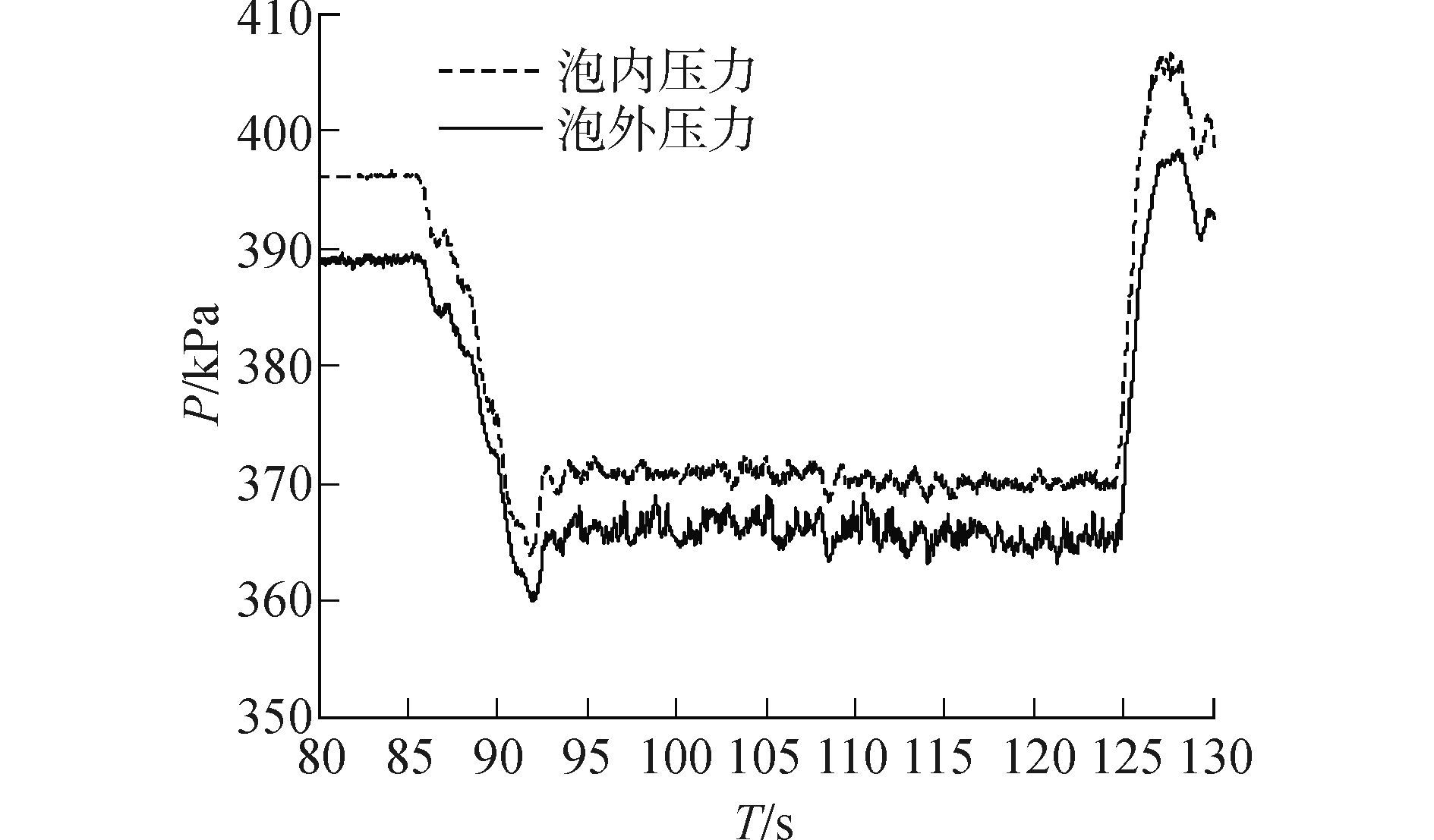
图 6为测量得到的整个实验过程的空泡内、外的压力数据。
|
图 6 超空泡内、外压力 Fig.6 Pressure of inner and outside supercavity |
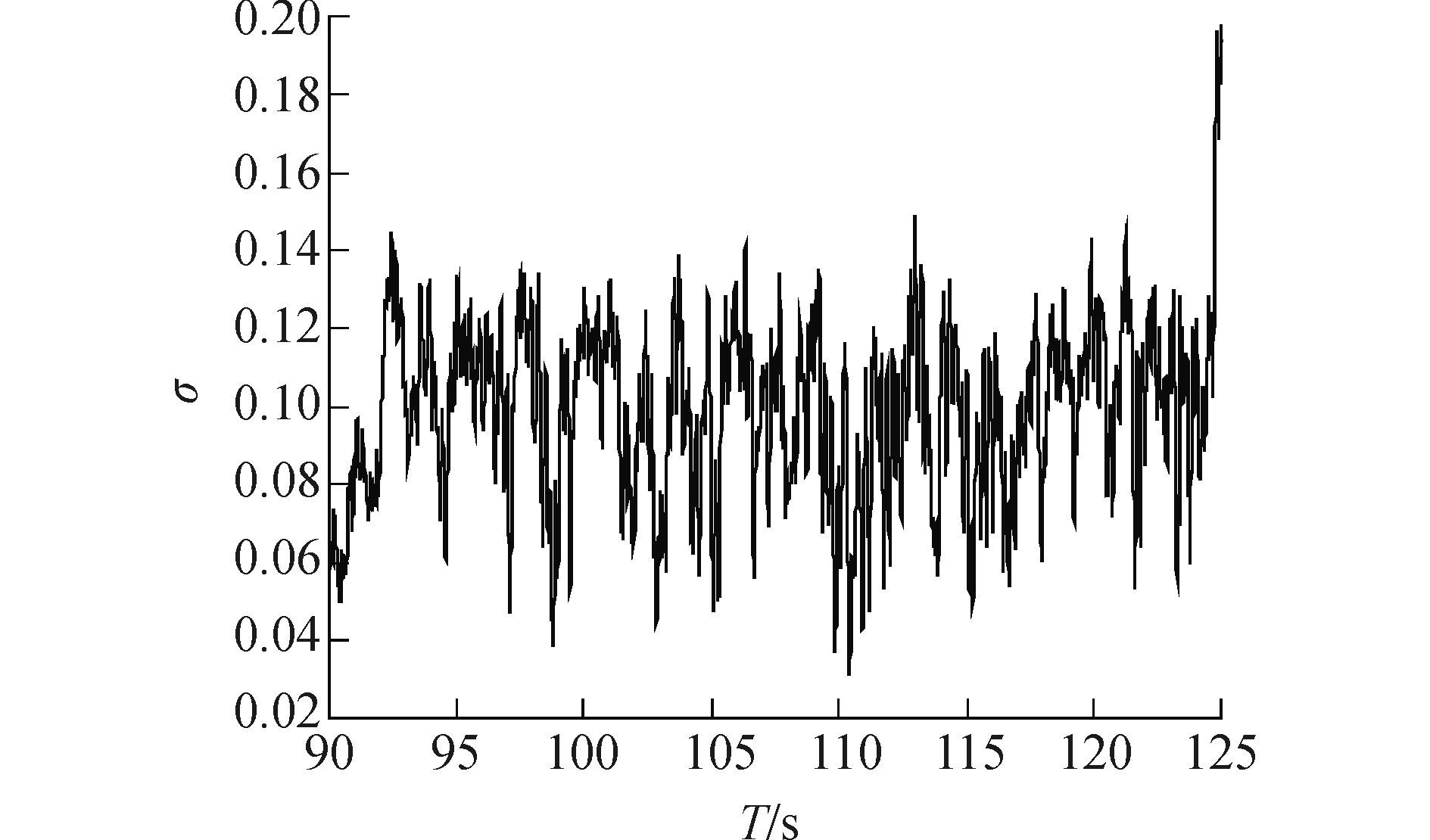
图 7为根据泡内的压力pc和泡外的压力p∞求得的空化数,空化数的计算公式如下
|
图 7 空化数 Fig.7 Cavitation number |
| $ \sigma = \frac{{2\left( {{p_\infty } - {p_c}} \right)}}{{\rho {\mathit{\boldsymbol{V}}^2}}} $ | (6) |
为准确求取空化数,泡外压力需考虑水洞舱盖与航行体模型表面的高度差0.2 m导致的压力差,将其与传感器取得的水洞盖板处压力相加,转换为实际泡外的压力。由于本次实验为准确取得泡内压力,选用一款小型压力传感器,将其安装在模型艉部,导致二者不是同一款压力传感器,因此在处理数据时应首先进行测试对准。
本次实验只对压力稳定的95~120 s时间段的数据进行分析。如图 5可见,当水流速度加快到预定值的时候,空泡逐渐成型,泡内外的压力同时减小,空泡成型后,泡外压力稳定在270 kPa左右,泡内压力稳定在266 kPa左右,重力水洞的水流速度存在一定不确定性,但根据数据可见在95~120 s为试验最为稳定的阶段,从求取的空化数的数值可知,其在稳定段的数值保持在0.1左右,符合预期。
3 超空泡航行体模型的修正由于条件所限,本文只针对某种实际环境中的空泡形态变化对超空泡航行体的控制进行研究,因此本文的模型修正只是针对此次水洞实验模拟的环境进行的,共进行3次同条件下的空化器动态实验,其数据基本类似。由于本文只考虑滑行力的变化,因此这里只提取可能产生滑行力的超空泡航行体艉部(模型以空化器中心为零点,沿中轴线的0.2 m处)的空泡半径(下部半径),具体可见表 1中的图片,因此文中只采用第二章中的数据对模型进行修正。
在Dzielski[3, 14]的模型中,航行体的空化器直径与实验中基本近似,且本次实验仅针对空化器动态运动时的空泡形态进行研究,所以本文直接引用Dzielski的模型,仅对其中的空泡形态公式根据实验数据进行修正。
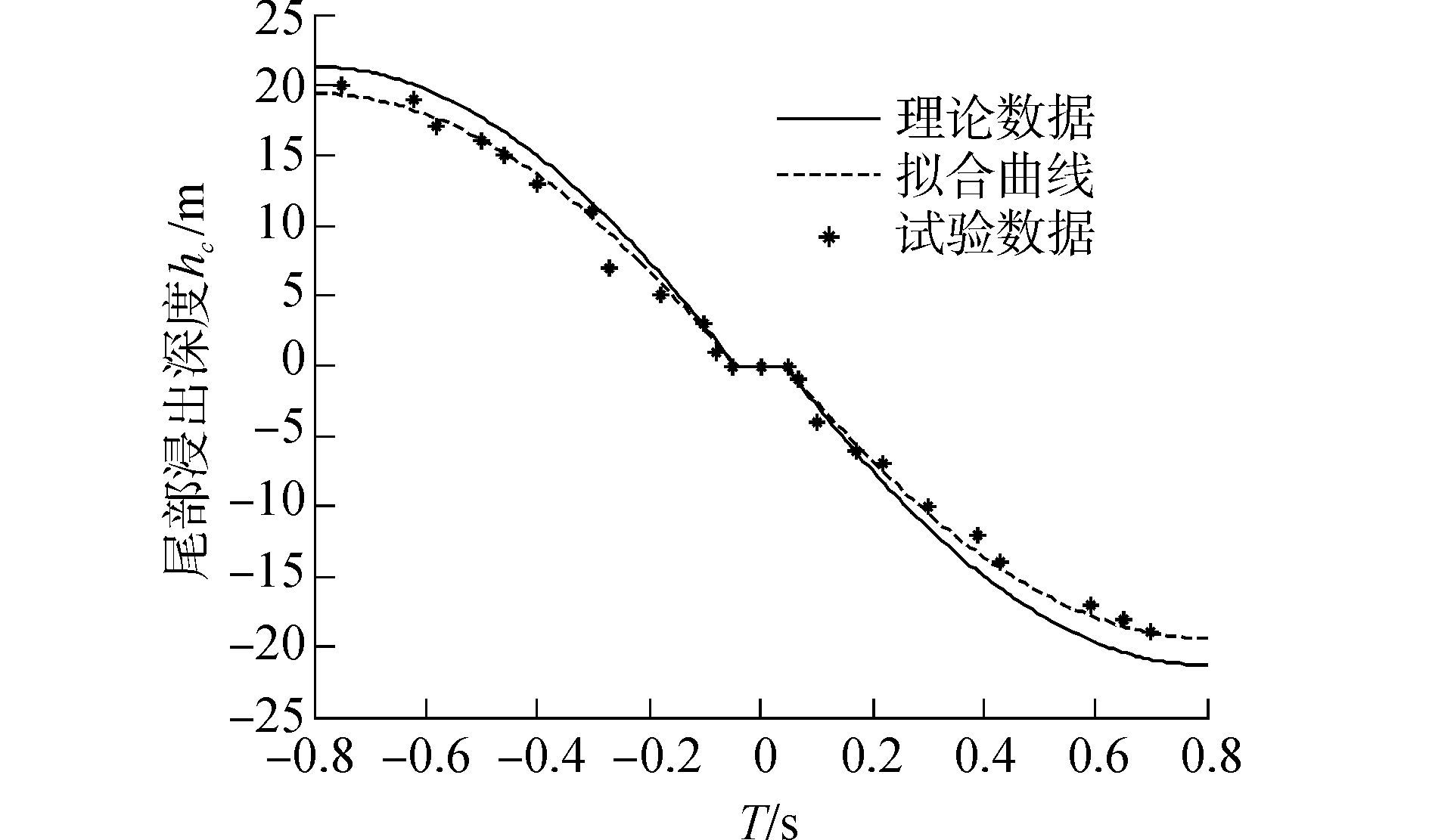
根据空化器与稳态空泡形态之间的关系公式[4-5]计算出本实验和Dzielski的模型之间的空化数和速度对应的艉部形态间的关系,然后等效得出与Dzielski的模型等效的实际空泡形态,并计算艉部浸出深度hc。然后在Matlab环境中运用最小二乘法绘制出hc和空化器偏转角δc的对应拟合关系曲线,再与理论计算所得的超空泡模型的浸入深度h随空化器偏转角δc变化的曲线对比。二者对比结果如图 8所示。
|
图 8 hc的理论曲线与实验拟合曲线 Fig.8 Comparison of the curves of hc of theory data and experiment data |
通过拟合曲线的对比情况,可得到hc(δc)=k·h(δc),其中k近似等于0.91,可对已建立的超空泡航行体的动力学模型做出如下改进:
| $ \begin{array}{*{20}{c}} {{h_c} = }\\ {\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {0,}\\ {\left( {L/R} \right)\left| {k\mathit{\boldsymbol{w}}/\mathit{\boldsymbol{V}}} \right|,} \end{array}}&\begin{array}{l} \left( {{R_c} - R} \right)/R > \left( {L/R} \right)\left| {kw/\mathit{\boldsymbol{V}}} \right|\\ 其他 \end{array} \end{array}} \right.} \end{array} $ | (7) |
式中k=0.91为常量,其他变量定义同公式(2)。相应原模型中滑行力在z轴上的分量Fp中的h变为hc,变化后的滑行力在z轴上的分量为
| $ \begin{array}{l} {F_p} = {\rm{ \mathsf{ π} }}\rho \mathit{\boldsymbol{R}}_c^2{\mathit{\boldsymbol{V}}^2}\sin \mathit{\boldsymbol{\alpha }}\cos \mathit{\boldsymbol{\alpha }} \cdot \\ \left( {\frac{{1 + h}}{{1 + 2h}}} \right)\left( {1 - {{\left( {\frac{{{R_c} - R}}{{hR + {R_c} - R}}} \right)}^2}} \right){a_p} \end{array} $ | (8) |
由于前文所述数学模型为简化后的模型,简化模型包括许多三角量和非线性量,若考虑得到的空化数是由传感器数据计算得来并计算噪声,则这些因素都将导致对航行体进行纵向运动控制和稳定性分析时出现较大的误差,所以本文对数学模型进一步变换,利用LPV方法为超空泡航行体设计控制器。基于LPV系统的控制方法,因其能够在理论上保证系统的鲁棒性及全局稳定性,并且克服了传统变增益控制存在的诸多缺点,近年来发展迅速[10]。
4.2 系统模型变换由前文所建立的数学模型可知,对于超空泡航行体的动力学方程,其右半部分只与w和q有关,对运动学方程,其右半部分存在3个状态变量z、θ和w,所以,两子系统级联这一形式可由原系统转换而成。为此,取η=[z θ]T,ζ=[w q]T。令A2=MI-1AI,B=MI-1BI,模型中的矩阵定义为如下形式:
| $ {\mathit{\boldsymbol{M}}_I} = \left[ {\begin{array}{*{20}{c}} {1/{m_l}}\\ {1/{m_l}L} \end{array}} \right]{\mathit{\boldsymbol{D}}^{ - 1}},{\mathit{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} 0&{ - \mathit{\boldsymbol{V}}}\\ 0&0 \end{array}} \right] $ | (9) |
式中,B和D为模型(5) 中的矩阵。
为使等式更加简略,这里令G=MI-1FgΛ,控制输入为u=[δf δc]T。
处于运动过程中的超空泡航行体,其受到系统内、外的噪声和扰动的影响是不可避免地。考虑存在噪声干扰时,系统模型(5) 可表示为如下形式:
| $ \mathit{\boldsymbol{\dot \eta = }}{\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{\eta }} + \mathit{\boldsymbol{\zeta }} $ | (10) |
| $ \mathit{\boldsymbol{\dot \zeta }} = {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{\zeta + Bu + G + DF}}_{pc}^\Lambda + {\mathit{\boldsymbol{B}}_\omega }\mathit{\boldsymbol{\omega }} $ | (11) |
式中Bω=I2表示的是噪声驱动矩阵,ω∈R2×1为噪声向量且满足ω(t)∈L2(0, ∞)。
由于按照给定指令进行跟踪控制并稳定运行是本文的仿真的目的之一,所以将式(10)、(11) 进一步转化。设zd、wd、θd和qd分别为给定的航行体的纵向位移、纵向速度、航行体俯仰角和俯仰角速度指令。令误差向量为ηe=η-ηd,ζe=ζ-ζd,其中ηd=[zd θd]T、ζd=[wd qd]T,代入(10)、(11) 替换式中的η和ζ,得到
| $ {{\mathit{\boldsymbol{\dot \eta }}}_{\rm{e}}}\mathit{\boldsymbol{ = }}{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{\eta }}_{\rm{e}}} + {\mathit{\boldsymbol{\zeta }}_{\rm{e}}} $ | (12) |
| $ {{\mathit{\boldsymbol{\dot \zeta }}}_{\rm{e}}} = {\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{\zeta }}_{\rm{e}}}\mathit{\boldsymbol{ + Bu + G + DF}}_{pc}^\Lambda + {\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{\zeta }}_d} - {{\mathit{\boldsymbol{\dot \zeta }}}_d} + {\mathit{\boldsymbol{B}}_\omega }\mathit{\boldsymbol{\omega }} $ | (13) |
为了得到反演跟踪模型[20],做如下变换:
| $ {{\mathit{\boldsymbol{\dot \eta }}}_{\rm{e}}} = \left( {{\mathit{\boldsymbol{A}}_1} - {\mathit{\boldsymbol{K}}_1}} \right){\mathit{\boldsymbol{\eta }}_{\rm{e}}} + {\mathit{\boldsymbol{\alpha }}_{\rm{e}}} $ | (14) |
式中:αe定义为
| $ {\mathit{\boldsymbol{\alpha }}_{\rm{e}}} = {\mathit{\boldsymbol{\zeta }}_{\rm{e}}} + {\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{\eta }}_{\rm{e}}} $ | (15) |
将αe作为新的状态变量,如此一来,新的跟踪模型变成了关于状态变量向量ηe和αe的方程,为了得到关于αe的状态方程,将式(15) 对时间求导得
| $ \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{v}}_{\rm{e}}} = \left( {{\mathit{\boldsymbol{K}}_1} + {\mathit{\boldsymbol{A}}_2}} \right){\mathit{\boldsymbol{\alpha }}_{\rm{e}}} + \mathit{\boldsymbol{Bu + \rho + DF}}_{pc}^\Lambda + {\mathit{\boldsymbol{B}}_\omega }\mathit{\boldsymbol{\omega }} $ | (16) |
其中,
| $ \begin{array}{l} \mathit{\boldsymbol{\rho = }}{\mathit{\boldsymbol{K}}_1}\left( {{\mathit{\boldsymbol{A}}_1} - {\mathit{\boldsymbol{K}}_1}} \right){\mathit{\boldsymbol{\eta }}_\varepsilon } + \left( {{\mathit{\boldsymbol{A}}_1}{{\mathit{\boldsymbol{\dot \eta }}}_\delta } - {{\mathit{\boldsymbol{\ddot \eta }}}_\delta }} \right) - {\mathit{\boldsymbol{A}}_2}\left( {{\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{\eta }}_\varepsilon } + } \right.\\ \;\;\;\;\;\;\left. {{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{\eta }}_\delta } - {{\mathit{\boldsymbol{\dot \eta }}}_\delta }} \right) + \mathit{\boldsymbol{G}} \end{array} $ |
综上所述,整理后的跟踪模型只与状态变量向量ηe和αe有关,其形式如下
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\eta }}{\mathit{\boldsymbol{v}}_{\rm{e}}} = \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{\eta }}_{\rm{e}}} + {\mathit{\boldsymbol{\alpha }}_{\rm{e}}}\\ {{\mathit{\boldsymbol{\dot \alpha }}}_{\rm{e}}} = \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{\alpha }}_{\rm{e}}} + \mathit{\boldsymbol{Bu + \rho + DF}}_{{\rm{pc}}}^\Lambda + {\mathit{\boldsymbol{B}}_\omega }\mathit{\boldsymbol{\omega }} \end{array} \right. $ | (17) |
式中:M=A1-K1是Hurwitz矩阵,N=K1+A2。
由滑行力公式并结合文献[5, 7]中所述,能够判断出滑行力是纵向速度w的函数,即滑行力可以改成如下形式:
| $ \mathit{\boldsymbol{F}}_{{\rm{pc}}}^\Lambda = \left\{ \begin{array}{l} \frac{{\mathit{\boldsymbol{F}}_{{\rm{pc}}}^\Lambda }}{\mathit{\boldsymbol{w}}}\mathit{\boldsymbol{w}},\;\;\;\;\;w \ne 0\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;w = 0 \end{array} \right. $ | (18) |
令时变参数
| $ \mathit{\boldsymbol{p}}\left( \mathit{\boldsymbol{w}} \right) = \left\{ \begin{array}{l} \mathit{\boldsymbol{F}}_{{\rm{pc}}}^\Lambda /w,\;\;\;\;w \ne 0\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;w = 0 \end{array} \right. $ | (19) |
可知时变参数p是有界的。
假设系统所有状态均为可观测,则时变参数也实时可测。站在航行体运动稳定性的角度,令期望的纵向速度wd=0,从而有w=w-wd=we,则
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot \alpha }}}_{\rm{e}}} = \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{\alpha }}_{\rm{e}}} + \mathit{\boldsymbol{Bu + \rho }} + \mathit{\boldsymbol{p}}\left( \mathit{\boldsymbol{w}} \right)\mathit{\boldsymbol{D}}\left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]{\mathit{\boldsymbol{\alpha }}_e} - }\\ {\mathit{\boldsymbol{p}}\left( \mathit{\boldsymbol{w}} \right)\mathit{\boldsymbol{D}}\left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]{\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{\eta }}_{\rm{e}}} + {\mathit{\boldsymbol{B}}_\omega }\mathit{\boldsymbol{\omega }}} \end{array} $ |
简化写成如下形式:
| $ {{\mathit{\boldsymbol{\dot \alpha }}}_e} = \mathit{\boldsymbol{N}}\left( \mathit{\boldsymbol{w}} \right){\mathit{\boldsymbol{\alpha }}_e} + \mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{w}} \right){\mathit{\boldsymbol{\eta }}_e} + \mathit{\boldsymbol{Bu}} + \mathit{\boldsymbol{\rho }} + {\mathit{\boldsymbol{B}}_\omega }\mathit{\boldsymbol{\omega }} $ | (20) |
其中
| $ \begin{array}{l} \mathit{\boldsymbol{N}}\left( \mathit{\boldsymbol{w}} \right) = \mathit{\boldsymbol{N}} + \mathit{\boldsymbol{p}}\left( \mathit{\boldsymbol{w}} \right)\mathit{\boldsymbol{D}}\left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]\\ \mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{w}} \right) = - \mathit{\boldsymbol{p}}\left( \mathit{\boldsymbol{w}} \right)\mathit{\boldsymbol{D}}\left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]{\mathit{\boldsymbol{K}}_1} \end{array} $ |
因为非线性的滑行力存在于系统中,想要进行控制器设计而直接采用线性系统理论是不可行的。所以进行控制器设计时,根据式(20) 可得到下式:
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{B}}^{ - 1}}\left( { - \mathit{\boldsymbol{N}}\left( \mathit{\boldsymbol{w}} \right){\mathit{\boldsymbol{\alpha }}_e} - \mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{w}} \right){\mathit{\boldsymbol{\eta }}_e} - \mathit{\boldsymbol{\rho + r}}} \right) $ | (21) |
令
| $ \mathit{\boldsymbol{u}} = - {\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{\rho }} - {\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{\eta }}_{\rm{e}}} - {\mathit{\boldsymbol{K}}_3}{\mathit{\boldsymbol{\alpha }}_{\rm{e}}} $ | (22) |
使得闭环系统(17) 是内部稳定的,并且使其在零初始条件下,具备给定的H∞扰动抑制水平γ。
为此定义受控输出o和目标函数Toω分别为
| $ \mathit{\boldsymbol{o}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_1}{\eta _{\rm{e}}} + {\mathit{\boldsymbol{D}}_1}\mathit{\boldsymbol{\omega }}}\\ {{\mathit{\boldsymbol{C}}_2}{\mathit{\boldsymbol{\alpha }}_{\rm{e}}} + {\mathit{\boldsymbol{D}}_2}\mathit{\boldsymbol{\omega }}} \end{array}} \right] $ | (23) |
| $ {\mathit{\boldsymbol{T}}_{o\omega }} = \int_0^\infty {\left( {{\mathit{\boldsymbol{o}}^{\rm{T}}}\mathit{\boldsymbol{o}} - {\mathit{\boldsymbol{\gamma }}^2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }}} \right){\rm{d}}t} $ | (24) |
式中:C1=C2=D1=D2=I2。对于给定的γ>0,把从噪声ω到受控输出o的传递函数Toω的H∞范数约束记做‖Toω‖<γ,因为H∞范数在时域内与诱导2范数等价,所以采用如下方法进行表示:
| $ {\left\| {\mathit{\boldsymbol{o}}\left( t \right)} \right\|_2} < \gamma {\left\| {\mathit{\boldsymbol{w}}\left( t \right)} \right\|_2},\forall \mathit{\boldsymbol{\omega }}\left( t \right) \in {L_2}\left( {0,\infty } \right) $ | (25) |
然后应用Lyapunov理论进行控制器设计,定义备选Lyapunov函数为
| $ \mathit{\boldsymbol{V}}\left( {{\mathit{\boldsymbol{\eta }}_{\rm{e}}},{\mathit{\boldsymbol{\alpha }}_{\rm{e}}}} \right) = \mathit{\boldsymbol{\eta }}_{\rm{e}}^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\eta }}_{\rm{e}}} + \mathit{\boldsymbol{\alpha }}_{\rm{e}}^{\rm{T}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{\alpha }}_{\rm{e}}} $ | (26) |
式中:对称矩阵P>0,Q>0。对上式沿着系统(17) 的轨迹求导,并将式(18) 代入得
| $ \begin{array}{l} {\mathit{\boldsymbol{o}}^{\rm{T}}}\mathit{\boldsymbol{o}} - {\mathit{\boldsymbol{\gamma }}^2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }} + \mathit{\boldsymbol{\dot V}}\left( {{\mathit{\boldsymbol{\eta }}_{\rm{e}}},{\mathit{\boldsymbol{\alpha }}_{\rm{e}}}} \right) = \\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\eta }}_{\rm{e}}}}\\ {{\mathit{\boldsymbol{\alpha }}_{\rm{e}}}}\\ \mathit{\boldsymbol{\omega }} \end{array}} \right]^{\rm{T}}}\underbrace {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{11}} + \mathit{\boldsymbol{C}}_1^{\rm{T}}{\mathit{\boldsymbol{C}}_1}}&{{\mathit{\boldsymbol{f}}_{12}}}&{\mathit{\boldsymbol{C}}_1^{\rm{T}}{\mathit{\boldsymbol{D}}_1}}\\ * &{{\mathit{\boldsymbol{f}}_{22}} + \mathit{\boldsymbol{C}}_2^{\rm{T}}{\mathit{\boldsymbol{C}}_2}}&{\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{B}}_\omega } + \mathit{\boldsymbol{C}}_2^{\rm{T}}{\mathit{\boldsymbol{D}}_2}}\\ * & * &{\mathit{\boldsymbol{D}}_1^{\rm{T}}{\mathit{\boldsymbol{D}}_1} + \mathit{\boldsymbol{D}}_2^{\rm{T}}{\mathit{\boldsymbol{D}}_2} - {\gamma ^2}\mathit{\boldsymbol{I}}} \end{array}} \right]}_\Xi \\ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\eta }}_{\rm{e}}}}\\ {{\mathit{\boldsymbol{\alpha }}_{\rm{e}}}}\\ \mathit{\boldsymbol{\omega }} \end{array}} \right] \end{array} $ | (27) |
式中:矩阵中的各元素分别定义为
| $ \begin{array}{*{20}{c}} {{\phi _{11}} = \mathit{\boldsymbol{M}}_I^{\rm{T}}\mathit{\boldsymbol{P + P}}{\mathit{\boldsymbol{M}}_I}}\\ {{\phi _{12}} = \mathit{\boldsymbol{P}} + {{\left[ {\mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{w}} \right) - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}_2}} \right]}^{\rm{T}}}\mathit{\boldsymbol{Q}}}\\ {{\phi _{22}} = {{\left[ {\mathit{\boldsymbol{N}}\left( \mathit{\boldsymbol{w}} \right) - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}_3}} \right]}^{\rm{T}}}\mathit{\boldsymbol{Q}} + \mathit{\boldsymbol{Q}}\left[ {\mathit{\boldsymbol{N}}\left( \mathit{\boldsymbol{w}} \right) - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}_3}} \right]} \end{array} $ |
由此,若定义于式(27) 中Ξ<0,那么有Toω<0,即在零初始条件下,闭环系统具有给定的H∞扰动抑制水平γ。根据前文及文献[21]提到的schur补引理,有Ξ<0成立等价于下式成立:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{11}}}&{{\mathit{\boldsymbol{f}}_{12}}}&0&{\mathit{\boldsymbol{C}}_1^{\rm{T}}}&0\\ * &{{\mathit{\boldsymbol{f}}_{22}}}&{\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{B}}_\omega }}&0&{\mathit{\boldsymbol{C}}_2^{\rm{T}}}\\ * & * &{ - {\mathit{\boldsymbol{\gamma }}^2}\mathit{\boldsymbol{I}}}&{\mathit{\boldsymbol{D}}_1^{\rm{T}}}&{\mathit{\boldsymbol{D}}_2^{\rm{T}}}\\ * & * & * &{ - \mathit{\boldsymbol{I}}}&0\\ * & * & * & * &{ - \mathit{\boldsymbol{I}}} \end{array}} \right] < 0 $ | (28) |
由于式(28) 含有决策变量的非线性项,无法直接利用Matlab中的LMI工具箱进行控制器设计,因此采用合同变换,对上式进行变换,通过左乘diag{P-1, Q-1, I, I, I}和右乘diag{P-1, Q-1, I, I, I}得到:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_{11}}}&{{\mathit{\boldsymbol{X}}_{12}}}&0&{{\mathit{\boldsymbol{L}}_1}\mathit{\boldsymbol{C}}_1^{\rm{T}}}&0\\ * &{{\mathit{\boldsymbol{X}}_{22}}}&{{\mathit{\boldsymbol{B}}_\omega }}&0&{{\mathit{\boldsymbol{L}}_2}\mathit{\boldsymbol{C}}_2^{\rm{T}}}\\ * & * &{ - {\gamma ^2}\mathit{\boldsymbol{I}}}&{\mathit{\boldsymbol{D}}_1^{\rm{T}}}&{\mathit{\boldsymbol{D}}_2^{\rm{T}}}\\ * & * & * &{ - \mathit{\boldsymbol{I}}}&0\\ * & * & * & * &{ - \mathit{\boldsymbol{I}}} \end{array}} \right] < 0 $ | (29) |
为方便表示令L1=P-1, L2=Q-1,则矩阵中的各元素分别定义为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_{11}} = {\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{ + M}}{\mathit{\boldsymbol{L}}_1}}\\ {{\mathit{\boldsymbol{X}}_{12}} = {\mathit{\boldsymbol{L}}_2} + {\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{H}}^{\rm{T}}}\left( \mathit{\boldsymbol{w}} \right) - \mathit{\boldsymbol{L}}_3^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{X}}_{22}} = {\mathit{\boldsymbol{L}}_2}{\mathit{\boldsymbol{N}}^{\rm{T}}}\left( \mathit{\boldsymbol{w}} \right) + \mathit{\boldsymbol{N}}\left( \mathit{\boldsymbol{w}} \right){\mathit{\boldsymbol{L}}_2} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{L}}_4} - \mathit{\boldsymbol{L}}_4^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}} \end{array} $ |
注意到式(29) 所示的矩阵不等式虽然是线性的,但是由于矩阵中含有依赖于时变参数变化的项N(w)和H(w)H(w),所以LMI对应的决策变量的约束条件有无穷多个,因而不可解。基于此,下面给出式(29) 成立的一个充分条件,该充分条件用有限个LMI即可保证系统的稳定性,从而使得控制器可解。
由于p∈[p p],所以矩阵N(w)和H(w)处于下式所描述的多胞形中:
| $ \left\{ {\mathit{\boldsymbol{N}}\left( \mathit{\boldsymbol{w}} \right),\mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{w}} \right)} \right\} = \sum\limits_{j = 1}^n {{\mathit{\boldsymbol{\alpha }}_j}\left( \mathit{\boldsymbol{w}} \right){{\left( {\mathit{\boldsymbol{N}},\mathit{\boldsymbol{H}}} \right)}_j}} $ | (30) |
式中:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_{11}}}&{{\mathit{\boldsymbol{L}}_2} - \mathit{\boldsymbol{L}}_3^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}} + {\mathit{\boldsymbol{L}}_1}\mathit{\boldsymbol{H}}_j^{\rm{T}}}&0&{{\mathit{\boldsymbol{L}}_1}\mathit{\boldsymbol{C}}_1^{\rm{T}}}&0\\ * &{ - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{L}}_4} - \mathit{\boldsymbol{L}}_4^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}} + {\mathit{\boldsymbol{L}}_2}\mathit{\boldsymbol{N}}_j^{\rm{T}} + {\mathit{\boldsymbol{N}}_j}{\mathit{\boldsymbol{L}}_2}}&{{\mathit{\boldsymbol{B}}_\omega }}&0&{{\mathit{\boldsymbol{L}}_2}\mathit{\boldsymbol{C}}_2^{\rm{T}}}\\ * & * &{ - {\gamma ^2}\mathit{\boldsymbol{I}}}&{\mathit{\boldsymbol{D}}_1^{\rm{T}}}&{\mathit{\boldsymbol{D}}_2^{\rm{T}}}\\ * & * & * &{ - \mathit{\boldsymbol{I}}}&0\\ * & * & * & * &{ - \mathit{\boldsymbol{I}}} \end{array}} \right] < 0,}\\ {j = 1, \cdots ,n} \end{array} $ | (31) |
综上所述,得到了有限个LMI表示的H∞绝对稳定控制器的约束条件:即对于给定的标量γ>0,若存在对称矩阵L1>0、L2>0和任意矩阵L3、L4使得式(31) 成立,则闭环系统(17) 在控制器K1及u=-B-1ρ-K2ηe-K3αe下是稳定的,其中,K1是使M为Hurwitz矩阵的任意矩阵,而其中的反馈矩阵K2和K3则可分别由K2=L3 L1-1和K3=L4L2-1得到。
当配置K1值如下:
| $ {\mathit{\boldsymbol{K}}_1} = \left[ {\begin{array}{*{20}{c}} 0&{16}\\ { - 0.48}&{10} \end{array}} \right] $ | (32) |
利用LMI工具箱可解得噪声抑制水平γ的最优解为1.414 2,此处取γ=2,得到式(31) 的一个可行解,从而得到对应的Lyapunov矩阵为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{P = }}\left[ {\begin{array}{*{20}{c}} {3.589\;0}&{ - 25.2712}\\ { - 25.271\;2}&{639.190\;2} \end{array}} \right] \times {{10}^5}}\\ {\mathit{\boldsymbol{Q = }}\left[ {\begin{array}{*{20}{c}} {0.937\;7}&{ - 0.071\;9}\\ { - 0.071\;9}&{0.354\;1} \end{array}} \right]} \end{array} $ |
对应的反馈矩阵如下:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_2} = \left[ {\begin{array}{*{20}{c}} {1.097\;4}&{ - 18.784\;8}\\ { - 0.249\;6}&{4.743\;9} \end{array}} \right]}\\ {{\mathit{\boldsymbol{K}}_3} = \left[ {\begin{array}{*{20}{c}} { - 8.373\;1}&{1.347\;4}\\ {1.958\;1}&{ - 0.443\;0} \end{array}} \right]} \end{array} $ |
由上所示,控制器如下式所示:
| $ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{Kx}} = - {\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{\rho }} - {\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{\eta }}_{\rm{e}}} - {\mathit{\boldsymbol{K}}_3}{\mathit{\boldsymbol{\alpha }}_{\rm{e}}} $ | (33) |
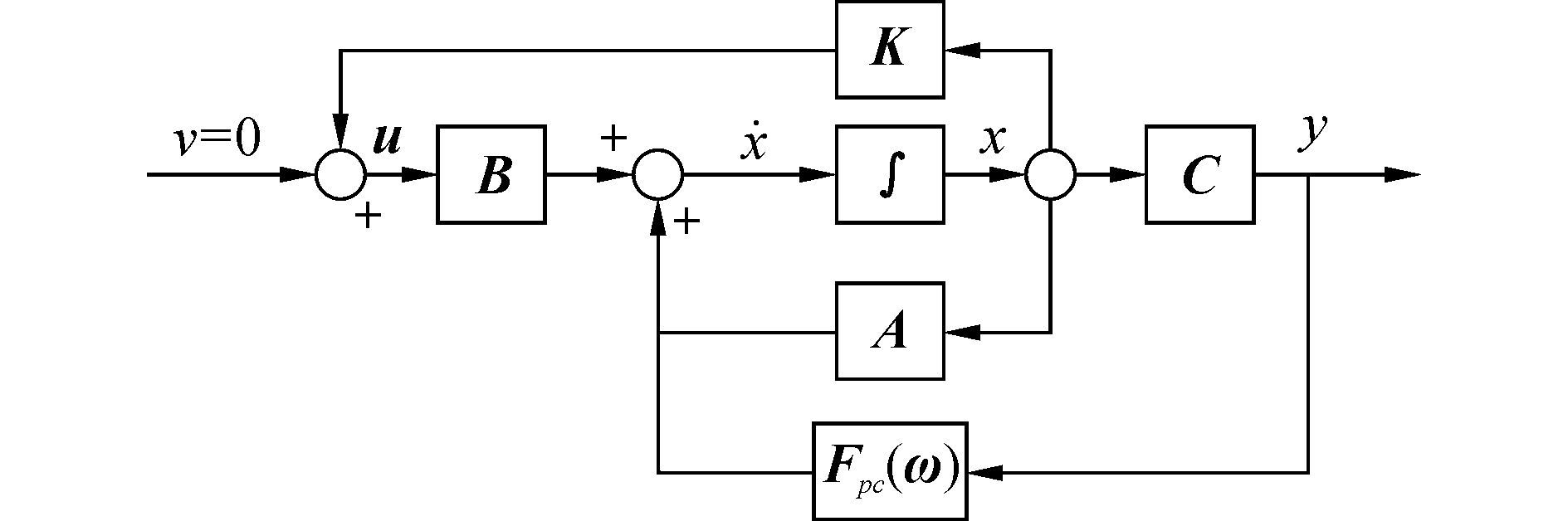
其中符号的定义见式(12)、(15)、(16) 的说明,控制结构如图 9所示。
|
图 9 控制系统方框图 Fig.9 Block diagram control system |
本节将在上文给出的水洞环境中对超空泡航行体的运动控制进行仿真分析和验证,主要对未经修正的模型和修正后的模型在运动控制中的性能进行仿真分析和比较。
在Matlab环境中,以Dzielski[3]的模型参数进行仿真。仿真时,将步长设为0.5 ms,仿真时间设为1.5 s,跟踪指令设定为zd=0.5,wd=75π/130,θd=π/130,qd=0,这样即改变了跟踪的纵向深度,且将最终跟踪的稳态设定为具有一定俯仰角的形式。此处wd为要跟踪的纵向速度指令,应该注意的是wd的方向与航行体轴线方向垂直,并不是垂向速度,实际速度方向仍是水平向前,所以可以定深。由前文航行体运动学方程可知其与俯仰角θd的关系,故设置此跟踪值。仿真初值取x0=[00π/800]T,反馈矩阵不变。
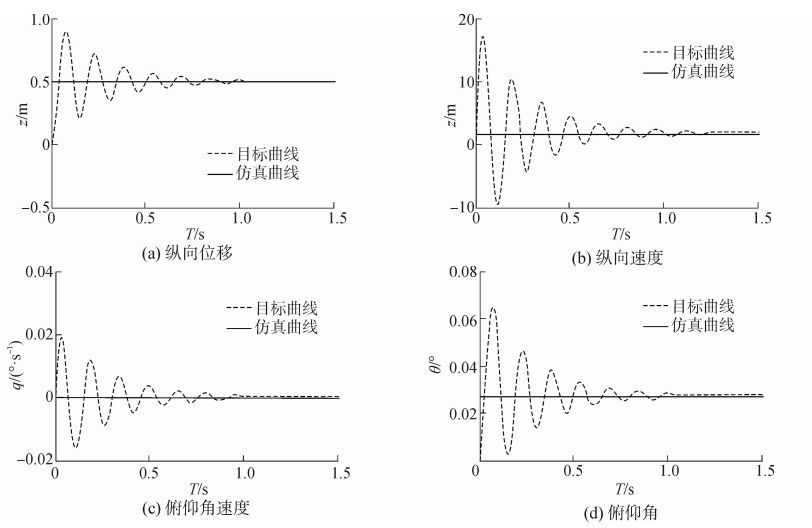
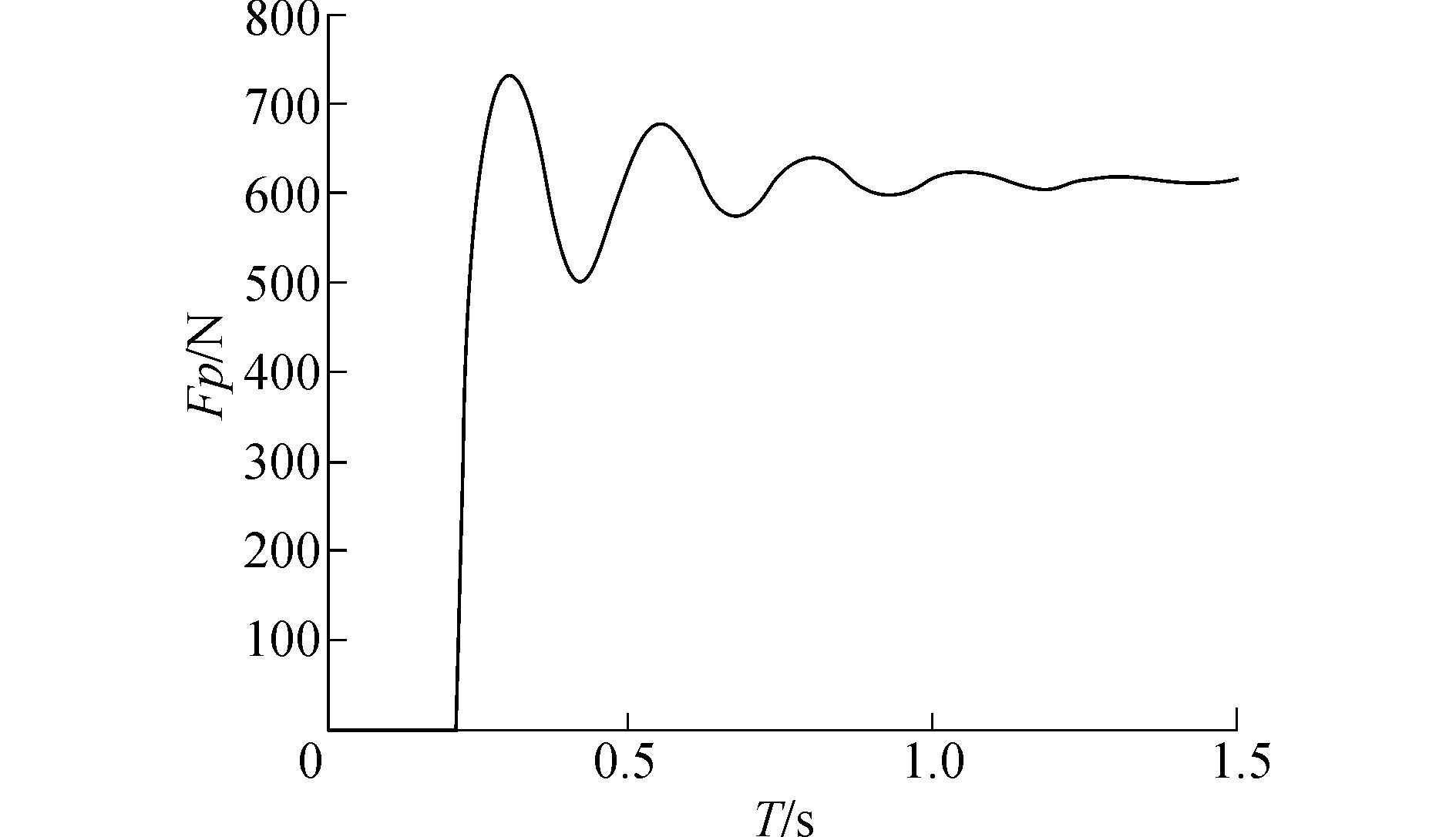
将未修正的模型代入实验数据进行仿真后得仿真图如图 10、11所示。
|
图 10 跟踪指令对应的响应曲线(未修正模型) Fig.10 Response curve of trace command(uncorrected model) |
|
图 11 滑行力响应曲线(未修正模型) Fig.11 Response curve of planing force(uncorrected model) |
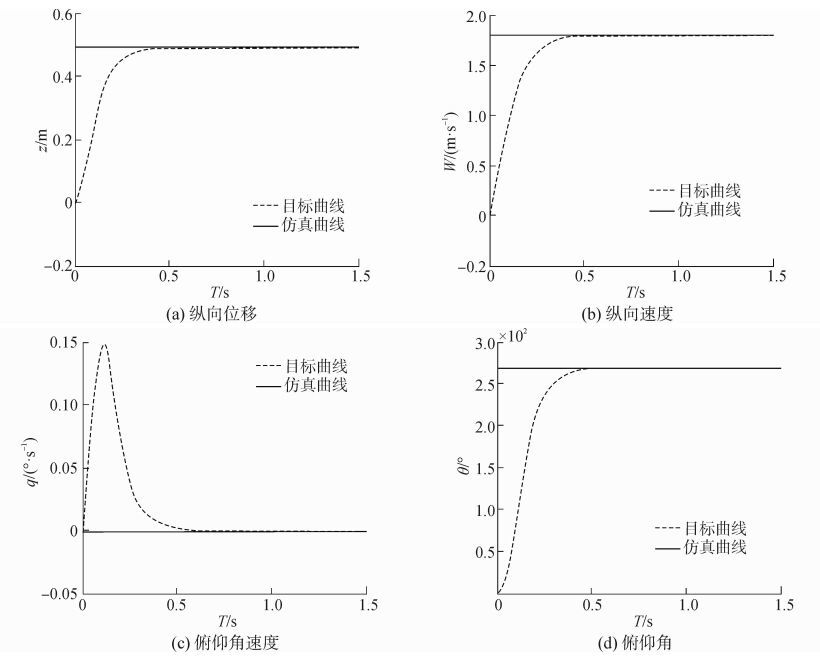
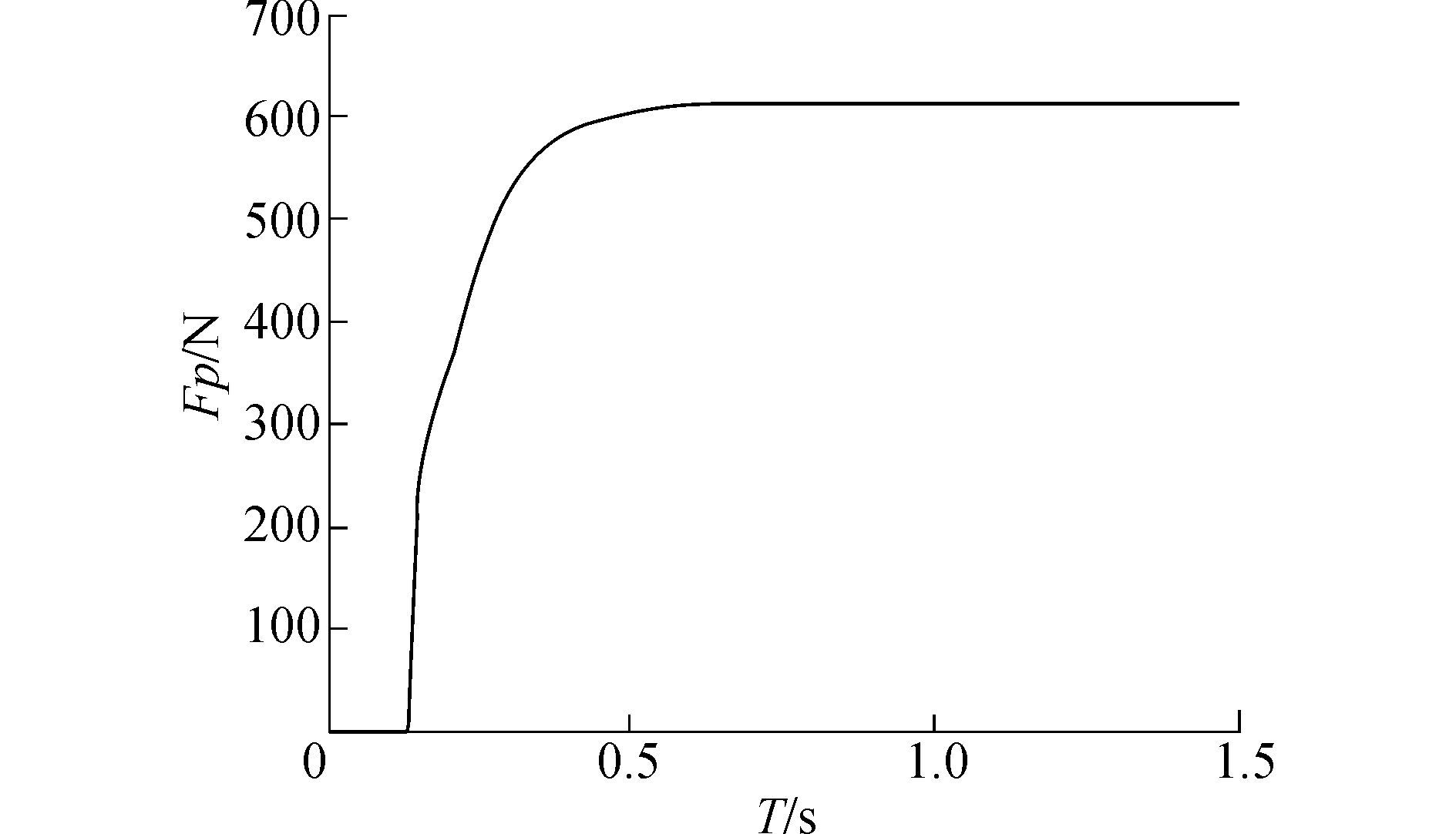
将修正的模型代入实验数据进行仿真后得仿真图如图 12、13所示。
|
图 12 跟踪指令对应的响应曲(修正后模型) Fig.12 Response curve of trace command(corrected model) |
|
图 13 滑行力响应曲线(修正后模型) Fig.13 Response curve of planing force(corrected model) |
可见,在仿真开始后,随着超空泡航行体的艉部的浸入深度的变化滑行力开始出现,导致航行体的各个状态发生改变,随着控制器对各个状态的不断矫正,航行体的各个状态在趋于平稳的过程中也对预设目标进行追踪,在滑行力迅速减小最终稳定在一个合理的范围的过程中,各个状态达到预定状态,从而达到控制目标。
经比较可知,虽然二者均能够在控制器的作用下在较短的时间内达到预定的稳定状态,但从各个状态在控制过程中的过渡时间、超调量、调整时间等指标和追踪效果可见,加入修正的模型的各项性能均优于未修正模型。
6 结束语本文得到结论如下:
1) 空化器可控的超空泡航行体的水洞实验数据,较固定空化器的水洞实验数据更加贴近实际控制环境;
2) LPV反演控制算法能够有效的解决超空泡航行体纵向运动控制中的一些干扰问题,在仿真条件下实现稳定控制。
本文的设计方法在一定程度上避免了完全理论仿真和使用静态控制器的数据进行仿真的弊端,能够较好的描述某一类环境中的超空泡航行体的纵向运动控制规律,能够为实际环境中的超空泡航行体控制器的设计提供有益的参考。
| [1] |
LOGVINOVICH G V. Hydrodynamics of flows with free boundaries[M]. Kiev, Russian: Naukova Dumka Publing House, 1980: 39-61.
( 0) 0)
|
| [2] |
曹伟, 魏英杰, 王聪. 超空泡技术现状、问题与应用[J]. 力学进展, 2006, 36(4): 571-579. CAO Wei, WEI Yingjie, WANG Cong. Current status problems and applications of supercavitation technology[J]. Advances in mechanics, 2006, 36(4): 571-579. DOI:10.6052/1000-0992-2006-4-J2005-083 (  0) 0)
|
| [3] |
DZIELSKI J, KURDILA A. A Benchmark control problem for supercavitating vehicles and an initial investigation of solutions[J]. Journal of vibration & control, 2003(9): 791-804. ( 0) 0)
|
| [4] |
SEMENNENKO V N. Supercavitation physics and calculation. RTO AVT Lecture Series on "Supercavitating Flows, " EN-010-11[R]. Brussels:Belgium, 2001.
( 0) 0)
|
| [5] |
SAVCHENKO Y N. Control of supercavitation flow and stability of supercavitating motion of bodies. RTO AVT lecture series on "supercavitating flows, " EN-010-14[R]. Brussels:Belgium, 2001.
( 0) 0)
|
| [6] |
SAVCHENKO Y N. Experimental investigation of supercavitating motion of bodies. RTO AVT lecture series on "supercavitating flows, " EN-010-04[R]. Brussels:Belgium, 2001.
( 0) 0)
|
| [7] |
VANEK B, BOKOR J, BALAS G J, et al. Longitudinal motion control of a high-speed supercavitation vehicle[J]. Journal of vibration and control, 2007, 13(2): 159-184. DOI:10.1177/1077546307070226 ( 0) 0)
|
| [8] |
SANABRIA D E, BALAS G, ARNDT R. Modeling, control, and experimental validation of a high-speed supercavitating vehicle[J]. Oceanic engineering IEEE journal, 2015, 40(2): 362-373. DOI:10.1109/JOE.2014.2312591 ( 0) 0)
|
| [9] |
DZIELSKI J E. Longitudinal stability of a supercavitating vehicle[J]. IEEE journal of oceanic engineering, 2011, 36: 562-570. DOI:10.1109/JOE.2011.2160470 ( 0) 0)
|
| [10] |
MAO Xiaofeng, WANG Qian. Nonlinear robust control design for a supercavitating vehicle[C]//ASME 2006 International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers. Chicago, USA, 2006:57-64.
( 0) 0)
|
| [11] |
王京华, 魏英杰. 水下超空泡航行体非线性动力学建模与仿真[J]. 工程力学, 2011, 28(12): 183-189. WANG Jinghua, WEI Yingjie. Nonlinear dynamic modeling and simulation of an underwater supercavitating vehicle[J]. Engineering mechanics, 2011, 28(12): 183-189. (  0) 0)
|
| [12] |
邹望. 基于Logvinovich原理的通气超空泡理论及其数值研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 93-109. ZOU Wang.Theoretical and numerical research[D]. Harbin:Harbin Institute of Technology, 2013:93-109. (  0) 0)
|
| [13] |
ZOU W, YU K P, ARNDT R. Modeling and simulations of supercavitating vehicle with planing force in the longitudinal plane[J]. Applied mathematical modelling, 2015, 39(19): 6008-6020. DOI:10.1016/j.apm.2015.01.040 ( 0) 0)
|
| [14] |
范辉, 张宇文. 超空泡航行器稳定性分析及其非线性切换控制[J]. 控制理论与应用, 2009, 26(11): 1211-1217. FAN Hui, ZHANG Yuwen. Stability analysis and nonlinear switching controller design for supercavitating vehicles[J]. Control theory & applications, 2009, 26(11): 1211-1217. (  0) 0)
|
| [15] |
ZHANG Xiaoyu, HAN Yuntao, BAI Tao, et al. H∞ controller design using LMIs for high-speed underwater vehicles in presence of uncertainties and disturbances[J]. Ocean engineering, 2015, 104: 359-369. DOI:10.1016/j.oceaneng.2015.05.026 ( 0) 0)
|
| [16] |
韩云涛, 强宝琛, 孙尧, 等. 基于圆判据的超空泡航行体非线性控制研究[J]. 工程力学, 2015, 32(8): 236-241. HAN Yuntao, QIANG Baochen, SUN Yao, et al. Nonlinear control research on supercavitating vehicles based on circle criterion[J]. Engineering mechanics, 2015, 32(8): 236-241. (  0) 0)
|
| [17] |
ZHAO Xinhua, SUN Yao, ZHAO Guoliang, et al. μ-Synthesis robust controller design for the supercavitating vehicle based on the BTT strategy[J]. Ocean engineering, 2014, 88: 280-288. DOI:10.1016/j.oceaneng.2014.06.035 ( 0) 0)
|
| [18] |
白涛, 毕晓君. 水下超空泡航行体纵向机动运动控制研究[J]. 哈尔滨工程大学学报, 2011, 32(4): 445-450. BAI Tao, BI Xiaojun. Studies on a longitudinal maneuvering motion control of underwater supercavitating vehicles[J]. Journal of Harbin engineering university, 2011, 32(4): 445-450. (  0) 0)
|
| [19] |
WANG Yadong, YUAN Xulong, ZHANG Yuwen. On the reentarnt jet of a supercavitating body[C]//Proceedings of the Eighth International Symposium on Cavitation (CAV 2012).Singapore, 2012:916-921.
( 0) 0)
|
| [20] |
VANEK B, BOKOR J, BALAS G. High-speed supercavitation vehicle control[C]//Collection of Technical Papers-AIAA Guidance, Navigation, and Control Conference. Colorado, USA, 2006:3165-3172.
( 0) 0)
|
| [21] |
MAO Xiaofeng, WANG Qian. Nonlinear control design for a supercavitating vehicle[J]. IEEE transactions on control systems technology, 2009, 17(4): 816-832. DOI:10.1109/TCST.2009.2013338 ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


