近几年来,随着计算机、信息处理与智能控制的迅猛发展,人们对于机器人的研究也在逐渐加深,机器人的功能也在慢慢完善,而本文所研究的移动机器人也是其中的一种[1]。现在移动机器人的研究已进入较为成熟的阶段,可以先前确定的任务地点为目标,提前对行走的地图做出规划,在移动的过程中根据周围复杂环境障碍物的情况,进行最短距离的判断,完美地避开障碍物。移动机器人按照运行环境,可分为海、陆、空3类[2-3]。本文主要解决如何使移动机器人在行走过程中可获取最短路径的问题,即移动机器人行进的路径规划问题。对此,国内外众多专家学者已进行探究并提出对应的解决办法。文献[4]针对无人机的航路规划问题,提出利用多个处理器来同时执行算法优化过程的思想,并通过仿真来对粒子群和遗传算法进行对应方案的验证,实验结果表明,算法的执行效率明显提升。文献[5]提出将改进的人工蜂群算法应用至机器人的路径规划中,并通过仿真结果将其与差分进化算法相比较,从而验证该改进蜂群算法的实用性。文献[6]提出将传统的ANN与蚁群算法相结合的优化算法运用到路径规划中,并进行相应的仿真实验,验证该优化算法在规划速度和更优路径上的优越性。文献[7]以蚁群算法为基础,引进人工势场的作用,两种算法之间优劣互补,在复杂的行走环境中共同作用以提升寻优能力。国际很多专家对人工鱼群算法进行了改进,应用在不同的领域,文献[8]将支持向量机与人工鱼群算法结合,来解决孪生支持向量机的参数选择问题;文献[9]针对深度神经网络AI研究的可解释性瓶颈,给出了有价值的解释;文献[10-12]利用改进的人工鱼群算法进行图像量化、WSN覆盖优化策略、资源调度算法;文献[13-16]研究改进的人工鱼群算法在时滞系统辨识和非线性优化问题中的应用,也有专家利用混合聚类或海洋流的流动功率对人工鱼群算法进行改进。
国外的专家对移动机器人的控制、组队进行了大量研究,美国专家研究拦截流氓机器人,捕获具有多个追踪器的多个逃逸者的算法[17];韩国的专家们研究多障碍下移动机器人避障、路径规划及不稳定网络下机器人的跟踪质量问题[18-20];印度专家对多机器人系统进行建模、实行分散控制[21-23];德国、法国和加拿大等的专家研究多机器人系统的运动冲突、测量与优化控制问题[24-27]。通过分析国内外的研究现状,可以发现现有的算法研究仍存在一些可优化项,例如:移动机器人的真实环境较为复杂,存在不定时的障碍物,这就要求机器人具备实时避免碰撞的能力。因此,利用更加即时的算法来实现该场景优化具有很强的实际应用意义。
本文针对复杂环境下寻找最短路径问题,提出基于视野自适应的改进人工鱼群(artificial fish-swarm algorithm based on adaptive vision, AVAFSA)的机器人路径规划算法,分别引入衰减函数和自适应算子来改善视觉效果,增强步长的自适应能力,从而避免因视野太小而陷入局部最小的情况,由此来缩减机器人在行走过程中的路径长度和时间。
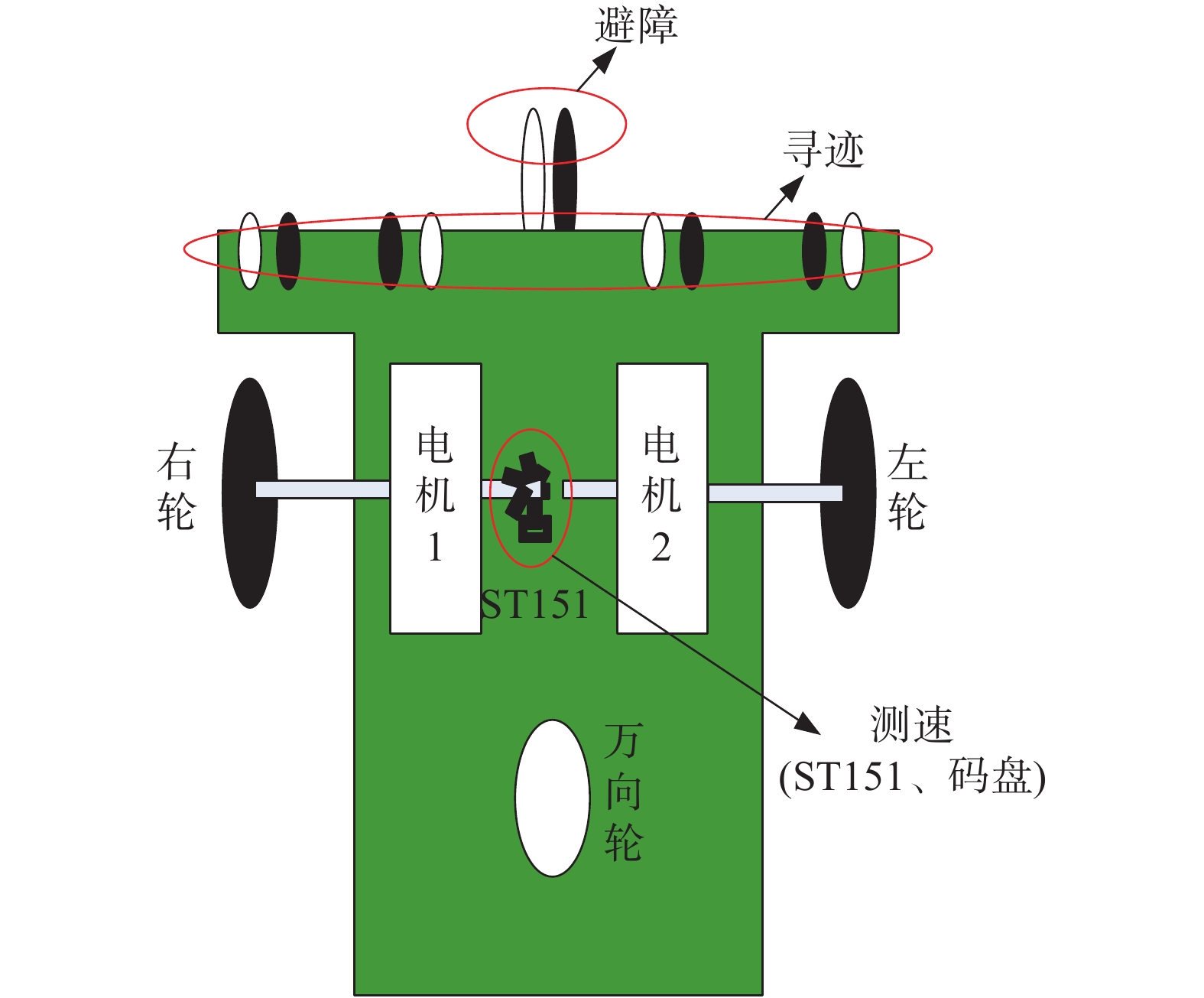
1 系统描述 1.1 结构设计本文研制的移动机器人设计主要由主控制器Arduino单片机、超声波测距模块、电机驱动模块、摄像头、RS232接口、光电感应以及电源等模块组成。其系统总体框架如图1所示。其中超声波测距和光电感应模块主要完成行走环境的信息获取,包括障碍物的距离和路线检测;Arduino可根据超声波测距和光电感应模块的输送信息来进行判断,从而驱动电机来合理地移动机器人。摄像机主要将机器人周边的环境信息通过RS232接口传送至上位机,由PC机来完成对路径的优化选择。图2给出了自制的移动机器人底部设计示意图。图2中,底部的前面中间的超声波传感器用作小车避障,其他4个红外传感器(红外对管)用作寻迹,左右车轮分别由2个12 V直流电机分别驱动,两轮之间装有型号为ST151的码盘测速器,万向轮配合左右车轮运动。

|
Download:
|
| 图 1 自动搬运机器人系统框图 | |
|
Download:
|
| 图 2 自制的移动机器人底部设计示意 | |
栅格图是目前在路径规划中应用较为广泛的一种表达方法,因此本文通过栅格法来建立移动机器人的运行模型。栅格法把移动机器人的操作环境投射为栅格二维空间,其中黑色区域为障碍物所在地,白色为机器人可行区域[8]。分析移动机器人的运动环境,特作以下假设。
1)运行环境处于二维空间内,在一个静态平面范围中。
2)在运行空间内,静态障碍物所处的初始位置、当前位置、目标位置与大小均知晓。
3)把移动机器人可看作质点。
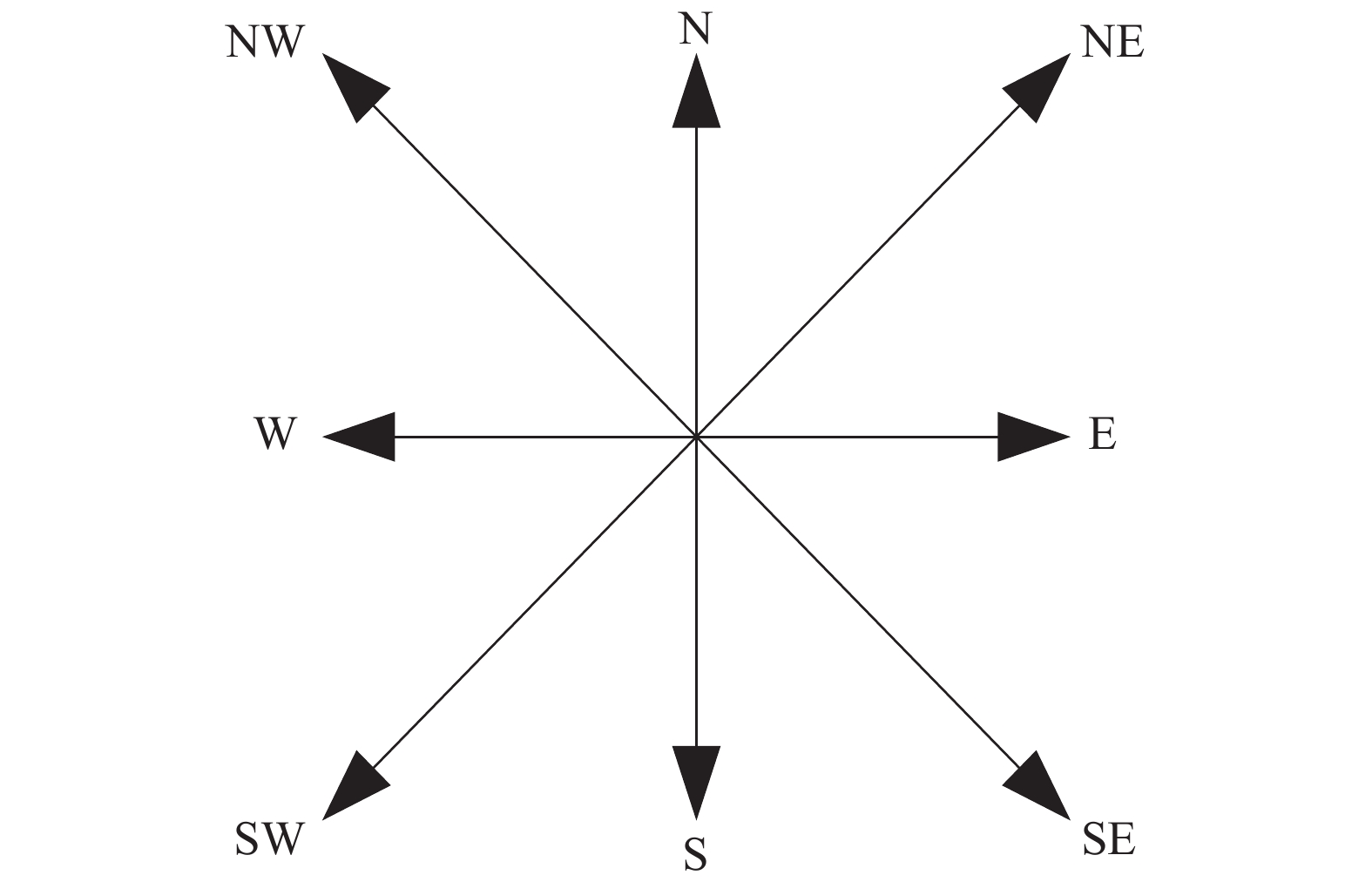
4)移动机器人可以随意变化方向[9],其变化方向如图3所示。
5)移动机器人可以随意改变行走速度,加速、减速、匀速或者停止等。
|
Download:
|
| 图 3 移动机器人移动方向 | |
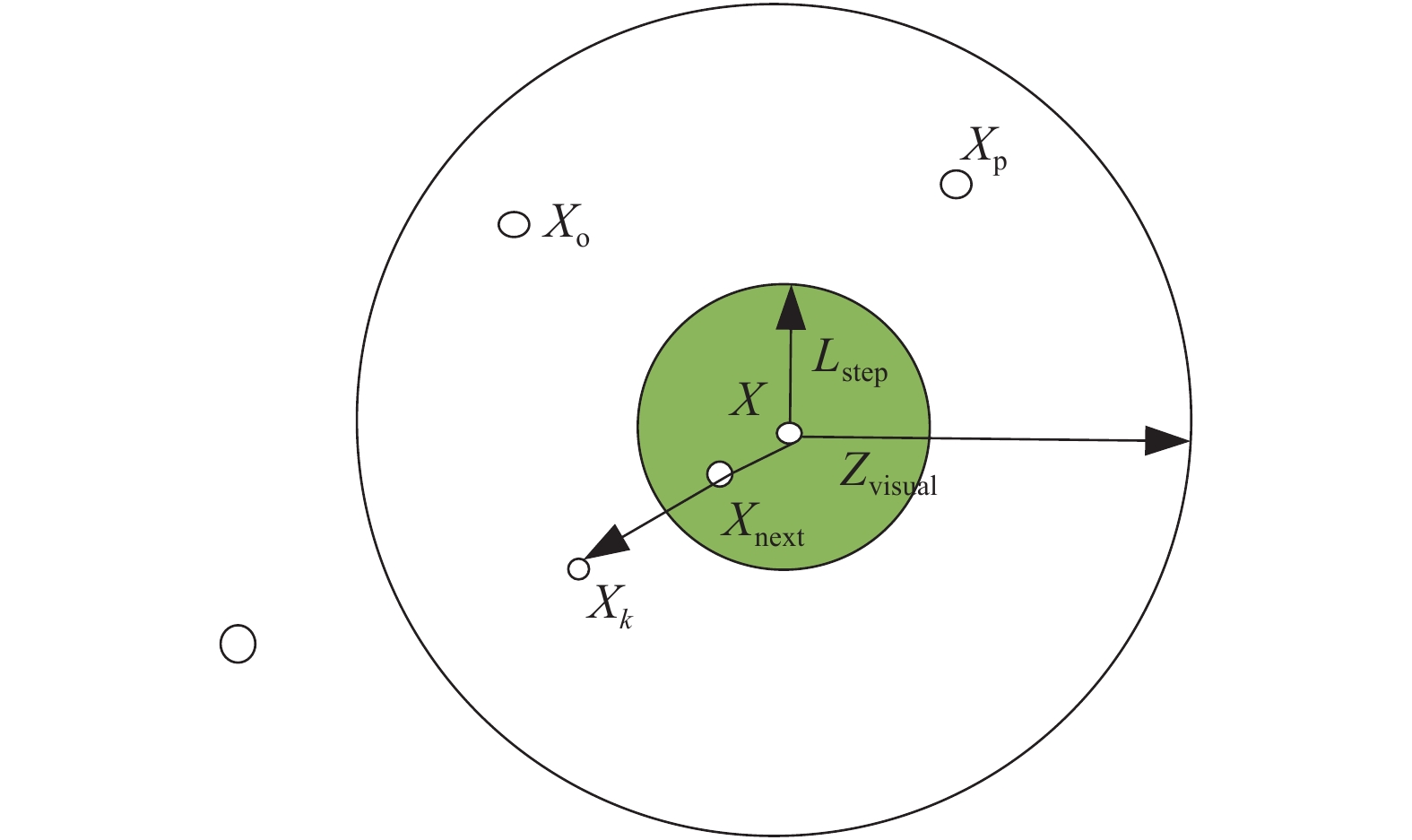
人工鱼群算法(artificial fish-swarm algorithm, AFSA)是由李晓磊博士在2002年提出的一种群体智能优化算法。其基本思想是仿照鱼群在一片水域当中寻找最优解的觅食、聚群和追尾等行为,水域中的每一条鱼都对应其中的一个优化解,该水域即为被优化问题的解空间。通过分析人工鱼群的优化理念,可得其人工鱼环境模型如图4所示。假设水域中一条鱼现时状态是
|
Download:
|
| 图 4 人工鱼环境模型 | |
AFSA在路径规划中的具体步骤如下。
1)初始化设置。对鱼群中的各个参数进行初始设置,包括:该人工鱼群的群体规模、视野、最大迭代次数、每一条鱼的最大移动步长Step(公式中用Lstep)等参数。
2)此时迭代的次数是0,由N条鱼组成初始鱼群,每个鱼表示从初始位置到目标位置的一条路径。
3)对每一条人工鱼都进行行为模拟:觅食、追尾、聚群与随机移动行为,选取其中最优的一种行为来操作。4种行为算法的数学表达如下。
觅食行为
| ${X_a}^{t + 1} = {X_a}^t + \frac{{{X_b} - {X_a}^t}}{{\left\| {{X_b} - {X_a}^t} \right\|}} \cdot {L_{{\rm{step}}}} \cdot {\rm{Rand}}()$ | (1) |
聚群行为
| ${X_a}^{t + 1} = {X_a}^t + \frac{{{X_c} - {X_a}^t}}{{\left\| {{X_c} - {X_a}^t} \right\|}} \cdot {L_{{\rm{step}}}} \cdot {\rm{Rand}}()$ | (2) |
追尾行为
| ${X_a}^{t + 1} = {X_a}^t + \frac{{{X_{{\rm{max}}}} - {X_a}^t}}{{\left\| {{X_{{\rm{max}}}} - {X_a}^t} \right\|}} \cdot {L_{{\rm{step}}}} \cdot {\rm{Rand}}()$ | (3) |
任意移动行为
| ${X_a}^{t + 1} = {X_a}^t + {Z_{{\rm{visual}}}} \cdot {\rm{Rand}}()$ | (4) |
式中Rand()为随机函数,产生0到1之间的随机数。
4)人工鱼在每次行为之后,选取自身状态和公告牌状态较优的一种进行实时更新。
5)判断是否已到最大迭代次数,若已到达,则输出,否则,转第3)继续运行。
根据以上对于AFSA基本理论和操作步骤的描述中可看出,视野起到了至关重要的作用。在移动过程中,视野值若不变,易引起算法收敛速度变慢,计算量变大。
2.2 AVAFSA机器人路径规划算法针对上述AFSA在路径规划中所存在的问题,本文提出基于视野自适应的改进人工鱼群算法的机器人路径规划算法。
人工鱼的4种行为中,觅食行为是决定算法是否收敛的关键,因此,仅对觅食行为采用自适应改进,其他的追尾、聚群以及随机移动行为对应的视野保持不变。在觅食行为执行初期,给予其较大的视野,随着过程迭代的进行慢慢减小。
但是,若行为执行到后期时,视野太小,易陷入局部最优。所以,设定在视野的当前值缩减至初始值的一半时,数值保持不变,停止减小。因此,现将觅食行为的数学表达式改写成式(5)数学模型,即目标函数。
| $\left\{ {\begin{array}{*{20}{c}} {{V_{k + 1}} = \alpha {V_k}},&{{\alpha ^k} \geqslant \beta } \\ {{V_{k + 1}} = \beta {V_o}},&{{\alpha ^k} < \beta } \end{array}} \right.$ | (5) |
式中:k为迭代数;
AVAFSA机器人路径规划算法实现步骤为
1)初始化设置。结合栅格图大小,设置每格的边长、障碍物的个数、机器人起点
2)迭代的次数从0开始,由N条鱼组成初始鱼群,每个鱼表示从初始位置到目标位置的一条路径。
3)对每一个人工鱼都进行行为模拟。包括觅食、追尾、聚群与随机移动行为(此处觅食行为的视野是改进后的,采用目标函数公式(5)迭代);在栅格图上机器人的当前位置,选取当中最优的一种行为来操作。
4)人工鱼在每次行为之后,选取自身状态和公告牌状态较优的一种进行实时更新。
5)判断运行次数是否等于初始设置的最大迭代次数,若是,则继续;否则,转到步骤3)继续。
6)判断机器人是否到达栅格图的终点
为了验证本文所提改进的人工鱼群算法与传统人工鱼群在移动机器人路径规划上的优越性,在此选择相同的运行环境作对比仿真实验。结合栅格法[28],利用MATLAB进行仿真验证,栅格图大小设为120 cm×120 cm,其每格的边长为4 cm,序号初始化值是0,在X、Y方向对各个栅格按照顺序进行编号,把障碍物所在的栅格位置标记成黑色,其他区域为白色,货物存放地47个,起点
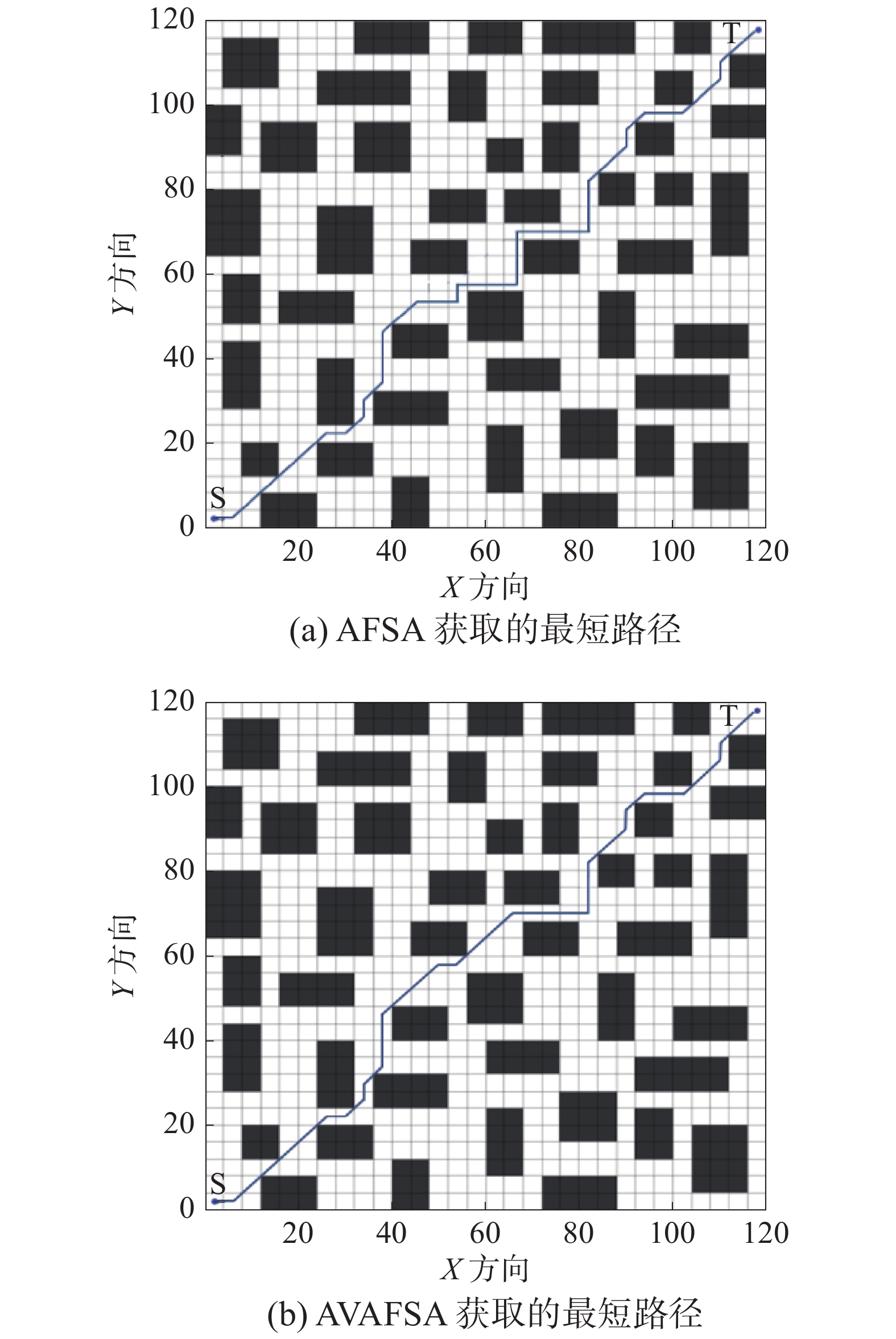
表1中,Lf为最优路径长度,Kmin为训练次数。由仿真图、实验及表中数据可得,2种算法在移动机器人路径规划的应用中,本文所改进的人工鱼群算法最优路径长度与迭代次数上均优于传统的人工鱼群算法。由图4可得,AVAFSA优化下的最优路径长度明显较AFSA短,为186 cm;从图5可看出,在路径寻优的整个过程中,AVAFSA最终找到最优路径所需迭代的次数为35次,比AFSA少了15次;此外,当2种算法的最大迭代次数均设置为100时,AVAFSA会最先达到次数上限,迭代用时较短,仅为10.15 s,比AVAFSA缩短了2.18 s。总之,本文所提出的基于视野自适应的改进人工鱼群优化算法较传统的人工鱼群算法在移动机器人的路径规划应用上存在明显的优势。
|
Download:
|
| 图 5 2种算法的最优路径搜索 | |
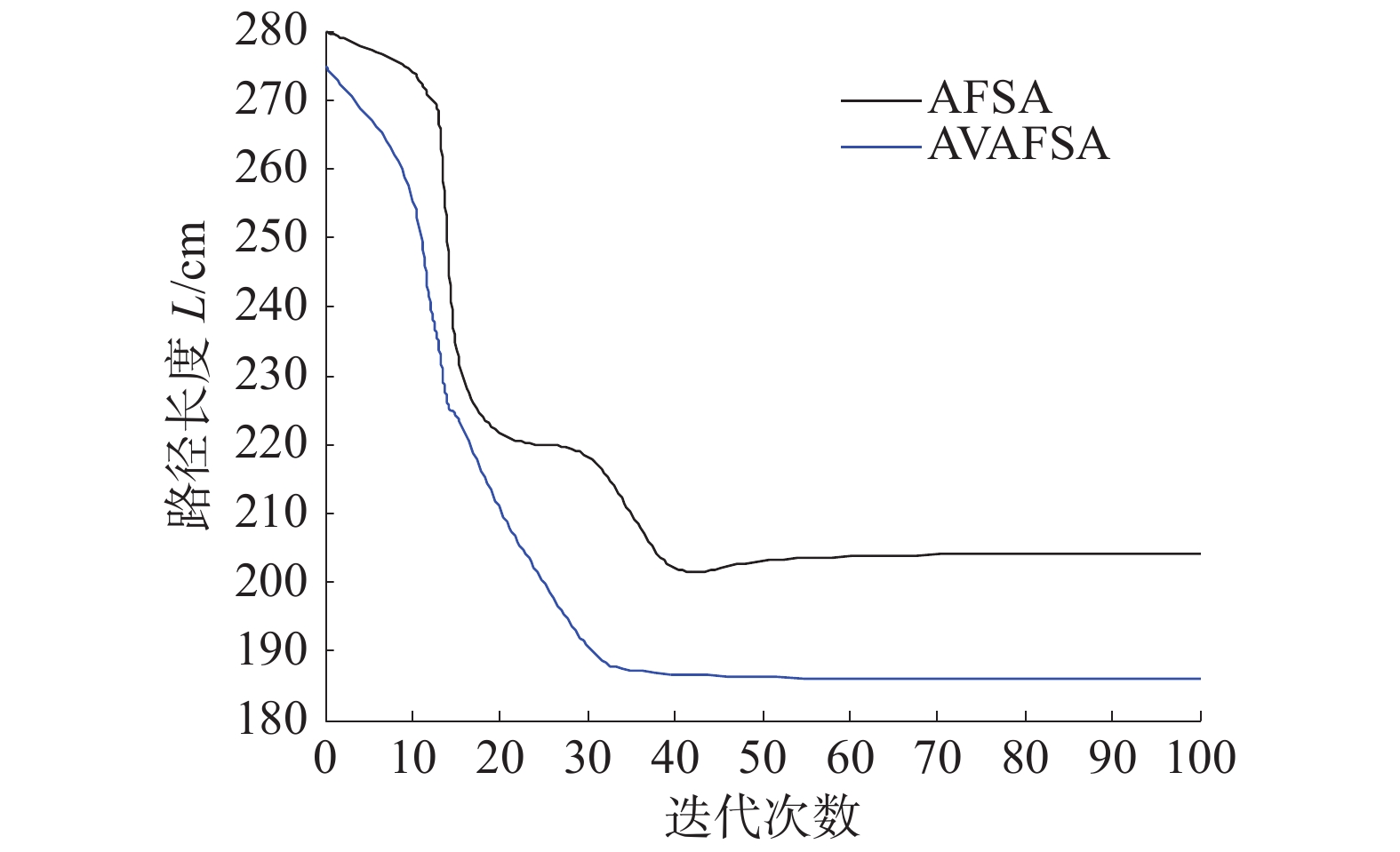
|
Download:
|
| 图 6 2种算法的收敛曲线 | |
|
|
表 1 2种算法最优路径相关参数对比 |

|
Download:
|
| 图 7 自制的移动小车在实际运行的状态 | |
本文通过建立移动机器人的环境模型,分析传统人工鱼群在路径优化方面存在的问题,提出基于视野自适应的改进人工鱼群优化算法,结合栅格图法的优点,形成了AVAFSA机器人避障和优化算法。该算法利用鱼群视野自适应的形式来对可见视线值的下限进行设定,引入衰减函数来改善视觉效果,引入自适应算子来增强步长的自适应能力,从而避免因视野太小而导致易陷入局部最小。计算机仿真和通过自制的小车实验结果表明,如果在环境中有未知障碍物,本文的AVAFSA机器人路径规划算法也能实时避障,重新优化运行的路径。在同样环境条件下,AVAFSA机器人避障和优化算法相比于传统的人工鱼群算法获取最优路径的迭代次数减少了,路径长度缩短了8.82%,收敛速度提高了17.68%。由此可见,视野自适应的人工鱼群优化算法在移动机器人的避障和路径规划上效果明显。
| [1] |
魏立新, 吴绍坤, 孙浩, 等. 基于多行为的移动机器人路径规划[J]. 控制与决策, 2019, 34(12): 2721-2726. ( 0) 0)
|
| [2] |
晋晓飞, 王浩, 宗卫佳, 等. 自主移动机器人避障技术研究现状[J]. 传感器与微系统, 2018, 37(5): 5-9. ( 0) 0)
|
| [3] |
吴姝源. 智能控制及移动机器人研究进展[J]. 信息与电脑, 2018(8): 127-129. ( 0) 0)
|
| [4] |
ROBERGE V, TARBOUCHI M, LABONTE G. Comparison of Parallel Genetic Algorithm and Particle Swarm Optimization for Real-Time UAV Path Planning[J]. IEEE Transactions on Industrial Informatics, 2013, 9(1): 132-141. DOI:10.1109/TII.2012.2198665 ( 0) 0)
|
| [5] |
屈鸿, 黄利伟, 柯星. 动态环境下基于改进蚁群算法的机器人路径规划研究[J]. 电子科技大学学报, 2015, 44(2): 260-265. DOI:10.3969/j.issn.1001-0548.2015.02.017 ( 0) 0)
|
| [6] |
HUANG Yunlong. Intelligent Technique for Robot Path planning Using Artificial Neural Network and Adaptive Ant Colony Optimization[J]. Journal of Convergence Information Technology, 2012, 7(9): 246-252. DOI:10.4156/jcit.vol7.issue9.30 ( 0) 0)
|
| [7] |
董哗. 基于混合算法的机器人路径规划及编队研究化[D]. 鞍山: 辽宁科技大学, 2016.
( 0) 0)
|
| [8] |
李景灿, 丁世飞. 基于人工鱼群算法的孪生支持向量机[J]. 智能系统学报, 2019, 14(6): 1121-1126. ( 0) 0)
|
| [9] |
何华灿. 重新找回人工智能的可解释性[J]. 智能系统学报, 2019, 14(3): 393-412. ( 0) 0)
|
| [10] |
El-SAID S A. Image quantization using improved artificial fish swarm algorithm[J]. Soft computing, 2015, 19(9): 2667-2679. DOI:10.1007/s00500-014-1436-0 ( 0) 0)
|
| [11] |
SONG Qiang, LIU Lingxia. WSN coverage optimization strategy based on improved artificial fish swarm algorithm[J]. International Journal of Signal Processing, Image Processing and Pattern Recognition, 2015, 8(8): 191-198. DOI:10.14257/ijsip.2015.8.8.21 ( 0) 0)
|
| [12] |
ZHAO Hongwei, TIAN Liwei. Resource schedule algorithm based on artificial fish swarm in cloud computing environment[J]. Applied Mechanics and Materials, 2014, 635(13): 1614-1617. ( 0) 0)
|
| [13] |
曹法如, 冯茂林. 改进人工鱼群算法及其在时滞系统辨识中的应用[J]. 工程科学学报, 2017, 39(4): 619-625. ( 0) 0)
|
| [14] |
XIAO H. Applications of a combinatorial heuristic artificial fish swarm algorithm in non-linear optimization problems[J]. Boletin Tecnico/Technical Bulletin, 2017, 55(5): 174-180. ( 0) 0)
|
| [15] |
ZHAO Hongwei, TIAN Liwei. Study of the artificial fish swarm algorithm for hybrid clustering[J]. International Journal Bioautomation, 2015, 19(2): 147-160. ( 0) 0)
|
| [16] |
WANG Hongbo, FAN Chengcheng, TU Xuyan. AFSAOCP: A novel artificial fish swarm optimization algorithm aided by ocean current power[J]. Applied Intelligence, 2016, 45(4): 992-1007. DOI:10.1007/s10489-016-0798-7 ( 0) 0)
|
| [17] |
PIERSON A, WANG Zijian, SCHWAGER M. Intercepting Rogue Robots: An Algorithm for Capturing Multiple Evaders With Multiple Pursuers[J]. IEEE Robotics and Automation Letters, 2017, 2(2): 530-537. DOI:10.1109/LRA.2016.2645516 ( 0) 0)
|
| [18] |
ZHAO Ran, LEE K L. Intelligent navigation for multiple mobile robots with dynamic obstacles[J]. Journal of Institute of Control, Robotics and Systems, 2017, 23(9): 711-717. DOI:10.5302/J.ICROS.2017.17.0101 ( 0) 0)
|
| [19] |
ZHAO Ran, LEE H K. Fuzzy-based path planning for multiple mobile robots in unknown dynamic environment[J]. Journal of Electrical Engineering and Technology, 2017, 12(2): 918-925. DOI:10.5370/JEET.2017.12.2.918 ( 0) 0)
|
| [20] |
YOO S J, KIM T H. Predesignated fault-tolerant formation tracking quality for networked uncertain nonholonomic mobile robots in the presence of multiple faults[J]. Automatica, 2017, 77(3): 380-387. ( 0) 0)
|
| [21] |
GAUTAM A, MOHAN S. STATE: Distributed algorithm for uniform circle formation by multiple mobile robots[J]. Intelligent Service Robotics, 2016, 9(4): 347-366. DOI:10.1007/s11370-016-0205-6 ( 0) 0)
|
| [22] |
SARKAR S, KAR I N. Formation of multiple groups of mobile robots: multi-timescale convergence perspective[J]. Nonlinear Dynamics, 2016, 85(4): 2611-2627. DOI:10.1007/s11071-016-2848-4 ( 0) 0)
|
| [23] |
RAZAK R A, SUKUMAR S, CHUNG H. Decentralized Adaptive Coverage Control of Nonholonomic Mobile Robots[J]. IFAC-PapersOnLine, 2016, 49(18): 410-415. DOI:10.1016/j.ifacol.2016.10.200 ( 0) 0)
|
| [24] |
HALMHEU R, OTTO B, HEGEL J. Layout optimization of a system for successive laser scanner detection and control of mobile robots[J]. Robotics and Autonomous Systems, 2018, 101(3): 103-113. ( 0) 0)
|
| [25] |
AL-DUJAILI A, MA Yajie, EL BADAOUI EL NAJJAR M, et al. Actuator Fault Compensation in Three Linked 2WD Mobile Robots Using Multiple Dynamic Controllers[J]. IFAC-PapersOnLine, 2017, 50(1): 13556-13562. DOI:10.1016/j.ifacol.2017.08.2364 ( 0) 0)
|
| [26] |
SHAHRIARI M, BIGLARBEGIAN M. A new conflict resolution method for multiple mobile robots in cluttered environments with motion-liveness[J]. IEEE transactions on cybernetics, 2018, 48(1): 300-311. DOI:10.1109/TCYB.2016.2633331 ( 0) 0)
|
| [27] |
BHATTACHARJEE P, RAKSHIT P, GOSWAMI I, et al. Multi-robot path—planning using artificial bee colony optimization algorithm[C]//Proceedings of the 3rd World Congress on Nature and Biologically Inspired Computing. Salamanca, Spain, 2011: 219–224.
( 0) 0)
|
| [28] |
梁嘉俊, 曾碧, 何元烈. 基于改进势场栅格法的清洁机器人路径规划算法研究[J]. 广东工业大学学报, 2016, 33(4): 30-36, 43. DOI:10.3969/j.issn.1007-7162.2016.04.006 ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


