在现代战场中，电磁环境日益复杂，电子装备体积和所占空间日趋庞大，为了解决这些问题，需要简化系统，提高系统利用效率。为此，许多学者提出了雷达通信一体化系统的概念^[1-3]。在雷达通信一体化系统中，一体化波形的设计是关键。目前设计集成波形的技术主要有以下几种：扩频编码技术、线性调频(LFM)技术^[4-5]、正交频分复用(OFDM)技术、多输入多输出技术(MIMO)和传统通信编码技术，这些技术各有优缺点。文献[6]采用多相频移键控直接序列扩频(MPSK-DSSS)技术来实现通信信息的传输和雷达检测的功能，但同时也降低了信息传输速率。线性调频技术已被广泛应用于通信领域，由于其高分辨率、良好的多普勒容差和恒模特性，在雷达应用中也具有很大的潜力^[7]。文献[8]将最小频移键控(MSK)技术与线性调频技术相结合，设计了雷达通信一体化波形。理论推导和仿真实验证明，MSK-LFM一体化信号的误码率(BER)与MSK信号的BER一致。但是，一体化波形还具有信息传输率低的问题，不能满足实际通信的要求。OFDM技术可以提高传输速率并获得更高的带宽以提高距离分辨率^[9]。文献[10]设计了一种自适应OFDM雷达通信一体化波形，设计的一体化波形通过加权因子折中选择雷达和通信性能，此时两者性能都不是最佳，但在低发射功率的情况下，设计的一体化波形比固定波形性能更优越。MIMO雷达在检测性能和空间分辨率上具有显著优势^[11]。MIMO技术在通信领域的应用也可以增加通信容量^[12]。鉴于其出色的雷达和通信性能，一些学者将其引入了雷达通信一体化波形设计上^[13]。文献[14]提出将OFDM-LFM技术与MIMO雷达技术相结合，所提出的系统可以执行远程监视，具有更高的数据速率和角度分辨率，并且增加脉冲重复频率(PRF)和每个脉冲中的符号数量，可以改善所提出系统的通信性能。但是，PRF和符号数量的增加会在一定程度上影响雷达性能。

基于以上问题，本文提出了在OFDM-LFM的波形基础上，分别与BPSK、MSK、16QAM这3种常见的通信调制技术相结合，设计出雷达通信一体化波形。分析这3种波形各自的优缺点，对其各自的通信性能和雷达性能进行了理论分析和仿真。在不影响雷达探测性能的情况下，实现通信信息的传输，从而达到雷达通信一体化的目的。

1 一体化信号模型 1.1 OFDM-LFM信号模型

线性调频信号具有较大的时间带宽积和系统处理增益，利用正交频分复用对线性调频信号进行调制，可以得到OFDM-LFM波形，其数学表达式为

$ s(t) = \sum\limits_{n = 0}^{N - 1} u (t - T)\exp \left[ {{\rm{j}}2{\text{π}} \left( {{f_n}t + {k_n}{t^2}/2} \right)} \right] $

(1)

式中： $t{\kern 1pt} {\kern 1pt} (0 \leqslant t \leqslant T)$ 为信号的时间样本； $u(t) = 1, $ $ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 \leqslant t \leqslant T)$ 为矩形窗函数； ${f_n}$ 和 ${k_n}$ 分别为在信号 $s(t)$ 的第 $ n$ 个子载波的起始频率和斜率。

当任意2个子载波的调频斜率相同时，其之间的内积可以表示为

$\begin{split}& \frac{1}{T}\int\limits_0^T {\left[ {\exp \left( {{\rm{j}}2{\text{π}} {f_n}t} \right)} \right]} {\left[ {\exp \left( {{\rm{j}}2{\text{π}} {f_{\tilde n}}t} \right)} \right]^*}{\rm{d}}t = {\rm{sinc}} \left[ {{\text{π}} \left( {{f_n} - {f_{\tilde n}}} \right)T} \right] \end{split}$

(2)

式中: $ *$ 是共轭算子； $n = 1,2, \cdots ,N；\tilde n = 1,2, \cdots ，N$ 为了使这2个子载波正交，应使 $ {\rm{sinc}} \left[ {{\text{π}} \left( {{f_n} - {f_{\tilde n}}} \right)T} \right]=0$ ，所以子载波频率 $ {f_n}$ 和 $ {f_{\tilde n}}$ 之间的频率间隔为

$ {f_n} - {f_{\tilde n}} = \frac{p}{T} $

(3)

式中 $ p$ 为任意整数 $p = 1,2, \cdots\cdots$ 。

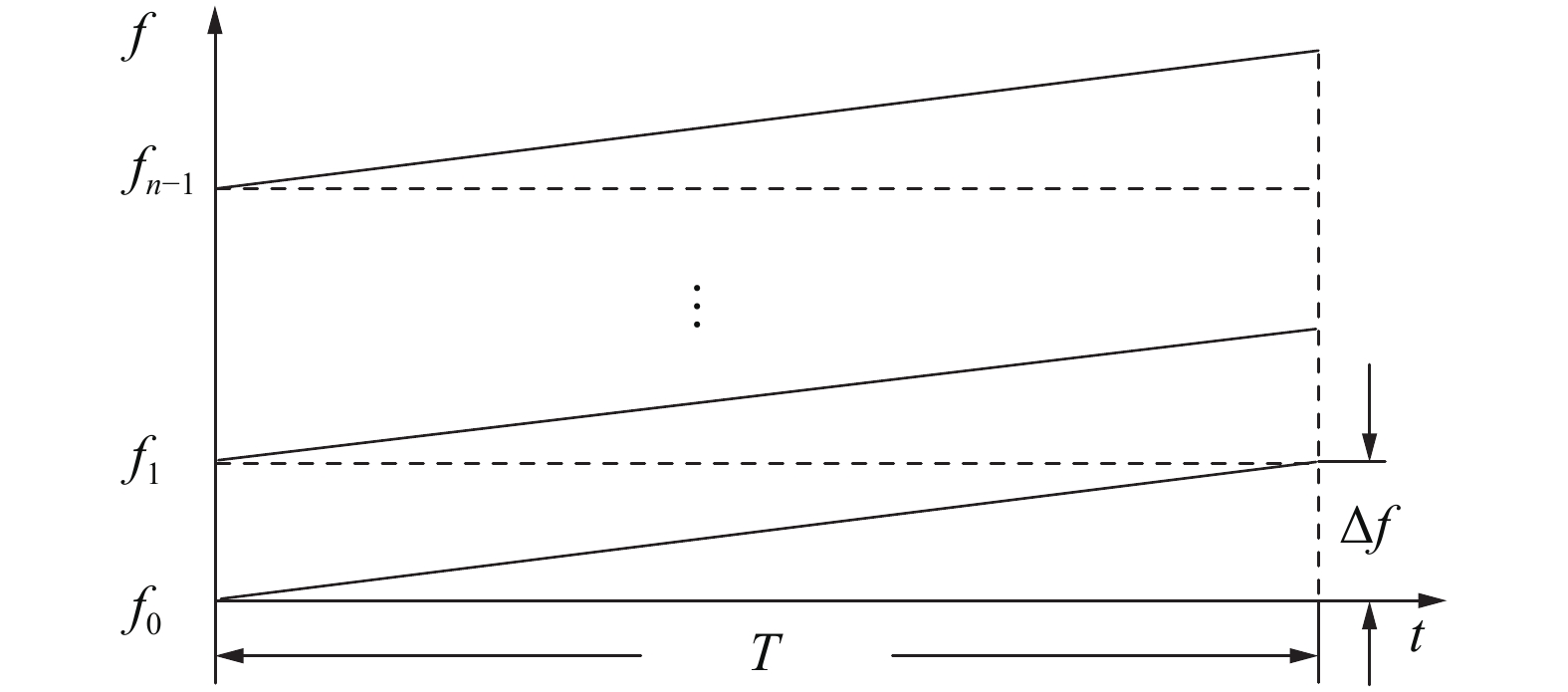
根据公式(1)及公式(3)可得到OFDM-LFM信号的时频关系图，如图1所示。

1.2 基于OFDM-LFM的一体化信号模型

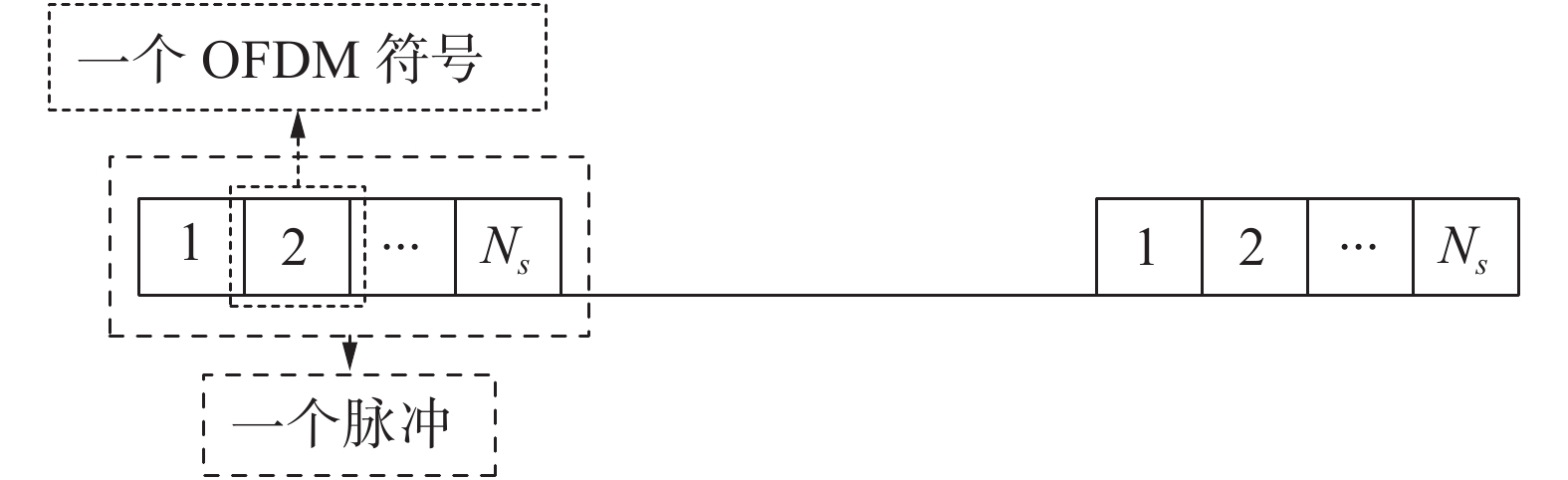
为了把通信信息调制在OFDM-LFM雷达上，对常见的BPSK、MSK和16QAM 通信调制方式进行研究分析，从而设计出3种一体化波形。以此设计的一体化波形由多个正交的LFM子载波组成，满足OFDM-LFM信号时频关系。每个子载波上调制有一个OFDM雷达脉冲，脉冲上则采用通信调制使OFDM符号搭载通信信息，图2为一个脉冲的OFDM一体化发射信号模型。

1.2.1 基于OFDM-LFM的BPSK一体化信号模型

BPSK是一种常见的相位通信调制，具有抗噪声能力强和运算简单的特点，但也具有低频带利用率的缺点。所以与OFDM-LFM技术结合可以提高频带利用率，且吸收了线性调频信号的优点。BPSK信号的第 $ k$ 个码元可以表示为

${s_{{\rm{BPSK}}}}\left( t \right) = \cos \left( {2{\rm{{\text{π}} }}{f_c}t + {\text{π}} {d_k}} \right)$

(4)

式中： ${f_c}$ 为载波频率； ${d_k}$ 为第 $ k$ 个通信码元。

结合OFDM-LFM技术得到一体化波形公式推导为

$ \begin{split} {s_1}(t) = \sum\limits_{m = 1}^{{N_s}} u \left( {t - (m - 1){T_s}} \right) \times \;\;\\ \sum\limits_{n = 0}^{{N_c} - 1} {\cos } \left( {2{\rm{{\text{π}} }}n\Delta ft + {\rm{{\text{π}} }}\mu {t^2} + {\rm{{\text{π}} }}{d_{m,n}}} \right) \end{split} $

(5)

式中： ${N_s}$ 为码元个数； ${N_c}$ 为载波个数； $\mu $ 为调频斜率； ${T_s}$ 为码元宽度； ${d_{m,n}}$ 为第 $n$ 个子载波上第 $m$ 个OFDM符号内调制的通信码元。

1.2.2 基于OFDM-LFM的MSK一体化信号模型

MSK 信号具有恒定的信息包络且每两个码元之间相位不会跳变，占用带宽也较小，将其与 OFDMLFM 信号相结合可得到一体化信号。MSK 信号的第k个码元可以表示为

$ \begin{split} {{s_{{\rm{MSK}}}}(t)} =& {\cos \left( {2{\rm{{\text{π}} }}{f_c}t + \frac{{{\rm{{\text{π}} }}{a_k}}}{{2{T_s}}} + {\varphi _k}} \right)} \end{split} $

(6)

式中： $ {a_k}$ 为第 $ k$ 个输入码元，取值为 $ \pm 1$ ； $ {\varphi _k}$ 为第 $ k$ 个码元的相位常数，在时间 $k{T_s} < t \leqslant (k + 1){T_s}$ 内保持不变，其作用是在 $ t=k{T_s}$ 处保持相位连续； ${k{T_s}} < $ $ {t \leqslant (k + 1){T_s}; \;k = 0,1, \cdots\cdots } $ 。

令 ${\varphi _k}(t) = 2{\rm{{\text{π}} }}{f_c}t + \dfrac{{{\rm{{\text{π}} }}{a_k}}}{{2{T_s}}} + {\varphi _k}+ {\varphi _k}$ ，可得

$ \frac{{d{\varphi _k}(t)}}{{dt}}2{\rm{{\text{π}} }}{f_c} + \frac{{{\rm{{\text{π}} }}{a_k}}}{{2{T_s}}} $

(7)

MSK信号的2个频率分别为

$ {f_1} = {f_c} + \frac{1}{{4{T_s}}},{f_0} = {f_c} - \frac{1}{{4{T_s}}} $

(8)

中心频率应选为 ${f_c} = \dfrac{n}{{4{T_s}}},n = 0,1, \cdots\cdots$ ，相位约束条件为

$ {\varphi _k} = {\varphi _{k - 1}} + \left( {{a_{k - 1}} - {a_k}} \right)\left[ {\frac{{\rm{{\text{π}} }}}{2}(k - 1)} \right]{\text{}} $

(9)

结合OFDM-LFM技术得到一体化波形公式推导为

$ \begin{split} {{s_2}(t) =}& {\sum\limits_{m = 1}^{{N_s}} u \left( {t - (m - 1){T_s}} \right)} {\sum\limits_{n = 0}^{{N_c} - 1} {\cos } ( {2{\rm{{\text{π}} }}n\Delta ft}} +\\& \quad\quad\quad\quad{{{\rm{{\text{π}} }}\mu {t^2} + \frac{{{\rm{{\text{π}} }}{a_k}}}{{2{T_s}}} + {\varphi _{m,n}}} )} \end{split} $

(10)

1.2.3 基于OFDM-LFM的16QAM一体化信号模型

16QAM具有较高的通信传输速率，将其与OFDM-LFM信号结合，既能扩大优势，又能实现雷达探测，形成一体化波形。固定频率载波16QAM信号通常表示为

$\begin{split} {s_{{\rm{QAM}}}}\left( t \right) = {a_o}\left( t \right)\cos \left( {2{\rm{{\text{π}} }}{f_c}t} \right) - {a_e}\left( t \right)\sin\left( {2{\rm{{\text{π}} }}{f_c}t} \right) \end{split}$

(11)

式中 ${a_o}\left( t \right)$ 和 ${a_e}\left( t \right)$ 为四进制通信数据。

结合OFDM-LFM技术得到一体化信号

$ \begin{split}& {s_3}(t) = \sum\limits_{m = 1}^{{N_s}} u \left( {t - (m - 1){T_s}} \right)\sum\limits_{n = 0}^{{N_c} - 1} {\left[ {{a_{{\rm{o}}_{{\rm{m,n}}}}}(t)\cos } \right.} (2{\text{π}} n\Delta ft +\\& \quad\quad\quad\quad \left. { { {\text{π}} \mu {t^2}}) - {a_{{\rm{e}}_{{\rm{m,n}}}}}(t)\sin \left( {2{\text{π}} n\Delta ft + {\text{π}} \mu {t^2}} \right)} \right] \end{split} $

(12)

通过对以上公式进行分析可以得出，BPSK和16QAM通过改变信号的相位或幅度来调制通信信息，而MSK调制则会改变信号的频率，因此会对载波之间的正交性产生一定的影响。

2 性能分析与仿真

本节从雷达和通信方面分析一体化波形的性能。仿真条件设置为：脉冲宽度为100 µs，符号宽度为1 µs，MSK调制的调频带宽为500 kHz，起始载波频率为2 MHz，LFM斜率为5 GHz，载波数为8，采样频率为15 MHz。

2.1 误码率分析

BER是评估系统通信性能的关键指标，代表数据通信的传输质量。因为OFDM-LFM信号平均误码率与其子载波的误码率保持一致，由子载波采用的调制方式决定，所以讨论设计的3种一体化波形的误码率就是讨论BPSK-LFM^[4]、MSK-LFM^[8]和16QAM-LFM^[5]的误码率，这3种波形的误码率如表1所示。

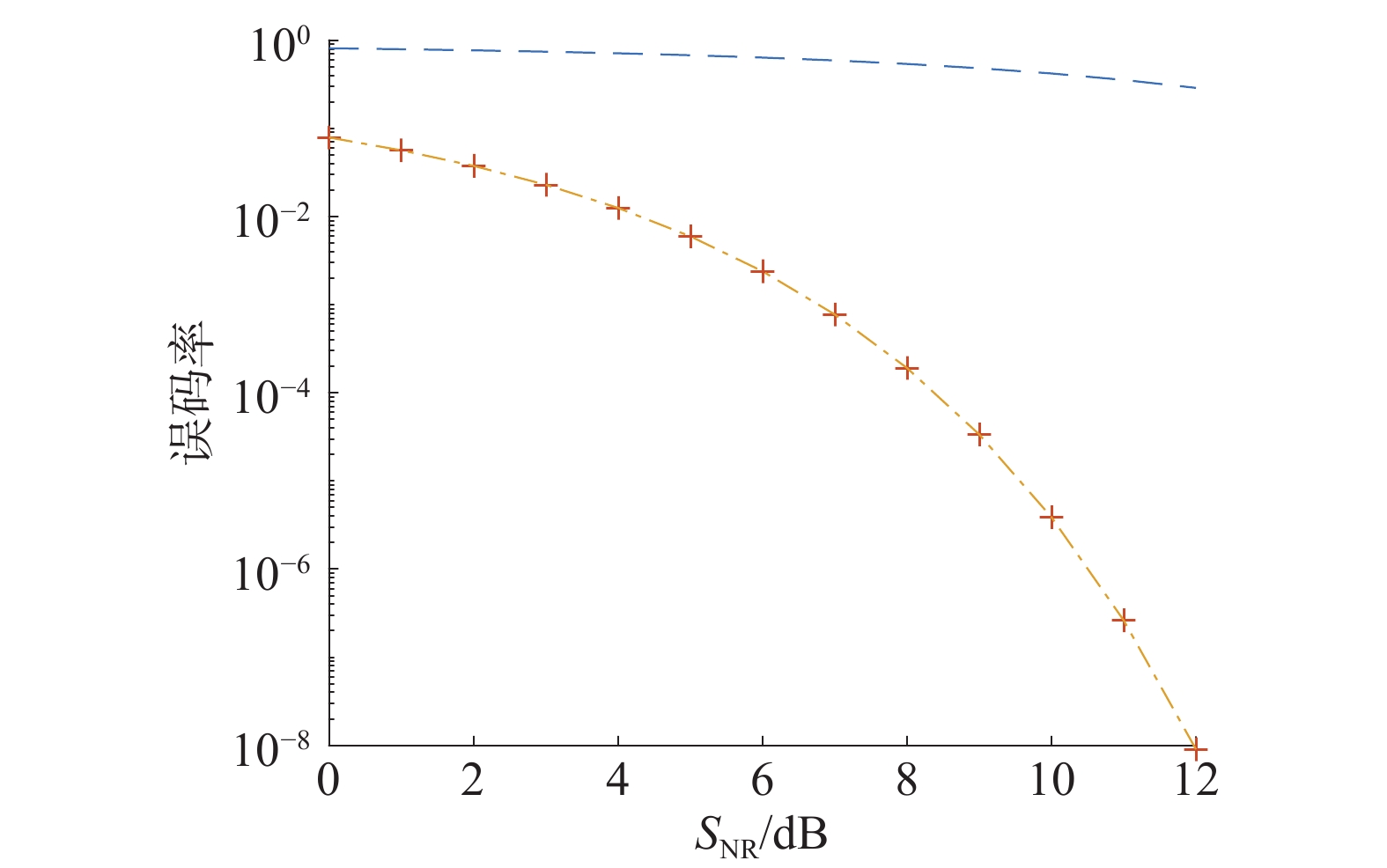
根据表1得到3种一体化波形误码率的理论曲线仿真图如图3所示，从图3可以看出，在相同的SNR情况下，BPSK-LFM和MSK-LFM信号的误码率一致且较低，而16QAM-LFM信号的误码率最高。因为在通信中，高阶调制牺牲了一定的误码率性能换取频带利用率。

2.2 雷达模糊函数分析

雷达模糊函数是评估雷达探测性能的重要依据，具有多种定义，本文采用式(13)的定义

$\chi \left( {\tau ,{f_d}} \right) = \int_{ - \infty }^{ + \infty } {s\left( t \right){s^*}\left( {t - \tau } \right)} \exp \left\{ {{\rm{j}}2{\rm{{\text{π}} }}{f_d}t} \right\}{\rm{d}}t$

(13)

式中： $ f_d$ 为多普勒频移；τ为时间延迟； $ s\left( t \right)$ 为雷达发射函数；*为共轭。

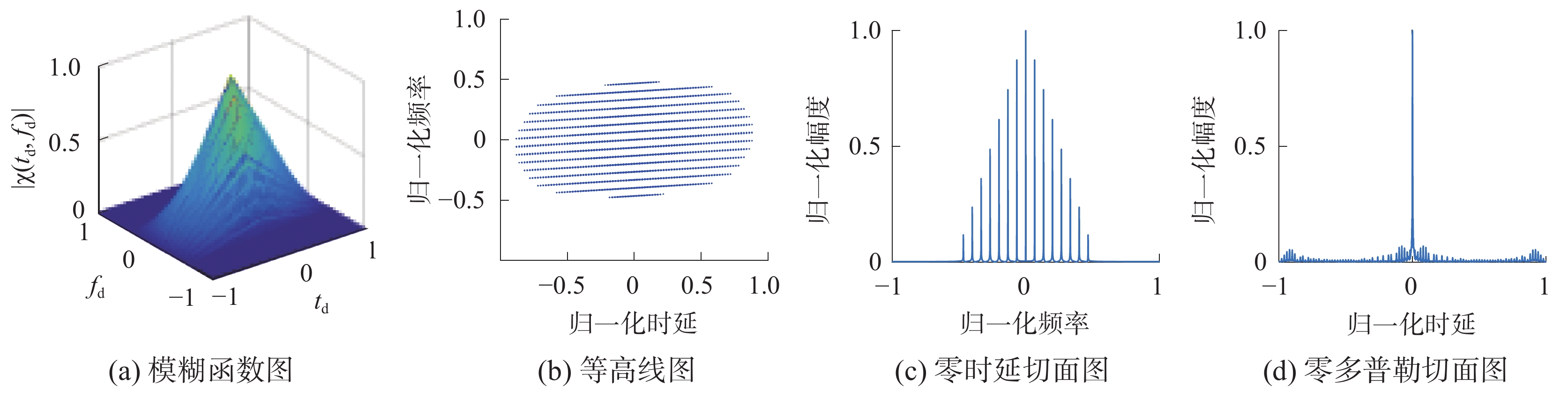
为了更为直观地判断信号的分辨能力，通常采用模糊函数图进行分析，并对其进行归一化处理。对基于OFDM-LFM的BPSK、MSK、16QAM这3种一体化波形进行仿真，得到仿真结果如图4—图6所示。

从图4可以看出，基于OFDM-LFM的BPSK一体化信号的模糊函数图为多个斜刃组成，与OFDM-LFM信号的模糊函数图非常相似，多个LFM载波之间的相关干扰比较严重，导致旁瓣较高。

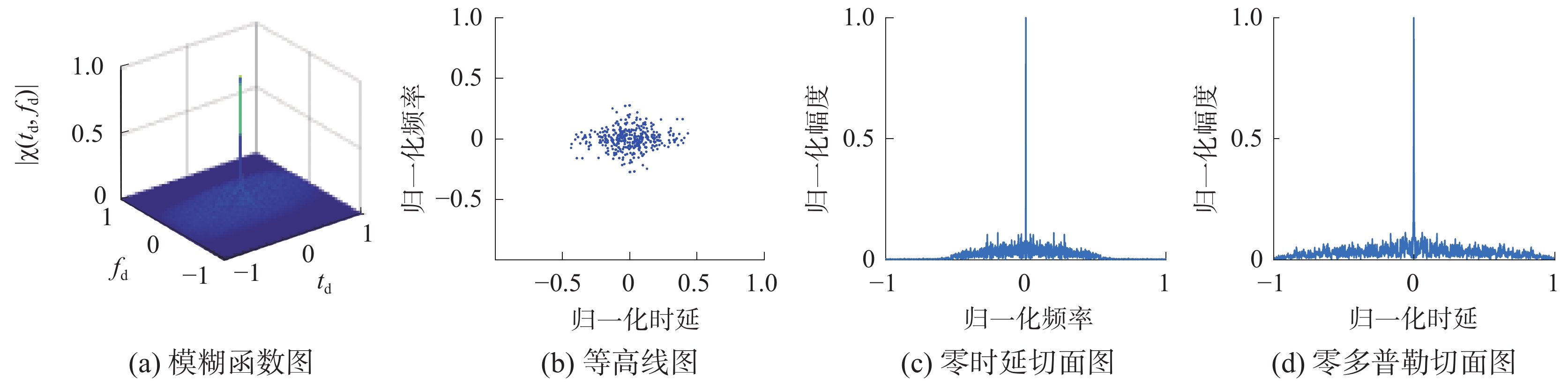
从图5可以看出，基于OFDM-LFM的MSK一体化信号的模糊函数图形类似图钉的形状，采用的MSK调制在一定程度上抑制了LFM载波之间的相关干扰，所以旁瓣较低，拥有较好的多普勒和时延分辨能力。

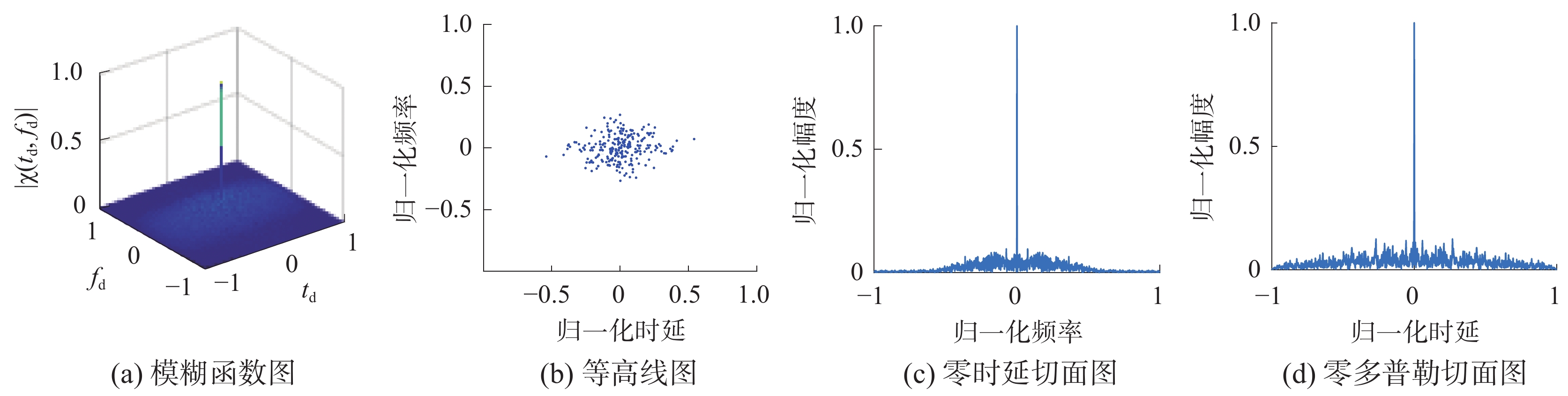
从图6可以看出，基于OFDM-LFM的16QAM一体化信号的模糊函数图形也类似于图钉的形状。因此，采用16QAM调制可以有效地抑制旁瓣，使一体化信号具有较好的多普勒和时延分辨率，但也对多普勒频移较为敏感。

3 结论

本文基于OFDM-LFM信号，采用BPSK、MSK和16QAM通信调制方法对通信信息进行调制，以实现雷达通信一体化波形的设计。讨论了OFDM-LFM信号的时频关系以及所提出的一体化信号模型的设计，分析了雷达的性能和通信性能。仿真结果表明，3种一体化信号可以实现雷达和通信功能，但各有优缺点。基于OFDM-LFM的BPSK一体化信号适用于需要高通信性能且对多普勒频移不敏感的场景。基于OFDM-LFM的16QAM一体化信号适用于低速信号检测和高通信速率场景。MSK调制会影响载波之间的正交性，但基于OFDM-LFM的16QAM一体化信号的通信和雷达性能均较好。