2. 32181部队,河北 石家庄 050000
2. 32181 Troops of PLA, Shijiazhuang 050000, China
正交频分复用(OFDM,Orthogonal Frequency Division Multiple)技术凭借抗多径能力强、频谱利用率高、易于与其他多种接入方法相结合等特性,在第四代移动通信(The Fourth Generation,4G)系统中广泛使用并被制定在多项标准中[1]。然而,OFDM也有着因为子载波叠加而导致的峰均比过高,和经过衰落信道后产生的非线性失真、多径衰落等问题,从而会严重影响到整个通信系统的误符号率(SER)性能[2]。
传统的信号检测方法有最小二乘(LS)法和最小均方误差(MMSE)法,LS算法虽然实现起来比较简单、计算复杂度较低,但是其忽略了噪声的影响,因此其信噪比低时性能较差[3]。MMSE算法考虑了噪声的影响,因此其性能比LS算法有所提升,但是这种性能优势需要事先知道信道的先验信息,因而实现起来较为困难,且这2种算法在导频数量较少时的信号检测性能较差[4-8]。
近年来,深度学习作为人工智能的基础技术,在计算机视觉和自然语言处理等学科取得巨大的成功,在图像分类、语音识别、面部识别和机器翻译风格转换等方面超越了传统机器学习方法的性能,使得无人驾驶、智能疾病诊断和个性化推荐等应用成为可能。神经网络在无线通信领域得到一些应用,例如直接采取端到端方式神经网络代替整个无线通信系统中的信道估计与均衡模块[8-11],也有用神经网络进行对信道估计的优化。文献[11]中利用深度学习采用端到端的方式隐式估计信道信息,直接恢复出传输信号,该方法所采用的神经网络为深度神经网络(Deep Neural Networks,DNN),与传统的信号检测方法相比在导频数较少时,具有较好的性能[12-15]。文献[16]中将信道矩阵看作二维图像,将神经网络融到迭代信号重建算法,设计一种基于深度学习去噪的近似信息传递网络,利用大量数据学习信道结构,在较短时间内有效地进行信道估计,解决了由射频链路数量有限导致的信道估计难题[16]。
本文提出了一种用于OFDM无线通信系统的基于BiLSTM (Bidirectional long short memory neural network,双向长短记忆神经网络)的信号检测框架。首先是构建BiLSTM信号检测网络,然后在信道模型下产生训练数据,对BiLSTM信号检测网络进行训练,训练之后将BiLSTM信号检测网络应用于OFDM通信系统进行信号检测。与长短记忆神经网络(Long Short Memory Neural Network, LSTM)信号检测网络不同,BiLSTM信号检测网络是前向LSTM和后向LSTM神经网络的结合,提高了信号检测的准确性,相比于传统的信号检测算法,BiLSTM信号检测网络在导频数较少时具有较好的性能。
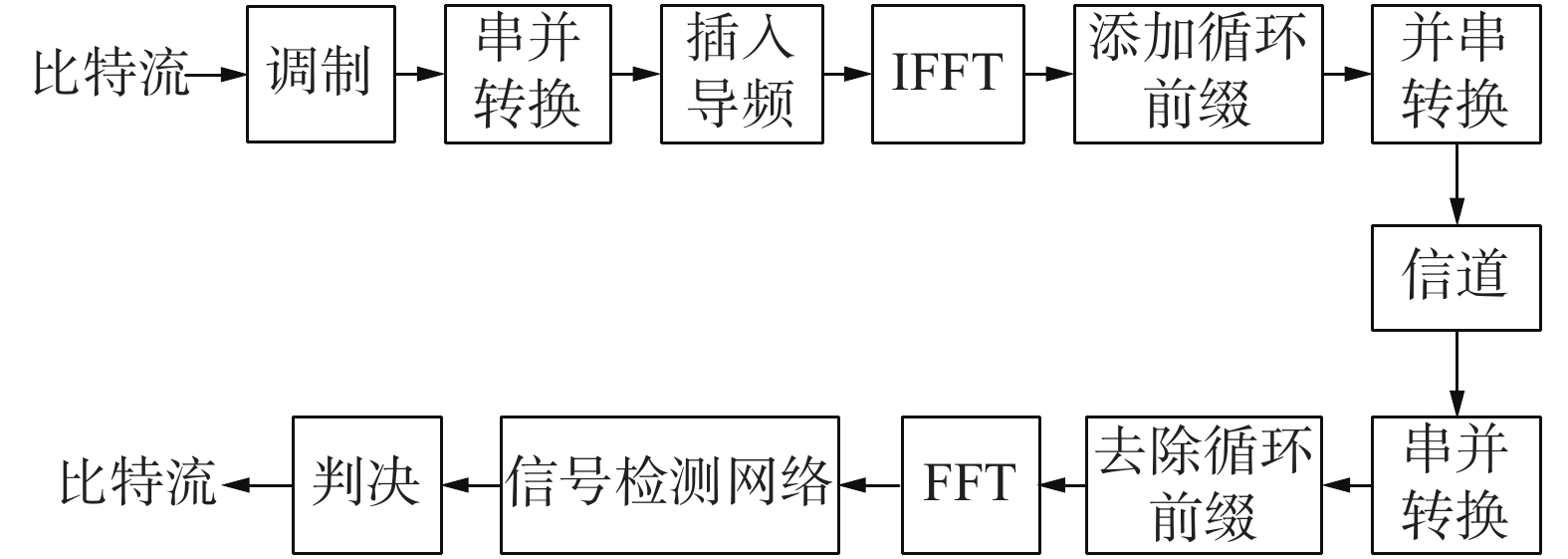
1 系统模型基于深度学习的OFDM系统具体的实现步骤如图1所示。该系统的结构与传统的OFDM系统相似,不过在该系统中,信道估计和均衡被信号检测网络替代。在发送端,需要对生成的比特流进行调制、串并转换、快速傅立叶逆变换(IFFT)、插入导频和添加循环前缀等步骤。IFFT是将信号从时域转换到频域,添加循环前缀是为了消除码间干扰对系统的影响,然后将处理好的信号传入信道。
|
Download:
|
| 图 1 OFDM系统框图 | |
设一个OFDM系统共有N个子载波,调制阶数为M,
则接收到的信号为
| $y(n) = x(n) \otimes h(n) + w(n){\text{}}$ |
式中:
接收到的信号去除循环前缀和FFT变换之后,接收到的频域信号为
| $ Y\left( k \right) = X\left( k \right)*{\rm{H}}\left( k \right) + W\left( k \right){\text{}} $ |
式中Y(k)、X(k)、H(k)和W(k)分别为y(n)、x(n)、h(n)和w(n)的FFT变换。
然后将接收端频域信号传输给信号检测网络,因为神经网络无法处理复数信号,因此需要在将信号传入信号检测网络前做一个预处理,该预处理为将接收信号的实部与虚部分离并串联起来。同时该系统的导频格式为
| $[{x_{{\rm{pilot}}}}\;{x_{{\rm{data}}}}]{\text{}}$ |
式中:xpilot为输入信号的导频部分;xdata为输入信号的数据部分。
2 信号检测网络模型基于神经网络的信号检测方法利用BiLSTM 神经网络设计一种端到端的信号检测网络,先通过OFDM系统仿真数据进行离线训练得到最优参数,再进行在线检测信号,该网络代替了传统方法中的信道估计和均衡。相比于传统的信号检测方法,此设计的信号检测网络在导频数较少时性能更加优异,同时与同为端到端的LSTM信号检测网络相比,本文所提出的BiLSTM采用的是以双向LSTM为基本单元的神经网络,提高了信号检测的能力。
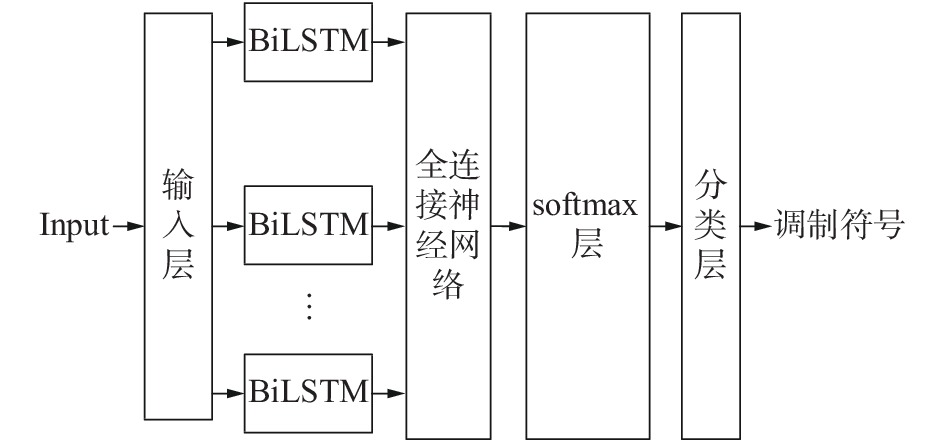
2.1 模型结构本文设计的神经网络结构如图2所示,神经网络由输入层、BiLSTM层神经网络、全连接层、softmax层和分类层组成。
|
Download:
|
| 图 2 信号检测网络结构图 | |
首先为输入层,输入层是将输入的数据进行分批次处理,再将数据逐个批次的传入后面的神经网络层;然后则是BiLSTM层,其主要功能是对输入数据进行处理;BiLSTM层之后则是全连接神经网络层;softmax层提供激活函数,激活函数为
| $ {S}_{i}=\frac{{e}^{{V}_{i}}}{\displaystyle\sum\nolimits_{i}^{C}{e}^{{V}_{i}}}{\text{}} $ |
式中:Vi为分类器前级输出单元的输出;i为类别索引;C为总的类别个数;Si为当前元素指数与所有元素指数和的比值。分类层提供损失函数,三者结合起到分类的作用。
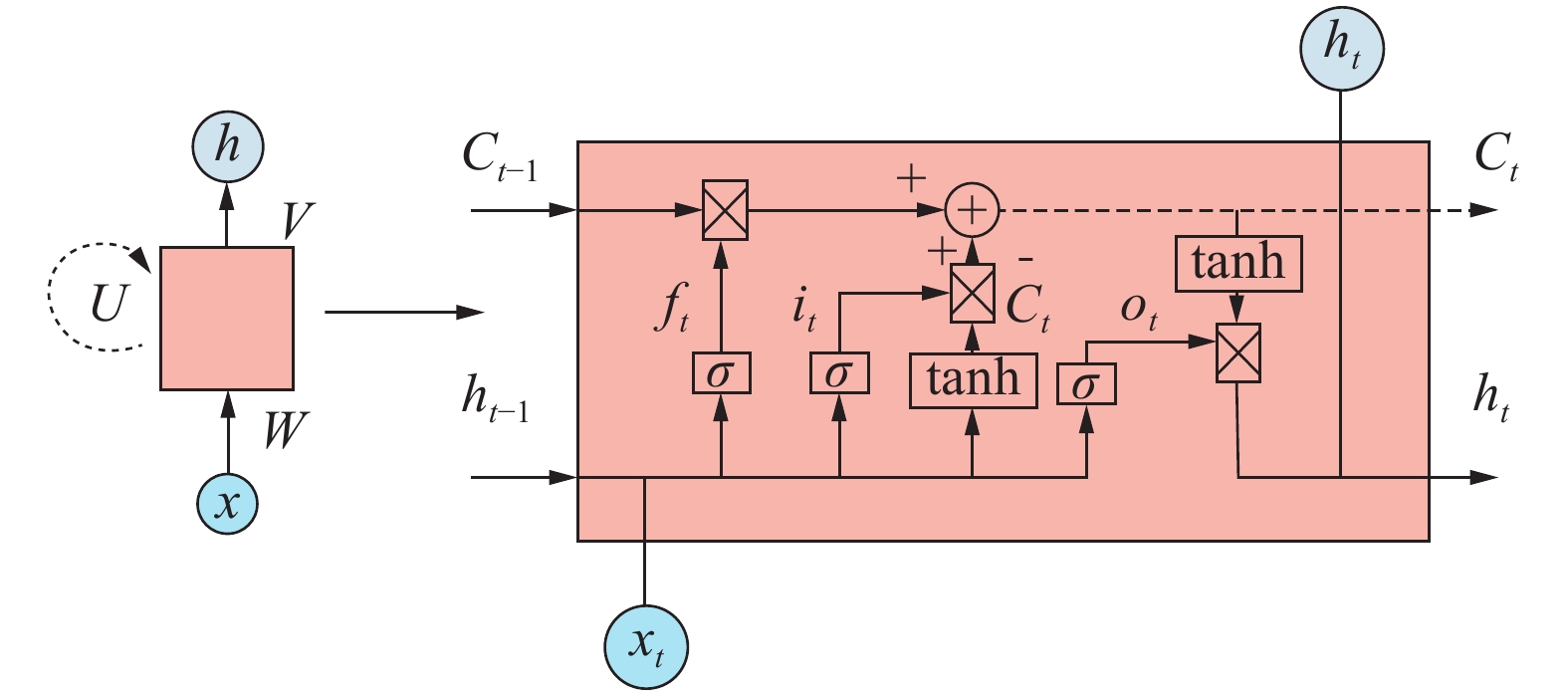
BiLSTM由正向、逆向2个LSTM构成,LSTM只能提取数据的单向信息,BiLSTM同时考虑前后数据的变化规律,展现出更加优越的性能。典型的LSTM结构如图3所示[17]。
|
Download:
|
| 图 3 典型LSTM结构 | |
图3中,x为输入;h为赋予网络记忆能力的隐藏状态;下标t−1、t和t+1为不同的时间步长;W、U、V为不同层的超参数。其节点之间的连接形成沿着序列的有向图,ht为基于前一层隐状态的输出和当前时刻的输入计算得到的。
典型的LSTM的重复单元主要有记忆存储单元状态(Ct)、遗忘门(ft)、输入门(it)和输出门(ot)。遗忘门、输入门和输出门实现对单元状态的控制,选择性地对单元状态添加或移除信息[18]。
| $ {f_t} = \sigma \left( {{{{W}}_f}{x_t} + {{{U}}_t}{{{h}}_{t - 1}} + {{{b}}_f}} \right){\text{}} $ |
| $ {i_t} = \sigma \left( {{{{W}}_i}{x_t} + {{{U}}_i}{{{h}}_{t - 1}} + {{{b}}_i}} \right){\text{}}\; $ |
| $\;\;\;\;\; {\tilde C_t} = \tanh \left( {{{{W}}_c}{x_t} + {{{U}}_c}{{{h}}_{t - 1}} + {{{b}}_c}} \right){\text{}} $ |
| $\; {C_t} = f \otimes {C_{t - 1}} + {i_t} \otimes {\tilde C_t}{\text{}}\;\;\;\quad $ |
| $\;\;\;\; {o_t} = \sigma \left( {{{{W}}_o}{x_t} + {{{U}}_o}{{{h}}_{t - 1}} + {{{b}}_o}} \right){\text{}} $ |
| $ {h_t} = {o_t} \oplus \tanh \left( {{{{C}}_t}} \right){\text{}}\quad\;\;\;\;\;\; $ |
式中:W为隐藏单元的输入权重矩阵;U为输出权重矩阵;b为偏置向量;下标f、i、o为遗忘门、输入门和输出门;
| $ \tanh \left( x \right) = \frac{{\exp \left( x \right) - \exp \left( { - x} \right)}}{{\exp \left( x \right) + \exp \left( { - x} \right)}}{\text{}} $ |
该信号检测网络实现其功能需要进行2个步骤:首先是进行线下训练,该步骤需要在一定的信道模型下生成训练数据,再将训练数据输入到信号检测网络进行训练;然后就是线上应用,该步骤是将经过训练的信号检测网络放入到OFDM系统中实现信道估计和均衡的功能,将OFDM系统经过预处理的接收信号输入到信号检测网络,即可得出调制符号。
2.2 训练模型信号检测网络的使用分为2个阶段,第1阶段是线下训练,即用训练数据集对构建好的神经网络进行训练;第2阶段则是线上应用,将训练好的信号检测网络加到OFDM系统中。而训练数据的收集也是十分重要,本文则在3GPP TR38.901信道模型下生成相应的训练数据。该训练数据的生成过程为:首先对原始二进制比特流进行调制,再对调制后的信号进行标签化处理,做成训练数据的标签,然后进行逆快速傅立叶变换、添加循环前缀以及并串转换生成OFDM发送信号,再将发送信号输入到信道之中,信道输出经过并串转换、去除循环前缀后和快速傅立叶变换,形成用于训练神经网络的样本数据。然后将生成的训练数据输入到信号检测网络中进行训练,其中,信号检测网络所采用的损失函数是交叉熵损失函数,其具体公式为
| $H(y) = - \sum\limits_i {y_i^{'}\log ({y_i})}{\text{}} $ |
式中:
在仿真实验中,OFDM系统所采用的调制方式为正交频移键控(quadrature phase shift keying,QPSK)调制,验证BiLSTM信号检测网络的误符号率性能,并与其他方法进行比较,对于OFDM无线通信系统,本文采用的信道模型为3GPP TR38.901信道模型,导频数目为16个,子载波数为64,循环前缀数量为16,使用的训练集和测试集的样本数目分别为100 000和10 000,训练学习率为0.01。该信号检测网络共包含5层,分别为:输入层、BiLSTM层、全连接层、softmax层和分类层,信道模型为3GPP TR38.901信道模型。信号检测网络中BiLSTM层包含16个神经元,全连接神经网络层包含4个神经元。
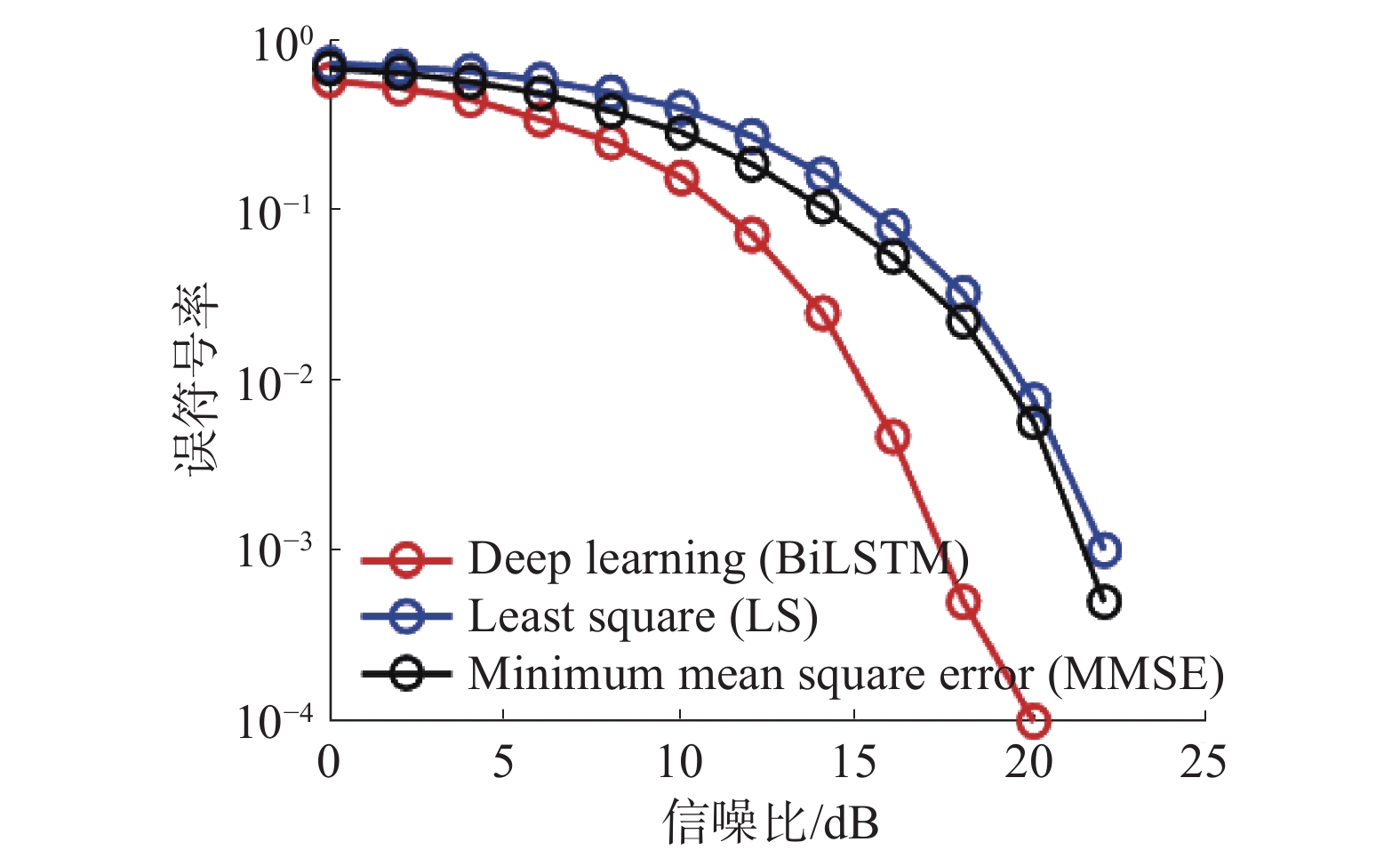
图4给出了LS算法、MMSE算法和BiLSTM信号检测网络的性能比较。由图4可见,本文所提算法在误符号率为10−3时,与传统的LS和MMSE算法相比有了5~6 dB的性能提升。由此可见本文所提出的算法与传统的OFDM信号检测方法相比,能够显著的降低OFDM系统传输信号误符号率。
|
Download:
|
| 图 4 LS、MMSE和BiLSTM信号检测网络性能比较 | |
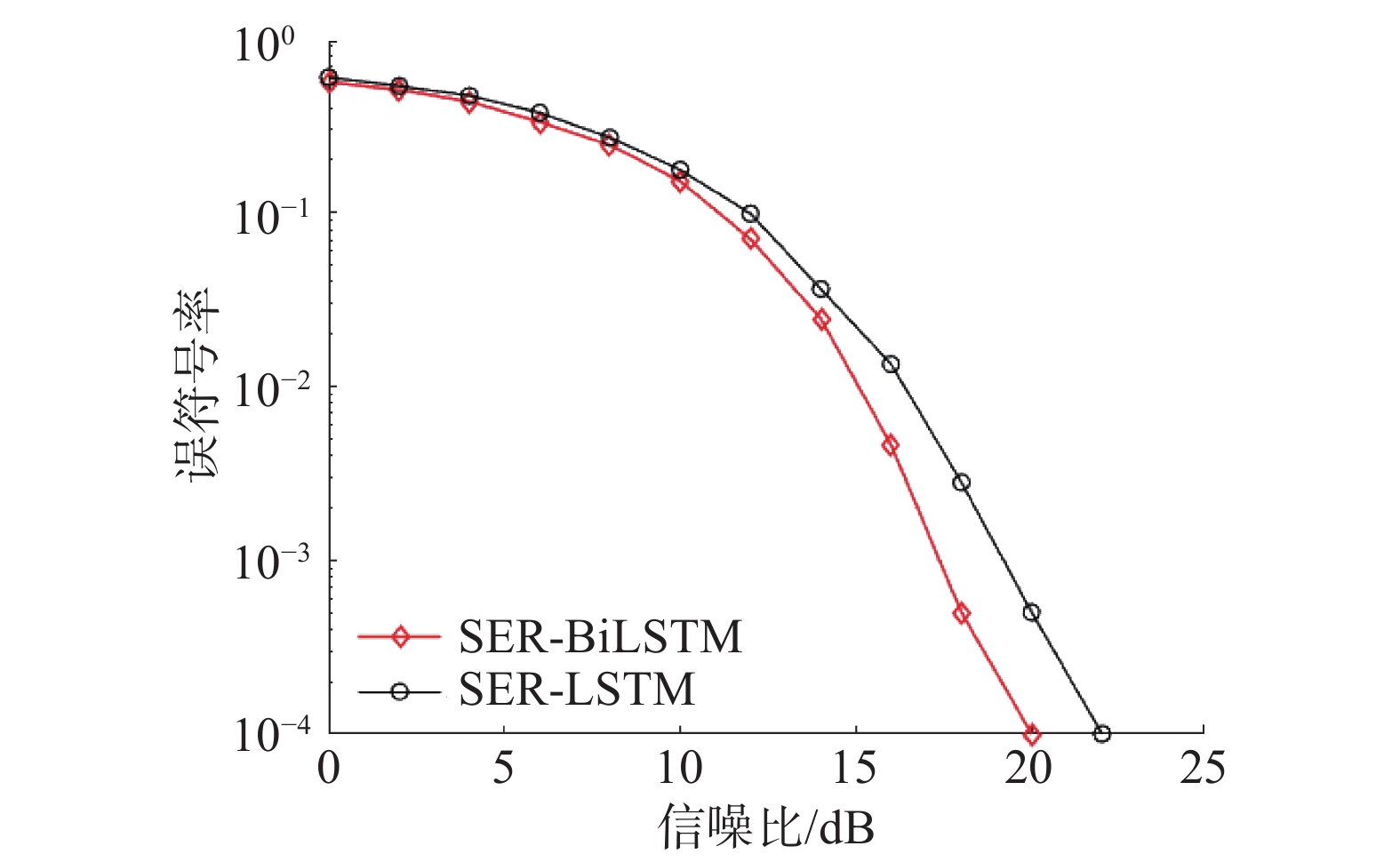
图5分别给出了BiLSTM信号检测网络和LSTM信号检测网络的性能比较。由图5可见,BiLSTM信号检测网络在误符号率为10−3时,与LSTM信号检测网络相比性能有了2~3 dB的提升,由此可见BiLSTM信号检测网络采用双向LSTM为基本单元,可以提高信号检测的准确性。
|
Download:
|
| 图 5 BiLSTM和LSTM信号检测网络性能比较 | |
本文针对传统的信号检测算法在OFDM系统导频较少时误符号率高的问题,提出了一种基于深度学习的OFDM信号检测方法。
1)该方法相比较于传统的算法,在误符号率为10−3时,性能有了5~6 dB的提升,提高了OFDM无线通信系统在导频数量较少时的信号检测性能。
2)该方法相比于LSTM信号检测方法,在误符号率为10−3时,性能有了2~3 dB的提升,并且因为采用端到端的方式从接收数据中恢复出调制信号,而不用估计出具体的信道冲激响应,实现起来较为简单,且性能较好。
| [1] |
李斌. OFDM基带系统关键技术及其FPGA设计与实现[D]. 长沙: 湖南大学, 2011.
( 0) 0)
|
| [2] |
丁凌琦, 穆道生, 蒋太杰, 等. OFDM技术应用现状分析[J]. 软件, 2016, 37(10): 130-134. DOI:10.3969/j.issn.1003-6970.2016.10.030 ( 0) 0)
|
| [3] |
SUTAR M B, PATIL V S. LS and MMSE estimation with different fading channels for OFDM system[C]//Proceedings of 2017 International conference of Electronics, Communication and Aerospace Technology. Coimbatore, India, 2017: 740–745.
( 0) 0)
|
| [4] |
DEEP BORAH A, BORA J. Post-processing noise of ZF detector with varying channel condition[C]//Proceedings of 2018 International Conference on Recent Innovations in Electrical, Electronics & Communication Engineering. Bhubaneswar, India, 2018: 360–362.
( 0) 0)
|
| [5] |
STERBA J, KOCUR D. Pilot symbol aided channel estimation for OFDM system in frequency selective Rayleigh fading channel[C]//Proceedings of 2009 19th International Conference Radioelektronika. Bratislava, Slovakia, 2009: 77–80.
( 0) 0)
|
| [6] |
HUSSEINI A H E, SIMON E P, ROS L. Optimization of the second order autoregressive model AR(2) for Rayleigh-Jakes flat fading channel estimation with Kalman filter[C]//Proceedings of 2017 22nd International Conference on Digital Signal Processing. London, UK, 2017: 1-5.
( 0) 0)
|
| [7] |
杨宗林, 刘梅. 第四代移动通信系统中的OFDM技术[J]. 通信技术, 2007, 40(11): 73-75. DOI:10.3969/j.issn.1002-0802.2007.11.028 ( 0) 0)
|
| [8] |
POLLET T, VAN BLADEL M, MOENECLAEY M. BER sensitivity of OFDM systems to carrier frequency offset and wiener phase noise[J]. IEEE transactions on communications, 1995, 43(2/3/4): 191-193. DOI:10.1109/26.380034 ( 0) 0)
|
| [9] |
范毅君, 蔡家麟. OFDM通信系统研究及其仿真分析[J]. 软件导刊, 2009, 8(1): 154-155. ( 0) 0)
|
| [10] |
王文博, 郑侃. 宽带无线通信OFDM技术[M]. 2版. 北京: 人民邮电出版社, 2007.
( 0) 0)
|
| [11] |
YE Hao, LI G Y, JUANG B H. Power of deep learning for channel estimation and signal detection in OFDM systems[J]. IEEE wireless communications letters, 2018, 7(1): 114-117. DOI:10.1109/LWC.2017.2757490 ( 0) 0)
|
| [12] |
MAO Zhendong, YAN Shi. Deep learning based channel estimation in fog radio access networks[J]. China communications, 2019, 16(11): 16-28. DOI:10.23919/JCC.2019.11.002 ( 0) 0)
|
| [13] |
SOLTANI M, POURAHMADI V, MIRZAEI A, et al. Deep learning-based channel estimation[J]. IEEE communications letters, 2019, 23(4): 652-655. DOI:10.1109/LCOMM.2019.2898944 ( 0) 0)
|
| [14] |
GIZZINI A K, CHAFII M, NIMR A, et al. Deep learning based channel estimation schemes for IEEE 802.11p standard[J]. IEEE Access, 2020, 8: 113751-113765. DOI:10.1109/ACCESS.2020.3003286 ( 0) 0)
|
| [15] |
CHUN C J, KANG J M, KIM I M. Deep learning-based joint pilot design and channel estimation for multiuser MIMO channels[J]. IEEE communications letters, 2019, 23(11): 1999-2003. DOI:10.1109/LCOMM.2019.2937488 ( 0) 0)
|
| [16] |
HE Hengtao, WEN Chaokai, JIN Shi, et al. Deep learning-based channel estimation for beamspace mmWave massive MIMO systems[J]. IEEE wireless communications letters, 2018, 7(5): 852-855. DOI:10.1109/LWC.2018.2832128 ( 0) 0)
|
| [17] |
VANKAYALA S K, KUMAR S, KOMMINENI I. Optimizing deep learning based channel estimation using channel response arrangement[C]//Proceedings of 2020 IEEE International Conference on Electronics, Computing and Communication Technologies. Bangalore, India, 2020: 1–5.
( 0) 0)
|
| [18] |
BALEVI E, DOSHI A, ANDREWS J G. Massive MIMO channel estimation with an untrained deep neural network[J]. IEEE transactions on wireless communications, 2020, 19(3): 2079-2090. DOI:10.1109/TWC.2019.2962474 ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


