没有干扰不了的雷达,也没有抵抗不了的干扰[1]。这说明干扰和抗干扰是协同发展的关系,随着DRFM技术的日益完善,这种新型雷达有源干扰呈现出灵活多变和脉压增益大的特点,对于主动雷达系统,回波信号伴随着敌军的有意干扰信号,它们一方面具有欺骗目标的干扰作用,另一方面具有压制目标信号的干扰作用,为雷达的追踪和检测带来了巨大的挑战。干扰对抗中最关键的一步就是干扰识别。文献[2]提出了一种提取信号频谱稀疏性的方法,用以识别出间歇采样转发干扰。文献[3]采用半监督生成对抗网络( secure steganography based on generative adversarial networks,SSGAN)和改进模型图卷积−半监督对抗生成神经网络(graph CNN-secure steganography based on generative adversarial networks,GC-SSGAN)实现了干扰样本的半监督学习,在分析了9种典型的有源干扰的前提下进行特征提取,使用合适的识别器和识别网络进行识别。文献[4]提出了一种宽带雷达非常规有源干扰识别方法。大量文献表明,干扰识别方法已成为抗干扰技术中的热点话题,为后续的抑制干扰做铺垫。
1 目标和干扰模型分析 1.1 新型压制干扰 1.1.1 噪声卷积灵巧干扰噪声卷积干扰定义为[5]
| $ {j_{\rm{1}}}(t) = n(t) \otimes s(t) $ |
式中:
噪声卷积干扰通过雷达匹配滤波之后的输出为
| $ {y_1}(t) = {j_1}(t) \otimes {{\rm h}{(t) = {\rm h}(t)}} \otimes s(t) \otimes n(t) $ |
式中
同时噪声卷积干扰信号的频谱为
| $ {J_1}(\omega ) = F[{j_1}(t)] = F[s(t) \otimes n(t)] = S(\omega )N(\omega ) $ |
式中:
由上述可知,噪声卷积干扰就是噪声信号与截获信号相乘积,而这相当于频域的乘积运算,这使得干扰的频谱无需引导就对准目标频谱。
1.1.2 噪声乘积灵巧干扰噪声乘积干扰可以定义为[6]
| $ {J_2}(t) = s(t)n(t) $ |
噪声乘积干扰信号的频谱为
| $ {J_{\rm{2}}}{\rm{(}}\omega {) = {{F}}[}{{{j}}_{\rm{2}}}{{(t)] = S(}}\omega {\rm{)}} \otimes {{N(}}\omega {\rm{)}} $ | (1) |
由式(1)可知,噪声乘积干扰是由噪声与截取信号相乘积而产生,这就相当于频域相卷积,表现为频谱的多普勒频移,以达到干扰的目的。
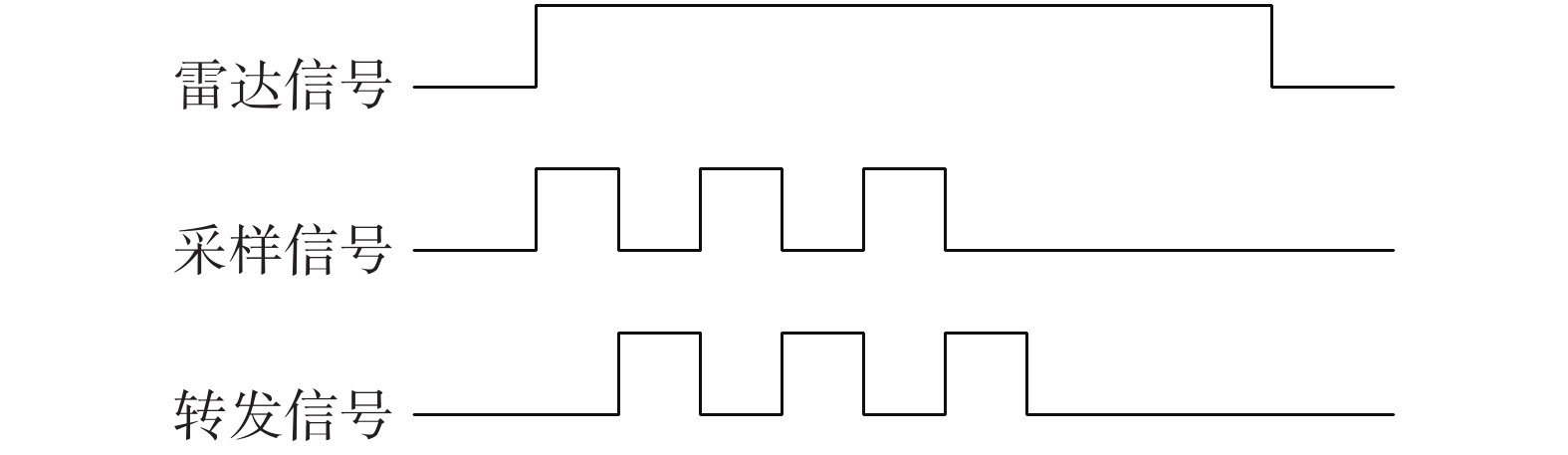
1.2 新型欺骗干扰 1.2.1 间歇采样直接转发干扰间歇采样直接转发的基本原理是[7]基于DRFM的干扰机接收端截获到雷达回波信号后,在脉冲信号内,先根据采样时长截取其中一小段信号做高保真采样,在采样间歇时,把采样信号处理转发,然后进入下一个循环:采样,转发。工作方式如图1所示。
|
Download:
|
| 图 1 间歇采样直接转发工作原理 | |
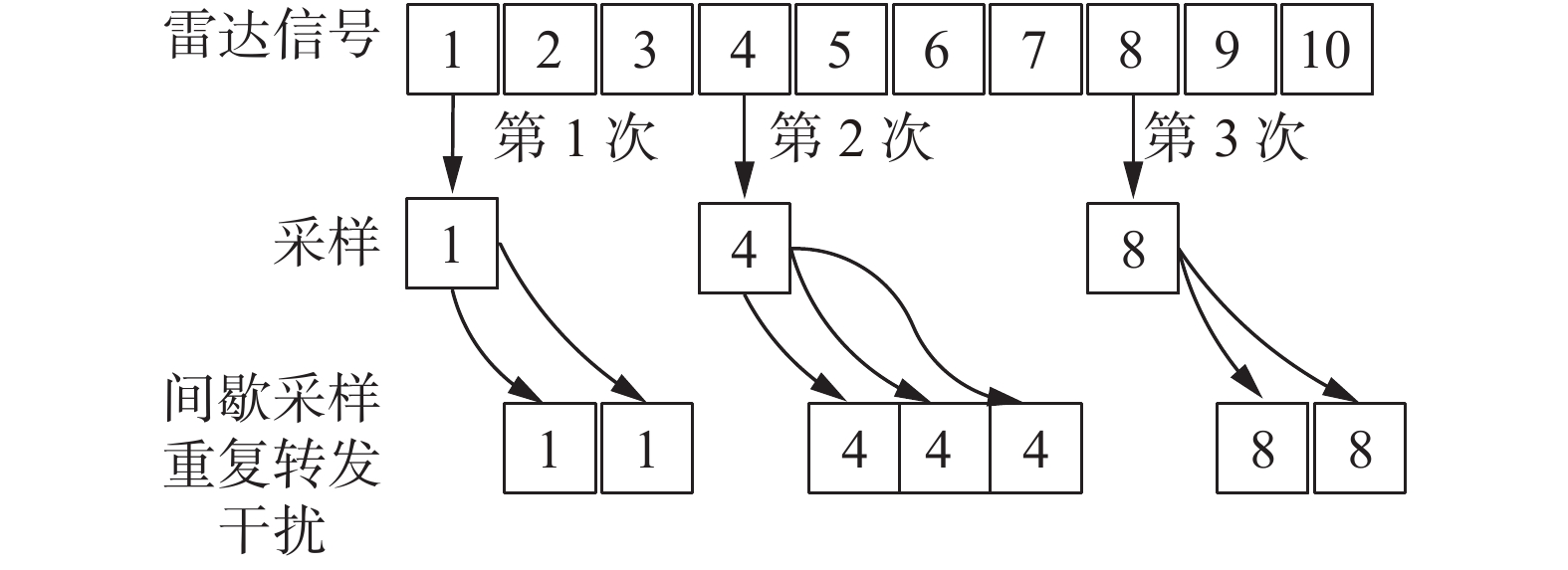
间歇采样重复转发干扰的产生原理[8]是基于DRFM的干扰机接收端截获到雷达回波信号后,在脉冲信号内,先根据采样时长截取其中一小段信号做高保真采样,在采样间歇时,对切片信号进行规定次数的不间断重复转发,然后进入下一个循环:采样,重复转发。工作原理如图2所示。一般情况,循环中的重复转发次数相同。
|
Download:
|
| 图 2 间歇采样重复转发工作原理 | |
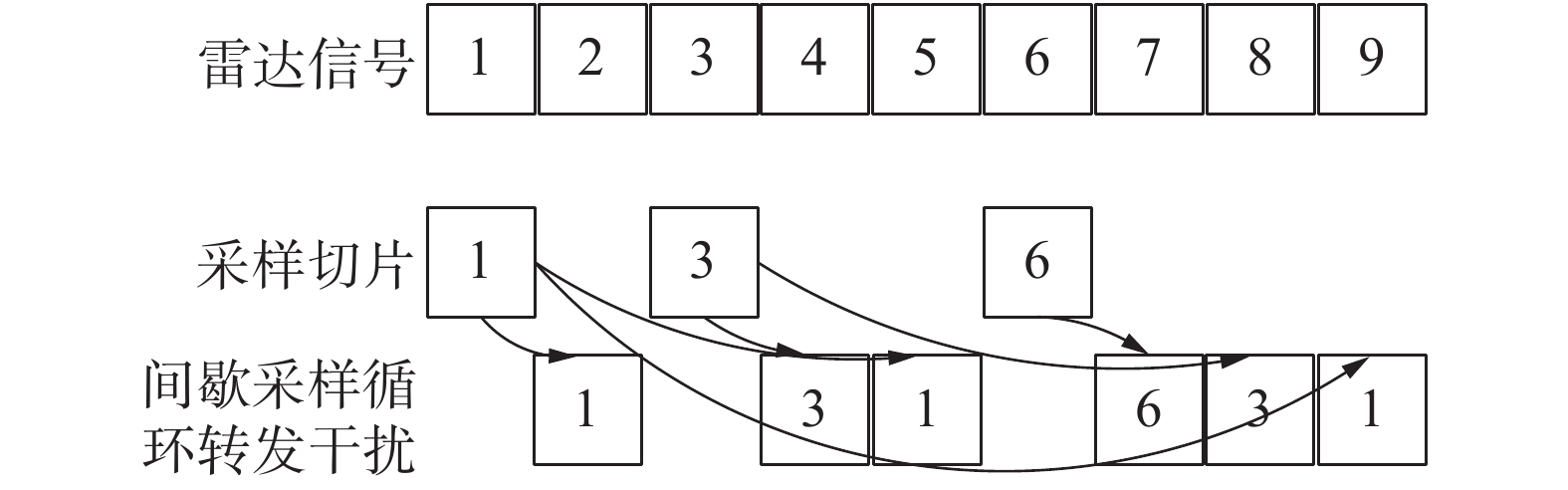
间歇采样循环转发干扰的产生原理[9]是基于DRFM的干扰机接收端截获到雷达回波信号后,在脉冲信号内,根据采样参数对截获信号进行截取,在采样间歇时,对切片信号进行转发,转发规则为对于每一个截取的切片在本循环立刻转发之外,在下第
|
Download:
|
| 图 3 间歇采样循环转发工作原理 | |
为了能够在低信噪比下分离出具有“冲击”特性的干扰分量,引入了一个概念−峭度[10]。峭度系数K可以定量表征出峭度特性,作为一个无量纲参数,其可以定义为
| $ K = \frac{{{\rm{E}}{{(x - \mu )}^4}}}{{{\sigma ^4}}} $ | (2) |
式中:
由式(2)可知,峭度值越大,则所求信号的观测值浮动就越大。由此可以得到结论:在低信噪下,信号的SSD分量的K值越大,则此分解分量的干扰信息就越丰富,干扰类型的特性就越明显,因此峭度系数可作为最佳参数选择的依据。
2.2 SSD算法及其参数选择SSD是现代信号处理的一种新方法,它能够解决非线性和非平稳时间序列信号的自适应分解问题,分解成若干成分,这些成分就称之为奇异谱分量(singular spectrum component,SSC),SSD算法是基于迭代算法把成分从高频向低频排列。
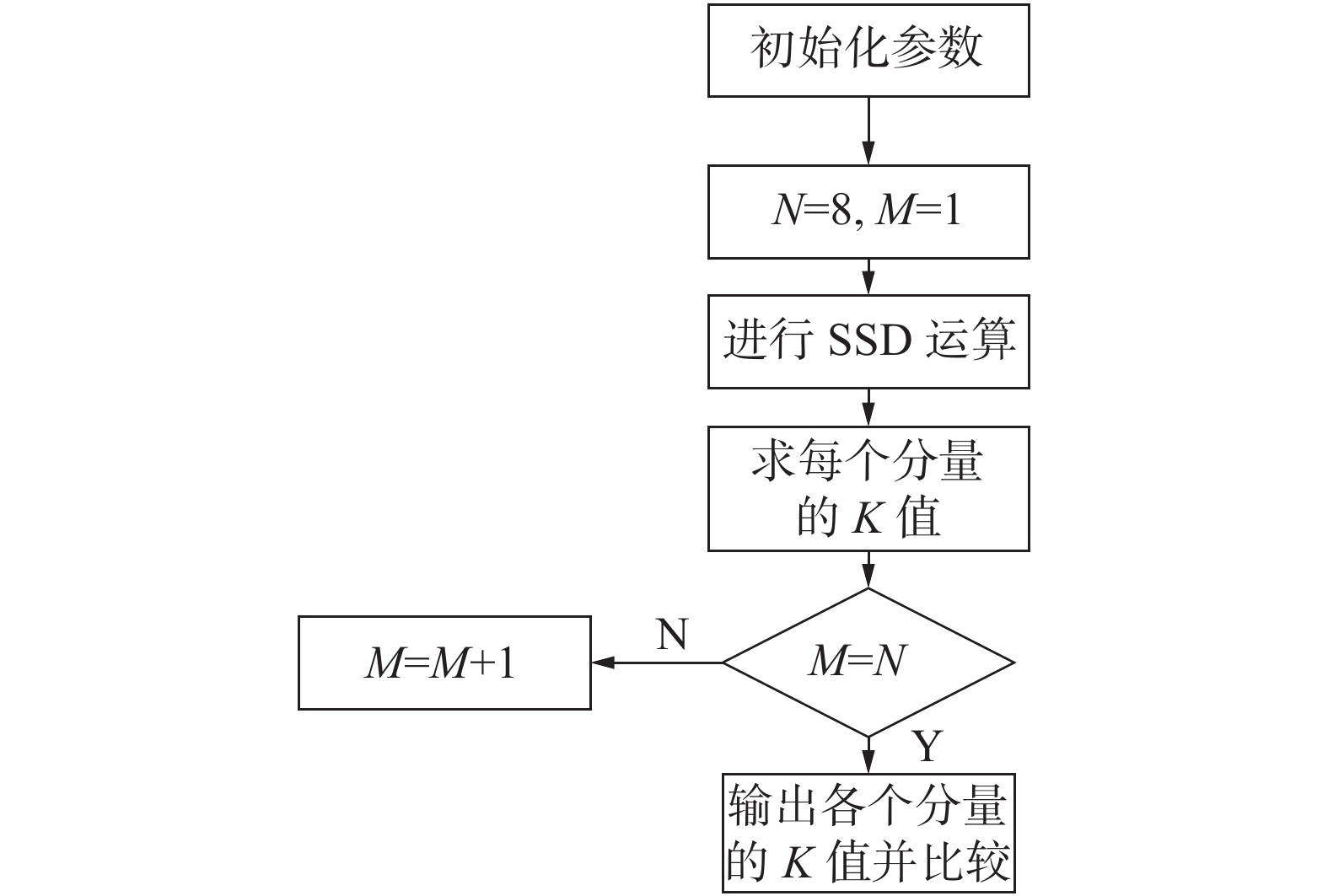
SSD算法需要选取分解个数和最优分量。以往需要人为的经验选取,不仅效率低下而且选取的参数可能也不是最优解[11]。为此,本文提出了一种基于峭度准则的自适应参数选择的方法,用以同时解决奇异谱分解算法中分解个数设置和最优分量选取的问题。奇异谱分解算法的自适应参数选择的流程如图4所示。
|
Download:
|
| 图 4 自适应SSD参数选择流程 | |
具体步骤如下:
1)预设一个最大分解个数
2)利用奇异谱分解算法对信号进行处理,得到M个分量,对这M个分量分别求峭度系数,并储存。
3)令
4)将储存的峭度系数进行比较,可以先把每个分解个数的第1个分量取出作比较得到,选取最佳分解个数,然后把该最佳分解个数的所有分解分量进行比较得到最佳分解分量。其依据就是K值大小,K值越大代表该分量的干扰特征明显,干扰信息丰富,更有特征提取的价值。
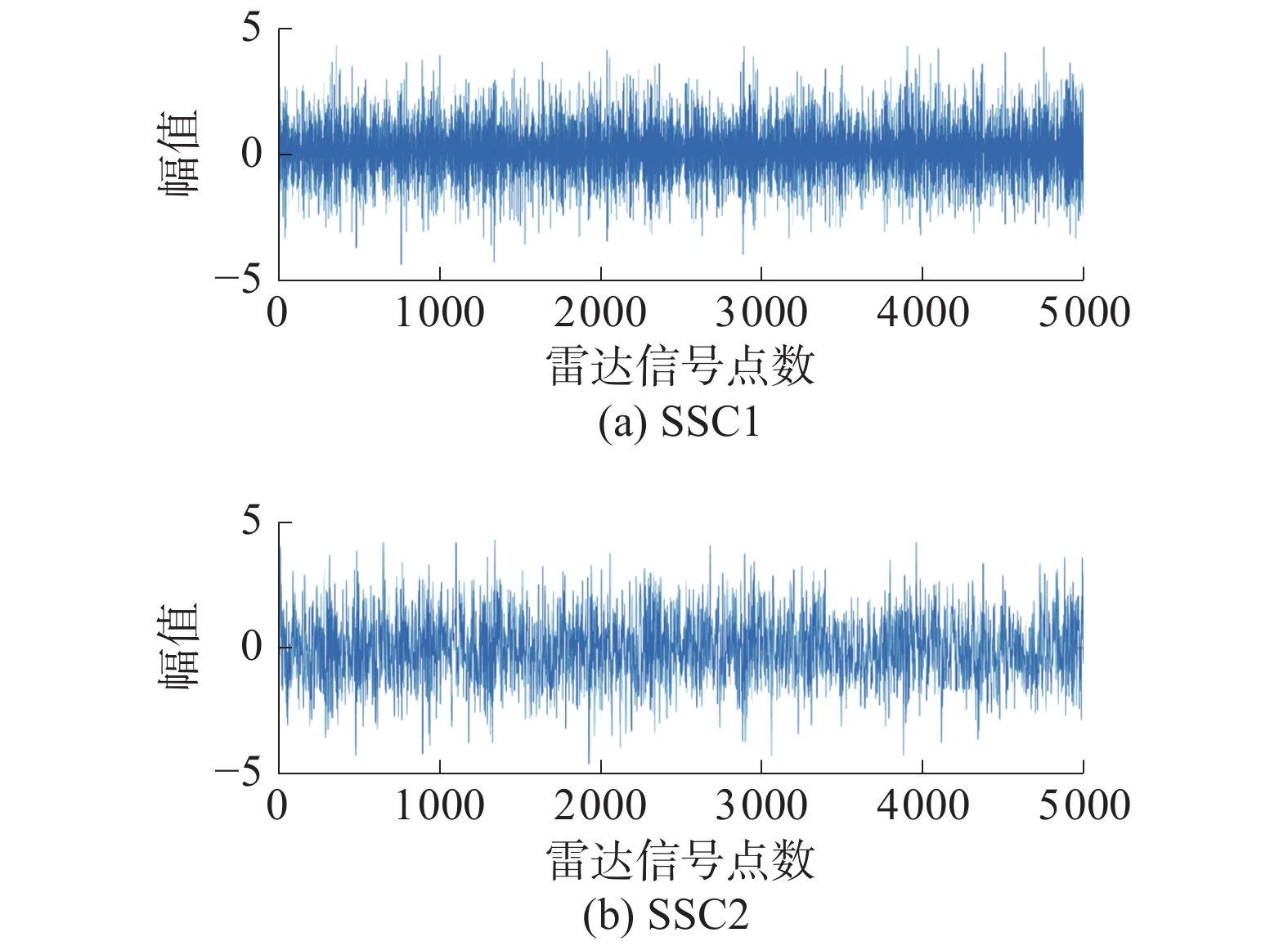
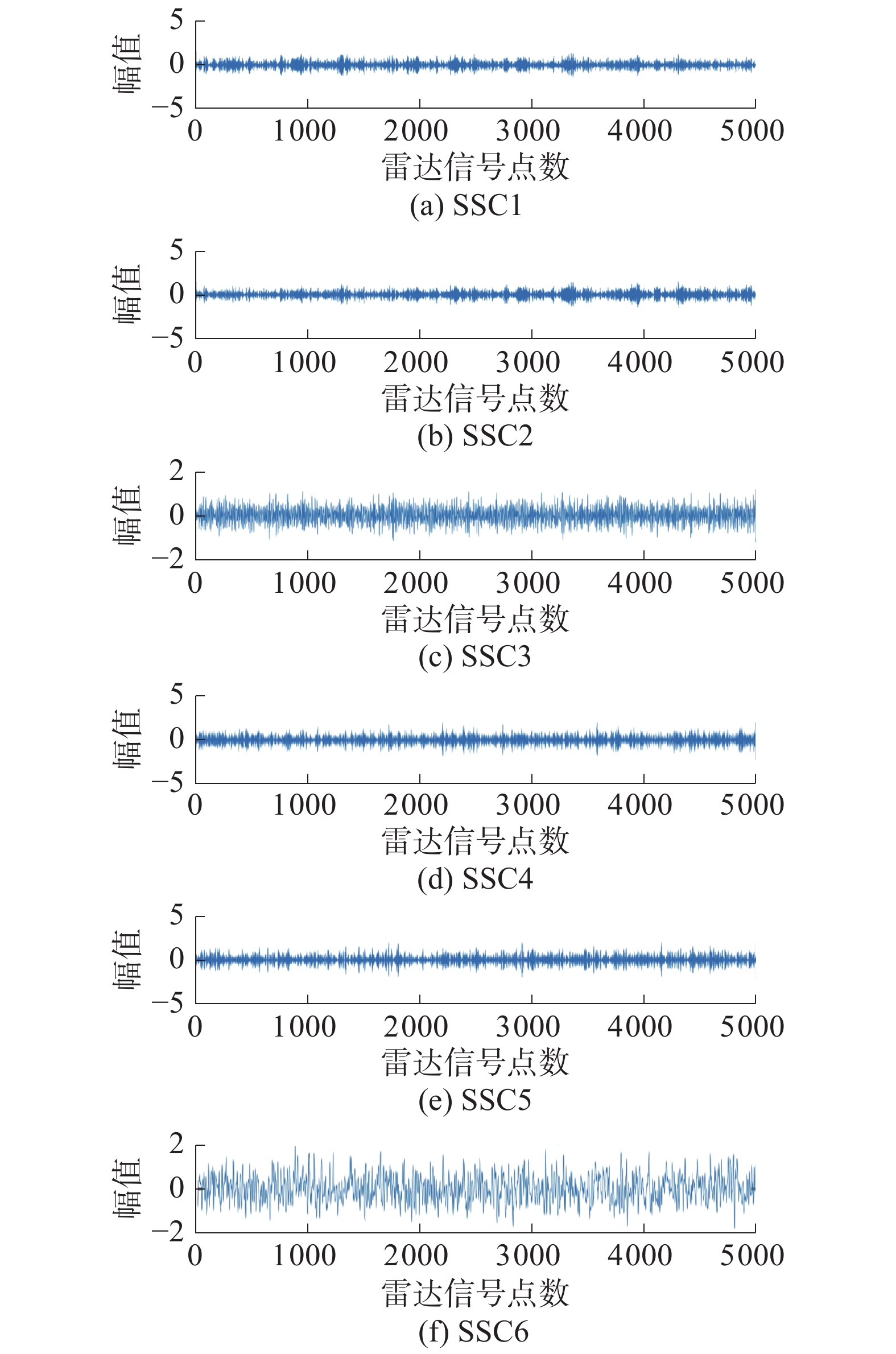
在此,以间歇采样直接转发干扰为例,设定了分解个数为2、6、8时,把混合信号进行奇异值分解,其结果如图5~7所示。从3个图可以看出,随着分解个数的增加,混合信号被分解的更加细致。
|
Download:
|
| 图 5 分量个数为2时SSD分解结果 | |
|
Download:
|
| 图 6 分量个数为6时SSD分解结果 | |

|
Download:
|
| 图 7 分量个数为8时SSD分解结果 | |
本文通过上述方法,得到最优选取分量个数为8。在选择完最佳分量个数后,分别得到了每个分解分量的峭度值如表1所示。从表中我们可以看出,第1个成分的峭度值最高,因此,本文选择第1个分解成分作为主要分析成分。
|
|
表 1 分量个数为8时各分量的峭度系数 |
对于一个非高斯的随机平稳信号x(t),其三阶累积量为[12]
| $ {C_{3X}}({\tau _1},{\tau _2}) = {\rm{E}}[x(n)x(n + {\tau _1})x(n + {\tau _2})] $ |
定义三阶累积量一维的对角切片为
| $ r_{1,2}^x(\tau )\mathop = \limits^\Delta {\rm{cum}}(x(t),x(t + \tau ),x(t + \tau )) = {C_{3x}}(\tau ,\tau ) $ |
定义三界累积量对角切片的傅里叶变换为x(t)的1.5维谱[13]
| $ B(\omega )\mathop = \limits^\Delta \int\limits_{ - \infty }^\infty {r_{1,2}^x(\tau )} \rm{e}^{ - {\rm{j}}\omega \tau }{\rm{d}}\tau \mathop = \limits^\Delta {C_{3x}}(\tau ,\tau ){{\rm{e}}^{ - {\rm{j}}\omega \tau }}{\rm{d}}\tau $ |
时变1.5维谱是高阶累积量,具有抑制高斯噪声和对称分布噪声的能力;且其计算量在高阶谱中最小,与功率谱相近;可增强谐波信号中的基频分量;可消除二次相位耦合时的谐波分量;能准确地提取出干扰的特征。
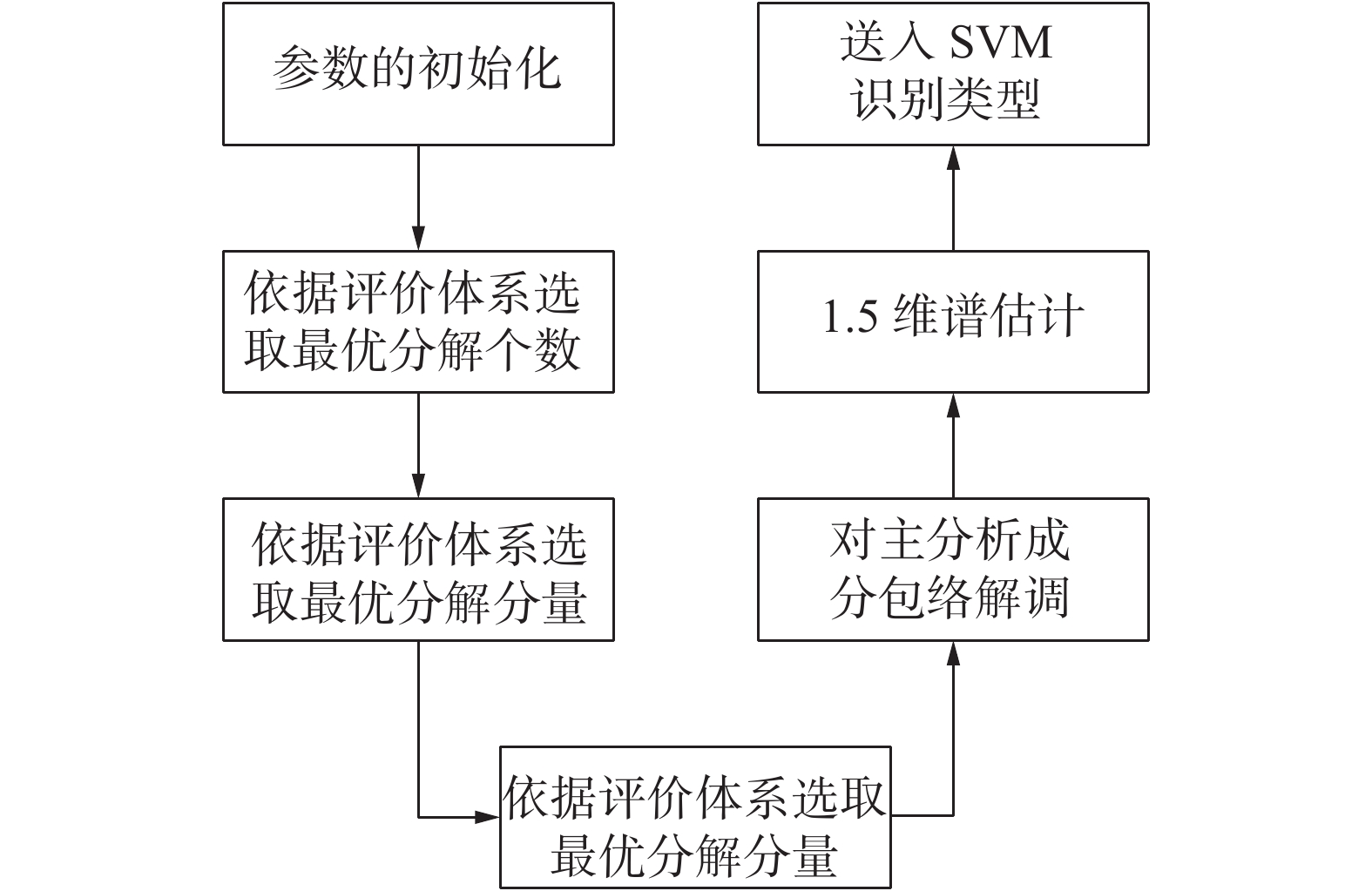
3.2 SSD算法和1.5维谱的新型雷达干扰识别 方法鉴于上面所述,论述了奇异值分解和1.5维谱的优势,SSD算法先对低信噪比下的信号进行处理,提高信噪比,把分解分量进行1.5维谱计算,提高信噪比的同时,把干扰的特征提取出来以做识别。本文结合了两者的优势提出了基于SSD算法和1.5维谱的自适应性雷达新型干扰识别方法,具体的方法流程如图8所示。
|
Download:
|
| 图 8 算法流程 | |
1)自适应SSD参数选择。混合信号送入参数评价系统,首先先设定最大分解个数,这里设置最大分解个数为8,依据图4所示流程,通过基于峭度准则的评价体系,不断迭代选取最优的奇异值分解个数。
2)主分析成分的选取。已知步骤1)中选取的最优分解个数,把混合信号通过SSD算法分解,再根据每个分解分量的K值,选取最优分解分量,把这个分解分量作为主分析成分。
3)主分析成分的特征提取。我们对主分析成分进行包络解调,对主分析成分的包络求取1.5维谱估计。
4)把1.5维谱估计的结果送入SVM中,进行识别,获得识别结果。
3.3 实验仿真和结果分析对间歇采样直接转发干扰,间歇采样重复转发干扰,间歇采样循环转发干扰,噪声卷积干扰,噪声乘积干扰分别与雷达回波信号混合,实验参数为信号采样率为50 MHz,雷达回波信号的脉宽为100 μs,带宽B为5 MHz。所有干扰的干信比设为20 dB。间歇采样直接转发干扰信号的仿真参数为:采样间隔为10 μs,采样占空比为50%。间歇采样重复转发干扰信号的仿真参数为:采样间隔为25 μs,采样占空比为20%。间歇采样循环转发干扰信号的仿真参数为:采样间隔为25 μs,采样占空比为20%。噪声卷积干扰信号的仿真参数为:调制噪声采用带限高斯白噪声,噪声带宽15 MHz,噪声长度100 μs。噪声乘积干扰信号的仿真参数为:调制噪声采用带限高斯白噪声,噪声带宽1 MHz,噪声长度100 μs。
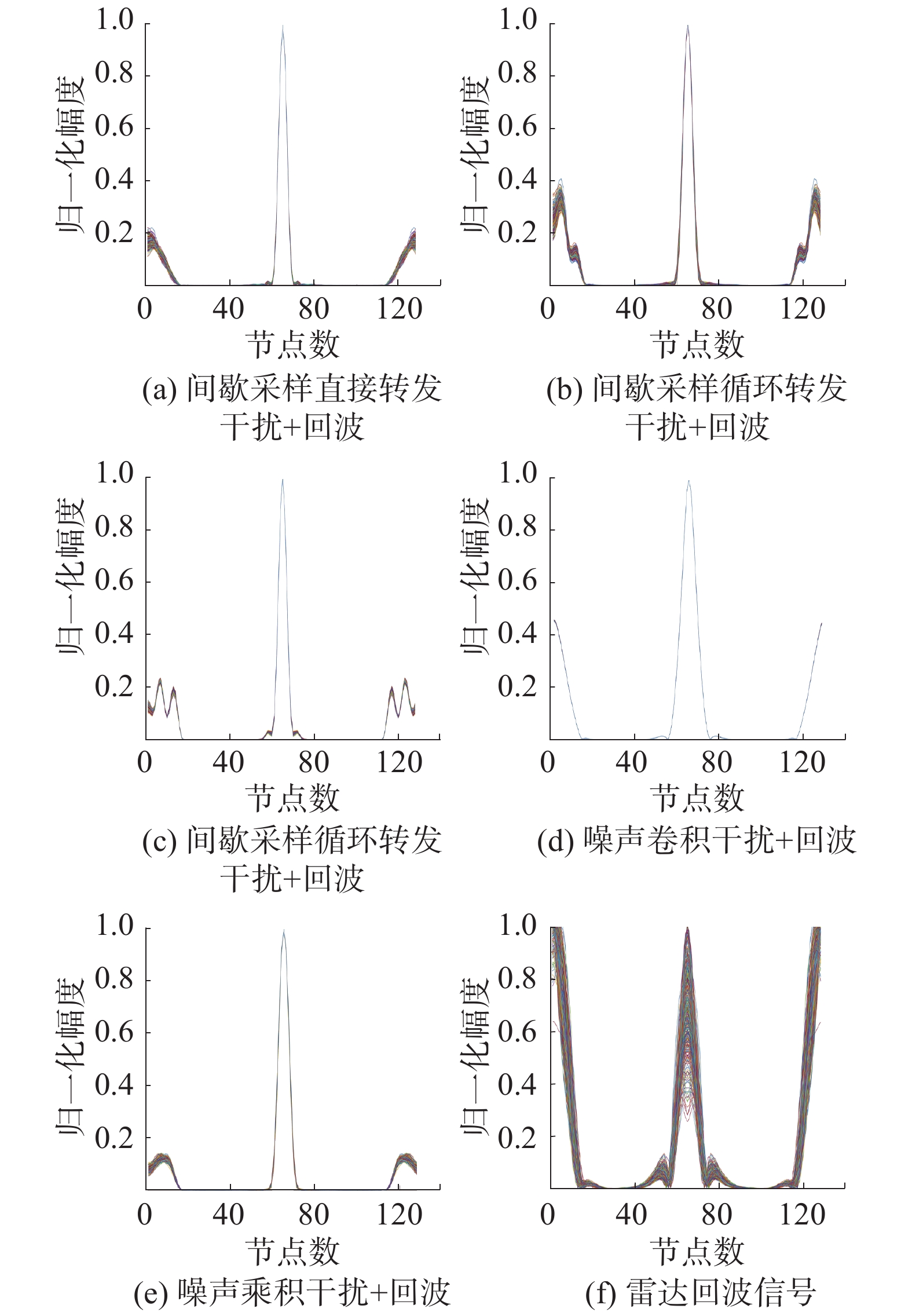
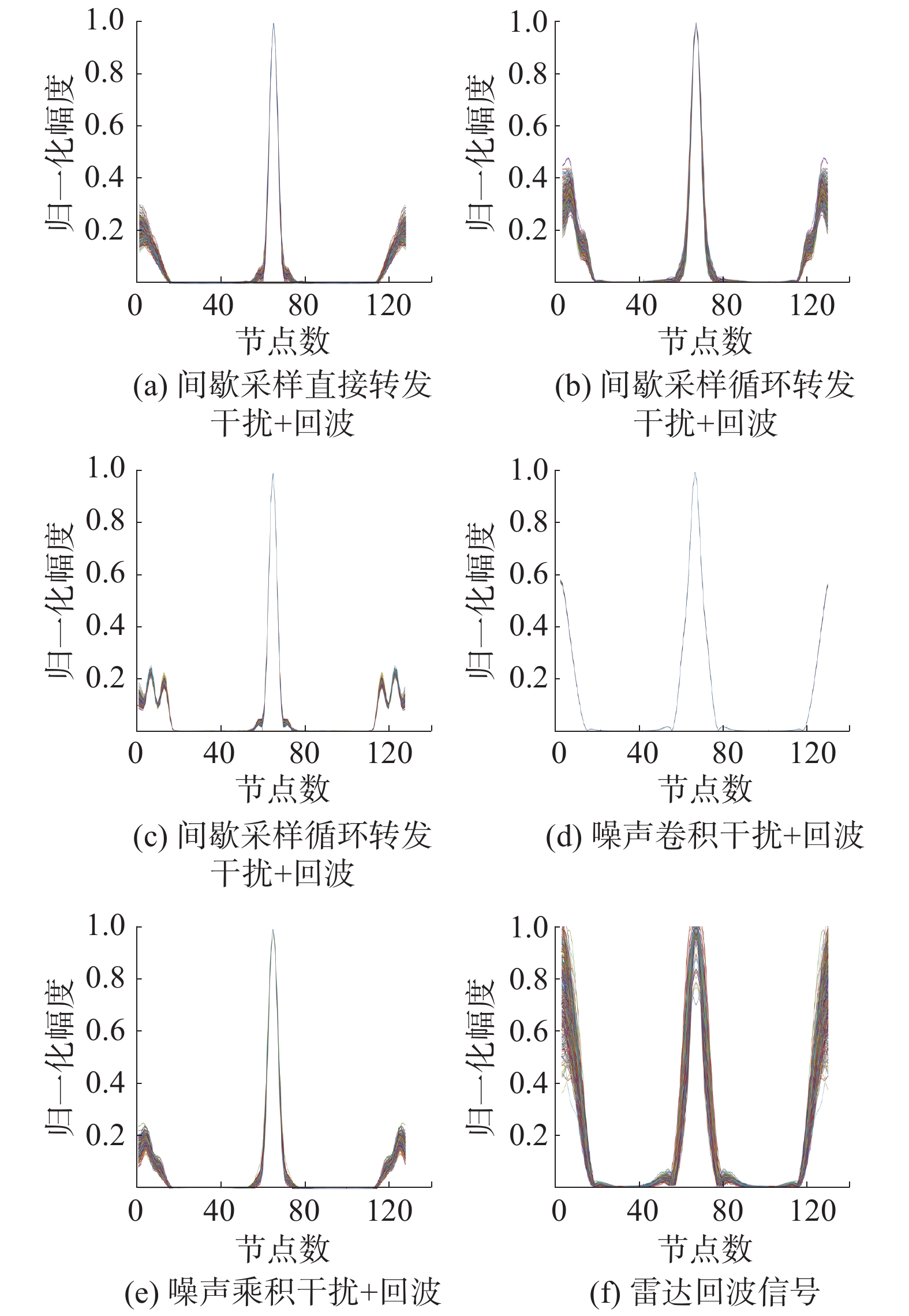
本实验先分别对信噪比为5 dB和0 dB的混合信号送入搭建的系统,得到归一化1.5维谱估计,每种信号类型仿真了400次,结果如图9、10所示。
|
Download:
|
| 图 9 信噪比为5 dB时的1.5维谱 | |
|
Download:
|
| 图 10 信噪比为0 dB时的1.5维谱 | |
从图9、10可以看出本文提出方法的优越性。由结果横向对比,可以看出5种干扰和回波的1.5维谱中峰的个数、峰面积、开始以及结束的图谱走势等不尽相同。对结果纵向对比,可以看出0 dB和5 dB两种信噪比下的5种新型干扰和雷达回波的1.5维谱基本相同,说明这种特征稳定。
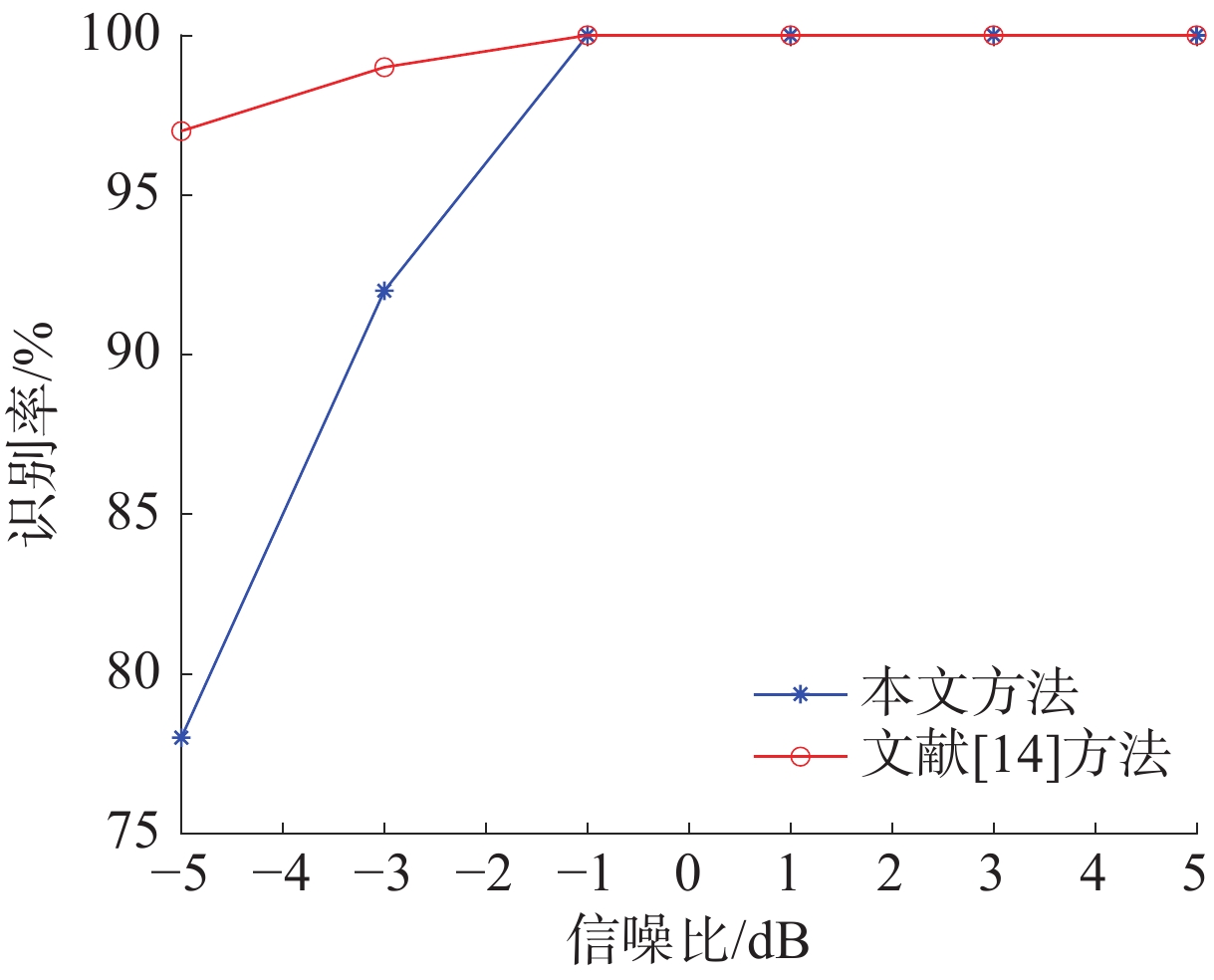
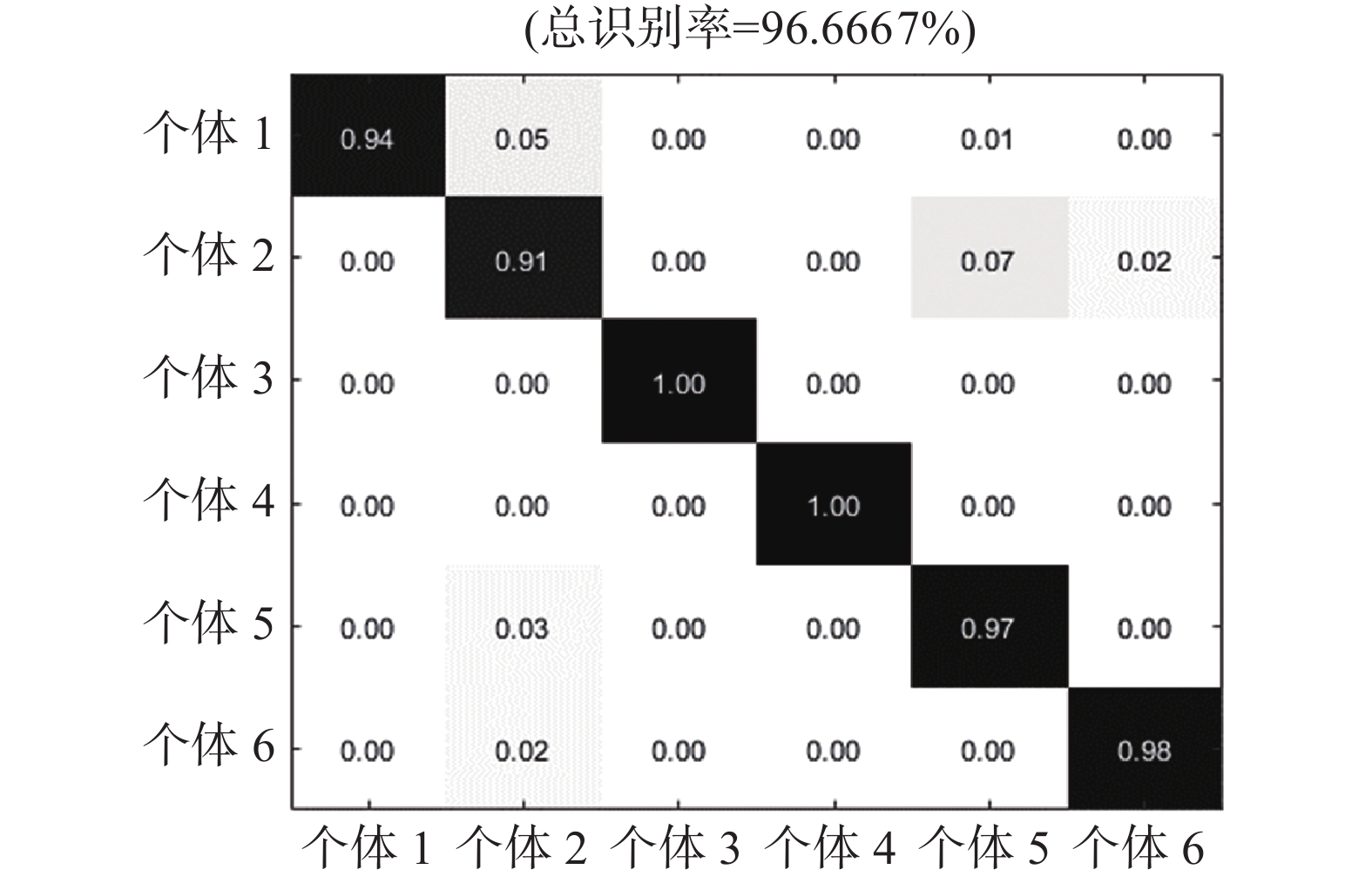
根据流程把5种干扰和回波的混合信号送入搭建的系统,设定实验中的信噪比范围为−5~5 dB,以步长为2 dB进行实验,每次实验进行400次蒙特卡洛仿真,选取280个特征样本作为支持向量机的训练集,选取另外的120个特征样本作为支持向量机的测试集,送入SVM中进行训练学习并识别,其识别结果与文献[14]的对比结果如图11所示,每种信号的各自识别率如表2所示,6种信号在信噪比为−5 dB下的混淆矩阵如图12所示。
|
Download:
|
| 图 11 本文方法和文献[14]的识别方法对比 | |
|
|
表 2 不同信噪比下的识别率 |
|
Download:
|
| 图 12 信噪比为−5 dB时的混淆矩阵 | |
从表2、图11和图12可以看出,在低信噪比下,本文提出的方法也具有很高的识别率,在信噪比高于−5 dB时,平均识别率高于95%,不仅可以识别出回波是否被干扰,而且还可以识别出干扰类型。与文献[14]中的方法相比,使用文献中的方法,信噪比在−2 dB以上、识别率在90%以上;信噪比在−4 dB时,识别率接近80%。
4 结论本文首先对干扰进行了仿真,依据干扰机理,分析提取目标在最佳SSD分解个数下的最佳分解分量的1.5维谱特征,所提特征因子在谱上体现了目标和干扰的差异。在上述特征提取的基础上,利用支持向量机分类器进行目标和干扰分类的识别,最终实现抗干扰的目的。作为一种新的处理非平稳非线性信号的自适应信号处理方法,SSD在抑制伪分量的产生和模态混叠方面具有优势,且表现出更好的鲁棒性。因此,将SSD应用于低信噪比下精确分离富含干扰信息特征的信号分量,提高原始信号的信噪比; 并将1.5维谱作为后续分析,进一步抑制信号分量中的无关噪声干扰。
| [1] |
UJAN S, NAVIDI N, LANDRY R JR. Hierarchical class-ification method for radio frequency interference recognition and characterization in satcom[J]. Applied sciences, 2020, 10(13): 4608. DOI:10.3390/app10134608 ( 0) 0)
|
| [2] |
蒋莹, 何明浩, 郁春来, 等. 基于频域稀疏性的间歇采样转发干扰识别[J]. 空军预警学院学报, 2015, 29(5): 318-321, 342. ( 0) 0)
|
| [3] |
刘强. 基于深度学习的雷达干扰识别技术[D]. 成都: 电子科技大学, 2020.
( 0) 0)
|
| [4] |
DU Congju, TANG Bin. Novel unconventional-active-jamming recognition method for wideband radars based on visibility graphs[J]. Sensors, 2019, 19(10): 2344. DOI:10.3390/s19102344 ( 0) 0)
|
| [5] |
GUO Yifan, LIAO Guisheng, LI Jun, et al. An improved range deception jamming recognition method for bistatic MIMO radar[J]. Digital signal processing, 2019, 95: 102578. DOI:10.1016/j.dsp.2019.102578 ( 0) 0)
|
| [6] |
HAO Honglian, ZENG Dazhi, GE Ping. Research on the method of smart noise jamming on pulse radar[C]//Proceedings of the Fifth International Conference on Instrumentation and Measurement, Computer, Communication and Control. Qinhuangdao, China, 2015: 1339-1342.
( 0) 0)
|
| [7] |
ZHANG Yanbin. Technology of smart noise jamming based on multiplication modulation[C]//Proceedings of 2011 International Conference on Electric Information and Control Engineering. Wuhan, China, 2011: 1-3.
( 0) 0)
|
| [8] |
刘明骞, 高晓腾, 张俊林. 多类型的雷达有源干扰感知新方法[J]. 西安交通大学学报, 2019, 53(10): 103-108, 121. ( 0) 0)
|
| [9] |
郑苡榕. 雷达有源干扰识别方法及高效实现[D]. 成都: 电子科技大学, 2019.
( 0) 0)
|
| [10] |
聂永辉, 徐明文, 张译丹. 基于多小波和峭度准则的风力发电机滚动轴承故障检测[J]. 东北电力大学学报, 2019, 39(6): 15-23. ( 0) 0)
|
| [11] |
檀鹏超. 雷达有源欺骗干扰多维特征提取与识别技术研究[D]. 成都: 电子科技大学, 2016.
( 0) 0)
|
| [12] |
祝存海. 基于特征提取的雷达有源干扰信号分类研究[D]. 西安: 西安电子科技大学, 2017.
( 0) 0)
|
| [13] |
王璐. 雷达新型有源干扰抑制技术研究[D]. 成都: 电子科技大学, 2019.
( 0) 0)
|
| [14] |
彭荣硕, 董鹏曙, 孟藏珍. 基于1.5维谱的欺骗干扰识别方法[J]. 空军预警学院学报, 2019, 33(5): 349-352. DOI:10.3969/j.issn.2095-5839.2019.05.009 ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


