注入锁定技术可以用一个高质量的小功率信号去锁定一个大功率的振荡器,产生高质量的大功率信号。该方式具有结构简单和效率高的优势,在通信领域和大功率微波源中扮演了重要角色,引起了国内外的广泛关注和重视[1-2]。注入锁定是一种受迫振荡的物理现象[3],以微波振荡器为例,如果注入的信号与自身振荡频率接近,振荡器的频率和相位就会向注入信号偏移。当注入信号幅度足够大的时候,振荡器的输出频率就会和输入信号频率保持相同[4]。
注入锁定技术可以用来调制、稳频和降噪等,已经被应用在通信系统、磁控管微波源以及相控阵系统中[5-6]。在之前的注入锁定研究中,主要有自注入、互注入和外部注入。上述注入方式均是通过环行器从振荡器输出端口馈入外部信号,不仅增加了系统的成本和损耗,而且不利于电路的小型化设计。本文提出一种通过VCO电压调谐端馈入基准信号的注入锁定方式,降低了电路的复杂度,亦具备良好的杂散抑制特性。
1 振荡器注入锁定理论基础注入锁定理论最早是由Alder在1946年提出的。通过注入锁定现象的精确推导,得到锁定范围的理论表达式,并提出了早期理论模型,简称为Alder模型[7]。通过Alder模型以及经典文献中可以得到注入锁定的带宽和注入信号功率之间的关系,由文献[8]中注入锁定的最大变化范围Δωmax公式可以变化为
| $\Delta {\omega _{{\rm{max}}}} = \sqrt {\frac{{{P_{{\rm{in}}}}}}{{{P_{{\rm{out}}}}}}} \frac{{{\omega _{\rm{0}}}}}{{{Q_{\rm{L}}}}}$ | (1) |
式中:ω0是振荡器自由振荡时的频率;ω是输入信号频率;Δω=ω0 − ω是振荡器在自由振荡时的中心频率与输入频率之差;QL是振荡器的有载品质因数[9];Pin为注入信号功率;Pout为输出功率。
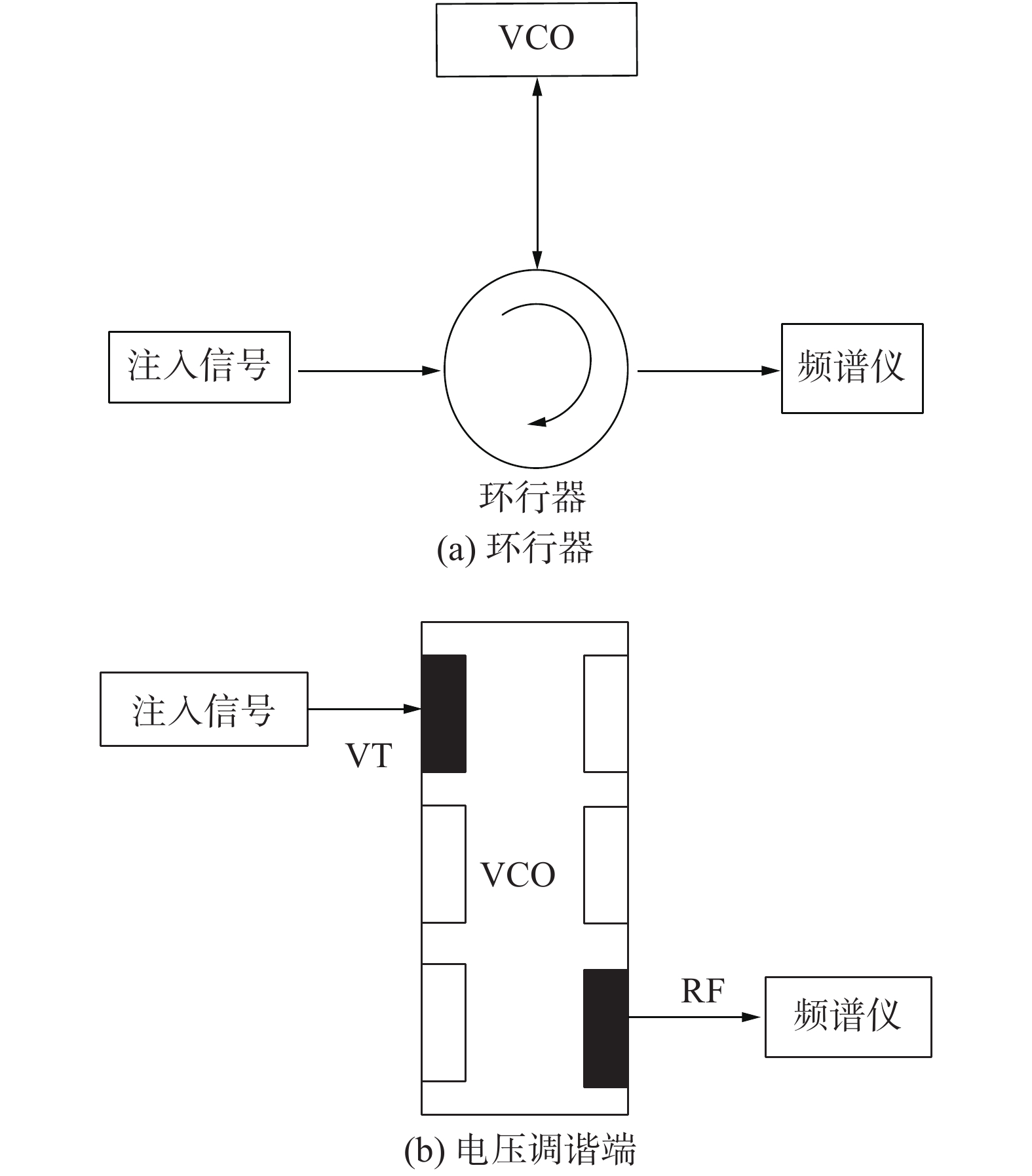
由式(1)可以看出,注入锁定振荡器的锁定范围与输入输出信号功率比、振荡频率以及振荡器的品质因数QL有关[10]。注入信号幅度越大,锁定带宽越宽[11-12]。通过改变注入信号的大小,可以得到在不同注入功率下的锁定带宽。图1(a)为传统环行器注入方式的示意图,图1(b)为VCO电压调谐端(VT)注入方式的示意图。
|
Download:
|
| 图 1 2种不同注入方式示意 | |
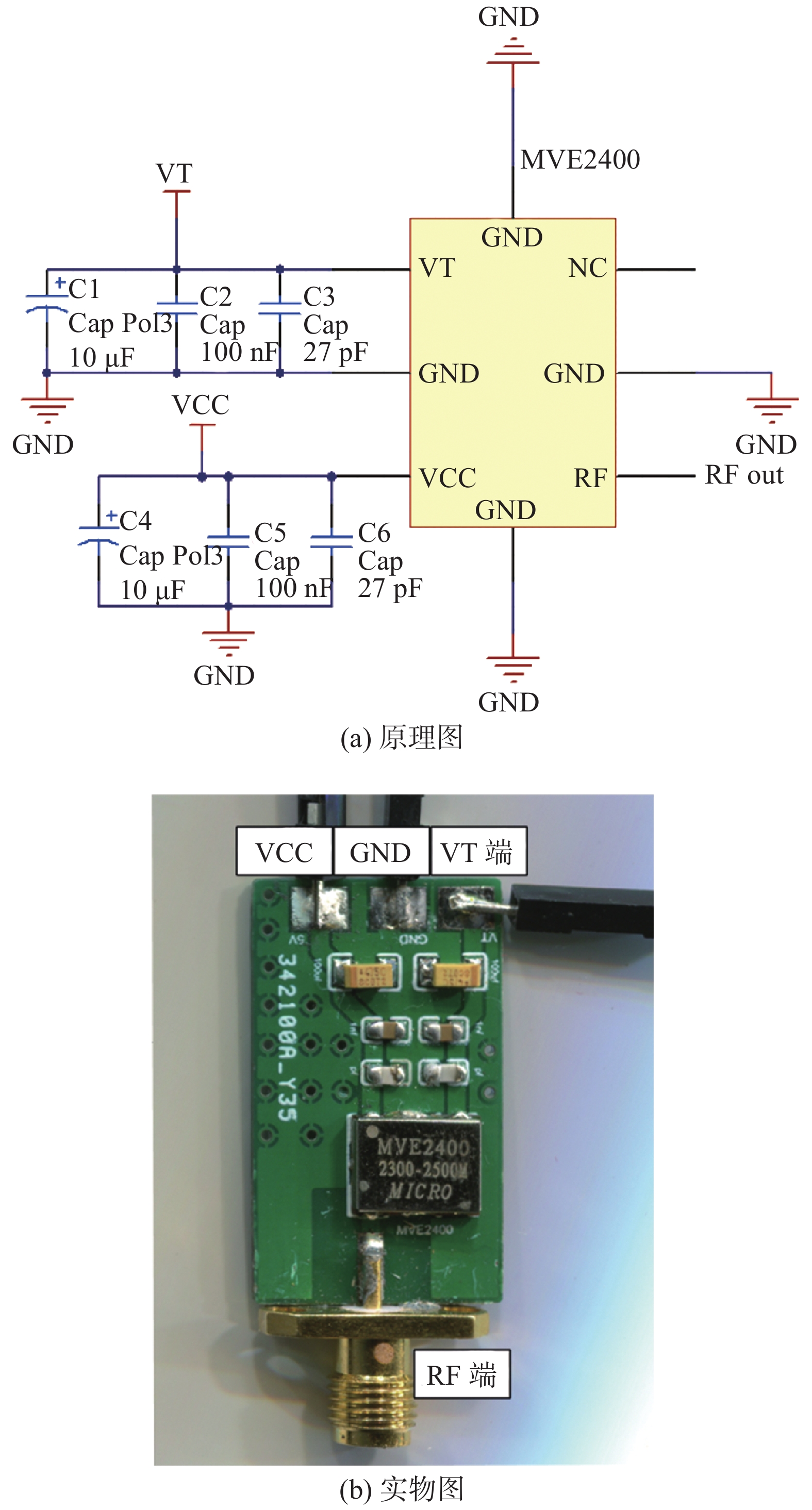
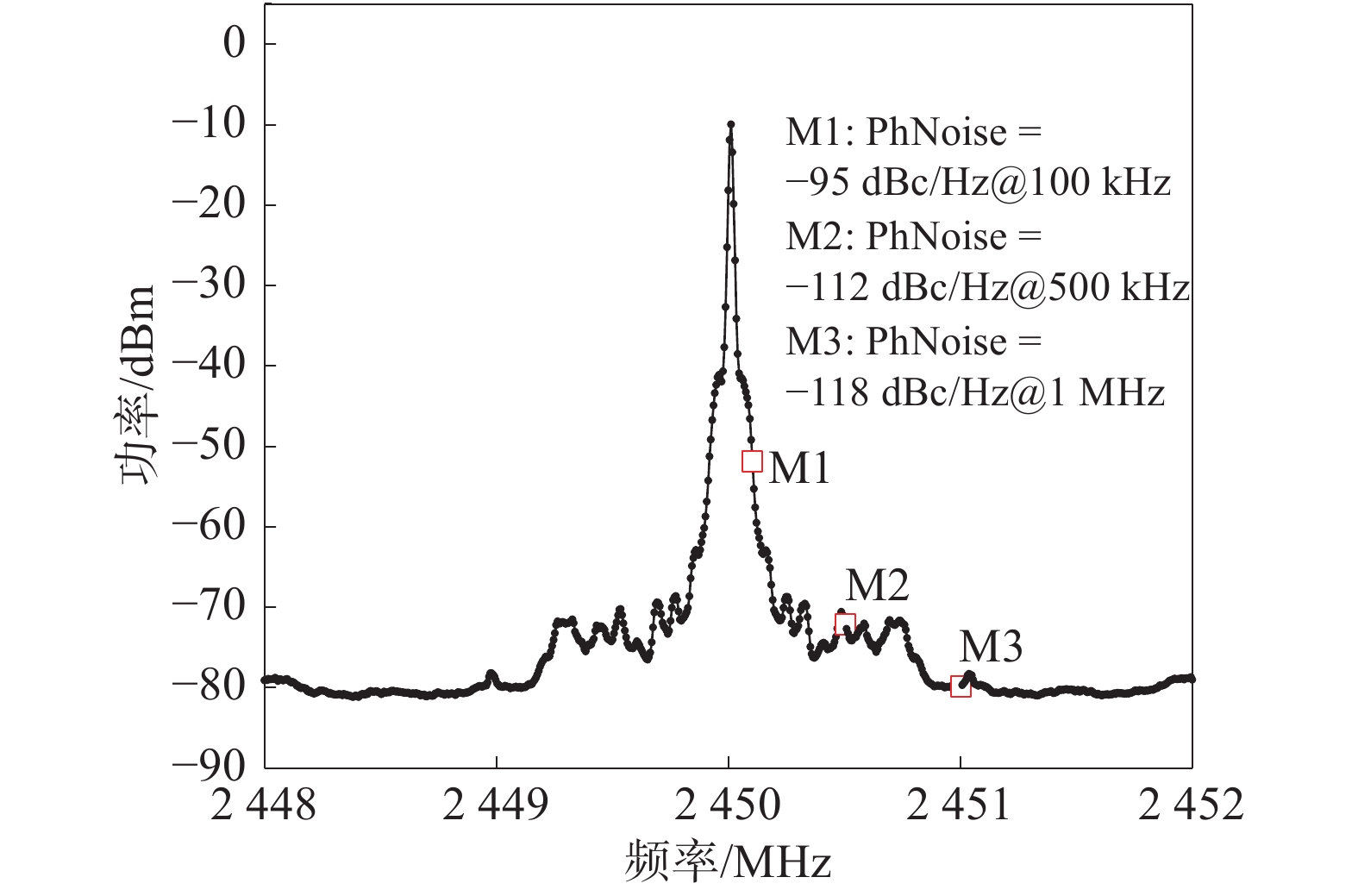
在本次电路设计中,采用的压控振荡器芯片型号为MVE2400,电源电压为5 V,工作频段为2 300~2 500 MHz,调谐灵敏度为50 MHz/V,调谐电压范围为0.2~4.5 V,调谐电压VT在1.95 V时,输出频率为2.45 GHz,输出幅度为3 dBm。图2(a)为VCO测试电路原理图,图2(b)为VCO测试电路实物图。实验中频谱仪的分辨率带宽设为10 kHz,测得的VCO的输出相位噪声特性如图3所示。从图3测试结果中可以得出,在偏离中心频率100 kHz处,相位噪声为−95 dBc/Hz;在偏离中心频率500 kHz处,相位噪声为−112 dBc/Hz;在偏离中心频率1 MHz处,相位噪声为−118 dBc/Hz。
|
Download:
|
| 图 2 VCO测试电路 | |
|
Download:
|
| 图 3 VCO的输出特性 | |
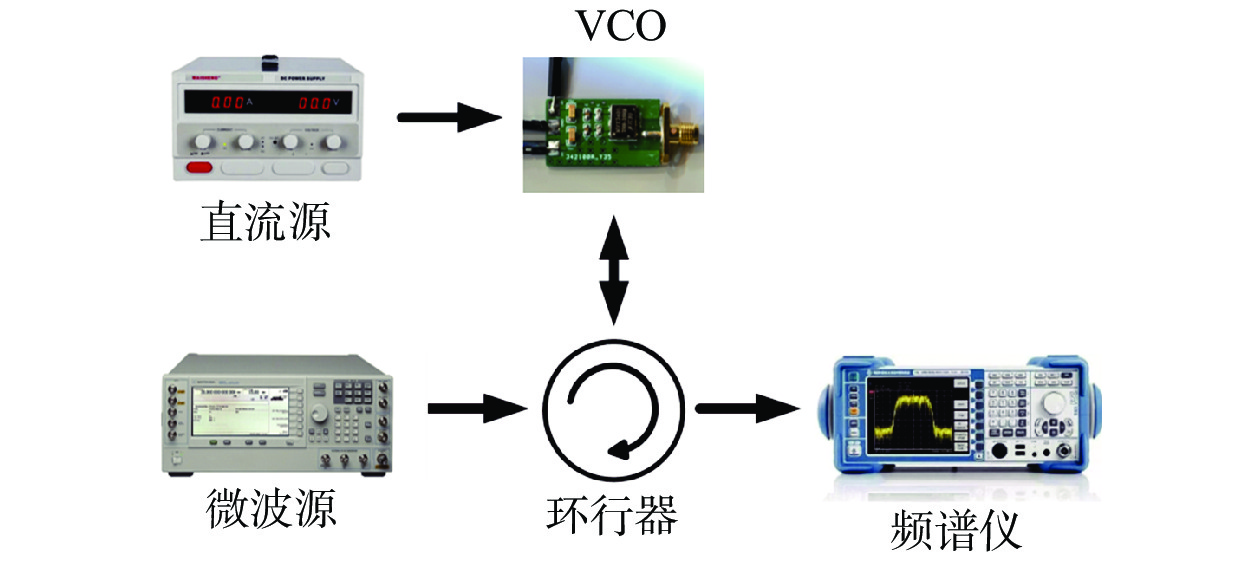
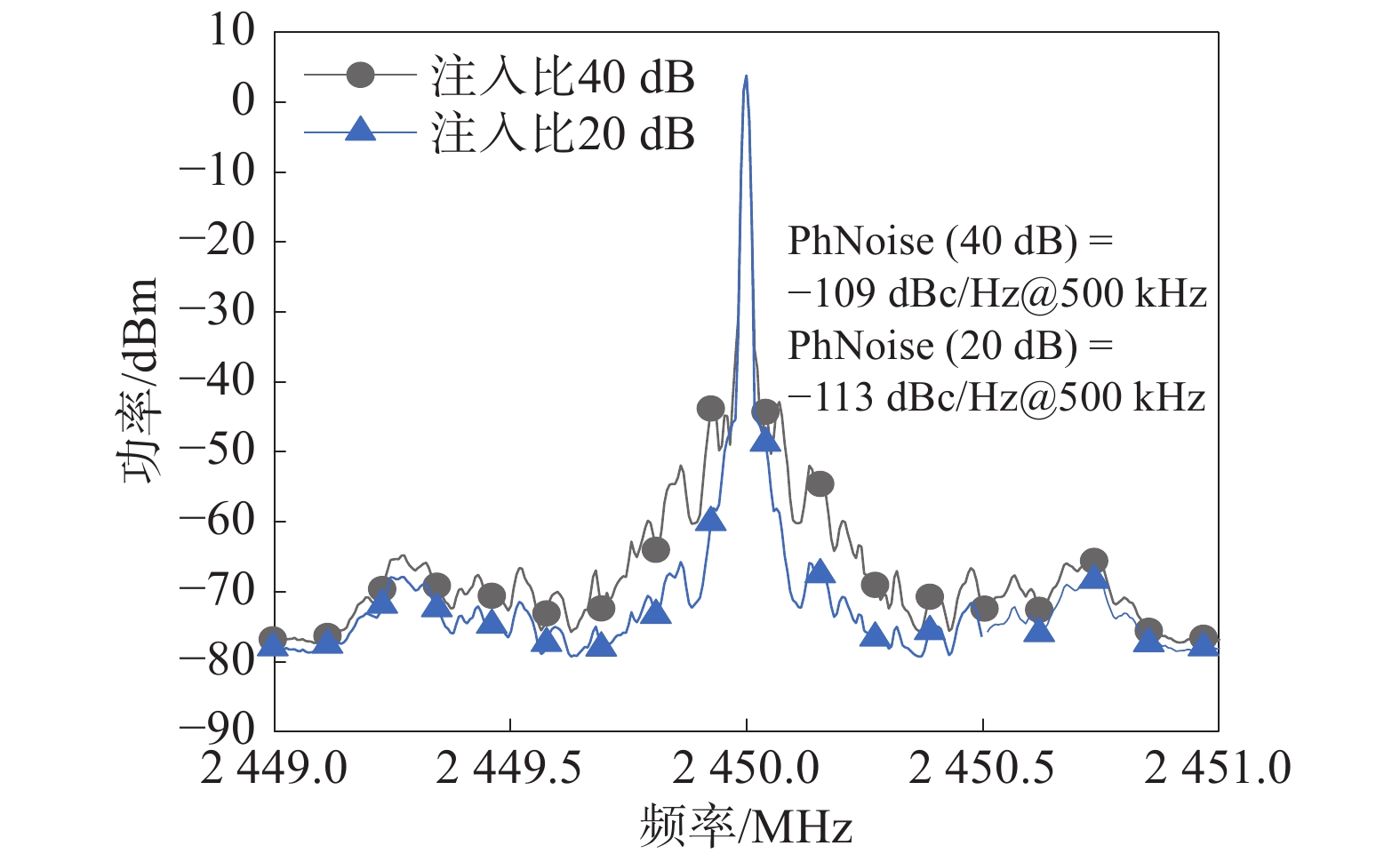
外部信号通过环行器从VCO的RF输出端注入振荡器中,图4为环行器注入方式的电路测试系统。直流源提供VCO的5 V工作电压和VT端电压,微波源提供外部信号源,信号通过环行器注入VCO的RF端,然后再通过环行器输出,最后在频谱仪上观察振荡器的输出特性。通过实验测试得到,当注入信号功率为−40 dBm时,输出功率为4 dBm,注入功率比最大可达44 dB,此时锁定带宽为50 kHz。图5为注入功率比分别为20、40 dB下VCO的输出相位噪声特性曲线。从图5结果可以看出,注入信号功率越大,注入功率比越小,VCO的输出相位噪声越好。当注入功率比为40 dB时,偏离中心频率500 kHz处,VCO的相位噪声为−109 dBc/Hz@500 kHz。
|
Download:
|
| 图 4 环行器注入方式的电路测试系统 | |
|
Download:
|
| 图 5 环行器注入方式不同注入比下VCO的输出特性 | |
外部注入信号通过VCO的电压调谐VT端注入振荡器中。图6(a)为对应的电路原理图,外部信号通过一个隔直电容注入VT端。隔直电容的作用是防止直流电进入微波信号源损坏信号源。50 Ω电阻的作用是减小端口的反射,实现端口的匹配。图6(b)为VT端注入方式的电路实物图,图7为VT端注入方式的电路测试系统。直流源提供VCO的5 V电源电压,微波信号源的输出端口和VCO的VT端用50 Ω同轴线连接,VCO的输出端口与频谱仪的端口连接。不断地减小外部注入信号的功率,观察信号锁定的范围,当注入信号功率最小为−37 dBm时,输出功率为3 dBm,注入功率比最大可达40 dB,此时锁定带宽为70 kHz。

|
Download:
|
| 图 6 VT端注入方式电路图 | |

|
Download:
|
| 图 7 VT端注入方式的电路测试系统 | |
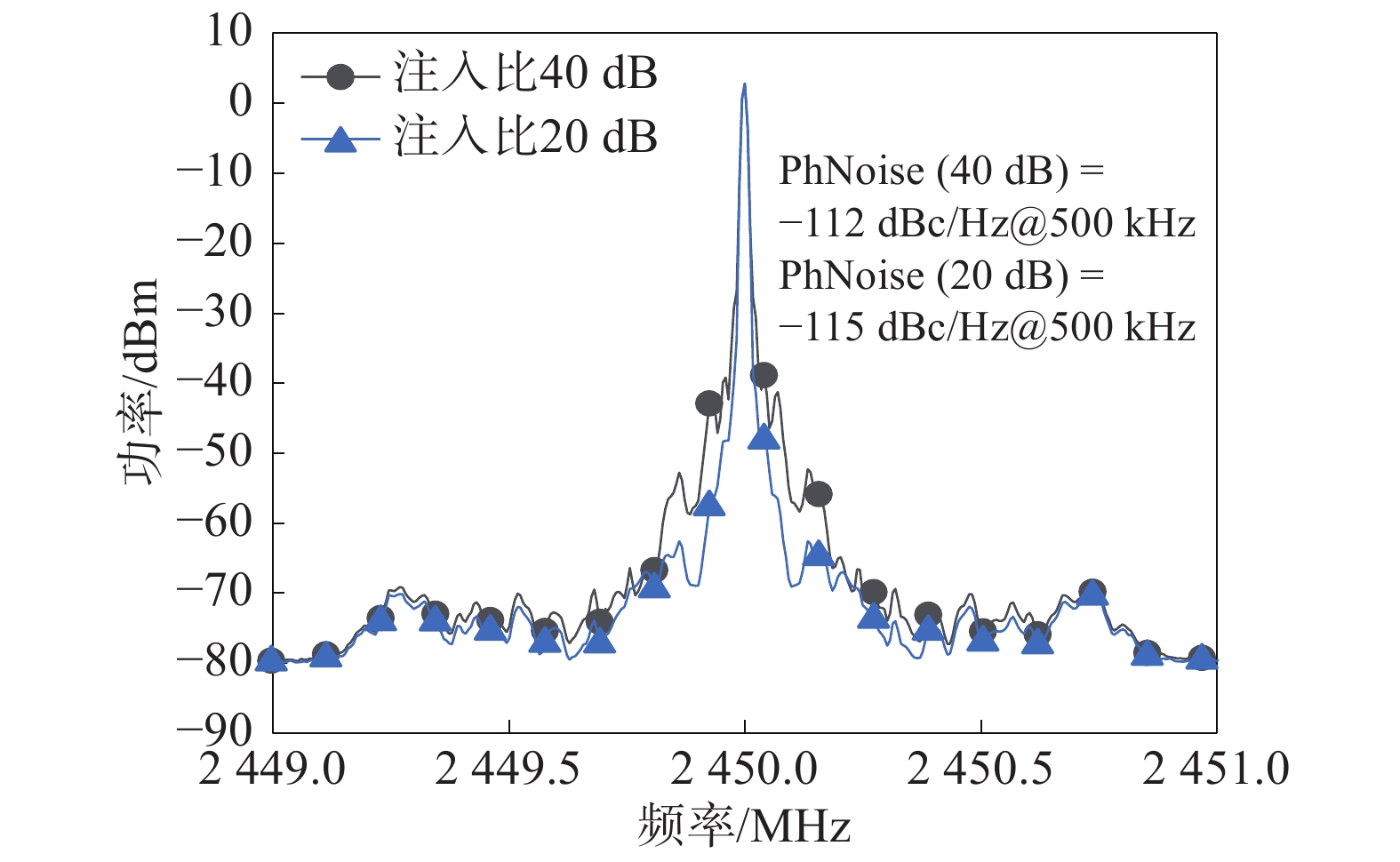
图8为注入功率比分别为20、40 dB下VCO的输出特性曲线。从图8测试结果可以看出,注入信号功率越大,注入比越小,VCO的输出相位噪声越小。当注入功率比为40 dB时,在偏移中心频率500 kHz处,频谱仪测得VCO的输出相位噪声为−112 dBc/Hz@500 kHz。
|
Download:
|
| 图 8 VT端注入方式不同注入比下VCO的输出特性 | |
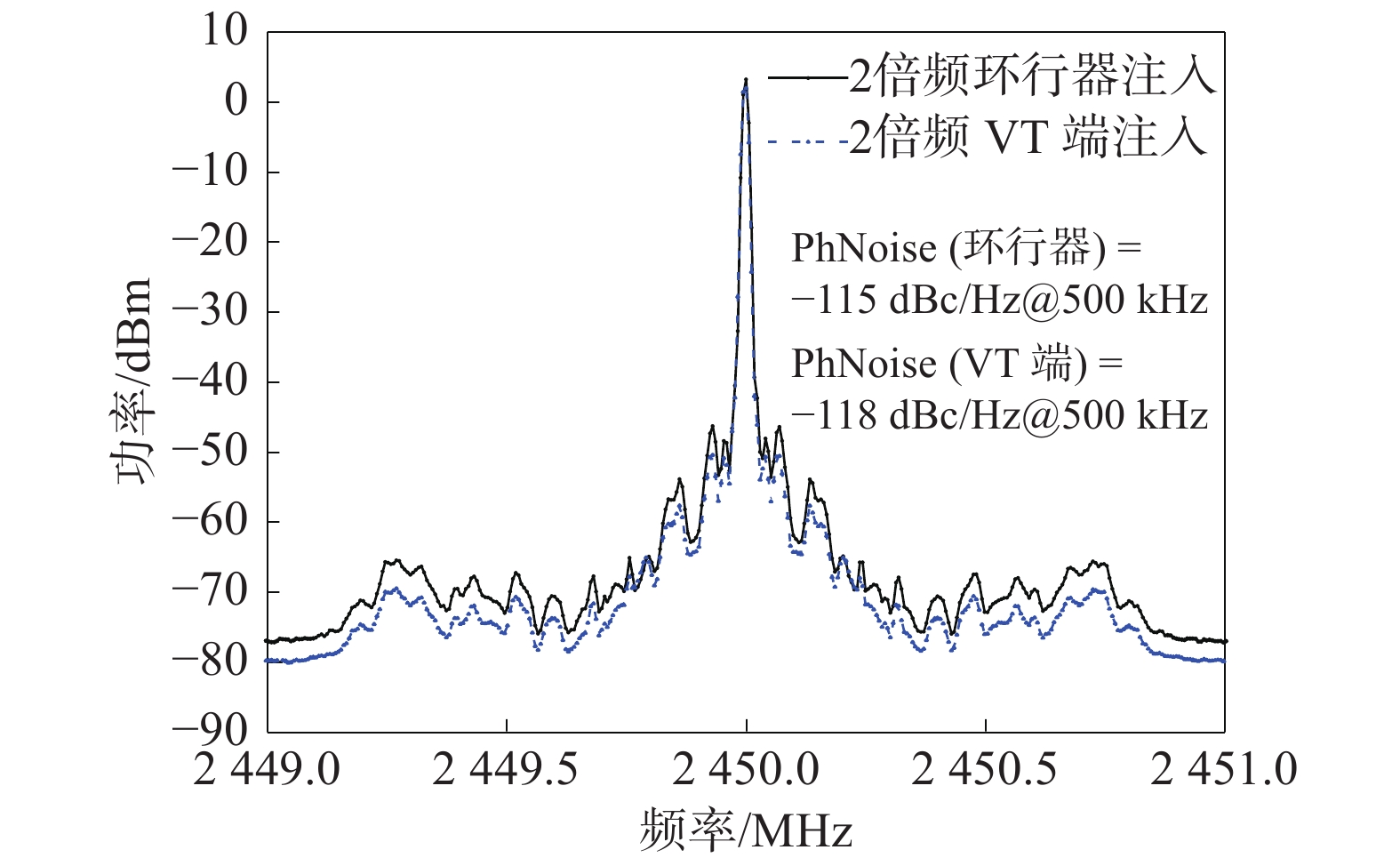
VCO的自由振荡频率为2.45 GHz,将外部注入信号的频率设置成2倍的振荡频率为4.9 GHz,然后将信号注入振荡器中,通过不断改变注入信号的功率来观察振荡器的输出特性。通过实验得出,采用环行器注入方式,能够实现锁定的最小输入功率为−12 dBm,注入比最大可达15 dB;采用VT端口注入方式,能够实现锁定的最小输入功率为−22 dBm,注入比最大为24 dB。在最大注入比下,2种注入方式的输出特性如图9所示。通过2种方式的对比,采用VT端注入方式的注入功率比、输出相噪特性都优于传统环行器注入方式,注入功率比提高9 dB,相位噪声降低3 dB。
|
Download:
|
| 图 9 2倍频2种不同注入方式的输出特性 | |
通过上面的测试结果可以看出,外部信号注入VCO后,VCO的输出更加稳定,同时VCO的输出相位噪声也有所改善,起到了很好的降噪和稳定输出的效果。采用传统环行器注入方式,注入功率比最大可达44 dB,采用VCO的VT端注入方式,注入功率比最大可达40 dB。在相同注入功率比下,VT端注入方式的相位噪声要优于环行器注入方式。2种注入方式的相位噪声都能小于−110 dBc/Hz@500 kHz。不断改变外部信号的注入功率,可以得到锁定的频率范围,从而可以得到注入信号的功率与锁定频率范围之间的关系,并和最先提出注入锁定技术的Alder模型进行对比。
从式(1)中可以看出,当自由振荡频率和品质因数不变时,锁定频率范围Δωmax与
|
Download:
|
| 图 10 环行器注入方式实测和曲线拟合的对比结果 | |
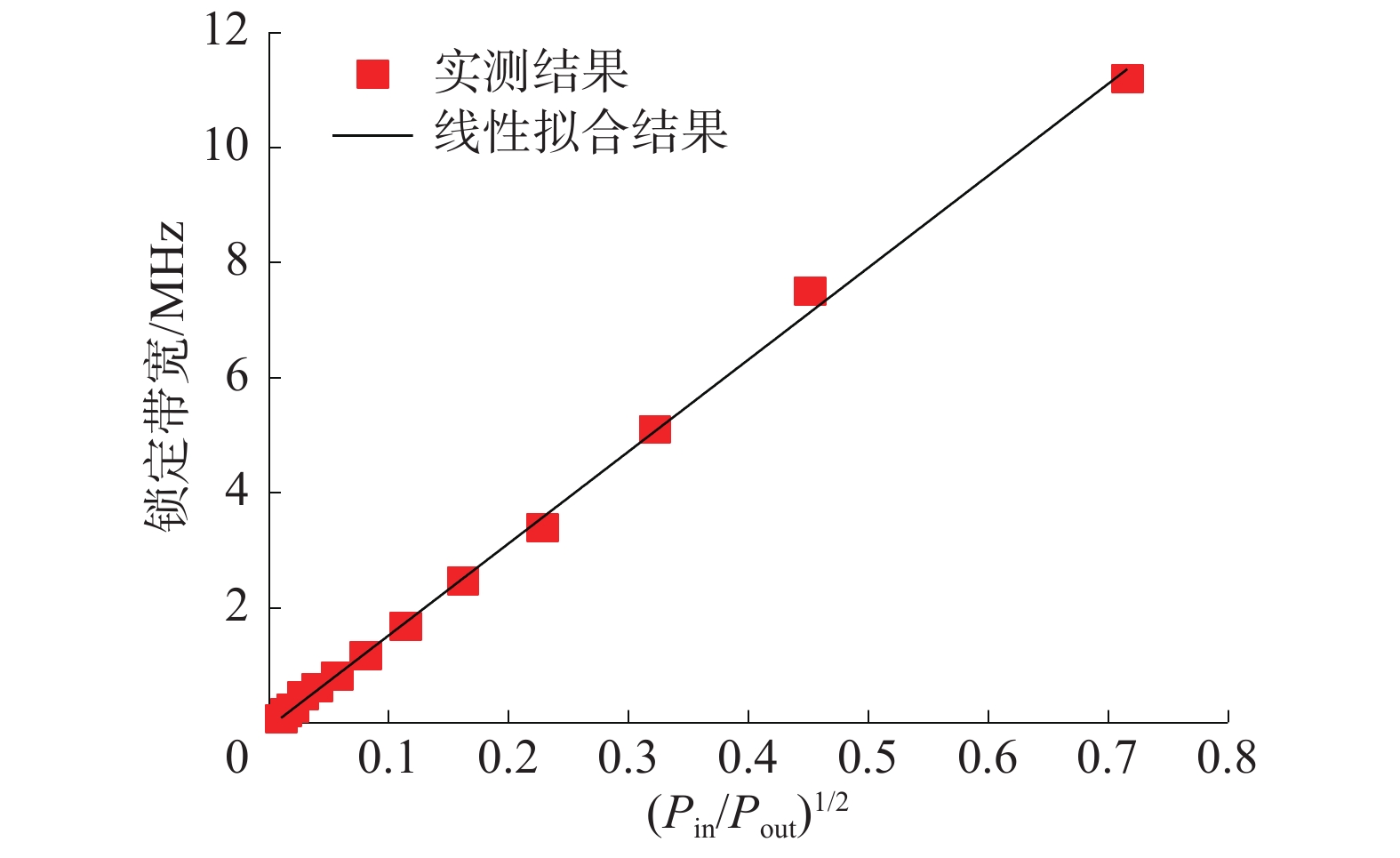
|
Download:
|
| 图 11 VT端注入方式实测和曲线拟合对比结果 | |
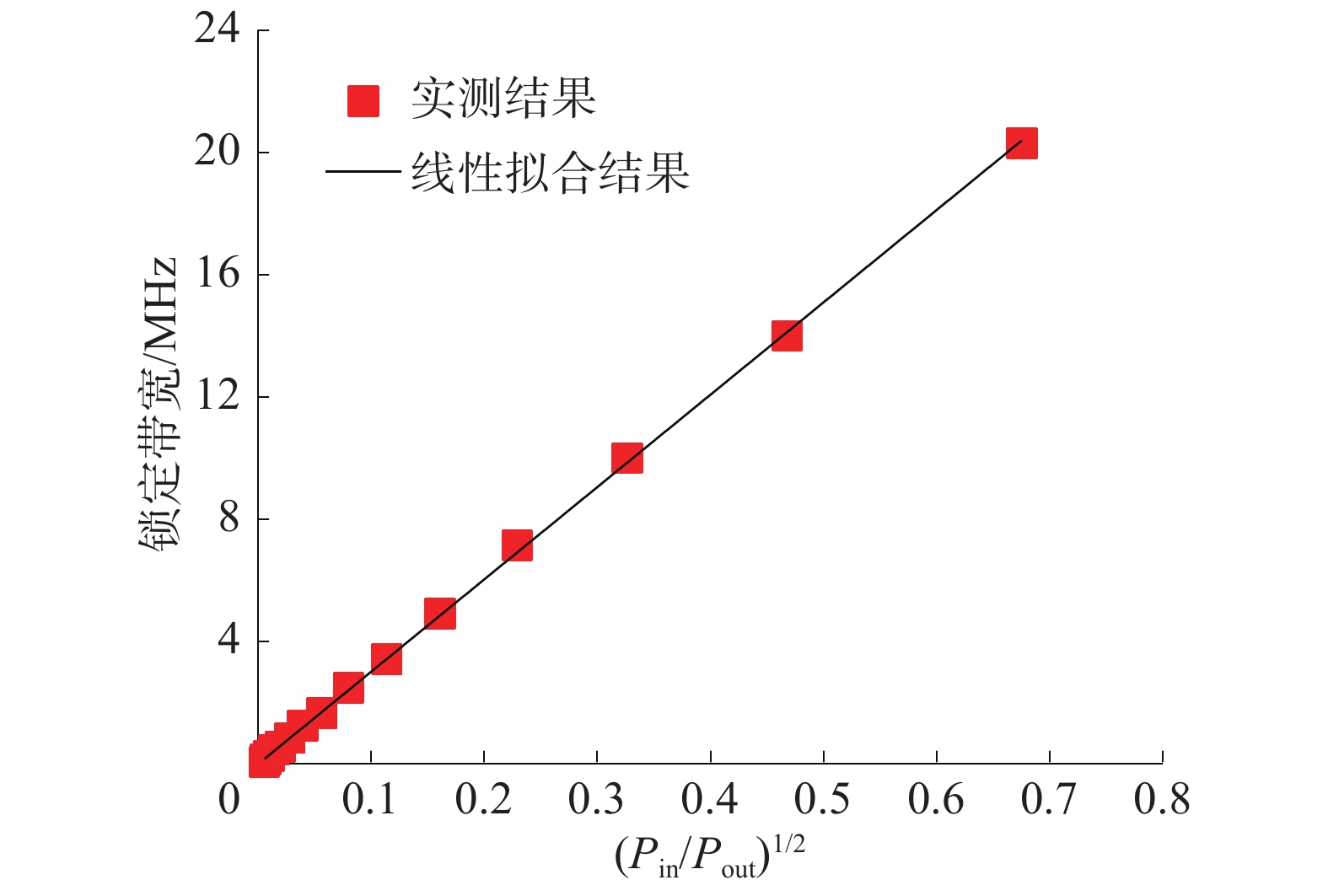
从图10和图11可以看出,实测结果和线性拟合的结果基本重合。因此可以得出,电压调谐端注入方式和传统环行器注入方式都符合Alder注入锁定理论模型。通过拟合结果可以计算得出直线的斜率,联合式(1)进一步算出振荡器的品质因数QL。得到环行器注入方式的等效品质因数QL为1 019。通过VCO的电压调谐端注入方式的等效品质因数QL为1 924。
在注入功率比相同的条件下,振荡器的品质因数越高,注入锁定的带宽越小[13]。这说明了振荡电路的品质因数越高,越不容易受外界干扰。因此,增大注入信号的幅度或者减小振荡器的品质因数可以提高锁定的范围[14]。在相控阵和微波射频系统中具有良好的应用前景[15]。
4 结论本文提出了一种VCO电路的新型注入锁定方式。通过实验得出结论如下。
1) 通过外部信号注入VCO的VT端来实现频率的锁定,避免引入环行器等外部电路元件,降低了电路系统的复杂度,节约成本,更易于实现。
2) 与传统的环行器注入方式相比,在相同注入功率比下,采用这种方式的输出相位噪声降低了3 dB,具有更好的降噪效果。
3) 在倍频锁定中,采用VT端注入方式的注入功率比、输出相位噪声特性都优于环行器注入方式,注入功率比提高9 dB,相位噪声低3 dB,具有极高的注入效率和良好的输出相位噪声特性。
| [1] |
IKEDA H, ITOH Y. 2.4-GHz-band high-power and high-efficiency solid-state injection-locked oscillator[J]. IEEE transactions on microwave theory and techniques, 2018, 66(7): 3315-3322. DOI:10.1109/TMTT.2018.2836393 ( 0) 0)
|
| [2] |
刘露, 刘长军. 一种2.45 GHz谐波抑制有源集成天线设计[J]. 应用科技, 2020, 47(4): 37-41. ( 0) 0)
|
| [3] |
RAZAVI B. A study of injection locking and pulling in oscillators[J]. IEEE journal of solid-state circuits, 2004, 39(9): 1415-1424. DOI:10.1109/JSSC.2004.831608 ( 0) 0)
|
| [4] |
廉琛. 基于注入锁定技术的锁相环、倍频器和分频器的研究与设计[D]. 上海: 复旦大学, 2012: 9-10.
( 0) 0)
|
| [5] |
杨梦琳, 刘臻龙, 刘长军. 一种S波段基于注入锁定技术高效的MOSFET大功率微波源[J]. 真空电子技术, 2018(1): 42-44, 51. ( 0) 0)
|
| [6] |
YANG Bo, MITANI T, SHINOHARA N. Injection-Locked CW Magnetron for a wirelessly-powered TV[C]//2019 International Vacuum Electronics Conference (IVEC). Busan, Korea (South), 2019: 1–2.
( 0) 0)
|
| [7] |
ADLER R. A study of locking phenomena in oscillators[J]. Proceedings of the IEEE, 1973, 61(10): 1380-1385. DOI:10.1109/PROC.1973.9292 ( 0) 0)
|
| [8] |
刘琨. W波段注入锁定放大器研究[D]. 成都: 电子科技大学, 2010: 33-60.
( 0) 0)
|
| [9] |
LO Y T, KIANG J F. Comparison of injection-locked and coupled oscillator arrays for beamforming[J]. IEEE transactions on microwave theory and techniques, 2015, 63(4): 1353-1360. DOI:10.1109/TMTT.2015.2403847 ( 0) 0)
|
| [10] |
刘长军, 黄卡玛, 朱铧丞. 射频通信电路设计[M]. 2版. 北京: 科学出版社, 2017: 101-104.
( 0) 0)
|
| [11] |
刘帮安. 基于注入锁定的高频倍频器设计[D]. 合肥: 中国科学技术大学, 2014.
( 0) 0)
|
| [12] |
EBRAHIMI N, BAGHERI M, WU Poyi. An E-band, scalable 2×2 phased-array transceiver using high isolation injection locked oscillators in 90nm SiGe BiCMOS[C]//2016 IEEE Radio Frequency Integrated Circuits Symposium (RFIC). San Francisco, USA, 2016: 178–181.
( 0) 0)
|
| [13] |
RATEGH H R, LEE T H. Superharmonic injection locked oscillators as low power frequency dividers[C]//Symposium on VLSI Circuits. Digest of Technical Papers (Cat. No. 98CH36215). Honolulu, USA, 1998: 132–135.
( 0) 0)
|
| [14] |
程一峰, 李家林, 王秉中. 一种宽带次谐波注入锁定振荡器的研究[C]//2013年全国微波毫米波会议论文集. 重庆, 中国, 2013: 1338-1341.
( 0) 0)
|
| [15] |
位宇, 陈潇杰, 刘臻龙, 等. 两路15kW连续波微波磁控管相干功率合成技术[J]. 应用科技, 2018, 45(2): 34-37. ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


