伴随着时代的发展与进步,大数据技术已深入到人们的生活中,比如在视频广告、交易平台和视频终端,每天产生海量的数据,如果将这些数据加以利用,就可以化“数字”为“神奇”,创造无穷价值,因此“数据挖掘”技术被广泛运用。而聚类[1-5]分析是数据挖掘的一项重要技术,是探索数据之间隐藏联系的重要一环。聚类分析源自分类学,但是聚类和分类并不一样。分类是已经知晓物品的标签,将其分到对应的标签下;而聚类是未知的,是一种无监督的分类方法。
密度峰值(DP)算法[6]是一种近几年流行的聚类算法。该算法的优势在于不受数据集形状的限制,可以识别出任意形状的数据,如流形、线形、环形和簇形等数据集;也很容易发现数据集中的噪声点。而且其参数唯一、易于使用,并具有很好的鲁棒性,广受学者们的欢迎。尽管如此,DP算法还是有一些不足:1)DP算法的局部密度计算方式是通过截断距离(
经过上述分析发现,实现自适应DP聚类算法关键是聚类中心的选取、
本文针对上述分析,提出以下内容:1)提出基于自然邻居的新内核;2)改进自然邻居的搜索算法;3)联合肘方法以自适应确定类数目。
1 相关工作 1.1 DP算法密度峰值算法的本质在于聚类中心,该算法在于提出一种方式高效地选取数据集中的聚类中心。Rodriguez等[6]提出2个关于聚类中心的假设:
假设1 聚类中心的密度应比其邻居密度都要大,即它任意邻居的密度均小于它。
假设2 聚类中心应与其他密度大于它的聚类中心的“距离”相对更大,即2个聚类中心应有一段距离。
设数据集
对于局部密度
| ${\rho _i} = \sum\limits_{j \in {F_D}\left\{ i \right\}} {X({d_{ij}} - {d_c})} $ |
式中
| $X\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {1,}&{x < 0} \\ {0,}&{x \geqslant 0} \end{array}} \right.$ |
其中,参数
| ${\delta _i} = \left\{ {\begin{array}{*{20}{c}} {\max \left\{ {{d_{ij}}} \right\},}&{F_D^i = \phi } \\ {\min \left\{ {{d_{ij}}} \right\},}&{F_D^i \ne \phi } \end{array}} \right.$ | (1) |
式中
| $F_D^i = \left\{ {k \in {F_D}:{\rho _k} > {\rho _i}} \right\},$ |
通过式(1)可知:若
文中提出一种新的参数
| $\gamma {\rm{ = }}{\rho _i}{\delta _i},i \in {I_S},$ |
显然,一个数据点的
自然邻居是一个新的邻居概念[12-14]。与k个最近邻居相比,此方法不需要设置任何参数,并且是自适应搜索邻居的方法。自然邻居主要受到人类社会关系的启发:假设2个人A和B,2个人之间的友谊应该是相互的,即A认识了解B,而B也认识了解A,此时才认为2个人是熟悉的;而当A认识B,但B不认识A时,可以说两者并没有任何关系。这说明一个数据点的自然邻居个数越多,其越紧密;反之,说明其越稀疏。
自然邻居的生成过程是这样实现的:首先初始化当前邻居个数r,通过不断增加r以扩大搜索范围,且每次计算每个点的逆最近邻居数量。当满足以下2个条件之一时,即:1)所有点具逆最近邻居;2)没有逆最近邻居的个数不变,可以认为达到了自然稳定状态。此时的搜索范围r是自然特征值
如图1所示,当r=2时,红色圆圈的K近邻为蓝、绿圆圈,其中,蓝色圆圈的K近邻为红、黑圆圈,绿色圆圈的K近邻为白色圆圈。此时,红、蓝互为自然邻居;反之红、绿不是自然邻居。
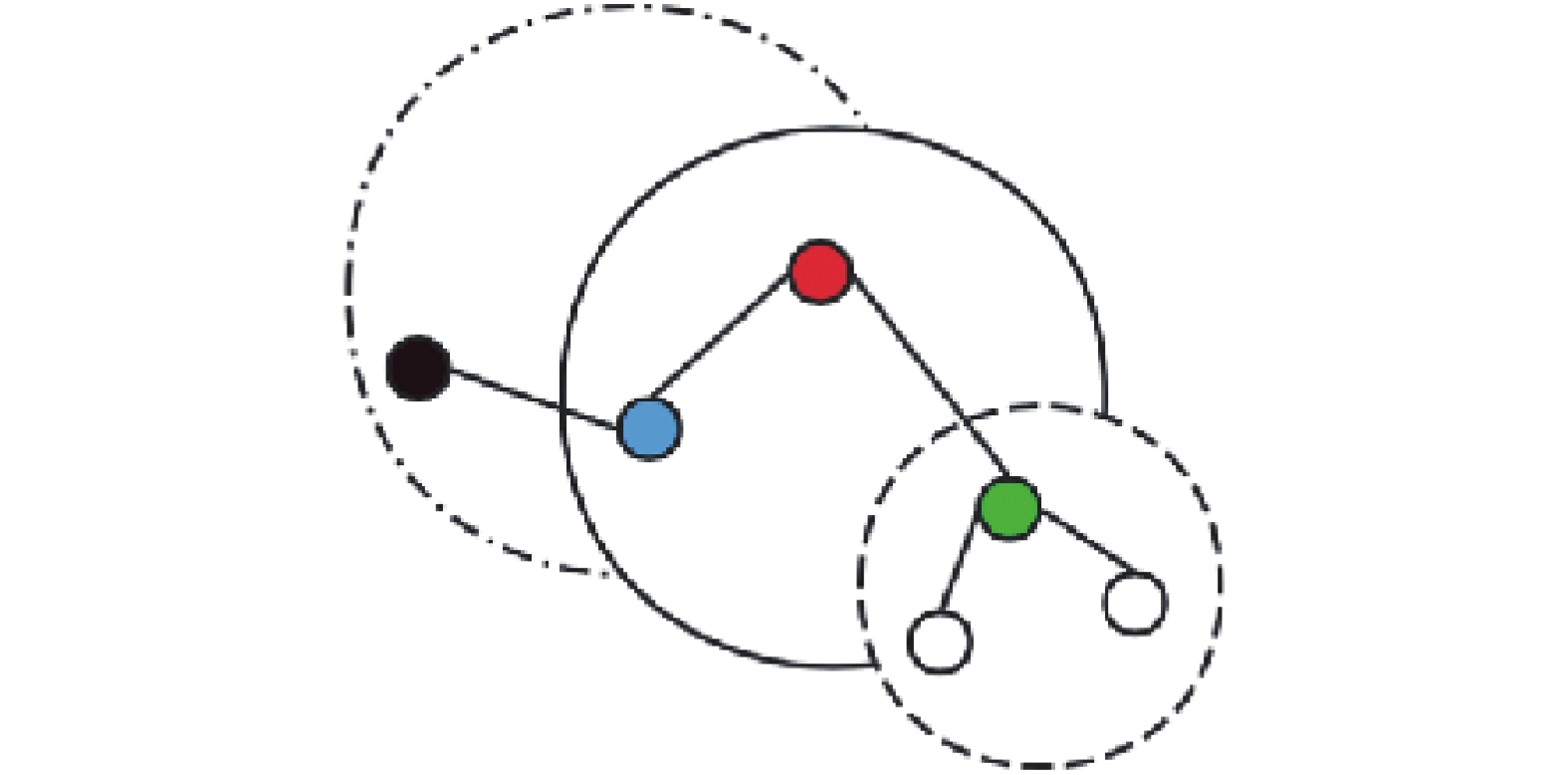
|
Download:
|
| 图 1 自然邻居示意 | |
肘方法顾名思义,就是类似人的手肘,有一个拐点存在[15]。肘方法就是通过这个拐点来得到最终的K值。它是基于2条曲线得到:一条是由误差平方和(sum of the squared errors,SSE)计算得到,另一条是搜索范围的起点和终点的SSE连线(
传统的密度峰值算法无法实现真正的自适应,其中的参数
对于传统的KNN算法,每个数据点要根据
由于肘方法的搜索范围往往是根据经验确定,设置数据集大小为N,搜索范围一般为
为了进一步减小时间成本,本文基于减而治之的思想改进了求自然邻居的算法,将原始时间复杂度从
密度峰值算法思想的核心是密集区域的局部密度要大于稀疏地区的局部密度,即密集区域的邻居之间的距离要更小,反之邻居之间的距离要更大。本文结合自然邻居思想给出局部密度
| ${\rho _i} = \frac{\omega }{{\displaystyle\sum\nolimits_{j \in N{N_\omega }\left( i \right)} {{\rm{dist}}\left( {i,j} \right)} }}$ | (2) |
式中:
由式(2)易知,基于自然邻居的思想,可以真正自适应地计算合适的邻居个数,为更准确地得到聚类结果提供保证。
2.2 肘方法的搜索范围假设肘方法的搜索范围
| $ {\theta _i} = \frac{{{n_{{b_i}}}}}{{F\left( {\displaystyle\sum\nolimits_{j \in {n_{{b_i}}}} {{{l}}\left( {{n_{{b_j}}}} \right)} } \right)}} $ |
式中:
候选因子
在选择候选聚类中心时,首先,计算每个数据点的候选因子
肘方法的核心思想是:随着聚类的类别数目K增加,数据集的误差平方和的下降幅度会骤减;然后随着K值的继续增大而趋于平缓,那么曲线图的拐点就是聚类中心。本文提出NDP指标,该指标由2条直线的差值计算得到,一条是由数据集的误差平方和计算得到(
| $I_{\rm{NDP}} = \left\{ {{y_i} - {z_i}|i \in C} \right\}$ |
式中C为候选聚类中心集合,
自然邻居的计算过程为,设置n初始值为1(n为自然邻居个数),遍历n直到满足以下任意条件其中一个:1)所有数据点的自然邻居集合不为空,即每个数据点都至少有1个自然邻居,
首先,算法的目标是找到一个n值使得每个数据点都至少有一个自然邻居。而对于数据来说,有这样一个趋势:随着n的递增,数据集中至少有1个自然邻居的数据点的个数是递增的,且当达到最大值时停止增加。即可以将求n值的问题转换为在一个递增序列中求这个最大值出现的位置。
二分查找的基本用法是在一个有序数组里查找目标元素,具体是检查区间中间元素的值与目标值的大小关系。如果等于,就可以直接返回;如果严格大于,就往右边查找;如果严格小于,就往左边查找。这也符合人类的逻辑思维。
由于一个元素出现多次,即当所有数据点都有自然邻居时,再增加n的值,得到的计算结果相同,此时的n值就是该序列中的最大值。算法具体可以分为3种情况:
1)如果当前看到的元素恰好等于目标值,那么当前元素有可能是目标值出现的第一个位置,因为要找第1个位置,此时应该向左边继续查找。
2)如果当前看到的元素严格大于目标值,那么当前元素一定不是要找的目标值出现的第一个位置(理论上不存在大于目标的值),此时应该向左边继续查找。
3)小于的情况与第2种情况类似。
Algorithm1总结了所提出的BNaN算法。
Algorithm1BNaN-Searching
Input
Ouput
Initializing:
While
end
3 实验结果为了证实新NDP指标和BNaN算法的性能,本文使用了12个人工数据集和3个真实数据集来测试NDP索引。此外,我们使用调整兰德指标来评估12个合成数据集和3个实际数据集的聚类结果。
通常,聚类K值的范围是
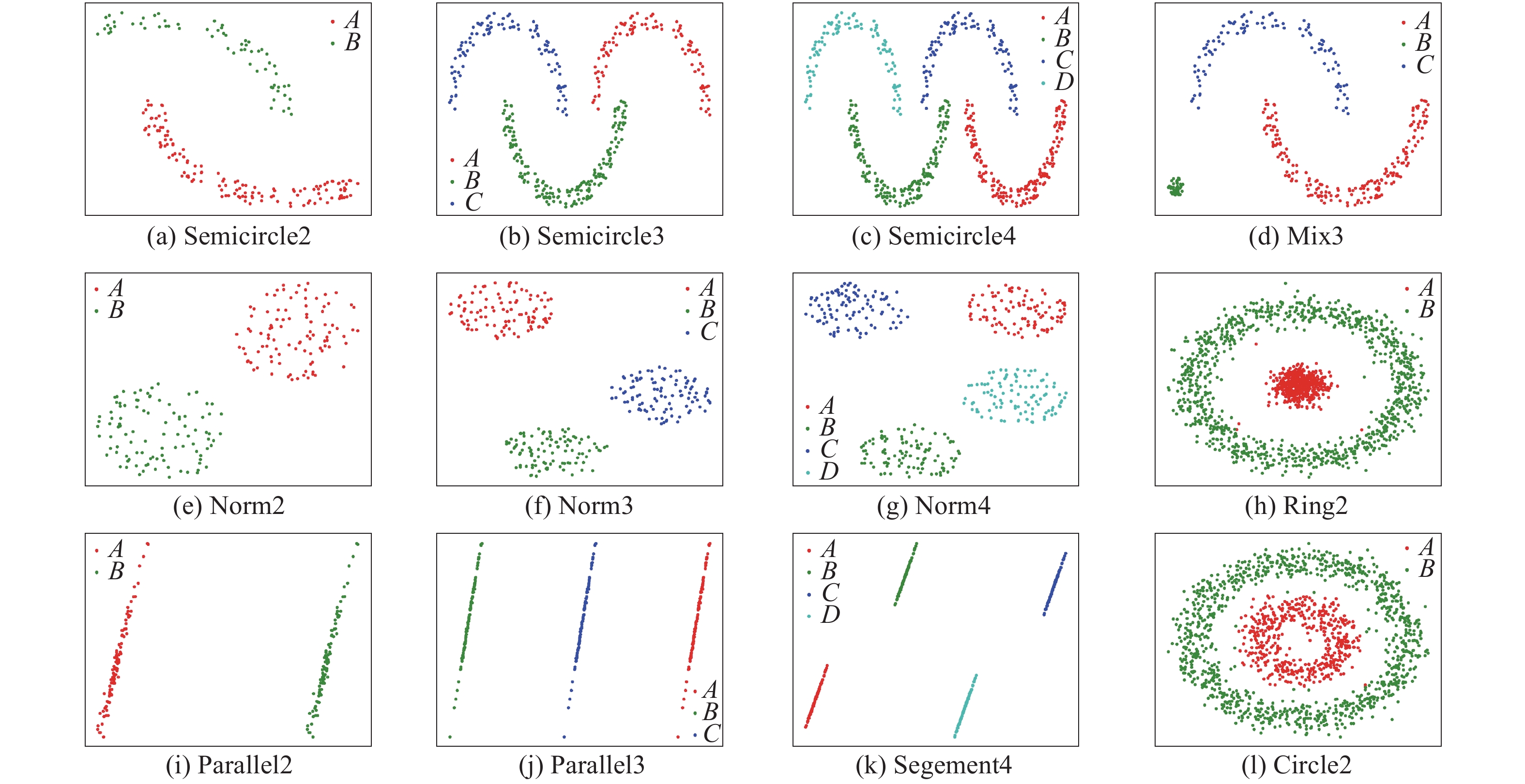
实验包括12个合成数据集,其中包括通过计算机模拟生成的二维随机数。这些数据集是Semicircle2、Semicircle3、Semicircle4、Mix3、Norm2、Norm3,Norm4,Ring2,Parallel2,Parallel3,Segenment4和Circle2。在这些数据集中,Parallel2、Parallel3、Segenment4数据集的结构是线性的,Semicircle2、Semicircle3、Semicircle4数据集的结构是多方面的,Ring2和Circle2数据集是环形的,Norm2、Norm3、Norm4数据集的结构是凸的,而Mix3数据集是混合的。12个数据集的聚类效果如图2所示。
对于Parallel2数据集,其正确的类数目为2。所得到的聚类结果也为2。通过实验发现,在给定最优类簇数目时,其余11个人工数据集的实验结果与Parallel2数据集的实验结果相似。因此,可以得出的结论,在给定最佳聚类数的情况下,可以正确划分12个人工数据集。
|
Download:
|
| 图 2 12个人工数据集的聚类结果 | |
实验包括3个真实数据集:Seeds、Iris和Titanic,这些数据集分别来自UCI机器学习存储库(
|
|
表 1 真实数据集上的运行结果 |
表1中加粗部分表示在当前数据集中得到的最大值。表1显示了通过候选因子限定了簇数的搜索范围,其中,Seeds簇数的搜索范围是2~14,Iris簇数的搜索范围是2~12,而Titanic簇数的搜索范围是2~6。可以看出通过候选因子,能减少搜索范围,提升计算效率。比如Titanic的样本数目是2201,若按照经验,K值的搜索范围应该是
表2列出了使用3个真实数据集确定最佳簇数的算法的运行时间,通过观察该表可以发现,通过改进自然邻居的搜索算法(BNaN-Searching),可以大幅减少算法的时间成本。
|
|
表 2 真实数据集上算法的运行时间 |
为了验证本文提出算法的有效性,将本文算法与自适应密度峰值算法(adaptive peak cluster,APC)、密度峰值算法(density peak cluster, DPC)、基于密度的聚类算法((density-based cluster,DBSCAN)和K-means算法进行比较。真实数据集的聚类结果采用综合评价指标(F值)、归一化互信息(NMI)、准确率(ACC)这3个聚类指标进行评价。通过表3数据可以看出NDP算法的各评价指标均高于其他算法。
|
|
表 3 真实数据集上聚类效果 |
密度峰值算法已经成为近几年流行的聚类算法,本文针对其依赖固有参数,对于不同数据集的聚类具有很大局限性这一缺点,引入自然邻居思想,实现真正的自适应密度峰值算法,并通过结合肘方法和候选因子,可以快速有效地得到类簇数目。最后对自然邻居的选取算法进一步改良,以实现更高效率的聚类。通过理论研究和实验结果证明,本文提出的新内核和方法可以准确地得到数据集的最优类簇数目,并适用于多种类型的数据集,如线形、流形、环形和凸形数据集。
本文还存在一些不足,所求的局部密度对于噪声点敏感,当噪声较多时,聚类效果和类簇数目的准确度会降低。后续会引入归一化来更好地求得数据点的密度。
| [1] |
MACQUEEN J B. Some methods for classification and analysis of MultiVariate observations[C]//Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley, USA, 1965.
( 0) 0)
|
| [2] |
MA L, FAN S H. CURE-SMOTE algorithm and hybrid algorithm for feature selection and parameter optimization based on random forests[J]. BMC bioinformatics, 2017, 18(1): 169. DOI:10.1186/s12859-017-1578-z ( 0) 0)
|
| [3] |
DENG Chao, SONG Jinwei, SUN Ruizhi, et al. GRIDEN: an effective grid-based and density-based spatial clustering algorithm to support parallel computing[J]. Pattern recognition letters, 2018, 109: 81-88. DOI:10.1016/j.patrec.2017.11.011 ( 0) 0)
|
| [4] |
XU Xiao, DING Shifei, SHI Zhongzhi. An improved density peaks clustering algorithm with fast finding cluster centers[J]. Knowledge-based systems, 2018, 158: 65-74. DOI:10.1016/j.knosys.2018.05.034 ( 0) 0)
|
| [5] |
ZHANG Kai, TANG Ming, KWOK J T. Applying neighborhood consistency for fast clustering and kernel density estimation[C]//Proceedings of 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, USA, 2005.
( 0) 0)
|
| [6] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 ( 0) 0)
|
| [7] |
杨震, 王红军, 周宇. 一种截断距离和聚类中心自适应的聚类算法[J]. 数据分析与知识发现, 2018, 2(3): 39-48. ( 0) 0)
|
| [8] |
王洋, 张桂珠. 自动确定聚类中心的密度峰值算法[J]. 计算机工程与应用, 2018, 54(8): 137-142. ( 0) 0)
|
| [9] |
LIU Rui, WANG Hong, YU Xiaomei. Shared-nearest-neighbor-based clustering by fast search and find of density peaks[J]. Information sciences, 2018, 450: 200-226. DOI:10.1016/j.ins.2018.03.031 ( 0) 0)
|
| [10] |
MEHMOOD R, ZHANG Guangzhi, BIE Rongfang, et al. Clustering by fast search and find of density peaks via heat diffusion[J]. Neurocomputing, 2016, 208: 210-217. DOI:10.1016/j.neucom.2016.01.102 ( 0) 0)
|
| [11] |
HOU Jian, PELILLO M. A new density kernel in density peak based clustering[C]//Proceedings of 2016 23rd International Conference on Pattern Recognition. Cancun, Mexico, 2016.
( 0) 0)
|
| [12] |
ZHU Qingsheng, FENG Ji, HUANG Jinlong. Natural neighbor: a self-adaptive neighborhood method without parameter K[J]. Pattern recognition letters, 2016, 80: 30-36. DOI:10.1016/j.patrec.2016.05.007 ( 0) 0)
|
| [13] |
LIU Yanchi, LI Zhongmou, XIONG Hui, et al. Understanding and enhancement of internal clustering validation measures[J]. IEEE transactions on cybernetics, 2013, 43(3): 982-994. DOI:10.1109/TSMCB.2012.2220543 ( 0) 0)
|
| [14] |
CHENG Dongdong, ZHU Qingsheng, HUANG Jinlong, et al. A novel cluster validity index based on local cores[J]. IEEE transactions on neural networks and learning systems, 2019, 30(4): 985-999. DOI:10.1109/TNNLS.2018.2853710 ( 0) 0)
|
| [15] |
SYAKUR M A, KHOTIMAH B K, ROCHMAN E M S, et al. Integration K-means clustering method and elbow method for identification of the best customer profile cluster[J]. IOP conference series: materials science and engineering, 2018, 336: 012017. DOI:10.1088/1757-899X/336/1/012017 ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


