2. 大连民族大学 机电工程学院,辽宁 大连 116600
2. College of Mechanical and Electronic Engineering, Dalian Minzu University, Dalian 116600, China
随着网络的普及和信息技术的发展,利用计算机和网络进行在线学习和考试已经成为一种趋势。为了让学生能够及时检验自己的学习情况,在线考试系统应运而生。在在线考试系统的研究与实现中,如何能实现达到用户满意的组卷功能一直是研究的重点。
在传统的组卷系统中,大多采用的是由教师人工组卷或者使用简单的随机法或回溯法进行组卷[1]。人工组卷不仅增加了教师的工作负担,而且容易使组成的试卷主观性太强,无法客观考察学生对知识的掌握情况。而简单的随机组卷法和回溯法又具有随机性太强的缺点,难以保证生成的试卷符合教师的期望。因此,本文提出采用遗传算法来实现组卷系统。遗传算法是一种全局优化搜索算法,具有自适应程度高、全局优化能力强等优点,适用于组卷系统的实现[2]。
1 遗传算法 1.1 算法概述遗传算法(genetic algorithm,GA)最早是由美国的John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的,是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法[3]。该算法通过数学的方式,用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生智能领域[4]。
1.2 算法执行过程1)初始化:设置进化代数计数器和最大进化代数,随机生成若干个体作为初代种群。
2)计算适应度:计算种群中每个个体适应度。
3)选择:从种群中以一定算法选择若干个体。
4)交叉:将选择得到的个体在一点或多点上交叉,得到新的种群。
5)变异:在种群中选若干个体,为每个体选择变异点位并改变该点位的基因。
6)重复执行步骤2)~5),直到适应度达到期望值或进化代数达到最大值。
2 系统设计与实现本系统采用B/S架构,教师只需要在网页上输入组卷的要求,如题目数量、分值,试卷难度,知识点覆盖数等,系统调用组卷算法并即刻返回组卷结果。教师可以对所组试卷进行查看检验,通过实验验证,本系统所组试卷达到了要求,能很好地满足课程考核的需求。
2.1 获得初始种群利用遗传算法实现组卷系统时,首先要建立试卷和试题等实体与遗传算法模型的映射关系。本系统将试题映射为个体上的基因,将试题组成的试卷映射为个体,并将一定数量的试卷组成的集合映射为种群[5]。
在设计获得初始种群的方法时,首先要在方法的参数列表提供以下几个参数:题目数量、题库中所有试题的集合以及种群包含的个体数。
在生成初始种群的每个个体时,为了避免选到重复的试题,需要首先初始化一个集合A,用于保存该个体中的试题。每当从试题库中选到一道题时,就判断该试题是否已在集合A中。如果存在,说明该试题已被选择,需要舍弃该试题并重新选择;如果不存在,则将试题加入试卷并添加到集合A中。当题目数量达到要求时,一个个体就生成了。重复执行上述过程,直到种群中的个体数量达到要求。
此外,在设计生成初始种群的方法时,需要考虑种群包含的个体数这个参数。这个参数的大小对算法的性能有直接影响。如果设置得太小,则很难从种群中找到合适的个体;如果设置得太大,则在初始化、交叉和变异等过程会消耗太多时间。实验表明,通常将这个值设置在20左右较为合适。
2.2 计算适应度在遗传算法中,通常使用适应度来评价个体的优劣程度和对环境的适应程度。适应度的值则取决于具体的适应度函数。因此,设计一个好的适应度函数对于评价个体的优劣程度十分关键[6]。
在设计组卷系统的适应度函数时,需要同时考虑多个指标对试卷的影响,这样才能全面地评价试卷的质量。为了使得适应度函数能够全面评价试卷的难度、知识点覆盖率和区分度等指标。本系统的适应度函数设计如下:
设一套试卷预期的难度系数为
| $n = 1 - r/R$ |
式中:
试卷预期的考察的知识点数为N0,而实际考察的知识点数为N。由于直接计算试卷的区分度较困难,因此本系统使用试卷中各题目难度的方差近似代替区分度,这样可以保证取得的试卷既有简单题,也有中等题和难题,不会出现所有题目难度接近而无法区分学生水平的问题。假设试卷预期的区分度为
| $f = 1 - \left| {n - {n_0}} \right|{k_1} - (1 - {N / {{N_0}){k_2} - \left| {s - {s_0}} \right|{k_3}}}$ |
式中k1、k2、k3分别是难度、知识点覆盖数、区分度这3个指标在评价适应度时所占的权重,用户可根据自己的需求设置这3个参数,但要保证这3个参数的和是1。
2.3 设计选择算子当某一代种群中没有满足适应度要求的个体时,就需要从这一代种群中选择适应度高的个体,使其通过交叉和变异产生新一代种群。选择算子就是选择过程中使用的算法。
在选择过程中,应当遵循的原则是优先选择适应度高的个体。基于这一原则,有2种常用的选择算法:直接选择法和轮盘赌选择法。直接选择法是将个体按照适应度降序排序,直接选择前面的若干个体;而轮盘赌算法是一种概率算法,采用轮盘赌算法,每一个个体都有概率被选到,被选到的概率和他的适应度成正比,这样,适应度越高的个体被选到的概率越大。
本系统选用的是轮盘赌算法[7]。假设种群共有
| ${p_i} = {{{A_i}} / {\sum\limits_{i = 1}^n {{A_i}} }}$ |
在遗传算法中,交叉是产生后代的重要步骤。在交叉的过程,首先需要从选择算法得到的个体中以某种方式选择2个个体,然后再选择一个或多个交叉点位,接着就可以将2个个体在该点位的试题进行互换,这样就得到了2个新的个体。重复执行上面过程若干次,使得到的新个体数等于上一代种群的个体数[8]。
在这个过程中,选择个体和选择交叉点位通常采用随机选择的方法。设计交叉算子时,确定交叉点位的数量是一个关键的问题。如果采用单点交叉,则算法执行速度较快,但是得到的后代和上一代区别不大;如果采用多点交叉则正好相反,选择的点位越多,得到的后代和上一代区别越大,但同时执行算法需要的时间也越长[9]。本研究通过多次的实验验证,交叉点位的数量保持在3个效果最好。
2.5 设计变异算子在实际的遗传过程中,变异发生的概率较小。因此本系统仅考虑在种群的每个个体上随机选择一个变异位置,而后从试题库中随机选择一道相同题型的题目来替换该位置的题目[10]。
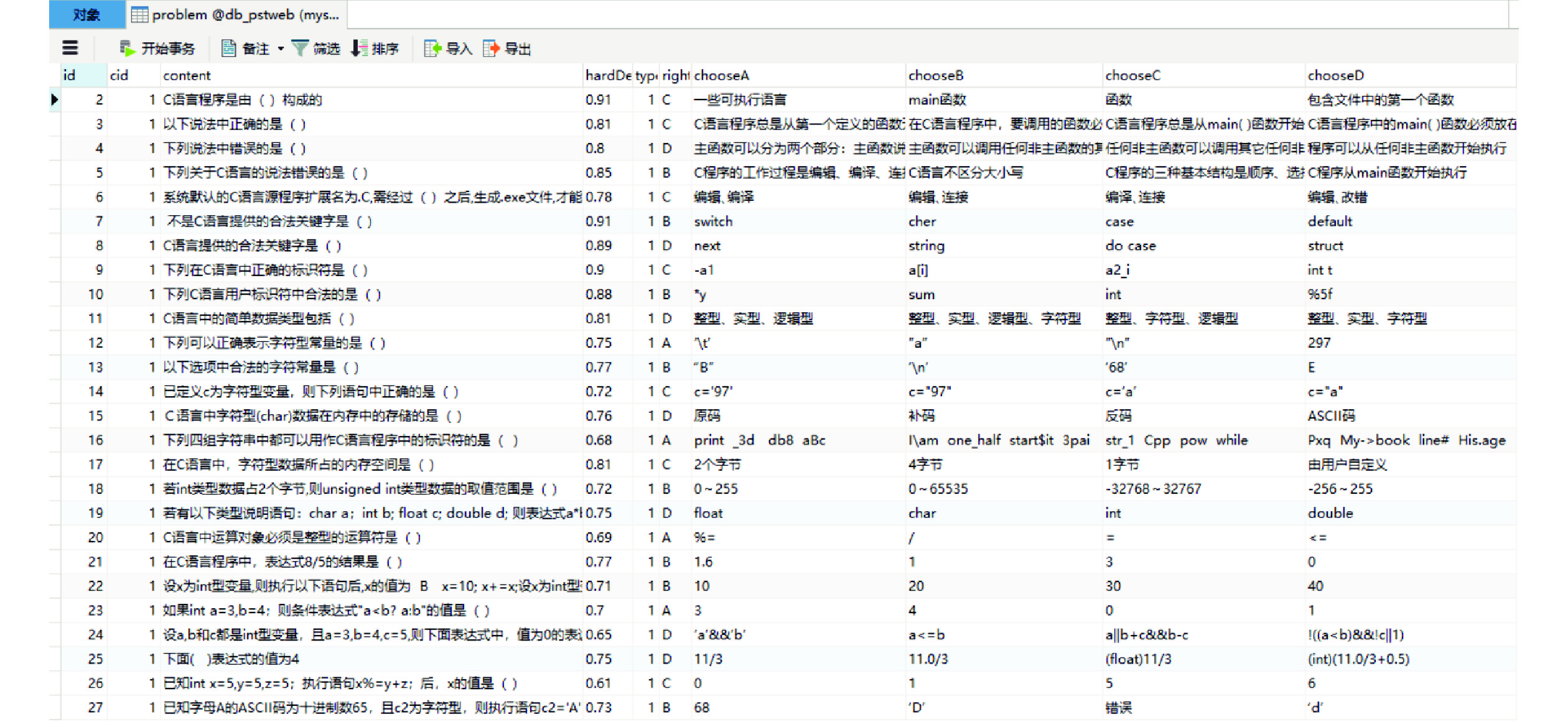
2.6 系统实现本系统采用Java语言开发,通过Servlet处理用户请求并返回响应,通过JSP向用户显示结果,试题及其他数据保存在Mysql数据库中,题库如图1所示。
|
Download:
|
| 图 1 试题库信息界面 | |
教师在登录系统后,可以在系统上发布考试。发布考试时教师需要输入与考试和试卷相关的信息,如考试名称、考试时长、题目数量、每题分值、预期难度和预期知识点考察数等,输入完成后点击生成试卷,即可将考试发布到系统中。本次实验中,教师将期望试卷难度设置为0.8,期望知识点考察数设置为50。发布考试界面如图2所示。
教师点击发布考试之后,页面将会跳转到组卷结果页,教师在此页面可以查看组卷的结果,包括试题难度、知识点覆盖数等信息和题目列表,查看组卷结果界面如图3和图4所示。根据图3的组卷结果,试卷的实际难度为0.788,这与用户输入的期望难度0.8接近,试卷考察的知识点数为56个,多于用户输入的预期知识点数50个。因此,可以认为该组卷算法生成的试卷能够满足用户的要求,试卷的质量能够得到保证。

|
Download:
|
| 图 2 发布考试界面 | |

|
Download:
|
| 图 3 组卷结果界面 | |
|
Download:
|
| 图 4 题目列表界面 | |
1)实验结果表明,该算法的成功率和组卷效率较高,组成的试卷在难度、知识点覆盖范围等指标上能够达到用户的要求,试卷的质量能够得到保证。
2)本文提出了一种高效的组卷策略,能够有效克服传统组卷算法存在的弊端,对于组卷算法的研究和智能组卷系统的设计与实现具有一定的参考价值。
本项目可以进一步扩展研究,通过增加试卷评价指标,进一步优化适应度函数,使组成的试卷令用户更加满意。
| [1] |
王宣策, 欧阳鑫玉. 基于改进遗传算法的智能组卷系统设计[J]. 电脑知识与技术, 2020, 16(2): 65-67. ( 0) 0)
|
| [2] |
贺建英, 王光琼, 唐青松. 一种基于遗传算法的智能组卷策略优化研究[J]. 计算机与数字工程, 2019, 47(1): 130-135. DOI:10.3969/j.issn.1672-9722.2019.01.029 ( 0) 0)
|
| [3] |
陈培培, 徐家喜. 基于SSM的自动组卷系统的设计与实现[J]. 电脑知识与技术, 2018, 14(20): 49-51. ( 0) 0)
|
| [4] |
黄国政. 基于遗传算法的自动组卷系统的设计与实现[D]. 南京: 南京理工大学, 2008.
( 0) 0)
|
| [5] |
李川, 张少茹. 一种分阶求解回溯组卷算法[J]. 电子测量技术, 2019, 42(3): 35-39. ( 0) 0)
|
| [6] |
邓明学. 基于遗传算法的开放教育在线考试系统组卷实现[J]. 广西广播电视大学学报, 2019, 30(2): 24-26. DOI:10.3969/j.issn.1008-7656.2019.02.006 ( 0) 0)
|
| [7] |
金玉苹, 李雨春. 一种改进的遗传算法在智能组卷上的应用[J]. 牡丹江师范学院学报(自然科学版), 2017(2): 38-40. ( 0) 0)
|
| [8] |
于萧榕. 在线考试系统在实验机房中的应用[J]. 现代电子技术, 2011, 34(8): 84-86, 90. DOI:10.3969/j.issn.1004-373X.2011.08.027 ( 0) 0)
|
| [9] |
朱敏, 马秀峰, 孙来福. 无纸化考试系统—新技术条件下教育考试的新视点[J]. 中国现代教育装备, 2005(3): 29-31. DOI:10.3969/j.issn.1672-1438.2005.03.011 ( 0) 0)
|
| [10] |
庄越, 黄君羡. 基于知识点和改进随机抽取算法的智能组卷方案研究[J]. 计算机与数字工程, 2009, 37(6): 16-18, 56. DOI:10.3969/j.issn.1672-9722.2009.06.004 ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


