随着电子对抗技术的不断发展，在复杂的作战环境中，单基地雷达定位往往很难得到理想的结果。而雷达组网定位在时域、频域、空域上都有很强的覆盖能力，通过雷达间的信息共享，对比于单基站雷达定位更加灵活多变，具有更高精度的定位能力和更快更广的搜索能力^[1-4]。在雷达组网对抗背景下，干扰机的干扰资源往往是有限的，如何通过有限的干扰资源去得到一个最优的干扰结果，就需要制定合理的干扰策略来实现干扰资源利用最大化。

诸多学者针对如何快速合理地分配干扰资源展开研究。文献[5]利用博弈论的方法去研究干扰资源分配问题，并证明纳什均衡的可行性与存在性，虽然算法结果能获得较高干扰效益，但系统开销和收敛速度之间关系很难平衡，算法复杂度较高。文献[6]研究了协同干扰对雷达组网对抗的影响，并利用智能算法中的遗传算法去寻找最优干扰资源分配方式，虽然用智能算法比博弈论迭代要快，但算法收敛时间太长，还伴随陷入局部最优风险。2015年，陈雅雯等^[7]提出了结合飞机突防位置变化过程，用概率加权来评估干扰效果，并通过蚁群算法去寻找最优干扰资源分配方式，这一方法虽然可以快速得到干扰策略，但由于目标函数建立靠经验加权，所以局限性较大。本次研究的目的就是为了寻找一个复杂度低、收敛速度快、不易陷入局部最优的干扰资源的分配方式，以适应复杂多变的雷达对抗环境。

在多部干扰机伴飞、突防雷达组网的研究背景下，本文把定位几何精度因子(geometric dilution precision，GDOP)作为目标函数，构建干扰效益分配模型，应用改进灰狼算法在满足目标函数和约束条件的前提下进行寻优，寻找一个最佳的干扰资源分配方案。最后通过仿真结果与常用的几个智能算法做对比，结果表明利用改进灰狼算法进行干扰资源分配的效果具有一定优势。

1 干扰资源分配数学模型 1.1 干扰资源分配评估指标

干扰资源分配的进行离不开干扰效果评估，根据对抗场景选择合适的干扰资源分配评估指标显得尤为重要。

通常在模拟雷达对抗时，进行干扰机对雷达干扰后的效果评估，都是通过检测概率(probability of detection，PD)或GDOP来作为判断标准，对于前者，当干扰的效果越好时，雷达的检测概率也就越低，不容易发现目标；而考虑干扰对雷达定位精度的影响时，干扰的效果越好，雷达的定位误差也就越大，对应的GDOP值也就越高^[7]。

若把所得的GDOP值作为目标函数值，首先要得到对应的信干比，根据文献[8]可得，在多部干扰机干扰同一部雷达时，对应雷达的信干比 ${J_{{\rm{SJR}}}}$ 为

${J_{{\rm{SJR}}}} = \frac{{{P_{{\rm{rs}}}}}}{{{P_{{\rm{rj}}}}}} = \frac{{{P_{\rm{t}}}G_{\rm{t}}^2\sigma }}{{4{\rm{{\text{π}} }}\left( {\displaystyle\sum\limits_i {{{{P_{ji}}{G_{ji}}{\gamma _{ji}}{G_{\rm{r}}}\left( {{\theta _i}} \right)} / {R_{ji}^2}}} } \right)R_{\rm{t}}^4}}$

式中： ${P_{{\rm{rs}}}}$ 和 ${P_{{\rm{rj}}}}$ 分别为雷达信号与干扰信号的功率； ${P_{\rm{t}}}$ 为雷达的发射功率； $i$ 和 $j$ 分别代表第 $i$ 部干扰机和第 $j$ 部雷达； ${P_{ji}}$ 为干扰机的峰值功率； ${G_{\rm{t}}}$ 为雷达天线主瓣增益； ${G_{ji}}$ 为干扰机的发射增益； ${G_{\rm{r}}}\left( {{\theta _i}} \right)$ 为在 $i$ 部干扰机方向上雷达天线的增益； $\lambda $ 为雷达信号的波长； ${\gamma _{ji}}$ 为干扰极化系数； $\sigma $ 为目标有效反射截面积； ${R_{ji}}$ 为第 $i$ 部干扰机和第 $j$ 部雷达之间的距离； ${R_{\rm{t}}}$ 为雷达与目标之间的距离。

据文献[6]可知，当雷达受到干扰时，测距误差 ${\sigma _{\rm{r}}}$ 为

${\sigma _{\rm{r}}} = \frac{{c\tau }}{{{k_1}\sqrt {{J_{{\rm{SJR}}}} \cdot {{{f_{\rm{r}}}} / {{\beta _{\rm{n}}}}}} }}$

式中： $c$ 为光速； ${k_1}$ 为一与雷达信号波形有关的常数，当雷达信号为脉冲压缩信号时， ${k_1} = 0.74$ ； ${f_{\rm{r}}}$ 为检测到的雷达信号重复频率； $\tau $ 为脉冲宽度； ${\beta _{\rm{n}}}$ 为对应的天线伺服带宽。

与此相对应的测角误差同样可求：

${\sigma _{\rm{\varphi }}} = \frac{{1.4{\theta _{0.5}}}}{{{k_2}\sqrt {B\tau \cdot {J_{{\rm{SJR}}}} \cdot {{{f_{\rm{r}}}} / {{\beta _{\rm{n}}}}}} }}$

式中： ${\theta _{0.5}}$ 为天线的半功率波束宽度； ${k_2}$ 为与角梯度相关的常数，单脉冲雷达 ${k_2} \approx 1.7$ ；B为接收机的带宽。

当利用雷达组网对目标进行定位时，将每一部雷达所获取的信息综合到一起来寻找目标位置。由于干扰信号的存在，雷达的测距和测角都会产生相应误差，使得最终定位结果产生偏差，而这个偏差的大小就是GDOP值（G_g）：

${G_{\rm{g}}} = \sqrt {\sigma _x^2 + \sigma _y^2 + \sigma _z^2} $

(1)

式中： $\sigma _x^2$ 、 $\sigma _y^2$ 、 $\sigma _z^2$ 分别为x、y、 $z $ 方向上的定位精度，可通过求得的斜距、测距误差和测角误差计算得到，将求得结果带入式(1)，即可求得定位精度GDOP的值。

每一种干扰资源分配方法都可以得到一组GDOP值，将GDOP值作为目标函数，根据选择的干扰资源分配算法，寻找目标函数最大值。对应目标函数值越大，干扰效果越好。

1.2 干扰资源分配效益模型

选择GDOP值作为干扰评估指标后，根据对抗双方的作战背景，确定干扰关系矩阵和干扰约束条件，建立干扰资源分配效益模型。

当研究背景为多部干扰机协同干扰雷达组网时，可假设有 $N$ 部干扰机，组网雷达数为 $M$ ，那么干扰关系就可构成一个关于干扰机与组网雷达的 $N \times M$ 的矩阵，干扰关系矩阵如下所示^[9-10]

${{Z}} = \left[ {\begin{array}{*{20}{c}} {{z_{11}}}&{{z_{12}}}& \ldots &{{z_{{\rm{1}}M}}} \\ {{z_{21}}}&{{z_{22}}}& \ldots &{{z_{{\rm{2}}M}}} \\ \vdots & \ldots &{}& \vdots \\ {{z_{N{\rm{1}}}}}&{{z_{N{\rm{2}}}}}& \ldots &{{z_{NM}}} \end{array}} \right]$

(2)

${z_{nm}} = \left\{ {{x_n},{y_m}} \right\}$ 表示第 $n$ 部干扰机对第 $m$ 部雷达是否实施干扰，如果干扰则函数值为1，反之为0。由于干扰过程中的干扰资源有限，不可能每一部干扰机同时干扰所有雷达，所以如何利用有限的干扰资源建立合理有效的干扰矩阵，是制定干扰策略的重点。

为了更合理地利用有限的干扰资源，这里用干扰资源利用率来约束干扰策略的制定。当雷达脉宽为 $\tau $ 、脉冲重复周期为t、总的研究时长为T、每个脉冲的干扰时长为 ${\tau _0}$ 时，假设干扰机n对多部雷达进行干扰，那么研究过程中，对该雷达所干扰的脉冲次数N为

$N{\rm{ = }}\frac{T}{t}$

对应干扰时间利用率为

${v_{nm}} = N \cdot \frac{{\left( {\tau + {\tau _0}} \right)}}{T}$

(3)

当一部干扰机同时干扰多部雷达时，就要求其干扰时间利用率小于1，以减少干扰时的脉冲丢失现象，可得约束条件为 $\displaystyle\sum\limits_{m = 1}^M {{v_{nm}}} \leqslant 1$ 。

同时，针对组网雷达的协同干扰，要求在协同干扰时，每一部雷达都会有至少一部干扰机对其干扰，以确保干扰资源的合理利用及干扰的有效性，可得约束条件为 $\displaystyle\sum\limits_{{\rm{n}} = 1}^N {{z_{nm}} \geqslant 1} $ ，所以最终可以得到干扰资源利用的约束条件为

$\left\{ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{m = 1}^M {{v_{nm}} \cdot {z_{nm}} \leqslant 1} } \\ {\displaystyle\sum\limits_{n = 1}^N {{z_{nm}} \geqslant 1\;\;\;\;\;} } \end{array}} \right.$

根据干扰资源利用的约束条件及干扰对抗关系矩阵，就可以建立干扰资源分配效益模型，选择合适的寻优算法^[11]，寻求一种最优的干扰资源分配方案。

2 干扰资源分配算法

通过对比研究，这里选用改进的灰狼算法去分配干扰资源^[12]。

首先对算法中灰狼的位置信息进行一定的处理，可得对应的干扰关系矩阵，继而求出此干扰策略的GDOP值，将其作为目标函数值后就可通过算法迭代去寻找一个最优的干扰资源分配方式，迭代方程为

${{D}} = \left| {{{C}} \cdot {{{X}}_{\rm{p}}}\left( t \right) - {{X}}\left( t \right)} \right|$

(4)

${{X}}\left( {t + 1} \right) = {{{X}}_{\rm{p}}}\left( t \right) - {{A}} \cdot {{D}}$

(5)

式中： $t$ 为此时的迭代次数； ${{{X}}_{\rm{p}}}$ 代表候选狼的位置向量； ${{X}}$ 表示灰狼的位置向量；向量A和 ${{C}}$ 是随迭代次数变化的随机参量，其大小分别为

${{A}} = 2{{{a}}_{\rm{g}}} {{{r}}_1} - {{{a}}_{\rm{g}}}$

${{C}} = 2 {{{r}}_2}$

式中： ${{{r}}_1}$ 和 ${{{r}}_2}$ 是随机控制因子； ${{{a}}_{\rm{g}}}$ 为非线性控制因子，是一组随着迭代从2非线性下降到0的数，这样在算法代数较小的时候，寻得的干扰资源分配结果可能性更多，扩大了搜索范围，防止陷入局部最优，

${{{a}}_{\rm{g}}} = {{a}} \exp \left( {bN\left( {0,1} \right) + c{N_j}\left( {0,1} \right)} \right) d$

其中： $b$ 和 $c$ 的值随着迭代次数的变化而变化，分别为 ${1 / {\sqrt {3n} }}$ 和 ${1 / {\sqrt {3\sqrt n } }}$ ；d为Beta分布的一随机数。

这里利用布谷鸟算法中的Lévy飞行策略。Lévy分布的表达式为

${\rm{Levy}}\left( \lambda \right) = \frac{\mu }{{{{\left| \nu \right|}^{\frac{1}{\beta }}}}}$

本次研究中 $\beta $ 设为1.5， $\mu $ 和 $\nu $ 服从正态分布：

$\left\{ \begin{array}{l} \mu ,{\rm{ }}N\left( {0,\sigma _\mu ^2} \right) \\ \nu ,{\rm{ }}N\left( {0,\sigma _\nu ^2} \right) \\ {\sigma _\mu } = {\left\{ {\dfrac{{\Gamma \left( {1 + \beta } \right)\sin \left( {{{{\rm{{\text{π}} }}\beta } / 2}} \right)}}{{{2^{{{\left( {\beta - 1} \right)} / 2}}}\Gamma \left[ {{{\left( {1 + \beta } \right)} / 2}} \right]\beta }}} \right\}^{\frac{1}{\beta }}} \\ \sigma _\nu ^2 = 1 \\ \end{array} \right.$

作为一种被人们广泛使用的智能算法，灰狼算法同样具有很大陷入局部最优的风险，所以在这里选用Lévy飞行策略的目的是减少随机性，增大对局部的搜索能力，避免算法陷入局部最优解，从而导致不能找到更好的干扰资源分配方案。

在每一代中都会通过 $\alpha $ 、 $\beta $ 和 $\delta $ 这3个最优解位置去更新每个粒子的位置，具体更新公式如下所示

${{X}}\left( {t + 1} \right) = \frac{{{{{X}}_1} + {{{X}}_2} + {{{X}}_3}}}{3}$

综上所述，灰狼算法的具体工作流程如下：

1)初始化算法，根据约束条件给 $\alpha $ 、 $\beta $ 和 $\delta $ 初始位置与适应度值，这里的适应度值为GDOP值，而对应解的位置信息经过处理后可得到对应干扰矩阵。

2)计算每个粒子的适应度值并与 $\alpha $ 、 $\;\beta$ 和 $\delta $ 做对比，并取其中最优解、次优解与第三优解作为新的 $\alpha $ 、 $\;\beta$ 和 $\delta $ 。

3)计算相应A、C和 ${{{a}}_{\rm{g}}}$ 的值。

4)根据式(4)、(5)去更新每一个粒子位置。

5)粒子位置更新完成后，若算法未到最大迭代次数，则返回步骤2)；若达到最大迭代次数，取 $\alpha $ 的目标函数值和位置信息作为最优解。

3 仿真结果

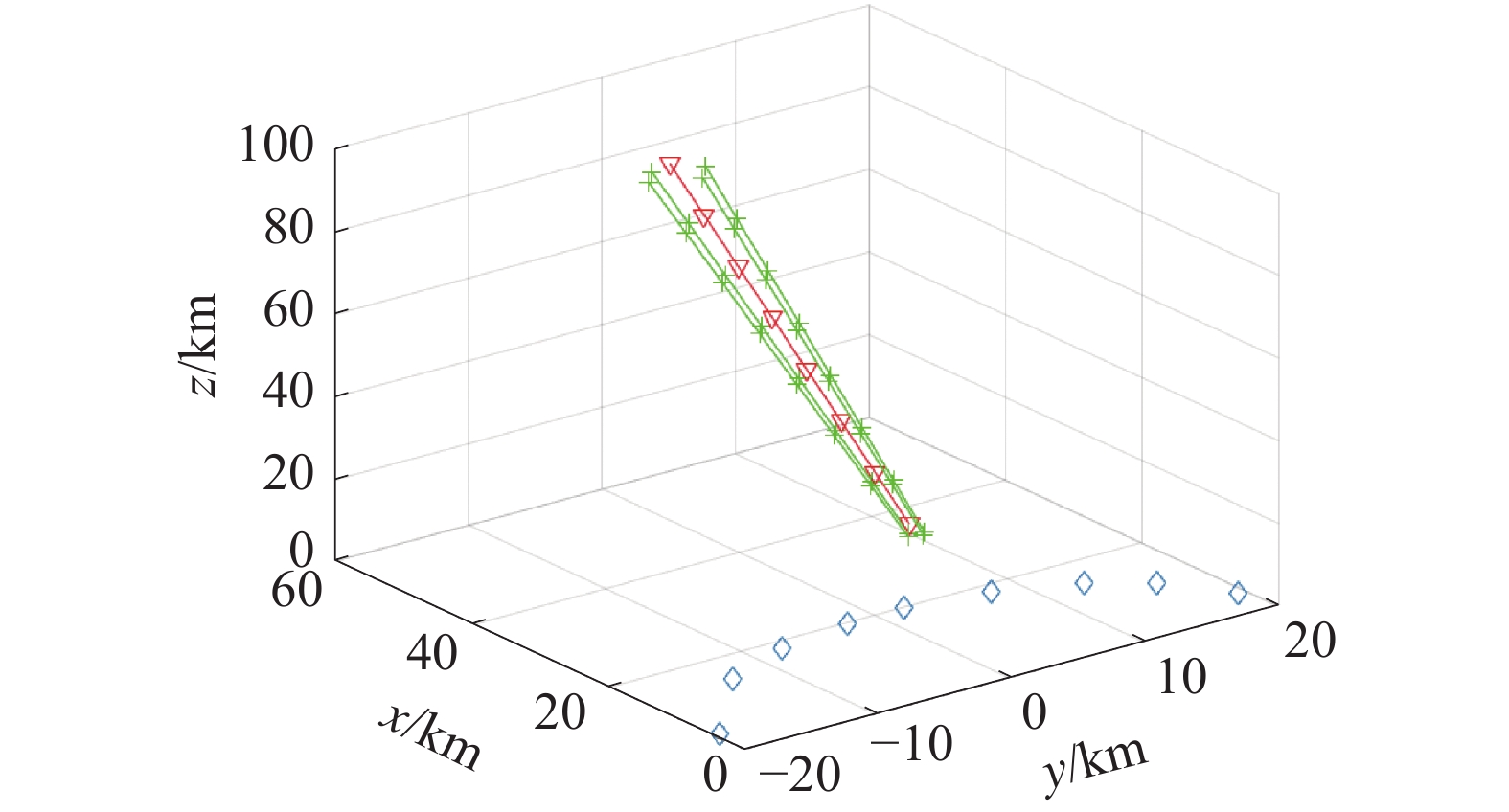
本次研究背景为4部干扰机围绕导弹伴随飞行，突防10部组网雷达，干扰机距离导弹2 km。具体如图1与表1所示。

在进行干扰前，干扰机会对雷达信号进行侦查与分选，提取有用信息来判断威胁程度，来制定合理的干扰资源分配方式。雷达参数信息如表2所示。

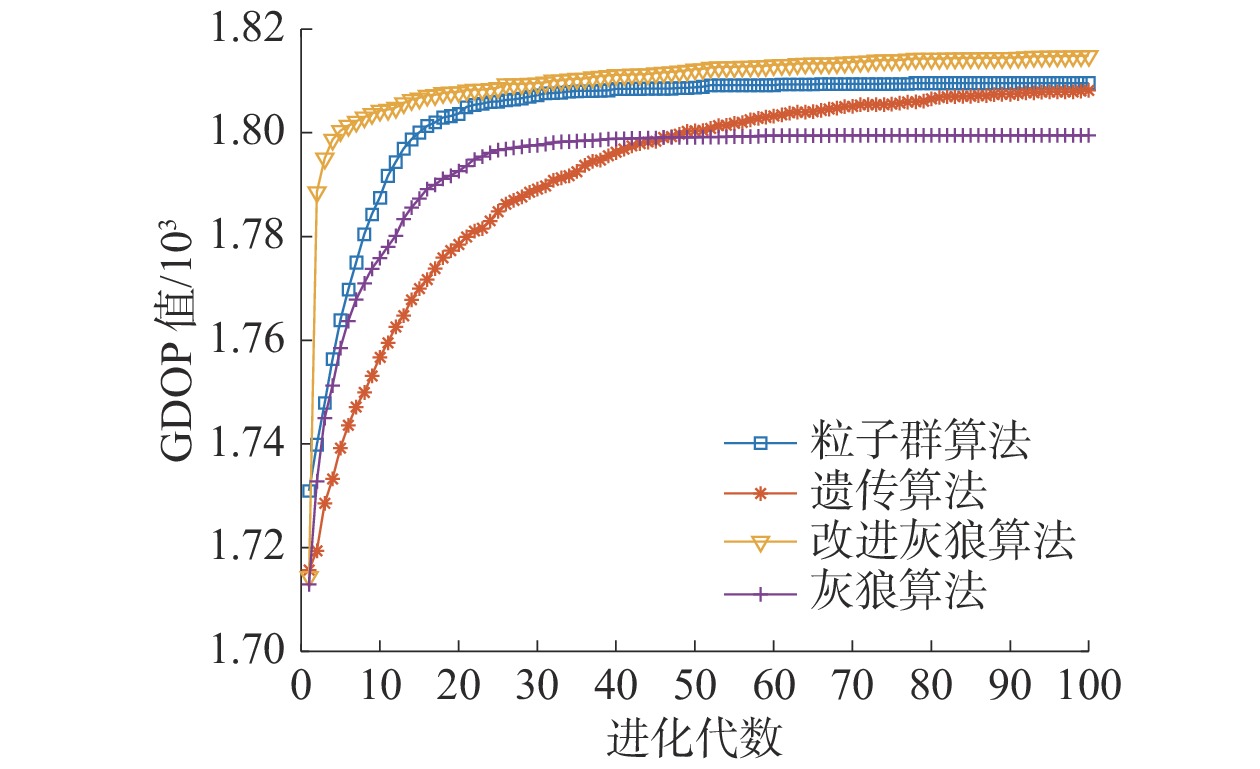
根据采集到的雷达参数，可判断雷达的威胁程度。本次研究中，除遵守单部干扰机的干扰时间利用率小于1以外，还要求1部雷达最少被1部、最多被3部干扰机干扰。设置种群数32，迭代次数100，干扰时长100 μs，总研究时长为300 ms。根据设定的研究背景和参数条件，即可通过算法去寻找一个最佳的干扰资源分配关系。进行100次蒙特卡罗试验，可得4种智能算法求得的GDOP值随迭代次数增加的变化趋势，对比结果如图2所示.

由图2可知，进行100次蒙特卡罗试验后，对结果取平均值可见，改进灰狼算法比灰狼算法、粒子群算法和遗传算法在寻优性能方面有了一定程度上的改进，不仅收敛速度更快，最终得到的分配结果也比其他3种算法要好。

由于干扰资源是有限的，所以在分配干扰资源时要有一定干扰效率和对抗关系的约束，利用式(2)与式(3)，将干扰关系矩阵与干扰效率相结合，可以得到对应的干扰效率矩阵，得到的最优干扰资源分配方案的干扰效率矩阵如表3所示。

由表4结果可见，改进后的灰狼算法比其他3种算法均方误差更小、稳定性更好，减少了陷入局部最优的概率，寻优性能有了很大的提高，在雷达组网对抗中可以更快、更有效地寻找到合理的分配干扰资源方法。

4 结论

本文针对雷达组网对抗中的干扰资源分配问题展开研究，根据研究成果可得出以下结论：

1）把GDOP值作为干扰效果评估的评判标准，可以有效地评估组网雷达的协同干扰问题。

2）验证改进灰狼算法在研究该类问题时良好的性能，为解决干扰资源分配问题提供了新的思路。

本次研究把定位精度作为评判干扰效果的标准不具备普遍性，下一步可以结合多种评估标准进行评判的研究。