船体几何重构是实现船舶概念设计、总体设计和船型优化的一种关键技术^[1]，对船舶的各种性能起着决定性影响。针对船体几何重构，找到一种简洁、高效的NURBS技术求解方法具有一定的现实意义。本文就这一问题对船体型线、曲面的重构和分割进行分析。

现阶段对船体曲面设计的研究相对成熟，钱宏等^[2]将NURBS技术成功运用于船体曲面重构，Wang H等^[3]利用NURBS曲面对船体进行几何建模，讨论了节点矢量的相容性处理问题，于亚如^[4]将NURBS技术运用到船体型线设计中，利用其卓越的局部修改性来设计船体型线，张伟等^[5]提出一种基于B样条的船体及自由面面元生成方法，这些研究主要是基于NURBS的船体曲面生成过程精确表达和曲面的修改方法等。

基于NURBS的船体曲面设计，有单一NURBS曲面表达方法^[6]、曲面分片表达方法和曲面细分方法^[7]等，它们主要是根据型值点生成船体曲面特征线进而生成船体曲面。陈军等^[8]对NURBS曲线曲面反求问题进行分析和研究，实现了船体的三维实体造型。Shi G等^[9]实现了快速插值给定型值点的船体曲面重构技术。Gianpaolo S等^[10]将一种在NURBS曲面上计算曲率和脐点的技术应用于船型设计。Yang C等^[11]采用NURBS曲面表示的船体，该技术可用于自动生成球艏，或根据水动力性能和几何约束修改船首或整个船型，也可以根据可移动的RBF控制节点来获得NURBS控制点的运动。

在基于NURBS方法关键技术的船体几何重构应用上，以上研究对控制顶点的反求算法较为复杂，对于曲线曲面的边界条件处理也各不相同。本文通过利用一种非节点边界条件下的曲线控制顶点反算算法^[12]，编写了船体型线和船体曲面重构程序，并探索一种求解算法用于船体曲面与水面快速求交。该程序可以通过修改控制顶点和权重因子对曲面进行变形，这种修改不破坏原有曲面的光顺、连续等几何特性，更方便用于船体型线设计领域。

1 NURBS曲线和曲面 1.1 NURBS曲线

由参数变量u定义的k次NURBS曲线方程^[13]为

$p(u) = \dfrac{{\displaystyle\sum\limits_{i = 0}^n {{{{w}}_i}{b_i}{N_{i,k}}(u)} }}{{\displaystyle\sum\limits_{i = 0}^n {{{{w}}_i}{N_{i,k}}(u)} }}\qquad i = 0,1, \cdots ,n$

(1)

式中： $p(u)$ 为参数 $u \in \left[ {0,1} \right]$ 下曲线上的点； ${b_i}$ 为曲线控制顶点， ${{{w}}_i}$ 为控制顶点对应的权重因子； ${N_{i,k}}(u)$ 为k次NURBS曲线的基函数，可根据deBoor-Cox的递推公式^[13]得出:

$\begin{split}& {N_{{{i}},0}}(u) = \left\{ \begin{array}{l} 1, \;\;\;\;\;\;u = {u_0}\;{\rm{and}}\; {u_i} < u \leqslant {u_{i + 1}}\\ 0, \;\;\;\;\;\;{\text{其他}} \end{array} \right.\\ &{N_{{{i}},{{k}}}}(u){\rm{ = }}\dfrac{{u - {u_i}}}{{{u_{i + k}} - {u_i}}}{N_{{\rm{i}},k - 1}}(u)\dfrac{{{u_{i + k + 1}} - u}}{{{u_{i + k + 1}} - {u_{i + 1}}}}{N_{{\rm{i + 1}},k - 1}}(u)\\ &{\text{规定}}\dfrac{0}{0}{\rm{ = }}0 \end{split}$

(2)

k次NURBS曲线的节点矢量， ${{\mathit{\boldsymbol{U}}}} = [{u_0},{u_1}, \cdots , $ $ {u_{n + k + 1}}]$ 。曲线的定义域 $u \in [{u_k},{u_{n + 1}}]$ ，共含有n−k+1个节点区间。去掉基函数为零的那些项，式(1)可化简为

$p\left( u \right) = \dfrac{{\displaystyle\sum\limits_{j = i - k}^i {{w_j}{b_j}{N_{j,k}}\left( u \right)} }}{{\displaystyle\sum\limits_{j = i - k}^i {{w_j}{N_{j,k}}\left( u \right)} }},\qquad u \in \left[ {{u_k},{u_{n + 1}}} \right]$

(3)

当k=3时，NURBS曲线的节点矢量和定义域分别为

$\begin{array}{c} U = [{u_0},{u_1}, \cdots ,{u_{n + 4}}] \\ u \in [{u_3},{u_{n + 1}}] \end{array} $

(4)

本文运用的三次NURBS曲线插值求解方程简化为

$p\left( u \right) = \dfrac{{\displaystyle\sum\limits_{j = i - 3}^i {{w_j}{b_j}{N_{j,3}}\left( u \right)} }}{{\displaystyle\sum\limits_{j = i - 3}^i {{w_j}{N_{j,3}}\left( u \right)} }}\qquad u \in \left[ {{u_3},{u_{n + 1}}} \right]$

(5)

1.2 NURBS曲面

由2个参数变量 $ \left( {u,v} \right)$ 定义的NURBS曲面方程^[13]：

$p\left( {u,v} \right) = \dfrac{{\displaystyle\sum\limits_{i = 0}^m {\displaystyle\sum\limits_{j = 0}^n {{w_{i,j}}{b_{i,j}}} } {N_{i,3}}\left( u \right){N_{j,3}}\left( v \right)}}{{\displaystyle\sum\limits_{i = 0}^m {\displaystyle\sum\limits_{j = 0}^n {{w_{i,j}}} } {N_{i,3}}\left( u \right){N_{j,3}}\left( v \right)}}$

(6)

式中： $p\left( {u,v} \right)$ 为参数 $\left( {u,v} \right)$ 下曲面上的点； ${b_{i,j}}$ 为 $\left( {m + 1} \right) \times $ $ \left( {n + 1} \right)$ 的曲面控制网格； ${w_{i,j}}$ 为控制网格对应的权因子； $ {N}_{i,3}\left(u\right)$ 、 $ {N}_{j,3}\left(v\right)$ 为曲面u和v两个参数方向的基函数，根据式(2)推导。曲面的控制网格可以根据曲线控制顶点的反算思路^[12]求解，给定 $\left( {m + 1} \right) \times \left( {n + 1} \right)$ 个数据点 $ {p}_{i,j},{p}_{0,i}$ 、 $ {p}_{n,i}$ 、 $ {p}_{j,0}$ 和 ${p_{j,m}}$ ， $i = 0,1, \cdots ,m,j = 1,2, \cdots , $ $ n - 1$ 作为曲面的边界。与NURBS曲线边界补充方式类似， $ {p}_{1,i}$ 、 $ {p}_{n-1,i}$ 、 $ {p}_{j,1}$ 和 ${p_{j,m}}$ ， $i = 1,2, \cdots ,m - 1,j = 2, $ $ 3, \cdots , n - 2$ 不再作为曲面分段连接点，由积累弦长参数化法可得出两个方向的节点矢量：

$\begin{array}{l} {{\mathit{\boldsymbol{U}}}} = [{u_0},{u_1}, \cdots ,{u_{m + 4}}] \\ {{\mathit{\boldsymbol{V}}}} = [{v_0},{v_1}, \cdots ,{v_{m + 4}}] \end{array} $

为了使其曲面控制网格求解更方便，NURBS曲面方程可改写为

$p\left( {u,v} \right) = \dfrac{{\displaystyle\sum\limits_{i = 0}^m {{w_i}\left( {\dfrac{{\displaystyle\sum\limits_{j = 0}^n {{w_{ij}}{b_{i,j}}} {N_{j,3}}\left( v \right)}}{{\displaystyle\sum\limits_{j = 0}^n {{w_{ij}}} {N_{j,3}}\left( v \right)}}} \right)} {N_{i,3}}\left( u \right)}}{{\displaystyle\sum\limits_{i = 0}^m {{w_i}{N_{i,3}}\left( u \right)} }}$

(7)

令

${a_i}\left( v \right) = \dfrac{{\displaystyle\sum\limits_{j = 0}^n {{w_{ij}}{b_{i,j}}{N_{j,3}}\left( u \right)} }}{{\displaystyle\sum\limits_{j = 0}^n {{w_{ij}}{N_{j,3}}\left( u \right)} }}$

(8)

则式(7)可简化为

$p\left( {u,v} \right) = \dfrac{{\displaystyle\sum\limits_{i = 0}^m {{w_i}{a_i}\left( v \right)} {N_{i,3}}\left( u \right)}}{{\displaystyle\sum\limits_{i = 0}^m {{w_i}} {N_{i,3}}\left( u \right)}}$

(9)

将两个方向的节点值代入式(7)，根据反算NURBS插值曲线控制顶点的方法分为两步求出，思路如下：1)在u方向上应用NURBS曲线反算，可解出式(9)中的 ${a_i}\left( v \right)$ 。2)在v方向上应用NURBS曲线反算，可解出式(8)中的 ${b_{i,j}}$ 控制网格。

2 控制顶点反算和数据点参数化 2.1 曲线的控制顶点反算

在实际应用中，给定样条曲线一系列数据点，对样条曲线进行插值的情况更为多见，也就是所谓的逆向工程。逆向工程就是根据一系列数据点可反算出样条曲线的多边形控制顶点，进而根据控制顶点和基函数对样条曲线进行插值。一般情况下，给出n−1个数据点和曲线端部的2个切矢量，可建立n+1个方程进而求解对应的n+1个控制顶点。通常在对船型进行建模时，给定的条件是船舶型值点或者型线图，没有端部切矢量。本文运用王飞^[12]提出的一种反算三次B样条插值开曲线控制顶点的算法求解NURBS的控制顶点，对船体进行几何重构，其主要特点是无需给定船舶型线首尾端切矢。

给定n+1个数据点 ${p_i}(i = 0,1, \cdots ,n,{p_0},{p_n})$ ，作为样条曲线的首末端点。 ${p_0},{p_2}, \cdots ,{p_{n - 2}},{p_n}$ 作为三次样条插值曲线的n−1个连接点， ${p_1},{p_{n - 1}}$ 不再为三次样条插值曲线的连接点。故对应的三次样条曲线的控制顶点个数为n+1，即 ${b_i}(i = 0,1, \cdots ,n)$ 。三次B样条曲线的节点矢量为

$u = \left[ {{u_0},{u_1}, \cdots ,{u_{n + 4}}} \right]$

(10)

式中： ${u_0} = {u_1} = {u_2} = {u_3},{u_{n + 1}} = {u_{n + 2}} = {u_{n + 3}} = {u_{n + 4}}$ ，三次样条曲线的定义域为 $u \in [{u_3},{u_{n + 1}}]$ 。将节点值依次代入式(5), 应满足插值条件:

$p({u_i}) = \displaystyle\sum\limits_{j = i - 3}^i {{b_j}{N_{j,3}}({u_i})} = {p_{i - 2}} \;\;\;i = 4,5, \cdots ,n$

(11)

求解n+1个控制顶点需要n+1个方程，式(11)有n−3个方程，需补充如下4个方程：

$\left\{ \begin{array}{l} {b_0} = {p_0} \\ {b_n} = {p_n} \\ p({t_1}) = \displaystyle\sum\limits_{j = 0}^3 {{b_j}{N_{j,3}}({t_1}) = {p_1}} \\ p({t_{n - 1}}) = \displaystyle\sum\limits_{j = 0}^3 {{b_j}{N_{j,3}}({t_{n - 1}}) = {p_{n - 1}}} \end{array} \right.$

(12)

式中： ${t_1},{t_{n - 1}}$ 分别是 ${p_1},{p_{n - 1}}$ 对应的参数节点值，其中 $ {t}_{1}\in [{u}_{3},{u}_{4}],{t}_{n-1}\in [{u}_{n},{u}_{n+1}]$ 。将式(11)、(12)合写成求解n+1个控制顶点 ${b_i},i = 0,1, \cdots ,n$ 的矩阵形式：

$\left[ {\begin{array}{*{20}{c}} 1&{}&{}&{}&{}&{}\\ {{N_{0,3}}({t_1})}&{{N_{1,3}}({t_1})}&{{N_{2,3}}({t_1})}&{{N_{3,3}}({t_1})}&{}&{}\\ {}&{{N_{1,3}}({u_4})}&{{N_{2,3}}({u_4})}&{{N_{3,3}}({u_4})}&{}&{}\\ {}& \ddots & \ddots & \ddots &{}&{}\\ {}&{}&{{N_{n - 3,3}}({u_n})}&{{N_{n - 2,3}}({u_n})}&{{N_{n - 1,3}}({u_n})}&{}\\ \begin{array}{l} \\ \end{array}&\begin{array}{l} \\ \end{array}&\begin{array}{l} {N_{n - 3,3}}({t_{n - 1}})\\ \end{array}&\begin{array}{l} {N_{n - 2,3}}({t_{n - 1}})\\ \end{array}&\begin{array}{l} {N_{n - 1,3}}({t_{n - 1}})\\ \end{array}&\begin{array}{l} {N_{n,3}}({t_{n - 1}})\\ 1 \end{array} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \begin{array}{l} {b_0}\\ {b_1} \end{array}\\ {{b_2}}\\ \vdots \\ {{b_{n - 2}}}\\ {{b_{n - 1}}}\\ {{b_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{p_0}}\\ {{p_1}}\\ {{p_2}}\\ \vdots \\ {{p_{n - 2}}}\\ {{p_{n - 1}}}\\ {{p_n}} \end{array}} \right]$

(13)

为了方便快速求解方程，将式(13)化简为三对角方程组的追赶法求解形式：

$\left[{\begin{array}{*{20}{c}} 1&{}&{}&{}&{}&{} \\ {{a_1}}&{{b_1}}&{{c_1}}&{}&{}&{} \\ {}&{{a_2}}&{{b_2}}&{{c_2}}&{}&{} \\ {}& \ddots & \ddots & \ddots &{}&{} \\ {}&{}&{{a_{n - 2}}}&{{b_{n - 2}}}&{{c_{n - 2}}}&{} \\ \begin{array}{l} \\ \end{array} &\begin{array}{l} \\ \end{array} &\begin{array}{l} \\ \end{array} &\begin{array}{l} {a_{n - 1}} \\ \end{array} &\begin{array}{l} {b_{n - 1}} \\ \end{array} &\begin{array}{l} {c_{n - 1}} \\ 1 \end{array} \end{array}}\right]\left[{\begin{array}{*{20}{c}} \begin{array}{l} {b_0} \\ {b_1} \end{array} \\ {{b_2}} \\ \vdots \\ {{b_{n - 2}}} \\ {{b_{n - 1}}} \\ {{b_n}} \end{array}}\right] = \left[{\begin{array}{*{20}{c}} {p{'_0}} \\ {p{'_1}} \\ {p{'_2}} \\ \vdots \\ {p{'_{n - 2}}} \\ {p{'_{n - 1}}} \\ {p{'_n}} \end{array}}\right]$

(14)

式中：

$\begin{split}& \quad\quad\quad\quad\quad{a_i} = \dfrac{{{{({u_{i + 3}} - {u_{i + 2}})}^2}}}{{({u_{i + 3}} - {u_i})}}\\ &{b_i} = \dfrac{{({u_{i + 3}} - {u_{i + 2}})({u_{i + 2}} - {u_i})}}{{({u_{i + 3}} - {u_i})}} + \dfrac{{({u_{i + 2}} - {u_{i + 1}})({u_{i + 4}} - {u_{i + 2}})}}{{({u_{i + 4}} - {u_{i + 1}})}}\\ &\quad\quad\quad\quad\quad{c_i} = \dfrac{{{{({u_{i + 2}} - {u_{i + 1}})}^2}}}{{({u_{i + 4}} - {u_{i + 1}})}}\\ &p{'_i} = ({u_{i + 3}} - {u_{i + 1}}) \cdot {p_i},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 2,3, \cdots ,n - 2 \end{split}$

(15)

$\begin{split} & \quad\quad\quad\quad\quad\quad\quad\quad\quad{a_1} = {c_2}{N_{0,3}}({t_1}) \\ &\quad\quad\quad\quad\quad\quad {b_1} = {c_2}{N_{1,3}}({t_1}) - {a_2}{N_{3,3}}({t_1})\quad\quad\quad\quad\quad\quad\quad \end{split} $

$\begin{split}\;\\ & \qquad {c_1} = {c_2}{N_{2,3}}({t_1}) - {b_2}{N_{3,3}}({t_1}) \\ & {a_{n - 1}} = {a_{n - 2}}{N_{n - 2,3}}({t_{n - 1}}) - {b_{n - 2}}{N_{n - 3,3}}({t_{n - 1}}) \\ & {b_{n - 1}} = {a_{n - 2}}{N_{n - 1,3}}({t_{n - 1}}) - {c_{n - 2}}{N_{n - 3,3}}({t_{n - 1}}) \\ & \quad\quad\quad\quad {c_{n - 1}} = {a_{n - 2}}{N_{n,3}}({t_{n - 1}}) \\ & \qquad\quad\quad\quad p{'_0} = {p_0} \\ & \qquad p{'_1} = {c_2}{p_1} - ({u_5} - {u_3}){N_{3,3}}({t_1}){p_2} \\ & p{'_{n - 1}} = {a_{n - 2}}{p_{n - 1}} - ({u_{n + 1}} - {u_{n - 1}}){N_{n - 3,3}}({t_{n - 1}}){p_{n - 2}} \\ &\qquad\quad\quad\quad p{'_n} = {p_n} \end{split} $

(16)

在式(16)中的基函数用式(2)deBoor-Cox递推公式求解，式(14)就可以用追赶法^[14]求解出NURBS曲线的n+1个控制顶点。

2.2 数据点参数化

对于数据点的参数化，即使相同的一组数据点采用同一种插值方法，选择数据点的参数化方法不同也可能求得的插值曲线不同。一般主要有4种参数化方法^[15]：均匀参数化法、积累弦长参数化法、向心参数化法和福利参数化法，本文NURBS曲线采用积累弦长参数化法确定节点值，使定义域内节点值与数据点 ${p_0},{p_2}, \cdots {p_{n - 2}},{p_n}$ 对应。

$\begin{split}& \quad \quad \quad \quad \quad \quad \quad \quad {{u'}_0} = 0 \\ & {{u'}_1} = {{u'}_{i - 1}} + \left| {{p_i} - {p_{n - 1}}} \right|,\;\;\;\;\;\;\;\;\;i = 1,2, \cdots, n \end{split} $

(17)

单位化处理：

${u'_t} = {u'_t}/{u'_n},\;\;\;\;i = 1,2, \cdots ,n$

(18)

节点取值：

$\begin{split}& \quad{u_0} = {u_1} = {u_2} = {u_3} = {{u'}_0} = 0 \\ &\quad\qquad\qquad{t_1} = {{u'}_1} \\ &\quad{u_i} = {{u'}_{i - 2}},\;\;\;\;\;\;i = 4,5, \cdots, n \\ &\quad\qquad\qquad{t_{n - 1}} = {{u'}_{n - 1}} \\ &\quad{u_{n + 1}} = = {u_{n + 2}} = {u_{n + 3}} = {u_{n + 4}} = {{u'}_n} = 1\end{split} $

(19)

从式(19)可以看出， ${t_1}$ 与 ${p_1}$ 对应， ${t_{n - 1}}$ 与 ${p_{n - 1}}$ 对应，为了避免首末曲线段的曲率突变，此非节点条件^[12]等价于边界条件。

3 几何重构 3.1 NURBS技术的程序实现

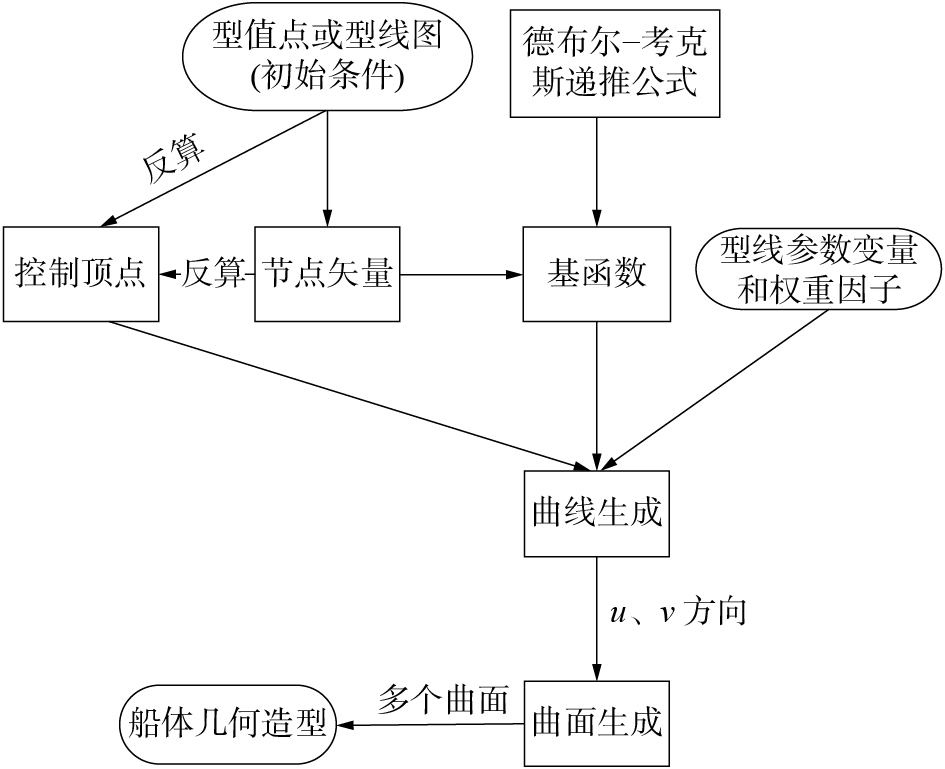
通过C++程序设计，图1为NURBS技术的实现流程图。根据论文前两节提供的算法计算NURBS曲线的控制顶点、节点矢量和基函数，运用u、v两个参数方向计算可以生成NURBS曲面，多个曲面拼接生成船体整个几何外型。给定船体型线的型值点初始条件，通过自行设计型线参数变量和权重因子，可以实现船体离散化表达和船体型线改变。

3.2 NURBS曲线重构

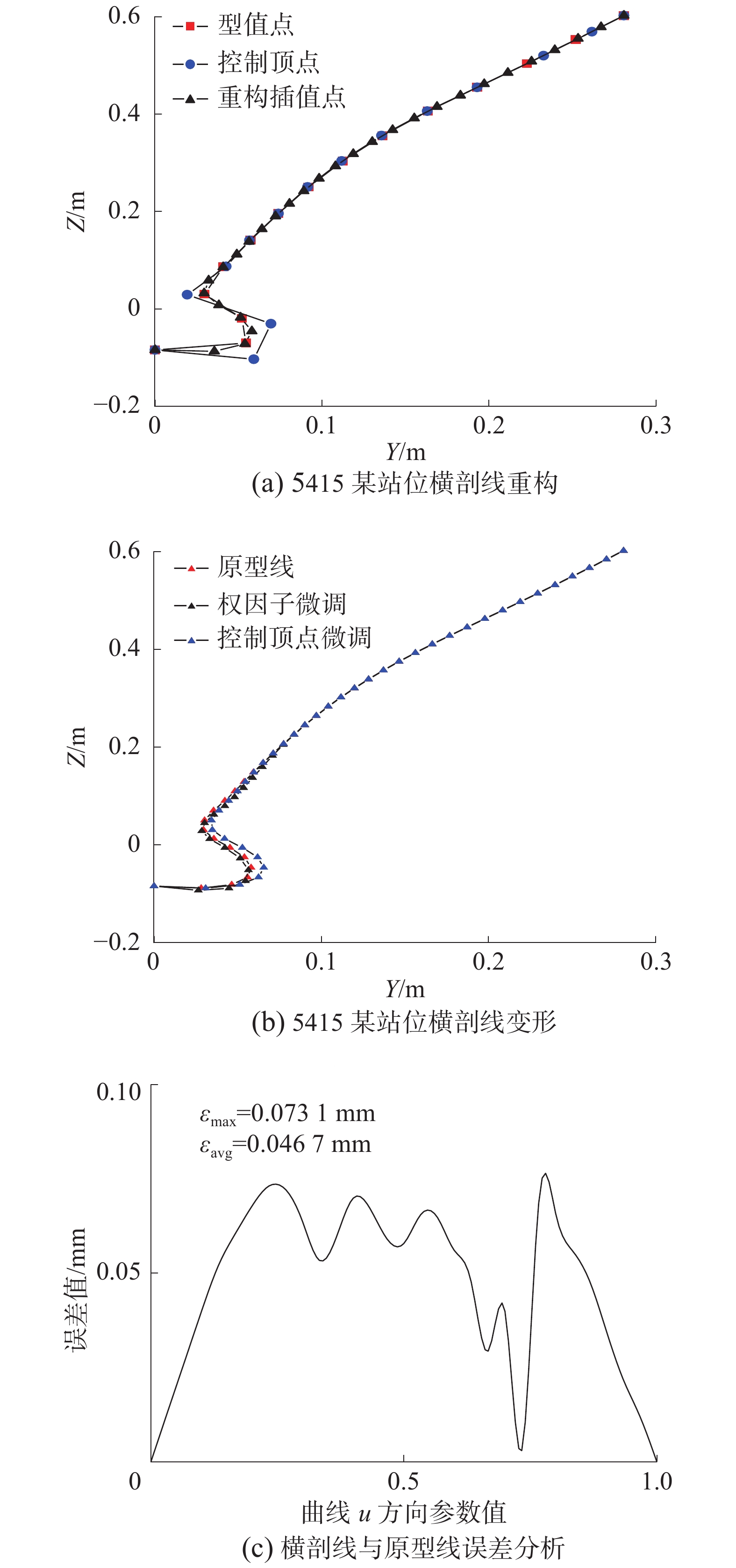
如图2(a)，以DTMB5415某站位横剖线为例，绘制出型线的插值点、控制顶点和型值点对比图。通过对第1~5个控制顶点和对应的权因子进行微调，图2(b)给出了原横剖型线和微调后的横剖型线的变形对比。可以看出，根据控制顶点(权因子为1)和基函数插值出来的点必定经过横剖线，多边形控制顶点和权因子改变可以控制横剖线的变形。本文用求解曲线与原型线的绝对误差 $\varepsilon $ 来评估曲线重构精度：

${\varepsilon _i} = \left| {{p_i} - p({u_i})} \right|$

(20)

式中： ${p_i}$ 为原型值点； $p({u_i})$ 为曲线u方向参数值对应的插值点。

如图2(c)，求解横剖线曲线误差，从图中可以看出，曲线最大误差不超过0.0731 mm，平均误差为0.0467 mm。

可以得出，通过本文前两节提供的算法计算NURBS曲线不需要型线首末端切矢量，不但简化了计算过程，且具有优良的变形能力，曲线精度较高。

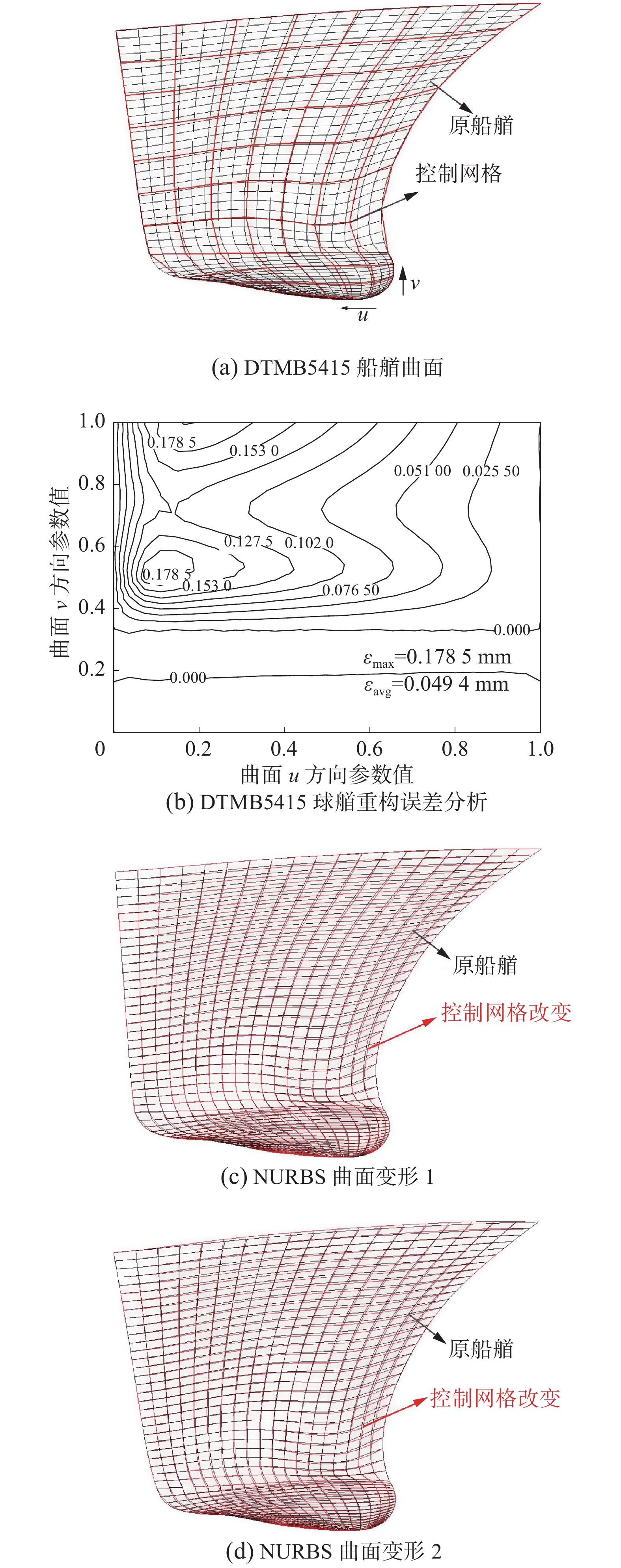
3.3 NURBS曲面重构

由一组数据点通过一次反算、插值可以得到NURBS曲线，从二维上升到三维，由一组曲线通过两个方向的反算、插值就可以得到NURBS曲面。 船体复杂曲面的重构与变形如图3。

图3(a)以DTMB5415船型船艏为例，初始条件为一组水平型线上的型值点，可以得到船艏的控制网格。通过改变船艏控制网和对应的权因子，图3(c)和图3(d)给出原船艏和改变后的原船艏对比。本文用求解曲面与原船型的绝对误差 $\varepsilon $ 来评估曲面重构精度。

${\varepsilon _{i,j}} = \left| {{p_{i,j}} - p({u_i},{v_j})} \right|$

(21)

式中： ${p_{i,j}}$ 为原型值点， $p({u_i},{v_j})$ 为曲面u、v方向参数值对应的插值点。

如图3(b)，以船体复杂曲面球艏为例，通过误差等高线分析可知，曲面插值最大误差为0.178 5 mm，平均误差为0.049 4 mm。可以得出，NURBS曲面具有良好的变形能力，且对于船体曲面的表达精度较高。

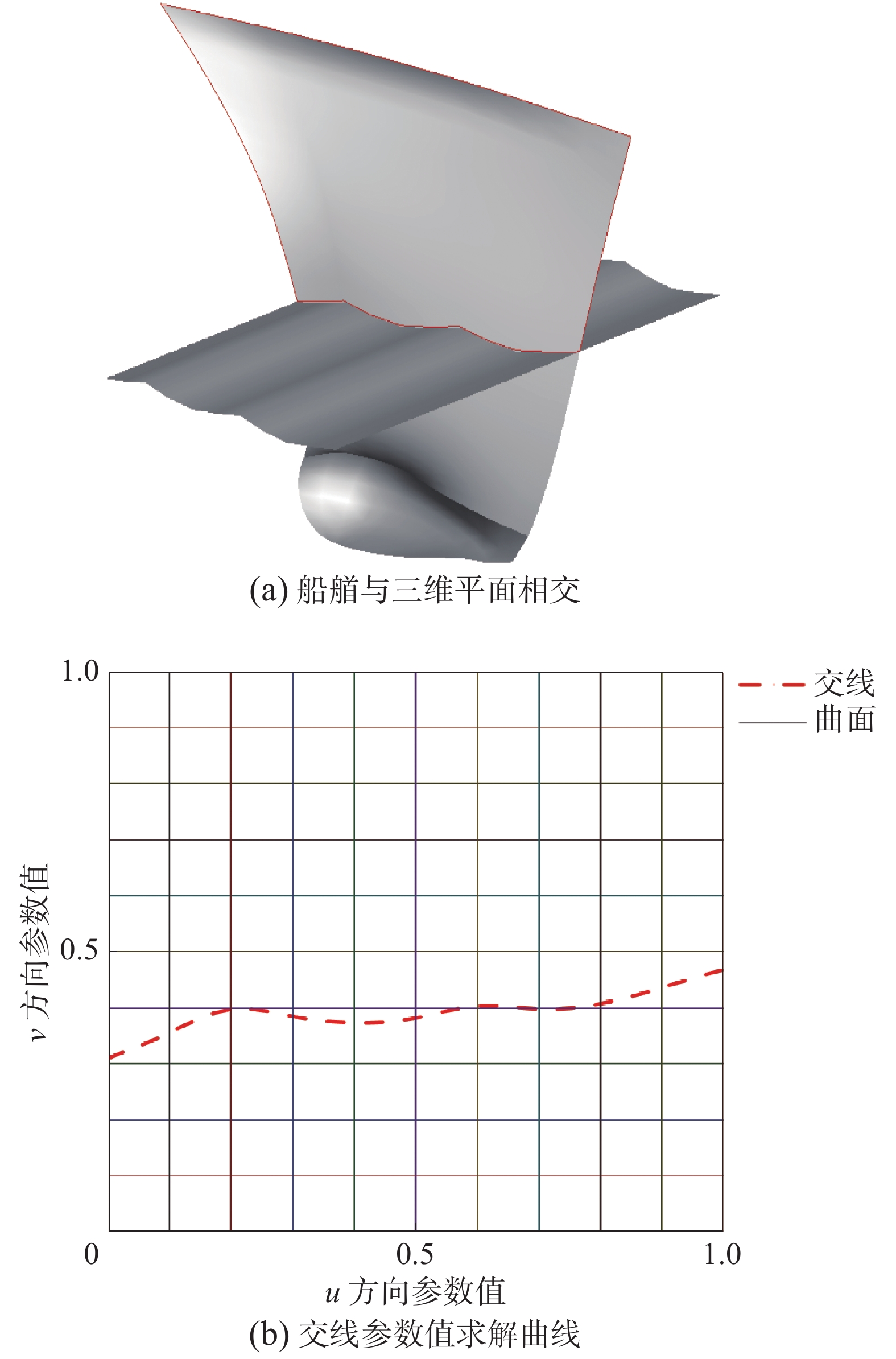
3.4 NURBS曲面求交

为了实现船体曲面快速分割，如图4(a)，DTMB5415船艏和三维平面相交，对其交线求解展开研究，本文采用了二分法、黄金分割、斐波那契法对交线参数区间进行迭代，交线参数值求解变化曲线如图4(b)，其交线参数区间收敛精度为0.000 1。如表1，在区间收敛精度为0.0001的情况下，通过对比船艏与三维平面求交算法的迭代次数和交线求解用时，二分法更适用于船体曲面分割。

3.5 船体型线和曲面重构

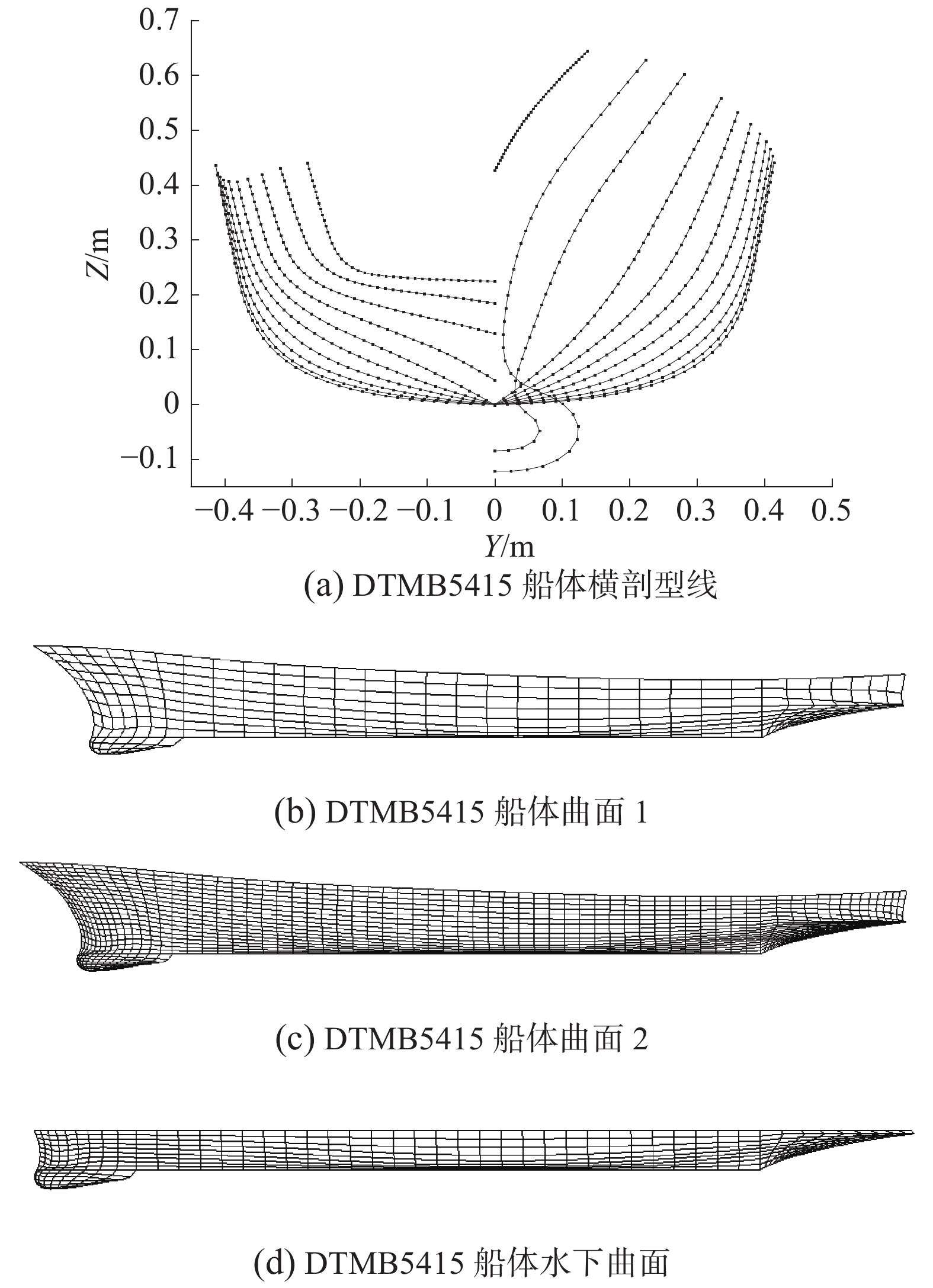
对于船体整个曲面构型，不同船型的曲面复杂度也不一样，本文以DTMB5415船型为例，其存在折角、曲率变化较大的曲面，图5(a)是通过NURBS曲线重构的DTMB5415船体横剖型线，图5(b)和图5(c)绘制的是多个NURBS曲面拼接构成DTMB5415船体曲面。图5(b)为面元数325的船体曲面，图5(c)为面元数1 399的船体曲面，且对艏艉部进行了加密。通过二分法快速分割曲面，图5(d)为面元数486的DTMB5415船体水下曲面，其可以为边界元法提供计算模型。从上述得出，在NURBS技术下可以实现船体曲面拼接、分割和局部区域加密等功能。

4 结论

本文基于NURBS技术实现了缩尺比为24.83的DTMB5415船体几何重构，对NURBS技术关键求解方法与几何重构效果展开研究与分析，可得出如下结论：

1)针对船体几何构型研究过程，将一种NURBS曲线(曲面)控制顶点(控制网)求解算法运用于船体几何重构，无需型线切矢量初始条件。通过本文编写的计算程序对DTMB5415船型几何重构过程研究发现，NURBS技术下的船体几何重构具有曲面变形、曲面拼接、曲面分割、局部区域加密等功能。

2)通过重构误差分析可知，基于该控制顶点反算算法的几何重构效果很好，其平均误差不超过0.05 mm，随机选取的横剖型线最大误差为0.0731 mm，船艉复杂曲面最大误差为0.1785 mm。

3)通过对比曲面求交算法的迭代次数和交线求解用时，在参数区间收敛精度为0.0001的情况下，二分法更适用于船体曲面分割。