所谓空化是因流体动力因素作用而在液体内部或在液体与固体界面上发生的液体与其蒸汽的相变过程和现象[1]。尽管空化作为一个水动力学热点问题已经被研究多年[2],但对于泡空化、梢涡空化[3-4]和云雾空化[5]等的数值模拟仍然是难点,表现在对各种类型的空化起始、发展及空泡溃灭的准确建模及高精度和高效率的算法实现上。
空化流数值模拟方法大致分为3种:势流方法、RANS方程求解及欧拉−拉格朗日混合方法。目前的几种空化模型,在模拟空化宏观形态和水动力整体参数方面取得一定的进展,但缺乏普适性,对空化的细节难以把握。空化的试验模拟仍然是空化研究的主要手段。梢涡空化及与其密切相关的“涡唱”现象近年来受到高度重视和广泛研究,后者在特定频率下噪声可以增加25 dB[6-8]。这些复杂物理现象对空化模型和相应的数值模拟技术提出了更高的要求。在梢涡区域进行网格加密对于梢涡及梢涡空化的捕捉是有成效的,但仍需进一步完善空化模型及与之匹配的湍流模型与算法。Budich等[9]首次采用可压缩隐式大涡模拟方法模拟了螺旋桨空化,与一般情形下的梢涡空化欠估计相反,他们的CFD结果是过度空化。
高精度流场计算方法尚在探索中,精确计算空化噪声的难度就更大了,用以校验数值方法的试验数据的获取与确认也存在难度,有必要将流场压力脉动信号和声压信号加以区分。文献[10]指出:近场压力脉动往往由湍流结构经过引起的压力扰动为主,但远场则以声信号辐射为主。作者发展了一种有效的小波滤波方法,成功地分离出水动力信号和声信号:流动信号即伪声信号是局部涡流动引起的压力扰动,具有间歇性的特征,可以认为是压缩的小波基函数,其有少量幅值较强的小波系数;声信号相对来说是连续的压力脉动,不能分解为小波基函数,所以可以认为是小波分解剩余的部分系数[11]。
PPTC(potsdam propeller test case)桨是第二届和第四届船舶推进器国际研讨会的算例桨,由德国波兹坦水池(SVA)设计以产生梢涡,其敞水性能、空化性能及螺旋桨压力脉动等试验数据均为开源,用以校验螺旋桨的各种势流或粘流分析程序[12-13]。文献[14]以SMP’15的算例桨PPTC’15为研究对象,基于Lighthill声类比方法及Ffowcs-Williams & Hawkings(FW-H)方程对斜流中的螺旋桨无空化和空化情形进行了噪声计算,并将声压与压力脉动进行了对比,但论文的篇幅限制一些问题没有展开论述。本文试图完整地叙述PPTC’15非定常流场及声场计算过程,并针对近场压力脉动在无空化情形下的计算与试验偏差,探讨试验数据的可靠性:试验测得的压力脉动里面是否包含了近场声压?流场压力脉动与声压之间的区别与联系究竟是什么?同时探讨声学积分面选取对噪声计算结果的影响。
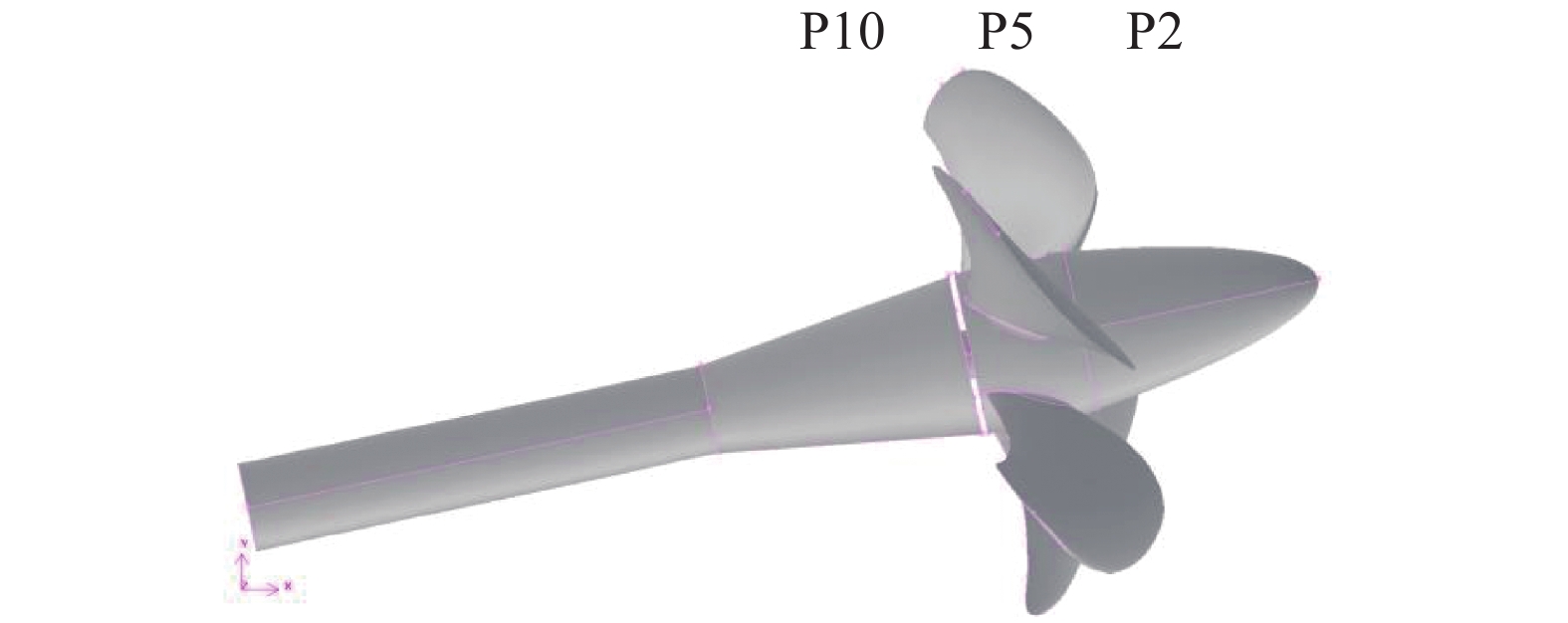
1 计算对象与工况本文的计算对象为SMP’15算例Case 3.2[13]。图1为PPTC’15及3个压力脉动测点位置示意图;表1给出了该设计工况下的试验参数。其中:α/αs为试验温度下的水中含气率与饱和含气率的比值,即相对含气量;两个工况下的转速均为20 r/s,进速系数为1.269。表中σn为以旋转线速度为特征速度的空化数。
|
Download:
|
| 图 1 PPTC'15及3个压力脉动测点 | |
|
|
表 1 计算工况 |
基于均质混合流模型和Zwart-Gerber-Belamri空化模型的非定常压力脉动及流场计算详见文献[13],此处不再赘述。
2 流激噪声流噪声预测方法主要有直接数值模拟方法和声类比方法。前者对系统资源的要求很高,而且计算时间也很长,不适于工程应用。声类比方法是使用最广泛的噪声预测方法,有积分方法、边界元方法和有限元方法。其中积分方法对于外流场问题,如机身噪声、螺旋桨噪声等,只需要非定常流场信息作为输入,不需要另外建立声学计算网格,计算速度很快。本节即采用基于Lighthill声类比的FW-H声学积分方程计算螺旋桨噪声。
2.1 FW-H方程FW-H方程适用于运动固壁在无界流场中的发声问题,能够预测单极子、偶极子、四极子等效声源产生的声音。一般而言,单极子源是由流体的可压缩性、液体的空化等引起的质量脉动源;偶极子源属于由流动涡脱落等引起的作用在流体上的力的脉动源;四极子源属于由流动自身粘性耗散引起的应力脉动源。在亚音速状态下,四极子对声压的贡献很小,当选取不可穿透的壁面作为噪声计算的声源面时,主要考虑的是单极子声源和偶极子声源。
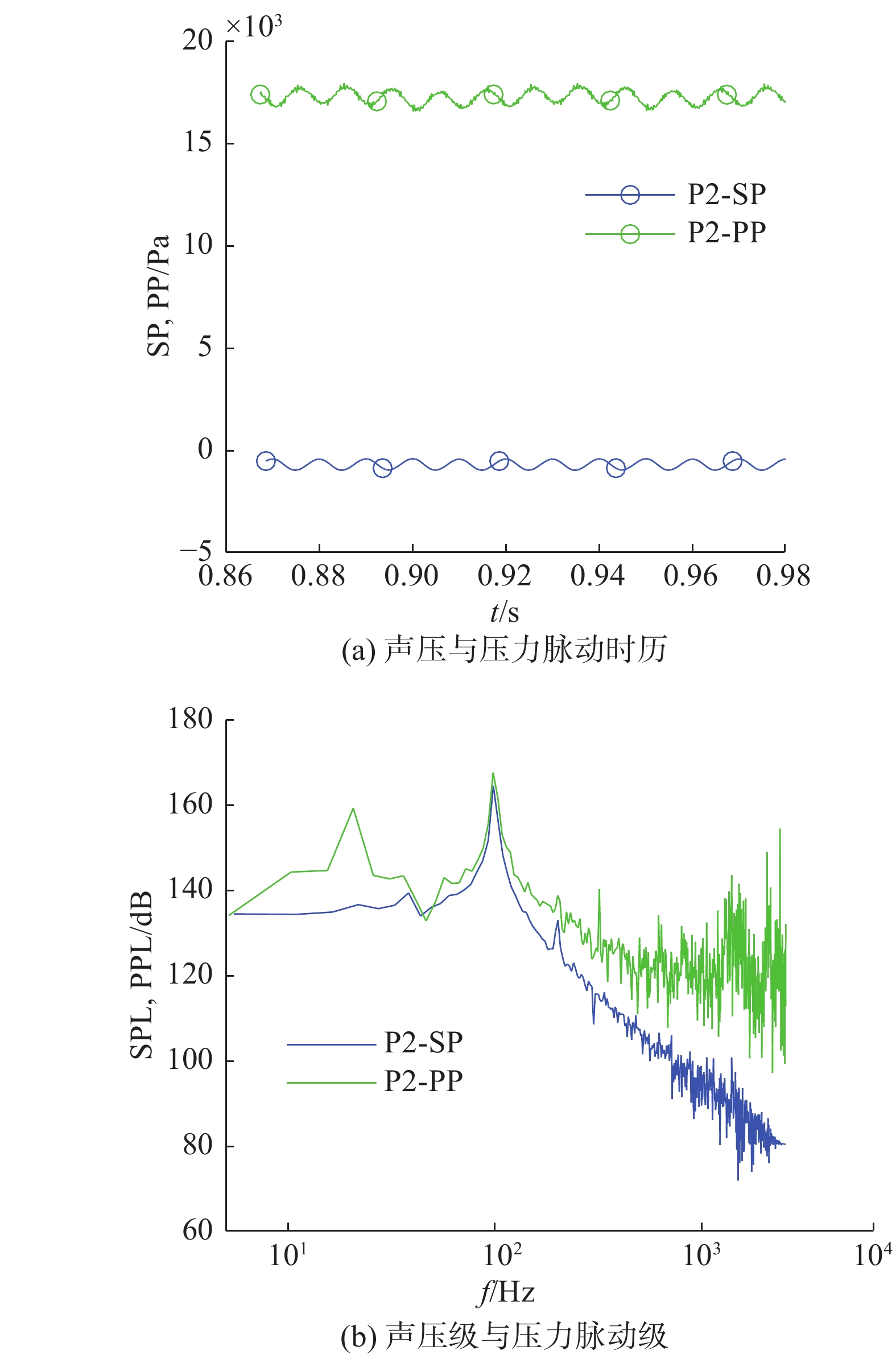
2.2 流场压力脉动与声压之间的区别与联系以Case 3.2中压力脉动测量点P2为例,图2给出了空化情形下,声压时历与压力脉动时历的比较以及声压频谱与压力脉动频谱的比较(参考压力均为10−6 Pa)。由图2(a)可以看出,声压与压力脉动特征频率一致,均为叶频,但二者反相——压力脉动达到波峰时,声压接近波谷;由图2(b)可以看出,声压与压力脉动均在叶频附近出现峰值,但高频段压力脉动衰减不显著,而声压随频率增大衰减显著;声压幅值低于压力脉动幅值。
表2给出了Case 3.2中3个压力脉动测量点上,空化前后的总声级和压力脉动级(参考压力均为10−6Pa),以此考察空化对声压和压力脉动的影响。由表可以看出,空化在各点上均使声压增加,而压力脉动则有增有减;空化前后各点上的声压计算值大小比较,均为P5>P2>P10,与压力脉动的试验结果完全一致。
|
Download:
|
| 图 2 声压与压力脉动比较 | |
|
|
表 2 空化对声压与压力脉动的影响 |
图3给出了空化前后3个点上的声压级频谱,由图上的叶频峰值可见,各点之间若采用叶频对应的声压峰值进行比较,其结果与表2中的总声级数值比较也完全一致,均为P5>P2>P10。

|
Download:
|
| 图 3 各点的声压级比较 | |
可见基频峰包含了主要的能量。也就是说,近场3个测点上的声压计算结果与试验[13]测得的压力脉动相对大小是符合的,而文献[13]中的压力脉动计算值本身倒与试验值不符合。这就引发人猜测:在声源附近进行压力脉动测量,测量结果中是否同时包含了水动力分量和声压分量,孰轻孰重、所占比例是多少?
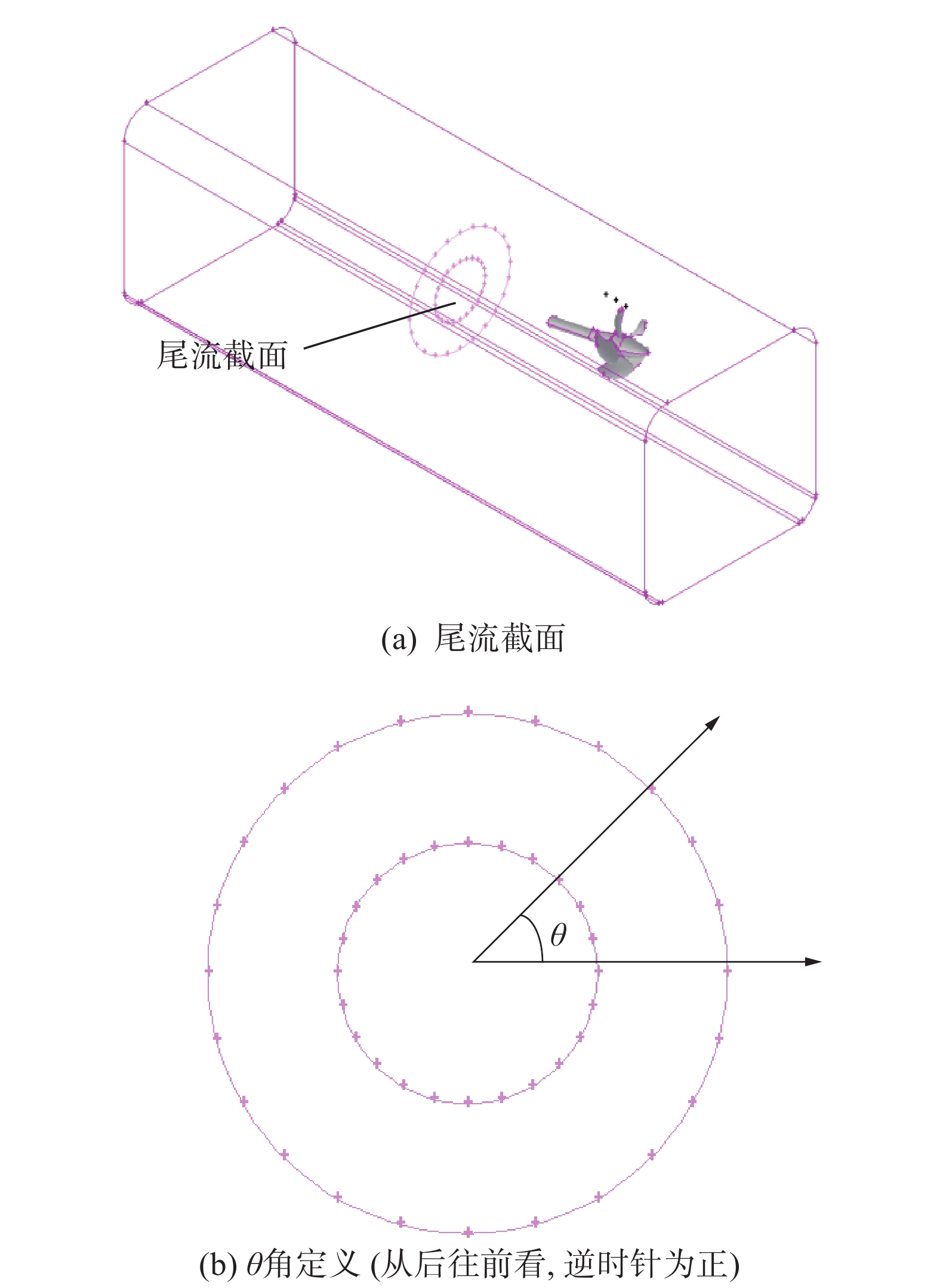
2.3 指向性分析沿螺旋桨桨轴尾流方向,在距离桨上方P5点后3.106Dp的铅垂截面上,以桨轴与截面的交点为圆心,做直径分别为1Dp和2Dp的两个圆弧,每15°取一个点,得到2×24共48个采样点,进行声辐射指向性分析。
|
Download:
|
| 图 4 指向性分析点阵 | |
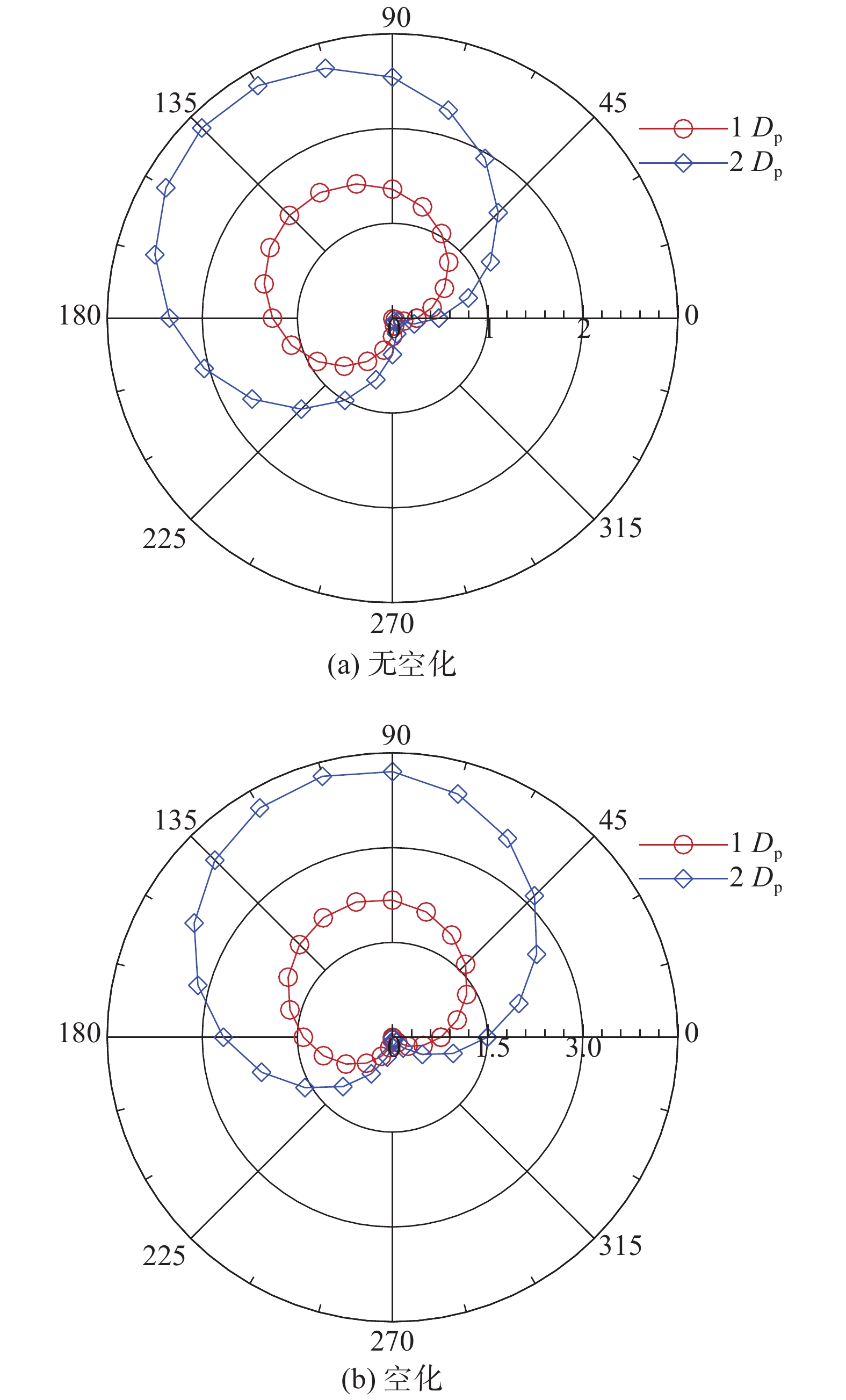
在等直径圆弧上进行指向性分析,为了凸显方向的差异性,需要减去各自圆弧上的最小声压级进行比较,得到ΔSPL。图5给出了空化前后尾流某截面上的声压指向性特征。由图可见:指向性曲线具有对称性,对称轴位于最大值与最小值两点的连线上——无空化情形的对称轴与y轴夹45°角,空化情形为15°角,方向沿螺旋桨旋转相反方向(与水流相对于桨的旋转方向相同);指向性曲线偏离圆弧中心整体上移(与螺旋桨桨轴上倾15°角相关);外圆弧(2Dp)上的指向性差异大于内圆弧(1Dp);指向性差异在无空化情形为2.83 dB,空化情形可达4.27 dB(注意2个极坐标图的纵坐标数值不同)。
|
Download:
|
| 图 5 声压的指向性 | |
表3给出了2个圆弧在空化前后的平均声压级,可以看出:空化显著增大声压级,达到7 dB;之前考察3个近场压力脉动测点,空化只略微增大近场声压级,不到1 dB(见表2)。由此得出结论:空化对远场声压的影响更为显著。
|
|
表 3 圆环上的平均声压级 |
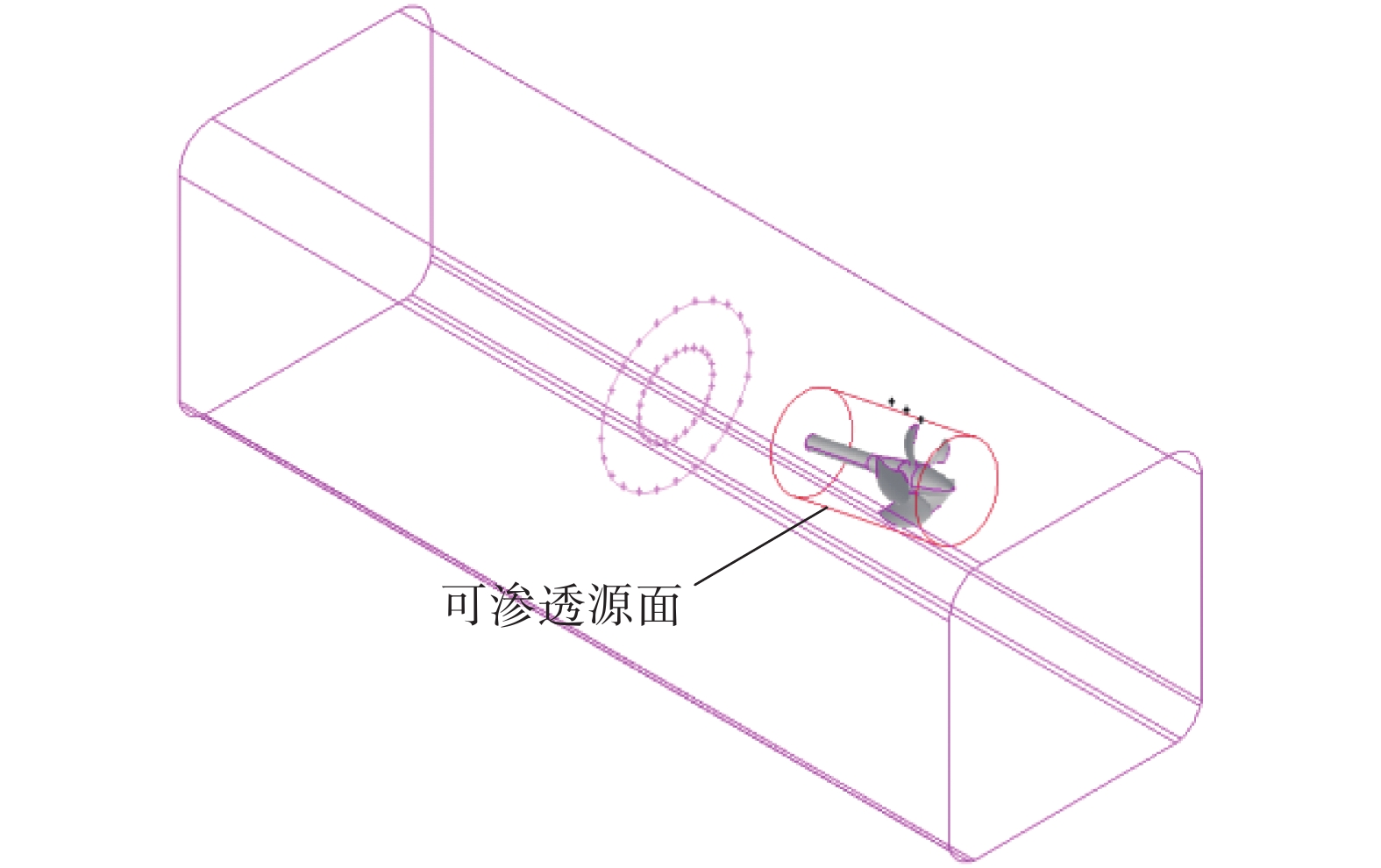
当源面仅取物面时,FW-H方程的解由单极子源和偶极子源组成;当在流体内部选取了可渗透表面,解就包含了源面内流体域中的四极子声源。之前的声学计算,源面仅为旋转叶片及桨毂部分(推力积分面);本节的声学计算,源面除推力积分面即物面之外,还包括一个流场内的可渗透源面,在此取为网格划分时在旋转区域与不动域之间生成的一对圆柱形交界面中的内侧面(如图6所示)。
|
Download:
|
| 图 6 可渗透源面 | |
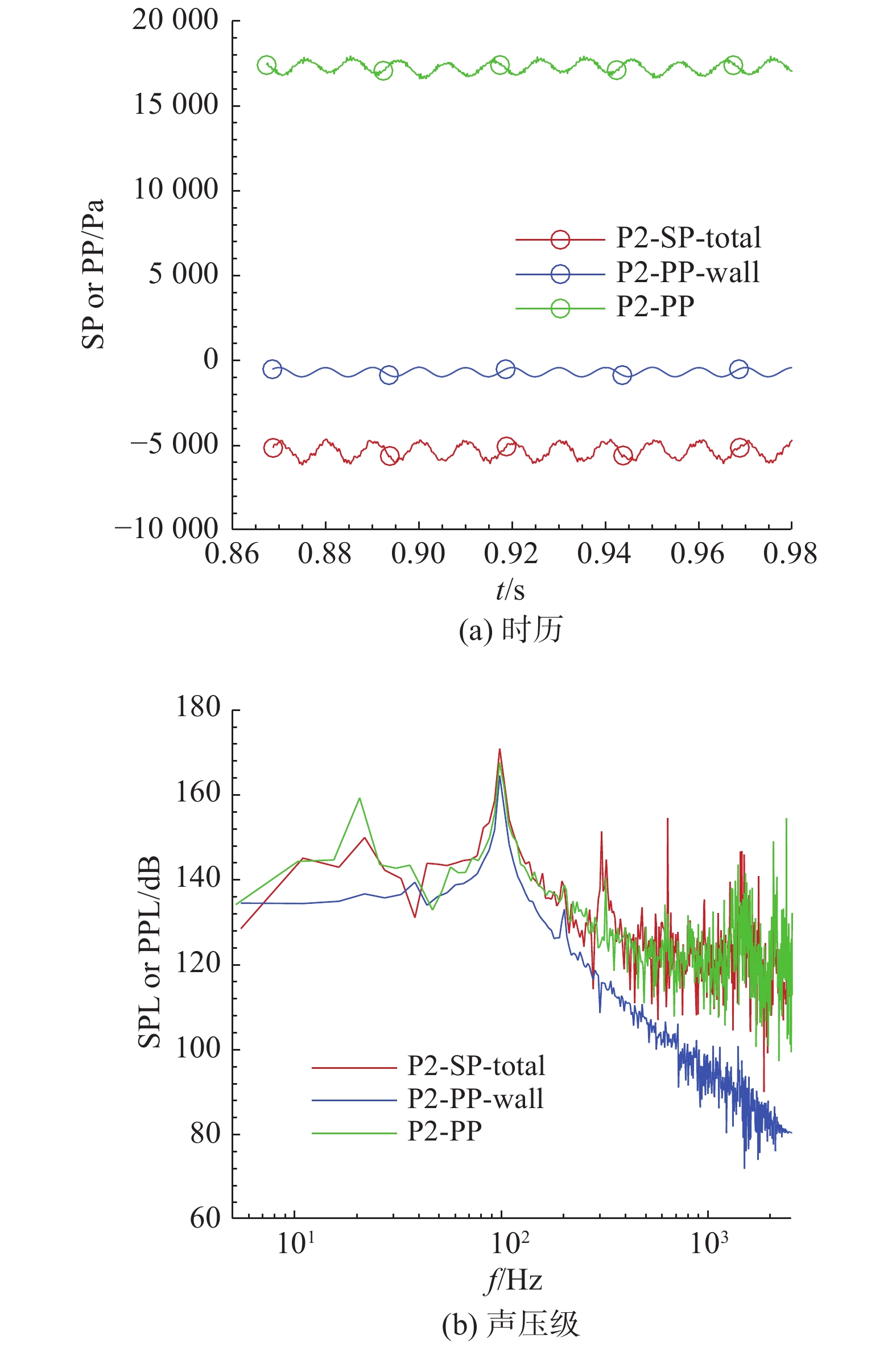
仍然以Case 3.2中压力脉动测量点P2为例,图7给出了空化情形下,仅考虑壁面(SP-wall)和同时考虑可渗透源面(SP-total)的声压计算结果比较。由图可见:仅考虑壁面的声压幅值低于同时考虑可渗透源面的声压幅值;后者在高频段更接近于压力脉动,即包含更多的高频成分。
|
Download:
|
| 图 7 声学积分面的影响 | |
表4给出了2种积分面选择对应的声压级对比。由表可见:当考虑可渗透源面时,总声级显著高于仅考虑壁面的声压级,且高于压力脉动级(见表2);空化仅使P5上的声压略微增加;空化后2种积分面的声压级均为P5>P2>P10;但当考虑可渗透源面时空化前各点上的声压级大小关系又变回了P2>P5>P10,得不到与压力脉动测量值相符的结果。
|
|
表 4 声学积分面对声压级的影响 |
图8给出了当考虑可渗透源面时,空化前后3点上的声压级频谱,由图上的叶频峰值可见,各点之间若采用叶频对应的声压峰值进行比较,其结果与表4中的总声级数值比较也完全一致,空化前为P2>P5>P10,空化后为P5>P2>P10,可见基频峰包含了主要的能量。

|
Download:
|
| 图 8 各点的声压级比较 | |
本节的研究表明:仅考虑壁面作为声源面的声压级满足“声压成分小于流动成分”的一般说法,当考虑可渗透源面时,声压则大于压力脉动。文献[15]指出:“选择与主流平行的面作为声学积分面是合适的;积分面不能在物体附近截断主流,否则会产生较大的虚假噪声”。然而开放的声源面物理意义上无法解释,封闭的声源面又很难避免在流向上“截断主流”。由此可见,可渗透源面的必要性以及选择方法还有待研究。
4 结论在利用近场压力脉动实验数据对CFD和计算声学方法进行校验时,有必要将水动力信号和声压信号分离出来,因为我们在计算时使用不同的模块分别进行流场和声场计算,而实验时,却是在声源附近进行压力脉动测量,如何从近场测量的压力脉动中分离出水动力分量和声信号成为关键。接下来的空化研究应从实验和数值研究两方面同时开展,实验测量和数值模拟都向更为精细的方向发展,最终实现流声耦合统一解。
虽然原则上采用旋转叶片作为壁面声源求解单极子和偶极子声源;采用封闭的包围壁面的可渗透源面求解流场内部的四极子声源;同时求解这两部分的积分之和作为FW-H方程的积分解,是合理的声学计算方式。然而,实际计算中如何具体选择这样的可渗透源面仍然有待进一步研究。
| [1] |
潘森森, 彭晓星. 空化机理[M]. 北京: 国防工业出版社, 2013.
( 0) 0)
|
| [2] |
JI B, LUO X W, PENG X X. Three-dimensional large eddy simulation and vorticity analysis of unsteady cavitating flow around a twisted hydrofoil[J]. Journal of hydrodynamics, 2013, 25(4): 510-519. DOI:10.1016/S1001-6058(11)60390-X ( 0) 0)
|
| [3] |
ZHANG L X, ZHANG N, PENG X X, et al. A review of studies of mechanism and prediction of tip vortex cavitation inception[J], Journal of hydrodynamics, 2015, 27(4): 488-495.
( 0) 0)
|
| [4] |
LIU Z H, WANG B L, PENG X X, et al. Calculation of tip vortex cavitation flows around three-dimensional hydrofoils and propellers using a nonlinear k-ε turbulence model[J], Journal of hydrodynamics, 2016, 28(2): 227-237.
( 0) 0)
|
| [5] |
LONG X P, CHENG H Y, JI B, et al. Large eddy simulation and Euler–Lagrangian coupling investigation of the transient cavitating turbulent flow around a twisted hydrofoil[J]. international journal of multiphase flow, 2018, 100: 41-56. DOI:10.1016/j.ijmultiphaseflow.2017.12.002 ( 0) 0)
|
| [6] |
ARNDT R E A. Cavitation in vortical flows[J], Annual review of fluid mechanics, 2002, 34: 143-181.
( 0) 0)
|
| [7] |
ARNDT R, PENNINGS P, BOSSCHERS J, et al. The singing vortex[J], Interface focus, 2015, 5(5): 1-11.
( 0) 0)
|
| [8] |
PENG X X, WANG B L, LI H Y. Generation of abnormal acoustic noise: singing of a cavitating tip vortex[J]. Physical review fluids, 2017, 2(5): 1-9. ( 0) 0)
|
| [9] |
BUDICH B, SCHMIDT S J, ADAMS N A. Implicit large eddy simulation of the cavitating model propeller VP1304 using a compressible homogeneous mixture model[C]//Proceedings of the 31th Symposium on Naval Hydrodynamics. Monterey, California, 2016.
( 0) 0)
|
| [10] |
FELLI M, FALCHI M, DUBBIOSO G. Direct and indirect experimental methodologies for the hydro-acoustic analysis of marine propellers[C]//Proceedings of the 30th Symposium on Naval Hydrodynamics. Hobart, Tasmania, Australia, 2014.
( 0) 0)
|
| [11] |
FELLI M, GRIZZI S, FALCHI M. A novel approach for the isolation of the sound and pseudo-sound contributions from near-field pressure fluctuation measurements: analysis of the hydroacoustic and hydrodynamic perturbation in a propeller-rudder system[J]. Experiments in fluids, 2014, 55(1): 1651-1667. DOI:10.1007/s00348-013-1651-y ( 0) 0)
|
| [12] |
冯学梅, 鲁传敬, 吴琼, 等. 均匀流场中螺旋桨空泡数值模拟[J], 中国造船, 2012, 53(3): 18-27.
( 0) 0)
|
| [13] |
傅慧萍, 李杰. 斜流中的螺旋桨空化及压力脉动计算[J]. 中国造船, 2018, 59(3): 1-12. DOI:10.3969/j.issn.1000-4882.2018.03.001 ( 0) 0)
|
| [14] |
FU H P, LI J. Hydro-acoustic analysis of the cavitating model propeller PPTC in oblique flow[EB/OL]. http://ebooks.asmedigitalcollection.asme.org/content.aspx?bookid=2565§ionid=206551535, 2019-01-25.
( 0) 0)
|
| [15] |
张楠, 王星, 谢华, 等. 流激噪声数值计算方法及声学积分面影响性研究[J]. 船舶力学, 2016, 20(7): 892-908. DOI:10.3969/j.issn.1007-7294.2016.07.013 ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


