曲柄摇杆机构是最简单、最普遍的平面四杆(体)机构，任何复杂的机构都可视为该机构经过演化或组合而形成的^[1-3]。连杆机构的运动具有连续性而没有运动冲击^[4]，其承载能力有限。由于间隙的作用，以转动副(属于二约束副)^[5]连接的构件(体)在承载时也是点线接触，且相对运动明显。一些轮廓线合理的高副(滚滑副，属于一约束副)机构反而可承受较大的载荷且耐用。这些构体的接触轮廓线须精心设计以避免运动冲击，如凸轮与从动件的接触轮廓^[6]、火车轮轨接触轮廓(包括车轮的车轨横截面在理论上可视为双曲柄机构经过高副低代(一副三代)而演化出的滚滑副机构)、链节与链齿的接触轮廓等。根据连杆机构的瞬心线设计滚滑副机构的接触轮廓具有重要的理论意义和实践价值。

曲柄摇杆机构的瞬心、瞬心线及瞬心圆^[7]的研究目前多见于图解法及连杆运动图谱研究。解析法研究主要有文献[8]的运动学辅助算例和文献[9]的消元法方程组研究。

运动学研究^[10-11]是动力学研究^[12]的基础。构体之间的速度瞬心属于机构运动学的研究范畴^[13-15]，可用于某些基于一副三代的少构体机构速度分析，例如飞机起落架机构、人工椎间盘设计^[16]等。本文基于直线方程、矩阵求逆和坐标变换等研究曲柄摇杆机构和5类双摇杆机构的瞬心线解析法方程。

1 平面四体机构的瞬心线 1.1 瞬心的位置

如图1所示的机构ABCD，共有4个构体、6个瞬心。作平面运动的3个物体之间有位于同一条直线上的3个瞬心(三心定理)。相邻构体之间的瞬心在其转动副中心。在运动过程当中，连杆2与机架(固定体)4之间的瞬心 ${P_{24}}$ 为曲柄(转杆)与摇杆延长线的交点。在主动连架杆(摆转杆)和从动摆转杆平行的位置，该瞬心位于无穷远处。

主动摆转杆1与从动摆转杆3之间的瞬心 ${P_{13}}$ 在连杆与固定体的延长线交点上，其轨迹与固定体AD共线。当连杆和固定体平行时，该瞬心位于无穷远处。

1.2 连杆与固定体之间的瞬心坐标

在图1当中，以A为坐标原点，以固定体AD为 ${x_1}$ 轴，建立平面直角固定坐标系 ${x_1}{\rm{ - }}A{\rm{ - }}{x_2}$ 。根据矢量方程的几何意义^[17]及构体之间的连接关系，建立矢量方程，采用基于谐波合成与分解的方法获得各构体的位置角^[18]，然后求出C、D点的坐标。根据AB和CD的两点式直线方程，该瞬心 ${P_{24}}$ 的坐标满足以下方程组：

$\left\{ \begin{array}{l} \dfrac{{{x_1} - {x_{1,A}}}}{{{x_{1,B}} - {x_{1,A}}}} = \dfrac{{{x_2} - {x_{2,A}}}}{{{x_{2,B}} - {x_{2,A}}}} \\ \dfrac{{{x_1} - {x_{1,D}}}}{{{x_{1,C}} - {x_{1,D}}}} = \dfrac{{{x_2} - {x_{2,D}}}}{{{x_{2,C}} - {x_{2,D}}}} \end{array} \right.$

(1)

整理式(1)，得

$ \begin{split}& \left[ {\begin{array}{*{20}{c}} {{x_{2,B}} - {x_{2,A}}}&{ - \left( {{x_{1,B}} - {x_{1,A}}} \right)} \\ {{x_{2,C}} - {x_{2,D}}}&{ - \left( {{x_{1,C}} - {x_{1,D}}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \end{array}} \right] = \\ &\;\;\left[ {\begin{array}{*{20}{c}} {\left( {{x_{2,B}} - {x_{2,A}}} \right){x_{1,A}} - \left( {{x_{1,B}} - {x_{1,A}}} \right){x_{2,A}}} \\ {\left( {{x_{2,C}} - {x_{2,D}}} \right){x_{1,D}} - \left( {{x_{1,C}} - {x_{1,D}}} \right){x_{2,D}}} \end{array}} \right] \end{split} $

根据二阶矩阵求逆运算的简化公式：

$\left[ {\begin{array}{*{20}{c}} a \\ c \end{array}} \right.\;\;{\left. {\begin{array}{*{20}{c}} b \\ d \end{array}} \right]^{ - 1}} = \dfrac{1}{{ad - bc}}\left[ {\begin{array}{*{20}{c}} d \\ { - c} \end{array}} \right.\;\;\left. {\begin{array}{*{20}{c}} { - b} \\ a \end{array}} \right]$

两条直线的交点即为 ${P_{24}}$ 。该点的坐标为

$\left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \end{array}} \right] = \dfrac{1}{d}\left[ {\begin{array}{*{20}{c}} { - \left( {{x_{1,C}} - {x_{1,D}}} \right)}&{ {{x_{1,B}} - {x_{1,A}}} } \\ { - \left( {{x_{2,C}} - {x_{2,D}}} \right)}&{{x_{2,B}} - {x_{2,A}}} \end{array}} \right]\cdot\\ \quad\quad \left[ {\begin{array}{*{20}{c}} {\left( {{x_{2,B}} - {x_{2,A}}} \right){x_{1,A}} - \left( {{x_{1,B}} - {x_{1,A}}} \right){x_{2,A}}} \\ {\left( {{x_{2,C}} - {x_{2,D}}} \right){x_{1,D}} - \left( {{x_{1,C}} - {x_{1,D}}} \right){x_{2,D}}} \end{array}} \right] \\ d = - \left( {{x_{2,B}} - {x_{2,A}}} \right)\left( {{x_{1,C}} - {x_{1,D}}} \right) - \\ \quad\quad \left[ { - \left( {{x_{1,B}} - {x_{1,A}}} \right)} \right]\left( {{x_{2,C}} - {x_{2,D}}} \right) \ne 0 \end{array} \right.$

(2)

与代入法和消元法^[9]相比，上述求解方程组的矩阵运算法更直观、更不易出错。

在式(2)中，如果d等于0，则该机构位置 ${P_{24}}$ 的2个坐标值均为无穷大，只能求出两者的比例。为了简化计算，本文不研究该位置。

为了绘制动瞬心线，在连杆上建立牵连坐标系 ${x'_1}{\rm{ - }}B{\rm{ - }}{x'_2}$ ，坐标原点为B， ${x'_1}$ 轴正方向为BC。将连杆平移，使B点平移到固定坐标系的原点，则连杆上的瞬心坐标转换为

$\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{x_{1,B}}} \\ {{x_{2,B}}} \end{array}} \right]$

(3)

再将 ${x'_1}$ 轴转平至 ${x_1}$ 轴正方向，即转动 $ - {\theta _2}$ ，则连杆上的瞬心坐标转换为

$\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \left( { - {\theta _2}} \right)}&{ - \sin \left( { - {\theta _2}} \right)} \\ {\sin \left( { - {\theta _2}} \right)}&{\cos \left( { - {\theta _2}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \end{array}} \right]$

(4)

再将B点平移到在固定坐标系当中的绘图位置，则该瞬心坐标转换为

$\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{x_{1,B'}}} \\ {{x_{2,B'}}} \end{array}} \right]$

(5)

式(4)为该瞬心在连杆牵连坐标系中的坐标。式(5)为将动瞬心线绘制在固定坐标系中的依据。

1.3 主动摆转杆与从动摆转杆之间的瞬心坐标

该瞬心为 ${P_{13}}$ 。固定体与 ${x_1}$ 坐标轴重合，AD的直线方程可采用点斜式，求得B、C点坐标之后，BC的直线方程可采用两点式。因此， ${P_{13}}$ 点的坐标满足以下方程组：

$\left\{ \begin{array}{l} \dfrac{{{x_1} - {x_{1,B}}}}{{{x_{1,{{C}}}} - {x_{1,B}}}} = \dfrac{{{x_2} - {x_{2,B}}}}{{{x_{2,{{C}}}} - {x_{2,B}}}} \\ {x_2} = 0 \end{array} \right.$

(6)

整理式（6）可得：

$\left\{ \begin{array}{l} {x_1} = {x_{1,B}} - \dfrac{{\left( {{x_{1,{{C}}}} - {x_{1,{{B}}}}} \right){x_{2,B}}}}{{{x_{2,C}} - {x_{2,B}}}} \\ {x_2} = 0 \end{array} \right.$

(7)

如果连杆与固定体平行，则 ${P_{13}}$ 在无穷远处，式(7)会被零除。

该瞬心在主动摆转杆和从动摆转杆上牵连坐标系中的坐标均可根据式(3)和式(4)获得。

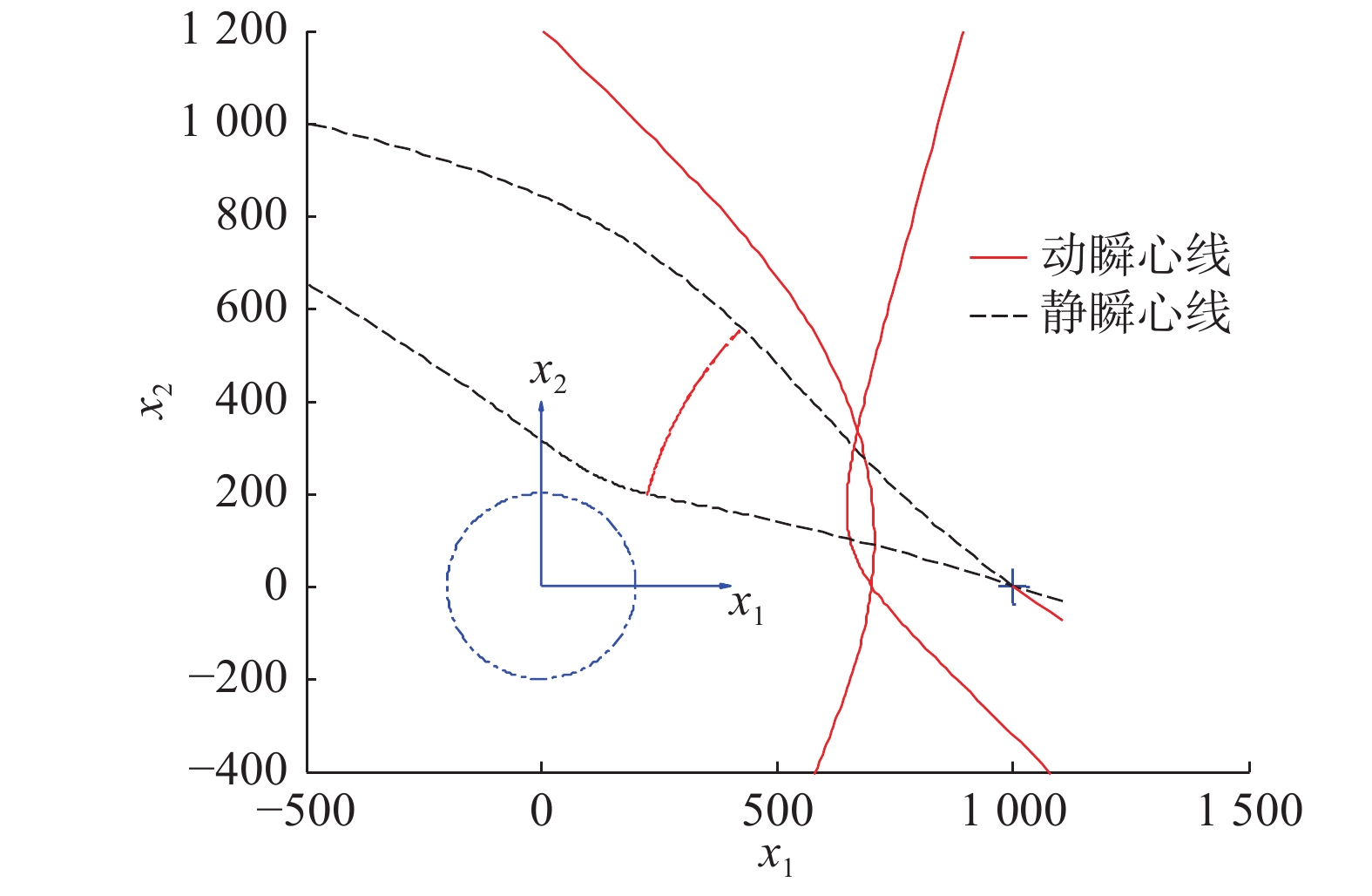
1.4 曲柄摇杆机构瞬心线的绘制

取曲柄长度为200，连杆长度为500，摇杆长度为800，固定体长度为1 000。当式(2)的d为零时，曲柄与摇杆平行，瞬心 ${P_{24}}$ 在无穷远处。在图2中， ${P_{24}}$ 在固定体上的轨迹为静瞬心线，如虚线所示； ${P_{24}}$ 在连杆上的轨迹随机构的运动而运动，称为动瞬心线，如实线所示；B点和C点的轨迹如点划线所示。静瞬心线在曲柄的延长线上，在该图可测出静瞬心与曲柄位置的对应关系。

2 双摇杆机构的瞬心线 2.1 摇杆的摆动范围

在摆转杆与固定体拉直共线或重叠共线的位置，如果另两杆均能组成三角形，则该摆转杆为曲柄，否则为摇杆。当另两杆重叠共线或拉直共线时，摇杆位于极限位置。据此，可确定摇杆的摆动范围。根据上述两个三角形成立的条件，可得平面四体机构存在周转副的杆长条件是：最短杆与最长杆之和小于另两杆之和。

双摇杆机构共有5种情况^[19]：

1)有周转副且最短杆对面的构体为固定体。由于上述2个三角形均不成立，2个摇杆均在固定体的同侧摆动。连杆和从动摇杆拉直共线时，主动摇杆位于左极限位置；连杆和从动摇杆重叠共线时，主动摇杆位于右极限位置。主动摇杆的转动范围为

${\theta _1} \in \left[{\begin{array}{*{20}{c}} {\arccos \dfrac{{l_1^2 + l_4^2 - {{\left( {{l_3} - {l_2}} \right)}^2}}}{{2{l_1}{l_4}}}},&{\arccos \dfrac{{l_1^2 + l_4^2 - {{\left( {{l_3} + {l_2}} \right)}^2}}}{{2{l_1}{l_4}}}} \end{array}}\right]$

(8)

2)无周转副且固定体最长。由于上述2个三角形必有一个成立，两摇杆均可在固定体两侧摆动。如果主动摇杆可对称摆动，则从动摇杆的摆动范围一般不对称，下同。从动摇杆和连杆只存在拉直共线的情况。2个摇杆摆动范围的开口方向相对。主动摇杆的转动范围为

$\;{\theta _1}\in\left[{\begin{array}{*{20}{c}} { - \arccos \dfrac{{l_1^2 + l_4^2 - {{\left( {{l_3} + {l_2}} \right)}^2}}}{{2{l_1}{l_4}}}},&{\arccos \dfrac{{l_1^2 + l_4^2 - {{\left( {{l_3} + {l_2}} \right)}^2}}}{{2{l_1}{l_4}}}} \end{array}}\right]$

(9)

3)无周转副且从动摇杆最长。连杆与从动摇杆只有重叠共线的情况。2个摇杆均可在固定体两侧对称摆动，且摆动范围的开口方向均向左。主动摇杆的转动范围为

${\theta _1} \in \left[{\begin{array}{*{20}{c}} {\arccos \dfrac{{l_1^2 + l_4^2 - {{\left( {{l_2} - {l_3}} \right)}^2}}}{{2{l_1}{l_4}}}},&{2{\rm{{\text{π}} }} - \arccos \dfrac{{l_1^2 + l_4^2 - {{\left( {{l_2} - {l_3}} \right)}^2}}}{{2{l_1}{l_4}}}} \end{array}}\right]$

(10)

4)无周转副且主动摇杆最长。连杆与从动摇杆只有拉直共线的情况。主动摇杆与从动摇杆均可在固定体两侧对称摆动，且摆动范围的开口均向右。主动摇杆的转动范围为

$\;{\theta _1}\in\left[ {{\rm{ - }}\arccos \dfrac{{l_1^2 + l_4^2 - {{\left( {{l_2}{\rm{ + }}{l_3}} \right)}^2}}}{{2{l_1}{l_4}}},\;\;\arccos \dfrac{{l_1^2 + l_4^2 - {{\left( {{l_2}{\rm{ + }}{l_3}} \right)}^2}}}{{2{l_1}{l_4}}}} \right]$

(11)

5)无周转副且连杆最长。连杆与从动摇杆只有重叠共线的情况。两个摇杆均可在固定体两侧对称摆动，且摆动范围的开口相背。主动摇杆的转动范围为

${\theta _1} \in \left[{\begin{array}{*{20}{c}} {\arccos \dfrac{{l_1^2 + l_4^2 - {{\left( {{l_2} - {l_3}} \right)}^2}}}{{2{l_1}{l_4}}}},&{2{\rm{{\text{π}} }} - \arccos \dfrac{{l_1^2 + l_4^2 - {{\left( {{l_2} - {l_3}} \right)}^2}}}{{2{l_1}{l_4}}}} \end{array}}\right]$

(12)

在上述5种情况当中，主动摇杆的极限位置存在运动分岔现象，属于歧运动位。如果机构静止，无论多么大的驱动力也会卡住，则该歧运动位也称为机构的卡位^[20-21]。卡位可用于锁紧机构。

2.2 瞬心线的绘制

对于式(8)的情况，参照1.4，取主动摇杆AB的长度为500，连杆BC的长度为200，从动摇杆CD的长度为800，固定体AD的长度为1 000。 ${P_{24}}$ 的瞬心线如图3所示，其中虚线为静瞬心线，实线为动瞬心线，点划线为主动摇杆上B点和从动摇杆上C点的摆动轨迹。

取4个构体的长度分别为1 000、800、500、400。对于式(9)~(12)的情况，在主动摇杆的一个摆动行程当中， ${P_{24}}$ 的瞬心线如图4所示，图线说明与图3的相同。

3 结论

1)本文推导的平面四体机构的瞬心线方程具有普适性。

2)基于该方程绘制的瞬心线可为滚滑副机构的轮廓线设计提供参考。

3)与当前经典机械原理学科的图解法相比，本文的研究更容易获得瞬心线。

4)对于平行四边形机构，两曲柄之间的瞬心在无穷远处，连杆与固定体之间的瞬心也在无穷远处。从动曲柄反转时，这两个瞬心也值得研究。