由于被动声呐探测隐蔽性好，被动定位技术已成为水下目标定位的重要技术手段。对于一个被动测向交叉定位系统，单一被动站不能很好地完成定位任务，通常联合多个被动站对目标进行联合定位。由于每个被动站之间存在一定的距离，其测量得到的目标辐射信号也不完全相同，有一定的差异。随着目标和观测站数目的增加，多条测向线两两相交，使虚假定位点的数目急剧增加。如何快速排除虚假点是目标方位数据关联的难点^[1]。

本文把目标的信息分为2类，即表示目标状态的方位信息和表示目标特征的物理信息，提出一种目标数据联合关联方法。该方法主要包括2个核心内容：一是辐射源方位数据关联，建立粗关联和细关联统计量，从多个不确定的角度集合中筛选出来自于同一个目标的信息^[2]；二是目标特征数据关联，利用目标属性对不同的目标进行区分。本文研究了利用自适应熵权灰色关联度和聚类分析对多条目标报文进行分类的方法，可用于实现多目标关联任务，把针对同一目标的方位角组合，提供给目标定位解算。

1 方位数据关联 1.1 方位粗关联

以3个声呐阵测向交叉定位为例，假设目标与声呐阵位于平面直角坐标系内。三阵测向交叉定位示意图如图1所示。图1中3个声呐阵分别位于 ${s_i}$ 、 ${s_j}$ 以及 ${s_k}$ 点。坐标分别为 $({x_i},{y_i})$ ， $({x_j},{y_j})$ 以及 $({x_k},{y_k})$ 。图中 ${l_i}$ 、 ${l_j}$ 、 ${l_k}$ 分别为各个声呐阵测量同一目标的3条测向线。对应的方位角测量值分别为 ${\theta _i}$ 、 ${\theta _j}$ 和 ${\theta _k}$ 。由于受到环境噪声影响，角度测量存在偏差，3条测向线不能完全交于一点。以测向线 ${l_i}$ 为基准、 ${l_j}$ 与其交于 $P$ 点， ${l_k}$ 与其交于 $Q$ 点。图中 $A$ 点表示实际目标位置，3条虚线表示各个阵相对于目标的真实测向线。 ${\theta _{iJ}}$ 是声呐阵 ${s_i}$ 与 ${s_j}$ 的基线和正北方向的夹角， ${\theta _{ik}}$ 是声呐阵 ${s_i}$ 与 ${s_k}$ 的基线和正北方向的夹角。假设各个声呐阵的测量相互独立，角度测量误差均服从均值为零的高斯分布^[3]。

根据正弦定理可知点 $P$ 与 ${s_i}$ 的距离为

$ {r_{P{s_i}}} = {r_{{s_i}{s_j}}}\sin ({\theta _j} + {\theta _{ij}})/\sin({\theta _i} - {\theta _j}) $

(1)

式中： ${r_{{s_i}{s_j}}}$ 为声呐阵 ${s_i}$ 与 ${s_j}$ 间的基线距离。由式(1)可知， ${r_{P{s_i}}}$ 是以 ${\theta _i}$ 、 ${\theta _j}$ 作为参数的函数。根据泰勒级数对 ${r_{P{s_i}}}$ 进行展开，并且取一阶偏导，近似计算得到 ${r_{P{s_i}}}$ 的误差方差的数学表达式为

$ \sigma _{rP{s_i}}^2 = {\left(\frac{{\partial {r_{P{s_i}}}}}{{\partial {\theta _i}}}\right)^2}\sigma _{{\theta _i}}^2 + {\left(\frac{{\partial {r_{P{s_i}}}}}{{\partial {\theta _j}}}\right)^2}\sigma _{{\theta _j}}^2 $

同理，点 $Q$ 与S_i的距离为

$ {r_{Q{s_i}}} = {r_{{s_i}{s_k}}}\sin({\theta _k} + {\theta _{ik}})/\sin({\theta _i} - {\theta _k}) $

声呐阵S_i与S_k间的基线距离用 ${r_{{s_i}{s_k}}}$ 表示。 ${r_{Q{s_i}}}$ 误差方差近似表达式为

$ \sigma _{rQ{s_i}}^2 = {\left(\frac{{\partial {r_{Q{s_i}}}}}{{\partial {\theta _i}}}\right)^2}\sigma _{{\theta _i}}^2 + {\left(\frac{{\partial {r_{Q{s_i}}}}}{{\partial {\theta _k}}}\right)^2}\sigma _{{\theta _k}}^2 $

交点 $P$ 与 $Q$ 之间距离 ${D_{PQ}}$ 为

$ {D_{PQ}} = \left| {{r_{P{s_i}}} - {r_{Q{s_i}}}} \right| $

根据3-σ准则，如果3条测向线均针对同一目标，则满足 ${D_{PQ}} < 3\sqrt {\sigma _{rP{s_i}}^2 + \sigma _{rQ{s_i}}^2} $ 。所以令 ${D_{PQ}}$ 作为检验统计量，令方位粗关联的判决门限为 $G$ ，数学表达式如下^[4]

$ G = 3\sqrt {\sigma _{rP{s_i}}^2 + \sigma _{rQ{s_i}}^2} $

(2)

式中 $\sigma _{rP{s_i}}^2$ 和 $\sigma _{rQ{s_i}}^2$ 分别为

$ \left\{ \begin{array}{l} \sigma _{rP{s_i}}^2 = \left(\dfrac{{{r_{{s_i}{s_j}}}\sin ({\theta _j} + {\theta _{ij}})\cos({\theta _i} - {\theta _j})}}{{{{\sin }^2}({\theta _i} - {\theta _j})}}\right)\sigma _{{\theta _i}}^2 + \\ \quad \quad \quad \left(\dfrac{{{r_{{s_i}{s_j}}}\sin ({\theta _i} + {\theta _{ij}})}}{{{{\sin }^2}({\theta _i} - {\theta _j})}}\right)\sigma _{{\theta _j}}^2 \\ \sigma _{rQ{s_i}}^2 = \left(\dfrac{{{r_{{s_i}{s_k}}}\sin ({\theta _k} + {\theta _{ik}})\cos({\theta _i} - {\theta _k})}}{{{{\sin }^2}({\theta _i} - {\theta _k})}}\right)\sigma _{{\theta _i}}^2 + \\ \quad \quad \quad \left(\dfrac{{{r_{{s_i}{s_k}}}\sin ({\theta _i} + {\theta _{ik}})}}{{{{\sin }^2}({\theta _i} - {\theta _k})}}\right)\sigma _{{\theta _k}}^2 \\ \end{array} \right. $

以3个声呐阵测量 $M$ 个目标为例，假设每个声呐阵都能检测到目标，且每个声呐阵的单条测向线只针对一个目标^[5]。图2为三阵测向交叉虚假点排除示意图。

图2中 ${L_{ij}}$ 表示第 $i$ 个声呐阵的第 $j$ 条测向线， ${p_i}$ 表示目标真实位置， ${q_i}$ 为虚假定位点。为了方便示意，图中3个声呐阵在同一水平线上，实际处理时不需要多个声呐阵位于同一水平线。

方位粗关联算法的详细步骤如下：

1)假设每个声呐阵都能测量到所有目标，针对 $M$ 个目标，每个声呐阵测得 $M$ 条测向线。对声呐阵1的每条测向线进行编号，记为 ${L_{1j}}(j = 1,2, \cdots ,M)$ ，分别统计声呐阵1与声呐阵2、声呐阵1与声呐阵3各条测向线交点。以声呐阵1的第 $j$ 条测向线 ${L_{1j}}$ 为基准，声呐阵2各条测向线与其交叉形成的定位点集合记为 $\{ {d_{1j,2l}} = ({x_{1j,2l}},{y_{1j,2l}})\} $ 。类似地，声呐阵3与声呐阵1的交叉定位点集合为 $\{ {d_{1j,3k}} = ({x_{1j,3k}},{y_{1j,3k}})\} $ 。

2)以声呐阵1测量1号目标的测向线 ${L_{11}}$ 为基准，搜索所有可能的候选关联组合。与 ${L_{11}}$ 有关的交叉定位点集合是 $\{ {d_{11,2l}}\} $ 和 $\{ {d_{11,3k}}\} $ ，由于角度测量误差的存在，每个集合里只有1个点是与目标真实定位点相关联的。遍历2个定位点集合，计算每2个点之间几何距离。记为集合{ ${D_{lk}} = \left| {{d_{11,2l}} - {d_{11,3k}}} \right|$ }。

利用式(2)得到判决门限 $G$ ，计算 ${L_{11}}$ 测向线上所有满足 ${D_{lk}} < G$ 的定位交叉点，其相关的测向线组合为 $R\{ 1,l,k\} $ ，是目标1方位关联集合 ${A_1}$ 中的一个元素。应当注意， ${A_1}$ 包含满足 ${D_{lk}} < G$ 这一约束的所有方位角组合，由于可能存在虚假的定位点，集合内元素并不是唯一的。

3)利用最小距离法，针对测向线 ${L_{11}}$ 上的关联集合 ${A_1}$ ，对每个候选组合的 ${d_{11,2l}}$ 与 ${d_{11,3k}}$ 几何距离由小到大排序，认为几何距离最小的关联组合是正确组合，记为 $R = \{ 1,l',k'\} $ 。由于1条测向线仅针对1个目标，与 ${L_{11}}$ 上的定位点关联后， ${L_{2{l^{'}}}}$ 与其他测向线形成的交叉定位点即为虚假定位点。如图2所示， ${p_1}$ 是 ${L_{11}}$ 上与声呐阵2的 ${L_{21}}$ 测向线确定的真实目标交叉点，则 ${L_{21}}$ 与 ${L_{12}}$ 测向线的交点 ${q_1}$ 、 ${L_{21}}$ 与 ${L_{13}}$ 测向线交点 ${q_2}$ 均被排除。

4)确定了 ${L_{11}}$ 上针对目标1的候选关联集合 ${A_1}$ 后，重复步骤2)和3)，确定 ${L_{12}}$ 上针对目标2的候选关联集合 ${A_2}$ 。由于之前计算测向线组合 $R\{ 1,l',k'\} $ 时，对测向线 ${L_{12}}$ 与其他测向线的交叉点做过排除处理，可能会导致 ${A_2}$ 是一个空集，即没有符合约束 ${D_{lk}} < G$ 的候选关联组合。此时需要在 ${A_1}$ 集合中，选择 ${d_{11,2l}}$ 和 ${d_{11,3k}}$ 几何距离次小的点，并把相关测向线作为目标1的方位关联组合，再次执行步骤4)，计算相应目标的方位候选关联集合。

5)计算出针对1号声呐阵的各个测向线 ${L_{1j}}(j = 1,2, \cdots ,M)$ ，针对各个目标的方位候选关联集合 ${A_m}(m = 1,2, \cdots ,M)$ 。对于 ${A_m}$ ，若其中元素超过1个，即包含多个方位组合，称为不确定关联集合；对于只含有1组方位关联的集合 ${A_m}$ ，称为确定集合。对于不确定关联集合，还需要利用细关联处理，筛选出唯一的方位关联组合。

从步骤4)可以看出，方位数据粗关联时，存在一种检验机制，即关联集合 ${A_m}$ 会受到 ${A_{m - 1}}$ 的限制。判决门限 $G$ 的取值对于候选方位集合的判定有着很大的影响，直接关系到方位数据关联的正确性。如果粗关联形成的不确定集合内元素过多，可以适当减小门限，提高方位关联正确率。

1.2 方位细关联

经过方位粗关联，有些候选关联集合 ${A_m}$ 含有多个方位组合。针对这种不确定集合，还需要进行细关联处理，最大程度上排除错误组合。对于任意不确定集合 ${A_m}$ ，其中含有 $n$ 个方位组合，根据每个方位组合的有效测量值，计算目标最小二乘估计位置为 ${{X}} = {[\hat x,\hat y]^{\rm{T}}}$ ，目标估计位置相对于声呐阵的方位估计值为

$ {\hat \theta _i} = \arctan (({y_{si}} - \hat y)/({x_{si}} - \hat x)) $

(3)

统计量建立如下：

$ \lambda = \sum\limits_{i = 1}^N {(({\theta _i} - {{\hat \theta }_i})/{\sigma _{\theta i}})} $

(4)

式中： $N$ 表示每个方位组合中有效测量值个数，由于存在假设每个声呐阵的每条测向线只针对1个目标，即 $N$ 与参与处理的声呐阵个数相等； ${\theta _i}$ 为第 ${s_i}$ 个声呐阵实际测得目标方位值； ${\sigma _{\theta i}}$ 为声呐阵测量方位角的标准差。

检验统计量 $\lambda $ 近似服从 ${\chi ^2}$ 分布，自由度为

$ n = N{n_z} - {n_x} $

式中： ${n_x}$ 为待估计参数个数， ${n_z}$ 为测量量个数。由于深度已知，只需要估计目标定位点二维坐标 $(x,y)$ ，则 ${n_x} = 2$ 。测量量只有目标方位角，则 ${n_z} = 1$ 。通过检验统计量 $\lambda $ 与显著检测水平 $\alpha $ 比较，判断该方位角集合是否针对同一目标。其中显著性检验就是事先对检测量做出假设，利用样本信息来判断这个假设是否合理，根据“小概率事件实际不可能性原理”来接受或否定假设。

综上所述，目标方位细关联步骤如下：1)对于不确定集合的每个方位组合进行最小二乘估计，计算目标最小二乘位置；2)利用式(3)计算目标方位估计值；3)根据式(4)建立检测统计量。确定显著检测水平 $\alpha $ 后，根据自由度 $n$ 查找 ${\chi ^2}$ 分布表，进而获得方位细关联判决门限 ${\lambda _a}(n)$ 。若检验统计量满足 $\lambda \leqslant {\lambda _a}(n)$ ，则此方位组合是正确的候选关联，否则为错误的方位关联，应该排除。在检测水平为 $\alpha = 0.001$ 并且自由度 $n = 1$ 时，判决门限 ${\lambda _a}(n) = 10.038$ 。如果某个方位组合计算的统计检测量小于判决门限，说明在99.9%概率下，该组合中的所有方位来自于同一个目标。由于方位粗关联时，已经过滤了一些候选关联组合，不确定集合 ${A_m}$ 中的候选方位组合较少，对应细关联次数减少，算法的运算速度得到提高。

2 目标特征数据关联

由于多个目标存在，虚假定位点数急剧增加，被动目标定位难度大大增加。但是被动声呐系统在获得目标方位角信息的同时，也可以获取目标的特征信息，如目标的固有频率、线谱个数和叶片转速等信息。在方位数据关联前，利用辐射源目标的特征信息进行关联，可以减少虚假点定位的计算量。

2.1 传统灰色关联

对于一个含有 $M$ 个声呐阵的分布式声呐系统，某次试验中共有 $N$ 个不同目标。同一时刻，系统的数据融合中心收到 $R$ 条报文，即 $R{\rm{ = }}MN$ 。以舰船目标为例，每条目标报文信息均包括线谱频率、线谱幅度、线谱个数等 $K$ 项目标特征，则某一时刻全部目标的特征属性值构成如下所示目标特征序列矩阵^[6]：

$ {{x}} = \left[ {\begin{array}{*{20}{c}} {{x_1}(1)}&{{x_1}(2)}& \cdots &{{x_1}(K)}\\ {{x_2}(1)}&{{x_2}(2)}& \cdots &{{x_2}(K)}\\ \vdots & \vdots &{}& \vdots \\ {{x_R}(1)}&{{x_R}(2)}& \cdots &{{x_R}(K)} \end{array}} \right] $

式中 ${x_i}(i = 1,2 \cdots ,R)$ 表示一条报文信息， $R$ 组特征向量既是比较序列，也是参考序列。

通常，采用平移标准差变换法，令变换后的第i个报文的第 $j$ 个特征值为 ${X_i}(j)$ ，其数学表达式如下：

$ \begin{array}{c} {X_i}(j) = \dfrac{{{x_i}(j) - \overline x (j)}}{{{S_j}}} \\ \overline x (j) = \dfrac{1}{R}\displaystyle\sum\limits_{i = 1}^R {{x_i}(j)} \\ {S_j} = \sqrt {\dfrac{1}{R}{{\left(\displaystyle\sum\limits_{i = 1}^R {({x_i}(j)} - \overline x (j)\right)}^2}} \\ \end{array} $

令去量纲化后的目标特征序列矩阵为 ${{X}}$ ，每条报文特征值序列记为 ${X_i}(j)$ ，即

$ {{X}} = \{ {X_i}(j)\left| {i = 1,2, \cdots ,R;\;j = 1,2, \cdots ,K} \right.\} $

任意2个特征序列 ${X_a}(j)$ 和 ${X_b}(j)$ 之间的第 $j$ 个特征差异值为

$ {\varDelta _{a,b}}(j) = \left| {{X_a}(j) - {X_b}(j)} \right| $

${X_a}(j)$ 和 ${X_b}(j)$ 这2个序列的第j个特征灰色关联系数为^[7]

$ \begin{array}{c} \zeta ({X_a}(j),{X_b}(j)) = \\ \dfrac{{\mathop {{\rm{Min}}}\limits_a \mathop {{\rm{Min}}}\limits_b \mathop {{\rm{Min}}}\limits_j {\varDelta _{a,b}}(j) + \rho \mathop {{\rm{Max}}}\limits_a \mathop {{\rm{Max}}}\limits_b \mathop {{\rm{Max}}}\limits_j {\varDelta _{a,b}}(j)}}{{{\varDelta _{a,b}}(j) + \rho \mathop {{\rm{Max}}}\limits_a \mathop {{\rm{Max}}}\limits_b \mathop {{\rm{Max}}}\limits_j {\varDelta _{a,b}}(j)}} \\ \end{array} $

式中： $\mathop {\rm{Min}}\limits_a \mathop {\rm{Min}}\limits_b \mathop {\rm{Min}}\limits_j {\varDelta _{a,b}}(j)$ 为2个序列特征值最小差； $\mathop {\rm{Max}}\limits_a \mathop {\rm{Max}}\limits_b \mathop {\rm{Max}}\limits_j {\varDelta _{a,b}}(j)$ 为2个序列特征值最大差； $\rho $ 为分辨系数， $\rho {\rm{ = }}0.5$ 时，分辨率最好。

由于关联系数并不唯一，不能直观地体现2个序列关联程度。定义灰色关联度^[8]：

$ \gamma ({X_a},{X_b}) = \sum\limits_{j = 1}^K {\zeta ({X_a}(j),{X_b}(j))} {w_{ab}}(j) $

式中： ${w_{ab}}(j)$ 表示第 $j$ 个特征项权重，且满足 $\displaystyle\sum\limits_{j = 1}^K {{w_{ab}}(j)} = 1,{w_{ab}}(j) \geqslant 0$ 。

在加权灰色关联算法中，权值的大小反映了该项特征的重要程度。特征项的权值越大，对关联结果的影响越大。

2.2 自适应熵权灰色关联度

在信息学理论中，用信息量度量信息的多少。信息量与事件发生的概率成反比，结合信息学中熵的概念，采用自适应熵为权重赋值，计算2个特征序列的相似程度，判断是否来自于同一目标^[9]。算法步骤如下：

1)目标特征矩阵的每一行既是参考序列，也是比较序列。选择参考序列为 ${X_a}$ ，计算参考序列与比较序列的绝对差，构成特征差矩阵^[10]：

$ {{{\varDelta}} _{\bf{a}}} = \left[ {\begin{array}{*{20}{c}} {{\varDelta _{a,1}}(1)}&{{\varDelta _{a,1}}(2)}& \cdots &{{\varDelta _{a,1}}(K)}\\ {{\varDelta _{a,2}}(1)}&{{\varDelta _{a,2}}(2)}& \cdots &{{\varDelta _{a,2}}(K)}\\ \vdots & \vdots &{}& \vdots \\ {{\varDelta _{a,a - 1}}(1)}&{{\varDelta _{a,a - 1}}(2)}& \cdots &{{\varDelta _{a,a - 1}}(K)}\\ {{\varDelta _{a,a + 1}}(1)}&{{\varDelta _{a,a + 1}}(2)}& \cdots &{{\varDelta _{a,a + 1}}(K)}\\ \vdots & \vdots &{}& \vdots \\ {{\varDelta _{a,R}}(1)}&{{\varDelta _{a,R}}(2)}& \cdots &{{\varDelta _{a,R}}(K)} \end{array}} \right] $

2)计算第 $j$ 个特征项出现的相对概率：

$ {P_{ai}}(j) = {{{\varDelta _{a,i}}(j)} \Bigg/ {\sum\limits_{i = 1}^R {{\varDelta _{a,i}}(j)} }} $

此时，第j个特征项的信息熵为 ${E_{ai}}\left( j \right)$ ：

$ {E_{ai}}(j) = - {1 / {\ln R}}\sum\limits_{i = 1}^R {{P_{ai}}(j)\ln{P_{ai}}(j)} $

定义第j个特征项的剩余度，也称差异性系数：

$ {D_{ai}}(j) = 1 - {E_{ai}}(j) $

参考序列与比较序列关于第j个特征项差异性系数越大，该特征项对于衡量比较序列和参考序列的差异性越重要，应该赋予的权重越大。

3)计算第 $j$ 个特征项的权重值：

$ {w_{ai}}(j) = \frac{{{D_{ai}}(j)}}{{\displaystyle\sum\limits_{j = 1}^K {{D_{ai}}(j)} }} $

各个特征序列与比较序列的加权灰色关联度矩阵为

${{\gamma}} = \left[ {\begin{array}{*{20}{c}} {\gamma ({X_1},{X_1})}&{\gamma ({X_1},{X_2})}& \cdots &{\gamma ({X_1},{X_R})}\\ {\gamma ({X_2},{X_1})}&{\gamma ({X_2},{X_i})}& \cdots &{\gamma ({X_2},{X_R})}\\ \vdots & \vdots &{}& \vdots \\ {\gamma ({X_R},{X_1})}&{\gamma ({X_a},{X_2})}& \cdots &{\gamma ({X_R},{X_R})} \end{array}} \right]$

2.3 系统聚类分析

系统聚类分析法的原则是首先把多个样本自成一类，每个类之间的距离描述各个类的相似程度^[11]，把距离最近的类合并，使类的数目减少。随后更新现有类之间的距离，再次进行类合并，使类的数目进一步减少，直至所有样本归为一类为止。本节采用样本的加权灰色关联度代替距离，以此作为分类依据，减少计算量^[12]。

假设共有 $S$ 个类，记为 $G{\rm{ = }}{{\{ }}{G_i}\left| {i = 1,2, \cdots ,S} \right.{{\} }}$ 。类间相似度用 $\mu $ 表示，则类 ${G_a}$ 和类 ${G_b}$ 之间的相似程度定义为

$ {\mu _{ab}} = \mathop {\max }\limits_{\scriptstyle{X_i} \in {G_a}\atop \scriptstyle{X_j} \in {G_b}} (\gamma ({X_i},{X_j})) $

式中若 $a = b$ ，则令 ${\mu _{ab}} = 1$ 。

初始时，数据中心收到 $R$ 条报文，令每条报文各自成为一类，记为 $G{\rm{ = }}{\mathbf{\{ }}{G_i}\left| {i = 1,2, \cdots } \right.,R{\mathbf{\} }}$ 。计算各类之间相似程度矩阵为

$ {{\mu}} = \left[ {\begin{array}{*{20}{c}} {{\mu _{11}}}&{{\mu _{12}}}& \cdots &{{\mu _{1R}}}\\ {{\mu _{21}}}&{{\mu _{22}}}& \cdots &{{\mu _{2R}}}\\ \vdots & \vdots &{}& \vdots \\ {{\mu _{R1}}}&{{\mu _{R2}}}&{\cdots}&{{\mu _{RR}}} \end{array}} \right] $

初始时刻，每条报文各自组成一个类，满足 ${\mu _{ab}} = \gamma ({X_a},{X_b})$ 。在相似度矩阵 ${{\mu}} $ 中，找出非对角线元素中最大值 ${\mu _{pq}}$ ，其对应类 ${G_p}$ 和 ${G_q}$ 。把这2个类合并为新的类 ${G_r} = \{ {G_p},{G_q}\} $ 。合并后，计算该类与其他类的类间相似度，新类 ${G_r}$ 与未发生改变的类 ${G_t}$ 之间 $\;{\mu _{rt}}$ 为

$ \begin{array}{*{20}{c}} {{\mu _{rt}} = \mathop {\max }\limits_{\scriptstyle{X_i} \in {G_r}\atop \scriptstyle{X_j} \in {G_t}}{\begin{array}{*{20}{l}} \end{array}} \{ (\gamma ({X_i},{X_j}))\} = \max\Bigg\{ \mathop {\max }\limits_{\scriptstyle{X_a} \in {G_p}\atop \scriptstyle{X_b} \in {G_t}}{\begin{array}{*{20}{l}} \end{array}} \{ \gamma ({X_a},{X_b})\} ,}\\ {\mathop {\max }\limits_{\scriptstyle{X_c} \in {G_q}\atop \scriptstyle{X_d} \in {G_t}}{\begin{array}{*{20}{l}} \end{array}} \{ \gamma ({X_c},{X_d})\} \Bigg\} = \max \{ {\mu _{pt}},{\mu _{qt}}\} } \end{array} $

最后，利用分类准则函数判断 $R$ 条报文应该融合分为几类。一个聚簇划分的合理性体现在不同聚簇之间相似度很低，同一聚簇相似度很高。假设R条报文融合分类形成z个聚簇，即 $C = \{ {C_1},{C_2}, \cdots , {C_z}\} $ 。其类内紧凑度函数为

$ {S_w}(C) = \frac{1}{z}\sum\limits_{i = 1}^z {\frac{1}{{\left| {{C_i}} \right| \cdot \left| {{C_i}} \right|}}} \sum\limits_{X,Y \in {C_i}} {\gamma (X,Y)} $

式中 $\left| {{C_i}} \right|$ 表示聚簇类中原始类个数。

类间分离函数为

${S_b}(C) = \frac{1}{{z(z - 1)}}\sum\limits_{i = 1}^z {\left( {\sum\limits_{j = 1,j \ne i}^z {\frac{1}{{\left| {{C_i}} \right| \cdot \left| {{C_j}} \right|}}\sum\limits_{X \in {C_i},Y \in {C_j}} {\gamma (X,Y)} } } \right)} $

令分类准则函数为

$ V(C) = {S_w}(C) + {S_b}(C) $

当分类准则函数值最大时，对应分类个数最为合理。理想情况下，对于目标个数为 $N$ 、声呐阵个数为M的被动定位系统，每个声呐阵均向数据融合中心传送 $N$ 条报文。由于受到环境因素影响，各个声呐阵上传报文数不完全相等，数据中心实际收到报文数为 $r$ 。此时合理的目标分类个数应该在 ${r / M}$ 附近，找出分类准则函数在分类数约为 ${r / M}$ 左右的最大值，对应分类个数为 $t$ ，记录此时分类结果。

2.4 目标方位−特征联合关联

由目标方位数据关联算法可知，由于多个目标存在，虚假定位点数急剧增加，被动目标定位难度大大增加。但是，被动声呐系统在获得目标方位角信息的同时，也可以获取目标的特征信息，如目标的固有频率、线谱个数和叶片转速等信息。当多目标轨迹交点分布较为聚集时，只利用方位数据关联算法正确率有所降低，此时在方位数据关联前，利用辐射源目标的特征信息进行关联，可以减少虚假点定位的计算量。如果目标属性关联结果不唯一，可以再进行方位数据关联。2种算法具有互补性，联合关联流程如图3所示。

3 仿真实例

3个声呐阵坐标分别为 $(0,0)$ 、 $(10,0)$ 和 $(20,0)$ 。同一时刻目标个数为3，每个目标间距d=2。其位置坐标如下：目标1(11,10)、目标2(11+d,10)和目标3(11−d,10)，单位均为km。各目标特征值如表1所示。线谱频率和归一化幅度测量(以最大幅度为准)误差服从均值为0、标准差分别为5 Hz和20 dB的高斯分布，线谱个数正确估计率为60%。

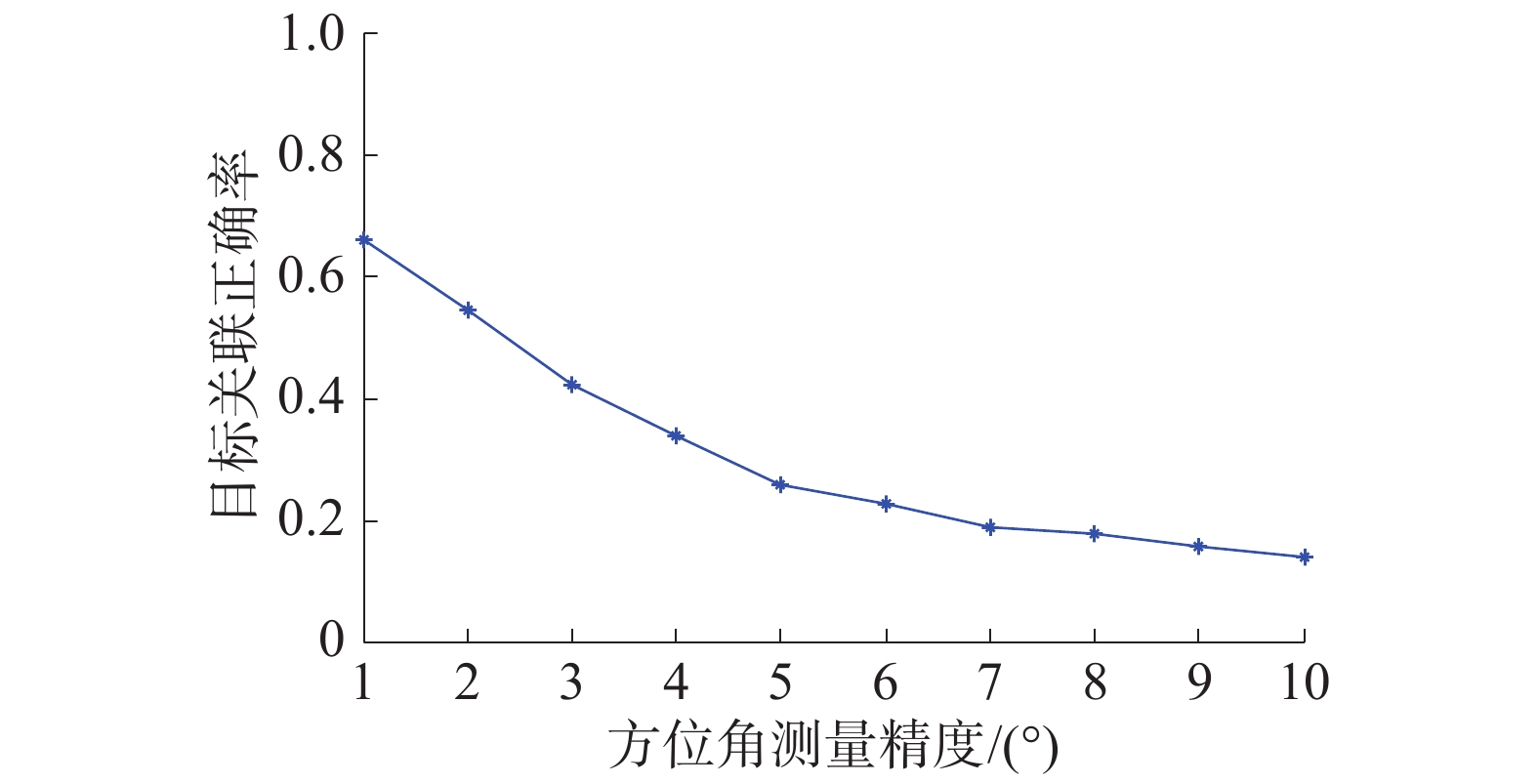
目标方位数据关联法进行1 000次蒙特卡洛试验，得到不同角度测量精度下的关联正确率如图4所示。其中，将3个目标都正确关联记为正确，有1个关联错误即为错误。

由图4可知，在目标间距较小时，只利用方位数据进行目标关联得到正确结果概率较低。在上述仿真条件下，只利用目标特征灰色关联算法，统计1 200个融合周期，最优分类函数分布状态如图5所示。

根据表1可知，3个目标中有2个目标的各个特征相似。在上述仿真测量误差下，2个目标的特征项存在模糊，只利用目标特征的灰色关联算法会发生错误关联。分析仿真中发生关联错误的原因发现，该算法会错误地将3个目标关联融合为2类，不能很好地区分1号目标和2号目标。

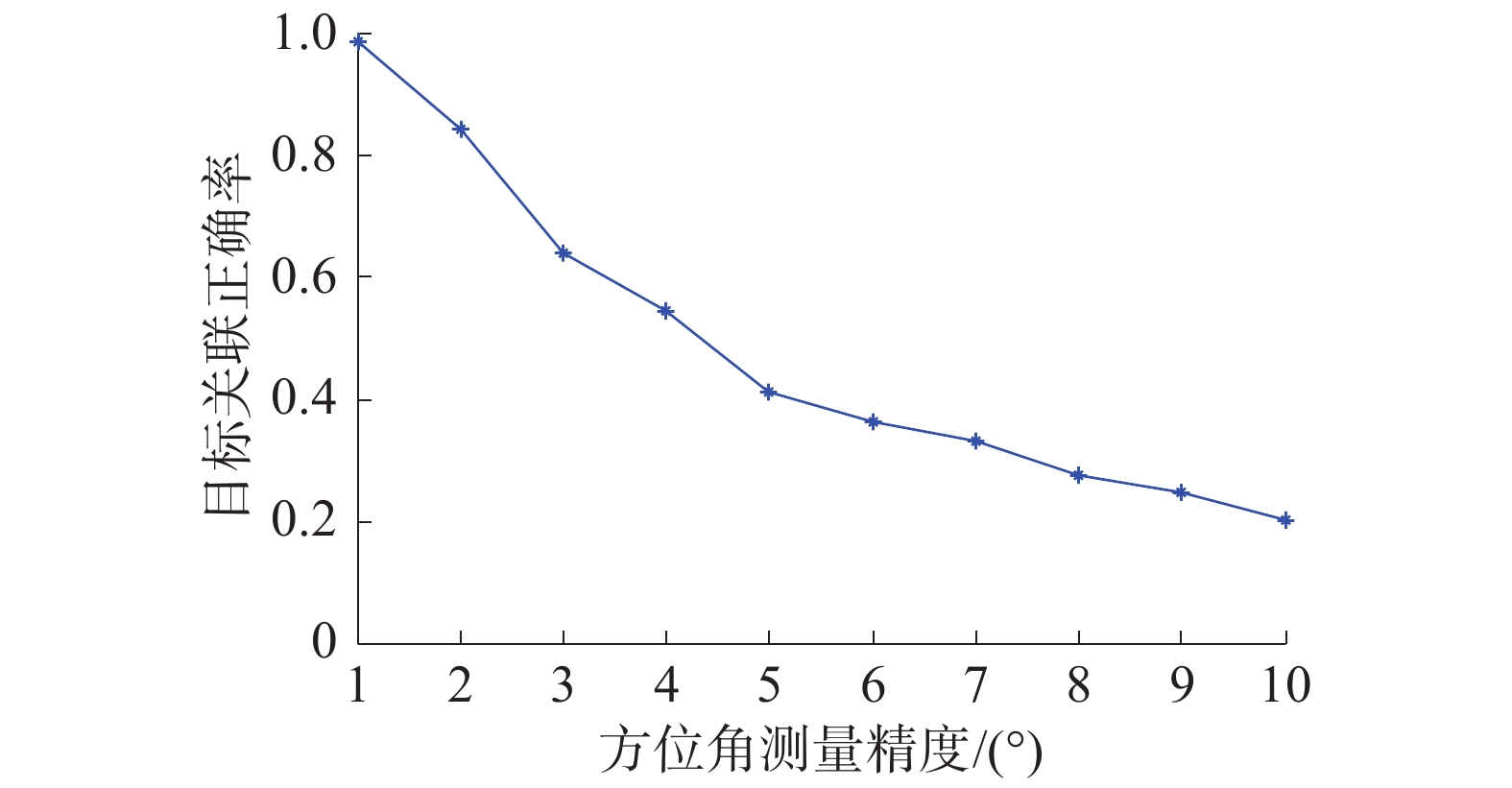
此时，利用目标特征灰色关联，得出最佳聚簇分类。针对报文条数多于 ${r / M}$ 的聚簇类，再次进行方位关联。在仿真条件不变的情况下，得到不同角度测量精度下的联合关联算法正确率如图6所示。

对比图4、5和6可知，在目标距离较近且目标特征测量误差较大时，单独使用方位数据关联或者特征关联的正确率都比较低。随着目标信息测量的精度增加，使用2种算法进行联合关联，可以有效减少虚假定位点个数。

4 结论

在目标间距较小时，各个声呐阵测向线交叉点分布较为集中，目标真实位置与虚假点位置间的距离较小，方位数据关联正确率较低。特征数据关联算法受到特征测量误差影响，不同目标属性值测量范围有重合，测量得到的目标特征值存在模糊，不能很好地区分不同目标。

本文基于上述方法对目标数据进行联合关联，弥补单一方法带来的不足，提高目标关联正确率。