为保障人民的生命与财产安全,对一些结构进行长期有效的实时在线健康监测十分重要。损伤识别技术的实际应用最早出现在航空和机械领域,20世纪末期,各种不同类型结构的损伤识别研究开始快速发展,1979年Cawley[1]和Adams等[2]对结构部分动力特性进行研究,提出了基于结构的固有频率对建筑结构损伤进行损伤识别的方法;1996年,Doebling等[3]对基于结构模态特性的结构损伤识别方法进行了综合研究;20世纪90年代,Masri等[4-6]分别研究了将频率、反应谱、振型等不同特征作为输入数据,BP神经网络对结构损伤的识别能力;21世纪以来,诸多学者都对不同类型的结构损伤识别方法进行了大量更深入的研究,Manson. G等[7-9]提出了一种以人工神经网络作为分类器,结合遗传算法的结构损伤识别方法,该算法还在飞机机翼健康监测上得到实验验证;基于模态参数的损伤识别方法也得到了进一步的发展和应用[10-11]。通过不断地研究与发展,结构损伤识别技术逐渐在实际工程中得到广泛应用,而如何提高结构损伤识别与定位在实际应用中的稳定性有待更深入的研究。本文结合人工神经网络与信息融合技术,讨论了基于BP神经网络的结构损伤识别技术的可行性,以及应用信息融合的损伤识别技术的优势。
1 损伤识别技术人工神经网络各层神经元之间以权值矩阵连接,在对网络训练的过程中,神经网络基于对样本数据特征的学习来选择网络的权值和偏置,从而使网络的输出结果不断接近期望输出。
1.1 BP神经网络的构建结构损伤识别中,不同工况将会对应不同的特征数据集,本文选择属于有监督学习的BP神经网络,通过网络本身的模式识别能力对所测得的特征进行分类。BP神经网络结构示意图如图1所示。

|
Download:
|
| 图 1 BP神经网络示意 | |
图中神经元结构如图2所示。

|
Download:
|
| 图 2 神经元示意 | |
以图2所示神经元为例,图中
应用BP神经网络对结构进行损伤识别包含以下4个步骤:
1)搭建神经网络结构。
本文采用3层神经网络结构,输入向量由损伤敏感特征组成。输出层神经元的节点数由网络目的来确定,如果是分类问题则由分类形式确定,初始学习率设置为0.01。
2)样本数据处理。
对数据进行标准化的处理,使用min-max标准化对数据进行标准化处理,使样本数据转换到[0,1]区间内。
3)网络训练。
对BP神经网络进行训练,也就是通过对训练数据集的学习调整网络参数,使网络最终的输出结果尽量接近期望输出。
4)网络测试。
利用测试集中的数据样本对训练成功的网络性能进行测试。
1.2 结构损伤敏感特征的选取结构损伤识别中,损伤敏感特征的选取是决定神经网络识别成功率的关键。结构的模态参数包括结构的固有频率、阻尼比和振型等。通过理论分析和实验验证,许多学者都证实了固有频率作为结构损伤指标在工程结构中应用的可行性[12-14]。
应变由位移求导所得,当结构产生损伤时,在损伤单元附近由于应力分布的变化,应变模态也会发生改变。李德葆等[15-16]通过一系列研究讨论了应变与位移模态的关系,并研究了将应变模态应用于损伤识别中的方法。
结构振型对结构的局部损伤较敏感,可用来进行确定结构损伤的位置。利用振型参数识别结构损伤最常用的方法为模态置信准则(modal assurance criterion,MAC)以及位移模态置信准则(coordinate modal assurance criterion,COMAC),W. M. West[17]与J. M. Ko[18]等对这2种方法用于结构损伤识别与定位的优劣分别进行了研究。MAC与COMAC相比,对结构损伤较敏感且结果简单明了。
综上所述,本文选用结构的频率、位移模态以及模态置信准则作为损伤敏感特征。
1.3 信息融合技术信息融合技术是利用计算机对按时序获得的观测信息,在一定准则下加以自动分析、综合,完成所需的决策和评估任务而进行的信息处理技术。
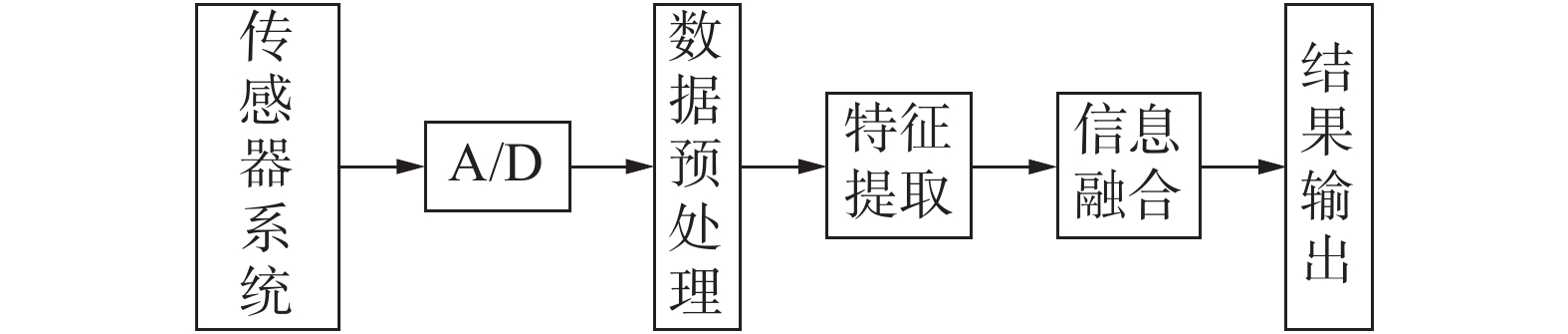
信息融合过程中,首先将检测到的信息转化为电信号,经过模数转换将电信号转化为数字信号。对转化后的信号进行预处理、除噪,然后提取处理后的信号特征进行融合或者直接对处理后的数据进行融合。信息融合过程如图3所示。
|
Download:
|
| 图 3 信息融合的过程 | |
本文将先分别选取单一特征对结构进行损伤识别,然后讨论信息融合技术在结构损伤识别中的应用优势。
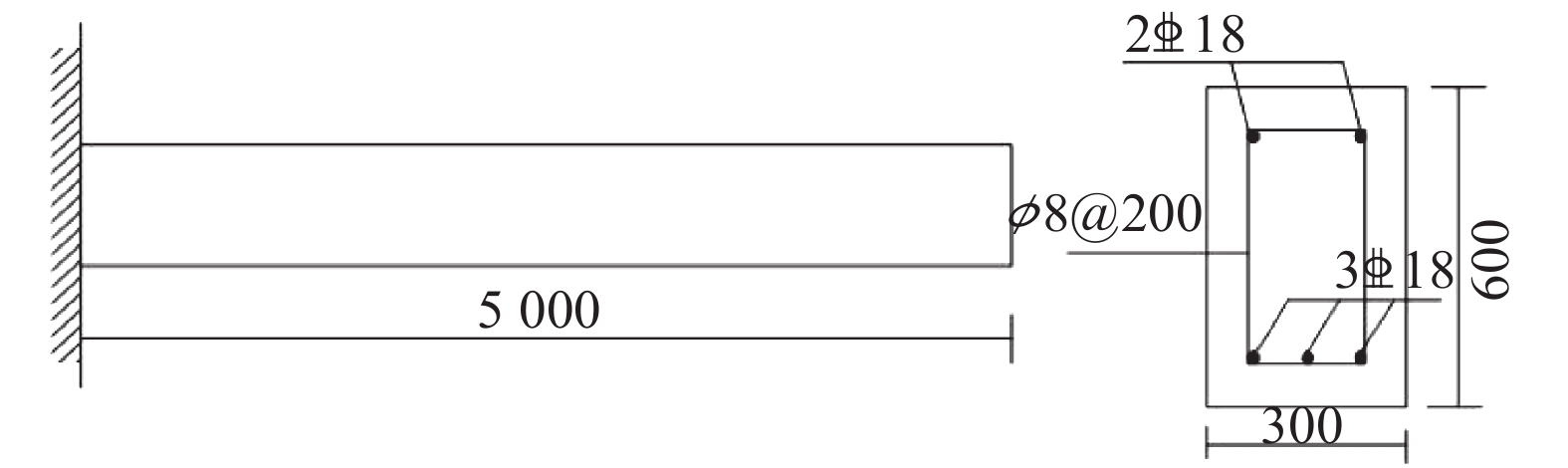
2 特征数据提取与处理 2.1 损伤敏感特征提取本文以悬臂梁为背景,利用仿真软件建立模型,获取各工况的损伤敏感特征。梁截面尺寸为300 mm×600 mm×5 000 mm,配筋如图4所示。
|
Download:
|
| 图 4 悬臂梁配筋 | |
结构所用材料参数如表1所示。
|
|
表 1 材料参数 |
为得到结构在不同状态下的特征参数,分别在悬臂梁悬臂端、跨中和支座附近选择3处划分损伤,在距离支座10 mm处设置损伤,该处命名为Ⅰ区;区域Ⅱ设置在钢筋混凝土梁的跨中位置,损伤中心距离支座2 500 mm;区域Ⅲ的损伤中心距离支座4 975 mm,位于悬臂端。
各区域损伤均位于梁结构上表面,分别设置a、b这2类损伤,其中a类损伤尺寸为100 mm×50 mm×20 mm,b类损伤尺寸为100 mm×50 mm×5 mm。各工况如表2所示。
|
|
表 2 梁工况分类 |
与传统的损伤识别方法相比,结合信息融合后,基于神经网络进行的结构损伤识别方法具有很强的自学习能力。但当样本数量过少时,神经网络可能会出现过拟合问题。
数据增强技术是在不改变数据标签和关键特征的前提下,引入某些类型的变换来扩充样本数量。本文参照文献[19]的方法,通过向样本数据中随机加入服从正态分布的高斯白噪声的方法来扩充样本数量。
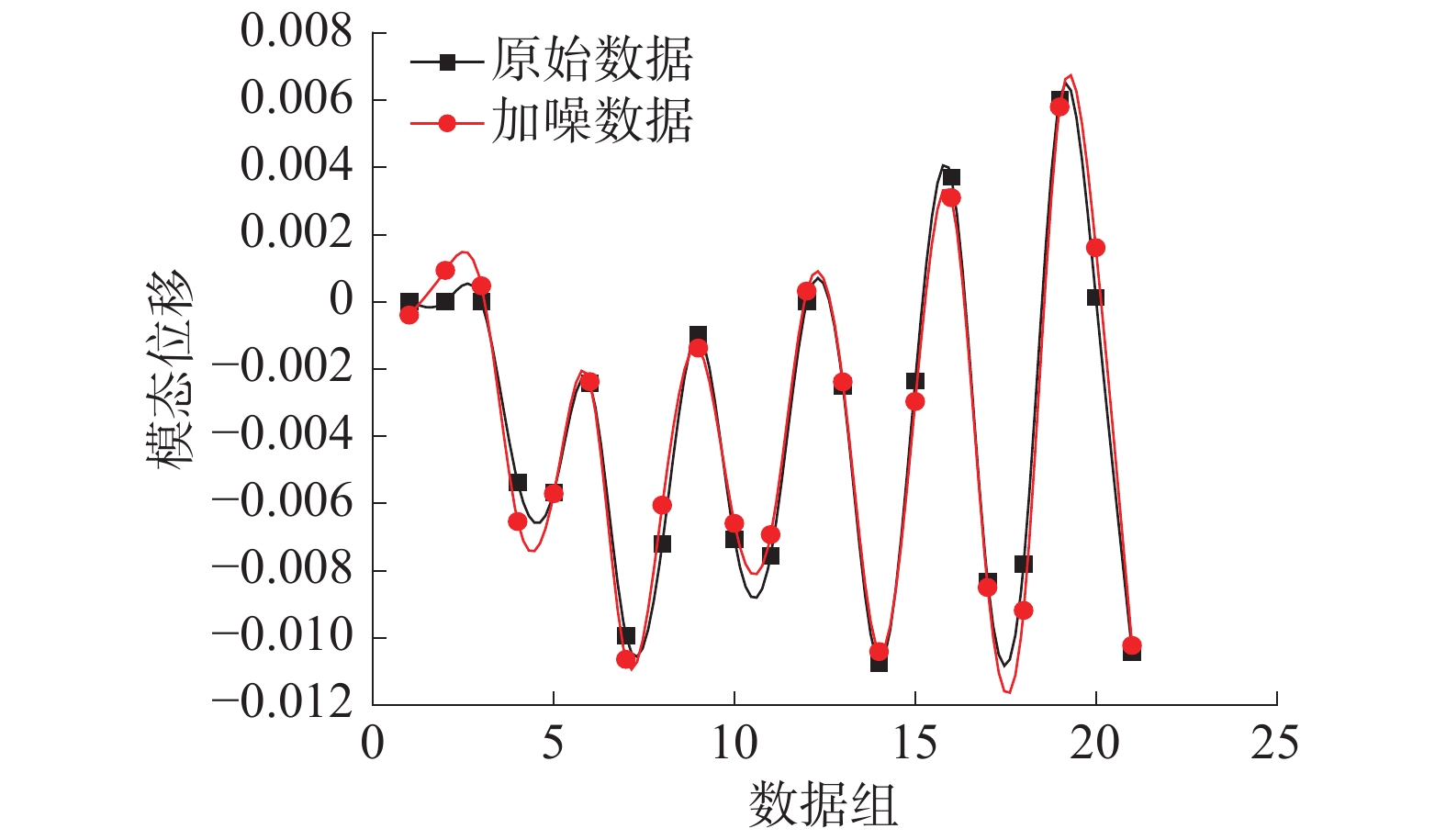
加入随机噪声的完整梁节点(150,300,1 500)处的位移模态数据与原始数据对比如图5所示,理论上通过这种方法可以扩充得到大量数据。
|
Download:
|
| 图 5 数据对比 | |
取模拟所得的特征参数,经过数据增强和处理之后作为特征向量输入网络,文中默认当网络输出大于0.8时为接近期望输出1,小于0.2时为接近期望输出0。
首先以损伤深度为20 mm对应的a类损伤与无损工况为例,进行基于单特征的损伤识别。
从4种工况中选取25组数据作为训练样本,剩余5组数据作为测试样本。网络训练数据为1×100的矩阵,测试集为1×20的矩阵。期望输出以数值的形式进行赋值,其中无损数据集的标签为0,损伤梁对应的特征数据集标签为1。
以位移模态作为特征数据时,针对同样的特征集输入和学习率,均方误差(mean squared error,MSE)随隐含层神经元节点数目的变化如表3所示。最终确定针对位移模态,隐含层神经元节点数为7、网络迭代193次时,网络性能达到最佳,网络输出记录于表4中,数据保留小数点后3位。
|
|
表 3 不同隐含层神经元节点数性能变化 |
|
|
表 4 结构损伤识别结果 |
对固有频率与MAC值组成的特征数据集,进行与位移模态相同的处理,分别将固有频率与MAC值对应的数据集作为网络输入,并对网络进行训练与调整,记录网络输出。
3.1.2 结果分析对应a类的工况Ⅰa、Ⅱa、Ⅲa以及工况Ⅳ,不同测试数据的输出结果如表4所示。
对网络测试结果进行分析可得,在位移模态做特征数据时,20组输出中有工况Ⅰa编号为4的数据输出为0.201,大于0.2,工况Ⅳ编号19的数据输出为0.704,小于0.8,2组输出不满足期望输出的要求。模态置信准则作为特征数据时,工况Ⅲa编号为11和15的2组数据输出为0.383与0.445,输出不满足要求。除此之外的输出均能满足对期望输出的接近,能实现目标要求的损伤识别。
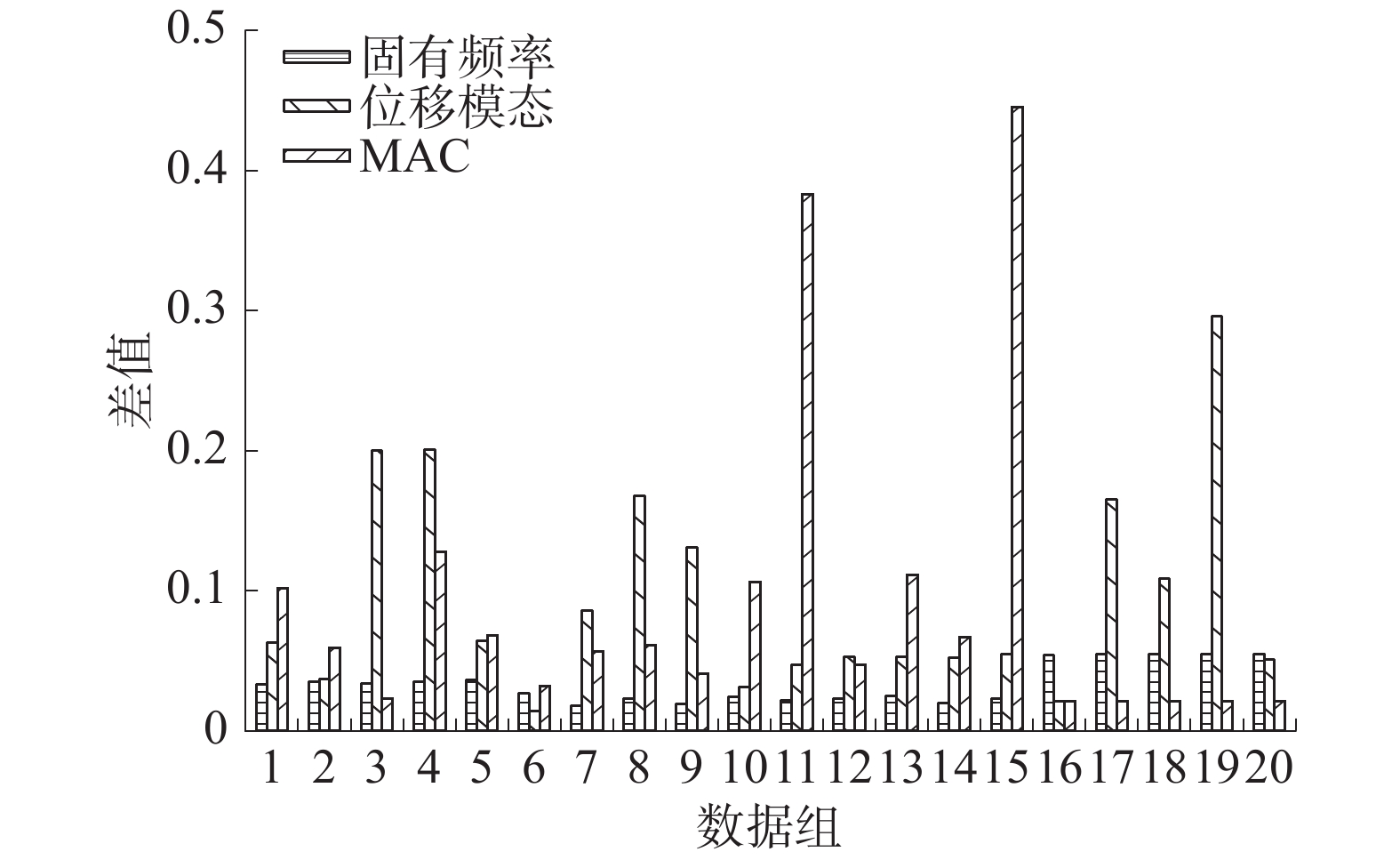
3类特征数据中,固有频率对应的输出结果对损伤的识别效果最佳。神经网络的实际网络输出与期望值之间差值的绝对值如图6所示。
|
Download:
|
| 图 6 网络输出与期望输出的差值 | |
网络输出证明位移模态、固有频率与MAC值均可以用作钢筋混凝土梁结构的损伤敏感特征,证明了基于MATLAB建立的BP神经网络应用于损伤识别的可行性。
同时对网络的输出进行对比发现,固有频率作为损伤敏感特征时,损伤识别精确度最高,输出结果与期望输出之间的均方误差MSE最小,对几种工况下的20组数据均能进行有效分类,满足期望要求的区分结果。由图6可知,固有频率作特征参数时,网络的输出结果最接近期望输出,网络识别效果良好。位移模态作为特征数据时,准确率达到90%,也能对结构进行损伤识别,但是识别结果之间波动较大,鲁棒性较差。
在用模态置信准则做损伤识别特征时,在结构没有损伤的情况下MAC值均为1;发生损伤时,结构振型发生变化,MAC值将小于1。但结构某些阶数对应的模态振型对结构损伤并不敏感,因此导致网络识别准确率仅达到90%,其中网络无法准确区分的数据主要集中在工况Ⅲa。
3.2 基于信息融合的结构损伤识别 3.2.1 相同损伤尺寸特征信息的信息融合首先仅考虑在同一损伤尺寸时,模型的损伤识别能力。
在损伤深度为20 mm时,取工况Ⅰa、Ⅱa、Ⅲa和Ⅳ的位移模态、固有频率以及MAC数据组成三维矩阵。从每种工况中抽取5组数据组成3×20的矩阵作为测试数据,剩余组成3×100的矩阵作为训练集,数据以矩阵的形式输入网络时,网络每次读取1列3个数,包含3种特征。对网络进行训练与测试得到1组结果。
损伤深度为5 mm时,各类数据集的设置与20 mm时一致。对工况Ⅰb、Ⅱb、Ⅲb和Ⅳ进行损伤识别并得到第2组结果。同样在网络进行损伤识别时,无损数据以1作为标签,损伤数据标签为0。
在损伤尺寸为20 mm的工况下,网络对应不同隐含层节点数目时的MSE变化如表5所示,最终确定隐含层神经元节点数为7、网络迭代208次时得到最佳识别结果。
|
|
表 5 不同隐含层神经元节点数性能变化 |
对于损伤深度为5 mm的工况,由表6可知,网络在隐含层神经元节点数取5、网络迭代165次时最佳。
|
|
表 6 不同隐含层神经元节点数性能变化 |
网络训练集数据由损伤深度20 mm和5 mm的特征数据共同组成。在损伤深度为20 mm的数据中,从每种工况特征数据中选取2组;从深度为5 mm的数据中每类选取3组,从完整梁特征数据中选取5组。将上述数据组合成3×20的测试集,剩余190组数据组成3×190的训练集。
网络的MSE与神经元节点数的关系如表7所示,最终确定神经元节点为6。
|
|
表 7 不同隐含层神经元节点数性能变化 |
3种不同训练情况下,网络输出结果如表8所示。
|
|
表 8 多数据融合损伤识别结果 |
图7给出了基于信息融合的结构损伤识别输出结果与期望输出之间的差值情况。图中A、B、C类分别代表损伤深度为20 mm、5 mm以及2种损伤深度混合对应的特征信息融合。

|
Download:
|
| 图 7 网络输出与期望输出的差值 | |
在仅考虑一种损伤深度的情况下,基于信息融合的输出结果表明网络能精确地区分损伤特征和无损特征。
将网络输出结果与基于单特征信息的损伤识别结果相比,基于信息融合的损伤识别对所设20组数据均能进行有效区分,不存在因为结构某几阶特征对损伤不敏感造成的误差所引起的无法区分损伤状况的数据。网络的输出结果相比单特征损伤识别精确度高,更接近期望输出。
在考虑2种损伤深度混合的情况下,网络输出证明了在信息融合的基础上,针对不同类型的损伤,BP神经网络也能做到准确地识别损伤,损伤数据的混合不会导致模型出现无法区分损伤的情况。
将混合2种损伤尺寸的网络输出与融合单尺寸损伤的结果相比,网络识别的精确度更高。这是因为神经网络的精确度受样本量的影响较大,在样本量足够大时,训练完成的网络测试结果可以无限逼近期望输出,因此当训练集样本数为190时,网络识别损伤的效果更好。
4 结论本文针对悬臂梁的损伤识别进行研究,基于人工神经网络和信息融合的理论,研究了BP神经网络在结构损伤识别上的应用,分析BP神经网络的构建流程,讨论BP神经网络中关键参数的选择方式。推导神经网络中的权值更新公式,最终建立BP神经网络,对结构进行损伤识别研究。本文得到的主要结论如下:
1)针对结构损伤识别进行研究。讨论分别用频率、位移模态以及MAC值作为网络输入时,BP神经网络识别损伤的能力。对输出结果分析得到基于上述3种特征,BP神经网络能对结构损伤进行准确的识别。在损伤尺寸发生变化时,网络依然能完成准确的损伤识别。3种特征中,位移模态作为特征输入时,网络识别精度最高,20组数据均能准确区分,应用频率与MAC值时准确率均达到90%。
2)讨论信息融合技术在结构损伤识别中的应用。相比仅用单类型特征作为网络输入参数,在融合3种特征的情况下,网络识别损伤的准确性更高,不存在因为结构某几阶特征对损伤不敏感造成的误差所引起的无法区分损伤状况的数据。网络的输出结果相比单特征损伤识别精确度高,更接近期望输出。
| [1] |
CAWLEY P, ADAMS R D. The location of defects in structures from measurements of natural frequencies[J]. The journal of strain analysis for engineering design, 1979, 14(2): 49-57. DOI:10.1243/03093247V142049 ( 0) 0)
|
| [2] |
ADAMS R D, CAWLEY P, PYE C J, et al. A vibration technique for non-destructively assessing the integrity of structure[J]. Journal of mechanical engineering science, 1978, 20(2): 93-100. DOI:10.1243/JMES_JOUR_1978_020_016_02 ( 0) 0)
|
| [3] |
DOEBLING S W, FARRAR C R, PRIME M B, et al. Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics: a literature review[M]. Los Alamos: Los Alamos National Lab, 1996.
( 0) 0)
|
| [4] |
MASRI S F, NAKAMURA M, CHASSIAKOS A G, et al. Neural network approach to detection of changes in structural parameters[J]. Journal of engineering mechanics, 1996, 122(4): 350-360. DOI:10.1061/(ASCE)0733-9399(1996)122:4(350) ( 0) 0)
|
| [5] |
WU X, GHABOUSSI J, GARRETT J H JR. Use of neural networks in detection of structural damage[J]. Computers & structures, 1992, 42(4): 649-659. ( 0) 0)
|
| [6] |
KIRKEGAARD P H, RYTTER A. Use of neural networks for damage detection and location in a steel member[C]//Proceedings of 3rd International Conference on the Application of Artificial Intelligence to Civil and Structural Engineering. Edinburgh, Britain, 1993.
( 0) 0)
|
| [7] |
WORDEN K, MANSON G, ALLMAN D. Experimental validation of a structural health monitoring methodology Part I: novelty detection on an aircraft wing[J]. Journal of sound and vibration, 2003, 259(2): 323-343. DOI:10.1006/jsvi.2002.5168 ( 0) 0)
|
| [8] |
MANSON G, WORDEN K, ALLMAN D. Experimental validation of a structural health monitoring methodology: Part Ⅲ. Damage location on an aircraft wing[J]. Journal of sound and vibration, 2003, 259(2): 365-385. DOI:10.1006/jsvi.2002.5169 ( 0) 0)
|
| [9] |
MANSON G, PAPATHEOU E, WORDEN K. Genetic optimisation of a neural network damage diagnostic[J]. The aeronautical journal, 2008, 112(1131): 267-274. DOI:10.1017/S0001924000002219 ( 0) 0)
|
| [10] |
SHABBIR F, KHAN M I, AHMAD N, et al. Structural damage detection with different objective functions in noisy conditions using an evolutionary algorithm[J]. Applied sciences, 2017, 7(12): 1245. DOI:10.3390/app7121245 ( 0) 0)
|
| [11] |
KUOK S C, YUEN K V. Investigation of modal identification and modal identifiability of a cable-stayed bridge with Bayesian framework[J]. Smart structures and systems, 2016, 17(3): 445-470. DOI:10.12989/sss.2016.17.3.445 ( 0) 0)
|
| [12] |
XIA Yong, HAO Hong. Statistical damage identification of structures with frequency changes[J]. Journal of sound and vibration, 2003, 263(4): 853-870. DOI:10.1016/S0022-460X(02)01077-5 ( 0) 0)
|
| [13] |
YANG Zhibo, CHEN Xuefeng, YU Jie, et al. A damage identification approach for plate structures based on frequency measurements[J]. Nondestructive testing and evaluation, 2013, 28(4): 321-341. DOI:10.1080/10589759.2013.801472 ( 0) 0)
|
| [14] |
JAHANGIRI M, NAJAFGHOLIPOUR M A, DEHGHAN S M, et al. The efficiency of a novel identification method for structural damage assessment using the first vibration mode data[J]. Journal of sound and vibration, 2019, 458: 1-16. DOI:10.1016/j.jsv.2019.06.011 ( 0) 0)
|
| [15] |
李德葆, 陆秋海. 实验模态分析及其应用[M]. 北京: 科学出版社, 2001.
( 0) 0)
|
| [16] |
李德葆, 诸葛鸿程, 王波. 实验动态应变分析中的模态分析方法[J]. 固体力学学报, 1990, 11(4): 360-364. ( 0) 0)
|
| [17] |
WEST W M. Illustration of the use of modal assurance criterion to detect structural changes in an orbiter test specimen[C]//Proceedings of the 4th International Modal Analysis Conference. Schenectady, USA, 1986: 1-6.
( 0) 0)
|
| [18] |
KO J M, WONG C W, LAM H F. Damage detection in steel framed structures by vibration measurement approach[C]//Proceedings of the 12th International Modal Analysis Conference. Honolulu, USA, 1994: 280-286.
( 0) 0)
|
| [19] |
郭耀华. 基于深度学习的车辆驾驶状态识别算法研究[D]. 北京: 北京邮电大学, 2019.
( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


