图像作为人们获取知识的主要载体,已经得到了一定的发展。但是,在图像去噪[1-2]这方面仍然有着需要改进的地方,图像去噪重构精度不够、时间开销比较大[3]等都需要进一步研究与学习。所以,本文主要针对这2个方面进行研究,通过结合压缩感知[4-6]和交替方向乘子法(alternating direction method of multipliers, ADMM)[7-9]的相关知识,以期找到一个更好的解决方法,从而可以达到更好的图像去噪效果。
1 一种基于熵函数的重构算法本节主要针对
| $\mathop {\min }\limits_x F\left( x \right) = \sum\limits_{i = 1}^n {{{\left| {{f_i}\left( x \right)} \right|}^p}} {\rm{, }} {0 \leqslant p \leqslant 1} $ | (1) |
显然,式(1)中的函数
| $ F\left( x \right) = \displaystyle\sum\limits_{i = 1}^n {|{f_i}\left( x \right){|^p}} = \displaystyle\sum\limits_{i = 1}^n {{{\left[ {\max \left\{ {{f_i}\left( x \right) - {f_i}\left( x \right)} \right\}} \right]}^p}} $ | (2) |
又因为存在以下关系:
| $ \mathop {\lim }\limits_{q \to \infty } \left[ {\dfrac{1}{q}\ln \left( {{{\rm{e}}^{qt}} + {{\rm{e}}^{ - qt}}} \right)} \right] = \mathop {\lim }\limits_{q \to \infty } \dfrac{{t{{\rm{e}}^{qt}} - t{{\rm{e}}^{ - qt}}}}{{{{\rm{e}}^{qt}} + {{\rm{e}}^{ - qt}}}} = \max \left( {t, - t} \right) = |t| $ | (3) |
所以,对比式(2)、(3)可以知道,非线性
| $ \mathop {\min }\limits_x F\left( {x,q} \right) = {\displaystyle\sum\limits_{i = 1}^n {\left[ {\dfrac{1}{q}\ln \left( {{{\rm{e}}^{q{f_i}\left( x \right)}} + {{\rm{e}}^{ - q{f_i}\left( x \right)}}} \right)} \right]} ^p} $ | (4) |
式中:
式(4)中函数
鉴于实验仿真的考虑,现将熵函数进行变形:
| $\begin{array}{c} \dfrac{1}{q}\ln \left( {{{\rm{e}}^{q{f_i}\left( x \right)}} + {{\rm{e}}^{ - q{f_i}\left( x \right)}}} \right) = \dfrac{1}{q}\ln \left[ {{{\rm{e}}^{q|{f_i}\left( x \right)|}}\left( {1 + {{\rm{e}}^{ - 2q|{f_i}\left( x \right)|}}} \right)} \right] =\\ {\rm{ }} |{f_i}\left( x \right)| + \dfrac{1}{q}\ln \left( {1 + {{\rm{e}}^{ - 2q|{f_i}\left( x \right)|}}} \right) \\ \end{array} $ |
则该熵函数的偏导为
| $\begin{array}{c} {\nabla _x}F\left( {x,q} \right) =\\ {\rm{ }} {\displaystyle\sum\limits_{i = 1}^n {p\left[ {\dfrac{1}{q}\ln \left( {{{\rm{e}}^{q{f_i}\left( x \right)}} + {{\rm{e}}^{ - q{f_i}\left( x \right)}}} \right)} \right]} ^{p - 1}} \dfrac{{{{\rm{e}}^{q{f_i}\left( x \right)}} - {{\rm{e}}^{ - q{f_i}\left( x \right)}}}}{{{{\rm{e}}^{q{f_i}\left( x \right)}} + {{\rm{e}}^{ - q{f_i}\left( x \right)}}}}{\nabla _x}{f_i}\left( x \right) =\\ {\rm{ }} {\displaystyle\sum\limits_{i = 1}^n {p\left[ {|{f_i}\left( x \right)| + \frac{1}{q}\ln \left( {1 + {{\rm{e}}^{ - 2q|{f_i}\left( x \right)|}}} \right)} \right]} ^{p - 1}} \dfrac{{1 - {{\rm{e}}^{ - 2q{f_i}\left( x \right)}}}}{{1 + {{\rm{e}}^{ - 2q{f_i}\left( x \right)}}}}{\nabla _x}{f_i}\left( x \right) \\ \end{array} $ |
基于上述理论,可以得到基于熵函数的重构算法,算法模型为
| ${L_p}\left( {{{x}},\lambda ,q} \right) = \frac{1}{2}\left\| {{{\varPhi x}} - {{y}}} \right\|_2^2 + \lambda F\left( {{{x}},q} \right)$ |
所以,基于一种熵函数的重构算法(reconstruction algorithm based on maximum entropy algorithm, MEA-RA)的求解步骤如下所示:
输入 压缩后的信号
输出 重构目标信号
初始化
1) 循环:
a) 通过求解式(5)来更新
| $\begin{array}{c} p{\left[ {|{{{x}}^{\left( {t + 1} \right)}}| + \dfrac{1}{q}\ln \left( {1 + {{\rm{e}}^{ - 2q|{{{x}}^{\left( {t + 1} \right)}}|}}} \right)} \right]^{p - 1}} \dfrac{{1 - {{\rm{e}}^{ - 2q{f_i}\left( x \right)}}{{{x}}^{\left( {t + 1} \right)}}}}{{1 + {{\rm{e}}^{ - 2q{{{x}}^{\left( {t + 1} \right)}}}}}}+ \\ {\rm{ }} \dfrac{1}{\lambda }{{{\varPhi }}^{\rm{T}}}\left( {{{\varPhi }}{{{x}}^{\left( t \right)}} - {{y}}} \right) = 0 \\ \end{array} $ | (5) |
b) 更新
c) 判断是否满足迭代终止条件:
2) 得到稀疏目标信号的解:
为了更好地体现重构效果,本文将上述方法与其他相关算法进行对比,来充分说明本文所提算法的优越性。评价的标准是峰值信噪比(peak signal to noise ratio, PSNR)、结构相似性(structural Similarity,SSIM)和所需时间t。具体分析与讨论下面将会介绍。
首先,本节与MEA-RA算法对比的是基于Lq最小化的稳定稀疏逼近(stable sparse approximation based on Lq minimization, StSALq)算法[15]、复合三角函数零空间重加权近似

|
Download:
|
| 图 1 Peppers原图 | |
去除噪声恢复后的效果图如图2~4所示,从图2~4中可以看出,当CR大于0.5时,所有算法都可以很好地恢复出原始的图片,尤其是MEA-RA算法的效果最好,但是其他4种算法恢复的图像仍然会有一些小的噪点。在CR等于0.4的时候,效果更加明显。尤其是StSALq算法,去除噪声后恢复的图像出现了一些线状的噪声,而且边缘地方恢复的效果也不是很好。而MEA-RA算法仍然可以恢复出很好的效果,并且没有明显的噪声。这些分析都是从主观上进行的,下面将从客观数据上对其进行更充分的说明。

|
Download:
|
| 图 2 压缩比CR=0.4,5种重构算法的恢复效果 | |

|
Download:
|
| 图 3 压缩比CR=0.5,5种重构算法的恢复效果 | |

|
Download:
|
| 图 4 压缩比CR=0.6,5种重构算法的恢复效果 | |
其次,本文将从PSNR和SSIM 2方面进行考虑,如表1所示。MEA-RA算法在PSNR方面,值是最大的,而且比其他最好的算法在数值上提升了至少1 dB以上,说明恢复的效果也是最好的。在SSIM方面,该算法也是最接近1的,也就说明本文所提算法恢复后的图像和原图像基本上是一致的。另外4种算法,相对来说没有那么理想,尤其是在压缩比比较低的时候,StSALq算法恢复的PSNR值只有21.811 dB、CTNRAL0算法只有24.989 dB,
|
|
表 1 不同算法在不同CR时恢复的图像的PSNR、SSIM值 |
最后,从运算所需时间上进行分析,如表2所示。MEA-RA算法的运行时间是相对最短的,其他几种算法的时间都比较长,尤其是StSALq算法、CTNRAL0算法和
|
|
表 2 不同算法在CR不同时去噪恢复所需要的时间 |
综上所述,在对比的几种算法中,MEA-RA算法的PSNR和SSIM值最高,在PSNR值上至少提升了1 dB,并且运行时间也是最短的,是这几种算法中最好的。但是仍然存在需要改进的地方,下节会对其进行进一步分析,在时间上进行进一步优化。
2 基于ADMM改进的去噪方法由第1节可以知道,在比较的几种重构算法中,MEA-RA算法的重构效果最好,并且时间也是相对比较少的。为了实现更快更好的去噪重构效果,本文将该算法与ADMM算法[19-20]进行结合,提出了一种更快而且图像去噪重构效果更好的算法。
所提算法是一种基于ADMM改进的重构算法。主要是将MEA-RA算法和ADMM算法进行结合,利用ADMM算法实现MEA-RA,所以提出一种速度更快的新算法——基于ADMM改进的MEA-RA算法(improved MEA-RA algorithm based on ADMM, MEA-RA-ADMM)。
该算法的具体实现步骤如下:
输入 压缩后的信号
输出 重构目标信号
初始化
1) 外部循环:
a) 内部循环:
| $ {{{x}}^{\left( {k + 1} \right)}} = \arg \mathop {\min }\limits_{{x}} \frac{1}{2}\left\| {{{y}} - {{\varPhi }}{{{x}}^{\left( k \right)}}} \right\|_2^2{\rm{ + }}\frac{\lambda }{{\rm{2}}}\left\| {{{{x}}^{\left( k \right)}} - \left( {{{{v}}^{\left( k \right)}} - {{{u}}^{\left( k \right)}}} \right)} \right\|_2^2 $ |
| $ {{{v}}^{\left( {k + 1} \right)}} = {\rm{BM3D}}\left( {1,\frac{{{y}}}{{\max \left( {{y}} \right)}},\sigma } \right) $ |
式中:BM3D是一种去噪模型;
| $ {{{u}}^{\left( {k + 1} \right)}} = {{{u}}^{\left( k \right)}} - \left( {{{{x}}^{\left( {k + 1} \right)}} - {{{v}}^{\left( {k + 1} \right)}}} \right) $ |
b) 将a)得到的结果赋值给
| $\begin{array}{c} p{\left[ {|{{{x}}^{\left( {t + 1} \right)}}| + \dfrac{1}{q}\ln \left( {1 + {{\rm{e}}^{ - 2q|{{{x}}^{\left( {t + 1} \right)}}|}}} \right)} \right]^{p - 1}} \dfrac{{1 - {{\rm{e}}^{ - 2q{f_i}\left( x \right)}}{{{x}}^{\left( {t + 1} \right)}}}}{{1 + {{\rm{e}}^{ - 2q{{{x}}^{\left( {t + 1} \right)}}}}}}+ \\ {\rm{ }} \dfrac{1}{\lambda }{{{\varPhi }}^{\rm{T}}}\left( {{{\varPhi }}{{{x}}^{\left( t \right)}} - {{y}}} \right) = 0 \\ \end{array} $ | (6) |
c) 更新
d) 判断是否满足迭代终止条件:
2) 得到稀疏目标信号的解:
本文由于涉及到
|
Download:
|
|
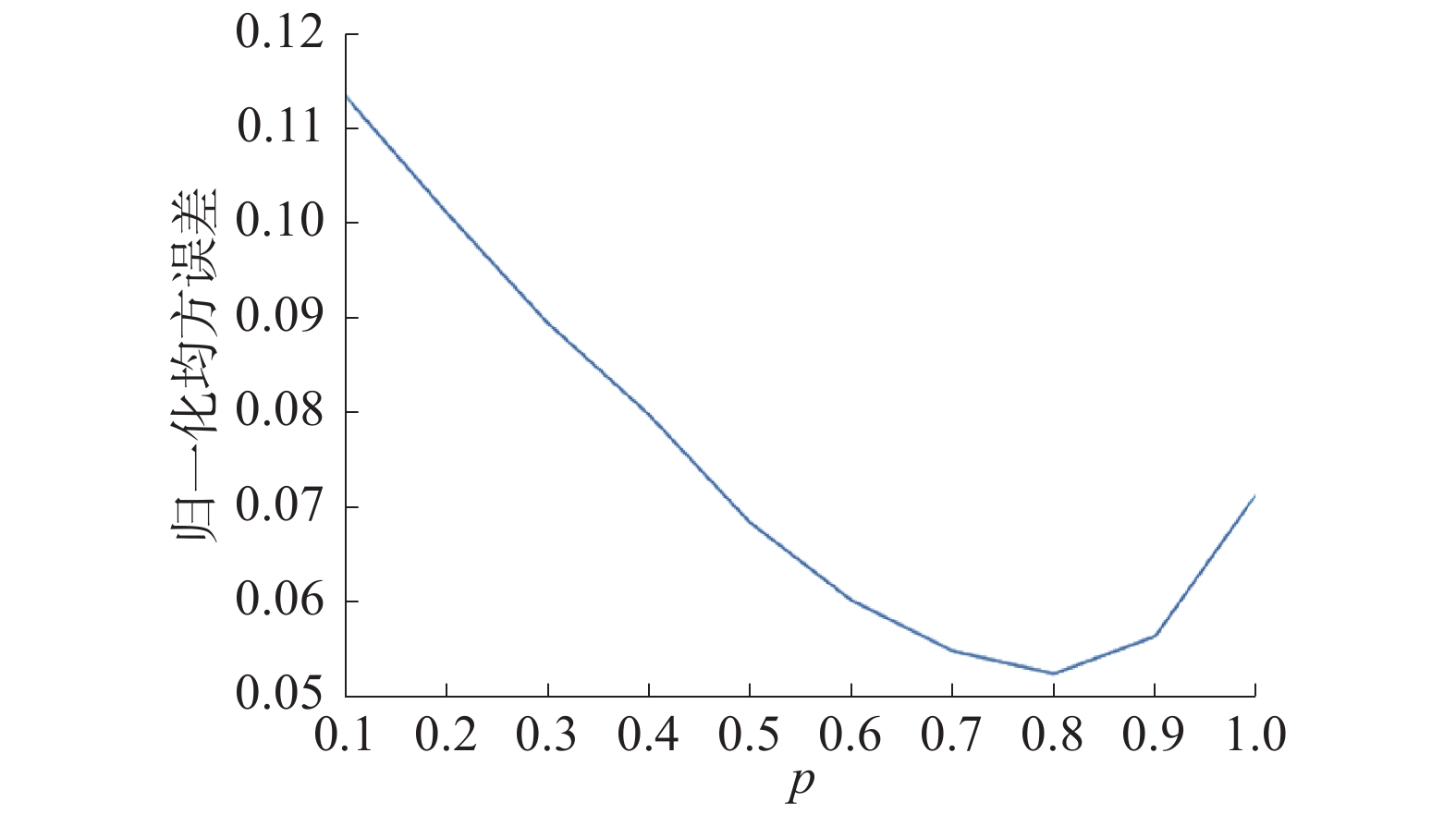
图 5 范数
|
|
本算法首先调节熵函数替换
|
Download:
|
|
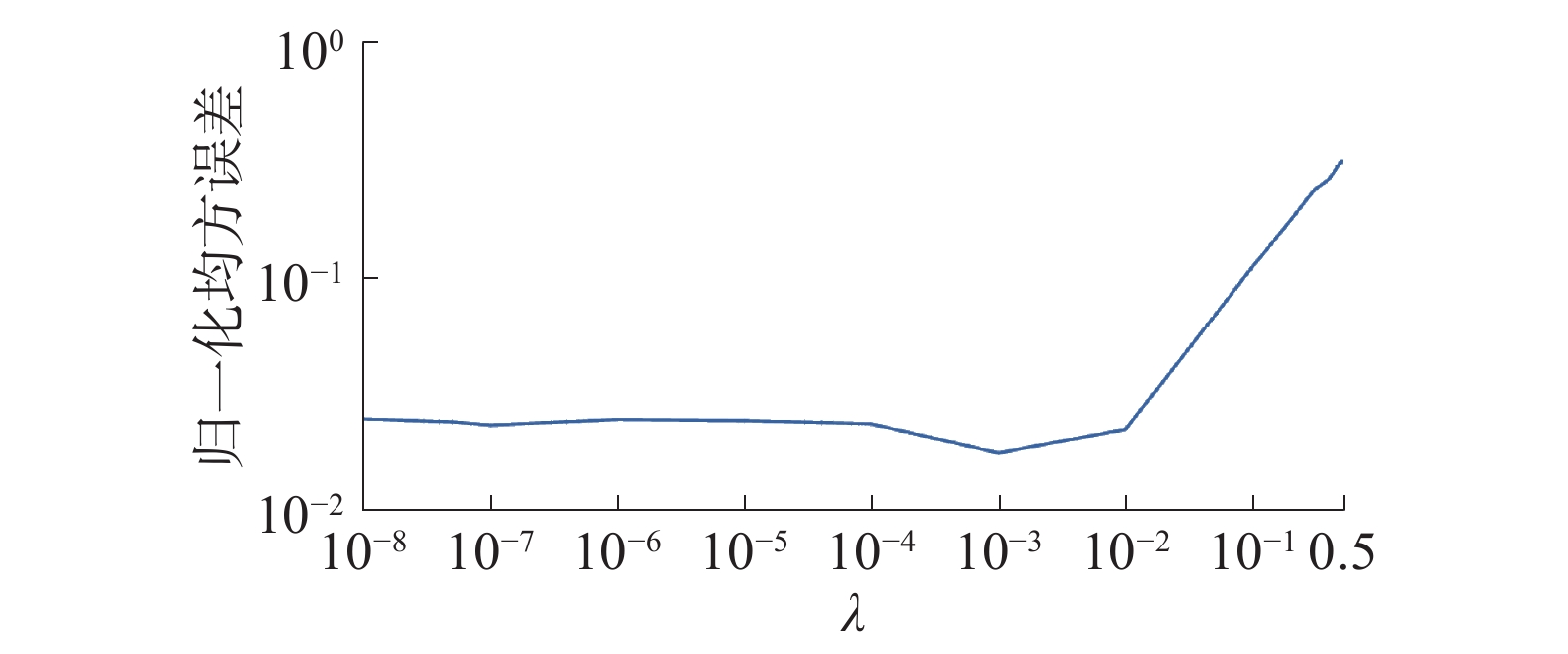
图 6 参数
|
|
本文以下面2幅图像作为实验对象,如图7所示。主要考虑高斯噪声对信号的影响。与MEA-RA-ADMM对比的算法选择MEA-RA和基于ADMM的BM3D算法2种。选择的一个依据是改进之前,通过实验可以知道这种改进方式是否有用、是否可以提升算法的性能;选择的另一个依据是该算法是典型的算法,BM3D是去噪效果很好的一种去噪算法,将其应用到ADMM,更有一定的说服力。所以,选择了这2种算法。接下来,将添加不同噪声强度的高斯信号,并且在不同压缩比下分别对这3种算法进行对比,并分析实验的结果。

|
Download:
|
| 图 7 Lenna和Parrots原图 | |
首先以Lenna图为目标图,如图8~11所示为3种算法在压缩比为0.6、添加噪声强度分别为0.07、0.09、0.10、0.20等4种情况下去噪的恢复效果图以及残差图。从图8~11中可以看出,MEA-RA-ADMM性能最好,恢复的图像最接近原始图像。而其他2种算法都存在一些噪声,尤其是帽子和头发部分。另外,随着噪声的增加,去除噪声后恢复的效果也在逐渐变差,但是MEA-RA-ADMM仍然可以恢复很好的效果。

|
Download:
|
| 图 8 噪声强度为0.07、压缩比为0.6,3种算法的去噪恢复图以及残差图 | |

|
Download:
|
| 图 9 噪声强度为0.09、压缩比为0.6,3种算法的去噪恢复图以及残差图 | |

|
Download:
|
| 图 10 噪声强度为0.10、压缩比为0.6,3种算法的去噪恢复图以及残差图 | |

|
Download:
|
| 图 11 噪声强度为0.20、压缩比为0.6,3种算法的去噪恢复图以及残差图 | |
图8~11中上方的图为3种算法的去噪恢复图,下方的图为残差图。上面仅仅是主观评价,为了使结果更具有说服力,本文从残差值、峰值信噪比(PSNR)、归一化均方误差(NMSE)和时间上分别进行比较,其中NMSE和SSIM均是对原图与恢复效果图误差的评估。
首先,从残差上进行分析和比较3种重构算法去除噪声后的恢复效果。如图8~11和表3所示,本文所提算法是三者中残差最小的,从残差图中基本看不到噪点。另外2种算法噪点相对比较多,也可以说明本文所提算法是最优的。
|
|
表 3 3种算法在不同压缩比(CR)、不同噪声强度(q)下的残差值 |
其次,从PSNR和NMSE 2方面进行分析和对比。从表3、4可以知道,本文所提算法MEA-RA-ADMM的PSNR是最大的,并且NMSE是最小的。从数值上看,本文所提算法在PSNR上比单纯的MEA-RA算法提升了1.3 dB,比基于ADMM的BM3D算法提升更多;在NMSE上比单纯的MEA算法降低了10%。所以本文所提MEA-RA-ADMM是一种恢复效果很好的重构算法。
|
|
表 4 3种算法在不同压缩比(CR)、不同噪声强度(q)下的PSNR、NMSE |
最后,从时间上进行比较。Lenna图和Parrots图在不同压缩比、不同噪声强度下的运行时间如表5所示。相对MEA-RA算法,本文所提MEA-RA-ADMM算法在噪声强度小于0.2时运行时间会有提升,这说明结合ADMM算法具有减少时间消耗的作用。虽然相对于ADMM算法,时间消耗大一些,但是若达到相同的去噪效果,时间也是最低的。而且在之前的分析可以看出,相对于MEA-RA算法,本文算法不但在PSNR上有一定的提升,而且也缩短了时间上的开销,进一步提升了该算法的图像去噪重构的效果。
|
|
表 5 3种算法在不同压缩比(CR)、不同噪声强度(q)下的运行时间t |
本文针对图像去噪的恢复效果较差以及恢复时间较长的问题,提出了解决方法。
1)首先根据熵函数提出了一种新的重构算法,即基于熵函数的重构算法——MEA-RA算法。
2)然后进行实验对比,对比的算法也都是与此相关的一些算法,经过仿真结果可以知道MEA-RA 算法具有很好的性能,而且时间复杂度相对也比较低。
3)为了进一步降低时间开销,本文将MEA-RA算法与ADMM算法进行结合,提出了一种新的基于ADMM的图像去噪算法——MEA-RA-ADMM算法。
4)对新提算法进行仿真分析,结果说明MEA-RA-ADMM是一个很好的算法,在PSNR值上有至少1 dB的提升,而且在时间上,当噪声强度小于0.2的时候,也得到了一定的提升。本文所提算法具有一定的工程实践价值。
| [1] |
张倩. 全变分高阶模型的快速去噪算法[J]. 电子世界, 2016(13): 165-166.
( 0) 0)
|
| [2] |
江唯奕. 数字图像去噪算法原理及应用[J]. 电子制作, 2019(6): 26-28. ( 0) 0)
|
| [3] |
YIN X, WANG L, YUE H, et al. A new nonconvex regularized sparse reconstruction algorithm compressed sensing magnetic resonance image recovery[J]. Progress in electromagnetics research C, 2018, 87: 241-253. DOI:10.2528/PIERC18072101 ( 0) 0)
|
| [4] |
DONOHO D L. Compressed sensing[J]. IEEE transactions on information theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 ( 0) 0)
|
| [5] |
戴琼海, 付长军, 季向阳. 压缩感知研究[J]. 计算机学报, 2011(3): 3-12. ( 0) 0)
|
| [6] |
焦李成, 杨淑媛, 刘芳, 等. 压缩感知回顾与展望[J]. 电子学报, 2011(7): 1651-1662. ( 0) 0)
|
| [7] |
TSAIG Y, DONOHO D L. Extensions of compressed sensing[J]. Signal processing, 2006(3): 549-571. ( 0) 0)
|
| [8] |
BOYD, STEPHEN, PARIKH, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and trends in machine learning, 2010, 3(1): 1-122. ( 0) 0)
|
| [9] |
WANG Yu , YIN Wotao , ZENG Jinshan .. Global convergence of ADMM in nonconvex nonsmooth optimization[J]. Journal of entific computing, 2018: 1-35. ( 0) 0)
|
| [10] |
HE B S, TAO M, YUAN X M. Alternating direction method with Gaussian back substitution for separable convex programming[J]. SIAM journal on optimization, 2012, 22: 313-340. DOI:10.1137/110822347 ( 0) 0)
|
| [11] |
CHEN C H, HE B S, YUAN X M. Matrix completion via an altemating direction method[J]. SIMA journal of numerical analysis, 2012, 32: 227-245. DOI:10.1093/imanum/drq039 ( 0) 0)
|
| [12] |
王天荆, 杨震. 非线性Lp问题的极大熵方法[J]. 南京工业大学学报(自然科学版), 2008, 30(1): 59-62. ( 0) 0)
|
| [13] |
ZHENG Le, ARIAN MALEKI, WENG Haolei, et al. Does lp-minimization outperform l1-minimization?
[J]. IEEE transactions on information theory, 2017, 63(11): 6896. ( 0) 0)
|
| [14] |
TANG G, LU G, WANG Z, et al. Robust tensor principal component analysis by lp-norm for image analysis[C]// 2016 2nd IEEE International Conference on Computer and Communications (ICCC). Chengdu, China. IEEE, 2016: 751–756.
( 0) 0)
|
| [15] |
SAAB R, CHARTRAND R, YILMAZ O. Stable sparse approximations via nonconvex optimization[C]// 2008 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE Transactions on Signal Processing. Las Vegas, Nevada, U.S.A, 2008: 3885–3888.
( 0) 0)
|
| [16] |
ZHANG C, HAO D, HOU C, et al. A new approach for sparse signal recovery in compressed sensing based on minimizing composite trigonometric function[J]. IEEE ACCESS, 2018, 6: 44894-44904. DOI:10.1109/ACCESS.2018.2855958 ( 0) 0)
|
| [17] |
PANT J K, LU W, ANTONIOU A. New improved algorithms for compressive sensing based on Lp-norm[J]. IEEE transactions circuits and systems II: express briefs, 2014, 3: 198-202. ( 0) 0)
|
| [18] |
RANGAN S. Generalized approximate message passing for estimation with random linear mixing[C]// In Proc IEEE Int Symp Inform Theory. Saint Petersburg, Russia, 2011: 2174–2178.
( 0) 0)
|
| [19] |
CHAN S H. Performance analysis of plug-and-play ADMM: a graph signal processing perspective[J]. IEEE transactions on computational Imaging, 2019, 5(2): 274-286. ( 0) 0)
|
| [20] |
BUZZARD G T, CHAN S H, SREEHARI S, et al. Plug-and-play unplugged: optimization free reconstruction using consensus equilibrium[J]. SIAM journal on imaging science, 2017, 11(3): 2001-2020. ( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


