分辨率是遥感图像的重要特征，高分辨率的遥感图像对后续目标识别的精度有重要影响。受到客观条件和硬件设备的限制，实际获取的遥感图像分辨率受到一定的影响。图像超分辨重建技术基于信号处理和模式识别理论，可以对低分辨率图像进行处理以获取更高分辨率的图像。

图像超分辨重建方法按原理大致可分为3类：基于重建模型的方法、基于插值的方法和基于学习的方法。基于重建模型的方法^[1-3]多用于多帧超分辨，多帧低分辨率图像间的运动估计误差会对超分辨效果产生较大影响。基于插值的方法^[4-6]可以快速地对单帧图像进行超分辨，缺点是不易加入合适的先验信息。为克服以上缺点，机器学习理论广泛引入到超分辨领域，使基于学习的超分辨方法取得了巨大的进展。该类方法基于神经网络或者冗余字典进行超分辨重建。基于神经网络的学习方法需要按照经验设定较多参数，训练需要较大的运算量，并且存在泛化能力问题^[7-9]。基于冗余字典的方法以稀疏表示和压缩感知作为理论基础，为求解图像超分辨重建这类典型的欠定问题提供了新的思路和方法，并且取得了较好的超分辨效果。文献[10-12]通过学习大量图像建立冗余字典，然后稀疏求解得到超分辨重建图像。由于建立的是单一字典，要求训练图像与要超分辨的图像具有一定的纹理相关性和算法的泛化能力。文献[13-14]将训练图像限定在要超分辨的图像本身，虽然一定程度上克服了上述问题，但字典是一次性的，并且低分辨率图像的纹理状况会对超分辨效果有一定的影响，比如过度模糊图像等。

由于图像纹理的复杂多样性，上述利用单一字典表示具有很大局限性。基于多字典学习将会改进超分辨的性能。文献[15-16]对学习的字典对进行聚类，分解成多个子字典，聚类的性能以及低分辨率块搜索所属类别的误差都将影响超分辨的效果。文献[17]按照图像块梯度大小将图像块分类，每类分别建立对应字典。该方法只根据图像块纹理复杂性进行分类而没有考虑图像纹理的方向性。文献[18]对每个图像块提取多个纹理，形成不同的子字典；超分辨重建阶段对每个低分辨率图像块都进行多次稀疏求解，提取纹理数目较多时计算量较大。由于小波变换可以将图像分解为多个频带且具有多分辨特性。但图像在小波域一般只能分解成4个频带，具有一定的局限性和改进空间^[19]。Contourlet变换是小波变换在二维图像的推广，相比小波具有更多良好的性能，在Contourlet域可以根据纹理方向建立更多的字典，取得更好的超分辨效果。

本文利用Contourlet变换将具有复杂多样的纹理遥感图像高频部分分解为多个不同的频带，对应建立多个残余字典来表示。基于压缩感知理论在不同频带分别进行稀疏求解，获得超分辨重建遥感图像。

1 压缩感知和Contourlet 变换理论基础 1.1 压缩感知

假定信号 $x \in {{\bf{R}}^N}$ ， $y = {{\varPhi }}x$ 为对该信号的一次测量，其中 $\varPhi \in {{\bf{R}}^{M \times N}}$ 为测量算子。令 $x = {{\varPsi }}a$ ，其中 ${{\varPsi }} \in {{\bf{R}}^{N \times N}}$ 为固定基或冗余字典。若 ${\left\| a \right\|_0} = S < N$ ，则称信号 $x$ 相对于 ${{\varPsi }}$ 是 $S$ 稀疏的，并且 ${{\varPhi }}$ 与 ${{\varPsi }}$ 具有一定的相干性。压缩感知理论^[17-19]认为，在满足一定条件下，可以通过较少的测量信号 $y$ 完美重建原始信号 $x$ 。完美重建所需的测量数目与 ${{\varPhi }}$ 和 ${{\varPsi }}$ 的相干性、 $x$ 的稀疏性密切相关。

1.2 Contourlet变换

Contourlet变换是小波变换在二维图像空间中的扩展，保持了小波变换的多尺度和时频定位功能，同时具有捕捉图像多方向纹理的能力，可以更好地表示图像的二维几何结构^[20]。Contourlet变换分2个阶段：子带分解和方向分解。子带分解利用Laplacian金字塔分解成多级频带。方向分解则利用方向滤波器组(the directional filter bank,DFB)将二维图像分解成整数次幂个锲形的方向频带。这2个分解阶段是相互独立的，因此，每个级别可根据需要分解成2的任意整数次幂个方向频带。

2 多尺度压缩感知超分辨重建

利用单字典表达复杂纹理图像有很大的局限性，利用多字典表达图像将会获得更好的效果。Contourlet变换可以将图像分解成多个不同纹理方向的频带，并且具有多分辨特性。本文将利用多级Contourlet变换建立多字典，基于压缩感知理论求解面向遥感图像的超分辨重建问题。

2.1 字典学习

字典学习即冗余字典的构建。假设 ${{{X}}_b}$ 表示第 $b$ 个高分辨率图像块矢量表示，则 ${{{X}}_b}$ 可以利用冗余字典D稀疏表示，两者关系为

${{{X}}_b} = {{D}}{{{\alpha }}_b}$

式中： ${{D}} \in {{\bf{R}}^{N \times K}}$ 为冗余字典； ${{{\alpha }}_b} \in {{\bf{R}}^K}$ 为稀疏表示系数，且有 ${\left\| {{{{\alpha }}_b}} \right\|_0} = r<<K$ 。

核奇异值分解(kernel singular value decomposition, K-SVD)算法是一种有效的字典学习方法^[21]。该方法借鉴K均值聚类的思想，通过求解式(1)所示的最优化问题同时获得冗余字典 ${{D}} \in {{\bf{R}}^{N \times K}}$ 和对应的稀疏表示 ${{{\alpha }}_b} \in {{\bf{R}}^K}$ 。

$ \mathop {\min }\limits_{{{D}},{{{\alpha }}_b}} \left\{ {\left\| {{{{X}}_b} - {{D}}{{{\alpha }}_b}} \right\|_2^2} \right\},\;{\left\| {{{{\alpha }}_b}} \right\|_0} \leqslant {T_0} $

(1)

式中 ${T_0}$ 为稀疏限制的阈值。

在Contourlet域，假定将图像分解为 $M$ 个频带，在各个频带分别求解式(1)，如式(2)所示：

$ \mathop {\min }\limits_{{{{D}}_k},{{{\alpha }}_{b,k}}} \left\{ {\left\| {{{{X}}_{b,k}} - {{{D}}_k}{{{\alpha }}_{b,k}}} \right\|_2^2} \right\},\;{\left\| {{{{\alpha }}_{b,k}}} \right\|_0} \leqslant {T_0} $

(2)

式中： ${{{X}}_{b,k}}$ 表示第 $k$ 频带第 $b$ 块； ${{{D}}_k}$ 表示第 $k$ 频带对应的冗余字典； ${{{\alpha }}_{b,k}}$ 表示对应的稀疏表达， $k = 1, 2,\cdots,M$ 。

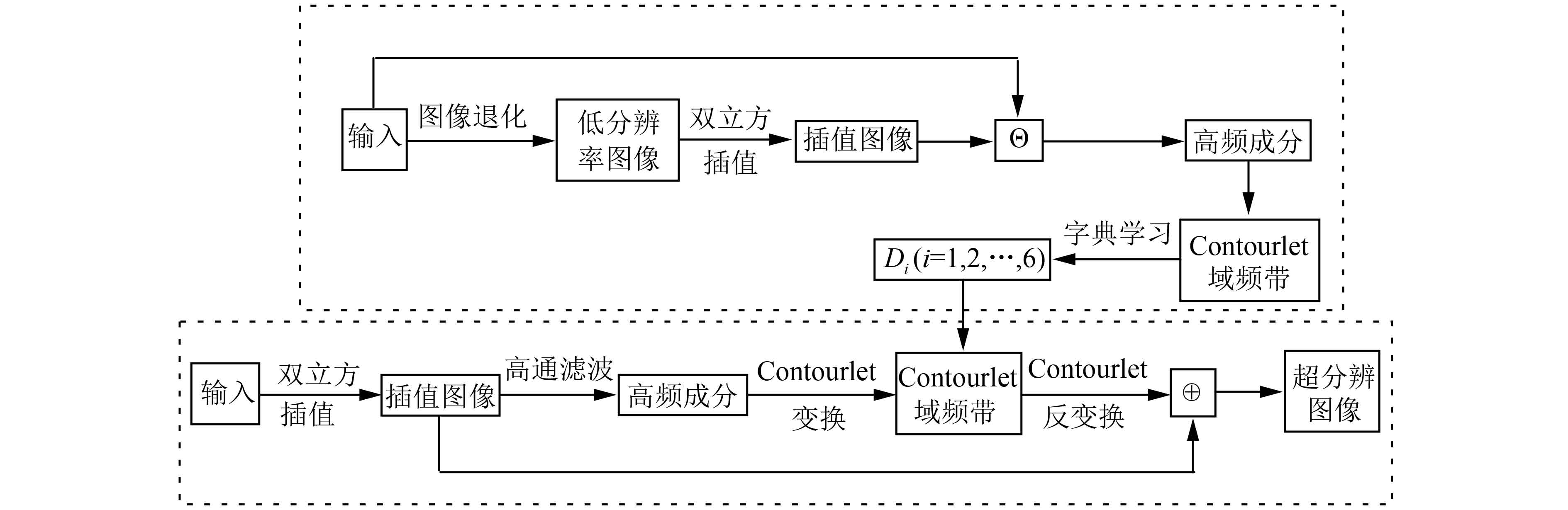
考虑到超分辨主要恢复图像的高频成分，只对高频成分进行分解并学习。字典学习与超分辨重建如图1所示。

字典学习算法步骤如下：

输入　高分辨率图像(high resolution image, HRI) ${I_H}$ 。

输出　方向频带的字典 ${D_i}(i = 1,2,\cdots,n)$ 。

1) 按照退化模型将输入高分辨率图像 ${I_H}$ 退化成低分辨率图像(low resolution image, LRI) ${I_L}$ ；

2) 对 ${I_L}$ 执行双立方插值，得到插值图像 ${I_{{\rm{BI}}}}$ ；

3) 将 ${I_H}$ 与 ${I_{{\rm{BI}}}}$ 相减，得到输入HRI的高频成分 ${I_{{\rm{HF}}}}$ ；

4) 对 ${I_{{\rm{HF}}}}$ 进行多级Contourlet变换；

5)在Contourlet域各方向频带利用K-SVD算法分别进行字典训练，获得多个方向频带的字典 ${D_i}(i = 1,2,\cdots,n)$ 。

2.2 超分辨重建

利用在Contourlet域建立的 $M$ 个冗余字典，通过稀疏编码即稀疏系数的求解可获得超分辨重建结果。在Contourlet域 $M$ 个频带分别求解如式(3)所示的最优化问题：

$ \mathop {\min }\limits_{{{{\alpha }}_{_{b,k}}}} {\left\| {{{{\alpha }}_{b,k}}} \right\|_0},\;\left\| {{{{Y}}_{b,k}} - {{{D}}_k}{{{\alpha }}_{b,k}}} \right\|_2^2 \leqslant \varepsilon $

(3)

式中： ${{{Y}}_{b,k}}$ 表示输入低分辨率图像双立方插值的高频分量第 $k$ 频带第 $b$ 块， $k = 1,2,\cdots,M$ ； ${{{D}}_k}$ 表示第 $k$ 频带对应的冗余字典； ${{{\alpha }}_{b,k}}$ 表示对应的稀疏表达。

在稀疏求解算法中，正交匹配追踪(orthogonal matching pursuit, OMP)算法是对匹配追踪(matching pursuits, MP)算法的改进，在分解的每一步对所选择的全部原子进行正交化处理，收敛速度更快^[22-23]。本文利用OMP算法进行求解。超分辨重建算法步骤如下：

输入　低分辨率图像 ${I_L}$ 。

输出　超分辨重建图像 ${I_{{\rm{SR}}}}$ 。

1) 对输入低分辨率图像 ${I_L}$ 进行双立方插值得到插值图像 ${I_{{\rm{BI}}}}$ ；

2) 对插值图像 ${I_{{\rm{BI}}}}$ 进行高通滤波，得到高频分量 ${I_{{\rm{HF}}}}$ ；

3) 对高频分量 ${I_{{\rm{HF}}}}$ 执行多级Contourlet变换；

4) 利用训练的多字典，对Contourlet域各方向频带进行稀疏编码，求取稀疏解；

5) 将步骤4)学习所得的各频带稀疏解执行Contourlet反变换，得到重建的高频分量 ${I_{{\rm{HC}}}}$ ；

6) 将 ${I_{{\rm{HC}}}}$ 与 ${I_{{\rm{BI}}}}$ 相加，得到超分辨重建图像 ${I_{{\rm{SR}}}}$ 。

3 实验结果 3.1 冗余字典参数对超分辨重建的影响

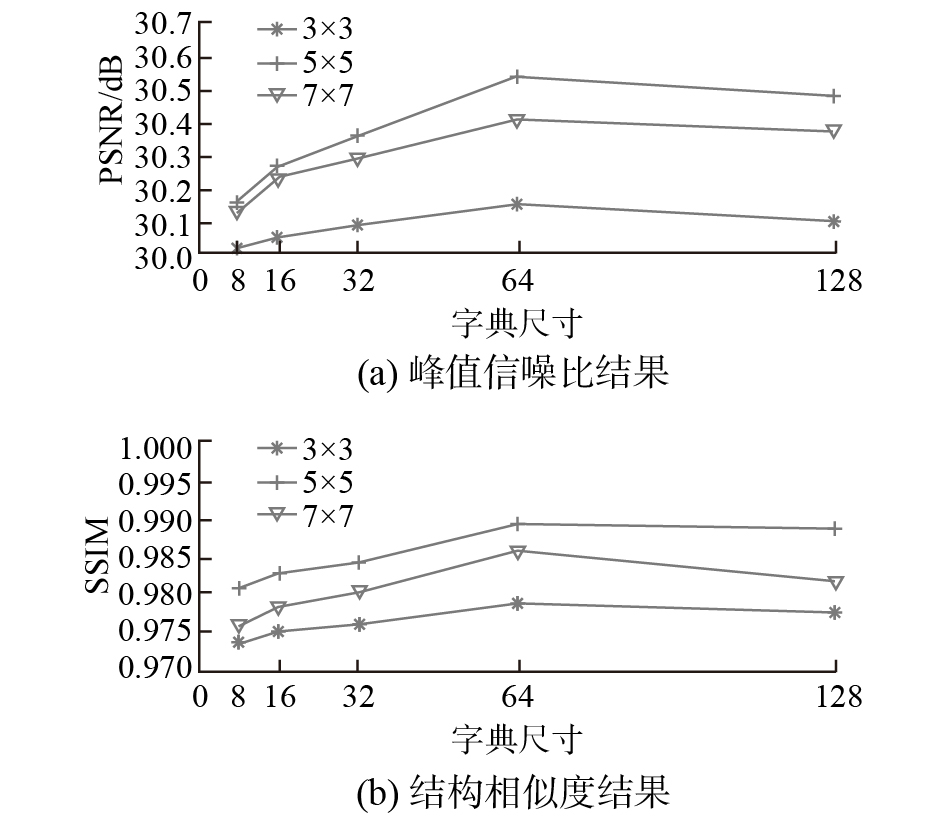
冗余字典中的原子数目和原子的尺寸是2个重要的参数，对超分辨重建的效果有一定的影响。采用实验的方法确定这2个参数。首先选取10帧1024×1024的遥感图像作为训练图像，建立Contourlet域冗余字典。单个字典的原子数目(字典尺寸)分别设置为8、16、32、64和128，而单个原子的尺寸即图像块大小分别设置为3×3、5×5和7×7，共建立15组字典。每组包含6个子字典。选取另外20帧256×256的遥感图像退化成低分辨率图像，对退化图像分别基于上述15组字典执行本文算法。基于每组冗余字典对算法结果图像求PSNR和SSIM值，并对20组参数求平均值。PSNR和SSIM的平均值如图2所示。

不考虑原子尺寸，PSNR和SSIM参数平均值都在字典尺寸为64处达到最大值。在128处反而有轻微的下降，这是由于字典尺寸过度冗余会导致过拟合以及测量矩阵和冗余字典的相干性增强，影响超分辨重建效果。因此，冗余字典的合适尺寸选取为64。另一方面，不考虑字典尺寸，PSNR和SSIM参数平均值都在原子大小为5×5处达到最大值。因此，图像块的合适尺寸应选取为5×5。

3.2 与其他方法对比分析

为证明本文算法有效性，基于建立的原子大小为5×5，数目为64的冗余字典进行超分辨重建实验，与双立方插值、文献[10]的单字典算法和文献[17]的多字典算法进行比较。选取训练图像之外的3组高分辨率遥感图像进行实验。首先对高分辨率原始遥感图像进行高斯模糊和1/2倍行列下采样，得到低分辨率图像；对低分辨率图像分别执行相应算法，得到超分辨结果图像。实验结果如图3所示，而图4给出了图3的局部纹理区域的放大结果。

可以看出，双立方插值图像比较模糊，分辨率较低。文献[10]单字典算法图像分辨率有了明显提高，而文献[17]多字典算法图像分辨率又高于单字典算法。本文算法结果图像取得了更好的超分辨效果，图像更加清晰，一些分辨不清的模糊纹理能够清楚地分辨出来。进一步进行定量分析，分别计算了峰值信噪比PSNR和结构相似度SSIM 2个评估参数，如表1、表2所示。相比文献[10]算法和文献[17]算法，本文算法的PSNR平均值分别提高6 dB、3.4 dB，SSIM平均值分别提高0.05、0.02。

4 结论

1)针对传统冗余字典表达能力有限问题，本文提出了一种基于Contourlet变换和压缩感知理论的多残余字典遥感图像超分辨重建方法。该方法将多尺度变换与压缩感知相结合，并利用残余字典代替冗余字典，在各高频子带建立对应的多个残余字典，圆满解决了遥感图像复杂纹理的训练和描述问题。

2)为获得最好的超分辨效果，通过实验验证了子残余字典和原子的最佳尺寸分别为64和5×5。

3)实验结果表明，与其他相关超分辨方法相比，本文方法取得了良好的超分辨效果，视觉质量明显改善，PSNR和SSIM都有明显提高。进一步考虑图像块之间的相关性以及更深入的理论研究是下一步的研究方向。