跳频通信是扩频通信系统中一种重要的技术手段，具有截获概率低、抗干扰性能强等优点，在军事通信中的数据链、卫星链路、战术电台等方面得到了广泛应用；此外，在民用通信系统中也发挥了重要作用^[1]。跳频通信利用伪随机序列进行频移键控，使载波频率不断跳变来完成频谱的扩展。通过这种方式，敌方在不知道我方频率跳变规律的条件下很难实施干扰，故跳频信号具有比其他通信信号更好的对抗性能。鉴于跳频信号在通信对抗上的优势，使得研究跳频信号的时频分析技术及参数估计问题迫在眉睫^[2]。目前，常用的跳频参数估计算法主要分为3类：基于自相关处理的跳频参数估计^[3]、基于时频分析的跳频参数估计^[4]和基于时频稀疏性的跳频参数估计^[5]。本文将针对时频分析类的跳频信号参数估计算法进行研究，以提高跳频信号参数估计的准确性为目标，一是对时频图进行修正，二是对现有的参数估计算法做出改进。

1 跳频信号数学模型

跳频通信系统的基本工作原理为：输入的信息在发射机中完成一次调制过程，对频率为 ${f_{\rm{c}}}$ 的载波进行调制，得到带宽为 $R$ 的调制信号；在跳频频率表中，根据跳频序列选取频率控制码，用于控制频率合成器，从而输出本振信号，此信号在不同的时隙内对应的频率不同；用本振信号对调制信号进行变频，得到射频信号，且射频信号的频率是按照跳频序列跳变的，从而得到跳频信号^[6]。

本文研究的跳频信号均是在单个跳频网台条件下，由单天线接收的跳频信号，该信号可以表示为

$x\left( t \right) = s\left( t \right) + n\left( t \right)$

式中： $s\left( t \right)$ 为跳频信号； $n\left( t \right)$ 为均值为0、方差为 ${\sigma ^2}$ 的加性高斯白噪声^[7]。

跳频信号在二维时频平面中表现为一组具有不同时移和频移的线段，这些线段在时间轴上首尾相连，在频率轴上随机跳变，其数学模型可表示为

$s\left( t \right) = \sum\limits_{k = 0}^{N - 1} {{s_k}\left( t \right)} = \sum\limits_{k = 0}^{N - 1} {{\rm{rec}}{{\rm{t}}_{{T_{\rm{h}}}}}\left( {t - k{T_{\rm{h}}} - {T_0}} \right){{\rm{e}}^{{\rm{j}}2{{\rm{{\text{π}} }}}{f_k}\left( {t - k{T_{\rm{h}}} - {T_0}} \right)}}} $

式中： ${s_k}\left( t \right)$ 表示第 $k$ 个跳频信号分量， $0 \leqslant t \leqslant T$ ； ${\rm{rec}}{{\rm{t}}_{{T_{\rm{h}}}}} \left( t \right)$ 表示宽度为 ${T_{\rm{h}}}$ 的矩形脉冲，其数学表达式为 ${\rm{rec}}{{\rm{t}}_{{T_{\rm{h}}}}}\left( t \right) =\left\{ \begin{array}{l} 1 ,\quad{t \in [0,{T_{\rm{h}}}]} \\ 0 ,\quad{{{\text{其他}}}} \end{array} \right.$ ； ${T_{\rm{h}}}$ 为跳频周期，其倒数形式表示跳频速率即 $1/{T_{\rm{h}}}$ ； ${T_0}$ 为起跳时间； ${f_k}$ 为跳变频率； $N$ 是跳变频率数； $T$ 为观测时间。

根据跳频信号的数学模型，结合Matlab对跳频信号进行仿真，仿真条件为：一次调制采用4FSK信号，其载波频率分别为 $500\;{\rm{ Hz}}$ 、 $1\;{\rm{ kHz}}$ 、 $1.5\;{\rm{ kHz}}$ 和 $2\;{\rm{ kHz}}$ ；跳频序列采用的是素数跳频序列族，序列长度为10；频率合成器产生的本振频率为 $3\sim 30\;{\rm{ kHz}}$ ，频率间隔为 $3\;{\rm{ kHz}}$ ，共10跳；跳频速率为 $250\;{\rm{ Hops/s}}$ ；跳频周期为 $0.004\;{\rm{ s}}$ ，采样频率为 $100\;{\rm{ kHz}}$ 。跳频信号对应的时域波形图及频谱图如图1所示。

2 基于时频矩的参数估计算法

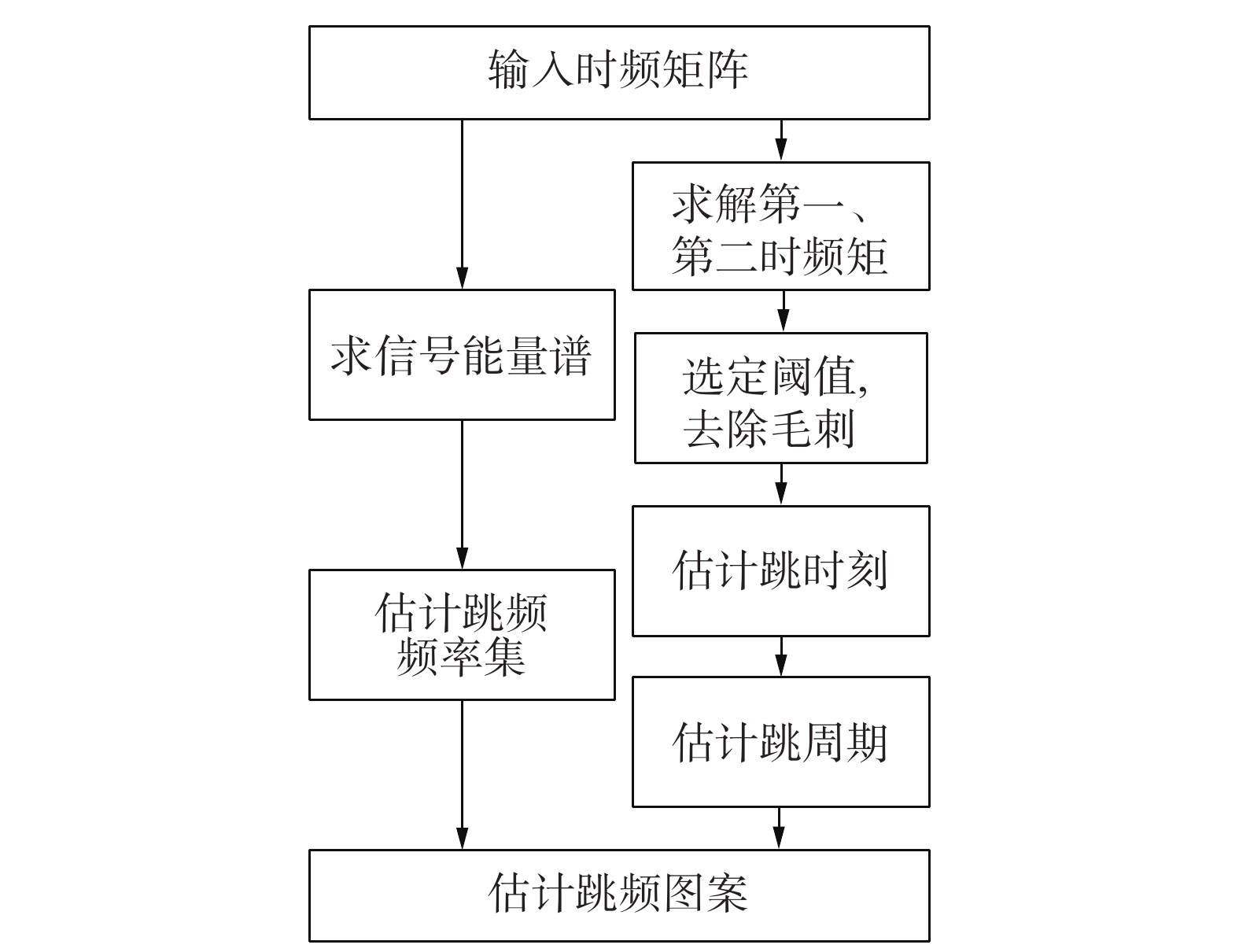
在理想情况下，通过观察跳频信号的时频图可以得到有关信号的载波频率、跳时刻、跳频周期等信息，因此时频分析类的跳频信号参数估计算法一般分为2个步骤：1)利用短时傅里叶变换（short-time Fourier transform，STFT)、平滑伪魏格纳−维尔分布(smoothed pseudo Wigner-Ville distri- bution, SPWVD)等时频分析工具得到跳频信号的时频分布以及相关时频域数据；2)基于步骤1)得到的时频图和数据来估计参数。

2.1 时频矩法

基于时频矩的参数估计算法能比较精确地估计跳频参数，该算法引入了频率矩的计算，分别利用第一频率矩和第二频率矩来估计跳频序列和跳频周期^[8]。其中第一频率矩的数学意义是频率平均值，自变量是时间 $t$ ；第二频率矩的数学意义是在每一个时刻频率方差的均值。

本文选择基本不受交叉项影响且时频聚集度高的SPWVD来分析跳频信号。根据时频图利用时频矩法来估计跳频信号参数，具体的操作步骤如下：

1)首先根据频率边缘特性得到信号能量谱，表达式为

${E_z}\left( f \right) = {\int_{t = 0}^T {{\rho _z}\left( {t,f} \right){\rm{d}}t = \left| {Z(f)} \right|} ^2}$

式中： $T$ 为跳频周期； $f$ 为频率。

2)取能量谱的峰值来估计跳频频率集

${\hat f_h} = \arg \left\{ {\mathop {\max }\limits_f \left[ {{\rm{E}}z(f)} \right]} \right\} ,\quad{1 \leqslant h \leqslant {M_h}} $

式中 ${M_h}$ 是跳频频率的总数量，在参数估计时视为已知量。

3)可以被当成瞬时频率的第一频率矩的定义式为

${f_i}\left( t \right) = \frac{{\displaystyle\int_0^T {f{\rho _z}\left( {t,f} \right){\rm{d}}f} }}{{\displaystyle\int_0^T {{\rho _z}\left( {t,f} \right){\rm{d}}f} }}$

可以被当成频率方差的第二频率矩的定义式为

$\sigma _f^2\left( t \right) = \frac{{\displaystyle\int_0^T {{f^2}{\rho _z}(t,f){\rm{d}}f} }}{{\displaystyle\int_0^T {{\rho _z}(t,f){\rm{d}}f} }} - {f_i}{\left( t \right)^2}$

4)第二频率矩的平方根值代表有效带宽，即当前跳和下一跳的频率间隔。在载波频率发生跳变的时刻,第二频率矩取得极大值，根据这个特征可以来估计跳时刻，表达式为

${\hat t_{{\rm{h}},k}} = \arg\left\{ {\max \left( {\sigma _f^2\left( t \right)} \right)} \right\} ,\quad{0 \leqslant k \leqslant {N_{\rm{h}}} - 1} $

式中 ${N_{\rm{h}}}$ 代表信号周期内的总跳数。

5)估计出跳时刻后，相邻跳时刻的时间差的平均值就是跳频周期的估计值，即

${\hat T_{{\rm{h}},k}} = {\hat t_{{\rm{h}},k}} - {\hat t_{{\rm{h}},k - 1}} ,\quad{0 \leqslant k \leqslant {N_{\rm{h}}} - 1} $

${\hat T_{\rm{h}}} = \frac{1}{{{N_{\rm{h}}}}}\sum\limits_{k = 0}^{{N_{\rm{h}}} - 1} {{{\hat T}_{{\rm{h}},k}}} $

6)估计出跳频周期后，计算一个跳频周期内的平均频率

${f_{{\rm{avg}},k}} = \frac{1}{{{{\hat T}_{{\rm{h}},k}}}}\int_{t = {{\hat t}_{{\rm{h}},k - 1}}}^{{{\hat t}_{{\rm{h}},k}}} {{f_i}(t)} {\rm{d}}t$

它与跳频频率集 ${\hat f_{\rm{h}}}$ 的绝对差为

${D_{{\rm{h}},k}} = \left| {{f_{{\rm{avg}},k}} - {{\hat f}_{\rm{h}}}} \right|$

那么，第 $k$ 跳的瞬时频率估计值为

${\hat f_{{\rm{h}},k}} = \arg \mathop {\min }\limits_k \left( {{D_{{\rm{h}},k}}} \right)$

重复此步骤，直至估计出所有跳的瞬时频率，跳频图案就被估计出来了^[9]。

2.2 改进的时频矩法

在跳频信号的实际处理过程中，会不可避免地受到噪声的影响。在这种情况下，利用时频图通过时频矩法进行跳频信号参数估计时得到的第一时频矩、第二时频矩图像，由于大量毛刺的存在，峰值变得不清晰。这样一来，基于时频矩来估计跳频参数的准确性会大大降低。

为了更准确地估计参数，本节对时频矩法做出改进。首先在求得时频矩参数后，选取阈值 $\gamma $ ，保留时频矩图像中幅值大于 $\gamma $ 的点，并将小于 $\gamma $ 的点看成时频矩图像中的无用信息，执行置零操作来去除，从而抑制噪声对时频矩的影响：

$ {\sigma }_{f}^{2}\left(t\right)=\left\{ \begin{array}{l}{\sigma }_{f}^{2}\left(t\right),\;{\sigma }_{f}^{2}>\gamma \\ 0,\;{\text{其他}}\end{array} \right.$

通过实验验证，阈值选取 $\gamma = 0.4\left[ {\max \left( {\sigma _f^2\left( t \right)} \right)} \right]$ 时效果最理想。然后根据时频矩来估计跳频参数，具体步骤见2.1节。改进后的流程图如图2所示。

2.3 基于时频图修正的改进时频矩法

在采用2.2节的改进时频矩法估计跳频参数之前，对时频图进行修正，可以进一步抑制噪声对该算法的影响。获取时频图是进行跳频信号参数估计前的关键步骤，其清晰程度与参数估计准确程度直接相关^[10]。所以为了获取清晰的时频图，提高跳频参数估计值的精确性，我们需要对经过经典的时频分析方法得到的时频图进行修正。本节将研究一种时频图修正算法——基于自适应门限的能量检测算法。利用该算法来修正时频图的基本思想是，令靠近真正载波频率的时频点保持不变，将其他时频点置零。然而，由于噪声的影响，时频图中时频点的幅值不总与真正的载波频率相关，但可以确定的是，靠近真正载波频率的时频点幅值相对较大。因此，为了提高参数估计的准确性和可靠性，这里不选择寻找幅度的最大值，而是找到一个更大的幅值范围^[11]。该种算法的流程如图3所示。

将时频图修正算法和改进时频矩法结合，基于时频图修正的改进时频矩法具体步骤如下：

1)利用SPWVD对输入的跳频信号进行时频分析，得到时频图，其定义式为^[12]

$ \begin{array}{c} {\rm{SPWV}}{{\rm{D}}_z}\left( {t,f} \right) = \\ \displaystyle\int_{ - \infty }^{ + \infty } {z\left( {t - u + \dfrac{\tau }{2}} \right){z^*}\left( {t - u - \dfrac{\tau }{2}} \right)g\left( u \right)h\left( \tau \right){{\rm{e}}^{ - {\rm{j}}2{\rm{{\text{π}} }}f\tau }}{\rm{d}}u{\rm{d}}\tau } \\ \end{array} $

式中： $z\left( t \right)$ 表示实信号 $s\left( t \right)$ 的解析形式； $g\left( u \right)$ 与 $h\left( \tau \right)$ 均为实窗函数，满足 $G\left( 0 \right) = 1$ 和 $h\left( 0 \right) = 1$ ，其中 $G\left( f \right)$ 是 $g\left( u \right)$ 的傅里叶变换^[13]。

2)利用基于自适应门限的能量检测算法对时频图进行修正，去除噪声影响对应在时频矩阵中的干扰值，保留真正信号对应在时频矩阵中的幅值；

3)根据清晰的时频图来提取时频矩参数，并选取阈值来进行处理，进一步抑制噪声的影响；

4)最后利用处理后的时频矩来估计跳频信号的跳时刻、跳频周期等参数。

3 算法仿真 3.1 时频图

在不加噪声的情况下，对输入的跳频信号求SPWVD，得到时频图，如图4所示。跳频信号源的参数如前文所述，SPWVD中时域和频域的窗函数均选用海明窗，窗长度是401个采样点。

根据清晰的时频图来提取时频矩参数，第一时频矩、第二时频矩示意图如图5所示，从图中可以看出明显的跳频信号特征。

3.2 改进前后的时频矩法对比

接下来对比改进前后的时频矩法估计跳频参数的准确性。仿真条件为：跳频信号源的相关参数见第1章，信噪比取值范围是 $0\sim 15\;{\rm{ dB}}$ ，在每个信噪比条件下蒙特卡洛仿真100次，采用相对误差来定量分析估计跳频周期的准确性，这里跳频周期估计的相对误差定义式为

${e_{{T_{\rm{h}}}}} = \frac{1}{U}\sum\limits_{u = 1}^U {\frac{{\left| {{T_{\rm{h}}} - \hat T_{\rm{h}}^{\left( u \right)}} \right|}}{{{T_{\rm{h}}}}}} $

(1)

式中： $\hat T_{\rm{h}}^{\left( u \right)}$ 表示第u次仿真时的跳频周期估计值； ${T_{\rm{h}}}$ 表示跳频周期实际值。 ${e_{{T_{\rm{h}}}}}$ 值越小则代表跳频周期估计得越准确。

改进前后的跳频周期估计误差曲线对比见图6。从图中可以看出，随着信噪比增加，2条曲线对应的跳频周期估计相对误差值均不断降低，直到趋于某个非零值，该值就是算法本身带来的误差。在相对误差值趋于稳定后，比较改进前后对应的2条相对误差曲线，可以看出：算法改进前的相对误差趋于0.1，改进后趋于0.003，这说明时频矩法经过改进后，算法本身带来的误差有所降低；在各个信噪比条件下，改进后的跳频周期估计相对误差值均比改进前对应的值小，这说明对时频矩法的改进是有效的；随着信噪比增加，改进前后对应的跳频周期估计相对误差差值在变大，这说明改进方案在信噪比比较高的条件下，效果比较显著；而在信噪比较低的条件下(小于 $0\;{\rm{ dB}}$ )，改进效果不明显。

3.3 基于时频图修正的改进时频矩法仿真

下面分别基于修正前后的SPWVD时频图使用2.2节分析的改进后的时频矩法来对跳频信号的跳频周期参数作出估计。仿真条件为：跳频信号源的相关参数同上，信噪比取值范围是 $0\sim 15\;{\rm{ dB}}$ ，在每个信噪比条件下蒙特卡洛仿真100次，采用式(1)定义的相对误差来定量分析估计跳频周期的准确性，SPWVD中时域和频域的窗函数均选用海明窗，窗长度是401个采样点。利用修正前后的SPWVD时频图分别来估计跳频周期得到的相对误差曲线如图7所示。

从图7可以看出：在相同的仿真条件下且使用同一种参数估计算法时，基于时频图修正的改进时频矩法在估计跳频周期时更准确；随着信噪比不断增加，时频图修正的性能提升效果逐渐变得不明显，但即使在高信噪比条件下2条曲线也没有重合。例如在 ${\rm{SNR}} = 15\;{\rm{dB}}$ 时，跳频周期估计相对误差值为0.003 1，而利用时频图修正的算法对应的相对误差值为0.002 2，这说明时频图修正的加入对于算法的改进是有意义的；在信噪比较低的条件下(小于 $0\;{\rm{ dB}}$ )，由于能量检测算法的弊端，时频图修正作用不大甚至可能会因为过修正产生反效果。

4 结论

本文提出了一种改进的时频矩法，通过引入门限对时频矩进行处理来实现。

1)改进后的时频矩法抑制了噪声对算法的干扰，估计跳频参数时的误差更小，在较高的信噪比条件下提升了参数估计性能。

2)基于时频图修正的改进时频矩法进一步提升了跳频参数估计精度，并结合仿真实验证明了算法的有效性。

经过Matlab仿真，本文提出的算法能够更准确地估计跳频参数，但在低信噪比条件下参数估计性能改进效果不大，仍需进一步研究。