在不断改变的战争形式中,信息化战争已取代传统战争形式成为当今战争的主流形式[1]。雷达信号分选是电子侦察的一个重要的环节,信号分选的成功与否成为电子战发挥作用的标志,甚至会影响战争的最终格局[2]。但是伴随科学技术水平的发展和提高,雷达信号分选面临的电磁环境越来越复杂多变,雷达数量和类型层出不穷,雷达信号错综复杂交叠,杂波干扰等问题。因此,如何对复杂多变的电磁环境中的错综交叠的脉冲信号进行精确和快速的分选,是当今雷达信号分选的重点和难点。
为了处理复杂电磁环境的雷达信号分选,赵贵喜等[3]将数据场引入雷达信号分选的领域,将数据场和K-means进行联合实现聚类,为雷达信号分选提供新的思路;徐赛等[4]将样本熵作为特征参数进行分选,也取得了不错的成果;Brendan J. Frey等[5]基于仿射思想提出了一种新的聚类算法,沙作金[6]将数据场结合平面变换技术实现了复杂电磁环境下的雷达信号分选。
现代电子侦察设备每秒能够接收到百万个脉冲信号,这些脉冲信号互相错杂、密集分布,直接应用于雷达信号分选会导致信号处理工作量大,浪费大量的时间,降低时效性。故而,需要对脉冲信号进行预分选处理,降低脉冲信号的密度。聚类是利用数据对象之间的相关性,可以作为预处理步骤,达到降低信号密度的目的。但是传统的如K-means聚类算法,需要人为预先设置具体的参数信息[7],且对噪声点敏感,聚类的质量受到初始人为设置参数信息的影响。为此,本文提出一种基于数据场和决策图的聚类算法。数据场主要通过计算数据对象的场强函数值累加形成势值,利用势值可以清楚快捷地识别孤立的噪声点。数据场聚类是利用势值的极值确定聚类中心和聚类数目,决策图是依据数据对象的局部密度参数值和到最近大密度点的距离值来确定聚类中心和聚类数目。由于数据场寻极值的步骤繁琐以及决策图对噪声点敏感,故将数据场和决策图做了不同程度的改进,并将两者进行联合聚类,按照数据对象的势值和到最近大密度点的距离实现聚类。
1 数据场“场”的概念最初是用来描述物质对象之间的作用力,受到场论思想的启发,李德毅院士将物理作用力引入到数据处理领域,创造性地提出数据场的概念。数据场理论认为每一个数据对象的状态值都是场中其他所有数据对象作用力的累积。类同库伦定律,数据对象的作用力与距离成反比,距离越远,作用力越小;距离越近,作用力越大。所有数据对象之间的作用力和作用范围构建了数据场[8]。
1.1 场强函数如万有引力和库仑定律,将数据场中描述数据对象之间的作用力用场强函数来表征,根据数据对象与距离的关系可以清楚地知晓,数据对象密集的地方场强函数值大,数据对象稀疏的地方场强函数值小。一般用高斯函数来描述数据对象的作用力,场强函数描述数据对象x与y点的作用力为
| ${f_y}(x) = \rho {{\rm{e}}^{ - \frac{{{d^2}(x,y)}}{{2{\sigma ^2}}}}}$ | (1) |
式中:
势函数是描述数据对象受到的场强函数的标量累加和,假设存在n个数据对象
| $F(y) = \sum\limits_{i = 1}^n {{f_y}({x_i}) = \rho \sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{d^2}(x,y)}}{{2{\sigma ^2}}}}}} } $ |
辐射因子
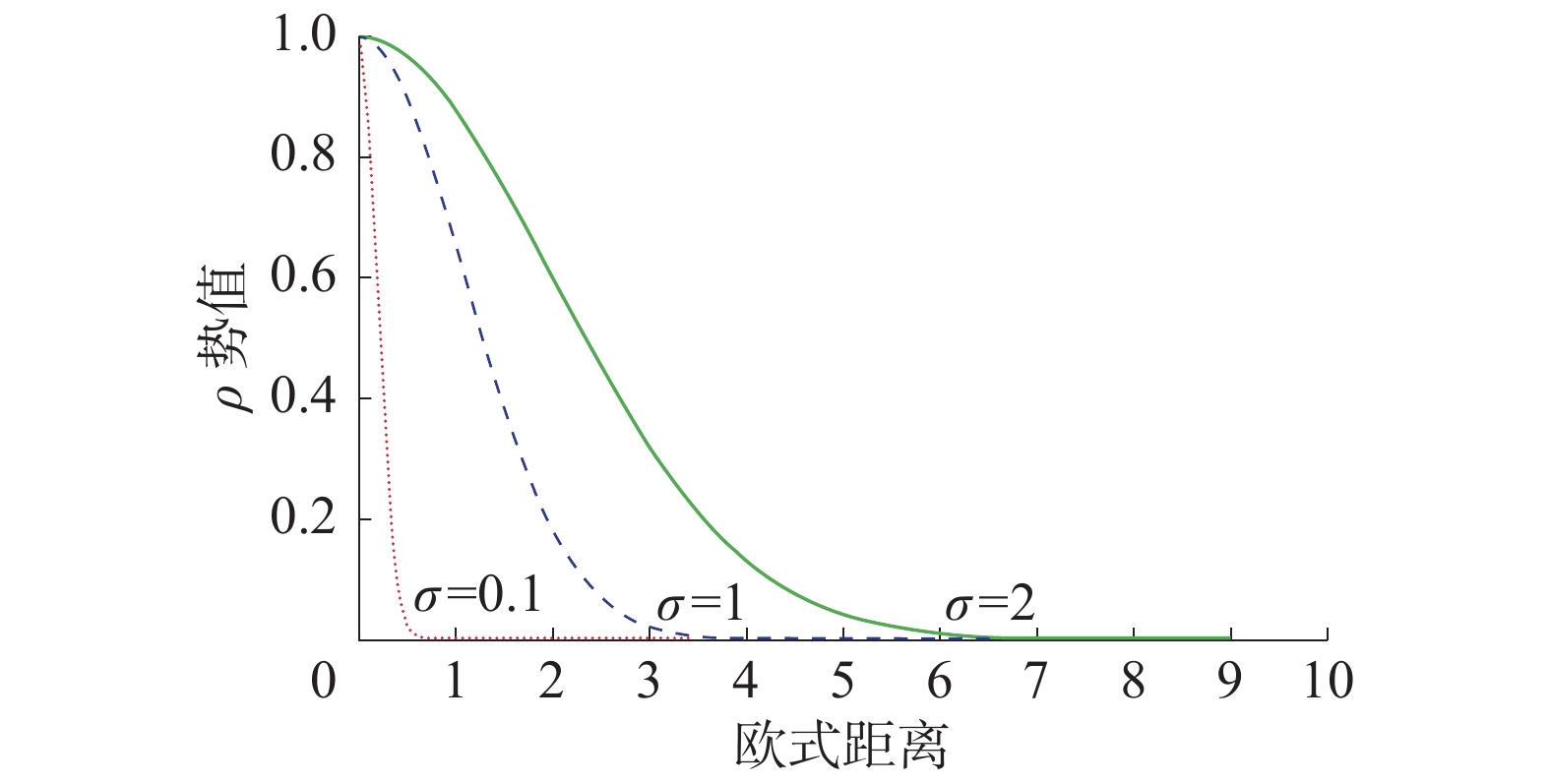
|
Download:
|
| 图 1 势值随距离关系曲线 | |
从图1中可以看出,势值随距离呈衰减趋势,且辐射因子
为了获取最优的辐射因子
| ${H_\varPsi } = - \sum\limits_{i = 1}^n {\frac{{{\varPsi _i}}}{Z}\log \Bigg(\frac{{{\varPsi _i}}}{Z}\Bigg)} $ | (2) |
式中
由式(2)可得,
数据对象的势熵与辐射因子的关系如图2所示。由图可知势熵与辐射因子的变化规律为,辐射因子
| $\mathop {\min }\limits_{\sigma > 0} H(\sigma ) = \mathop {\min }\limits_{\sigma > 0} - \sum\limits_{i = 1}^n {\frac{{{\varPsi _i}}}{Z}\log \Bigg(\frac{{{\varPsi _i}}}{Z}\Bigg)} $ | (3) |

|
Download:
|
| 图 2 势值与辐射因子关系 | |
由式(3)可以看出,选择最小势熵就是无约束的一维极值问题,可以采取斐波那契法解决此问题。假设
1)令
2)求出
3)设定
4)如果
5)
6)
7)令
8)将
对数据场进行改进就是需要对场强函数进行改进,但是基于式(1)可知,只要改进辐射因子
| ${f_y}(x) = \left\{ \begin{array}{l} {{\rm{e}}^{ - \frac{{{d^2}(x,y)}}{{2{\sigma ^2}}}}},\;d(x,y) \leqslant 3\sigma \\ 0, \; d(x,y) > 3\sigma \end{array} \right.$ | (4) |
鉴于现实电磁环境中不只存在脉冲信号,还存在大量的噪声干扰等因素,聚类的效果还会受到信号噪声等干扰因素影响。但是噪声点不是真实的脉冲信号,距离会超过聚类中心点的辐射范围,即距离值大于
按照目前存在的聚类算法,大多数都是基于数据对象之间的距离信息进行数据的簇类划分处理,但是这些算法处理数据会需要大量的工作量,消耗大量的时间。2014年,Rodriguez等[10]在基于密度聚类算法的基础上进行改进优化,提出了一种快速简捷的搜索聚类中心的聚类算法,并将该算法命名为密度峰值聚类算法。该算法主要是利用数据对象的局部密度值和到最近大密度点的距离形成决策图,再在决策图中处理参数信息得到聚类中心和聚类数目,所以该算法也被称为决策图聚类算法。决策图聚类算法可以实现自动选择聚类中心和聚类数目,且相较于其他聚类算法,决策图聚类算法需要处理的步骤少,能够快捷地得到聚类簇组,节省大量数据处理时间。
2.1 决策图基础决策图聚类算法可以实现数据对象的快速聚类,核心思想是对聚类中心或密度峰值点进行相关的理论假设:1)每个数据聚类簇组中的聚类中心拥有最大的局部密度参数值,聚类簇组中其他相邻数据点的局部密度值低于聚类中心的局部密度值[11];2)不同数据聚类簇组的聚类中心之间有着比较远的距离,即高局部密度的数据点分布比较远。基于决策图聚类算法的2个理论假设,决策图聚类算法引入了2个重要的参数变量,局部密度
假设待聚类的数据对象为
1)局部密度
| ${\rho _i} = \sum\limits_{j = 1}^N {{{\rm{e}}^{ - {{(\frac{{{d_{ij}}}}{{{d_c}}})}^2}}}} $ |
式中参数
| $0.02N = \sum\limits_{i = 1}^N {{\rho _i}} $ |
2)最近大密度点的距离
| ${\delta _i}{\rm{ = }}\left\{ \begin{array}{l} \mathop {\min }\limits_{j:{\rho _i} > {\rho _j}} ({d_{ij}}) , \; i \geqslant 2\\ \mathop {\max }\limits_j ({d_{ij}}),\; i = 1 \end{array} \right.$ |
与K-modes聚类算法类似,峰值密度聚类算法首先需要得到待聚类数据对象的聚类中心,该算法是利用
对决策图的改进主要就是要解决人为选择
| $\gamma = \rho \times \delta $ |
这样可以将变量
| $\frac{{{\gamma _i}}}{{{\gamma _{i + 1}}}} < \varepsilon ,\;\varepsilon \in (1,2)$ |
式中变量
数据场聚类所需要的步骤冗杂,需要利用势值参数进行极值判断来确定聚类中心和聚类数目,再来处理脉冲归属问题。孤立噪声点在数据场聚类中能够轻易地被识别剔除,决策图聚类只需要得到变量
1)对输入的待聚类的雷达数据的脉宽(pulse width, PW)、射频(radio frequency, RF)、波达方向(direction of arrival, DOA)进行归一化处理;
2)根据DOA参数值对待分选的脉冲信号进行排序,并计算两两脉冲信号之间的欧式距离形成距离矩阵;
3)利用斐波那契法计算得出最佳的辐射因子
4)利用距离矩阵和最佳的辐射因子
5)对势值
6)设置变量
7)对剩余的脉冲信号按照靠近原则划分到最近的聚类中。
4 聚类算法仿真 4.1 仿真条件本文选择了12部雷达辐射源信号,其中包括常规雷达信号、参差雷达信号、抖动雷达信号、脉组捷变和脉间捷变雷达信号,具体的参数信息如表1所示,图3是待聚类的雷达信号。其中,设置脉宽的精度为1 μs,载频的精度为1 MHz,方位角的精度为1°[12]。为了统一待聚类的数据对象之间各个参数的维度量纲,采用min-max标准将数据对象进行归一化处理,结果为
| ${x_i}' = \frac{{{x_i} - \min (D)}}{{\max (D) - \min(D)}}$ |
|
|
表 1 雷达参数设置表 |
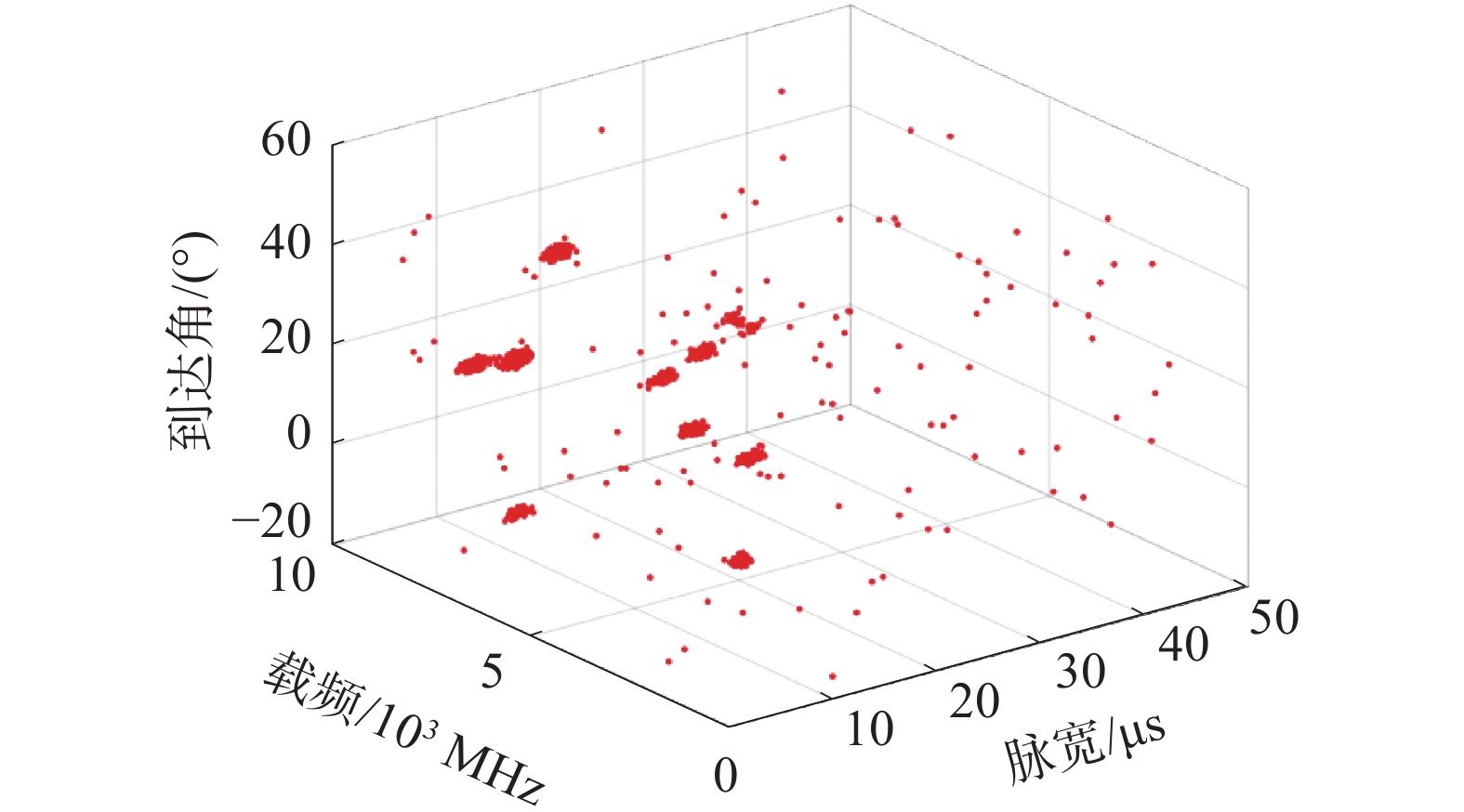
|
Download:
|
| 图 3 待聚类的雷达信号 | |
实验1 为了验证数据场聚类算法的正确性,对算法进行仿真验证。用Matlab模拟实际环境中的雷达信号,根据表1的参数信息生成对应的雷达信号并进行数据场聚类,得到的聚类中心如表2所示。
|
|
表 2 聚类中心参数表 |
实验2 利用式(1)、(4)不同的场强函数重新计算势函数,按照数据场聚类得出每个簇组的聚类中心,并与理论值进行比较,得出不同场强函数下的聚类算法的误差,并进行500次蒙特卡洛实验,对误差处理得到方差值,图4是不同场强函数对应的聚类误差图。
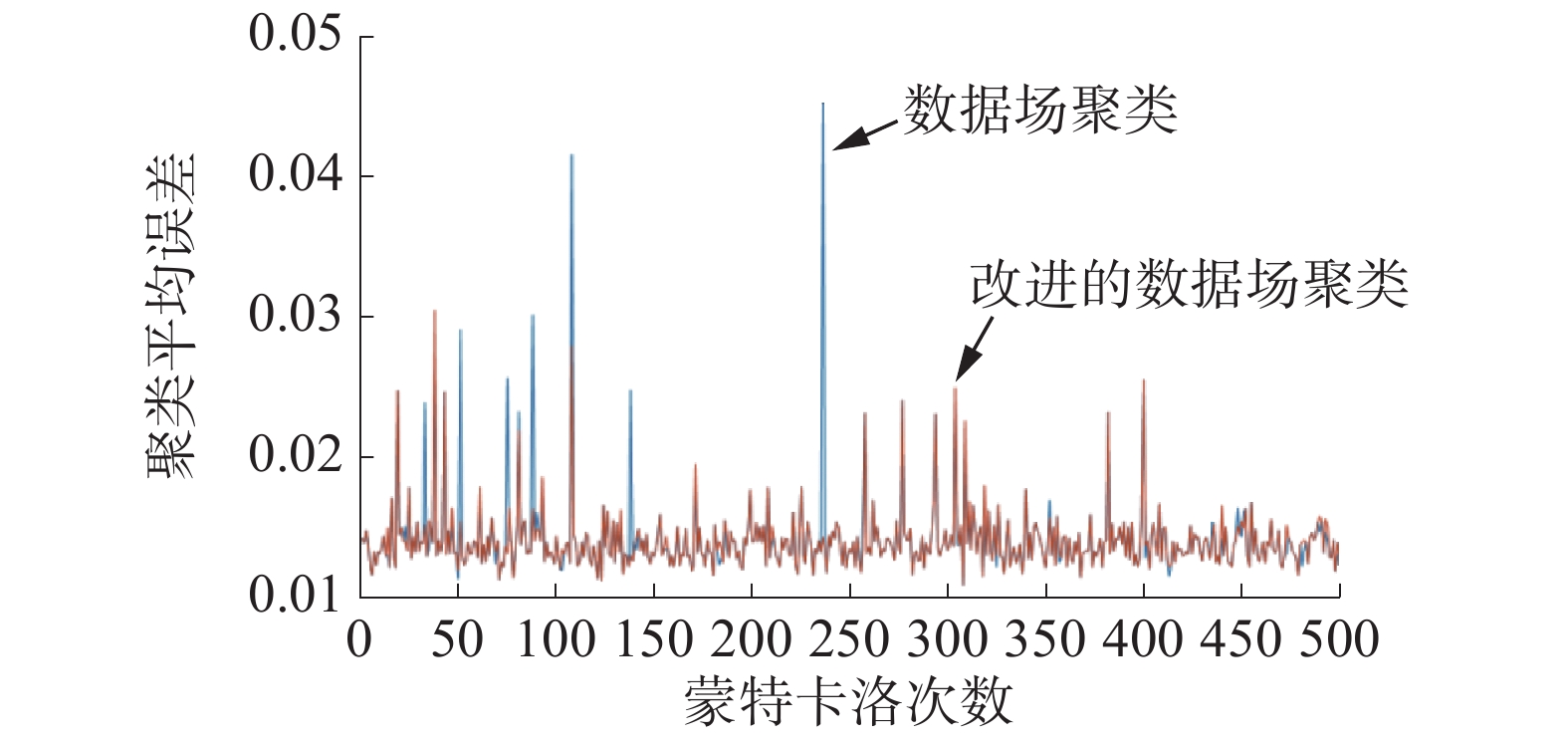
|
Download:
|
| 图 4 数据场改进前后平均误差对比 | |
仿真结果显示改进的数据场聚类的平均误差要比数据场聚类的误差小,虽然误差值没有得到大幅度改进,但是改进的数据场聚类算法的方差值小,聚类效果稳定,分析图中出现几次误差远大于平均误差的原因是聚类数目比真实聚类数目多,造成同一组数据被分到不同的聚类簇组中,改进的数据场明显减少了这些现象,同时,改进的数据场减少了运算步骤,降低时间的复杂性,加快了聚类的效果,所以改进后的数据场对数据对象聚类的效果会更加好。
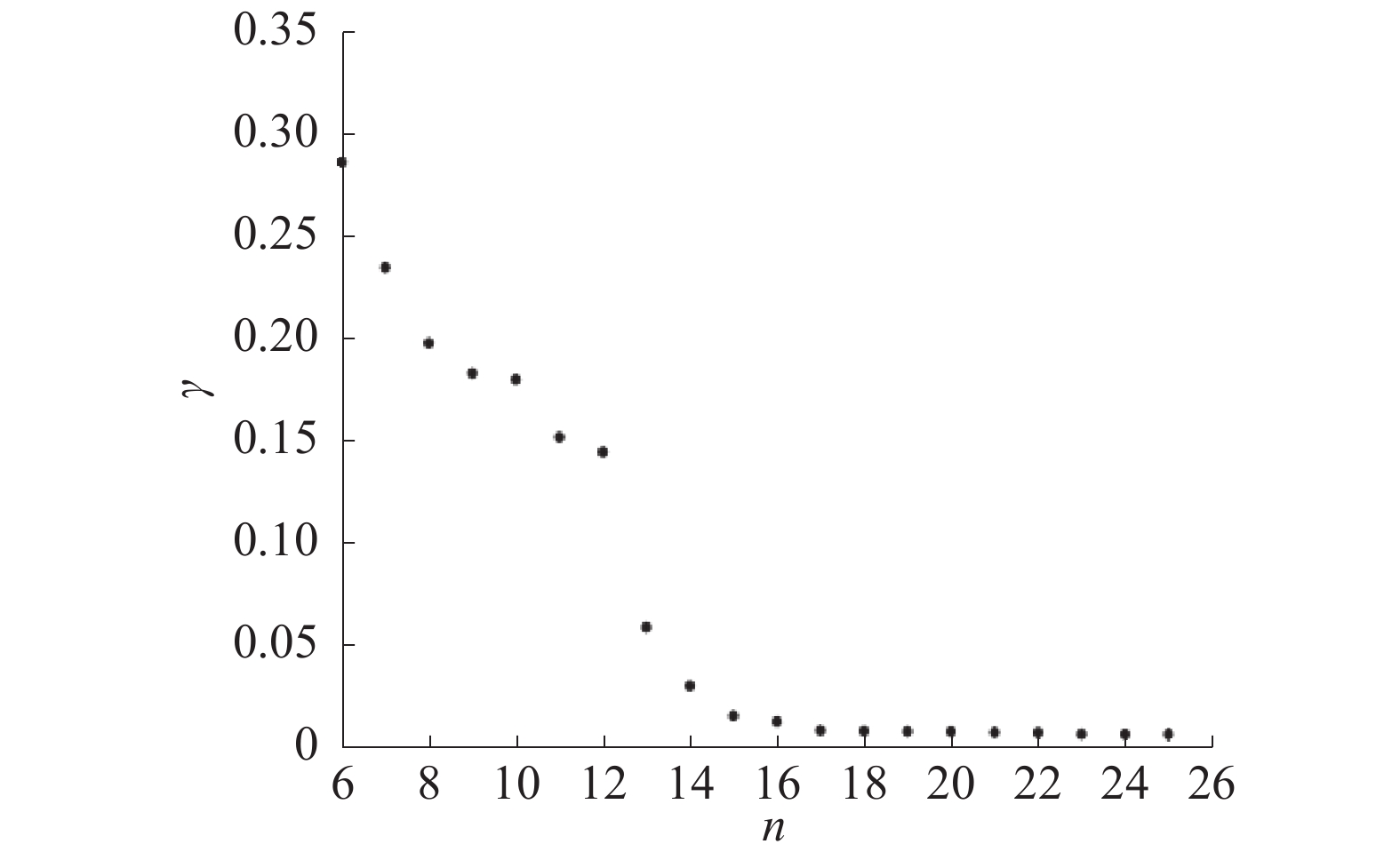
实验3 利用改进的决策图聚类仿真,忽略脉冲丢失和噪声干扰的情况下,形成图5基于
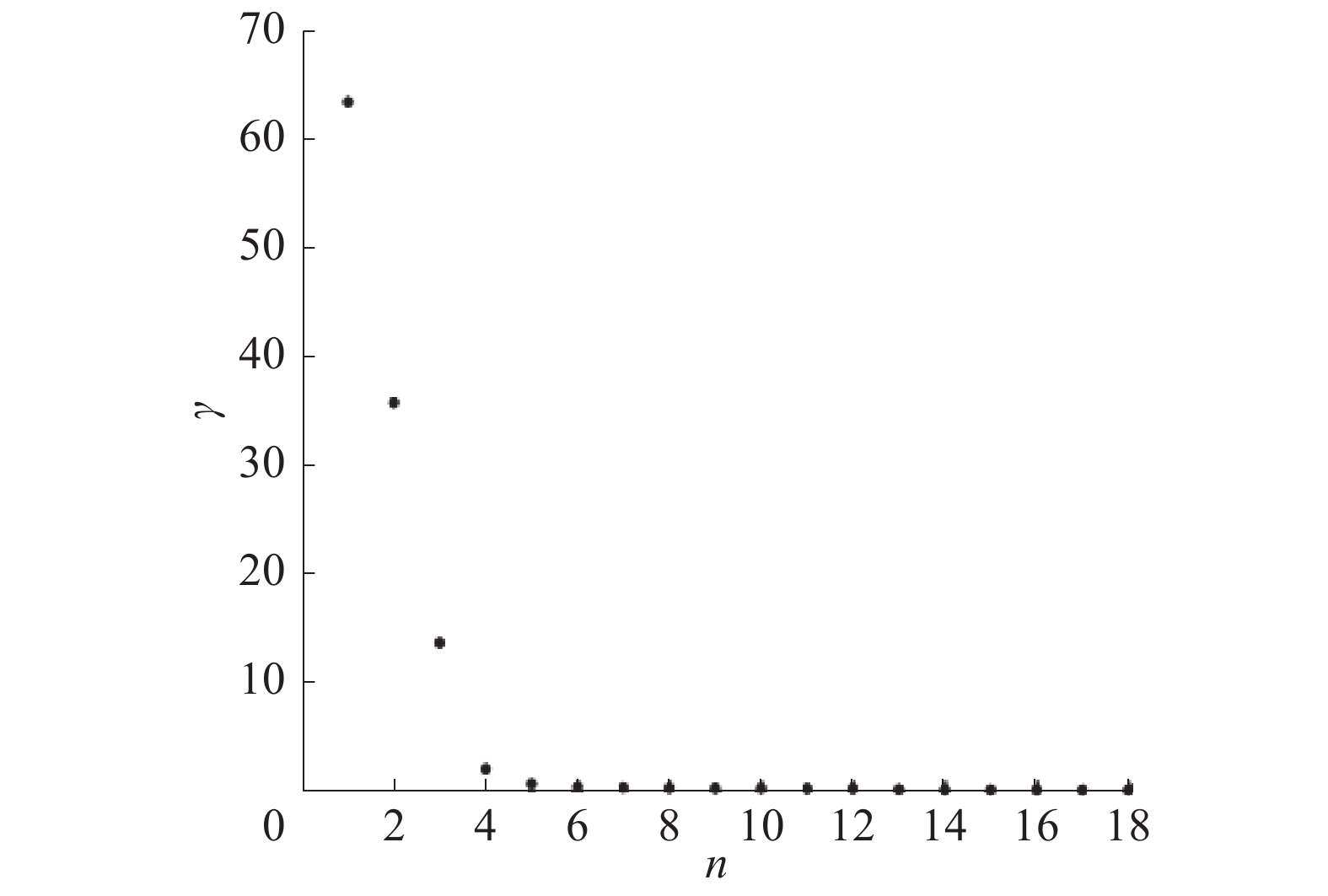
|
Download:
|
|
图 5 基于
|
|
|
Download:
|
|
图 6 基于
|
|
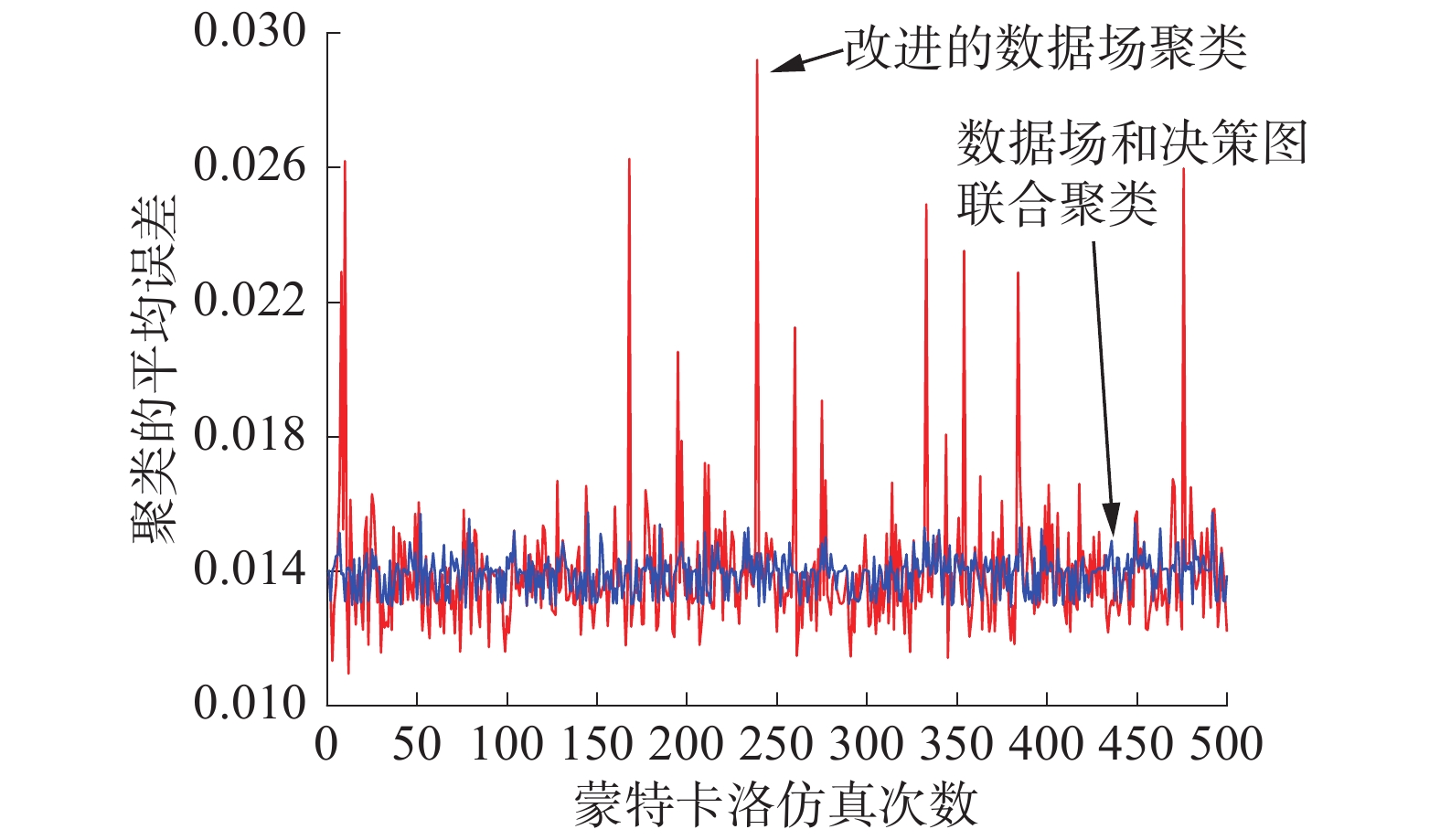
实验4 利用改进的数据场联合改进的决策图进行聚类得到聚类中心,连同原数据场聚类得出的每个簇组的聚类中心,分别与理论值进行比较,得出2种聚类算法的误差,并进行500次蒙特卡洛实验,对误差处理得到方差值,图7是不同聚类方式得到的聚类平均误差对比图。
|
Download:
|
| 图 7 不同聚类方式的聚类平均误差对比 | |
从仿真结果中可以看出,数据场联合决策图的聚类平均误差比改进的数据场的聚类平均误差小,同时对应的方差函数值也比改进的数据场小,说明数据场联合决策图的聚类效果更加稳定,聚类效果更加好。而图中改进的数据场出现几次误差远大于平均误差的原因是聚类数目比真实聚类数目多,造成同一组数据被分到不同的聚类簇组中,数据场联合决策图明显对这种现象做了进一步的改进,基本上解决了这一问题。
5 结论本文采取了一种改进的数据场和决策图联合聚类算法,主要是根据数据对象的势值和到最近大密度点的距离实现了聚类,且取得了理想的聚类效果。
1)改进的数据场能够更加快捷地处理孤立的噪声点,聚类的平均误差更加小,聚类效果更加稳定。
2)决策图实现了快速获得聚类中心和聚类数目的效果,在无噪声和脉冲丢失的情况下,聚类效果好。
3)数据场联合决策图聚类算法在能够处理孤立噪声点的基础上,克服了决策图对噪声和脉冲丢失的缺陷,联合聚类的效果更加显著。
经过仿真实验表明,本文提出的聚类算法在复杂的电磁环境下能够实现聚类功能,且有很好的聚类效果。但是联合聚类算法需要的时间复杂性更高些,聚类的时间会比数据场略多,后续需要对时间复杂性作进一步的研究,以缩短聚类的时间。
| [1] |
赵国庆. 雷达对抗原理[M]. 西安: 西安电子科技大学出版社, 1999: 1-7.
( 0) 0)
|
| [2] |
刘志鹏, 张国毅. 一种新的雷达信号实时分选方法[J]. 航天电子对抗, 2016, 32(2): 6-9, 17. DOI:10.3969/j.issn.1673-2421.2016.02.002 ( 0) 0)
|
| [3] |
赵贵喜, 刘永波, 王岩, 等. 数据场和K-Means算法融合的雷达信号分选[J]. 雷达科学与技术, 2016, 14(5): 517-520, 525. DOI:10.3969/j.issn.1672-2337.2016.05.012 ( 0) 0)
|
| [4] |
徐赛, 金炜东. 一种基于样本熵的雷达辐射源信号分选[J]. 电子世界, 2018(21): 8-10. ( 0) 0)
|
| [5] |
FREY B J, DUECK D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976. DOI:10.1126/science.1136800 ( 0) 0)
|
| [6] |
沙作金. 数据场聚类与平面变换雷达信号分选算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
( 0) 0)
|
| [7] |
张霓, 陈天天, 何熊熊. 基于数据场和单次划分的聚类算法[J]. 浙江工业大学学报, 2016, 44(1): 52-57. DOI:10.3969/j.issn.1006-4303.2016.01.011 ( 0) 0)
|
| [8] |
冯鑫, 胡晓曦, 匡银. 基于数据场的多模雷达信号分选算法[J]. 电子设计工程, 2018, 26(23): 139-142. DOI:10.3969/j.issn.1674-6236.2018.23.031 ( 0) 0)
|
| [9] |
简艳, 贾洪勇. 一种基于数据场的K-均值算法[J]. 计算机应用研究, 2010, 27(12): 4498-4501. ( 0) 0)
|
| [10] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 ( 0) 0)
|
| [11] |
黄栋. 基于词向量的短文本聚类研究与应用[D]. 大连: 大连理工大学, 2017.
( 0) 0)
|
| [12] |
纪风有. 基于概率关联的信号分选方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


