随着科学技术的发展,现代电子战信号的电磁环境变得越发复杂[1-2],接收机作为电子战中无线信号接收的重要系统,其接收到的信号往往具有非合作、先验信息未知、接收信号中所包含的子带信号数目、带宽及位置均未知的特点[3]。为了能够动态地适应电子战系统中低截获概率(low probability of intercept,LPI)雷达信号等大瞬时带宽的信号在传统的均匀宽带数字信道化接收机中存在的跨信道的情况,动态数字信道化接收机应运而生。在动态数字信道化接收机中,正确地对子带信号的频谱实施检测,判断子信道中信号的有无,继而对存在信号的子信道进行综合,重构出相应的原始信号,实现宽带信号中多个信号的提取与分离是动态数字信道化技术的关键,对后续的信号处理起着关键作用[4]。
频谱检测作为动态信道化结构中的重要组成部分,对子带信号检测的正确与否,影响着整个接收机的性能,是后续信号处理的基础。以往的经典频谱检测处理方法主要包括能量检测法(energy detection,ED)[5]、匹配滤波法(matched filtering detection,MFD)[6]以及循环平稳特征检测法(cyclostationary feature detection,CFD)[7]。ED检测方法的优势是实现简单,无需已知信号的先验信息,但是需要根据噪声估计检测门限,受噪声的可变性影响较大。MFD方法的优点是检测精度高,在一定条件下是最佳检测,但是其需要了解信号和噪声的先验信息,这在现代电子战中的雷达信号接收中是很难做到的。而CFD方法的优点是抗噪性能强,但是其实现过程复杂,进行信号检测的时间较长,不具备实时性。近年来,随机矩阵理论(random matrix theory, RMT)作为一种新的理论,其发展促进了人们对频谱检测技术的研究[8-9]。基于随机矩阵理论的频谱检测方法,通过分析接收信号的采样协方差矩阵的特征值来进行频谱检测,具有实现简单、不需要先验信息以及检测效果好的优点而受到学者们的关注,并出现了包括最大最小特征值之比(maximum-minimum eigenvalue,MME)[9]、最大最小特征值之差(different between the maximum and minimun eigenvalue,DMM)[10]等优秀的算法及其相应的改进算法。然而,已有的算法大多根据最大特征值所具有的分布规律确定门限,获得的门限精度有待进一步提升,并且他们的检验统计量通常只利用到了采样协方差矩阵的最大特征值和最小特征值的信息,其余特征值因没有用到而被舍弃,与此同时,最大最小特征值并不能完整地反馈出采样协方差矩阵的所有特征值信息,因而会造成资源浪费,也会对性能造成相应的损失。同时,特征值之差一类算法的最终门限表达式与噪声有关,检测结果受噪声影响。
从大数据的观点来看,根据系统观测采集到的所有数据进行分析和计算,能够从高维度的角度提取到多维数据的固有属性,从而能够更加清晰准确地认识到系统的内部特性,并以此做出相应的判决。对于信号的采样协方差矩阵来说,其所有的特征值共同反映了信号的特征信息,与只利用最大和最小特征值的信息相比较,对全部特征值进行合理利用将能获得更好的检测效果。基于以上想法,本文利用随机矩阵理论的最新研究成果,应用更为精确的最小特征值的分布[11],结合采样协方差矩阵的全部特征值信息,将判决统计量表示为平均特征值与最小特征值之比的形式,在2种不同条件下推导出了更优的检测门限表达式,提出了2种基于特征值的改进检测方法:平均特征值与最小特征值之比(average eigenvalue-minimum eigenvalue,AEME)算法和性能更优的平均特征值与最小特征值之比(improved average eigenvalue-minimum eigenvalue,IAEME)算法。给出了算法的推导过程和算法流程,并通过Matlab仿真实验与其他文献中已有的方法进行对比分析,验证了所提算法的性能。
1 基于特征值的动态信道化子带频谱检测模型基于特征值的动态信道化子带频谱检测结构可以表示为如图1所示。

|
Download:
|
| 图 1 基于特征值的动态信道化子带频谱检测结构 | |
假设系统信道个数为
| ${x_i}(n) = {s_i}(n) + {\omega _i}(n),\;i = 0,1,\cdots,K - 1$ |
式中:
| ${x_i}(n) = \left\{ {\begin{array}{*{20}{l}} {{\omega _i}(n), {H_0}} \\ {{s_i}(n) + {\omega _i}(n), {H_1}} \end{array}} \right.$ |
式中:
当用某种检测算法对频谱进行检测时,需要对各子带输出信号的观测数据进行处理,得到根据某种数据形式计算得到的检验统计量
| $\left\{ \begin{array}{l} T[{x_i}(n)] > \gamma ,{\kern 1pt} {H_1} \\ T[{x_i}(n)] \leqslant \gamma , {H_0} \\ \end{array} \right.$ |
在动态数字信道化接收机中,各子带的输出数据通常都是单通道形式的,即为一个
延时扩展法采用延时处理的方式将观测数据进行延时获得多段数据,以此构造虚拟通道,进而将各个通道的数据组合在一起构造接收数据矩阵。其优点是操作简单且计算量小,但是需要的采样点数较多。
经验模态分解法以信号本身的局部时间特性为依据,将要处理的信号分解为一系列固有模态函数(intrinsic mode function,IMF)的和的形式,从而使一般复杂的信号能够分解为单分量信号。一个单通道的观测信号经过经验模态分解后,可以将其扩展成为IMF分量与残余量组合的多通道形式,进而获得数据矩阵。其优点是能够自适应地将信号分解为多通道接收形式,但是其计算复杂度高,不利于数据的实时处理。
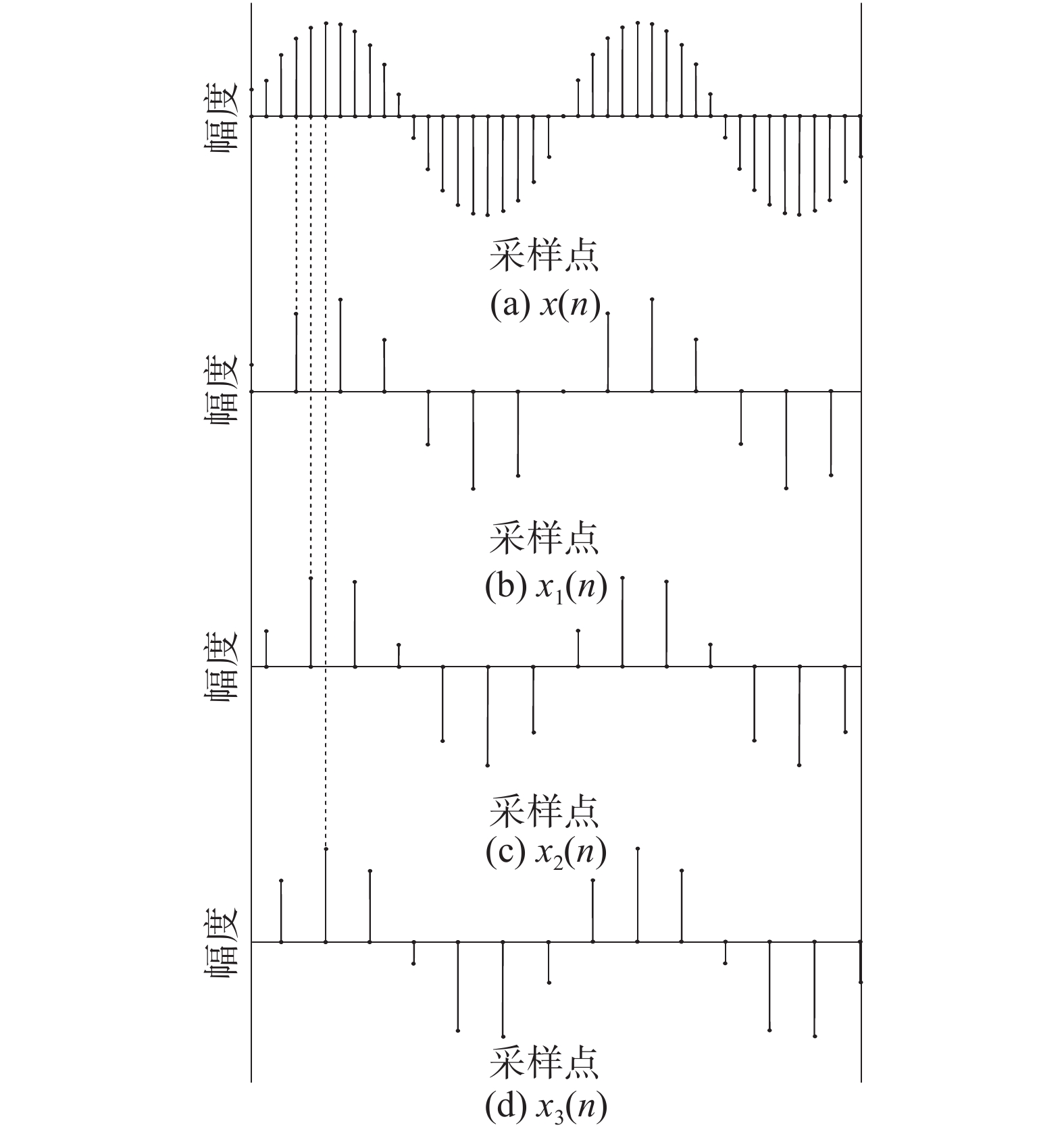
所谓间隔采样法,是指输入信号为过采样信号,对输入信号进行重采样可以获得新的数据向量,用重采样得到的数据向量即可构成多维矩阵。假设输入的单通道接收观测数据向量为
| ${x_i}(n) = x[Mn + i - 1],\;i = 1,2, \cdots ,M$ |
因而可以通过间隔采样把观测信号的单通道接收数据转换为多通道的接收形式。
| $\begin{array}{l} {{X}} = \left[ {\begin{array}{*{20}{c}} {{x_1}(n)} \\ {{x_2}(n)} \\ \vdots \\ {{x_M}(n)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {x(nM)} \\ {x(nM + 1)} \\ \vdots \\ {x(nM + M - 1)} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {x(0)}&{x(M)}& \cdots &{x((N - 1)M)} \\ {x(1)}&{x(M + 1)}& \cdots &{x((N - 1)M + 1)} \\ \vdots & \vdots & & \vdots \\ {x(M - 1)}&{x(2M - 1)}& \cdots &{x(NM - 1)} \end{array}} \right] \\ \end{array} $ |
式中,
|
Download:
|
| 图 2 间隔采样法构造多通道数据 | |
由于信道化处理中的分析滤波器组的输出子带带宽远小于输入信号带宽,每个子带的输出均为过采样信号,因此,间隔采样法较适合信道化处理中的信号维数转换。
对第
| $\begin{array}{l} {{{X}}_i} = \left[ {\begin{array}{*{20}{c}} {{x_{i1}}(n)} \\ {{x_{i2}}(n)} \\ \vdots \\ {{x_{iM}}(n)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_i}(nM)} \\ {{x_i}(nM + 1)} \\ \vdots \\ {{x_i}(nM + M - 1)} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {{x_i}(0)}&{{x_i}(M)}& \cdots &{{x_i}((N - 1)M)} \\ {{x_i}(1)}&{{x_i}(M + 1)}& \cdots &{{x_i}((N - 1)M + 1)} \\ \vdots & \vdots & & \vdots \\ {{x_i}(M - 1)}&{{x_i}(2M - 1)}& \cdots &{{x_i}(NM - 1)} \end{array}} \right] \\ \end{array} $ | (1) |
式中
由式(1)可以求得第
| $ {{{R}}_{ix}}(N) = \frac{1}{N}{{{X}}_i}{{X}}_i^{\rm{H}} = {{{R}}_{is}}(N) + {{{R}}_{i\omega }}(N) = \\ {{{R}}_{is}}(N) + {\sigma ^2}{{{I}}_M} $ | (2) |
当
| ${{{R}}_{ix}}(N) = {{{R}}_{i\omega }}(N) = \frac{1}{N}{{{W}}_i}{{W}}_i^{\rm{H}} = {\sigma ^2}{{{I}}_M}$ |
根据随机理论可知,此时的
对
基于上述分析,我们利用特征值的平均值与最小特征值的差异,采用二者的比值作为检验统计量进行频谱检测。则检验统计量可表示为
| $T = \frac{{{{\bar \lambda }_i}}}{{\mathop {\min }\limits_{j = 1,2,\cdots,M} \lambda _i^j}}{\rm{ = }}\left\{ \begin{array}{l} {\dfrac{{\bar \rho }}{{{\sigma ^2}}} + 1,}\quad {{H_1}}\\ {1,}\quad {{H_0}} \end{array} \right.$ | (3) |
式中
显然,当采用检验统计量
| $\left\{ \begin{array}{l} T > 1,{\kern 1pt} {H_1} \\ T = 1, {H_0} \end{array} \right.$ | (4) |
然而,
| $\left\{ \begin{array}{l} T > \gamma ,{\kern 1pt} {H_1} \\ T \leqslant \gamma , {H_0} \end{array} \right.$ | (5) |
算法检测性能的优劣取决于
Wishart随机矩阵的联合概率密度表达式复杂度很高,根据文献[15-17],利用随机矩阵的渐进理论,可以得出Wishart随机矩阵的特征值满足下面的几个定理。
定理1 假设噪声为实信号,令
| ${{A}}(N) = \frac{N}{{{\sigma ^2}}}{{{R}}_\omega }(N)$ |
| $\mu = {\left( {\sqrt {N - 1} + \sqrt M } \right)^2}$ |
| $\upsilon = \left( {\sqrt {N - 1} + \sqrt M } \right){\left( {\frac{1}{{\sqrt {N - 1} }} + \frac{1}{{\sqrt M }}} \right)^{1/3}}$ |
假设
定理2 假设噪声为复信号,令
| ${{A}}\left( N \right) = \frac{N}{{{\sigma ^2}}}{{{R}}_\omega }\left( N \right)$ |
| $\mu ' = {\left(\sqrt N + \sqrt M \right)^2}$ |
| $\upsilon ' = \left(\sqrt N + \sqrt M \right){\Bigg(\frac{1}{{\sqrt N }} + \frac{1}{{\sqrt M }}\Bigg)^{1/3}}$ |
假设
定理3 根据M-P律,当
| $\mathop {\lim }\limits_{N \to \infty } {\lambda _{\max }} = \frac{{{\sigma ^2}}}{N}{\left( {\sqrt N + \sqrt M } \right)^2}$ |
| $\mathop {\lim }\limits_{N \to \infty } {\lambda _{\min }} = \frac{{{\sigma ^2}}}{N}{\left( {\sqrt N - \sqrt M } \right)^2}$ |
伴随着人们对于随机矩阵理论研究的深入,学者们指出当
定理4 假设噪声为实信号,令
| ${{A}}(N) = \frac{N}{{{\sigma ^2}}}{R_\omega }(N)$ |
| $\mu = {\left( {\sqrt {N - 1} - \sqrt M } \right)^2}$ |
| $\upsilon = \left( {\sqrt {N - 1} - \sqrt M } \right){\left( {\frac{1}{{\sqrt {N - 1} }} - \frac{1}{{\sqrt M }}} \right)^{1/3}}$ |
假设
定理5 假设噪声为复信号,令
| ${{A}}(N) = \frac{N}{{{\sigma ^2}}}{{{R}}_\omega }(N)$ |
| $\mu ' = {\left(\sqrt N - \sqrt M \right)^2}$ |
| $\upsilon ' = \left(\sqrt N - \sqrt M \right){\Bigg(\frac{1}{{\sqrt N }} - \frac{1}{{\sqrt M }}\Bigg)^{1/3}}$ |
假设
由于检验统计量选取为待检测子带信号采样协方差矩阵特征值的平均值与最小特征值的比值,而在
| ${\sigma ^2} = \frac{1}{{M - 1}}\Bigg(\sum\limits_{i = 1}^M {{\lambda _i}} - {\lambda _{\max }}\Bigg)$ | (6) |
由式(6)可以将
| $\bar \lambda = \frac{1}{M}\sum\limits_{i = 1}^M {{\lambda _i}} = \frac{1}{M}\left( {(M - 1){\sigma ^2} + {\lambda _{\max }}} \right)$ |
根据定理3可知,
| $\begin{array}{l} \bar \lambda = \dfrac{{M - 1}}{M}{\sigma ^2} + \dfrac{1}{M}\dfrac{{{\sigma ^2}}}{N}{\left( {\sqrt N + \sqrt M } \right)^2} = \\ \dfrac{{{\sigma ^2}}}{N}\left( {\dfrac{{N(M - 1)}}{M} + \dfrac{{{{\left(\sqrt N + \sqrt M \right)}^2}}}{M}} \right) \end{array} $ | (7) |
另一方面,在
| $\bar \lambda = \frac{{{\lambda _{\max }} + {\lambda _{\min }}}}{2}$ |
根据定理3有
| $\bar \lambda = \frac{{{\sigma ^2}}}{{2N}}\left[{\left(\sqrt N + \sqrt M \right)^2} + {\left(\sqrt N - \sqrt M \right)^2}\right]$ | (8) |
根据式(7)和式(8)中特征值的平均值的2种形式,能够推导出2种检测门限值,继而得到2种频谱检测算法,将前者称之为平均特征值与最小特征值之比(average eigenvalue-minimum eigenvalue,AEME)检测算法,后者称之为IAEME检测算法,并用
当利用AEME算法对动态信道化的子带进行频谱检测时,
假设信号为实信号,若
| ${P_f} = P\left\{ {\frac{{\bar \lambda }}{{{\lambda _{\min }}}} > {\gamma _{{\rm{AEME}}}}\Bigg|{H_0}} \right\} = P\left\{ {{\lambda _{\min }} < \frac{{\bar \lambda }}{{{\gamma _{{\rm{AEME}}}}}}\Bigg|{H_0}} \right\}$ | (9) |
根据定理4可以将式(9)变换为
| $\begin{array}{c} {P_f} = P\left\{ {{\lambda _{\min }} < \dfrac{{\bar \lambda }}{{{\gamma _{{\rm{AEME}}}}}}\Bigg|{H_0}} \right\} = \\ P\left\{ {\dfrac{{{\sigma ^2}}}{N}{\lambda _{\min }}(A(N)) < \dfrac{{\bar \lambda }}{{{\gamma _{{\rm{AEME}}}}}}} \right\} = \\ P\left\{ {\dfrac{{{\lambda _{\min }}(A(N)) - \mu }}{\upsilon } < \dfrac{{\dfrac{N}{{{\sigma ^2}}}\dfrac{{\bar \lambda }}{{{\gamma _{{\rm{AEME}}}}}} - \mu }}{\upsilon }} \right\} = \\ {F_1}\left(\dfrac{{\dfrac{N}{{{\sigma ^2}}}\dfrac{{\bar \lambda }}{{{\gamma _{{\rm{AEME}}}}}} - \mu }}{\upsilon }\right) \end{array} $ |
因而,能够得到AEME算法的检测门限为
| $\begin{array}{c} {\gamma _{{\rm{AEME}}}} = \dfrac{{N\overline \lambda /{\sigma ^2}}}{{F_1^{ - 1}({P_f})\upsilon + \mu }} = \\ \dfrac{{\left[{{\left(\sqrt N + \sqrt M \right)}^2} + N(M - 1)\right]/M}}{{F_1^{ - 1}({P_f})\upsilon + \mu }} \end{array} $ |
式中
从判决门限的表达式可以看出,检测门限与噪声无关,只与虚警概率
当利用IAEME算法对动态信道化的子带进行频谱检测时,
假设信号为实信号,若
| $ {P_f} = P\left\{ {\dfrac{{\bar \lambda }}{{{\lambda _{\min }}}} > {\gamma _{{\rm{IAEME}}}}\Bigg|{H_0}} \right\} = P\left\{ {{\lambda _{\min }} < \dfrac{{\bar \lambda }}{{{\gamma _{{\rm{IAEME}}}}}}\Bigg|{H_0}} \right\} $ | (10) |
根据定理4可将式(10)变换为
| $\begin{array}{c} {P_f} = P\left\{ {{\lambda _{\min }} < \dfrac{{\bar \lambda }}{{{\gamma _{{\rm{IAEME}}}}}}\Bigg|{H_0}} \right\} = P \left\{ {\dfrac{{{\sigma ^2}}}{N}{\lambda _{\min }}(A(N)) < \dfrac{{\bar \lambda }}{{{\gamma _{{\rm{IAEME}}}}}}} \right\} = \\ P\left\{ {\dfrac{{{\lambda _{\min }}(A(N)) - \mu }}{\upsilon } < \dfrac{{\dfrac{N}{{{\sigma ^2}}}\dfrac{{\bar \lambda }}{{{\gamma _{{\rm{IAEME}}}}}} - \mu }}{\upsilon }} \right\} = \\ {F_1}\left(\dfrac{{\dfrac{N}{{{\sigma ^2}}}\dfrac{{\bar \lambda }}{{{\gamma _{{\rm{IAEME}}}}}} - \mu }}{\upsilon }\right) \\ \end{array} $ |
因而,能够得到IAEME算法的检测门限为
| $\begin{array}{c} {\gamma _{{\rm{IAEME}}}} = \dfrac{{N\overline \lambda /{\sigma ^2}}}{{F_1^{ - 1}({P_f})\upsilon + \mu }} = \\ \dfrac{{\left[{{\left(\sqrt N + \sqrt M \right)}^2} + {{\left(\sqrt N - \sqrt M \right)}^2}\right]/2}}{{F_1^{ - 1}({P_f})\upsilon + \mu }} \end{array} $ |
式中
从判决门限的表达式可以看出,检测门限同样与噪声无关,且只与虚警概率
Tracy-Widom分布函数的表达式非常复杂,其1阶累积分布函数
| ${F_1}(t) = \exp \left( { - \frac{1}{2}\int_t^\infty {(q(u) + (u - t){q^2}(u)){\rm{d}}u} } \right)$ | (11) |
| ${F_2}(t) = \exp \left( {\int_t^\infty {(u - t){q^2}(u){\rm{d}}u} } \right)$ | (12) |
式中
| $q''(u) = uq(u) + 2{q^3}(u)$ | (13) |
来获得。
由式(11)~(13)可以看出,要获得Tracy-Widom分布的闭式表达式非常困难。为了能够方便地使用Tracy-Widom分布的累积分布函数,在文献[17]中Johnstone等采用级数展开的方法求得了它的一些离散值,如表1所示。
|
|
表 1 Tracy-Widom分布的1阶和2阶函数数值 |
这样就可以通过查找表的方式方便地使用Tracy-Widom分布的函数值。
上述讨论均基于实信号,当信号为复信号时,只需将
综合前面的内容可知,AEME和IAEME这2种算法的检验统计量是相同的,但检测门限不同,因而可以将2种算法的执行步骤统一归纳如下:
1)对信道化输出的第
2)对各子带信号的采样协方差矩阵
3)根据实际情况设定的虚警概率
4)根据相应的检测算法的判决表达式确定信号是否存在,即当
为了验证本文所提算法的有效性,本节在Matlab仿真实验平台上对算法进行仿真并对算法的性能进行分析。
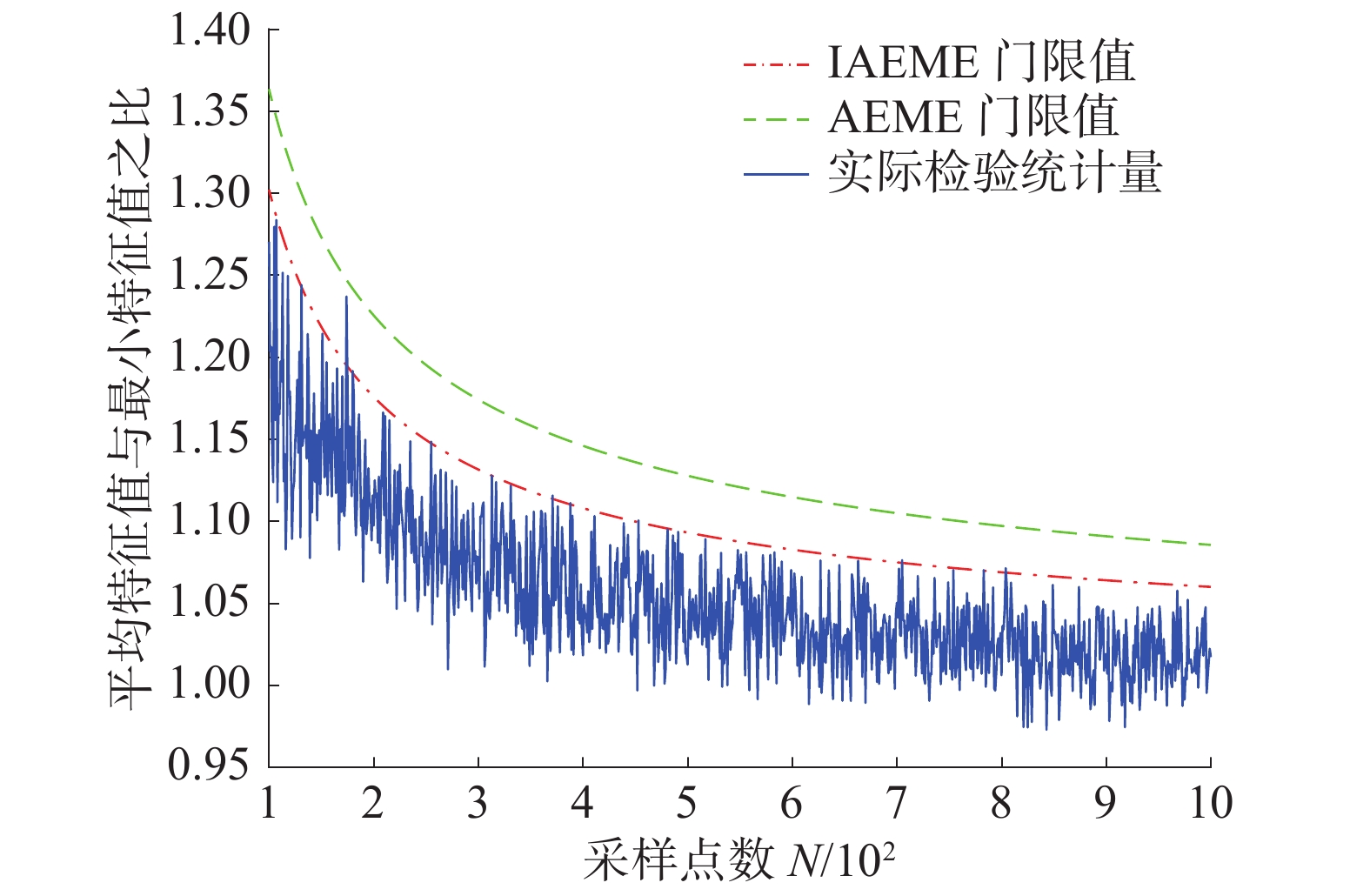
6.1 检测门限的有效性设置单通道信号的多通道转换之后的行数
|
Download:
|
| 图 3 检测门限的有效性 | |
从图中3可以看出,在虚警概率较低时,IAEME算法的门限值与AEME算法的门限值非常接近,但IAEME算法的检测门限相比较AEME算法的检测门限更低,且二者随着采样点数的增加差距逐渐减小。另一方面,当信道中只存在噪声的情况下,根据式(5)可知,检验统计量应该小于等于算法的检测门限值。另外,二者的检测门限值曲线均位于检验统计量的上方,由于存在一定的虚警概率,检验统计量中有少数点越过了IAEME算法的检测门限。
由于2种算法的检验统计量相同,但IAEME算法的检测门限更低,因而在实际的检测中,IAEME算法会获得更好的检测效果。从图中还可以了解到,由于AEME算法距离实际的检验统计量较远,虽然其能获得更低的虚警概率,但其是以牺牲检测性能为代价,不利于实际检测的应用。从图中还可以看出,算法的检测门限随着采样点的变化也在动态变化,因而在实际检测中能够动态地适应不同的检测情况,验证了算法的检测门限的有效性。
6.2 算法性能的比较分析为了确定本文所提方法的可行性和有效性,对本文提出的基于特征值的频谱检测算法AEME以及IAEME与已有文献中的基于特征值的频谱检测算法MME、AME、MMAE、MEMAE、IMEMAE和MMGAE[20]等几种算法的检测性能进行对比,考察在一定的虚警概率
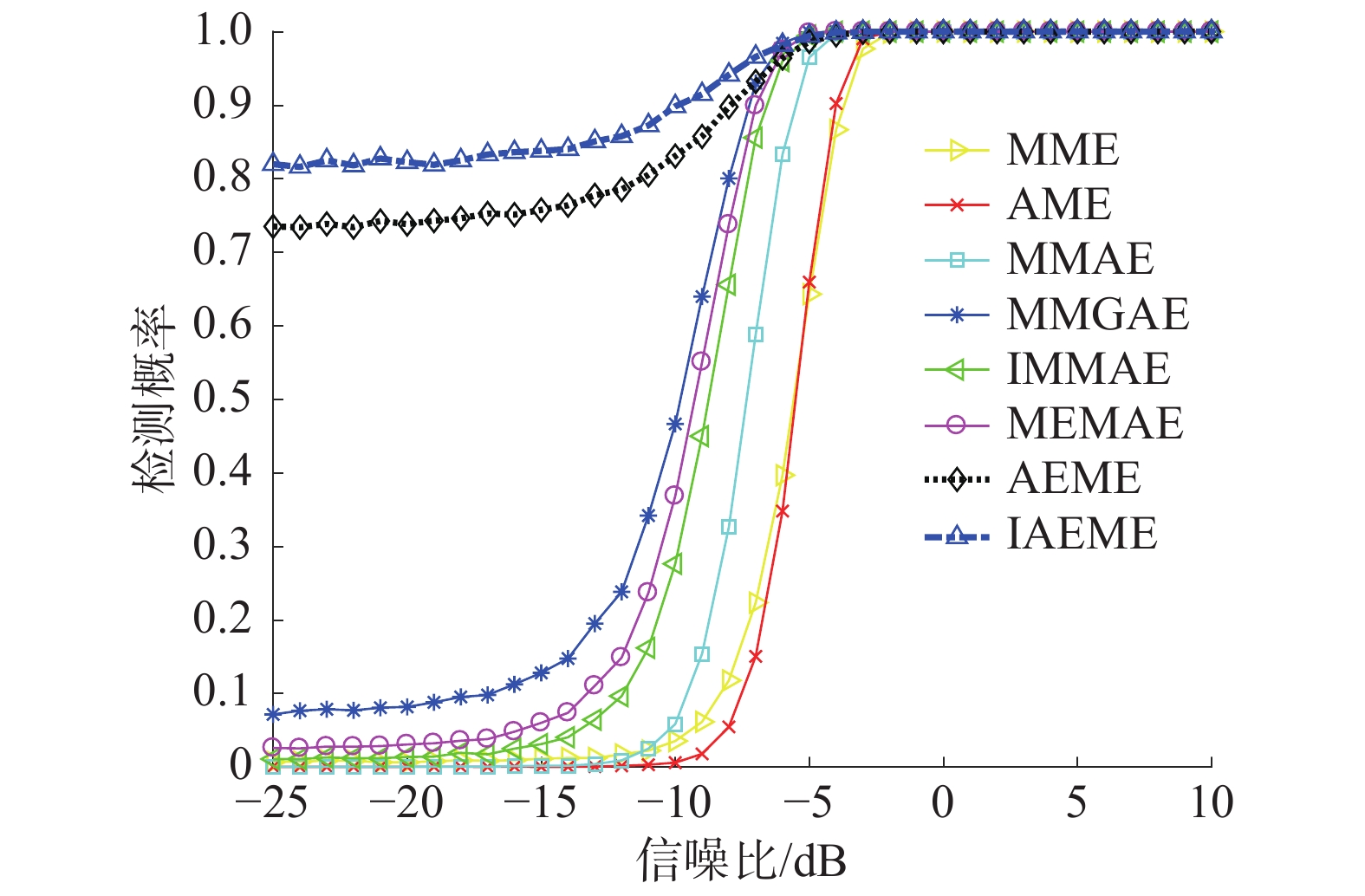
设置每个子信道的采样点数
|
Download:
|
| 图 4 不同算法在不同信噪比下的检测性能曲线 | |
从图4中能够看出,随着信噪比的提升,各个算法的检测性能均呈现出上升趋势。本文提出的2种算法采用特征值的均值
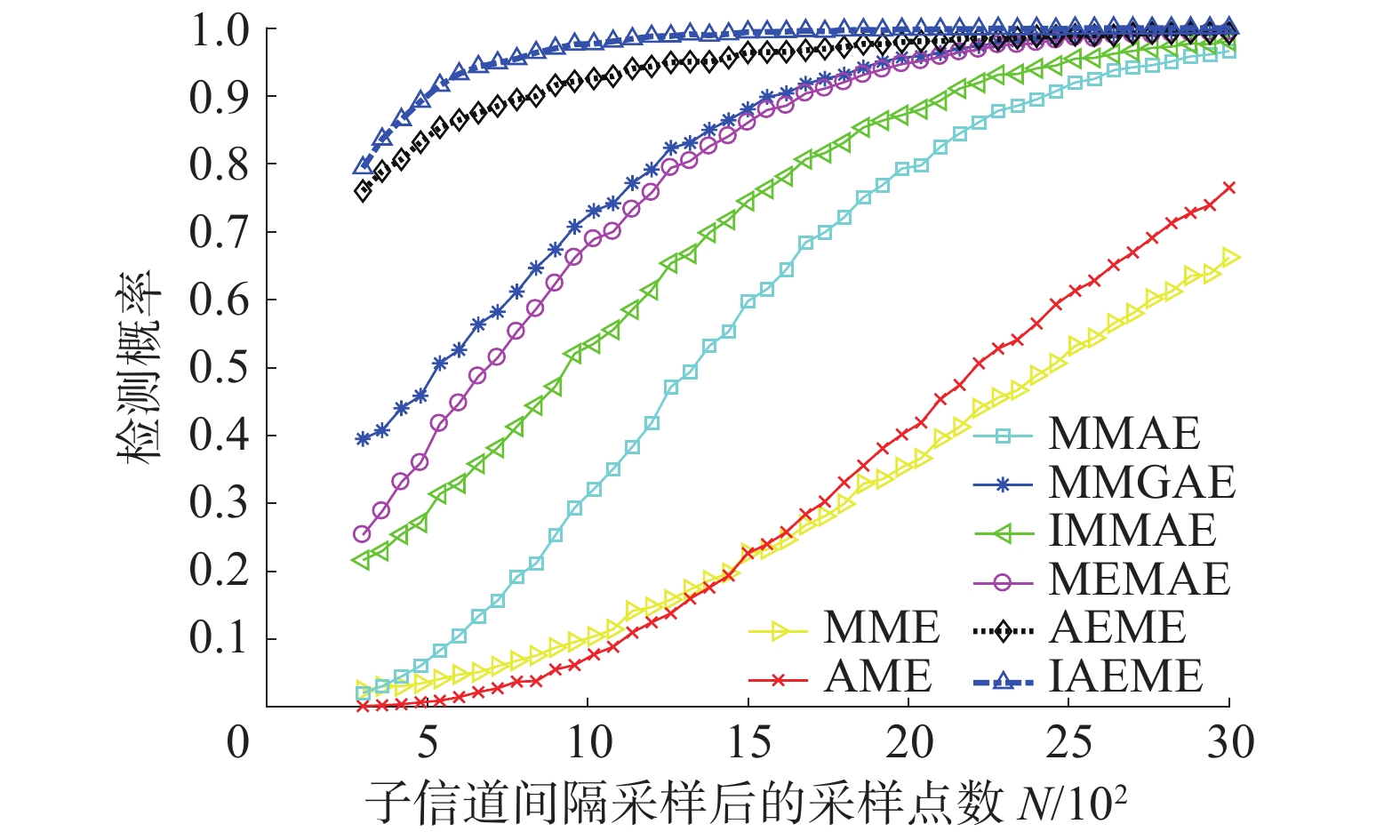
由于算法的检测门限表达式与信道化子带信号间隔采样后得到的
|
Download:
|
| 图 5 不同算法的检测性能与子信道采样点数的关系曲线 | |
从图5中可以看出,随着子信道采样点数的增加,各个算法的检测性能均得到了提升,由于在检验统计量中采用了最小特征值的极限分布,并且对最小特征值的极限分布在低维度下的描述更为准确、性能更加良好,因此会使算法的检测性能得到提升。因而与已有的算法相比,新提出的2种算法在较低的采样点数下会获得更高的检测概率。其中IAEME算法的性能最好,在子信道间隔采样后的的采样点数
将
|
Download:
|
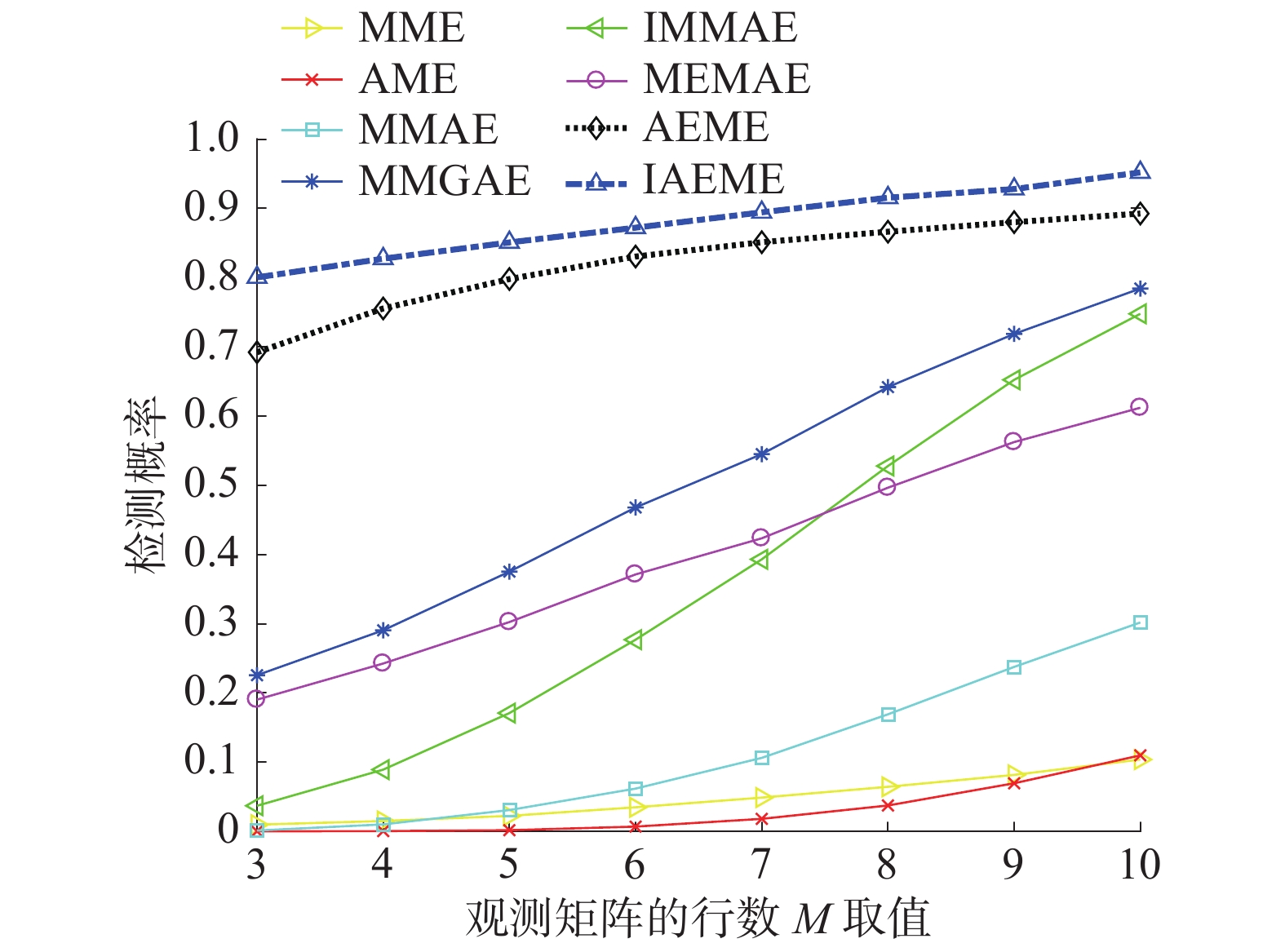
| 图 6 不同算法的检测性能与M值的关系曲线 | |
从图6中可以看出,随着
综上,通过以上8种算法的仿真对比实验可知,8种算法随着信噪比
本文提出算法的检测门限表达式只与虚警概率
本文对基于特征值的频谱检测算法进行了研究,提出了2种基于特征值的动态信道化子带频谱检测改进算法,给出了算法的详细推导过程,并通过仿真实验验证了算法的有效性。
1)算法综合考虑了采样协方差矩阵所有特征值对信号特征的描述,利用采样协方差矩阵的特征值的平均值和更为精确的最小特征值的极限分布推导出了更为精确的检测门限表达式,提高了检测性能。
2)算法的检测门限表达式只与虚警概率
3)算法可以根据实际情况需要对虚警概率进行调整获得不同的检测判决门限,可以适应不同的应用场景。
4)由于信号与噪声的特征值差异在任何情况下都是存在的,不论何种形式的信号,都可以通过特征值进行信号与噪声之间的区分,因此该方法对多种信号均具有检测性能,具有可以适应复合信号检测的优点。
5)算法与已有的算法相比在低信噪比、低采样点数
综上所述,本文提出的算法具有实现简单、不需要先验信息、适用能力强、检测性能好等优点,更符合未来电子战中的信号电磁环境,具有良好的应用前景。
| [1] |
汪连栋, 申绪涧, 韩慧, 等. 复杂电磁环境概论[M]. 北京: 国防工业出版社, 2015: 1-50.
( 0) 0)
|
| [2] |
龚仕仙, 魏玺章, 黎湘. 宽带数字信道化接收机综述[J]. 电子学报, 2013, 41(5): 949-959. DOI:10.3969/j.issn.0372-2112.2013.05.019 ( 0) 0)
|
| [3] |
刘小蒙, 邵高平, 汪洋, 等. 一种改进的动态信道化滤波方法[J]. 信息工程大学学报, 2016, 17(4): 448-453. DOI:10.3969/j.issn.1671-0673.2016.04.013 ( 0) 0)
|
| [4] |
刘小蒙, 邵高平, 汪洋, 等. 基于双门限的动态信道化子带频谱检测方法[J]. 信息工程大学学报, 2017, 18(2): 176-180. DOI:10.3969/j.issn.1671-0673.2017.02.010 ( 0) 0)
|
| [5] |
DIGHAM F F, ALOUINI M S, SIMON M K. On the energy detection of unknown signals over fading channels[J]. IEEE transactions on communications, 2007, 55(1): 21-124. DOI:10.1109/TCOMM.2006.887483 ( 0) 0)
|
| [6] |
CABRIC D, MISHRA S M, BRODERSEN R W. Implementation issues in spectrum sensing for cognitive radios[C]//Proceedings of 38th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA, 2004: 772−776.
( 0) 0)
|
| [7] |
王颖喜, 卢光跃. 基于循环平稳特征的OFDM主用户感知的仿真研究[J]. 西安邮电学院学报, 2009, 14(5): 72-76. ( 0) 0)
|
| [8] |
CARDOSO L S, DEBBAH M, BIANCHI P, et al. Cooperative spectrum sensing using Random matrix theory[C]//Proceedings of the 3rd International Symposium on Wireless Pervasive Computing. Santorini, Greece, 2008: 334−338.
( 0) 0)
|
| [9] |
ZENG Yonghong, LIANG Yingchang. Eigenvalue-based spectrum sensing algorithms for cognitive radio[J]. IEEE transactions on communications, 2009, 57(6): 1784-1793. DOI:10.1109/TCOMM.2009.06.070402 ( 0) 0)
|
| [10] |
卢光跃, 弥寅, 包志强. 特征值极限分布的改进合作频谱感知[J]. 信号处理, 2014, 30(3): 261-267. DOI:10.3969/j.issn.1003-0530.2014.03.002 ( 0) 0)
|
| [11] |
PENNA F, GARELLO R, SPIRITO M A. Cooperative spectrum sensing based on the limiting eigenvalue ratio distribution in Wishart matrices[J]. IEEE communications letters, 2009, 13(7): 507-509. DOI:10.1109/LCOMM.2009.090425 ( 0) 0)
|
| [12] |
彭耿, 黄知涛, 姜文利, 等. 单通道盲信号分离研究进展与展望[J]. 中国电子科学研究院学报, 2009, 4(3): 268-277. DOI:10.3969/j.issn.1673-5692.2009.03.008 ( 0) 0)
|
| [13] |
GAO Bin, WOO W L, DLAY S S. Single-channel source separation using EMD-subband variable regularized sparse features[J]. IEEE transactions on audio, speech, and language processing, 2011, 19(4): 961-976. DOI:10.1109/TASL.2010.2072500 ( 0) 0)
|
| [14] |
WARNER E S, PROUDLER I K. Single-channel blind signal separation of filtered MPSK Signals[J]. IEEE Proceedings- Radar, Sonar and Navigation, 2003, 150(6): 396-402. DOI:10.1049/ip-rsn:20031007 ( 0) 0)
|
| [15] |
TULINO A M, VERDÚ S. Random matrix theory and wireless communications[M]. Hanover, USA: Now Foundations and Trends, 2004: 3−73.
( 0) 0)
|
| [16] |
JOHANSSON K. Shape fluctuations and random matrices[J]. Communications in mathematical physics, 2000, 209(2): 437-476. DOI:10.1007/s002200050027 ( 0) 0)
|
| [17] |
JOHNSTONE I M. On the distribution of the largest eigenvalue in principal components analysis[J]. Annals of statistics, 2001, 29(2): 295-327. DOI:10.1214/aos/1009210544 ( 0) 0)
|
| [18] |
宋昱辉. 认知无线电中频谱检测算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
( 0) 0)
|
| [19] |
TRACY C A, WIDOM H. On orthogonal and symplectic matrix ensembles[J]. Communications in mathematical physics, 1996, 177(3): 727-754. DOI:10.1007/BF02099545 ( 0) 0)
|
| [20] |
李善双. 基于动态信道化接收机的子带频谱检测技术的研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


