近年来,随着能源需求的快速增长、化石能源的日益枯竭及核能的限制性发展,清洁能源因其自身的优势而被大规模应用于电力系统中[1]。现今,如何合理地解决环境问题和能源问题已经成为世界各国的研究热点[2]。太阳能是现在热门的清洁能源,尽管它占有很大优势,但还是受到环境的制约,如风速、温度、光照强度等。因此,对光伏发电进行准确的预测,可以节约资源,保证电力系统运行的稳定性,对清洁能源应用很有意义。
光伏出力预测的研究方法主要有统计法与物理法2种[3-4]。物理法主要通过建立物理模型来进行预测;统计法则依靠大量的数据,通过优化算法进行预测。文献[5]只采用了一种预测模型,由于环境影响因素较大,这种单一预测模型预测结果的准确度较差。文献[6]使用SVM对数据进行分类后使用BPNN和自回归与滑动平均模型分别预测,但SVM的分类误差较大。本文的研究对象是小型光伏发电站,构建基于BP神经网络的预测模型,由于BP神经网络易陷入局部极小值,并且具有收敛速度慢等缺陷,提出基于EMD分解的GA-BP神经网络预测模型,优化网络结构中的权值和阈值。然后利用某光伏电站的历史数据作为输入变量,输入到搭建好的预测模型中,最后经过对比得出结论。
1 光伏发电输出功率影响因素本文通过记录某小型光伏发电站2015年5月3日—7月3日的温度、海拔、云层密度、空气湿度以及发电量数据,通过SPSS数据分析软件,选用Person相关系数进行分析。在对数据进行聚类讨论时,首先确定变量的相似性程度
| ${x_i},{y_i} \in R$ |
式中:
| $r = \frac{{\displaystyle\sum\limits_{i = 1}^n {({x_i} - \overline x } )({y_i} - \overline y )}}{{{{\Bigg[\displaystyle\sum\limits_{i = 1}^n {({x_i}} - \overline x )^2}}\displaystyle\sum\limits_{i = 1}^n {({y_i}} - \overline y {)^2}\Bigg]^{1/2}}}$ |
式中:
由此可得,光伏发电量与温度以及湿度具有较强的相关关系,与海拔、气压等因素相关较小[7]。在分析了相关因素的基础上,本文为了提高预测的精度往往会在天气因素变化大体相同的基础上采用相似日的选取原理。
2 建模原理 2.1 经验模态分解经验模态分解是根据数据自身的时间尺度把信号分解,不用预设其他基函数。由于该方法具有这样的优点,它可以应用在任何的信号分解,在处理数据时有很大的优势,广泛应用于分析非平稳信号,信噪比很高。经验模态分解方法假设任何复杂信号都是由简单且独立的固有模态函数(intrinsic mode function,IMF)组成的[8]。EMD分解法能将不平稳数据进行平稳化处理,然后进行希尔伯特变换获得时频谱图,获得有意义的频率。这种方法较直观、具有自适应性[9]。所谓经验模态分解就是从非平稳、非线性的原始信号里面拆分出特征尺度各不相同的信号,从而获取多个不一样的本征模函数及一个剩余分量。具体分解步骤如下[10]:
1)假设原始信号为
2)求上包络线与下包络线的均值
| ${h_1}(t) = {x_1}(t) - {m_1}(t)$ |
若
3)如
| ${h_{11}}(t) = {h_1}(t) - {m_{11}}(t)$ |
然后经过重复的筛选,得到
| ${h_{1k}}(t) = {h_{1(k - 1)}}(t) - {m_{1k}}(t)$ |
4)从
| ${r_1}(t) = x(t) - {c_1}(t)$ |
| ${r_2}(t) = {r_1}(t) - {c_2}(t)$ |
| ${r_n}(t) = {r_{n - 1}}(t) - {c_n}(t)$ |
当
| $x(t) = \sum\nolimits_{i = 1}^n {{c_i}} (t) + {r_n}(t)$ |
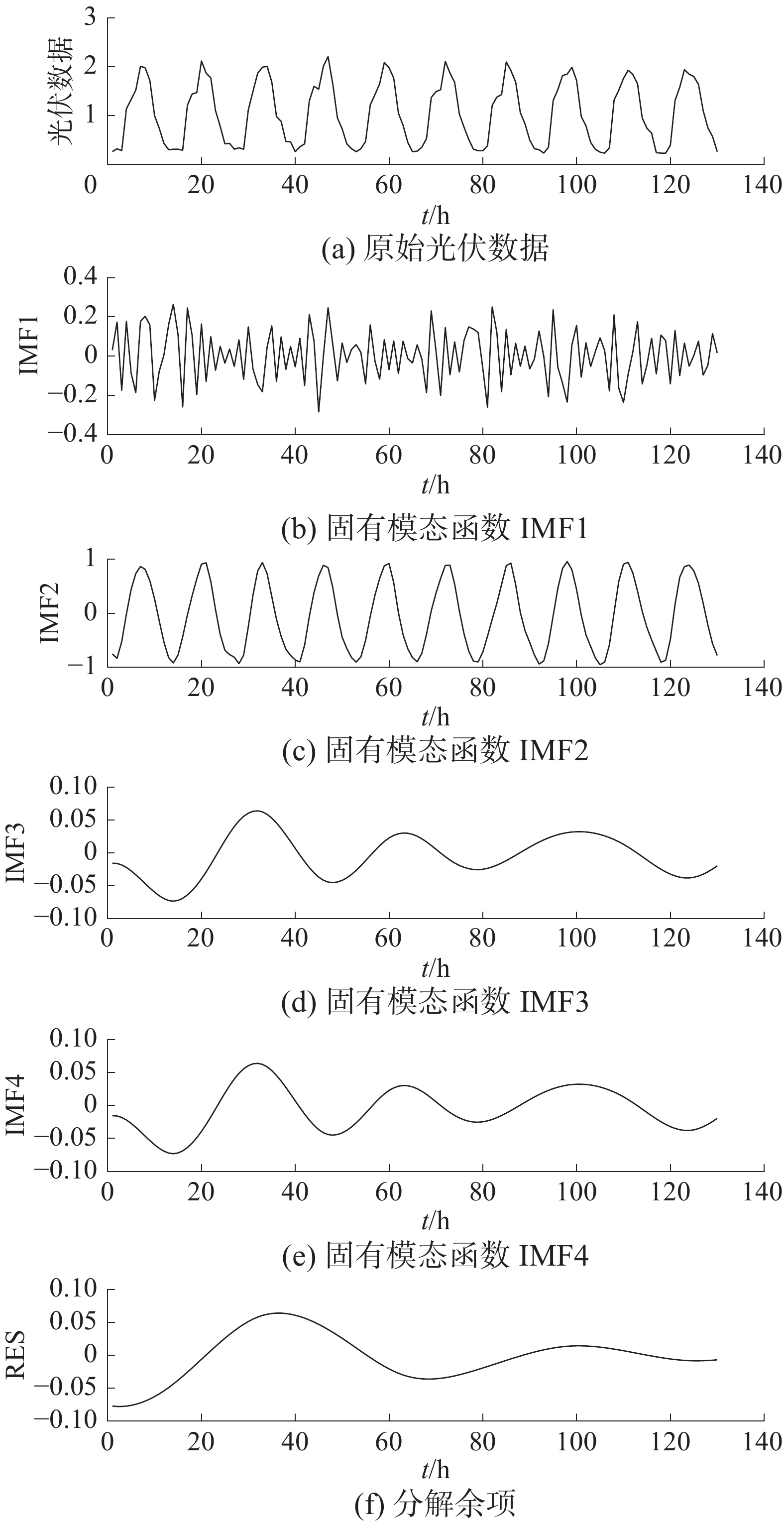
从记录的小型光伏发电站中选取10天的光伏数据,把原始信号做EMD分解处理。由于外界因素影响,如温度、湿度和云层变化的随机性等特点,经验模态分解法的自适应性与完备性等特点与优势才得以显现出来[11]。EMD分解图如图1所示。
|
Download:
|
| 图 1 EMD分解 | |
从图1中可知,原始光伏数据与IMF1形状有明显的日周期性,体现了光伏出力的特点。由于光照强度的影响,早上和傍晚的力度较弱,正午时光照强度大、出力强。IMF2、IMF3与IMF4为低频周期分量,它们的幅值较低,而剩余信号(residual, RES)分量占比较高,可以体现出整体光伏发电趋势。
2.2 BP神经网络模型神经网络则是一类相对复杂的计算网络。BP神经网络由输入层(input),隐含层(hidden),输出层(output)和权重(weight)组成。
BP神经网络的整个学习过程为信号正向传播和误差的方向回传[12]。假设训练样本数为
1)将权值
2)输入
3)如果
4)得到的误差逐层反向传回之前的各层,并将误差信号加载到连接的权值上,使得整个神经网络误差减小。
5)重复训练每一个输入与输出样本,直到误差符合要求为止。
2.2.1 输入层、输出层与隐含层设计由前文可知,光伏出力强度受多种因素的影响。在众多因素中,光照强度、温度、风速3个为主要影响因素,因此考虑进输入层结点。而光伏出力受时间的影响,集中在上午6点到下午18点之间,所以我们将光伏电站的光伏出力限制在此区间,选取1 h为周期,所以共取13个功率数据与13个温度数据。此外太阳辐照强度与日平均风速也是2个重要影响因素,应加入研究,因此共28个输入层节点数。输出层的神经元传递函数通常采用线性传递函数,公式如下:
| ${\rm{pureline}}(x) = x$ | (10) |
在BP神经网络中,有一个公式可以确定隐含层节点数目:
| $h = \sqrt {m + n} + a$ | (11) |
式中:
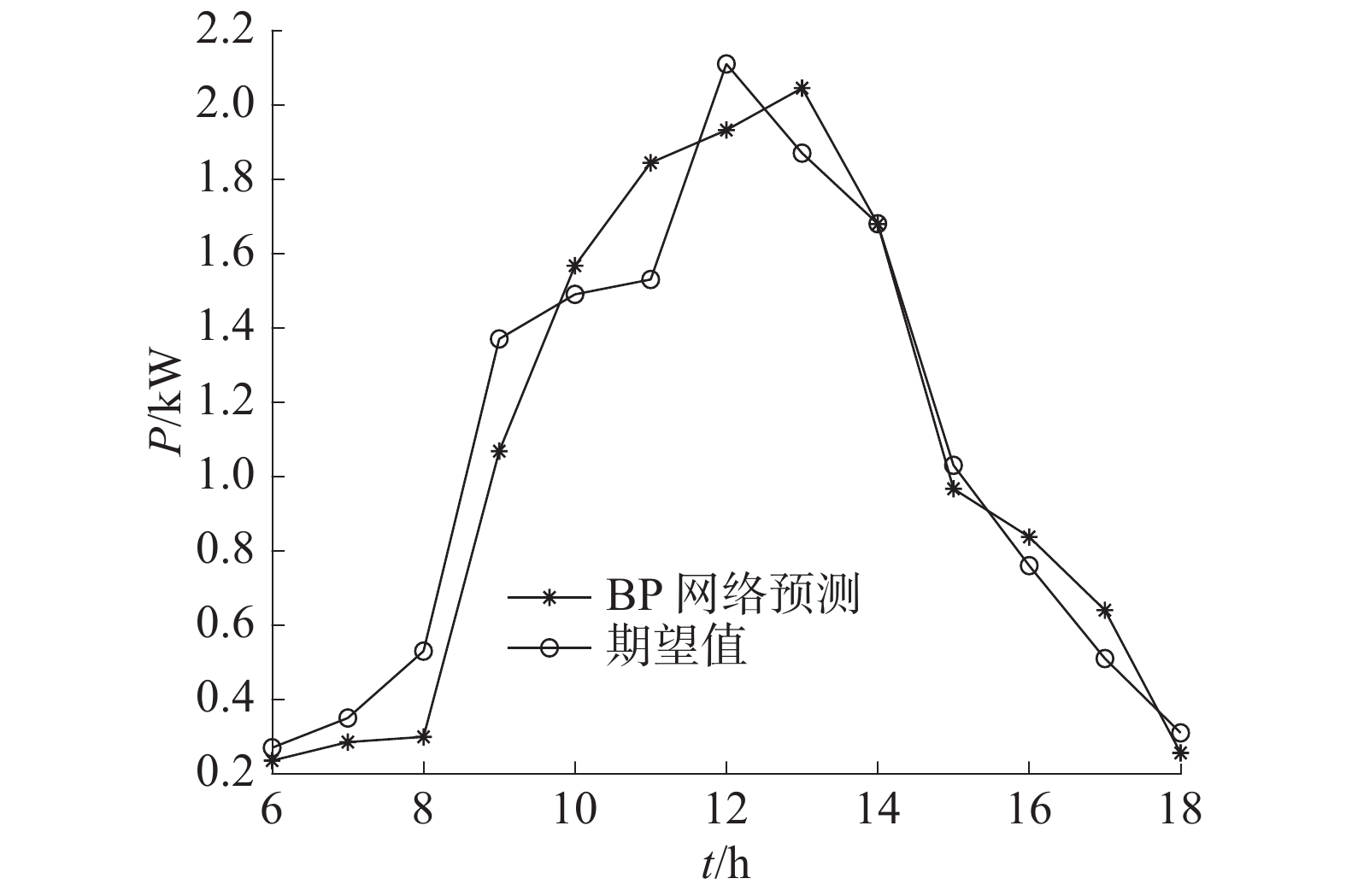
将收集的数据作为训练样本,然后将误差反向传播到神经网络中,对第1—9日的数据进行训练,再利用第9日的数据预测第10日的发电值,然后将预测的结果与实际值比较,结果如图2所示。
|
Download:
|
| 图 2 BP神经网络预测光伏出力数据与期望值对比 | |
从图2可知,BP神经网络的预测值与期望值之间的误差较大,尤其在中午时,光照强度较强,误差较为明显。
3 基于EMD分解的GA-BP光伏出力预测 3.1 遗传算法遗传算法(GA)的思想基于达尔文的进化论、魏茨曼的物种选择学说和孟德尔的群体遗传学说[13]。遗传算法模拟生命进化,在自然选择中交配、繁殖、突变。在GA中,有选择、交叉、变异3种遗传算子。选择算子依据规则从群体中选出部分个体作为下一代种群个体;交叉算子按照遗传模拟充足、选取最佳的基因转移给下一代中,从而获得新个体;变异算子模拟在自然进化中出现的基因突变现象,依据变异的概率获得新个体。
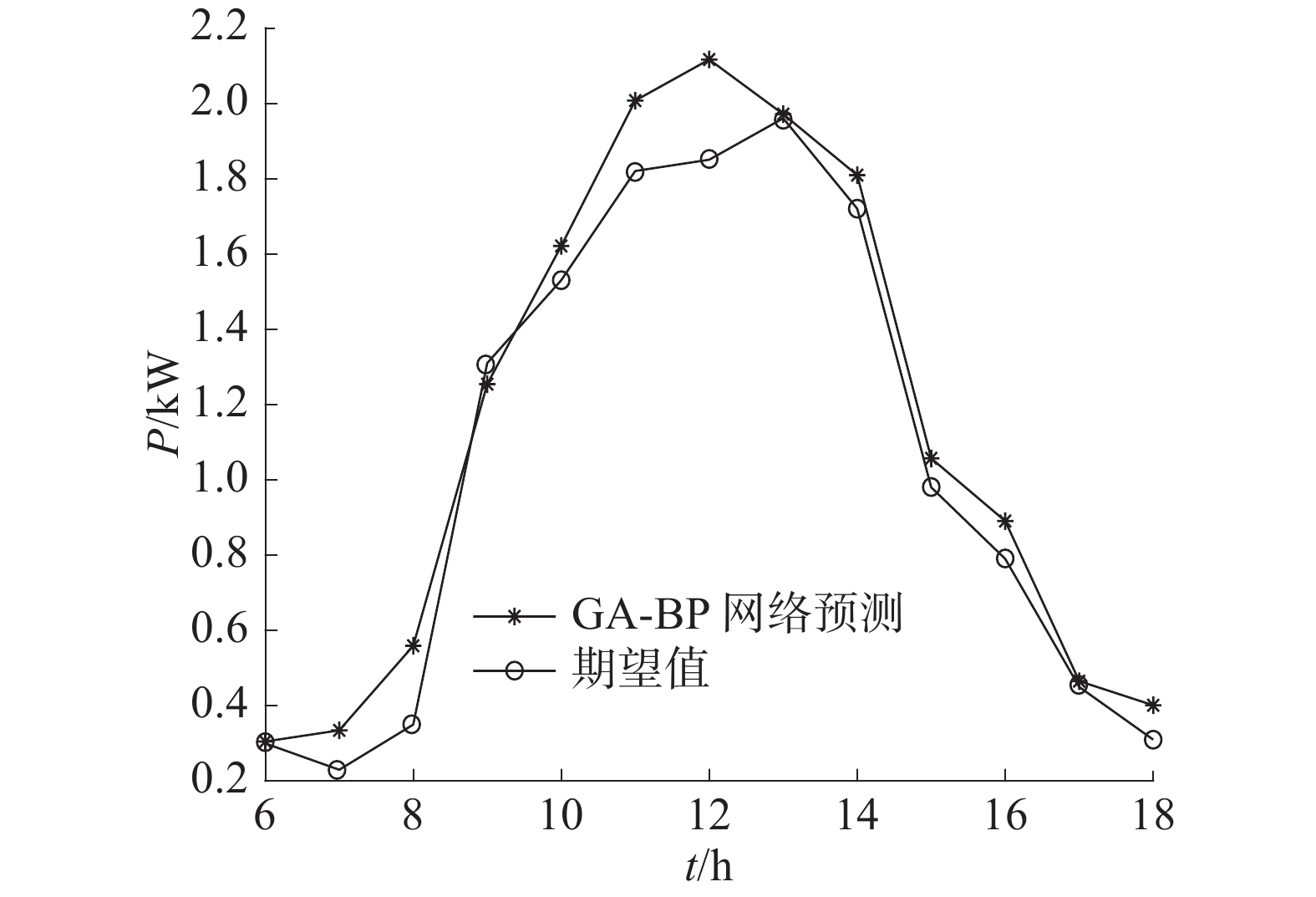
3.2 GA-BP模型光伏出力预测为了克服神经网络的缺陷,一些学者提出采用GA优化BP神经网络的权值和阈值的方法,建立了GA-BP模型[14]。GA-BP模型构建如图3所示。然后选择数据作训练样本,进行仿真模拟,得到GA-BP神经网络预测模型,如图4所示。

|
Download:
|
| 图 3 GA-BP构建流程 | |
|
Download:
|
| 图 4 GA-BP预测光伏出力数据与期望值对比 | |
由图4可知,GA-BP神经网络的预测精确度要较单一BP神经网络的高,但是该模型在太阳出力强的阶段仍具有较大误差,因此还需要进一步改进。
3.3 基于EMD分解的GA-BP神经网络光伏出力预测由于GA-BP模型虽然优化了精度,但是耗费了一定的时间,于是建立基于EMD组合预测模型。EMD能够分解出不同频率特性的信号,然后对每一个信号用GA-BP算法进行预测,基于EMD分解的组合预测模型流程图和结果如图5、6所示。

|
Download:
|
| 图 5 EMD-GA-BP预测流程 | |

|
Download:
|
| 图 6 3种模型预测光伏出力数据与实际值对比 | |
由图6可知,EMD-GA-BP的拟合效果较其他2种预测方法更精确,但模型预测结果与实际值仍存在一定误差,经过反复训练,表1为各模型均方误差(mean squared error,MSE)与平均绝对误差(mean absolute error,MAE)的对比。
|
|
表 1 3种模型预测误差对比 |
由表1可知,BP神经网络的预测结果误差较大,GA-BP模型的预测结果较单一BP模型精确,而EMD-GA-BP组合预测模型的预测精度高于前两者,说明本文的组合预测模型具有较强的适应性。
4 结论利用神经网络对光伏系统进行短期的出力预测是当今的热点,也是电网正常运行的基础,对电力的发展与电力部门的经济效益有着重要的意义。本文通过收集某光伏电站的数据,进行仿真预测,结果证明,使用本文的基于经验模态分解算法改进BP神经网络的光伏出力预测结果,误差较单一使用BP神经网络与GA-BP神经网络的小,虽然与实际发电量相比,仍有一定的误差,但是随着样本的增加和实验次数的增加,误差会逐渐变小,预测值也会变得更加精准,最终达到要求。
| [1] |
应飞祥, 何民, 姜燕波, 等. 光伏发电及其所处电力系统可靠性评估研究进展[J]. 云南民族大学学报(自然科学版), 2019, 28(5): 523-530. ( 0) 0)
|
| [2] |
李凯晗. 光伏发电并网逆变器供电稳定性控制研究[J]. 通信电源技术, 2019, 36(2): 26-27. ( 0) 0)
|
| [3] |
陈树勇, 鲍海, 吴春洋, 等. 分布式光伏发电并网功率直接控制方法[J]. 中国电机工程学报, 2011, 31(10): 6-11. ( 0) 0)
|
| [4] |
EHSAN R M, SIMON S P, VENKATESWARAN P R. Artificial neural network predictor for grid-connected solar photovoltaic installations at atmospheric temperature[C]//Proceedings of 2014 International Conference on Advances in Green Energy. Thiruvananthapuram, India, 2014.
( 0) 0)
|
| [5] |
李英姿, 贺琳, 牛进苍. 基于马尔可夫链的光伏并网发电量预测[J]. 太阳能学报, 2014, 35(4): 611-616. DOI:10.3969/j.issn.0254-0096.2014.04.010 ( 0) 0)
|
| [6] |
高阳, 张碧玲, 毛京丽, 等. 基于机器学习的自适应光伏超短期出力预测模型[J]. 电网技术, 2015, 39(2): 307-311. ( 0) 0)
|
| [7] |
孙祥晟, 陈芳芳, 吴孟礼, 等. 基于EMD分解的AR模型光伏发电预测方法探讨[J]. 电工技术, 2019(11): 8-10. DOI:10.3969/j.issn.1002-1388.2019.11.003 ( 0) 0)
|
| [8] |
CHERKASSKY V. The nature of statistical learning theory[J]. IEEE transactions on neural networks, 1997, 8(6): 1564. DOI:10.1109/TNN.1997.641482 ( 0) 0)
|
| [9] |
刘晓光, 郝沙沙, 王光磊, 等. 基于自相关特性的经验模态分解微机械陀螺去噪方法[J]. 中国惯性技术学报, 2016, 24(4): 537-541. ( 0) 0)
|
| [10] |
杨茂, 张强. 基于集合经验模态分解和相关向量机的风电功率实时预测研究[J]. 太阳能学报, 2016, 37(5): 1093-1099. DOI:10.3969/j.issn.0254-0096.2016.05.002 ( 0) 0)
|
| [11] |
王守相, 王亚旻, 刘岩, 等. 基于经验模态分解和ELM神经网络的逐时太阳能辐照量预测[J]. 电力自动化设备, 2014, 34(8): 7-12. DOI:10.3969/j.issn.1006-6047.2014.08.002 ( 0) 0)
|
| [12] |
SAHA A K, CHOWDHURY S, CROSSLEY P A. Modeling and performance analysis of a microturbine as a distributed energy resource[J]. IEEE transactions on energy conversion, 2009, 24(2): 529-538. DOI:10.1109/TEC.2009.2016123 ( 0) 0)
|
| [13] |
THANGIAH S R, NYGARD K E, JUELL P L. GIDEON: a genetic algorithm system for vehicle routing with time windows[C]//Proceedings the 7th IEEE Conference on Artificial Intelligence Application. Miami Beach, USA, 1991.
( 0) 0)
|
| [14] |
郭海湘, 诸克军, 胡杰, 等. GA-BP嵌套算法的理论及应用[J]. 数学的实践与认识, 2008, 38(1): 116-125. ( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


