近年来,隔离型三端口变换器在新能源发电、混合动力汽车、燃料电池汽车以及储能系统应用等需要同时连接和控制多个电源或者负载的场合中受到越来越广泛的关注,是电力电子技术研究领域研究和应用的热点问题[1-4]。隔离型三端口变换器通过三绕组高频变压器进行能量的传递,具有电气隔离、能够自由匹配电压等级等诸多优点。通过合理的设计变压器匝数比,隔离型三端口变换器可以实现在不同电压等级之间的电能传输,并且可以实现各个端口全桥变换器的软开关运行[5-7]。这对于提高功率变换器效率、降低损耗、提高功率密度是非常有益的。然而当端口电压或者负载功率在比较宽的范围变化时,会出现1个或者2个端口不能实现软开关的情况,导致开关损耗增加[8-10]。因此在三端口变换器设计阶段,通过理论分析可以准确地确定出在端口电压和负载功率变化情况下的三端口变换器软开关范围,这是一件非常有意义的工作,有助于整个变换器系统效率和功率密度设计的优化。本文通过分析隔离三端口变换器各端口与全桥变换器连接的变压器绕组中的电流波形和全桥变换器桥臂中点电压波形之间的关系,通过理论计算得出全桥变换器各开关管实现软开关运行的条件,进而利用MATLAB软件形象地绘制在特定电气参数条件下实现功率器件软开关的范围,并通过仿真和实际硬件电路实验进行验证。
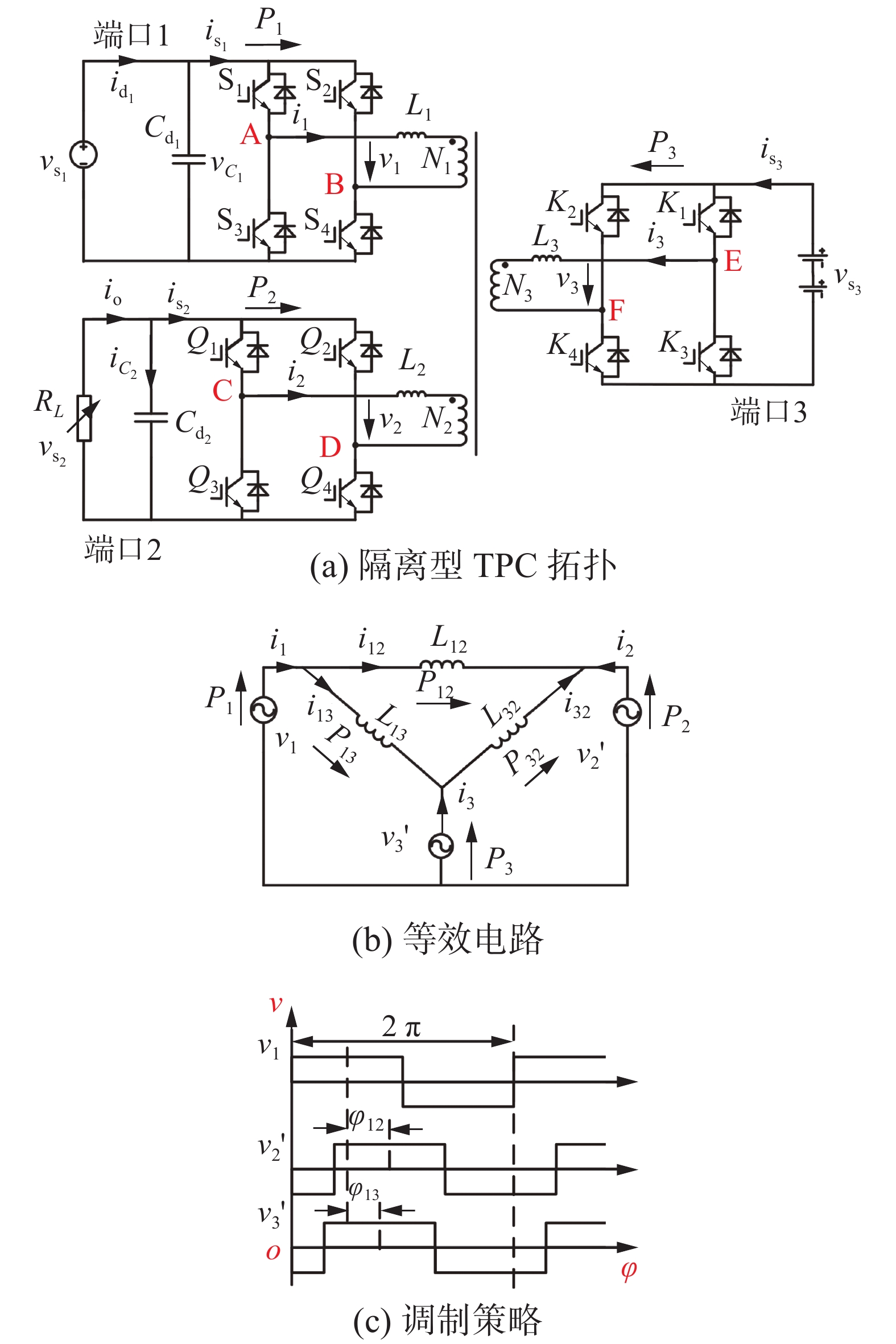
1 拓扑结构与软开关分析本文所研究的隔离型三端口变换器如图1所示。图中端口1为输入电源端口(可以为新能源发电系统的太阳能电池板等)。其全桥开关管为S1~S4,其中S1和S3,S2和S4均工作在互补状态,占空比均为50%。桥臂A和桥臂B之间的移相角为180°。端口2和端口3分别为负载端口和储能端口,其开关管的工作模式与端口1的情况完全一致。端口2和端口3对应的参数都折算到端口1,可得到图1(b)所示的△连接的等效电路[11],如图中v'2、v'3分别为v2和v3折算到端口1的对应桥臂中点电压。
|
Download:
|
| 图 1 隔离型三端口变换器 | |
以v1为参考,v2(v2')和v3(v3')与v1之间的移相角分别为φ12和φ13,它们之间的关系可以用图1(c)来表示。图1(a)中的L1、L2和L3分别为3个端口与变压器绕组串联的电感,经变换后得到在图1(b)所示的△连接的等效电路中的L12、L13和L32,可表示为
| $\left\{ {\begin{array}{*{20}{l}} {{L_{12}} = {L_1} + {L_2}^\prime + {{{L_1}{L_2}^\prime } / {{L_3}^\prime }}} \\ {{L_{32}} = {L_2}^\prime + {L_3}^\prime + {{{L_2}^\prime {L_3}^\prime } / {{L_1}}}} \\ {{L_{13}} = {L_3} + {L_1} + {{{L_1}{L_3}^\prime } / {{L_2}^\prime }}} \end{array}} \right.$ |
式中
| $\left\{ {\begin{array}{*{20}{c}} {{L_2}^\prime = {{N_1^2L_2^{}} / {N_2^2}}} \\ {{L_3}^\prime = {{N_1^2L_3^{}} / {N_3^2}}} \end{array}} \right.$ |
式中N1、N2和N3分别表示3个端口的绕组匝数。
根据图1(b)的△等效电路可以看出,隔离型三端口变换器可以看成3个两两作用的双有源桥变换器,因此通过分析双有源桥变换器中高频变压器绕组的电流,可以得出隔离型三端口变换器的各端口电流状况,进而可以对其实现软开关的条件进行分析研究。假设端口3开路,则可将端口1和端口2可看作一个双有源桥变换器,如图2所示。

|
Download:
|
| 图 2 双有源桥变换器拓扑结构 | |
根据图2,将端口2参数折算到端口1,可得到双有源桥变换器的简化等效电路模型如图3所示。

|
Download:
|
| 图 3 双有源桥变换器的简化等效电路模型 | |
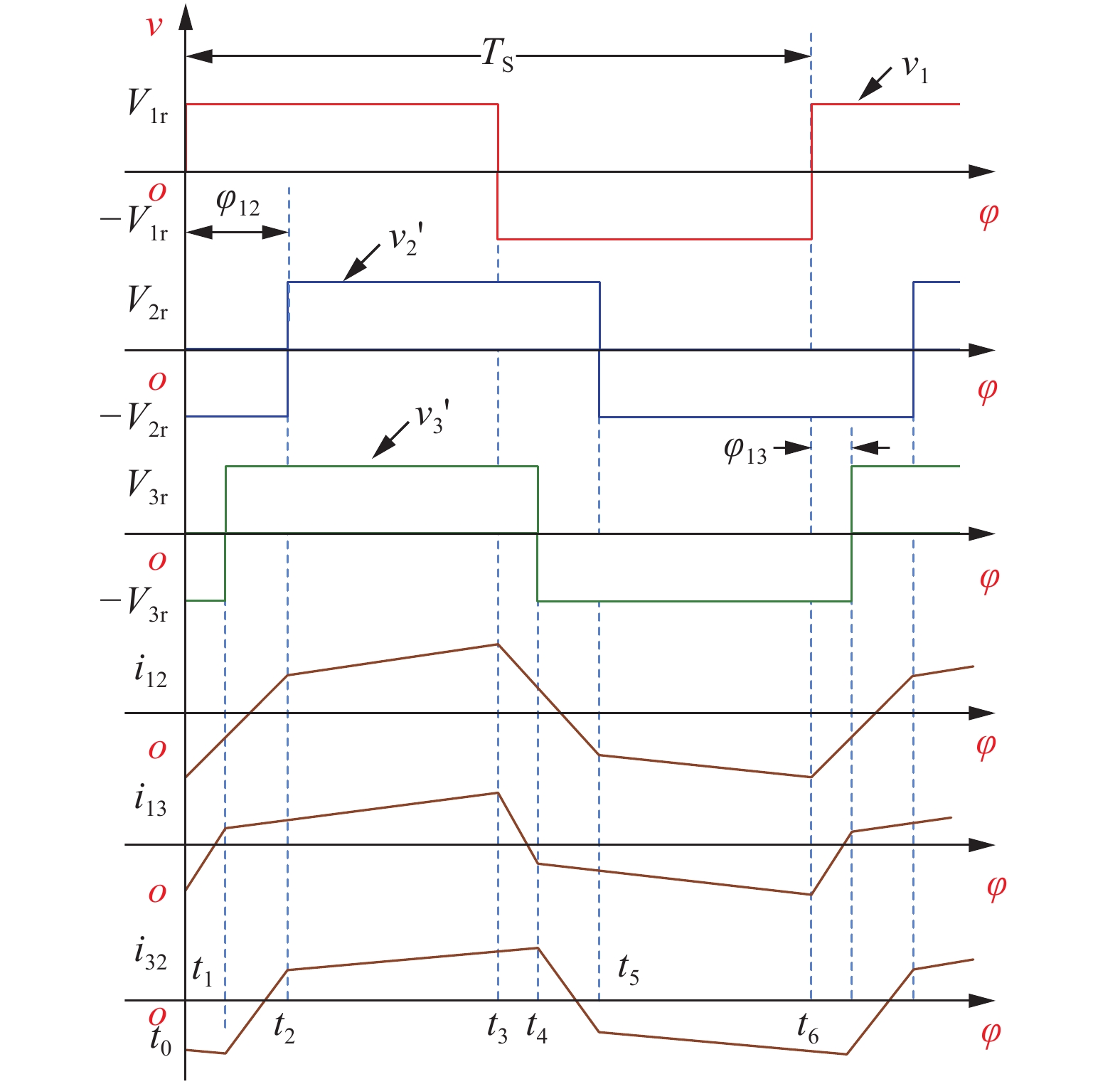
假设V1r和V2r表示v1和v2′的稳态幅值,其中V1r=vS1,V2r=vS2/n1,n1=N2/N1。同理,可设V3r=vS3/n2,n2=N3/N1。忽略死区时间,假设开关过程瞬时完成,即电流从一个桥臂开关管转移到另一个桥臂的开关管瞬时完成,则可得图4所示的电压与电流波形。
|
Download:
|
| 图 4 双有源桥电压和电流波形 | |
如图4所示,端口1桥臂中点的电压超前端口2桥臂中点的电压,在一个开关周期中根据v1和v2'的上升和下降边沿有4种开关模态。根据图3所示等效电路和图4所示开关模态,可得4种模态下折算后的端口1绕组中的电流i12:
| ${i_{12}}\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{V_{1{\rm{r}}}} + {V_{2{\rm{r}}}}}}{{{L_{12}}}}\left( {t - {t_0}} \right) + {i_{12}}\left( {{t_0}} \right)\;,\;\;{t_0} \leqslant t < {t_2}} \\ {\dfrac{{{V_{1{\rm{r}}}} - {V_{2{\rm{r}}}}}}{{{L_{12}}}}\left( {t - {t_2}} \right) + {i_{12}}\left( {{t_1}} \right)\;,\;\;{t_2} \leqslant t < {t_3}} \end{array}} \right.$ | (1) |
同理可得i13:
| ${i_{13}}\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{V_{1{\rm{r}}}} + {V_{3{\rm{r}}}}}}{{{L_{13}}}}\left( {t - {t_0}} \right) + {i_{13}}\left( {{t_0}} \right)\;,\;\;{t_0} \leqslant t < {t_1}} \\ {\dfrac{{{V_{1{\rm{r}}}} - {V_{3{\rm{r}}}}}}{{{L_{13}}}}\left( {t - {t_1}} \right) + {i_{13}}\left( {{t_1}} \right)\;,\;\;{t_1} \leqslant t < {t_3}} \end{array}} \right.$ | (2) |
根据电流的对称性可知:
| $\left\{ {\begin{array}{*{20}{l}} {{i_{12}}\left( {{t_3}} \right) = - {i_{12}}\left( {{t_0}} \right)} \\ {{i_{13}}\left( {{t_3}} \right) = - {i_{13}}\left( {{t_0}} \right)} \end{array}} \right.$ | (3) |
联立式(1)~(3),可得i12和i13在t0、t1和t2时刻(转折点处)的值分别为
| $\left\{ {\begin{array}{*{20}{l}} {{i_{12}}\left( {{t_0}} \right) = - \dfrac{{\left( {{V_{1{\rm{{\rm{r}}}}}} - {V_{2{\rm{{\rm{r}}}}}}} \right){\rm{{\text{π}} }} + 2{V_{2{\rm{{\rm{r}}}}}}{\varphi _{12}}}}{{4{\rm{{\text{π}} }}{f_{\rm{S}}}{L_{{\rm{12}}}}}}} \\ {{i_{12}}\left( {{t_2}} \right) = \dfrac{{\left( {{V_{2{\rm{{\rm{r}}}}}} - {V_{1{\rm{{\rm{r}}}}}}} \right){\rm{{\text{π}} }} + 2{V_{1{\rm{{\rm{r}}}}}}{\varphi _{12}}}}{{4{\rm{{\text{π}} }}{f_{\rm{S}}}{L_{{\rm{12}}}}}}} \end{array}} \right.$ |
| $\left\{ {\begin{array}{*{20}{l}} {{i_{13}}\left( {{t_0}} \right) = - \dfrac{{\left( {{V_{1{\rm{{\rm{r}}}}}} - {V_{{\rm{3{\rm{r}}}}}}} \right){\rm{{\text{π}} }} + 2{V_{{\rm{3{\rm{r}}}}}}{\varphi _{13}}}}{{4{\text{π}} {f_{\rm{S}}}{L_{{\rm{13}}}}}}} \\ {{i_{13}}\left( {{t_1}} \right) = \dfrac{{\left( {{V_{{\rm{3{\rm{r}}}}}} - {V_{1{\rm{{\rm{r}}}}}}} \right){\rm{{\text{π}} }} + 2{V_{1{\rm{{\rm{r}}}}}}{\varphi _{13}}}}{{4{\rm{{\text{π}} }}{f_{\rm{S}}}{L_{{\rm{13}}}}}}} \end{array}} \right.$ |
根据图1(b),由KCL定律可得:
| $\left\{ {\begin{array}{*{20}{l}} {{i_1} = {i_{1{\rm{2}}}}{\rm{ + }}{i_{1{\rm{3}}}}} \\ {{i_2}^\prime = - {i_{32}} - {i_{12}}} \\ {{i_3}^\prime = - {i_{13}} + {i_{32}}} \end{array}} \right.$ |
对照图1(a)以端口1为例。若要实现端口1全桥变换器的零电压开通(zero voltage switch ON,ZVS ON),则需要使i1在相位上滞后v1,即i1的过零点滞后于v1的过零点,这样可以保证在开关管触发信号到来时刻,其反并联二极管处于导通续流状态。例如对应v1的下降沿对应时刻t3需满足:
| ${i_1}({t_3}) = {i_{1{\rm{2}}}}({t_3}){\rm{ + }}{i_{1{\rm{3}}}}({t_3}) > 0$ |
即有
| $\frac{{\left( {{V_{1{\rm{{\rm{r}}}}}} - {V_{2{\rm{{\rm{r}}}}}}} \right){\rm{{\text{π}} }} + 2{V_{2{\rm{{\rm{r}}}}}}{\varphi _{12}}}}{{4{\rm{{\text{π}} }}{f_{\rm{S}}}{L_{12}}}} + \frac{{\left( {{V_{1{\rm{{\rm{r}}}}}} - {V_{3{\rm{{\rm{r}}}}}}} \right){\rm{{\text{π}} }} + 2{V_{3{\rm{{\rm{r}}}}}}{\varphi _{13}}}}{{4{\rm{{\text{π}} }}{f_{\rm{S}}}{L_{13}}}} > 0$ | (4) |
同理,可得到为了实现端口2和端口3变换器ZVS ON,需满足条件:
| $\left\{ {\begin{array}{*{20}{l}} {{i_2}^\prime ({t_5}) = - {i_{32}}({t_5}) - {i_{12}}({t_5}) > 0} \\ {{i_3}^\prime ({t_4}) = - {i_{13}}({t_4}) + {i_{32}}({t_4}) > 0} \end{array}} \right.$ |
对应有(过程省略):
| $\left\{ {\begin{array}{*{20}{l}} {\dfrac{{\left( {{V_{2{\rm{{\rm{r}}}}}} - {V_{3{\rm{{\rm{r}}}}}}} \right){\rm{{\text{π}} }} + 2{V_{3{\rm{{\rm{r}}}}}}{\varphi _{32}}}}{{4{\rm{{\text{π}} }}{f_{\rm{S}}}{L_{32}}}} + \dfrac{{\left( {{V_{{\rm{2{\rm{r}}}}}} - {V_{{\rm{1{\rm{r}}}}}}} \right){\rm{{\text{π}} }} + 2{V_{{\rm{1{\rm{r}}}}}}{\varphi _{12}}}}{{4{\rm{{\text{π}} }}{f_{\rm{S}}}{L_{12}}}} > 0} \\ {\dfrac{{\left( {{V_{3{\rm{{\rm{r}}}}}} - {V_{1{\rm{{\rm{r}}}}}}} \right){\rm{{\text{π}} }} + 2{V_{1{\rm{{\rm{r}}}}}}{\varphi _{13}}}}{{4{\rm{{\text{π}} }}{f_{\rm{S}}}{L_{13}}}} + \dfrac{{\left( {{V_{3{\rm{{\rm{r}}}}}} - {V_{2{\rm{{\rm{r}}}}}}} \right){\rm{{\text{π}} }} + 2{V_{2{\rm{{\rm{r}}}}}}{\varphi _{32}}}}{{4{\rm{{\text{π}} }}{f_{\rm{S}}}{L_{32}}}} > 0} \end{array}} \right.$ | (5) |
定义d12=vS2/(n1vS1)、d13=vS3/(n2vS1)、φ32=φ12−φ13,并假设L12=L13=L32,根据式(4)、(5)可以得到:
| $\left\{ \begin{array}{l} \left[ {\left( {1 - {d_{12}}} \right){\rm{{\text{π}} }} + 2{d_{12}}{\varphi _{12}}} \right] + \left[ {\left( {1 - {d_{13}}} \right){\rm{{\text{π}} }} + 2{d_{13}}{\varphi _{13}}} \right] > 0 \\ \left[ {\left( {{d_{12}} - 1} \right){\rm{{\text{π}} }} + 2{\varphi _{12}}} \right] + \left[ {\left( {{d_{12}} - {d_{13}}} \right){\rm{{\text{π}} }} + 2{d_{13}}{\varphi _{32}}} \right] > 0 \\ \left[ {\left( {{d_1}_3 - 1} \right){\rm{{\text{π}} }} + 2{\varphi _{13}}} \right] + \left[ {\left( {{d_{13}} - {d_{12}}} \right){\rm{{\text{π}} }} + 2{d_{12}}{\varphi _{32}}} \right] > 0 \end{array} \right.$ | (6) |
求解式(6)并化简整理后可得实现三端口变换器软开关的条件为(按照端口1到端口3的顺序自上而下排序)
| $\left\{ \begin{array}{l} {d_{12}} < \dfrac{{2{\rm{{\text{π}} }} + {d_{13}}(2{\varphi _{13}} - {\rm{{\text{π}} }})}}{{{\rm{{\text{π}} }} - 2{\varphi _{12}}}} \\ {d_{12}} > \dfrac{{{\rm{{\text{π}} }} - 2{\varphi _{12}} + {\rm{{\text{π}} }}{d_{13}} - 2{d_{13}}({\varphi _{12}} - {\varphi _{13}})}}{{2{\rm{{\text{π}} }}}} \\ {d_{12}} < \dfrac{{2{\varphi _{13}} - {\rm{{\text{π}} }} + 2{\text{π}} {d_{13}}}}{{{\rm{{\text{π}} }} - 2{\varphi _{12}} + 2{\varphi _{13}}}} \end{array} \right.$ | (7) |
或
| $\left\{ \begin{array}{l} {d_{13}} < \dfrac{{2{\rm{{\text{π}} }} - {d_{12}}({\rm{{\text{π}} }} - 2{\varphi _{12}})}}{{{\rm{{\text{π}} }} - 2{\varphi _{13}}}} \\ {d_{13}} < \dfrac{{2{d_{12}}{\rm{{\text{π}} }} - ({\rm{{\text{π}} }} - 2{\varphi _{12}})}}{{{\rm{{\text{π}} }} - 2({\varphi _{12}} - {\varphi _{13}})}} \\ {d_{13}} > \dfrac{{({\rm{{\text{π}} }} - 2{\varphi _{13}}) + {d_{12}}({\rm{{\text{π}} }} - ({\varphi _{12}} - {\varphi _{13}}))}}{{2{\rm{{\text{π}} }}}} \end{array} \right.$ |
根据式(7),在MATLAB中用m语言编程可形象地绘制出变换器的软开关范围。例如,当固定vS3和φ13时,可得实现三端口变换器软开关(ZVS ON)时d12与φ12需要满足的关系,如图5所示。图5中,阴影部分表示3个端口的变换器可以同时实现ZVS ON的范围。由图5分析可见,当任意两端口的移相角和电压等级确定后,三端口变换器开关管的ZVS ON范围与各个端口之间的移相角绝对值的大小有密切的关系,绝对值越大,实现软开关范围也越大。此外,由图5(a)、(c)和(d)对比可知,三端口变换器软开关的范围与3个端口间电压相对大小(即d12、d13)有关,某一端口电压增大,则该端口实现软开关范围变大而其他2个端口减小;反之,则该端口实现软开关范围减小而其他2个端口增大。对于隔离三端口变换器而言,d12=1且d13=1时所有端口实现软开关的范围最大[12-13]。

|
Download:
|
| 图 5 不同条件下软开关范围 | |
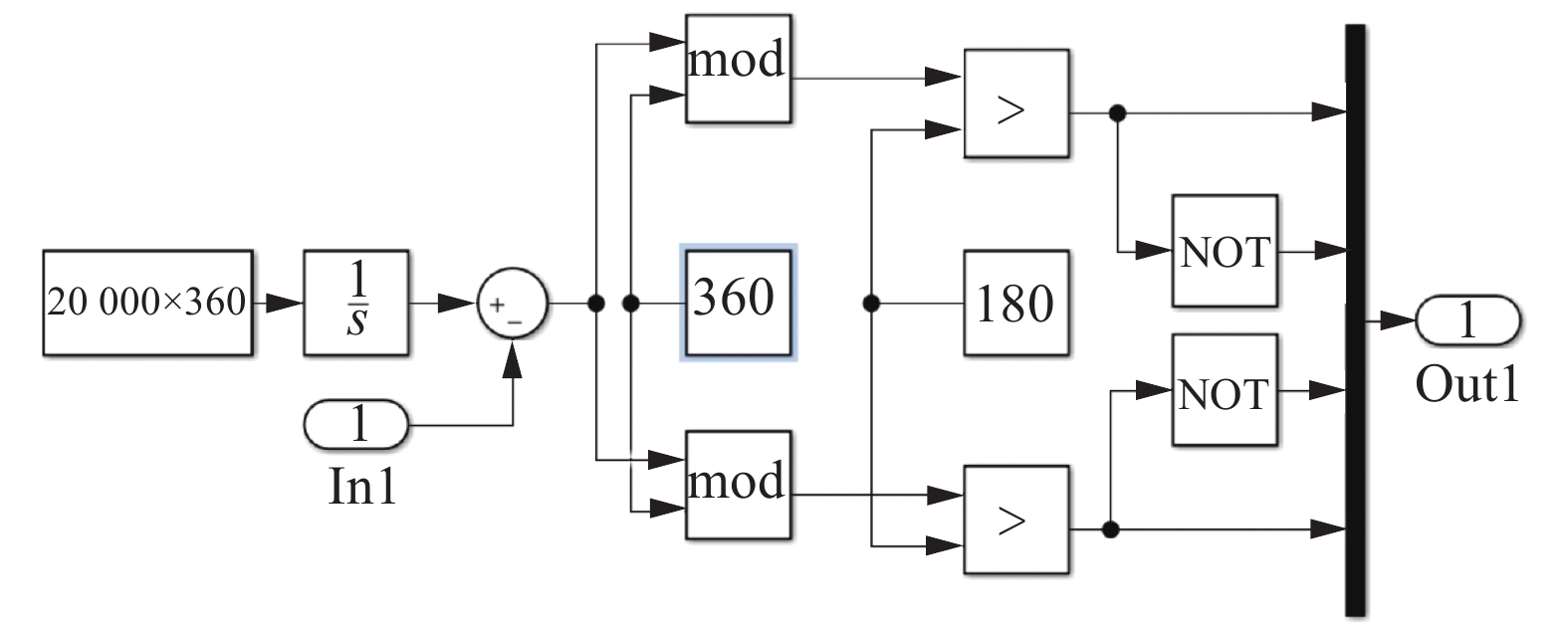
利用MATLAB/Simulink仿真软件,通过搭建隔离三端口变换器的仿真模型来验证上述理论分析的正确性。所搭建的Simulink仿真模型如图6所示。其中,移相模块的内部结构如图7所示(以图6中的PSPWM2模块为例)。

|
Download:
|
| 图 6 Simulink仿真模型 | |
|
Download:
|
| 图 7 移相模块内部结构图 | |
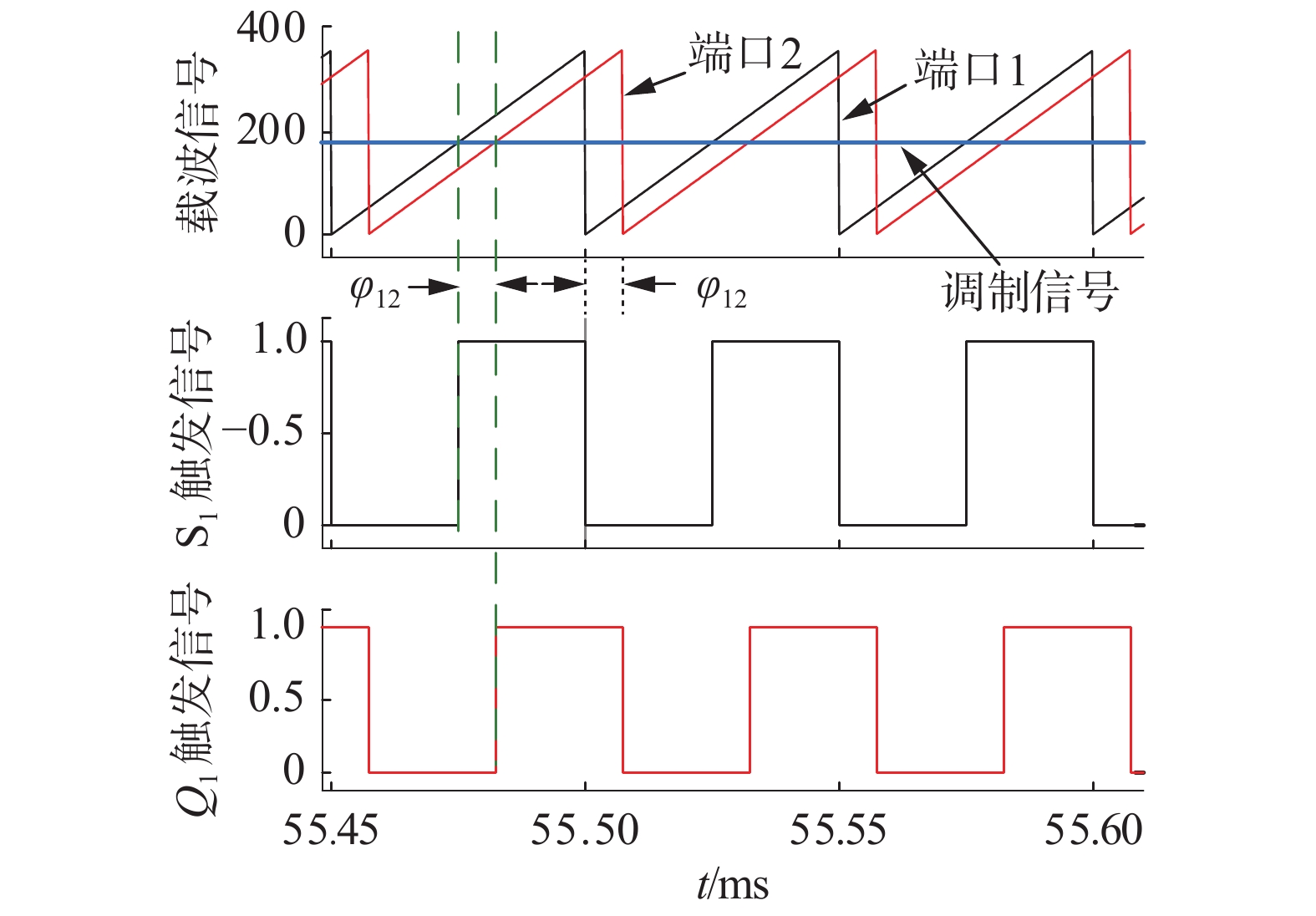
通过对开关频率与一个开关周期(2π)所对应的角度(360°)乘积的积分所产生的斜坡信号与所设置移相角作差,其结果以360为模进行取余运算。这样便产生了频率为20 kHz、幅值为360的周期性锯齿波信号,将其作为载波信号。所产生的脉冲信号用来控制开关管的通断。端口1和端口2的移相模块的输出波形如图8所示。
|
Download:
|
| 图 8 移相模块波形 | |
可以看出,端口1的载波信号超前于端口2的载波信号。因此,3个端口在相同的调制信号下(本文为180,即载波幅值的一半,产生50%占空比的脉冲信号)。端口1的开关管触发脉冲将超前于端口2的开关管触发信号,这是因为三端口变换器载波信号之间的相位差即为触发信号之间的移相角,从而实现了不同端口之间的移相控制。
2.2 仿真过程本文分别对2种负载情况进行开环仿真,仿真参数如表1所示。情况A为RL=45 Ω,情况B为RL=25 Ω。2种情况下负载电压vS2均保持为180 V。通过计算,RL=45 Ω时移相角φ12=35.5°,φ13=21.7°;而在RL= 25 Ω时φ12=52°,φ13=7.1°。这样使得在2种负载情况下,端口2的输出电压保持不变。如图5(a)、(b)中的标注所示。观察工作点A、B可见,处于较轻负载的情况A时,图5(a)中A点的位于阴影区所示的公共软开关区域之外,根据式(7)可知端口1和端口2均能实现软开关,端口3无法实现ZVS ON。当处于较重负载的情况B时,图5(b)中的B点位于阴影区域内部,故端口1、2和3均能实现ZVS ON。
|
|
表 1 仿真模型的主要参数 |
接下来分别对情况A和B进行仿真测试。对于较轻负载的情况A,三端口变换器桥臂中点电压和变压器原边绕组的电流仿真波形如图9所示。
|
Download:
|
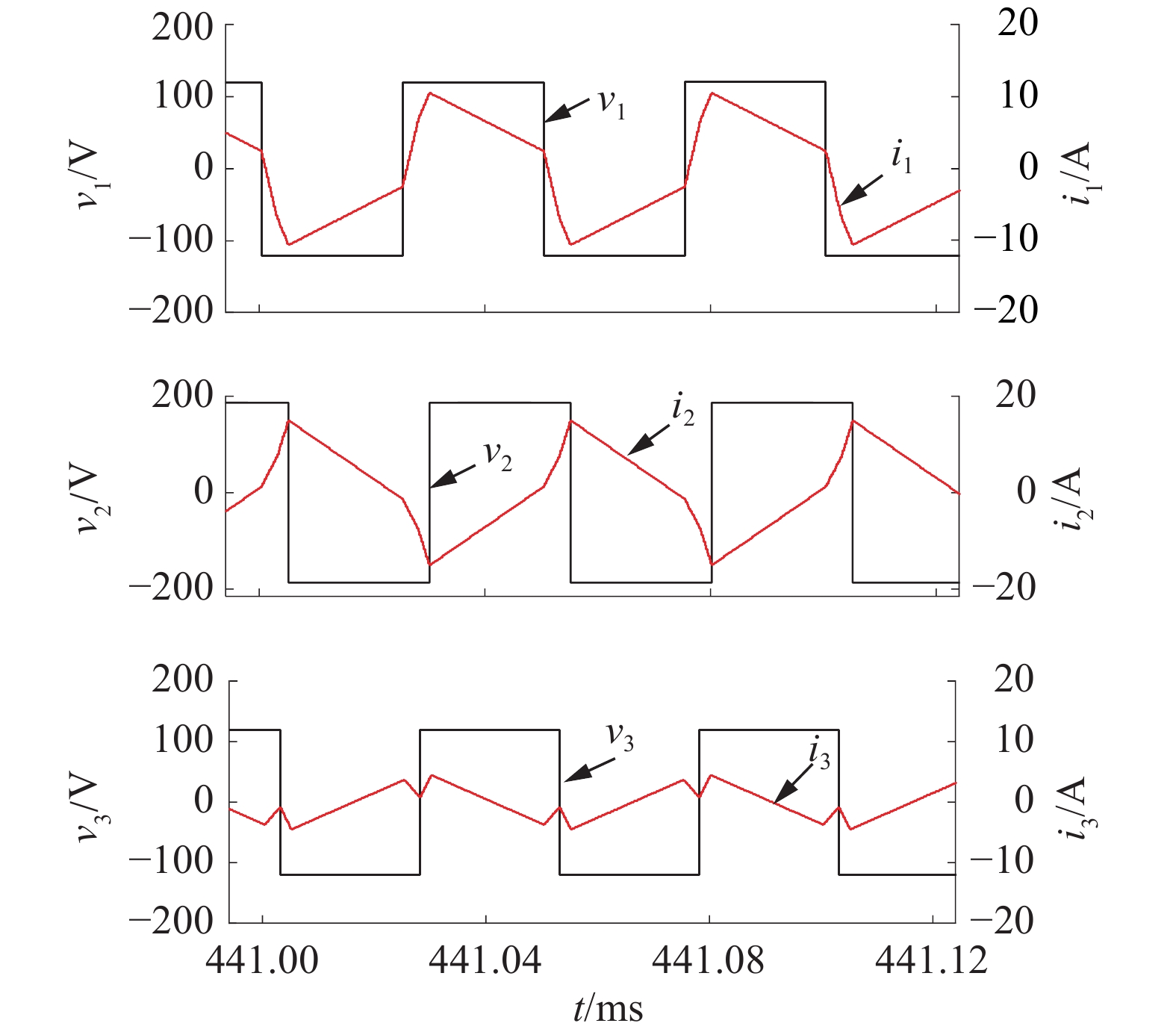
| 图 9 RL=45 Ω时的电压和电流仿真波形 | |
由图9可知,在此情况下,端口1和端口2的变压器绕组电流i1和i2分别在电压v1和v2上升沿时为负值,而在电压v1和v2的下降沿时为正,因此端口1和端口2可以实现ZVS ON;而端口3变压器绕组电流i3在电压v3的下降沿时为负值,因此无法实现软开通。在实际应用时,硬关断会产生更多的损耗。
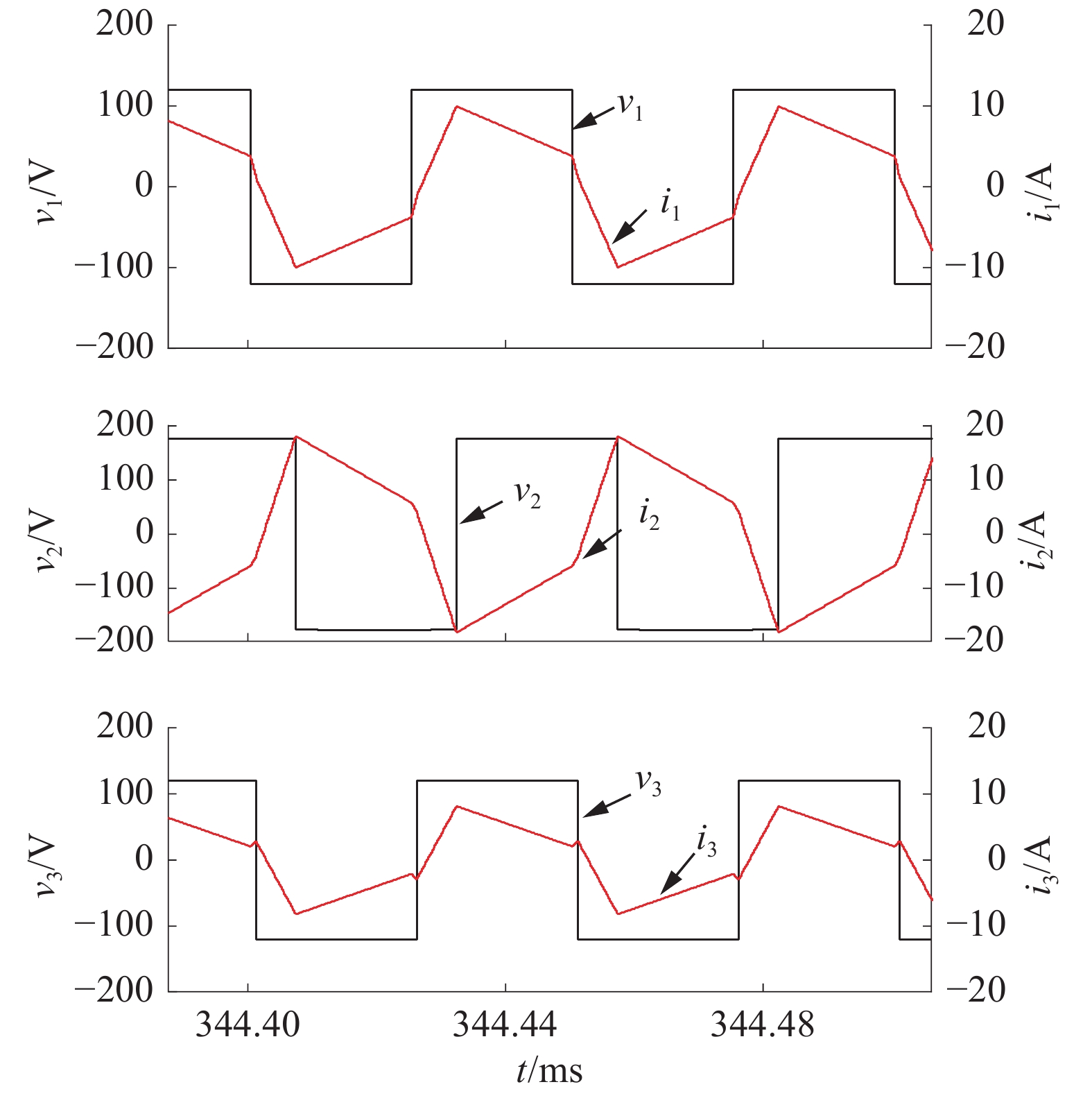
对于较重负载的情况B,3个端口变换器桥臂中点电压和变压器原边绕组的电流波形图如图10所示。可见,在此情况下对应v1、v2和v3的上升沿,i1、i2和i3均为负值,而在三端口变换器桥臂中点电压的下降沿时为正值,因此3个端口的全桥变换器的开关管都可以在此情况下实现ZVS ON。这与前文理论分析的结果是吻合的。
|
Download:
|
| 图 10 RL=25 Ω时的电压和电流仿真波形 | |
在理论分析和仿真验证的基础上,搭建了一台实验样机进行实验验证。隔离三端口变换器的硬件实物图如图11所示,硬件电路的主电路部分包括3个相同的控制板、含驱动电路的全桥变换器、三绕组高频变压器、负载电阻、直流输入电源和蓄电池。控制以STM32F407IGT6控制器为核心,通过其集成的可变静态存储控制器(flexible static memory controller,FMSC)总线与FPGA芯片EP4CE6E22C8接口,由后者产生12路移相控制脉冲信号。

|
Download:
|
| 图 11 硬件实验电路 | |
在实验过程中,通过STM32F407IGT6设定各端口的移相角,将这个移相角信号通过FSMC总线传输至EP4CE6E22C8芯片。对于较轻负载的情况A,分别设置移相角φ12=35.5°、φ13=21.7°。实验波形如图12所示。由图可知,在此情况下,端口1和端口2的变压器绕组电流i1和i2都分别在其变换器桥臂中点电压v1和v2的上升沿时为负值,而在桥臂中点电压的下降沿时为正值,因此可以实现ZVS ON。而端口3的变压器绕组电流在其全桥变换器桥臂中点电压v3的下降时为负,因此该变换器在此情况下是硬开通的。

|
Download:
|
| 图 12 RL=45 Ω时的电压和电流实验波形 | |
对于负载较重的情况B,分别设置移相角φ12=52°、φ13=7.1°。实验波形如图13所示。

|
Download:
|
| 图 13 RL=25 Ω时的电压和电流实验波形 | |
可见,3个端口的变压器绕组电流都分别在各变换器桥臂中点电压的上升沿时为负值,而在各变换器桥臂中点电压下降沿时为正值,因此3个端口的全桥变换器的开关管在此情况下都可以工作在ZVS ON状态。上述实验结果表明,理论分析和仿真与实验测试的结果具有很好的一致性。
4 结论基于隔离三端口变换器的拓扑结构和工作原理,本文分析了隔离型三端口变换器实现ZVS ON的工作范围,利用MATLAB/Simulink仿真工具对理论分析进行了验证,并在此基础上利用硬件电路对理论分析和仿真的结果进行了相应的验证。结果表明:理论分析所得出的特定条件下三端口变换器的软开关范围表达式的准确性得到了仿真和实验验证,可以用于实际系统研制时的辅助设计和参数优化,有助于整个变换器系统效率和功率密度的提高。
| [1] |
YOU Jiang, LIAO Mengyan, FAN Weiyan. Linear active disturbance rejection control for isolated three-port converter[C]//Proceedings of 2018 International Power Electronics Conference, Niigata, 2018: 1421–1425.
( 0) 0)
|
| [2] |
廖梦岩. 三端口变换器及其在配电系统中应用的研究[D]. 哈尔滨: 哈尔滨工程大学, 2019: 3–7.
( 0) 0)
|
| [3] |
邓明杰. 隔离型三端口变换器的分析和控制[D]. 哈尔滨: 哈尔滨工程大学, 2018: 1-6.
( 0) 0)
|
| [4] |
KARANAYIL B, CIOBOTARU M, AGELIDIS V G. Power flow management of isolated multiport converter for more electric aircraft[J]. IEEE transactions on power electronics, 2017, 32(7): 5850-5861. DOI:10.1109/TPEL.2016.2614019 ( 0) 0)
|
| [5] |
储凯. 三端口隔离型双向直流/直流变换器的设计与控制[D]. 南京: 东南大学, 2015: 2-10.
( 0) 0)
|
| [6] |
丁勇. 基于多端口变换器的电动汽车与电网集成网络研究[D]. 合肥: 合肥工业大学, 2015: 16-21.
( 0) 0)
|
| [7] |
LIU K H, LEE F C Y. Zero-voltage switching technique in DC/DC converters[J]. IEEE transactions on power electronics, 1990, 5(3): 293-304. DOI:10.1109/63.56520 ( 0) 0)
|
| [8] |
王政, 储凯, 张兵, 等. 移相占空比控制的三端口双向直流变换器[J]. 电机与控制学报, 2015, 19(7): 81-87. ( 0) 0)
|
| [9] |
ZHAO Chuanhong, ROUND S D, KOLAR J W. An isolated three-port bidirectional DC-DC converter with decoupled power flow management[J]. IEEE transactions on power electronics, 2008, 23(5): 2443-2453. DOI:10.1109/TPEL.2008.2002056 ( 0) 0)
|
| [10] |
肖建国. 用于新能源混合发电的三端口DC/DC变换器的研究[D]. 杭州: 浙江大学, 2011: 30-37.
( 0) 0)
|
| [11] |
TAO H, KOTSOPOULOS A, DUARTE J L, et al. A soft-switched three-port bidirectional converter for fuel cell and supercapacitor applications[C]//Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 2005: 2487–2493.
( 0) 0)
|
| [12] |
潘子周. 隔离型多端口桥式直流变换器软开关技术的研究[D]. 南京: 南京航空航天大学, 2013: 27-33.
( 0) 0)
|
| [13] |
蒋永杰. 三端口全桥变换器的优化零功率流控制策略[D]. 南京: 南京航空航天大学, 2014: 9-21.
( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


