近代多光谱辐射测温技术起源于20世纪70年代末期，Svet等^[1]利用四波长辐射测温方法对物体表面温度进行了测量，多波长辐射测温技术进入了一个快速发展的新时代。进入20世纪80年代后，一些西方国家开始尝试将多波长辐射测温技术应用于解决较难进行接触式测温的超高温物体表面温度的动态测量^[2]。符泰然等^[3]设计出紫外至近红外波段多光谱高温计，在测量波长接近时，将发射率模型近似为波长的简单线性模型，可测量波段域更广。周培森等^[4]提出了调谱平衡测温方法，采用信号平衡、零值调幅的方法，不必测量信号绝对值，可以直接依据普朗克公式对仪器进行标定。1995年，戴景民等^[5]研制出了棱镜分光无干涉滤光片式35波长高温计及国内第一套实用型金属凝固点(Cu，Al及Zn)黑体炉，为辐射温度精确定标做出了巨大贡献。1998年，孙晓刚等^[6]提出了利用BP神经网络处理光谱数据，在发射率模型已知的情况下，利用大量样本训练后的BP神经网络能大幅提高测量精度。1999年，杨立等^[7]通过分析影响测温误差的各种因素，给出了测温误差的理论计算公式。2017年，张福才等^[8]提出了将温差影响因子引入发射率模型的多光谱辐射测温方法并进行了可行性分析，通过引入温差变量，使该发射率模型变化趋势更接近实际发射率变化，有效提高了测温精度和稳定程度。

多光谱辐射测温最根本的问题为通过N个通道测量N组数据后，有N个通道的发射率和测量温度，共N+1个未知数。由于欠定方程解不唯一，为了减少方程个数，使方程组具有唯一解，目前比较通用的办法是假设不同通道的发射率变化趋势符合某种函数变化规律，从而减少未知数维度^[9]。以往研究通常是假设一个经典发射率模型，受温度、被测物体表面材料等因素影响，发射率与波长之间的关系较为复杂，不同表面材料的被测物体发射率模型一般不同；表面材料相同时，发射率模型一般相同，参数有所变化。随着温度的变化，反射率真实值仍与发射率模型计算值有一定误差^[10]。本文在传统发射率模型的基础上增加了温度修正，结合对关键算子改进后的非支配排序遗传算法(non-dominated sorting genetic algorithm II，NSGA-II)，改良其编译、交叉算子，选取适当参数后，在保证速度的基础上，进一步提高了计算精度，并进行了相应的实验验证。

1 多光谱辐射测温的基本原理

绝对黑体即能将入射的所有波长的光谱辐射吸收的物体。根据普朗克定律可知，当物体温度大于绝对零度时，会释放出热辐射。黑体的光辐射强度 ${M_{\rm{b}}}$ 与波长λ、绝对温度T之间的关系可以表示为

${M_{\rm{b}}}\left( {\lambda ,T} \right) = \frac{{{C_1}{\lambda ^{ - 5}}}}{{{{\rm{e}}^{{{{C_2}} / {\lambda T}}}} - 1}}$

式中： ${C_{\rm{1}}}$ 和 ${C_{\rm{2}}}$ 为光谱辐出度常数，当 $\lambda T < < 1$ 时，根据韦恩公式，黑体辐射定律可近似表示为

${M_{\rm{b}}}\left( {\lambda ,T} \right) = {C_{\rm{1}}}{\lambda ^{ - 5}}{\rm{exp}}\left( { - \frac{{{C_{\rm{2}}}}}{{\lambda T}}} \right)$

设温度测量系统有n个通道，则其中i通道的光谱强度V_i为

${V_i} = {\varepsilon _i}\left( {{\lambda _i},T} \right){M_{\rm{b}}}\left( {{\lambda _i},T} \right)$

(1)

式中：λ_i为第i通道波长；T为相应通道测量温度； ${\varepsilon _i}\left( {{\lambda _i},T} \right)$ 为被测物体表面发射率。对于n个通道的测量系统，得到的数据可以构成n个测量方程，其中含有n+1个未知数(n个ε和T)，这属于欠定方程问题，从理论上有无限个解，无法求出唯一的有效解。为解决这一问题，以往主要研究的方法通过含有λ_i的表达式替换 ${\varepsilon _i}\left( {{\lambda _i},T} \right)$ ，从而将未知数降到n个以下。但是在实际测试中，含有λ_i的表达式往往不能完全替代发射率，其中会引入一定误差。在张福才等^[8]的研究中引用了温差模型，通过迭代的方式解算出物体温度。但是迭代初始时必须通过黑体炉标定出物体在某一初始温度下的发射率，而实际应用中，同一材料不同物体的发射率也不一定相同，在应用过程中测量其发射率很难实现。将传统发射率模型与温差模型结合，无需测量初始发射率，通过非支配排序算法，即可计算出物体温度。

2 基于发射率温差模型的测温算法 2.1 发射率模型 2.1.1 经典发射率模型

为求解出测量温度T，必须对方程进行降维，目前应用较多的发射率模型有

$\varepsilon (\lambda ,T) = {a_0} + {a_1}\lambda $

$\ln \varepsilon (\lambda ,T) = \sum\limits_{i = 0}^m {{a_i}{\lambda ^i}} \;\;(m \leqslant n - 2)$

$\varepsilon (\lambda ,T) = {{\rm{e}}^{\left[ { - {{\left( {{a_0} + {a_1}\lambda } \right)}^2}} \right]}}$

$\varepsilon (\lambda ,T) = \frac{1}{2}\left[ {1 + \sin ({a_0} + {a_1}\lambda )} \right]$

不同的材料一般有不同的模型，当所选发射率模型与实际发射率变化趋势相符时，测温误差一般可以控制在一定范围内。目前还没有一个发射率模型可以应用于所有材料上。在实际应用中，最重要的就是确定合适的发射率模型。一个发射率模型确定的测温系统应该应用在某一特定的材料测温中，如需测量多种材料温度，一般应加入发射率模型判断系统。

2.1.2 引入温差算子的发射率模型

发射率的变化是无法准确计算的，实际上它不仅仅与波长相关，和被测物体温度、材料表面状态等都有关系。为了提高测温精度，本文改进了传统发射率模型，引入了温差算子，使发射率模型的变化趋势更符合实际情况。发射率模型设定为

$\varepsilon (\lambda ,T) = \Bigg(1 + k_{\rm{T}}{\Bigg(\frac{{T - {T_0}}}{{{T_0}}}\Bigg)^2}\Bigg) \times \sum\limits_{i = 0}^2 {{a_i}{\lambda ^i}} $

(2)

式中：k_T为温差系数；T₀为温度中心点。此模型在考虑到发射率随波长变化的同时，引入了影响发射率变化的温度因子，在测量某种材料的物体时，引入的温差系数使发射率更加贴合实际值，从而进一步降低误差。

2.2 非支配排序算法 2.2.1 经典非支配排序算法

在求解测量温度时，n个通道共可以列出n个方程。由式(1)和(2)可知，其中共有5个未知数，分别为温差系数、测量温度及3个发射率系数。为求解测量温度，通道数n应不小于5。由于测量每通道辐射强度数据时会引入测量误差，为提高系统信息冗余度，通道数n应大于等于6，本文取n为6。由于方程数多于未知数个数，属于超定方程，可能无法解出有效结果，可以转换成多目标优化类问题，设测量温度为T，目标函数记为

$\delta = \sum\limits_{i = 1}^6 {{{\left( {{M_i} - {M_{i0}}} \right)}^2}} $

理论上各通道测量温度需要相同，但由于误差的存在，各通道的测量温度可能是一组相近的温度值。为使误差最小，应令目标函数值尽量趋近于最小。目前解决此类问题应用最为广泛的多目标优化算法是带有精英策略的NSGA-II算法，可在一次运行过程中得出多个高质量的解^[11]。但是NSGA-II算法在求解时更关注最优解的质量，然而解集的分布性方面相对较差，且经典NSGA-II算法收敛速度较慢。本文从自适应角度出发，改进了NSGA-II算法的选择、变异、交叉算子，改善了算法解集前期多样性及后期收敛速度。

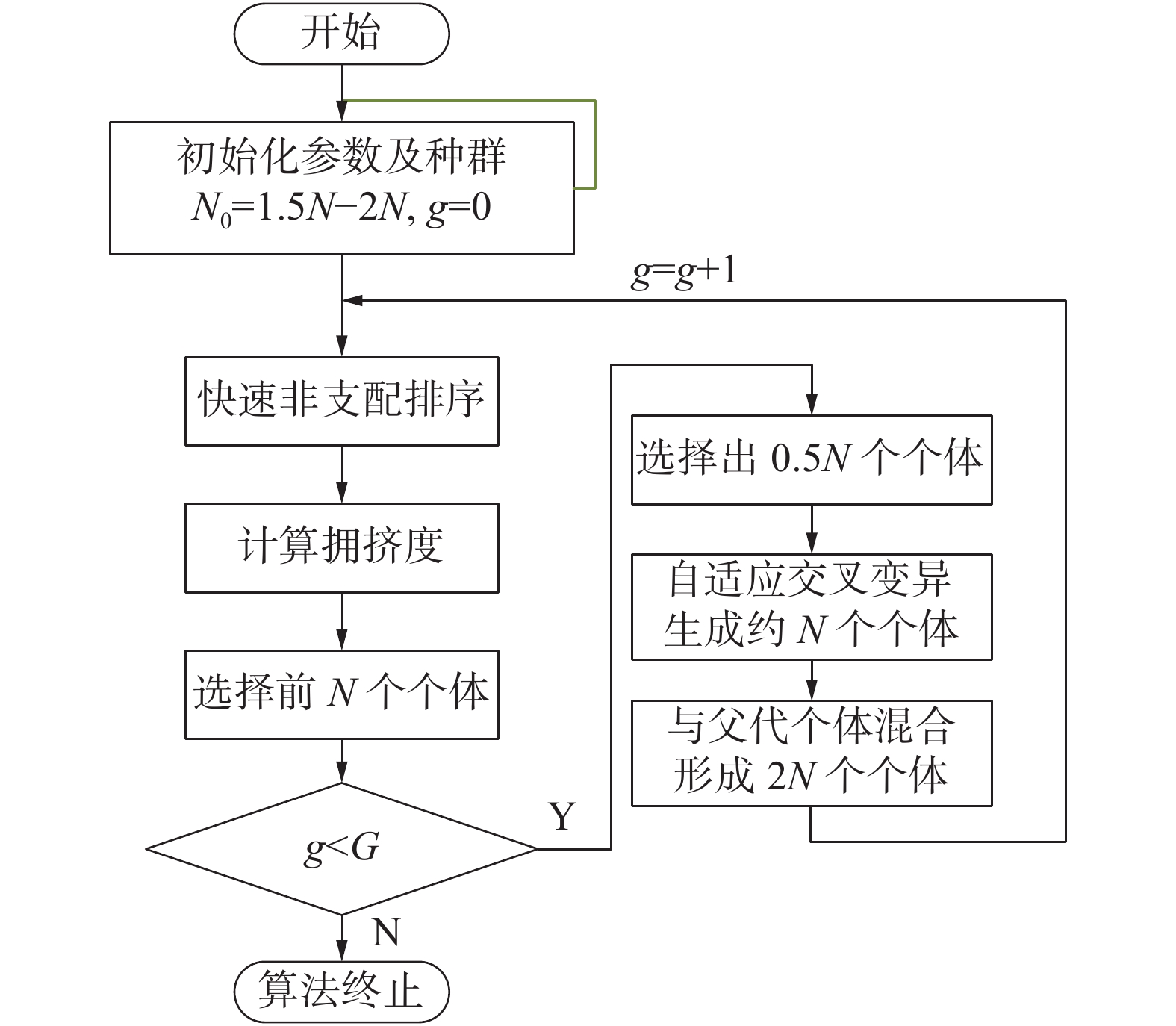
2.2.2 改进的非支配排序算法

在整个变量取值空间内分布较为均匀的初始化种群可以使遗传算法更好地在整个空间内寻找最优解，避免计算结果陷入局部最优解，本文的初代种群初始化是在变量取值范围内取随机值，种群数量较少时，可能出现种群在局部最优解处聚堆现象，而过多的种群数量会使遗传算法的计算时间变长。本文采取增加初始化种群数量而子代种群数量不变的方式，提高初始化种群分布性，在保证遗传算法初始进化方向的同时，运算时间较短。同时，本文从非支配排序算法中的选择、交叉、变异等关键算子方面进行了改进，并保留传统NSGA-II算法中的快速非支配排序、拥挤度计算算子，改进后的NSGA-II算法流程如图1所示。

2.2.3 改进的自适应概率选择算子

选择算子的作用是选出父代种群中的优良个体，通过交叉变异形成新的子代种群，它决定了进化的方向。经典NGSA-II算法的选择算子通常采用二元竞赛选择，随机从上一代种群取2个不同的子代个体，比较出排序等级较小、拥挤度较大的个体，然而这种方法很有可能使结果陷入局部最优解或者出现早熟^[12]。

选择算子的作用主要是为了令进化能向着全局最优解前进。在进化初期，为了增加种群的分布性，可使选择算子以相对较大的概率选择非最优解。随着进化的进行，当进化到中期后，降低选择算子选择非最优解的概率，提高算法的收敛性。改进的选择算子如下

${P_{\rm{s}}} = \frac{1}{{1 + {\rm{exp}}\left( {\dfrac{{ - kg}}{G}} \right)}}$

式中：k为选择系数，本文建议取为10，g和G分别为遗传算法当前进化代数和进化总代数。在进化初期，P_s约等于1/2，选择算子有一半的概率选择非最优解，可以提高种群的分布性，而在进化后期，此时种群主要分布在最优解附近，P_s约等于1，可提高种群的收敛速度。该算子从进化整体过程的角度考虑，对进化不同进程中的不同情况，加入了适应性策略，可以提高种群对进化环境的适应能力。

2.2.4 改进的个体交叉率及变异率算子

交叉变异算子是遗传算法的重要部分，如果设置交叉变异率过小，很容易使种群陷入局部最优或者早熟，而如果概率偏大则可能造成种群收敛变慢甚至不收敛^[13]。本文采用自适应概率策略，引入进化代数、种群数量等信息，动态地调整交叉变异概率。在不同阶段，使用不同的概率模型。在同一阶段内，交叉变异概率会随着种群进化的进行而逐渐下降，从而保证了算法的收敛性。由于NSGA-II算法更新到一定代数时，新的父代种群多样性会急剧下降^[14]。此时经过选择算子筛选出来的当前最优解总是围绕在一个点周围，很可能最终结果是局部最优解。

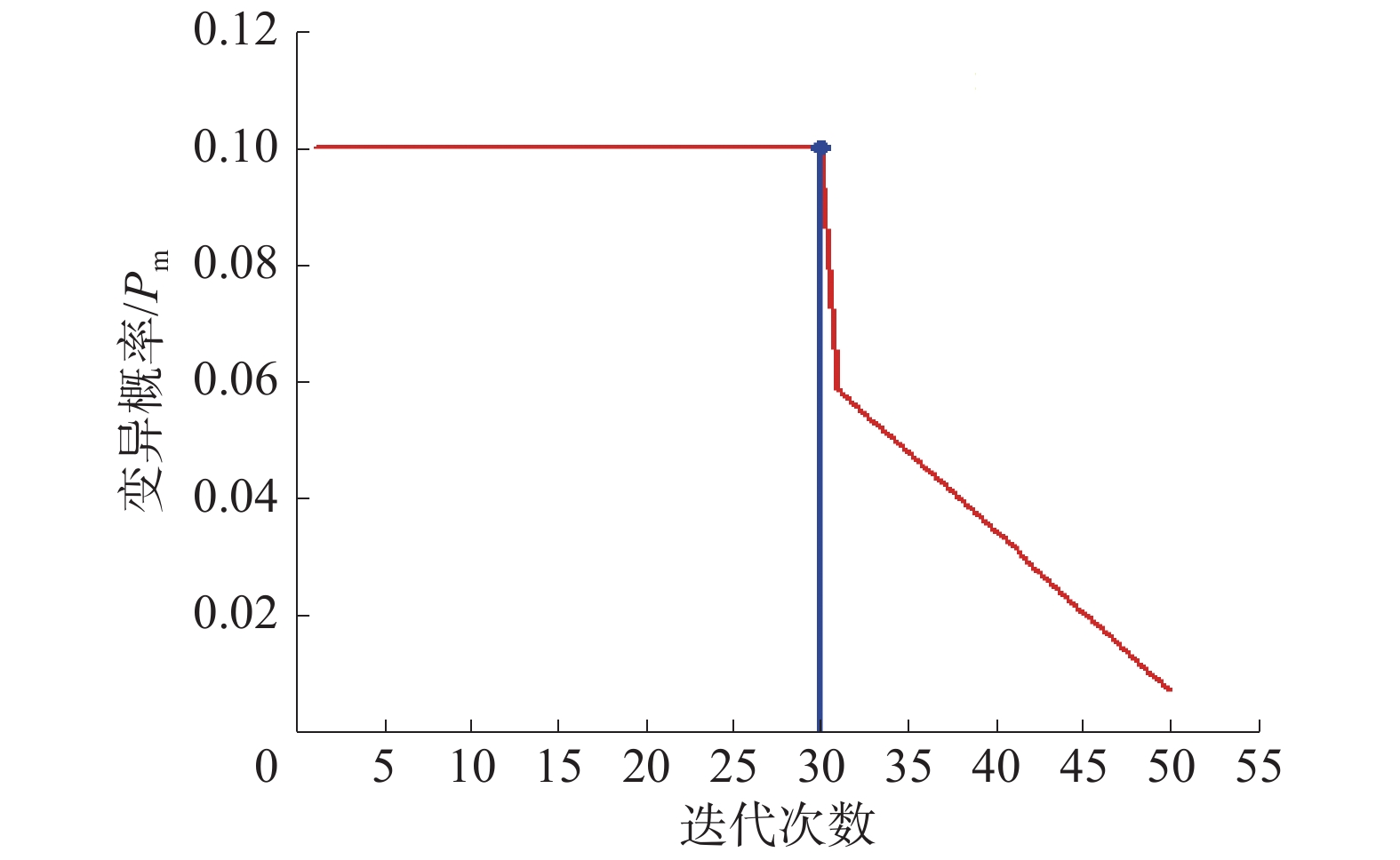
本文中的变异概率算子引入了当前子代中非支配个体数作为判定条件，若当前子代中存在支配解，即非支配排序层数大于1时，变异概率有

${p_{\rm{m}}} = \left\{ \begin{array}{l} 0.1,\;g \leqslant \left( {1 - \alpha } \right)G \\ \dfrac{{0.1\beta }}{V} + \dfrac{{0.1\left( {1 - \dfrac{1}{V}} \right)\left( {G - g} \right)\left( {1 - \beta } \right)}}{{\alpha G}},\;g > \left( {1 - \alpha } \right)G \end{array} \right.$

(3)

式中：V为变量个数；β为进化概率系数，本文取0.35；α为进化阶段划分参数，一般取为0.382。此时，变异概率随着进化变化曲线如图2所示，变异概率始终小于0.1，且随着进化的进行而变异概率不断变小，最后接近于0但不为0。

若当前子代中不存在支配解，即非支配排序层数等于1时，变异概率有

${p_{{\rm{m}}i}} = \left\{ \begin{array}{l} {P_{\rm{m}}},\;i \leqslant 0.5N \\ \dfrac{{{P_{\rm{m}}} + 0.1}}{2},\;{\rm{ 0}}{\rm{.5}}N < i \leqslant {\rm{0}}{\rm{.75}}N \\ {\rm{0}}{\rm{.1, }}\;i > {\rm{0}}{\rm{.75}}N \end{array} \right.$

式中：i为当前种群中第i个个体；N为种群数；P_mi为第i个个体的变异概率。当子代种群中所有个体不存在支配关系时，种群分布性较差、多样性下降。令子代种群前50%的变异概率为式(3)中计算结果，同时提高种群后50%的变异概率，可以提高子代种群分布多样性，保证种群的进化方向且使进化不会陷入早熟和局部最优。

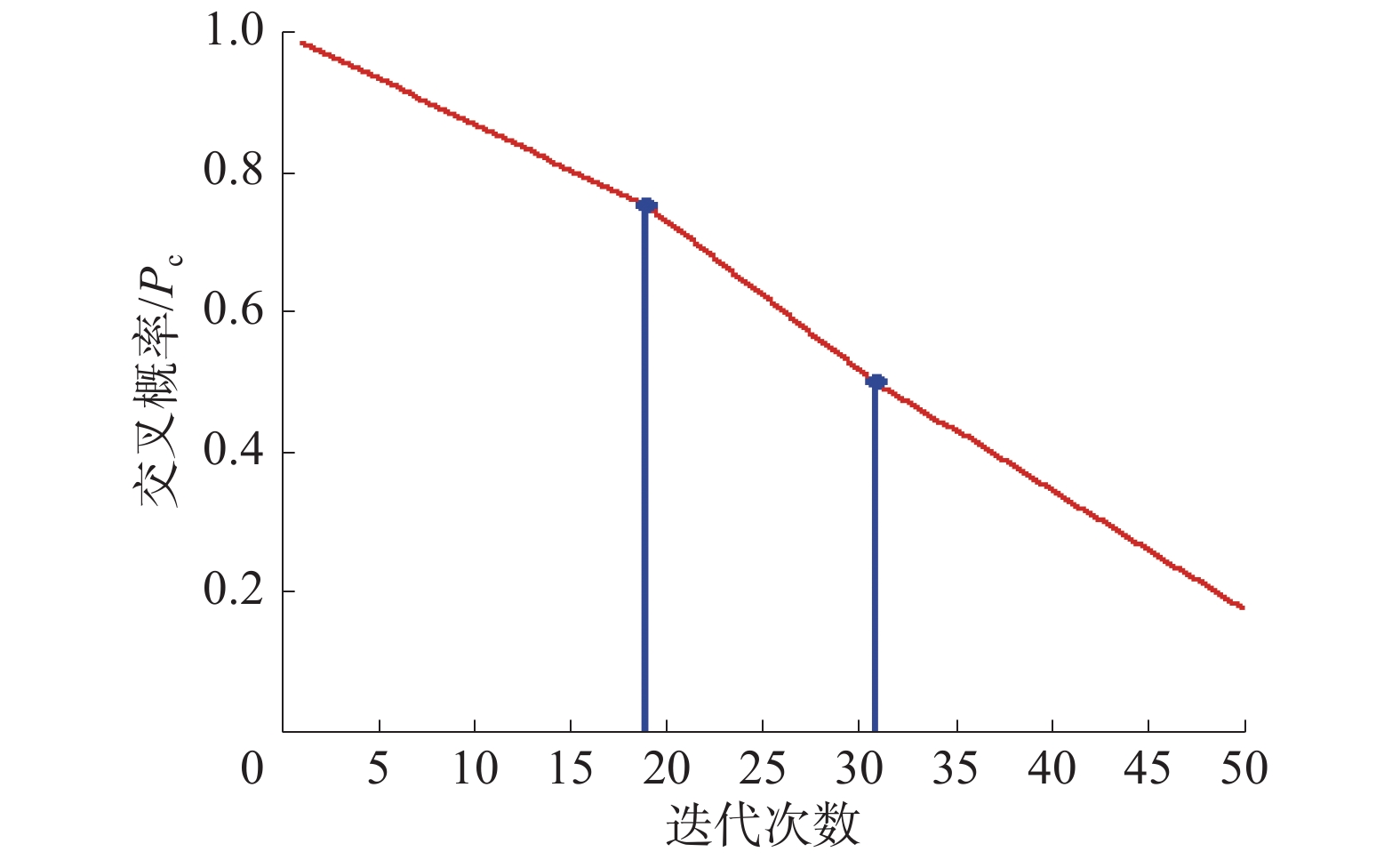
本文使用的交叉率算子最大交叉率为1，且随着进化的不断进行，在进化的不同阶段，交叉率不断下降且最终下降为一个接近于0的非零值，交叉概率算子可以表示为

${P_{\rm{c}}} = \left\{ \begin{array}{l} 0.75 + \dfrac{{0.25\left( {{T_1} - g} \right)}}{{{T_{\rm{1}}}}}{\rm{, }}\;g \leqslant {T_1} \\ 0.5 + \dfrac{{0.25\left( {{T_2} - g} \right)}}{{\left( {{T_2} - {T_1}} \right)}},\;{T_1} < g \leqslant {T_2} \\ 0.5\beta + \dfrac{{0.5\left( {G - g} \right)\left( {1 - \beta } \right)}}{{G - {T_2}}}{\rm{, }}\;{T_2} < g \end{array} \right.$

式中阶段划分值 ${T_1} = \alpha G$ ， ${T_2} = \left( {1 - \alpha } \right)G$ 。交叉概率变化曲线如图3所示。交叉概率变化曲线分为3个阶段。第1阶段为NGSA-II算法初始阶段，为提高种群多样性，可将交叉概率设置较高，交叉概率范围为[0.75,1)，较高的交叉概率可以保证初始种群以较大概率分布在整个决策变量取值范围；在第2阶段，种群中有个体在最优解周围分布，此时减小交叉概率，交叉概率范围为[0.5,0.75)，使子代种群不断向最优解靠拢，保证了种群的进化方向；在第3阶段，为了使种群快速收敛，令交叉概率变化范围为[0.5β,0.5)，随着交叉概率逐渐趋于0，种群中的个体也不断向全局最优解附近收缩并趋于稳定。

本文引用的交叉变异概率算子，既考虑了种群整体进化进程，又考虑了种群中个体进化程度，能够动态自适应地调节子代交叉变异概率。

2.2.5 交叉算子及变异算子的调整

经典NSGA-II所采用的交叉变异算子未考虑算法的进化进程，在全局搜索能力上较弱，可能陷入局部最优解。本文采用模拟二进制交叉(simulated binary crossover, SBX)混合正态分布交叉算子(normal distribution crossover, NDX)，引入进化代数g变量，动态地调节交叉算子系数，令子代个体变量值在两父代个体之间根据系数变化。在进化初期，为提高种群多样性，令NDX算子权值增加，使搜索空间增大；在进化后期，为提高种群的收敛性，令SBX算子权值增加，使子代个体在最优解附近收敛。取u为服从区间(0，1)内均匀分布的随机变量，当 $u \leqslant 0.5$ 时，交叉算子计算公式为

$\left\{ \begin{array}{l} {\rm{child}}1\left( i \right) = \dfrac{g}{{2G}}\left( {{S_1} + \alpha {S_2}} \right) + \dfrac{{G - g}}{{2G}}\left( {{S_1} + 1.841{S_2}r} \right) \\ {\rm{child}}2\left( i \right) = \dfrac{g}{{2G}}\left( {{S_1} - \alpha {S_2}} \right) + \dfrac{{G - g}}{{2G}}\left( {{S_1} - 1.841{S_2}r} \right) \\ \alpha = {\left( {2u} \right)^{\frac{1}{{\eta + 1}}}} \end{array} \right.$

当 $u > 0.5$ 时，交叉算子计算公式为

$\left\{ \begin{array}{l} {\rm{child}}1\left( i \right) = \dfrac{g}{{2G}}\left( {{S_1} + \alpha {S_2}} \right) + \dfrac{{G - g}}{{2G}}\left( {{S_1} - 1.841{S_2}r} \right) \\ {\rm{child}}2\left( i \right) = \dfrac{g}{{2G}}\left( {{S_1} - \alpha {S_2}} \right) + \dfrac{{G - g}}{{2G}}\left( {{S_1} + 1.841{S_2}r} \right) \\ \alpha = {\left( {\dfrac{1}{{2\left( {1 - u} \right)}}} \right)^{\frac{1}{{\eta + 1}}}} \end{array} \right.$

式中： ${S_1} = {\rm{parent}}1(i)\; + \;{\rm{ parent}}2(i)$ 、 ${S_2} = {\rm{parent}}1(i) - $ ${\rm{parent}}2(i)$ ；child1(i)、child2(i)为第i个变量交叉后产生的子代；r为服从N(0，1)高斯分布的随机变量；η为交叉变异算子参数，计算公式为

$\eta = 1 + \frac{{\left( {{\eta _{\max }} - 1} \right)g}}{G}$

式中： ${\eta _{\max }}$ 取为20，η随着进化的不断进行而增加，子代与父代距离逐渐缩短。

本文引入的变异算子为

${\rm{child}}\left( i \right) = \left\{ \begin{array}{l} {\rm{parent}}\left( i \right) + {\left( {2r} \right)^{\frac{1}{{\eta + 1}}}} - 1,\;r < 0.5 \\ {\rm{parent}}\left( i \right) + 1 - {\left( {2\left( {1 - r} \right)} \right)^{\frac{1}{{\eta + 1}}}},\;r \geqslant 0.5 \\ \end{array} \right.$

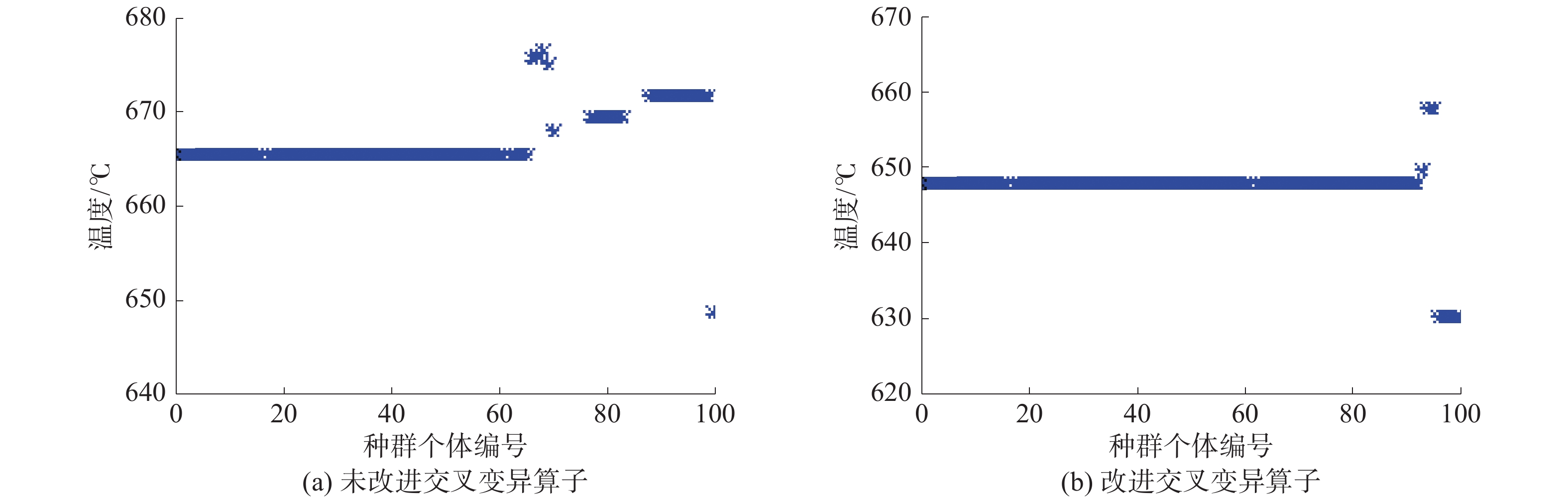
在进化初期，变异算子使子代个体在距离较远距离内波动；在进化后期，子代个体向父代个体收缩，算法迅速收敛。未改进交叉变异算子与改进后算法进化末期种群温度值结果如图4所示。

3 实验验证

待测物体为涡轮叶片，将涡轮叶片置于黑体炉中，用热电偶测量其表面温度，同时用HIT−4型多光谱辐射测温仪测量其表面辐射强度，并在500~900 ℃变化，用6波长GA算法、NSGA-II算法、改进的NSGA-II算法分别测量涡轮叶片表面温度，实验中使用的部分数据如表1所示。

GA算法参数设置及3种算法的变量搜索空间如表2、3所示。为衡量算法测温的稳定程度，引入均方误差定义为

$\begin{split}\;\\ &{s^2} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{T_i} - {T_{i0}}} \right)}^2}} \end{split}$

式中：N为计算总点数；T_i为第i点计算温度，T_i0为第i点真实温度。

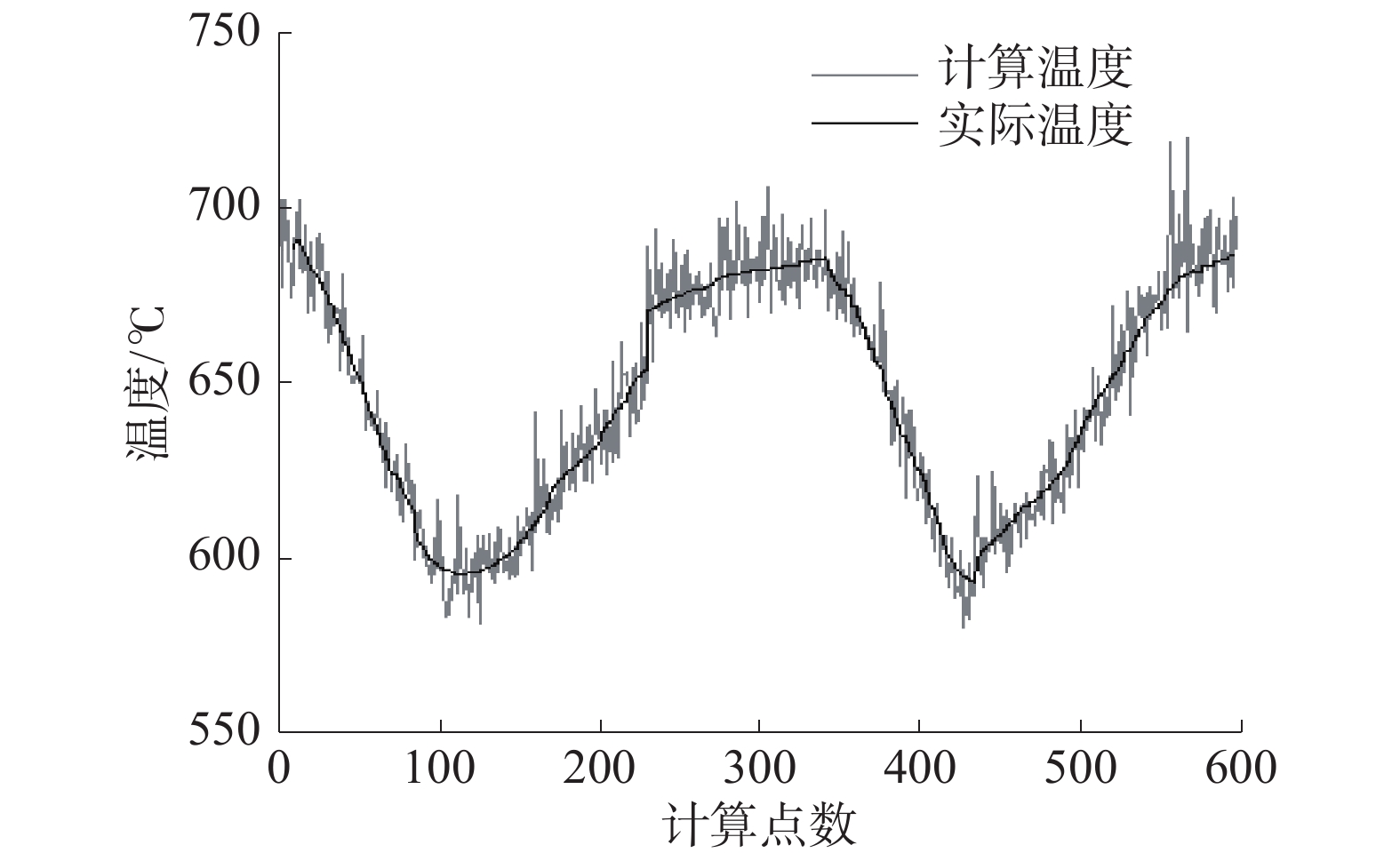
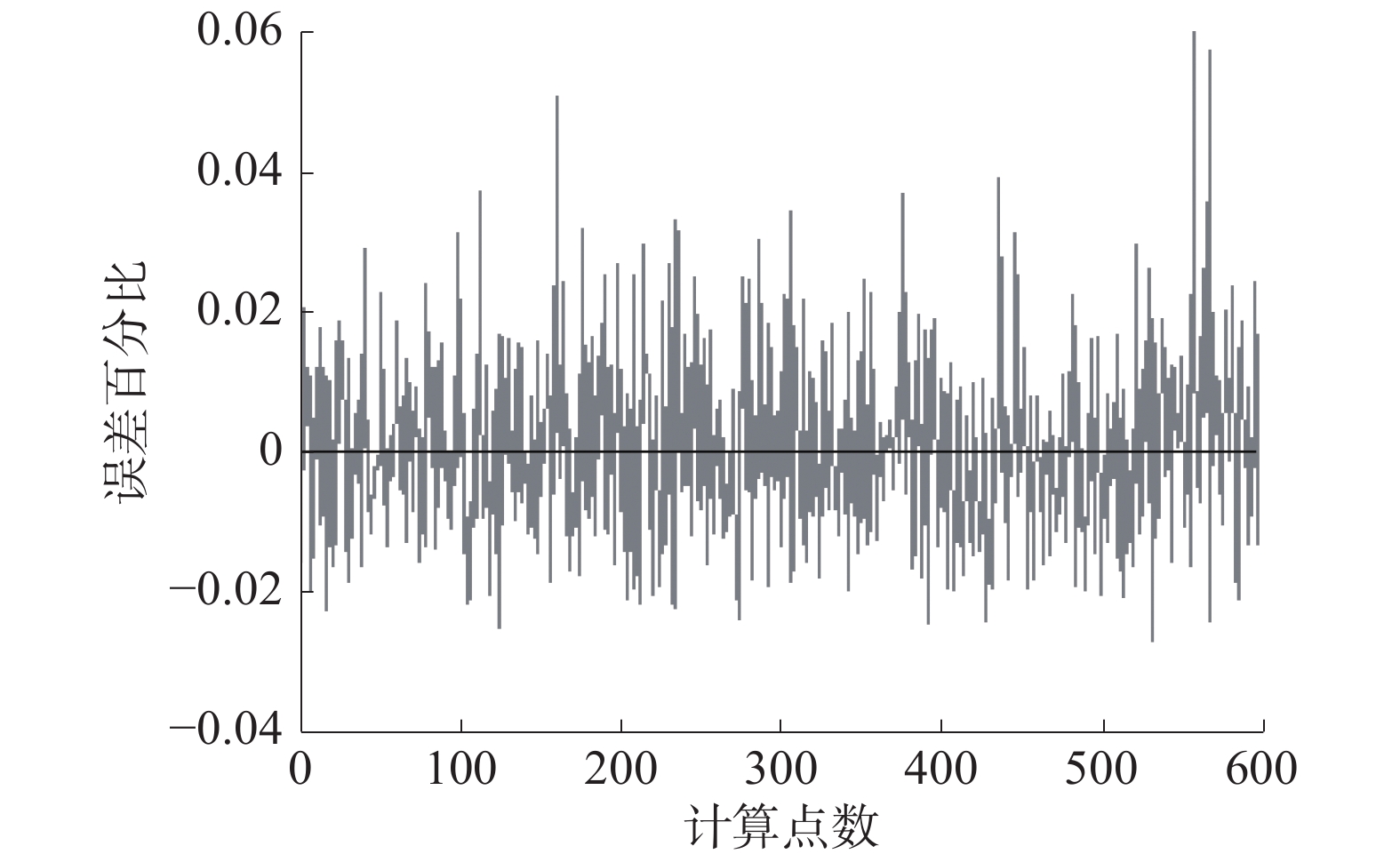
图5、6为GA算法使用传统发射率模型计算出的温度与实际温度曲线及温度误差百分比曲线。经计算得知，GA算法测温误差最大值为42 ℃，正偏移误差百分比最大值为6.3%，负偏移最大误差百分比为−3.1%，均方误差为75.162 0，单点计算平均时间为2.448 1 s。

未改进的NSGA-II算法参数设置如表4所示。

改进后的NSGA-II算法参数设置如表5所示。

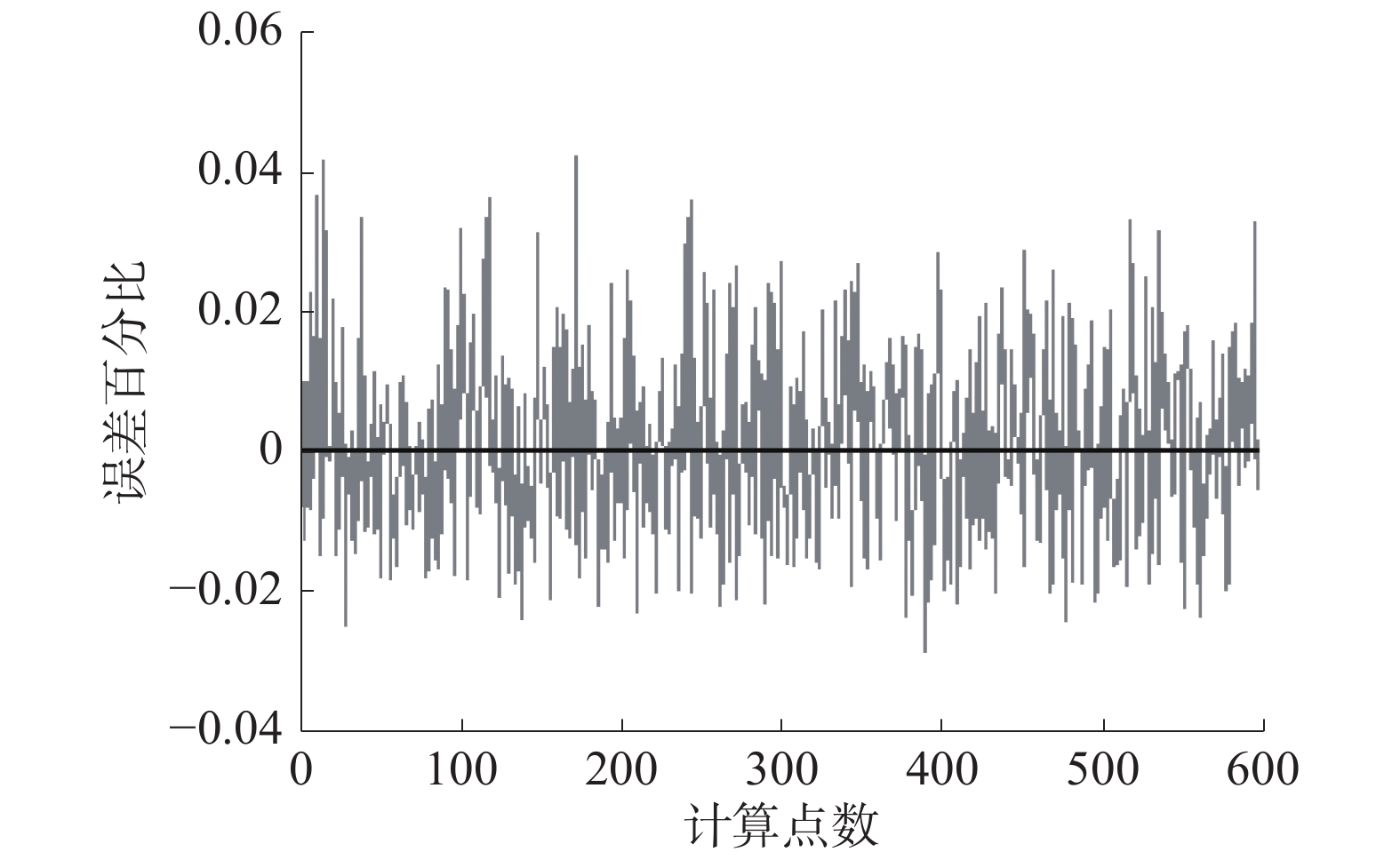
图7、8为未改进的NSGA-II算法使用传统发射率模型计算出的温度与实际温度曲线及温度误差百分比曲线。经计算得知，未改进的NSGA-II遗传算法测温误差最大值为28.5 ℃，正偏移误差百分比最大值为4.1%，负偏移最大误差百分比为−2.9%，均方误差为73.283 6，单点计算平均时间为2.440 7 s。

图9、10为改进后的NSGA-II算法使用传统发射率模型计算出的温度与实际温度曲线及温度误差百分比曲线。

经计算得知，改进后的NSGA-II算法测温误差最大值为10.6 ℃，正偏移误差百分比最大值为1.8%，负偏移最大误差百分比为−1.7%，均方误差为30.96，单点计算平均时间为8.91 s。

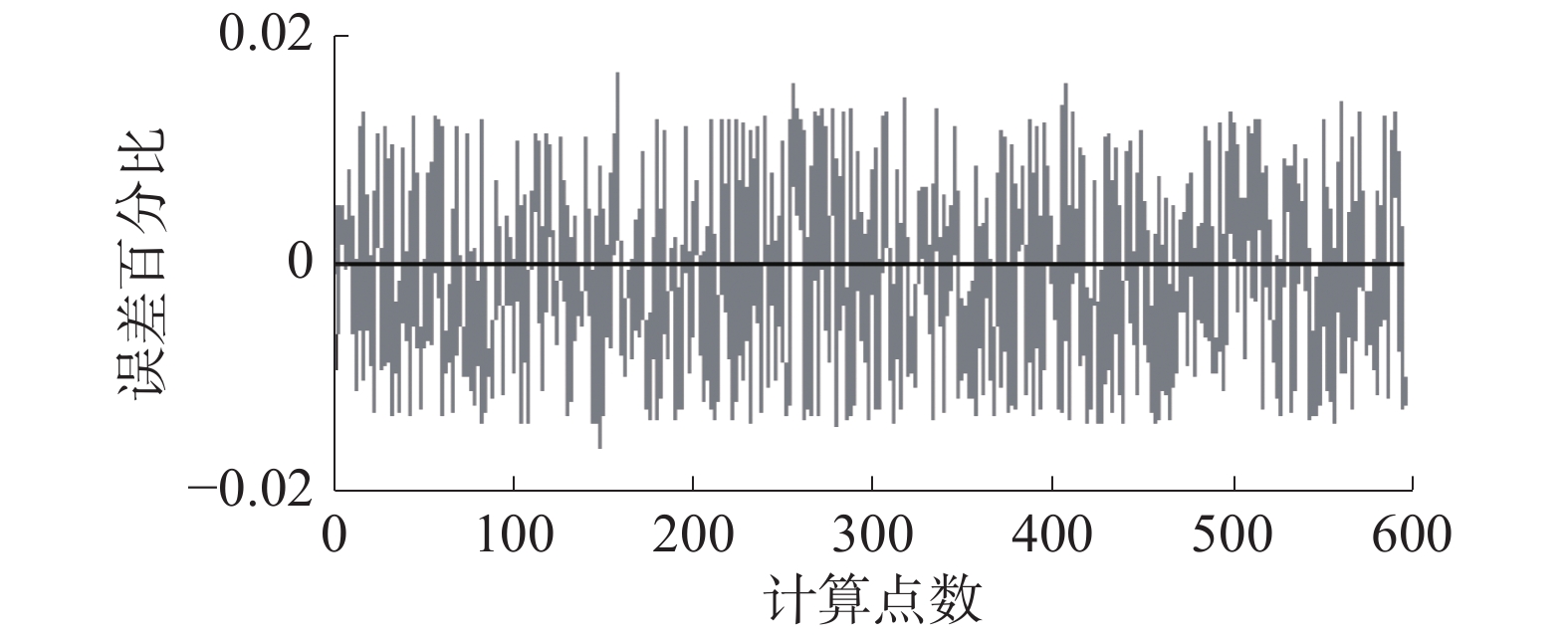
上述算法得到的测温结果都是应用传统发射率模型计算得出，为对比发射率模型对测温结果的影响，现改用引入温差变量的改进发射率模型算法进行测温，算法其余参数取值范围不变，图11、12为改进后的NSGA-II算法使用引入温差变量的改进发射率模型计算出的温度与实际温度曲线及温度误差百分比曲线。

经计算得知，改进后的NSGA-II遗传算法改用引入温差变量的改进发射率模型后测温误差最大值为10.4 ℃，正偏移误差百分比最大值为1.6%，负偏移最大误差百分比为−1.6%，均方误差为13.927 0，单点计算平均时间为7.31 s。

从上述6种情况下测温计算结果(图5~12)可以看出，使用GA算法和未改进过的NGSA-II算法进行测温时，计算速度较快，但是计算误差较大；而使用改进的NGSA-II算法后，虽然计算时间增加，但是有效地提高了精度。同时，对不同的发射率模型对比可知，使用改进发射率模型时，均方误差减小，测温稳定程度有所提高。

4 结论

本文通过对使用GA、NSGA-II、改进的NSGA-II这3种遗传算法及带有温差变量的发射率模型、线性发射率模型2种模型测温效果进行比对，说明了改进NSGA-II算法及改进发射率模型对辐射测温的作用，改进的NSGA-II算法能提高温度测量的准确性，而使用改进发射率模型能提高测量结果的稳定程度。

1)改进发射率模型结合改进的NSGA-II算法能在提高温度测量准确性的同时，提高测量准确度的稳定程度，计算时间稍有增加。在对反应时间要求不高且对测温准确度要求较高的情况下，可以考虑使用本文中的计算方法测温。

2)受不同被测物体不同材料以及表面涂层等因素影响，本文使用的改进发射率模型不一定适用于所有情况，对于不同材料的被测物体，如测量效果较差，应该考虑更换其他形式的温差发射率模型。