氦透平膨胀机是一种通过高速旋转,利用工质流动速度变化进行能量转换的低温设备[1]。应用于逆布雷顿循环微型低温氦制冷机中的氦透平膨胀机,因其重量轻、结构简单、可靠性高等优点,引起众人关注和研究[1-3]。随着对飞机环控系统的不断深入研究,对于系统中微型低温制冷机的要求愈来愈高,设计运行安全可靠的高效率微型氦透平膨胀机对中国国内航空领域和国防部门具有重大意义[4]。祝勇仁等[5-6]以一元流设计方法为基础对膨胀机特性比、反动度和轮径比等参数进行多目标优化;侯予等[7]在多目标优化的基础上,在优化过程中无需给出显式的目标函数,无需求导和微分,在优化过程中可以全面考虑约束条件,自动从数据库中选取其他热力及结构参数,并可方便地加入专家经验以提高搜索效率。熊联友等[8]得到优化后较好的热力性能及较高的失稳转速,开展不同工质的相似模化研究,以便更好地预测氦透平膨胀机的热力性能。孙立佳等[9]提出一种氦制冷系统流程设计,采用NREC对氦透平膨胀机优化通流部分,采用FLUENT分析气体轴承性能,优化气体轴承机构,采用ANSYS分析优化转子结构参数,提高转子临界转速。
1 微型氦透平膨胀机设计基于图1的微型氦透平膨胀机模型,提出如图2所示设计流程。本文采取一元流动分析的方法对向心透平中的流动过程进行“宏观地”考察与总体分析,并进行模型筛选,完成透平的方案选择与初步设计工作;在此基础上利用二元或三元的分析方法在CFturbo对所得参数进行改进,得到三维模型;通过IGG模块划分网格,在NUMECA计算模拟分析向心透平进气腔及进气管整机流场,保证运行高效率;利用转子动力学分析软件构建转子动力学计算模型,使转子可安全运行;对涡轮和压气机叶片施加载荷进行应力分析,对自由振动进行模态分析,避免叶轮在共振频率工作,确保叶轮工作可靠性。

|
Download:
|
| 图 1 微型氦透平膨胀机模型 | |

|
Download:
|
| 图 2 系统性设计流程 | |
根据初始边界条件(如表1所示)计算叶轮几何模型参数,采用最佳速比法结合经验模型参数来确定与最高轮周效率对应的级的速比和反动度[10]。
|
|
表 1 设计参数 |
气体在喷嘴内的流动存在气流与壁面的摩擦和气体内部分子相互间的摩擦,导致气流内部能量交换产生损失,使喷嘴出口气流的实际速度C1低于理想速度C1s,实际的出口比焓值高于理论的比焓值。在一元流动时,这一损失通常用经验的速度系数来反映。速度系数是一种综合性的损失系数,影响因素包括喷嘴的气流参数、结构尺寸、加工质量、叶片形状等。反动度的选取应保证在流道内部不发生扩压流动时,考虑涡轮的经济性和低温工作环境。反动度
| $\rho {\rm{ = }}\frac{{1 - {{\left( {{u_1}\varphi/\cos {\alpha _1}^\prime } \right)}^2}}}{{2{h_s}^\prime }}$ |
PR能量方程为
| $P = \frac{{RT}}{{{V_m} - b}} - \frac{{\alpha a}}{{V_m^2 + 2b{V_m} - {b^2}}}$ | (1) |
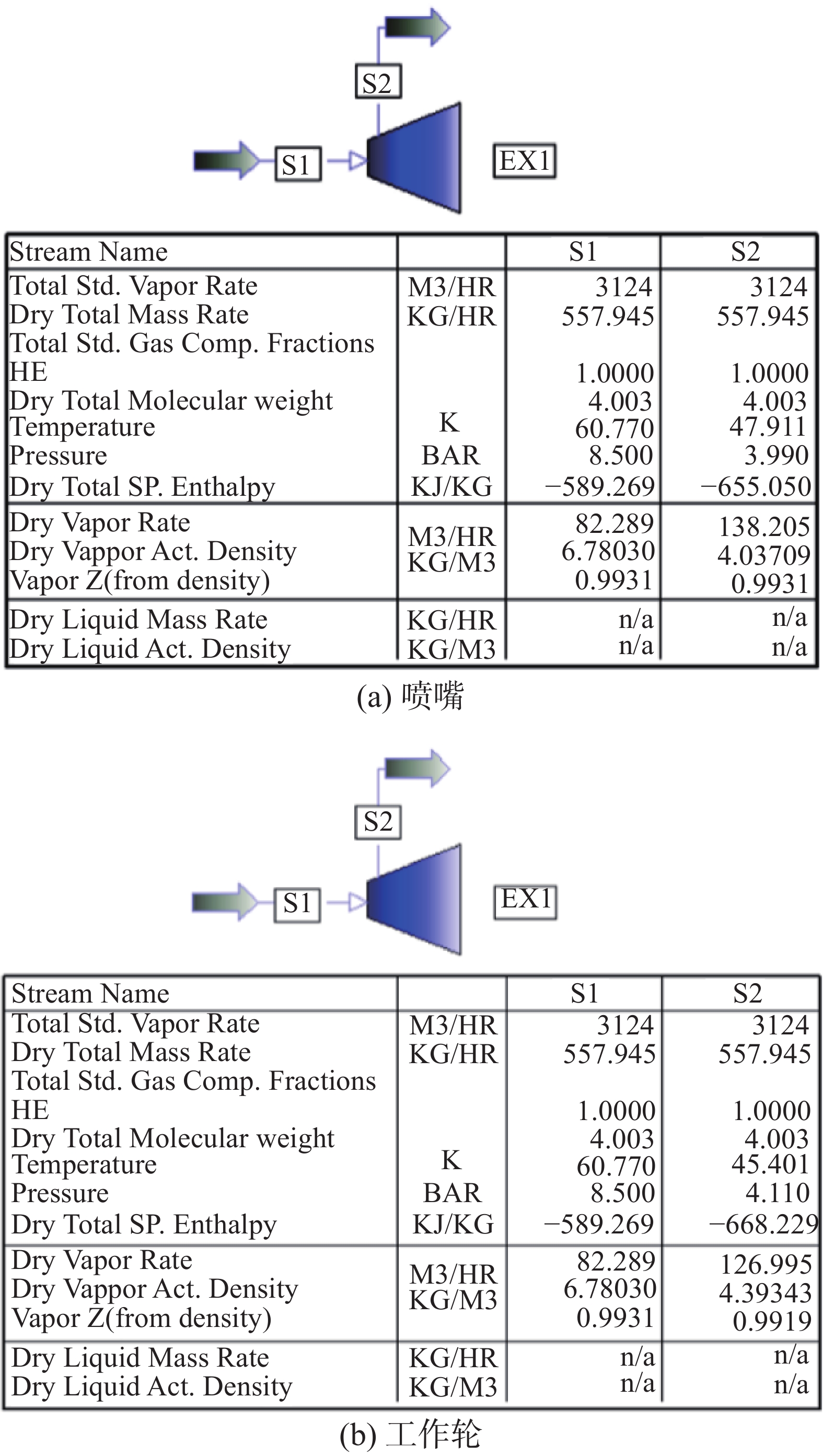
根据式(1)及氦气物性参数,利用流程模拟程序 PRO/II v9.4进行热力计算,可得如图3所示喷嘴和工作轮进出口状态参数计算结果。
|
Download:
|
| 图 3 PRO-II参数 | |
依据热力计算结果参数,在CFturbo软件中给定设计参数,并将氦气物性参数调入,根据结构参数和经验参数调整计算结果,得到如图4所示合理区间内的子午面设计。

|
Download:
|
| 图 4 涡轮子午面设计 | |
根据经验选取喷嘴z-r子午面,设定叶片进出口r边线在喷嘴径向长度10.83%和91.67%处,调整叶片中线,包角设定为47°,设计得到调整喷嘴叶片叶型。设计得到叶轮几何参数已在表1给出。
通过CFturbo中经验值的选取及对叶型轮廓的调整最,终得到图5所示9叶喷嘴叶片和10叶工作轮叶片的涡轮三维轮廓模型。经处理,将三维轮廓模型填充成三维实体模型,用于CFD软件仿真分析计算。

|
Download:
|
| 图 5 9叶喷嘴和10叶工作轮三维模型 | |
某型号的氦透平膨胀机设计参数如表2所示。根据表2透平设计参数及要求,采用最佳速比法结合经验模型参数,优化与最高轮周效率对应的级的速比和反动度。采用一元流设计方法对透平膨胀机流通部分进行设计,确保透平的最佳工作性能,选取参数为涡轮叶轮直径35 mm,转速141 384 r/min。
|
|
表 2 设计参数 |
采用商业CAE数值模拟仿真软件NUMECA对涡轮通流部分进行数值模拟,在旋转坐标系下采用角速度为ω的笛卡尔参考坐标系雷诺数 Navicer-stokes 方程来表示:
| $\frac{{\partial U}}{{\partial t}} + \nabla {F_1} + \nabla {F_V} = Q$ |
采用Spalart-Allmaras模型,引入湍流运动粘性系数ut:
| ${v_t} = \frac{{{u_t}}}{\rho } = v \times 100\% \times{f_{v_1}}$ |
遵循的输运方程:
| $\begin{array}{c} \dfrac{{\partial v \times 100\% }}{{\partial t}} + W \cdot v \times 100\% = \\ \dfrac{1}{\sigma }\left\{ {\nabla \cdot \left[ {{v} + \left( {1 + {c_{b_2}}} \right)v \times 100\% \cdot \nabla v} \right] - {c_{b_2}}v \times } \right.\\ \left. {100\% \nabla v} \right\} + Q \end{array} $ |
运行效率为
| $ \eta =\frac{1-{T}_{2}/{T}_{1}}{1-{\mathrm{\pi }}^{\left(k-1/k\right)}} $ |
利用IGG/AutoGrid5对iges格式几何叶轮进行前处理结构化网格绘制,如图6所示。叶片的空间离散网格在IGG中贴体生成,计算模拟和分析向心透平内部和进气腔及进气管的整机流场。

|
Download:
|
| 图 6 动静叶和通流部分网格划分 | |
B2B截面为相邻叶片间流体流动区域,图7分别给出5%、50%、95%叶高处B2B截面的相对马赫数、压力、流线分布云图。

|
Download:
|
| 图 7 B2B截面性能分布云图 | |
在叶栅间流动部分数值模拟基础上,对向心涡轮整机和周期性内部全流道流动数值模拟进行对比,得到图8所示的流量−效率性能曲线。由图8可看出,整机运行效率比周期性部分效率有所下降,但仍可保证在80%左右。相对现有设计,氦透平膨胀机效率有所提升,验证了设计的向心涡轮透平机械具有高效运行的优势。

|
Download:
|
| 图 8 向心涡轮的效率特性曲线 | |
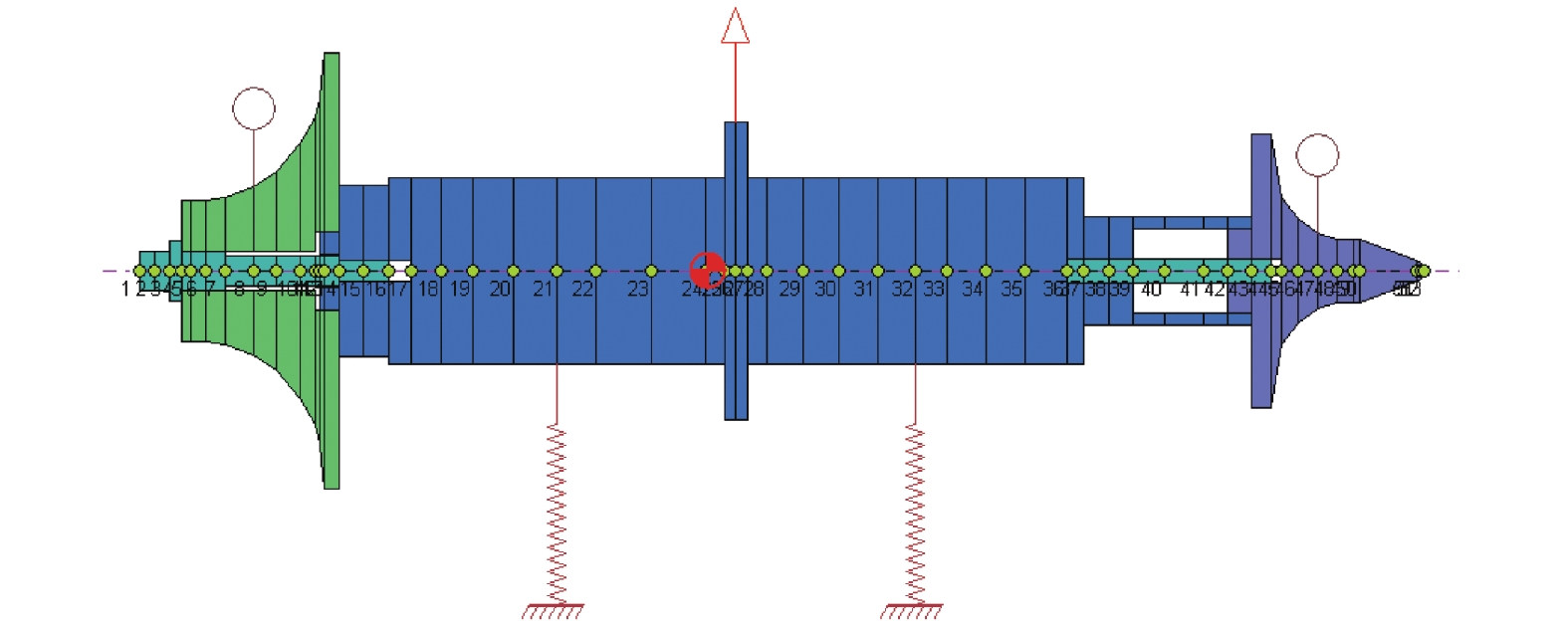
转子是透平膨胀机中唯一的高速运转部件,对膨胀机稳定性有很大影响[11]。转子在运行时,存在共振转速、不平衡转子、转子失稳等不利于运行安全的因素,系统设计时需进行转子动力学分析[12]。利用转子动力学分析软件建立转子支撑系统动力学模型。为了减少轴向导热和转子质量,采用钢为主轴材料。选用传递矩阵法计算,确定所研究的轴系各阶临界转速的数值,使轴系的工作转速避开各阶临界转速,防止发生共振危害。基于透平膨胀机叶轮尺寸,设计整机轴系,并在转子动力学分析软件中建立如图9所示微型氦透平膨胀机转子支撑系统动力学模型。
|
Download:
|
| 图 9 转子支撑系统动力学模型 | |
基于该模型进行自由振动模态分析,得到图10转子弹性支撑下临界转速及振型,工作转速141 373 r/min介于二阶和临界转速之间,证明工作转速下运行安全。

|
Download:
|
| 图 10 转子弹性支撑下临界转速及振型 | |
根据API617标准,不平衡量的施加应根据无阻尼振型的具体形状施加。施加的不平衡量应该根据悬臂端的总重量计算而得,施加在轴系上最大位移处,如图9模型,施加在26号节点,0.188 6 g·mm。不平衡量计算公式为
| $U = 6\;350\left( {{W_1} + {W_2}} \right)/N$ |
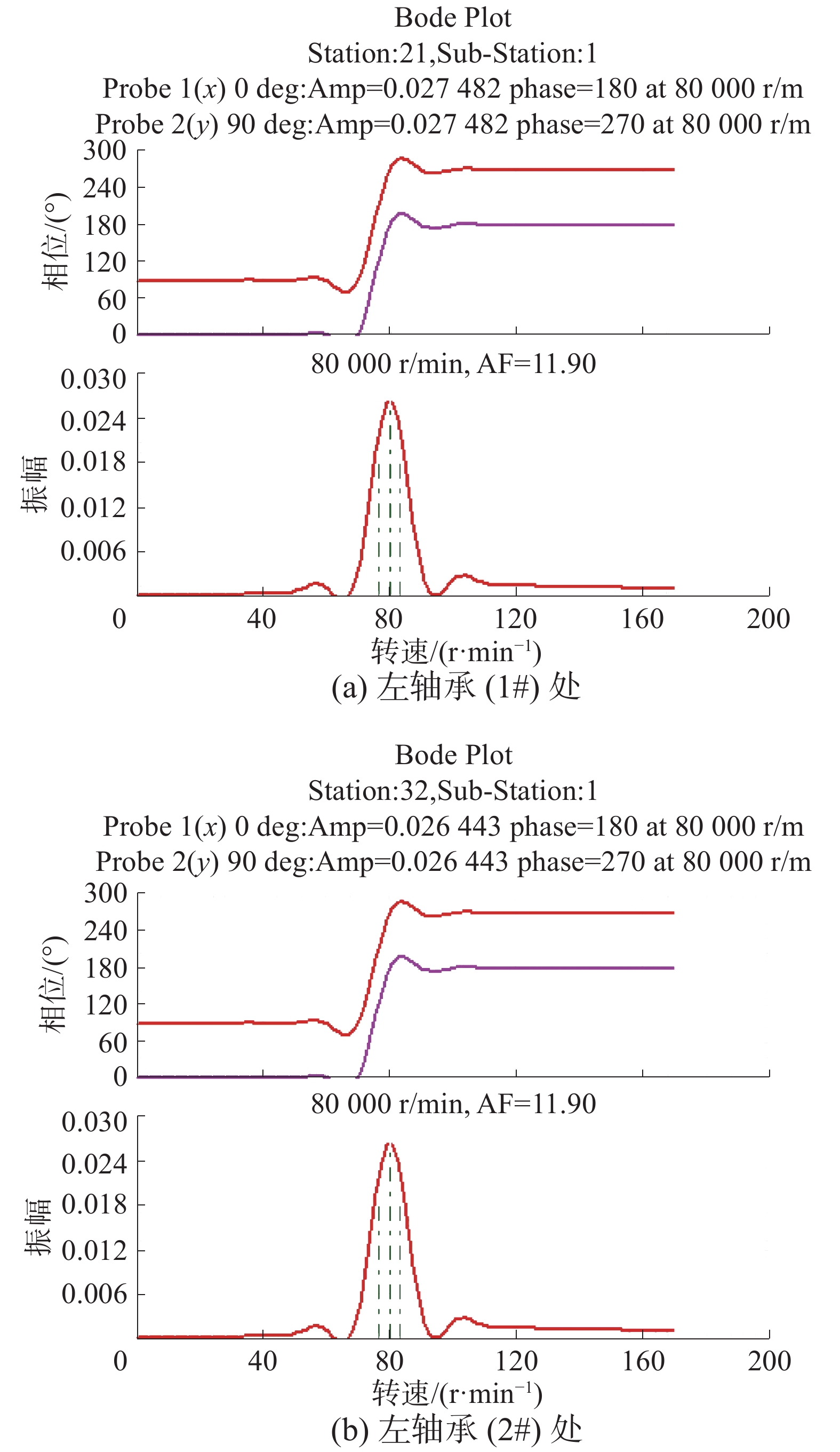
图11为轴系一阶不平衡响应分析结果。
|
Download:
|
| 图 11 轴系一阶不平衡响应分析 | |
如图11所示,左轴承(1#)在计算不平衡响应时存在一个峰值80 000 r/min,其对应的放大因子AF值为11.90,对这个AF值进行隔离裕度核算:
| ${\rm{SM}} = 17\left( {1 - \frac{1}{{{\rm{AF}} - 1.5}}} \right)$ |
左轴承在80 000 r/min时产生振动峰值较大,其隔离裕度为15.36%,工作转速141 273 r/min落在了隔离裕度67 712~92 288 r/min之外。根据API617细则2.1.3规定,左轴承处不平衡响应验证合格。
右轴承(2#)不平衡响应峰值对应的AF值为11.90,进行隔离裕度核算,计算结果和左轴承相近。根据API617细则2.1.3规定,右轴承处不平衡响应验证合格。从零到跳闸转速,不存在运转的峰峰值,左、右轴承的横向振动符合API安全性要求,验证合格。
2.3 运行可靠性对涡轮和制动压气机叶轮几何进行网格划分,在Abaqus中进行材料属性设定,对计算模型设置约束条件和施加载荷,约束类型为完全约束。离心叶轮的结构载荷包括惯性载荷和气动载荷,气动载荷暂不考虑,叶轮的重力载荷忽略不计,只需施加叶轮的离心力载荷。
经过计算机求解得到Mises应力值,涡轮应力分布云图如图12所示。根据云图可得到涡轮的最大应力值发生在叶片的尾缘根部,值为49.4 MPa,材料的屈服强度为330 MPa,相比于材料的容许应力,涡轮工作轮不容易发生屈服失效,处在运行可靠范围内。

|
Download:
|
| 图 12 涡轮工作轮应力分布云图 | |
压气机叶轮的应力分布云图如图13所示,根据云图显示可以得到,叶轮最大应力值在叶片的前缘根部,应力值为84.9 MPa,运行可靠。

|
Download:
|
| 图 13 压气机叶轮应力分布云图 | |
在外界扰动力的影响下,叶片受迫振动,径流式叶轮会出现叶片破坏现象。当一种弹性体在外加短暂的扰力使其偏离平衡位置后,将发生自由振动。图14给出了涡轮叶片模型前四阶模态分布。

|
Download:
|
| 图 14 涡轮模态分析 | |
此模态分析类型为完全固定式,可进行固定式模态计算分析。一阶固有频率为13 045 r/s,远大于工作转速,不会发生共振现象,运行安全。
图15给出了压气机叶片模型前四阶固定模态分析。第一阶固有频率为15 521 r/s,一阶固有频率大于工作转速,同样不会发生共振现象,确保透平膨胀机运行可靠性。

|
Download:
|
| 图 15 压气机模态分析 | |
基于现有的数值模拟仿真软件,建立设计微型氦透平膨胀机的系统性数值模拟。经过基本热力设计方案选取,利用CFturbo建立透平膨胀机三维模型,并对设计造型进行仿真性能分析。
1)通过NUMECA对微型氦透平膨胀机通流部分运行效率进行分析;建立转子动力学分析模型,对转子临界转速、不平衡量和稳定性进行计算,确保转子运行安全性。
2)将前处理划分网格后的涡轮和压气机叶片导入Abaqus中进行应力计算,计算各阶模态,保证叶轮的固有频率在工作频率外不会产生自由振动,保证透平机械可靠运转。
该套对微型氦透平膨胀机的数值模拟流程方案,系统地总结了透平机械的设计仿真过程,针对氦透平膨胀机设计指标,完善优化设计仿真过程。进一步进行样机实验,验证仿真分析的正确性,并根据结果对计算数据进行误差和可靠性分析。
| [1] |
朱朝辉, 姚艳霞, 杨金焕, 等. 低温氦透平膨胀机的研究进展[J]. 低温与特气, 2003, 21(1): 1-6. DOI:10.3969/j.issn.1007-7804.2003.01.001 ( 0) 0)
|
| [2] |
计光华. 透平膨胀机[M]. 西安: 西安交通大学出版社, 1988.
( 0) 0)
|
| [3] |
花严红, 罗涛, 汪永根, 等. 氦透平膨胀机在空间技术中的应用现状及展望[J]. 通用机械, 2008(8): 44-47. DOI:10.3969/j.issn.1671-7139.2008.08.013 ( 0) 0)
|
| [4] |
常旭宁, 孙俊芳, 乔佳, 等. 氦透平膨胀机在我国的发展[J]. 低温与超导, 2014, 42(2): 30-34, 91. DOI:10.3969/j.issn.1001-7100.2014.02.007 ( 0) 0)
|
| [5] |
祝勇仁, 张炜, 韩澎. 氦气体轴承透平膨胀机研制[J]. 机械研究与应用, 2014, 27(5): 124-126. DOI:10.3969/j.issn.1007-4414.2014.05.043 ( 0) 0)
|
| [6] |
侯予, 陈纯正, 熊联友, 等. 低温氦透平膨胀机的热力设计及性能分析[J]. 西安交通大学学报, 2003, 37(7): 666-669. DOI:10.3321/j.issn:0253-987X.2003.07.002 ( 0) 0)
|
| [7] |
侯予, 王瑾, 熊联友, 等. 径-轴流低温透平膨胀机整体性能多目标优化设计[J]. 低温工程, 2001(4): 13-17. DOI:10.3969/j.issn.1000-6516.2001.04.003 ( 0) 0)
|
| [8] |
熊联友, 陈纯正, 刘立强, 等. 新型氦气体轴承透平膨胀机的研制[J]. 低温与特气, 2002, 20(1): 23-25. DOI:10.3969/j.issn.1007-7804.2002.01.008 ( 0) 0)
|
| [9] |
孙立佳, 孙郁, 任小坤, 等. 氦制冷系统气体轴承透平膨胀机设计[J]. 低温工程, 2013(3): 7-10. DOI:10.3969/j.issn.1000-6516.2013.03.002 ( 0) 0)
|
| [10] |
王新军. 汽轮机原理[M]. 西安交通大学出版社, 2014.
( 0) 0)
|
| [11] |
侯予, 陈纯正, 熊联友, 等. 低温氦气体轴承透平膨胀机的设计[J]. 低温工程, 2003(3): 7-11, 16. DOI:10.3969/j.issn.1000-6516.2003.03.002 ( 0) 0)
|
| [12] |
王正. 转动机械的转子动力学设计[M]. 北京: 清华大学出版社, 2015: 3-31.
( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


