2. 江苏方天电力技术有限公司, 江苏 南京 211102;
3. 东南大学 电气工程学院,江苏 南京 210096
2. Jiangsu Frontier Electric Technologies Co., Ltd., Nanjing 211102, China;
3. School of Electrical Engineering, Southeast University, Nanjing 210096, China
随着经济和科技的高速发展,人们对电能的与日俱增。在传统化石能源短缺和生态恶化加剧的大背景下,充分利用可再生能源已经成为全球共识[1]。以屋顶光伏为代表的分布式光伏(photovoltaic,PV)快速发展起来,PV的大规模渗透已经成为新型配电网不可阻挡的发展趋势。分布式光伏的高渗透率对配电网的规划和运行带来了包括电压上升、反向功率流、网损增加、电能质量下降等问题[2-4]。此外,由于分布式光伏受外界环境影响较大,其功率输出具有显著的不确定性[5]。所以,我们需要研究一种方法来评估分布式光伏接入配电网的容量极限。
目前,国内外已经开展了相关研究。文献[6]对分布式电源(distributed generation, DG)接入配网后的谐波情况进行分析,给出多台DG谐波叠加估计算式,以此推出以谐波限值为约束条件的DG准入容量。文献[7]从规划设计角度出发,提出了一种分布式电源最大渗透率综合计算模型和求解方法,并分析了极端情况下配电线路和主变压器供电区域内可接入的分布式电源的最大渗透率。文献[8]提出了一种考虑短路电流、电压质量指标以及系统潮流等约束的分布式电源准入功率优化模型,并采用分布度、分散度和渗透率3个指标来表征分布式电源的接入状态。文献[9]基于加权因子方法,建立了以能量损失最小为目标函数的评估风力发电接入容量的模型。文献[10]提出一种矩阵化描述的准入容量计算方法,避免在应用电压约束进行准入容量计算时的潮流迭代问题,采用遗传算法计算各节点准入容量,得出以电压为约束的准入容量值。
综上研究,目前的研究主要存在以下几个问题:
1)分布式电源的接入使得潮流在配电网络上的分布特性发生变化,从而导致配网线路存在潮流越限、节点电压存在失稳风险。因此,安全约束是分析分布式电源准入容量的关键因素。但目前许多文献集中在考虑继电保护、谐波约束分析以及能量损失等方面问题。
2)分布式电源出力具有波动性,而负荷水平也具有明显的不确定性。目前的研究大都将其视为确定性因素,很少涉及分布式电源和负荷的时序性以及不确定性,少数文献利用基于场景的随机优化来处理不确定性。然而由于难以获得完整的历史数据和预测数据,无法得到多个不确定变量的概率分布,所以随机优化方法具有一定的局限性。
3)主动配电网(active distribution network, ADN)是消纳大规模DG的有效手段[11-12]。然而大多数的研究仅针对传统配电网中DG的准入容量,并未考虑主动管理措施(active network management, ANM)。电压控制和无功补偿设备在传统配电网中得到了广泛的应用。因此,在评估DG准入容量时要考虑电压调整和无功补偿。
综上问题,本文考虑了分布式光伏和负荷的不确定性以及时序性,利用鲁棒方法对不确定因素进行建模,并考虑了电压控制和无功补偿等配电网的ANM措施,提出了最大化分布式光伏准入容量的优化配置方案,通过鲁棒性指标来权衡系统可靠性和解的最优性。在本文的研究中,电压控制和无功补偿仅考虑了有载变压器分接头(on-load tap changer, OLTC)和静态无功补偿器(static var compensator, SVC)。
1 分布式电源准入容量模型 1.1 目标函数分布式光伏准入容量模型的优化目标为可配置节点的分布式光伏安装容量之和最大:
| $\max {\rm{ }}f = \sum\limits_{j \in G} {p_j^G} $ | (1) |
式中:G为分布式光伏候选节点集合;
模型的约束条件如下:等式约束包括配网潮流约束;不等式约束包括节点电压约束、线路容量约束、变压器容量约束、变压器功率约束、OLTC分接头约束以及无功补偿容量约束。具体表达式如下所示:
1)配网潮流约束
如图1所示,将一典型链式配电网络各节点和每段线路的阻抗依次编号,则每个节点的潮流等式可表示如为:
| ${V_0} = {V_{{\rm{sub}}}}(1 + {t_p} \cdot a)$ |
| ${P_{i + 1,t}} = {P_{i,t}} - {r_i}(P_{i,t}^2 + Q_{i,t}^2)/{U_{i,t}} - {p_{i + 1,t}}$ | (2) |
| ${Q_{i + 1,t}} = {Q_{i,t}} - {x_i}(P_{i,t}^2 + Q_{i,t}^2)/{U_{i,t}} - {q_{i + 1,t}}$ | (3) |
| ${U_{i + 1,t}} = {U_{i,t}} - 2({r_i}{P_{i,t}} + {x_i}{Q_{i,t}}) + \frac{{(r_i^2 + x_i^2)(P_{i,t}^2 + Q_{i,t}^2)}}{{{U_{i,t}}}}$ | (4) |
式中:
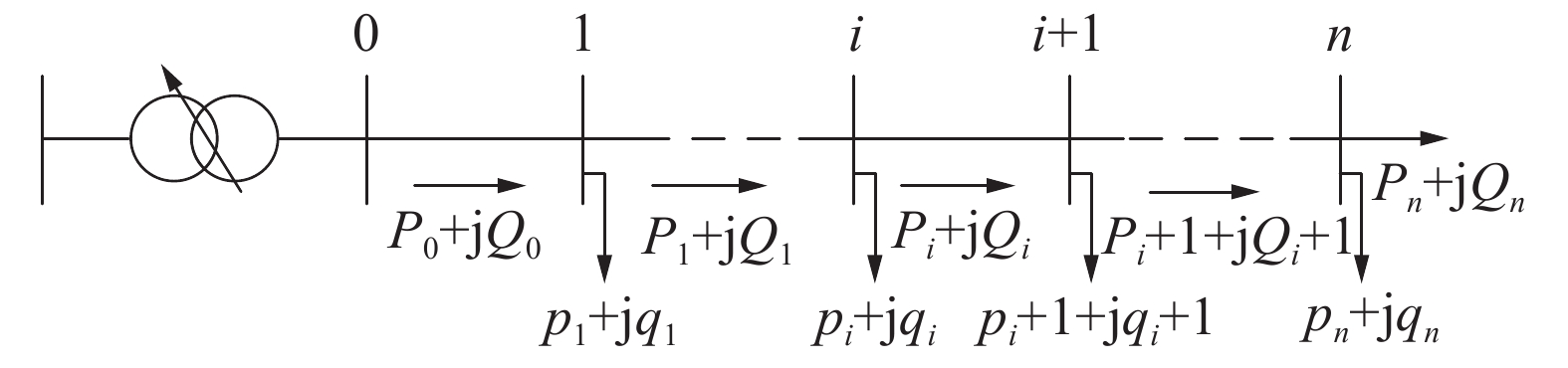
|
Download:
|
| 图 1 典型辐射网络 | |
| ${U_{i,t}} = {({V_{i,t}})^2};\; {p_{i,t}} = p_{i,t}^L - p_{i,t}^g;\; {q_{i,t}} = q_{i,t}^L - q_{i,t}^g - q_{i,t}^s;\; p_{i,t}^g = {\omega _{i,t}}p_i^G $ |
为了避免配网潮流方程的非线性,文献[13]给出了上述潮流方程的线性转换式,具体而言,式(2)~(4)可以简化如下:
| ${P_{i + 1,t}} = {P_{i,t}} - {p_{i + 1,t}}$ |
| ${Q_{i + 1,t}} = {Q_{i,t}} - {q_{i + 1,t}}$ |
| ${V_{i + 1,t}} = {V_{i,t}} - \frac{{({r_i}{P_{i,t}} + {x_i}{Q_{i,t}})}}{{{V_{{\rm{sub}}}}}}$ |
进而,支路潮流和节点电压可以用首节点电压和各节点有功无功注入来表示。如图1所示,辐射网络总共有N+1个节点,节点0代表首节点,因此,这个网络有N个独立的节点和N条支路。引入网络拓扑矩阵T(
| ${{B}} = {{{T}}^{\rm{T}}}$ |
| ${P_i} = \sum\limits_{j \in N} {{B_{ij}}{p_j}} $ | (5) |
| ${Q_i} = \sum\limits_{j \in N} {{B_{ij}}{q_j}} $ | (6) |
| ${V_i} = {V_0} - \frac{1}{{{V_{{\rm{sub}}}}}}\sum\limits_{j \in N} {({p_j}{R_{ij}} + {q_j}{X_{ij}})} $ | (7) |
式中:Rij和Xij为从首节点到i节点与首节点到j节点两条支路重叠部分的电阻和电抗。
2)节点电压约束
| ${V_{i,\min }} \leqslant {V_{i,t}} \leqslant {V_{i,\max }},\forall i \in N$ | (8) |
式中Vi,min和Vi,max分别为节点i的电压下限值与电压上限值。
3)设备容量约束
| $p_{{\rm{sub}},t}^2 + q_{{\rm{sub}},t}^2 \leqslant S_{{\rm{sub}},\max }^2$ | (9) |
| $p_{i,t}^2 + q_{i,t}^2 \leqslant S_{ij,\max }^2,\forall i \in N$ | (10) |
式中:psub,t和qsub,t分别为变压器在t时刻发出的有功和无功;Ssub,max为变压器容量;Si,max为线路i的容量。
式(9)、(10)的可行域是圆的内部,采用文献[14]介绍的二次约束线性化方法,用正十二边形来近似表示,如图2所示。则设备容量约束可以转化为线性不等式(11)和(12)。

|
Download:
|
| 图 2 设备容量线性化示意 | |
| ${\alpha _n}{p_{{\rm{sub}},t}} + {\beta _n}{p_{{\rm{sub}},t}} + {\delta _n}{S_{{\rm{sub}},\max }} \leqslant 0,\forall c \in \left\{ {1,2, \cdots ,12} \right\}$ | (11) |
| ${\alpha _n}{p_{i,t}} + {\beta _n}{p_{i,t}} + {\delta _n}{S_{i,\max }} \leqslant 0,\forall c \in \left\{ {1,2, \cdots ,12} \right\}$ | (12) |
式中
|
|
表 1 设备容量线性化系数 |
4)变压器功率约束
| ${p_{{\rm{sub}},\min }} \leqslant {p_{{\rm{sub}},t}} \leqslant {p_{{\rm{sub}},\max }}$ | (13) |
| ${q_{s{\rm{ub}},\min }} \leqslant {q_{{\rm{sub}},t}} \leqslant {q_{s{\rm{ub}},\max }}$ | (14) |
式中psub,max、psub,min、qsub,max和qsub,min分别为变压器有功功率和无功功率限值。
5)OLTC分接头约束
| ${t_{p,\min }} \leqslant {t_{p,t}} \leqslant {t_{p,\max }}$ |
式中
6)SVC运行约束。
| $q_{j,\min }^s \leqslant q_{j,t}^s \leqslant q_{j,\max }^s,\forall j \in S$ |
式中:S为SVC安装节点;
将式(5)~(7)分别代入式(8)和式(11)~(14)可得:
| $\begin{split} & {V_{i,\min }}{V_{{\rm{sub}}}} \leqslant V_{{\rm{sub}}}^2(1 + {t_p} \cdot a) + \sum\limits_{j \in G} {{\omega _{j,t}}p_j^G({R_{ij}} + {X_{ij}}\tan\; \varphi _j^G)} + \\ & \quad \quad \sum\limits_{j \in S} {q_{j,t}^S{X_{ij}} - \sum\limits_{j \in N} {p_{j,t}^L({R_{ij}} + {X_{ij}}\tan\; \varphi _j^L) \leqslant } } {V_{i,\max }}{V_{{\rm{sub}}}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$ | (15) |
| $\begin{split} & \sum\limits_{j \in N} {({\alpha _n}{B_{1j}} + {\beta _n}{B_{1j}}\tan\; \varphi _j^L)p_{j,t}^L - \sum\limits_{j \in S} {{\beta _n}{B_{1j}}q_{j,t}^s} } + \\ & \quad \quad {\delta _n}{S_{{\rm{sub,max}}}} - \sum\limits_{j \in G} {({\alpha _n}{B_{1j}} + {\beta _n}{B_{1j}}\tan \; \varphi _j^G){\omega _{j,t}}p_j^G \leqslant 0} \end{split} $ | (16) |
| $\begin{split} & \sum\limits_{j \in N} {({\alpha _n}{B_{ij}} + {\beta _n}{B_{ij}}\tan \; \varphi _j^L)p_{j,t}^L - \sum\limits_{j \in S} {{\beta _n}{B_{ij}}q_{j,t}^s} } + \\ & \quad \quad {\delta _n}{S_{i,\max }} - \sum\limits_{j \in G} {({\alpha _n}{B_{ij}} + {\beta _n}{B_{ij}}\tan\; \varphi _j^G){\omega _{j,t}}p_j^G \leqslant 0} \end{split}$ | (17) |
| ${p_{{\rm{sub,min}}}} \leqslant \sum\limits_{j \in N} {{B_{1j}}p_{j,t}^L - \sum\limits_{j \in G} {{B_{1j}}{\omega _{j,t}}p_j^G \leqslant {p_{{\rm{sub,max}}}}} } $ | (18) |
| $\begin{split} {q_{{\rm{sub,min}}}} \leqslant & \sum\limits_{j \in N} {{B_{1j}}p_{j,t}^L\tan\; \varphi _j^L - \sum\limits_{j \in G} {{B_{1j}}{\omega _{j,t}}p_j^G\tan\; \varphi _j^G} } - \\ & \sum\limits_{j \in S} {{B_{1j}}q_j^s} \leqslant {q_{{\rm{sub,max}}}} \end{split} $ | (19) |
式(15)~(19)分别为转化后的电压约束、变压器容量约束、线路容量约束以及变压器有功无功上下限约束。
2 基于鲁棒线性优化理论的模型求解 2.1 鲁棒线性优化理论1973年,Soyster[15]首次提出了鲁棒线性优化方法,经过几十年的发展,鲁棒优化(robust optimization, RO)已在多个领域得到广泛应用,其中鲁棒线性优化最为成熟。Seng-Cheol Kang[16]提出了基于随机变量分布信息的鲁棒线性优化方法,用区间和期望值的形式描述不确定参数,引入一个对鲁棒优化保守性判断的可调节参数,以实现对不确定参数取值区间的缩放,从而可将难以处理的不确定区间约束条件转化为一般确定性约束。本文正是基于随机变量分布信息的鲁棒线性优化方法对配电网中分布式电源准入容量问题中的不确定因素进行处理,并将其转化为易于处理的鲁棒对等式。
2.2 基于随机变量分布信息的可调节鲁棒线性优化方法对于最小化线性问题:
| $\left\{ \begin{array}{l} \min {\rm{ }}{{cx}} \\ {\rm{s}}{\rm{.t}}{\rm{. }}{{Ax}} \leqslant {{b}} \\ {\rm{ }}{{l}} \leqslant {{x}} \leqslant {{u}} \\ \end{array} \right.$ | (20) |
式中:
| $\begin{gathered} {\Re _i}({\mathit{\Gamma} _i}) = \Bigg\{ {{a_i}|{a_{ik}} \in \left[ {{{\overline a }_{ik}} - {\beta _{ik}}t_{ik}^B,{{\overline a }_{ik}} + {\beta _{ik}}t_{ik}^F} \right],} \\ {\rm{ }} {0 \leqslant {\beta _{ik}} \leqslant 1,\sum\limits_{k \in {J_i}} {{\beta _{ik}}} \leqslant {\Gamma _i}} \Bigg\} \\ \end{gathered} $ |
式中:
| $\left\{ \begin{array}{l} \min {\rm{ }}{{cx}} \\ {\rm{s}}{\rm{.t}}{\rm{. }}\displaystyle\sum\limits_{j = 1}^n {{{\bar a }_{ij}}{x_j}} + {\mathit{\Gamma }_i}{z_i} +\displaystyle \sum\limits_{k \in {J_i}} {{p_{ik}}} \leqslant {b_i},i = 1,2, \cdots ,m \\ {{\rm{ }}{z_i} + {p_{ik}} \geqslant t_{ik}^F{x_k},}\quad{{\rm{ }}i = 1,2, \cdots ,m,\forall k \in {J_i}} \\ {{\rm{ }}{z_i} + {p_{ik}} \geqslant - t_{ik}^B{x_k},}\quad {i = 1,2, \cdots ,m,\forall k \in {J_i}} \\ {{\rm{ }}{z_i} \geqslant 0,{p_{ik}} \geqslant 0,}\quad {i = 1,2, \cdots ,m,\forall k \in {J_i}} \\ {\rm{ }}{{l}} \leqslant {{x}} \leqslant {{u}}{\rm{ }} \\ \end{array} \right.$ | (21) |
式中zi和pik为鲁棒转化过程中引入的新决策变量,没有实际物理意义,具体的转化过程可参考文献[16]。鲁棒对等模型是确定性线性规划模型,可以采用常规的线性规划方法求解。文献[16]已经证明,线性规划模型式(21)的优化解是含随机变量的原规划模型式(20)的优化解,转化过程等价。
2.3 不确定时序场景集为解决分布式电源出力以及负荷的不确定性,通过搜集历史数据来统计预测分布式光伏的均值及波动范围。为了体现分布式光伏和负荷的不同时序特征,使用24 h数据作为模拟运行研究对象[17]。根据鲁棒优化理论,随机变量光伏出力和负荷描述为鲁棒区间集合:
| $\begin{split} \Re ({\mathit{\Gamma} _t}) =& \Bigg\{ {{{\omega }_t},{p}_t^L|{\omega _{j,t}} \in \left[ {{{\bar \omega }_{j,t}} - {\mu _{j,t}}{{\hat \omega }_{j,t}},{{\bar \omega }_{j,t}} + {\mu _{j,t}}{{\hat \omega }_{j,t}}} \right]} \forall j \in G,\\ p_{j,t}^L \in & \left[ {\bar p_{j,t}^L - {\nu _{j,t}}\hat p_{j,t}^L,\bar p_{j,t}^L + {\nu _{j,t}}\hat p_{j,t}^L} \right]\forall j \in N,0 \leqslant {\mu _{j,t}} \leqslant 1,\\ {0} \leqslant & {{\nu _{j,t}} \leqslant 1,\displaystyle\sum\limits_{j \in G} {{\mu _{j,t}}} + \displaystyle\sum\limits_{j \in G} {{\nu _{j,t}}} \leqslant {\mathit{\Gamma} _t}} \Bigg\} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$ | (22) |
式中:
由式(22)知,当
对上述的分布式电源准入容量模型中含不确定参数的约束进行转化,得到鲁棒对等模型,以简化求解。由于转化的过程对于各个约束是相似的,因此使用电压上限约束作为示例。
根据RO的基本概念,电压上限约束可转化为:
| $\begin{split} & V_{{\rm{sub}}}^2(1 + {t_p} \cdot a) + \sum\limits_{j \in S} {q_{j,t}^s{X_{ij}}} + \sum\limits_{j \in G} {{{\bar \omega }_{j,t}}p_j^G({R_{ij}} + {X_{ij}}\tan\; \varphi _j^G)} - \\ & \quad \quad \sum\limits_{j \in N} {\bar p_{j,t}^L({R_{ij}} + {X_{ij}}\tan \varphi _j^L)} + \\ & \quad \quad \mathop {\max }\limits_{\sum\limits_{j \in G} {{\mu _{j,t}} + \sum\limits_{j \in N} {{\nu _{j,t}} \leqslant {\Gamma _{j,t}}} } } \left\{ {\sum\limits_{j \in G} {{\mu _{j,t}}{{\hat \omega }_{j,t}}\left| {{R_{ij}} + {X_{ij}}\tan \; \varphi _j^G} \right|p_j^G} } \right. + \\ & \quad \quad\left. { \sum\limits_{j \in N} {{\nu _{j,t}}\hat p_{j,t}^L\left| {{R_{ij}} + {X_{ij}}\tan \varphi _j^L} \right|} } \right\} \leqslant {V_{i,\max }}{V_{{\rm{sub}}}} \\ \end{split} \!\!\!\!\!\!\!\!\!\!\!\!$ | (23) |
由于式(23)是一个含max函数的不可解析的不等式约束,所以首先对式(23)中的max函数进行转化,将其单列如下:
| $\begin{split} & \max \left\{ {\sum\limits_{j \in G} {{{\hat \omega }_{j,t}}} \left| {{R_{ij}} + {X_{ij}}\tan \; \varphi _j^G} \right|p_j^G\mu _{j,t}^{}} \right. + \\ & \quad \quad\left. { \sum\limits_{j \in N} {\hat p_{j,t}^L\left| {{R_{ij}} + {X_{ij}}\tan \; \varphi _j^L} \right|\nu _{j,t}^{}} } \right\} \end{split} $ | (24) |
约束条件:
| $\sum\limits_{j \in G} {{\mu _{j,t}}} + \sum\limits_{j \in N} {{\nu _{j,t}}} \leqslant {\mathit{\Gamma} _t}$ | (25) |
| $0 \leqslant {\mu _{j,t}} \leqslant 1$ | (26) |
| $0 \leqslant {\nu _{j,t}} \leqslant 1$ | (27) |
根据文献[18]中的对偶理论,式(24)~(27)可以转化为:
| $\min \left\{ {{\mathit{\Gamma} _{t,i}}{z_{ub,t,i}} + \sum\limits_{j \in G} {h_{ub,t,ij}^G} + \sum\limits_{j \in N} {h_{ub,t,ij}^L} } \right\}$ | (28) |
约束条件:
| ${z_{{\rm{ub}},t,i}} + h_{{\rm{ub}},t,ij}^G \geqslant {\hat \omega _{j,t}}\left| {{R_{ij}} + {X_{ij}}\tan\; \varphi _j^G} \right|p_j^G$ |
| ${z_{{\rm{ub}},t,i}} + h_{{\rm{ub}},t,ij}^L \geqslant {\hat p^L}_{j,t}\left| {{R_{ij}} + {X_{ij}}\tan\; \varphi _j^G} \right|$ |
| $h_{{\rm{ub}},t,ij}^G \geqslant 0$ |
| $h_{{\rm{ub}},t,ij}^L \geqslant 0$ |
| ${z_{{\rm{ub}},t,i}} \geqslant 0$ |
式中
将式(28)带入式(23),则由式(1)和式(23)组成的分布式电源准入容量问题可以转化为max-min问题:
| $\max \sum\limits_{j \in G} {p_j^G} $ | (29) |
约束条件:
| $\begin{split} & V_{{\rm{sub}}}^2(1 + {t_p} \cdot a) + \sum\limits_{j \in S} {q_{j,t}^s{X_{ij}}} + \sum\limits_{j \in G} {{{\bar \omega }_{j,t}}p_j^G({R_{ij}} + {X_{ij}}\tan \; \varphi _j^G)} - \\ & \quad \quad \sum\limits_{j \in N} {\bar p_{j,t}^L({R_{ij}} + {X_{ij}}\tan \; \varphi _j^L)} + \min \left\{ {{\Gamma _t}{z_{{\rm{ub}},t,i}} + \sum\limits_{j \in G} {h_{{\rm{ub}},t,ij}^G} } \right. + \\ & \quad \quad \left. { \sum\limits_{j \in N} {h_{{\rm{ub}},t,ij}^L} } \right\} \leqslant {V_{i,\max }}{V_{{\rm{sub}}}} \end{split} \!\!\!\!\!\!\!\!\!\!\!$ | (30) |
由文献[19]所证,由式(29)和(30)组成的优化问题可以转化为如下线性模型:
| $\max \sum\limits_{j \in G} {p_j^G} $ |
约束条件:
| $\begin{split} & V_{{\rm{sub}}}^2(1 + {t_p} \cdot a) + \sum\limits_{j \in S} {q_{j,t}^s{X_{ij}}} + \sum\limits_{j \in G} {{{\bar \omega }_{j,t}}p_j^G({R_{ij}} + {X_{ij}}\tan \; \varphi _j^G)} - \\ & \quad \quad \sum\limits_{j \in N} {\bar p_{j,t}^L({R_{ij}} + {X_{ij}}\tan \; \varphi _j^L)} + {\Gamma _t}{z_{{\rm{ub}},t,i}} + \sum\limits_{j \in G} {h_{{\rm{ub}},t,ij}^G} + \\ & \quad \quad \sum\limits_{j \in N} {h_{{\rm{ub}},t,ij}^L} \leqslant {V_{i,\max }}{V_{sub}} \\ \end{split} $ |
根据上述过程,式(15)~(19)也可以类似地转化为鲁棒对等模型。至此,原问题就转化为混合整数线性规划(mixed integer linear programming,MILP)问题,可以采用商业软件如cplex、lingo等求解器求解。
3 算例分析 3.1 算例描述本文采用改进的IEEE33节点配电网络作为测试系统,在IEEE33节点标准算例的基础上考虑了OLTC以及SVC(S1和S2),拓扑结构如图3所示。分布式光伏的候选节点集合可以结合配网地理实际情况选择,不同的候选节点组合都可以验证本文方法的有效性,本文给出的分布式光伏待选位置集合为G1~G7。

|
Download:
|
| 图 3 修正的IEEE33节点配网模型 | |
分布式光伏取单位功率因数。有载变压器容量为6 MVA,变压器传输最大有功无功分别为6 MW和3 MVar,分接头具有17个档位。SVC可以从−100~300 kVar连续调节。
为了模拟实际情况,本文考虑居民负荷、工业负荷以及商业负荷3种负荷模式,配电网相应地被分为3个区域[20]。光伏出力曲线和3种日负荷曲线如图4所示。
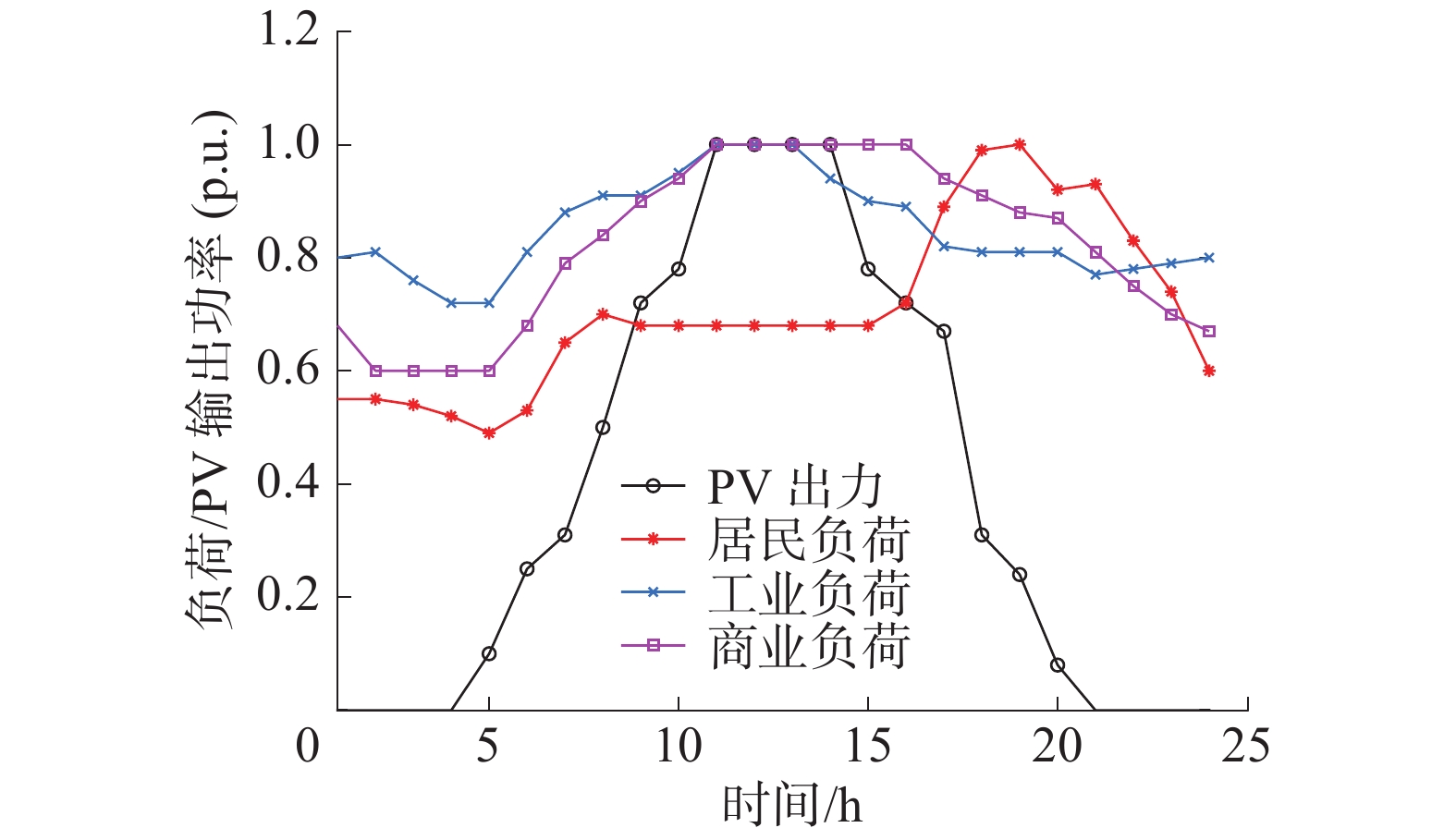
|
Download:
|
| 图 4 PV出力及负荷需求曲线 | |
1)所提鲁棒优化算法的有效性
如图3所示,本算例考虑了32个负荷点以及7个候选位置的光伏接入点,不确定功率的注入总数为39,因此Γ的取值区间为[0, 39]。为了验证所提出的基于RO模型的可行性,需要评估在最保守条件下(Γ=39),配电网PV准入容量。表2给出了Γ=39时各节点PV接入容量,PV总接入容量为6.631 MW。同时,RO方法也推导出其他关键控制变量包括SVC无功补偿器容量和OLTC分接头位置的最优值,如表3所示。
|
|
表 2 PV接入容量(Γ=39) |
|
|
表 3 模型1SVC无功补偿容量以及OLTC分接头位置(Γ=39) |
根据RO的思想,即使最坏的情况发生,表2所示的PV接入容量也不会影响图3所示的配电网络的安全性。一般来说,最坏的情况通常对应于:
1)场景1:最大负荷水平下最小光伏输出;
2)场景2:最小负荷水平下最大光伏输出。
为了直观地证明所提出的评估方法的鲁棒性,对场景1和场景2进行潮流计算,基于潮流计算结果,可以验证模型是否满足约束条件。
假定根据表2中的容量分配,在IEEE33节点配电网中安装分布式PV,同时,OLTC分接头位置和SVC的无功补偿按照表3中给出的数据设置。潮流计算的结果如图5、6和表4所示。由图表中数据可知,场景1和2中的电压和功率都满足约束。另外从图5中可以看出,某些节点的电压值已经达到0.95或1.05,所以此时的PV安装容量已经达到极限值。在最坏情况下,所有的安全约束都没有越限。因此,所提出的RO方法的有效性得到验证。

|
Download:
|
| 图 5 电压计算结果 | |

|
Download:
|
| 图 6 支路视在功率 | |
|
|
表 4 变压器交换功率 |
2)不同模型的对比
为了进一步验证本文模型的有效性,将本文方法(下称方法1)所求结果与基于机会约束的随机规划方法(下称方法2)所求结果来做对比。
基于机会约束的随机规划模型为:
| $\left\{ \begin{array}{l} \max {\rm{ }}f({x})\\ {\rm{s}}{\rm{.t}}{\rm{. }}\quad {p_r}\left\{ {{g_j}({x},{\xi }) \leqslant 0,j = 1,2, \cdots ,p} \right\} \geqslant {\alpha _j} \end{array} \right.$ |
将本文模型用上述随机规划模型表示,其中,ξ为随机向量,即分布式光伏出力与负荷需求;pr{•}为事件{•}成立的概率,即本文模型提出的电压约束、线路容量约束、变压器容量约束以及变压器交换功率约束;αj为事先给定的约束条件的置信水平,取值0.95。
方法1和方法2求得的分布式光伏的接入容量如表5所示。方法2优化得到的无功补偿器容量和OLTC分接头位置如表6所示。由表5各PV接入节点的PV接入容量可知,方法1得到的分布式光伏的总接入容量为6.631 MW,方法2求得的分布式光伏的总接入容量达到6.814 MW。由于基于机会约束的随机规划方法对每个约束都进行松弛,导致最后评估PV接入容量时偏乐观。
|
|
表 5 PV接入容量对比 |
|
|
表 6 模型1SVC无功补偿容量以及OLTC分接头位置(Γ=39) |
对方法2求得的PV容量配比仍然考虑上述所提极端场景1、2时,潮流电压计算结果如图7所示;各支路结果如图8所示。

|
Download:
|
| 图 7 方法2电压计算结果 | |
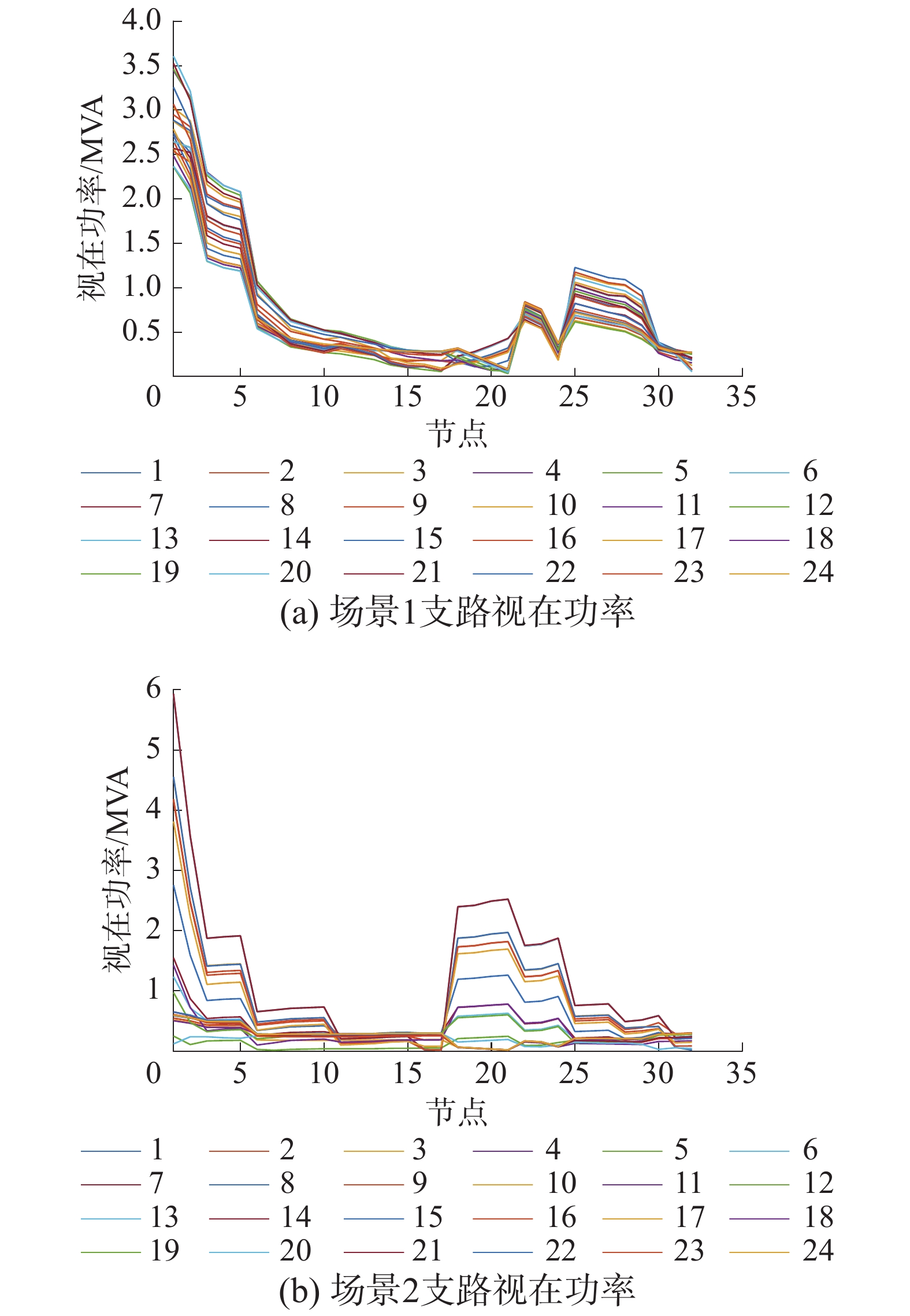
|
Download:
|
| 图 8 方法2支路视在功率 | |
由图7可知,对于场景1,电压越下限;而对于场景2,电压越上限。而本文所提模型1可以满足极端场景下电力系统的安全性,相对于随机规划来说,求得的结果更加安全。当极端场景发生概率较小时,也可以通过调节Γ值来适当缓解所得结果的保守性。
3)参数Γ的选择
在使用本文所提出的RO方法评估分布式电源准入容量之前,配网运营商(distribution network operator, DNO)首先需要预先定义Γ值。根据RO的思想,Γ取值越大,得到的结果就越保守;而较低的Γ值可以使PV的安装容量更大。因此下面给出定量分析以探讨Γ值与PV安装容量之间的关系。
对应于不同Γ值的PV安装容量如图9所示。
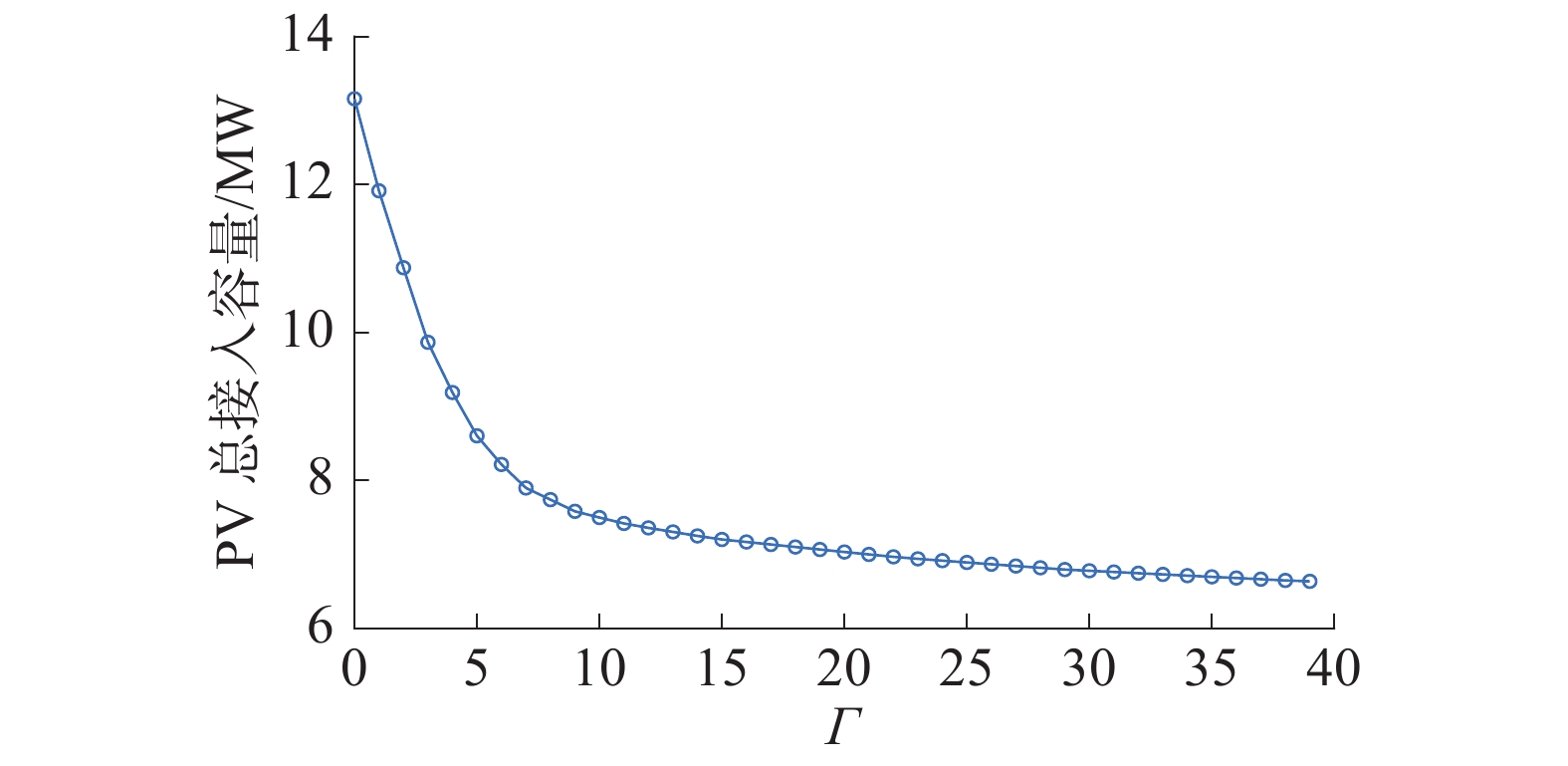
|
Download:
|
| 图 9 不同Γ值对应的PV接入容量 | |
从图9中可以看出,当Γ<9时曲线陡峭;当Г>9时曲线变得平缓。具体来说,Γ=0与Γ=39相比,PV安装容量增加了98.4%,而Γ=9与Γ=39相比,PV安装容量只增加了2.15%。即参数Γ降低到一定程度后,DG接入容量才会显著增加。
当Γ=0时,即DNO以最乐观的态度评估DG的接入容量,此时意味着所得结果存在违反技术约束的风险。当Γ=39,即DNO以最保守的态度评估DG接入容量,此时所得结果偏保守,但是解的鲁棒性最强。面对实际电网,我们可以在允许风险范围内,通过调整参数Γ来改善配电网的DG接入容量。
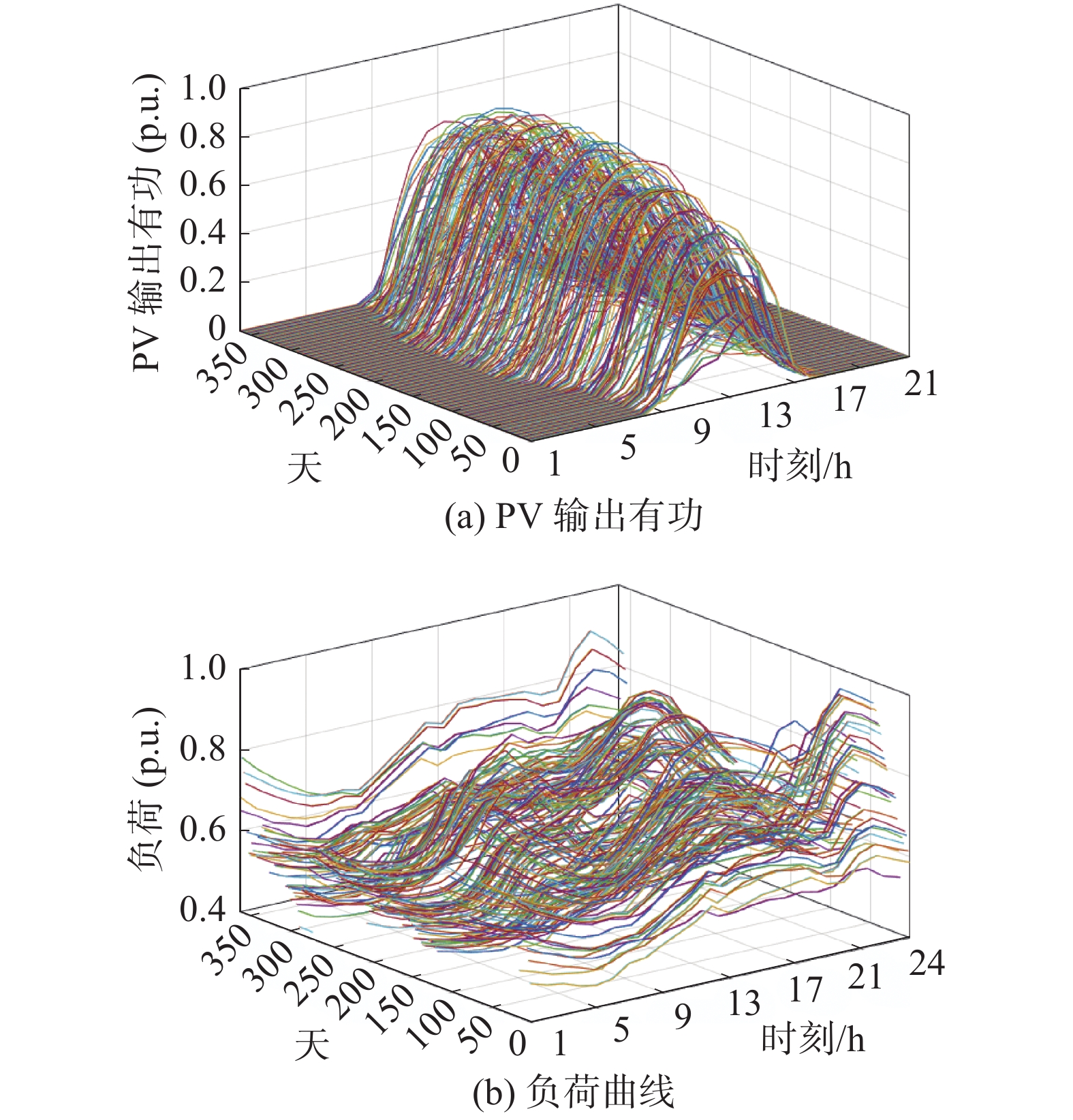
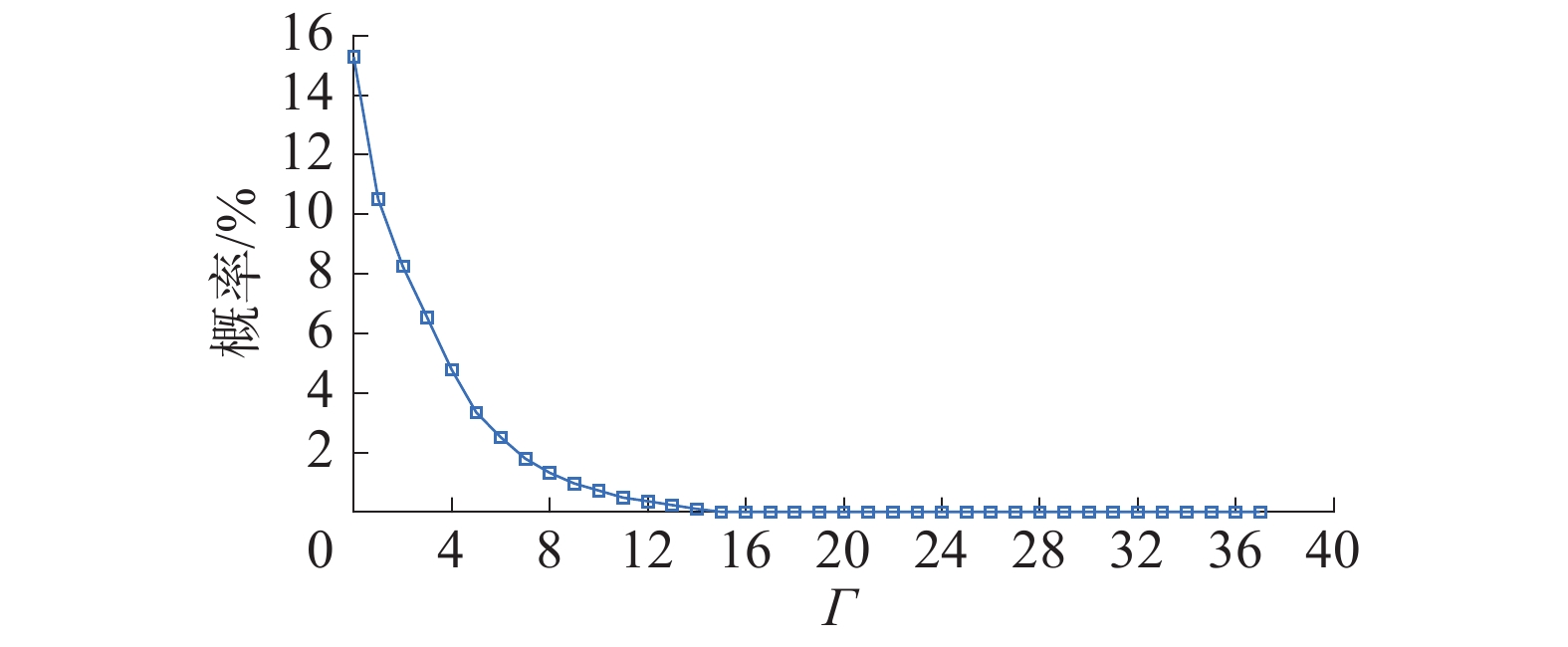
在所提出的基于RO的评估方法中,得到的鲁棒优化解对应于多个负荷和DG出力水平的场景,因为它们是给定的不确定参数,而不是RO中的决策变量。事实上,RO的一种解决方案可以应对多个负荷和DG出力水平的情况,即能够在大量的不同的负荷和DG出力水平下,不违反约束使DG接入容量最大化。随着Γ的减小,得到的鲁棒最优解可以处理的场景也就越少,但始终包含大量的场景。利用一年的负荷数据和PV出力数据来对不同Γ值下违约风险进行定量评估,图10给出了负荷和光伏发电的曲线,而图11为不同Γ值下越限概率曲线图。
|
Download:
|
| 图 10 负荷和光伏发电的曲线 | |
|
Download:
|
| 图 11 不同Γ值下的越限风险 | |
如图11所示,较低的Γ值会导致较高的风险水平。根据图9和图11,DSO可以基于系统的主动调节能力选择适当的Γ值作为DG接入容量与风险之间的权衡。如果有足够的负载和PV功率数据,DSO可以用不同的Γ值评估风险并选择合适的Γ值;否则,DSO可以通过预定义最大Γ值来选择最保守的方案。
4)安全约束分析
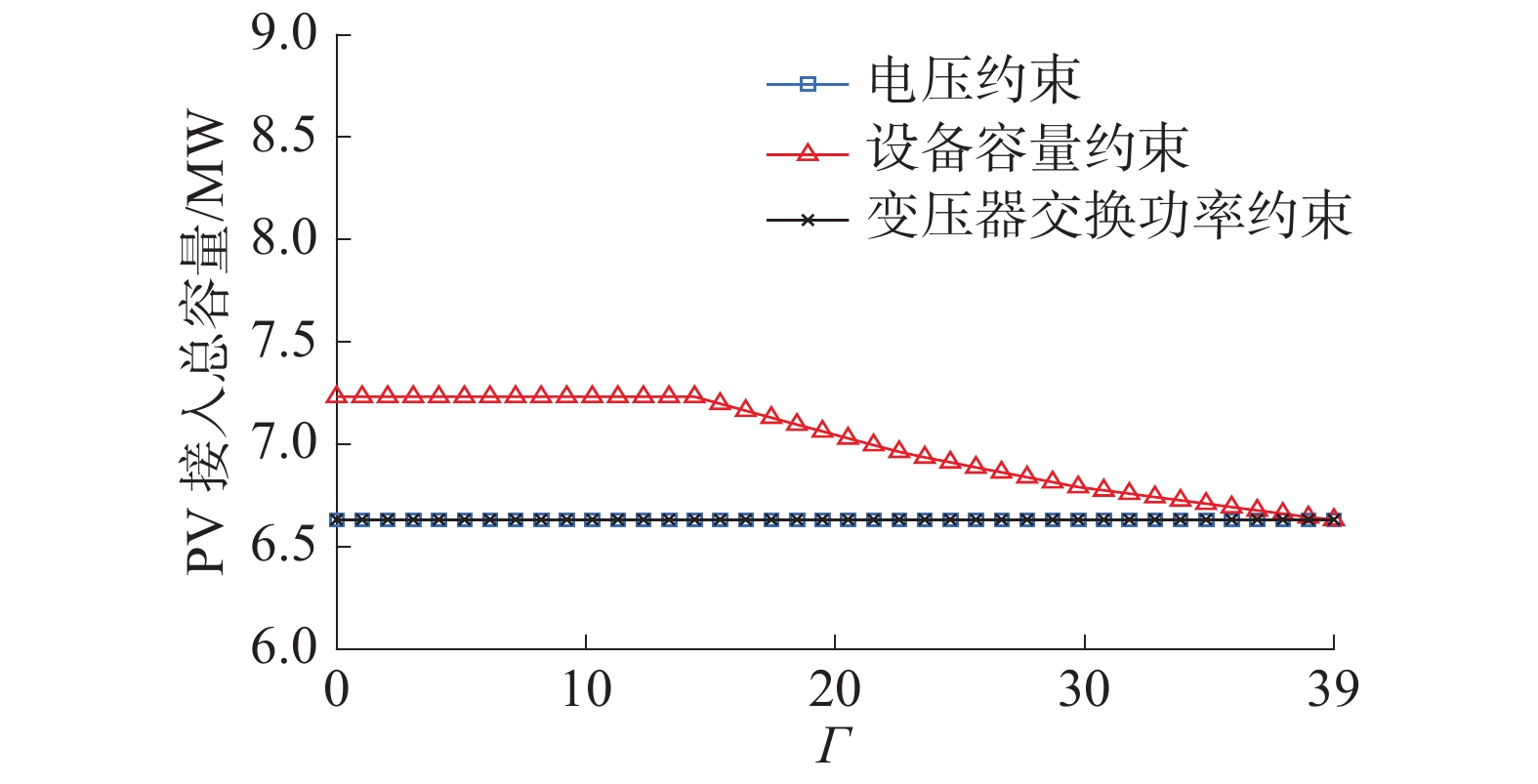
由本文所得模型可知,配电网的分布式电源最大安装容量受到一系列安全约束的限制,但是它们的影响程度是不相同的。如果DNO想要增加PV的接入容量,就需要找出限制PV接入的技术瓶颈。在此处的分析中,假设所有电压约束的参数Γ采用相同的值,由Γv表示。类似的,Γs表示设备容量约束的参数Γ,Γpq表示变压器与上级电网交换功率约束的参数Γ。对于Γv、Γs和Γpq,轮流进行以下操作:令其中2个参数取最大值39,并使另外一个参数Γ在0~39变化,计算PV的安装容量。结果如图12所示。
|
Download:
|
| 图 12 不同Γ值对应的PV接入容量 | |
从图12可以明显看出,电压约束和变压器交换功率约束的Γ值改变不会影响PV接入容量,而较低的Γs值可以增加PV接入容量。因此,在这种情况下,设备容量约束是限制PV接入容量的关键因素。
为了进一步证明上述方法的可行性,进行另一组仿真,将电压约束收紧,让电压约束的取值范围由原来的[0.95, 1.05]变为[0.96, 1.04],此时得到的结果如图13所示。

|
Download:
|
| 图 13 不同Γ值对应的PV接入容量 | |
结果表明,Γv值越小,PV接入容量越大,不论Γs和Γpq设置何值,PV接入容量保持不变。因此,在这种情况下,电压约束是限制PV接入容量的最关键因素。
从上述仿真可以得出结论,所提出的RO方法可以帮助DNO识别可能影响PV接入总容量的最关键因素,从而DNO可以采取相应的措施来提高配电网容纳更多PV的能力。
4 结论本文提出了一种基于RO的方法用于评估配电网中分布式光伏的准入容量。该方法使用无分布有界区间来模拟分布式光伏功率输出和负荷的不确定性,利用鲁棒性指标来协调安全性与接入容量,其显著优越性在于:
1)该方法通过区间和期望值的形式描述分布式光伏功率输出和负荷水平的不确定性,更贴近工程实际,参数获取容易;
2)引入一个用来描述决策者对鲁棒优化保守性判断的可调节参数,实现对不确定参数取值区间缩放,用来权衡系统安全与优化结果值;
3)为了适应新型配电网,考虑了主动管理措施带来的约束,包括电压控制和无功补偿,来更好地评估分布式光伏的接入容量。
在改进的IEEE33节点配电系统上进行了仿真计算,得到在最保守的情况下,所有极限场景安全约束均满足的结果,验证了本文所提方法的有效性。此外,通过2个仿真场景来说明的基于RO的方法可以用于识别限制分布式光伏接入容量的技术瓶颈。
| [1] |
邱坚石, 陈铁. 配电网中分布式电源规划研究综述[J]. 东北电力大学学报, 2017, 37(2): 89-92. DOI:10.3969/j.issn.1005-2992.2017.02.016 ( 0) 0)
|
| [2] |
吴鸣, 于辉, 熊雄. 分布式电源接入配电网的基本原则[J]. 供用电, 2017, 34(12): 32-38. ( 0) 0)
|
| [3] |
丁磊, 刘俊勇, 刘友波, 等. 考虑分布式发电商投资的区域配电网光伏储能容量配置[J]. 可再生能源, 2017, 35(3): 374-383. ( 0) 0)
|
| [4] |
王威, 王晴, 虞殷树, 等. 分布式电源接入配电网的极限容量计算研究[J]. 电力信息与通信技术, 2017, 15(3): 14-19. ( 0) 0)
|
| [5] |
何英静, 李帆, 沈舒仪, 等. 新能源及分布式电源接入浙江配电网适应性研究[J]. 浙江电力, 2018, 37(1): 32-36. ( 0) 0)
|
| [6] |
钟清, 高新华, 余南华, 等. 谐波约束下的主动配电网分布式电源准入容量与接入方式[J]. 电力系统自动化, 2014, 38(24): 108-113. DOI:10.7500/AEPS20131214002 ( 0) 0)
|
| [7] |
刘志文, 董旭柱, 黄豫, 等. 考虑多种约束的分布式电源最大渗透率计算方法[J]. 电力系统及其自动化学报, 2019, 31(6): 85-92. ( 0) 0)
|
| [8] |
雷金勇, 黄伟, 夏翔, 等. 考虑相间短路影响的分布式电源准入容量计算[J]. 电力系统自动化, 2008, 32(3): 82-86. DOI:10.3321/j.issn:1000-1026.2008.03.019 ( 0) 0)
|
| [9] |
UGRANLI F, KARATEPE E. Optimal wind turbine sizing to minimize energy loss[J]. International journal of electrical power & energy systems, 2013, 53: 656-663. ( 0) 0)
|
| [10] |
商立群, 郭伟. 一种矩阵化描述的分布式光伏准入容量计算方法[J]. 电力系统保护与控制, 2018, 46(16): 25-30. DOI:10.7667/PSPC171142 ( 0) 0)
|
| [11] |
任智君, 郭红霞. 基于风光荷时序特性和主动管理的配电网分布式电源准入容量模型及应用[J]. 水电能源科学, 2019, 37(6): 183-186, 191. ( 0) 0)
|
| [12] |
CAPITANESCU F, OCHOA L F, MARGOSSIAN H, et al. Assessing the potential of network reconfiguration to improve distributed generation hosting capacity in active distribution systems[J]. IEEE transactions on power systems, 2015, 30(1): 346-356. DOI:10.1109/TPWRS.2014.2320895 ( 0) 0)
|
| [13] |
YEH H G, GAYME D F, LOW S H. Adaptive VAR control for distribution circuits with photovoltaic generators[J]. IEEE transactions on power systems, 2012, 27(3): 1656-1663. DOI:10.1109/TPWRS.2012.2183151 ( 0) 0)
|
| [14] |
CHEN Xin, WU Wenchuan, ZHANG Boming. Robust restoration method for active distribution networks[J]. IEEE transactions on power systems, 2016, 31(5): 4005-4015. DOI:10.1109/TPWRS.2015.2503426 ( 0) 0)
|
| [15] |
SOYSTER A L. Technical note—convex programming with set-inclusive constraints and applications to inexact linear programming[J]. Operations research, 1973, 21(5): 1154-1157. DOI:10.1287/opre.21.5.1154 ( 0) 0)
|
| [16] |
KANG S C. Robust linear optimization using distributional information[D]. Boston: Boston University, 2008. http://www.oalib.com/references/16849026
( 0) 0)
|
| [17] |
彭春华, 谢鹏, 陈臣. 大规模光伏电站接入电网可调节鲁棒优化调度[J]. 中国电机工程学报, 2014, 34(25): 4324-4332. ( 0) 0)
|
| [18] |
BAZARAA M S, JARVIS J J, SHERALI H D. Linear programming and network flows[M]. 4th ed. Hoboken, NJ, USA: Wiley, 2010.
( 0) 0)
|
| [19] |
朱嘉远, 刘洋, 许立雄, 等. 考虑风电消纳的热电联供型微网日前鲁棒经济调度[J]. 电力系统自动化, 2019, 43(04): 54-65. ( 0) 0)
|
| [20] |
CHEN Xin, WU Wenchuan, ZHANG Boming, et al. Data-driven DG capacity assessment method for active distribution networks[J]. IEEE transactions on power systems, 2017, 32(5): 3946-3957. DOI:10.1109/TPWRS.2016.2633299 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


