复杂的电磁环境下，保持电磁静默，实现隐蔽突防是重要的战术手段。电磁静默条件下对辐射源目标进行侦察时，无源定位便成为重要的探测手段，也备受各国的关注和重视^[1]。无人机相较于当前先进的有人驾驶飞机而言，具有低成本、长航时、易维护和安全风险系数低等特点。而无源探测设备又具备体积小、功耗低的特点^[2]。无人机编队作为新型作战系统，将多站时差无源定位系统应用于无人机编队具有良好的实用性。

采用多站时差无源定位时，衡量定位系统性能的重要指标之一便是系统的定位精度。其中，定位精度的影响因素包含定位算法、时差测量精度、站址坐标测量精度和站址布局等。在不同布站方式中，Y型和倒Y型布站方式的定位精度要高于其他布站方式^[2-3]。对于多站时差定位而言，在其他测量误差不变的条件下，多机编队的站址构形是影响定位精度的重要因素之一。

无人机编队在进行多站时差定位的过程中，不仅需要考虑敌方雷达探测区域、编队飞行高度、无人机间最大通信距离、地球曲率、辐射源信号侦收等问题，还需要考虑针对探测区域的辐射源目标的定位效果^[4]。无人机编队具有灵活的特点，可针对目标出现区域的不同和其他限制条件，动态调整编队方式，从而获取针对目标所在区域定位精度最优的站址构形^[5-6]。

2017年，MIRJALILI S等^[7]、陈涛等^[8]提出一种樽海鞘群算法(SSA)，该算法是以深海生物樽海鞘群体作为研究对象。樽海鞘群体中个体间的行为联系密切，不同于大多数动物群体，在每次迭代过程中都将进行排序，单个个体均跟随前一个体移动，从而形成一种链状结构。这种跟随式的更新方式不是所有个体均向最优值移动，减少了出现局部最优解的情况。

本文利用樽海鞘群算法来解决站址构型优化问题，以最小化目标所在区域内平均定位误差作为目标函数，对无人机编队被动时差定位时的站址构形进行调整优化，实现在测量误差不变的条件下，对辐射源目标进行被动时差定位时定位精度的提升^[9]。

1 多站时差定位原理

无人机编队四站时差定位模型如图1所示，该雷达发射具有良好的距离分辨率和径向速度分辨率的线性调频脉冲信号。利用辐射源发出信号到达不同无人机的时间差可以确定一条以2架无人机为焦点的双曲线，通过解算多条双曲线的交点获得辐射源位置信息^[10]。时差测量是多站时差定位中的重要环节，往往根据实际工程要求选择测时差方式。如根据主观测站对自身接收到的信号与辅观测站传输来的信号做相关运算^[11]求取相应的时间差，或是基于统一高同步时统模块，各站分别记录信号到达时间，传输至主站计算获得时差^[12]。本文所用时差信息是基于后一种模式获取得到的。

当无人机进行四站时差定位时，设主站与3个辅站的坐标分别为 $({x_0},{y_0},{z_0})$ 、 $({x_1},{y_1},{z_1})$ 、 $({x_2},{y_2},{z_2})$ 、 $({x_3},{y_3},{z_3})$ ；目标辐射源的坐标为 $(x,y,z)$ ； $\Delta {r_i}$ 表示的目标到各无人机的距离的差值； ${r_i}(i = 0,1,2,3)$ 表示辐射源到各无人机之间的距离，使用的距离均为真实距离，实际应用中观测站位置信息往往由GPS给出基于大地直角坐标系下的经纬高坐标，通过转换公式转换为以地球表面某点为原点的空间直角坐标系用于仿真计算^[13]； $\Delta {t_i}$ 为主站到各个辅站所对应的时间差； $c$ 表示电磁波的传播速度。通过几何关系可以得到如下所示定位方程组：

$\left\{\!\!\!\!\!\! {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {{r_0}^2 = {{(x - {x_0})}^2} + {{(y - {y_0})}^2} + {{(z - {z_0})}^2}}&{}&{} \end{array}} \\ {\begin{array}{*{20}{c}} {{r_i}^2 = {{(x - {x_i})}^2} + {{(y - {y_i})}^2} + {{(z - {z_i})}^2}}&{}&{} \end{array}} \\ {\begin{array}{*{20}{c}} {\Delta {r_i} = {r_i} - {r_0} = c\Delta {t_i}}&&{} \end{array}} \end{array}} \right.$

(1)

式中 ${i = 1,2,3} $ 。

将式(1)的多站时差定位方程组重写为

$\left\{ {\begin{array}{*{20}{c}} {{f_1} = {r_1} - {r_0} - c \cdot \Delta {t_1}\; } \\ {{f_2} = {r_2} - {r_0} - c \cdot \Delta {t_2}} \\ {{f_3} = {r_3} - {r_0} - c \cdot \Delta {t_3}} \end{array}} \right.$

其矩阵表达式为

${{F}}({{x}}) = {\bf{0}}$

(2)

式中： ${{F}} = {\left[ {{f_1}\; {f_2}\; {f_3}} \right]^{\rm{T}}}$ ； ${{x}} = {\left[ {x\; y\; z} \right]^{\rm{T}}}$ 。

若 ${{{x}}^{(k)}}$ 是式(2)方程的近似解，且 ${{F}}({{x}})$ 在 ${{{x}}^{(k)}}$ 邻域内可微，则 ${{F}}({{x}})$ 可在 ${{{x}}^{(k)}}$ 附近进行线性化，得到近似的线性方程：

${{F}}({{x}}) = {{F}}\left( {{{{x}}^{(k)}}} \right) + {{F}}'({{{x}}^{(k)}})({{x}} - {{{x}}^{(k)}}) = {\bf{0}}$

${{F}}'({{{x}}^{(k)}})$ 非奇异情况下，式(2)的线性方程存在唯一解：

${{{x}}^{(k + 1)}} = {{{x}}^{(k)}} - {[{{F}}'({{{x}}^{(k)}})]^{ - 1}}{{F}}({{{x}}^{(k)}})$

(3)

式中：

${{{x}}^{(k)}}{\rm{ = }}\left[ {{{{x}}^{(k)}}\;{y^{(k)}}\;{z^{(k)}}} \right]$

$\begin{array}{c} {{F}}'({{x}}) = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {f_1}}}{{\partial x}}}&{\dfrac{{\partial {f_1}}}{{\partial y}}}&{\dfrac{{\partial {f_1}}}{{\partial z}}} \\ {\dfrac{{\partial {f_2}}}{{\partial x}}}&{\dfrac{{\partial {f_2}}}{{\partial y}}}&{\dfrac{{\partial {f_2}}}{{\partial z}}} \\ {\dfrac{{\partial {f_3}}}{{\partial x}}}&{\dfrac{{\partial {f_3}}}{{\partial y}}}&{\dfrac{{\partial {f_3}}}{{\partial z}}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\dfrac{{x - {x_1}}}{{{r_1}}} - \dfrac{{x - {x_0}}}{{{r_0}}}}&{\dfrac{{y - {y_1}}}{{{r_1}}} - \dfrac{{y - {y_0}}}{{{r_0}}}}&{\dfrac{{z - {z_1}}}{{{r_1}}} - \dfrac{{z - {z_0}}}{{{r_0}}}} \\ {\dfrac{{x - {x_2}}}{{{r_2}}} - \dfrac{{x - {x_0}}}{{{r_0}}}}&{\dfrac{{y - {y_2}}}{{{r_2}}} - \dfrac{{y - {y_0}}}{{{r_0}}}}&{\dfrac{{z - {z_2}}}{{{r_2}}} - \dfrac{{z - {z_0}}}{{{r_0}}}} \\ {\dfrac{{x - {x_3}}}{{{r_3}}} - \dfrac{{x - {x_0}}}{{{r_0}}}}&{\dfrac{{y - {y_3}}}{{{r_3}}} - \dfrac{{y - {y_0}}}{{{r_0}}}}&{\dfrac{{z - {z_3}}}{{{r_3}}} - \dfrac{{z - {z_0}}}{{{r_0}}}} \end{array}} \right]\\[-35pt] \end{array} $

(4)

将式(4)代入式(3)中，依次迭代，直至 $\left\| {{{{x}}^{(k)}} - {{{x}}^{(k - 1)}}} \right\| < \varepsilon $ 时，迭代结束，最后获得定位结果。

2 多站时差定位精度分析

定位精度是无源定位系统性能的重要衡量指标。定位精度指标通常采用几何精度因子(geometrical dilution of precision，GDOP)，精度越高，GDOP数值越小。

对式(1)中的 $\Delta {r_i}$ $(i = 1,2,3)$ 求微分：

$\begin{split} {\rm{d}}(\Delta {r_i}) = \dfrac{{\partial \Delta {r_i}}}{{\partial x}}{\rm{d}}x + \dfrac{{\partial \Delta {r_i}}}{{\partial y}}{\rm{d}}y + \dfrac{{\partial \Delta {r_i}}}{{\partial z}}{\rm{d}}z + \dfrac{{\partial \Delta {r_i}}}{{\partial {x_i}}}{\rm{d}}{x_i} + \\ \dfrac{{\partial \Delta {r_i}}}{{\partial {y_i}}}{\rm{d}}{y_i} + \dfrac{{\partial \Delta {r_i}}}{{\partial {z_i}}}{\rm{d}}{z_i} + \dfrac{{\partial \Delta {r_i}}}{{\partial {x_0}}}{\rm{d}}{x_0} + \dfrac{{\partial \Delta {r_i}}}{{\partial {y_0}}}{\rm{d}}{y_0} + \dfrac{{\partial \Delta {r_i}}}{{\partial {z_0}}}{\rm{d}}{z_0} \end{split} $

(5)

令

$\left\{ {\begin{array}{*{20}{c}} {{c_{ix}} = \dfrac{{\partial {r_i}}}{{\partial x}} = \dfrac{{x - {x_i}}}{{{r_i}}}} \\ {{c_{iy}} = \dfrac{{\partial {r_i}}}{{\partial y}} = \dfrac{{y - {y_i}}}{{{r_i}}}} \\ {{c_{iz}} = \dfrac{{\partial {r_i}}}{{\partial z}} = \dfrac{{z - {z_i}}}{{{r_i}}}} \end{array}} \right.$

(6)

式中 $i = 0,1,2,3$ 。

将式(6)代入式(5)：

$\begin{array}{l} {\rm{d}}\left( {\Delta {r_i}} \right) = ({c_{ix}} - {c_{0x}}){\rm{d}}x + ({c_{iy}} - {c_{0y}}){\rm{d}}y + ({c_{iz}} - {c_{0z}}){\rm{d}}z + ({k_0} - {k_i}) \end{array} $

式中

${k_i} = {c_{ix}}{\rm{d}}{x_i} + {c_{jy}}{\rm{d}}{y_i} + {c_{iz}}{\rm{d}}{z_i}$

写成矩阵的形式为

${\rm{d}}\Delta {{R}} = {{C}} \cdot {\rm{d}}{{X}} + {\rm{d}}{{{X}}_s}$

式中： ${\rm{d}}{{X}} = {\left[ {{\rm{d}}x,{\rm{d}}y,{\rm{d}}z} \right]^{\rm{T}}}$ 为对辐射源的定位误差； ${\rm{d}}\Delta {{R}} = {\left[ {{\rm{d}}\Delta {r_1},{\rm{d}}\Delta {r_2},{\rm{d}}\Delta {r_3}} \right]^{\rm{T}}}$ 为各站的站址测量误差； ${\rm{d}}{{{X}}_s} = {\left[ {{k_0} - {k_1},{k_0} - {k_2},{k_0} - {k_3}} \right]^{\rm{T}}}$ 为主站与辅站间的到达时间差的测量误差。

进一步转换得相关系数矩阵：

${{C}} = \left[ {\begin{array}{*{20}{c}} {{c_{1x}} - {c_{0x}}}&{{c_{1y}} - {c_{0y}}}&{{c_{1z}} - {c_{0z}}} \\ {{c_{2x}} - {c_{0x}}}&{{c_{2y}} - {c_{0y}}}&{{c_{2z}} - {c_{0z}}} \\ {{c_{3x}} - {c_{0x}}}&{{c_{3y}} - {c_{0y}}}&{{c_{3z}} - {c_{0z}}} \end{array}} \right]$

所以可得辐射源的定位误差估计值：

${\rm{d}}{{X}} = {\left( {{{{C}}^{\rm{T}}}{{C}}} \right)^{ - 1}}{{{C}}^{\rm{T}}}\left[ {{\rm{d}}\Delta {{R}} - {\rm{d}}{{{X}}_s}} \right]$

令

${{D}} = {({{{C}}^{\rm{T}}}{{C}})^{ - 1}}{{{C}}^{\rm{T}}} = {\left[ {{b_{ij}}} \right]_{3 \times 3}}$

则

${\rm{d}}{{X}} = {{D}}\left[ {{\rm{d}}\Delta {{R}} - {\rm{d}}{{{X}}_s}} \right]$

定位误差的协方差为

$\begin{array}{l} {{{P}}_{{\rm{d}}{{X}}}} \!=\! {\rm{E}}\left[ {{\rm{d}}{{X}}\;\;\;{\rm{d}}{{{X}}^{\rm{T}}}} \right] \!=\!{{D}}\left\{ {{\rm{E}}\left[ {{\rm{d}}\Delta {{R}}\;\;\;{\rm{d}}\Delta {{{R}}^{\rm{T}}}} \right] \!+\! {\rm{E}}\left[ {{\rm{d}}{{{X}}_s}\;\;\;{\rm{d}}{{{X}}_s}^{\rm{T}}} \right]} \right\}{{{D}}^{\rm{T}}} \end{array} $

式中：

$\begin{array}{l} {\rm{E}}\left[ {{\rm{d}}\Delta {{R}}\;\;\;{\rm{d}}\Delta {{{R}}^{\rm{T}}}} \right] \!=\! \left[ {\begin{array}{*{20}{c}} {\sigma _{\Delta {r_1}}^2}&{{\eta _{12}}{\sigma _{\Delta {r_1}}}{\sigma _{\Delta {r_2}}}}&{{\eta _{13}}{\sigma _{\Delta {r_1}}}{\sigma _{\Delta {r_3}}}} \\ {{\eta _{21}}{\sigma _{\Delta {r_2}}}{\sigma _{\Delta {r_1}}}}&{\sigma _{\Delta {r_2}}^2}&{{\eta _{23}}{\sigma _{\Delta {r_2}}}{\sigma _{\Delta {r_3}}}} \\ {{\eta _{31}}{\sigma _{\Delta {r_3}}}{\sigma _{\Delta {r_1}}}}&{{\eta _{32}}{\sigma _{\Delta {r_3}}}{\sigma _{\Delta {r_2}}}}&{\sigma _{\Delta {r_3}}^2} \end{array}} \right] \end{array} $

其中：标准差 $\sigma _{\Delta {r_i}}^2$ 为第 $i$ 站与主站间距的测量误差； ${\eta _{ij}}$ 为 $\Delta {r_i}$ 与 $\Delta {r_j}$ 的相关系数， ${\eta _{ij}} = \dfrac{{{\rm{cov}} \left( {\Delta {r_i},\Delta {r_j}} \right)}}{{{\sigma _{\Delta {r_i}}}{\sigma _{\Delta {r_j}}}}} $ 。

$\begin{array}{c} {\rm{E}}\left[ {\begin{array}{*{20}{c}} {{\rm{d}}{{{X}}_S}}&{{\rm{d}}{{{X}}_S}^{\rm{T}}} \end{array}} \right] = {\rm{diag}}[c_{1x}^2\sigma _{x1}^2 + c_{1y}^2\sigma _{y1}^2 + c_{1z}^2\sigma _{z1}^2, \\ c_{2x}^2\sigma _{x2}^2 + c_{2y}^2\sigma _{y2}^2 + c_{2z}^2\sigma _{z2}^2, c_{3x}^2\sigma _{x3}^2 + c_{3y}^2\sigma _{y3}^2 + c_{3z}^2\sigma _{z3}^2] + \\ \left( {c_{0x}^2\sigma _{x0}^2 + c_{0y}^2\sigma _{y0}^2 + c_{0z}^2\sigma _{z0}^2} \right){{{Q}}_{3 \times 3}} \end{array} $

其中 ${{{Q}}_{3 \times 3}}$ 为三阶方阵。

假设观测站的站址测量误差各分量为相等的标准差，即有

$ \begin{array}{l} \sigma _{xi}^2 = \sigma _{yi}^2 = \sigma _{zi}^2 = \sigma _s^2,\;\;{i = 0,1,2,3} \\ c_{ix}^2 + c_{iy}^2 + c_{iz}^2 = 1,\;\;{i = 0,1,2,3} \end{array}$

可得

${\rm{E}}\left[ {{\rm{d}}{{{X}}_S}{\rm{d}}{{{X}}_S}^{\rm{T}}} \right] = \sigma _s^2\left( {{{{I}}_{3 \times 3}} + {{{Q}}_{3 \times 3}}} \right)$

式中 ${{{I}}_{3 \times 3}}$ 为三阶单位矩阵。令

$ \begin{array}{c} {\rm{E}}\left[ {{\rm{d}}{{{X}}_S}{\rm{d}}{{{X}}_S}^{\rm{T}}} \right] + {\rm{E}}\left[ {{\rm{d}}\Delta {{R}}{\rm{d}}\Delta {{{R}}^{\rm{T}}}} \right] = {\left[ {{\sigma _{ij}}} \right]_{3 \times 3}}\\ \;\;\;\;\;\;\;\;{{{P}}_{{\rm{d}}{{X}}}} = {\left[ {{B_{lh}}} \right]_{3 \times 3}} \end{array}$

式中

${\sigma _{ij}} = \left\{ {\begin{aligned} & {\sigma _{\Delta {r_i}}^2 + 2\sigma _s^2,\quad {i = j} } \\ & {{\eta _{ij}}{\sigma _{\Delta {r_i}}}{\sigma _{\Delta {r_j}}} + \sigma _s^2,\quad {i \ne j} } \end{aligned}} \right.$

其中： $i=1,2,3; j=1,2,3$ 。

${B_{lh}} = \displaystyle\sum\limits_{i = 1}^3 {\displaystyle\sum\limits_{j = 1}^3 {{b_{li}}{b_{hj}}\sigma _{ij}^2\begin{array}{*{20}{c}} {}&{} \end{array}} } $

其中： $l=1,2,3; h = 1,2,3$ 。

可得在 $x,y,z$ 方向上定位误差的方差分别为

$\left\{ {\begin{array}{*{20}{c}} {\sigma _{{x}}^2 = {B_{11}} = \displaystyle\sum\limits_{i = 1}^3 {\displaystyle\sum\limits_{j = 1}^3 {{b_{1i}}{b_{1j}}\sigma _{ij}^2} } } \\ {\sigma _y^2 = {B_{22}} = \displaystyle\sum\limits_{i = 1}^3 {\displaystyle\sum\limits_{j = 1}^3 {{b_{2i}}{b_{2j}}\sigma _{ij}^2} } } \\ {\sigma _z^2 = {B_{33}} = \displaystyle\sum\limits_{i = 1}^3 {\displaystyle\sum\limits_{j = 1}^3 {{b_{3i}}{b_{3j}}\sigma _{ij}^2} } } \end{array}} \right.$

所以四站时差定位的 ${\rm{GDOP}}$ 值为

$\begin{array}{l} {P_{{\rm{GDOP}}}} = \sqrt {\sigma _{{x}}^2 + \sigma _y^2 + \sigma _z^2} {\rm{ = }}\sqrt {{\rm{trace(}}{{{P}}_{{\rm{d}}{{X}}}}{\rm{)}}} = \\ \sqrt {\displaystyle\sum\limits_{i = 1}^3 {\displaystyle\sum\limits_{j = 1}^3 {({b_{1i}}{b_{1j}} + {b_{2i}}{b_{2j}} + {b_{3i}}{b_{3j}})} } {\sigma _{ij}}^2} \end{array} $

在测量误差不变的条件下，通过调整无人机编队布局方式，可有效提升定位精度。本文以最小化目标所在区域内平均定位误差作为目标函数，采用樽海鞘群算法寻找最优布局方式。

设 $S$ 为目标所在的区域，为衡量无人机编队在该区域内的时差定位效果，在目标区域内采用离散取值的方式来近似计算无人机编队对目标区域时差定位的平均定位误差，从而避免复杂的积分运算^[14]。定义 ${\sigma _a}$ 为区域的平均定位误差：

${\sigma _a} = \dfrac{1}{K}\displaystyle\sum\limits_{i = 1}^K {{A_{{\rm{GDOP}}}}\left( {{T_i}} \right)} $

(7)

式中： $K$ 为在目标区域选取的观测点数； ${A_{{\rm{GDOP}}}}\left( {{T_i}} \right)$ 为无人机编队在点 ${T_i}$ 处的定位精度，且 ${T_i}$ 位于目标区域 $S$ 中。

根据空间位置限制条件，并以平均定位误差最小作为编队站址布局的优化目标函数，无人机编队布局优化问题可描述为

${{{P}}_{i,{\rm{opt}}}} = \arg \mathop {\min }\limits_{{{{P}}_i} \in {{{D}}_{\rm{L}}}} {\sigma _a}, \;\;{i = 1,2, \cdots ,M} $

式中： ${{{P}}_{i,{\rm{opt}}}}$ 为无人机的最优位置坐标； ${{{P}}_i}$ 为无人机位置坐标； $M$ 为无人机架数； ${{{D}}_{\rm{L}}}$ 为位置约束条件下的三维空间区域。

3 基于反向学习策略的樽海鞘群算法

本节采用反向学习策略(OBL)对樽海鞘群算法进行优化，建立反向学习樽海鞘群算法(opposition salp swarm algorithm，OSSA)，用于解决站址优化问题^[15-16]。采用反向学习策略提高樽海鞘群算法中种群的多样性，通过优化初始种群，提高初始种群的质量，并在更新过程中采用反向学习策略对种群进行适当优化，使改进后的樽海鞘算法具有更快的收敛速度。

3.1 算法描述

樽海鞘生活在海洋深处，通过吸取身体周围的水，让水泵过自己的身体来向前移动。不同于其他大多数群居生物，樽海鞘是以链的形式，一个跟随一个移动。排在樽海鞘链的第一个个体被视为领导者，其对周围环境具有最好的识别，后续个体视为跟随者。樽海鞘群的领导者并不直接引导全部个体的移动方向，而是采取由前往后顺次跟随的领导方式，领导者的影响力逐层锐减，使跟随者也可保持自己的多样性。

3.1.1 种群初始化

设捕食空间为 ${D_w} \times N$ 的欧式空间， ${D_w}$ 为空间的维数， $N$ 为樽海鞘群的种群规模。 ${{F}} = {[{f_1},{f_2}, \cdots ,{f_{{D_w}}}]^{\rm{T}}}$ 为空间中的食物。 ${{{X}}_i} = {[{x_{i1}},{x_{i2}}, \cdots ,{x_{i{D_w}}}]^{\rm{T}}}$ 为樽海鞘群个体位置，其中 $i = 1,2, \cdots ,N$ 。 ${{{L}}_{\rm{B}}} = [{l_{{{\rm{b}}_1}}},{l_{{{\rm{b}}_2}}}, \cdots ,{l_{{{\rm{b}}_{{D_w}}}}}]$ 为搜索下界，上界为 ${{{U}}_{\rm{B}}} = [{u_{{{\rm{b}}_1}}},{u_{{{\rm{b}}_2}}}, \cdots ,{u_{{{\rm{b}}_{{D_w}}}}}]$ 。所以，算法产生的随机初始种群为

${{{X}}_{N \times {D_w}}} = {\rm{rand}}(N,{D_w}) \times ({{{U}}_{\rm{B}}} - {{{L}}_{\rm{B}}}) + {{{L}}_{\rm{B}}}$

(8)

式中： $x_d^1$ 为第 $d$ 维领导者状态； $x_d^m$ 为第 $d$ 维跟随者状态。其中 $d = 1,2, \cdots ,{D_w}$ ，为空间维数； $m = 2,3, \cdots ,N$ ，为跟随者的代数。

3.1.2 领导者位置更新

领导者负责引导整个樽海鞘群的移动，其位置的更新需具有高度随机性，更新方式遵循：

$x_d^1 = \left\{ \begin{array}{l} {f_d} + {c_1}(({u_{{{\rm{b}}_d}}} - {l_{{{\rm{b}}_d}}}){c_2} + {l_{{{\rm{b}}_d}}}),\;\;\;\;\;{c_3} \leqslant 0.5 \\ {f_d} - {c_1}(({u_{{{\rm{b}}_d}}} - {l_{{{\rm{b}}_d}}}){c_2} + {l_{{{\rm{b}}_d}}}),\;\;\;\;\;{c_3} > 0.5 \end{array} \right.$

(9)

式中 ${c_1}$ 、 ${c_2}$ 和 ${c_3}$ 为控制参数。其中： ${c_2}$ 和 ${c_3}$ 为随机数，在[0,1]变化，用于加强领导者位置更新的随机性，从而增强全局勘探能力； ${c_1}$ 为收敛因子，其作为最主要的控制参数，设置为数值在区间[2,0]内单调递减的函数，大于1时侧重全局搜索，小于等于1时则着重进行局部开发。

${c_1} = 2{{\rm{e}}^{ - {{\left(\frac{{4I}}{{{I_{\max }}}}\right)}^2}}}$

式中：I为当前迭代次数； ${I_{\max }}$ 为最大迭代次数。

3.1.3 跟随者位置更新

在樽海鞘群算法中，由于整个种群是链状分布，跟随者采用顺次跟随移动，跟随者的随机性比较低。其运动方式满足牛顿第二运动定律，跟随者的移动距离 $R$ 满足：

$R = \dfrac{1}{2}a{t^2} + {v_0}t$

式中： $t$ 为2次迭代间的时间差值； $a$ 为迭代过程中加速度； ${v_0}$ 为运动速度，每次迭代开始时跟随者的速度为0。

因此，跟随者的更新过程满足：

$x_d^{m'} = \dfrac{1}{2}(x_d^{m - 1} + x_d^m)$

(10)

式中： $x_d^{m'}$ 是跟随者更新后的位置； $x_d^m$ 为第 $m$ 个跟随者的第 $d$ 维在更新前的位置。

3.2 算法改进

通过研究发现，樽海鞘群算法应用于无人机编队时差定位站址布局优化问题中时，存在一定缺陷。其中领导者较少，种群的多样性不足。

3.2.1 优化初始种群位置

在没有先验信息的条件下，优秀的初始种群可在一定程度上提升寻优效果，利用反向学习策略优化初始种群，获取较好的初始解。

1）随机生成初始种群 $K$ 。

2）获取反向种群 $O$ :

${O_{a,b}} = {X_{a,\min }} + {X_{a,\max }} - {K_{a,b}}$

(11)

式中： $a = 1,2, \cdots ,{D_w}$ 为空间维数； $b = 1,2, \cdots ,N$ 为种群组数； ${K_{a,b}}$ 和 ${O_{a,b}}$ 分别为原始种群位置和对应反向种群位置中的第 $a$ 维第 $b$ 个元素的值； ${X_{a,\min }}$ 和 ${X_{a,\max }}$ 分别为第 $a$ 维元素的最小值和最大值。

3）计算原始种群与反向种群中个体的适应度值，对所有个体根据适应度值好坏进行排序，选取适应度较好的前 $N$ 个个体组成新的初始种群 $K'$ 。

3.2.2 优化迭代过程中种群位置

在种群更新过程中应用反向策略，增大算法搜索范围，提升全局勘探能力。

1）生成在区间[0,1]内的随机数 $p$ ，当 $p < 0.2$ 时执行步骤2)，否则进入步骤4)。

2）计算动态反向种群 $M$ ：

${M_{a,b}} = {X_{a,\min }}(t) + {X_{a,\max }}(t) - {K'_{a,b}}$

(12)

式中 ${X_{a,\min }}(t)$ 和 ${X_{a,\max }}(t)$ 分别为第 $t$ 次更新后的第 $a$ 维元素的最小值和最大值。

3）计算产生的动态反向种群个体的适应度值，与更新的原种群个体适应度值进行比较，选取适应度更好的个体用于下一步更新计算。

4）进行下一次的迭代。

3.3 算法步骤

结合反向学习策略对樽海鞘群算法进行优化，提升其初始种群的丰富性，增加其全局勘探能力。使用OSSA对无人机编队四站时差定位站址布局优化的具体步骤如下：

1）设定参数。如最大迭代次数 ${I_{{\rm{max}}}}$ 、樽海鞘群的种群规模 $N$ ，搜索区间 ${{{U}}_{\rm{B}}}$ 和 ${{{L}}_{\rm{B}}}$ 等。

2）种群初始化。利用式(8)生成规模为 $N \times D$ 的初始樽海鞘群。采用式(11)计算反向种群，进行优劣排序，择优组成新的初始种群。

3）计算适应度值。根据式(7)计算 $N$ 个个体的适应度值。

4）选择食物位置。根据适应度值的优劣对樽海鞘群中的个体排序，把位于最前的樽海鞘选作此刻食物的位置。

5）确定领导者与跟随者。食物位置确定后，剩余的 $N{\rm{ - }}1$ 个樽海鞘个体按照之前的适应度值先优后劣的顺序，将靠前的一半樽海鞘作为领导者，剩余的均为跟随者。

6）生成 ${\rm{rand}}\left( {0,1} \right)$ ，当 ${\rm{rand}}\left( {0,1} \right) < p$ 时，根据式(12)计算反向动态种群。计算新生成的反向动态种群的适应度值，与原种群适应度值进行对比。利用适应度值好的个体替换适应度值不好的种群个体，并组成新的种群；否则直接进入步骤9)。

7）种群位置更新。分别根据式(9)和(10)依次更新领导者和跟随者的位置。

8）计算更新后种群适应度值。比较此刻食物的适应度值与更新后的樽海鞘个体的适应度值的优劣，选取适应度值更好的个体成为更新后的食物位置。

9）判断是否满足最大迭代次数 ${I_{{\rm{max}}}}$ 。若满足，则输出无人机时差定位的最优编队布局方式的站址优化结果；否则，重复步骤4）~9），直至达到迭代次数，将当前的最优樽海鞘个体位置作为无人机时差定位的编队布局方式的站址优化结果输出。

4 仿真实验与分析

本节通过仿真实验验证OSSA在无人机编队时差定位过程中的站址布局方式的优化效果。以下仿真实验过程均以最小化目标所在区域内平均定位误差作为目标函数。

仿真条件设置：设无人机编队中主站位置固定在 $\left[ {0,0,6} \right]\;{\rm{km}}$ ，无人机编队中的其余3架无人机在三维空间 $x \in \left[ { - 50,50} \right]\;{\rm{km}}$ , $y \in \left[ { - 50,50} \right]\;{\rm{km}}$ , $z \in \left[ {4,8} \right]\;{\rm{km}}$ 中调整自身的空间位置坐标，辐射源目标所在区域为 $S$ ： $\left\{ {x \in \left[ { - 100,100} \right]\;{\rm{km}},y \in \left[ {150,200} \right]\;{\rm{km}},z = 0 \;{\rm{ km}}} \right\}$ ，站址测量误差设置为10 m，时差测量误差为20 ns，种群规模均设置为36。以下实验均基于上述仿真条件进行。

4.1 OSSA与SSA、PSO、IPSO、AGPSO、DE对比

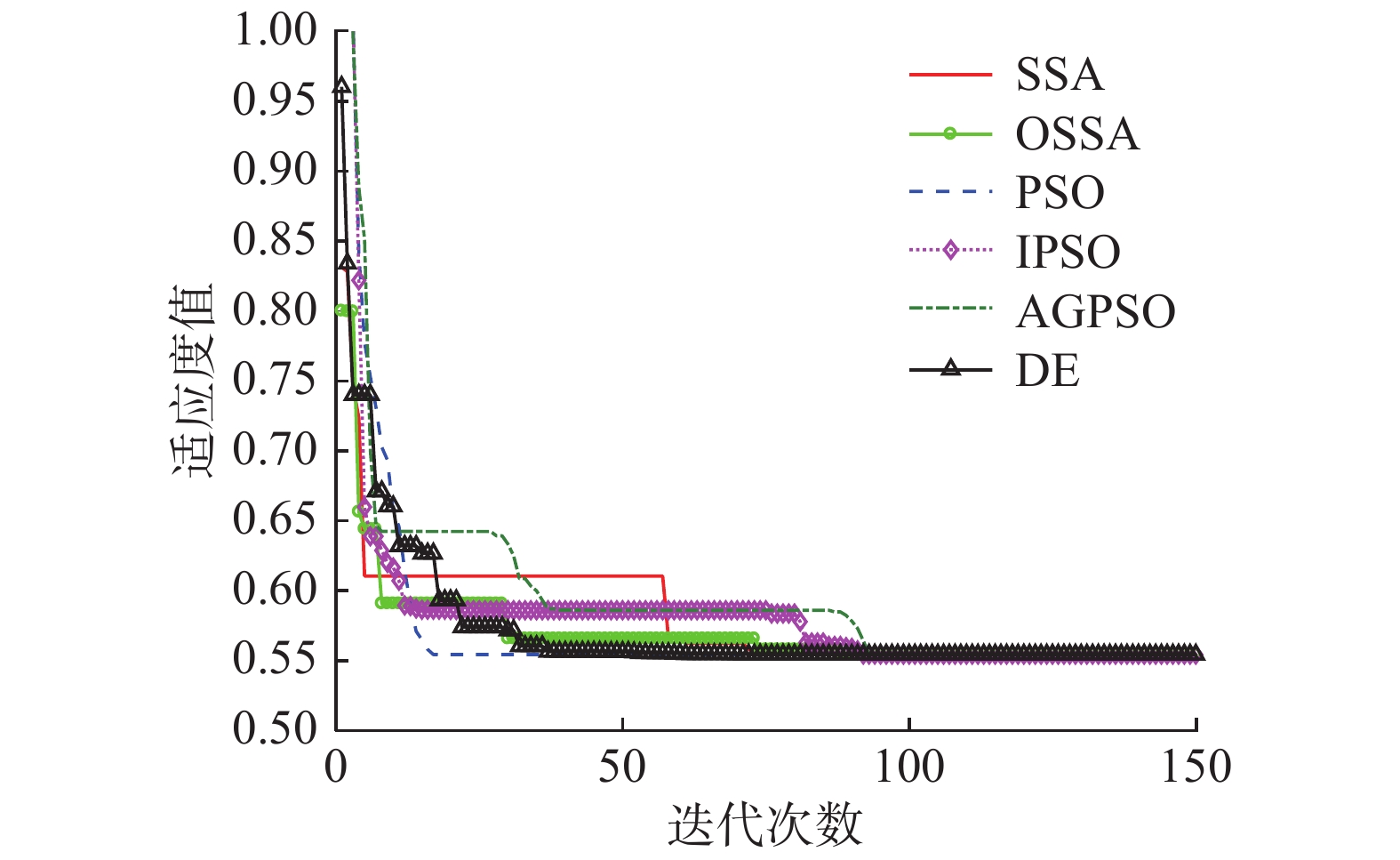
本次实验中，采用SSA、OSSA与PSO、IPSO、AGPSO、DE这4种优化算法^{[12, 14, 17]}进行无人机编队站址优化实验，最大迭代次数设置为600次，进行1000次蒙特卡洛实验。实验中假设当平均定位误差小于0.555 km时，认为实现了站址布局最优，未陷入局部最优解，能够获得正确寻优结果。适应度值收敛曲线如图2所示，为便于对比，将图中的 $x$ 轴坐标缩减为150。

采用SSA、OSSA、PSO、DE、IPSO和AGPSO进行优化时，6种优化算法均收敛至最优解的收敛曲线由图2所示，表明6种优化算法均可以解决无人机编队站址布局问题的优化。6种算法正确率对比如表1所示。

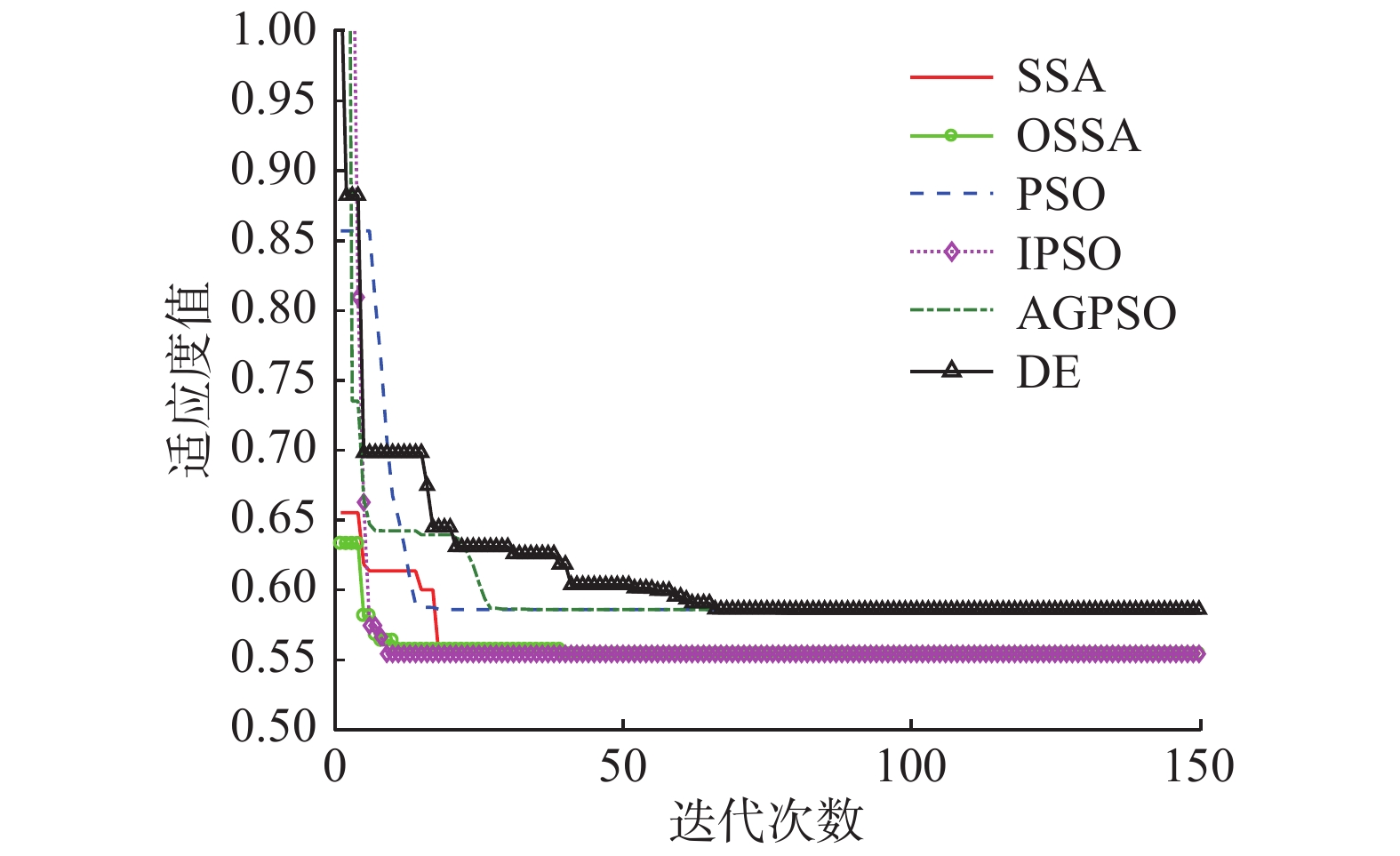
从蒙特卡洛实验中发现，除OSSA以外，其他5种优化算法均会出现陷入了局部最优的情况，如图3所示。图3中展示部分算法陷入局部最优的情况，其中PSO陷入局部最优的次数最多，PSO的改进算法AGPSO、IPSO跳出局部最优能力明显提升，但效果均不及DE、SSA、OSSA，而SSA和OSSA优化稳健性更优。在相同实验条下，改进后的SSA算法跳出局部最优能力得到加强，稳健性优于其他5种算法。所以，在无人机编队的站址布局优化应用场景下，采用OSSA比其他5种智能优化算法具有更稳定可靠的优化性能。

4.2 改进后的算法收敛速度对比

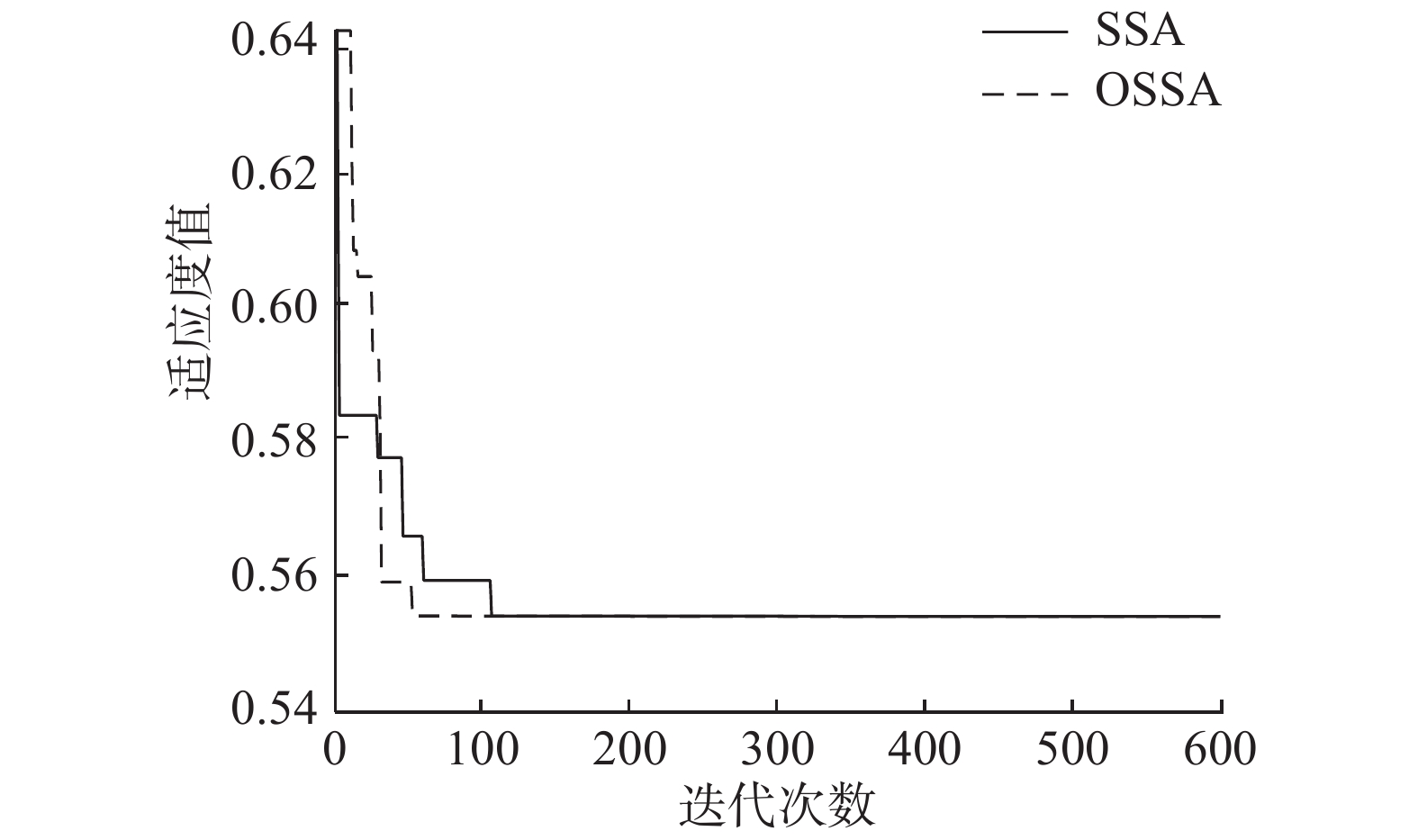
本次实验中，对SSA与OSSA的收敛速度进行对比。迭代次数设置为600次，进行蒙特卡洛实验，统计每次迭代开始至适应度值收敛时的时间。2种方法在优化过程中达到无人机编队对目标区域最小定位误差时耗时的平均时长分别为SSA耗时92.28 s，OSSA耗时79.80 s。

无人机编队进行站址布局优化时，采用SSA与OSSA进行优化的适应度值收敛曲线如图4所示。2种方法均能实现限制空域内的无人机编队对目标所在区域进行时差定位的最优布局。通过对比图4中的单次实验收敛曲线可知，OSSA要早于SSA实现适应度值收敛。由蒙特卡洛实验结果可知，采用OSSA进行无人机编队站址布局优化时的速度要优于采用SSA进行优化的速度。

4.3 站址布局优化效果对比

采用OSSA对执行多站时差定位的无人机编队进行三维空间的站址布局优化。通过优化后获得4架无人机在限制区域内的站址坐标如表2所示，陷入局部最优时的站址布局位置坐标如表3所示，倒Y型布局方式4架无人位置坐标如表4所示。

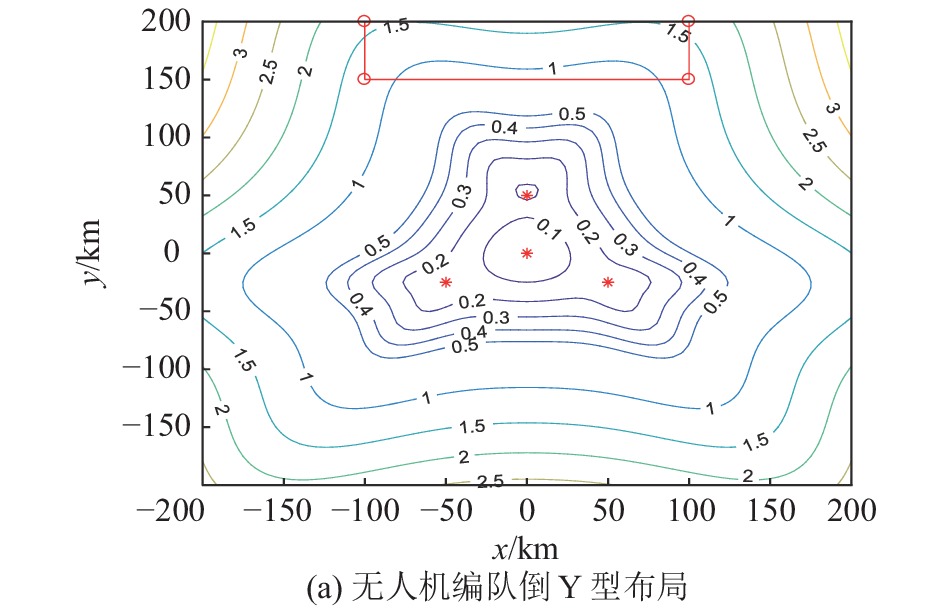
根据表2~4中无人机编队各机的坐标绘制几何精度因子（geometric dilution of precision，GDOP）图，如图5所示。在图5中，图片上方矩形区域为目标所在区域，“*”为4架无人机所在位置在二维平面的投影点。由图5的实验结果可以明确知道，采用优化后的无人机编队布局方式的定位精度优于倒Y型布局的无人机编队的定位精度。

2种无人机编队布局方式下针对图5中矩形目标区域进行多站时差定位的平均定位误差如表5所示。

无人机编队采用OSSA优化后的布局方式相对于倒Y型布局，在目标区域内的平均定位误差减小约54.6%，相对于PSO、DE等算法出现局部最优时的站址布局平均定位误差减小约5.4%。所以对无人机编队布局方式采用OSSA、PSO等优化后获得的站址布局方式可以有效提升编队对目标区域内的平均定位精度，但OSSA相对而言优化效果表现更加稳定。

5 结论

本文提出一种基于樽海鞘群算法的群体智能优化算法的改进算法，用于解决无人机编队针对特定目标区域进行时差定位时的站址布局问题。

1）该算法结合反向学习策略提高了樽海鞘群算法种群的多样性，提升全局搜索能力，降低陷入局部最优的概率，有效提升原算法寻优速度。

2）以目标所在区域内平均定位误差最小作为优化目标函数，对无人机编队被动时差定位时的站址构形进行调整优化。从而在测量误差不变的条件下，实现对目标区域中的辐射源进行被动时差定位时定位精度的有效提升。

仿真结果表明，解决无人机编队的站址布局优化问题时，用于对比的5种算法均出现了陷入局部最优的情况。而采用OSSA未出现局部最优情况，寻优的稳健性要更高，速度也要优于SSA。无人机编队站址布局优化后的定位精度明显优于传统站址最优布局形式的倒Y型站址布局的定位精度。本文所采用的无人机编队站址布局优化方法可根据限制条件的不同进行调整，可以适应多种应用场景。改进算法也可用于解决其他优化问题。