与常规化石能源动力装置相比,核动力装置具有功率密度高、燃料装载量小、持续工作时间长以及工作时无需氧气等突出优点,已被广泛用作船舶的推进装置,也在航天动力、深海航行器、离岸电站或海洋动力平台等领域具有潜在应用前景,获得了研究者的关注。在航天、深海、船舶等领域,整个装置的重量和体积又是制约其综合性能的瓶颈之一。如何在保证核动力装置正常发挥其功能的前提下,尽量减少其重量或体积,无疑是设计者和用户都十分关心的问题。
以此为背景,本文选择压水反应堆核动力装置中的关键设备之一——稳压器为研究对象,采用几种典型的优化算法,对稳压器的重量进行优化实例分析,并评估各类型算法在进行稳压器重量优化时的性能,为后续核动力装置的优化方法设计提供参考。
1 稳压器计算模型稳压器是压水反应堆核动力系统中一回路压力边界的重要组成部分,其主要设计功能为:1)压力控制。包括反应堆正常稳态运行、功率变化以及某些事故工况下保证反应堆冷却剂系统的压力变化在一定范围之内;2)压力保护。一旦反应堆冷却剂系统压力变化超过允许范围,稳压器应能提供压力保护功能,以防止反应堆或其他主设备损坏;3)辅助容积控制。在反应堆启停堆过程中提供对一回路水容积变化的补偿功能。在压水反应堆中,大都采用电加热式稳压器,即稳压器内由蒸汽与水两相组成。在进行稳压器重量计算之前,需首先对稳压器的容积进行设计,然后根据容积设计结果和结构设计规范,计算出稳压器筒体以及上下封头的壁厚,最后可由材料的密度和相应的体积计算出稳压器的重量。
1.1 稳压器容积计算模型稳压器的总容积构成如图1所示[1-2],包括下封头区水体积、加热元件区水体积、水位仪表偏差体积、摇摆水体积(针对船用反应堆,若为陆基反应堆,则可认为倾角为0)、蒸发水体积、负瞬变水体积、回路温度测量引起的体积偏差、静态功率变化引起的体积变化、正瞬变水体积以及最小蒸汽体积等10部分构成,详细计算模型可参见文献[1-3]。

|
Download:
|
| 图 1 稳压器内部容积构成示意 | |
稳压器封头最小壁厚应满足:
| ${\delta _1} = \frac{{PDk}}{{2[\sigma ]\varphi - 0.5P}}$ |
式中:
稳压器筒体的壁厚应不低于式(1)所得结果:
| ${\delta _2} = \frac{{PD}}{{2[\delta ]\varphi - P}}$ | (1) |
稳压器电加热元件区的筒体壁厚应满足:
| ${\delta _3} = \frac{{PD}}{{2[\delta ]r - P}}$ |
式中
1)若稳压器采用椭圆封头,则其重量可由式(2)确定:
| ${M_1} = \left\{ {\frac{{{\rm{2{\text{π}} }}{{(D + 2{\delta _1})}^2}}}{{\rm{3}}}{{h'}_1} - \frac{{{\rm{2{\text{π}} }}{D^2}}}{{\rm{3}}}{h_{\rm{1}}}} \right\}\rho $ | (2) |
式中:标准椭圆封头的曲面深度
| $ {M_1} = \left\{ {\frac{{{\text{π}}}}{6}\left[ {{{\left( {D + 2{\delta _1}} \right)}^3} - {D^3}} \right]} \right\}\rho $ |
式中
若稳压器采用球形封头,则其重量可表示为
| $ {M_1} = \left\{ {\frac{{2{{\text{π}}}}}{3}\left[ {{{\left( {D + 2{\delta _1}} \right)}^3} - {D^3}} \right]} \right\}\rho $ |
2)圆柱筒体重量
| $ \begin{array}{l} {M_2} = \dfrac{{{\text{π}}}}{4}\left[ {{{\left( {D + 2{\delta _2}} \right)}^2} - {D^2}} \right]{H_y}\rho \\ \;\;\;\;{H_y} = {H_{{\rm{PR}}}} - 2{H_s} - {H_2} \end{array}$ |
式中
3)电加热区筒体重量
| ${M_3} = \frac{{{\text{π}}}}{4}\left[ {{{\left( {D + 2{\delta _3}} \right)}^2} - {D^2}} \right]{H_2}\rho $ |
4)稳压器总重量
稳压器筒体及封头的重量为
| $M = 2{M_1} + {M_2} + {M_3}$ |
稳压器的总重量还包括电加热元件重量
| ${M_{{\rm{PR}}}} = 2{M_1} + {M_2} + {M_3} + {M_4}$ |
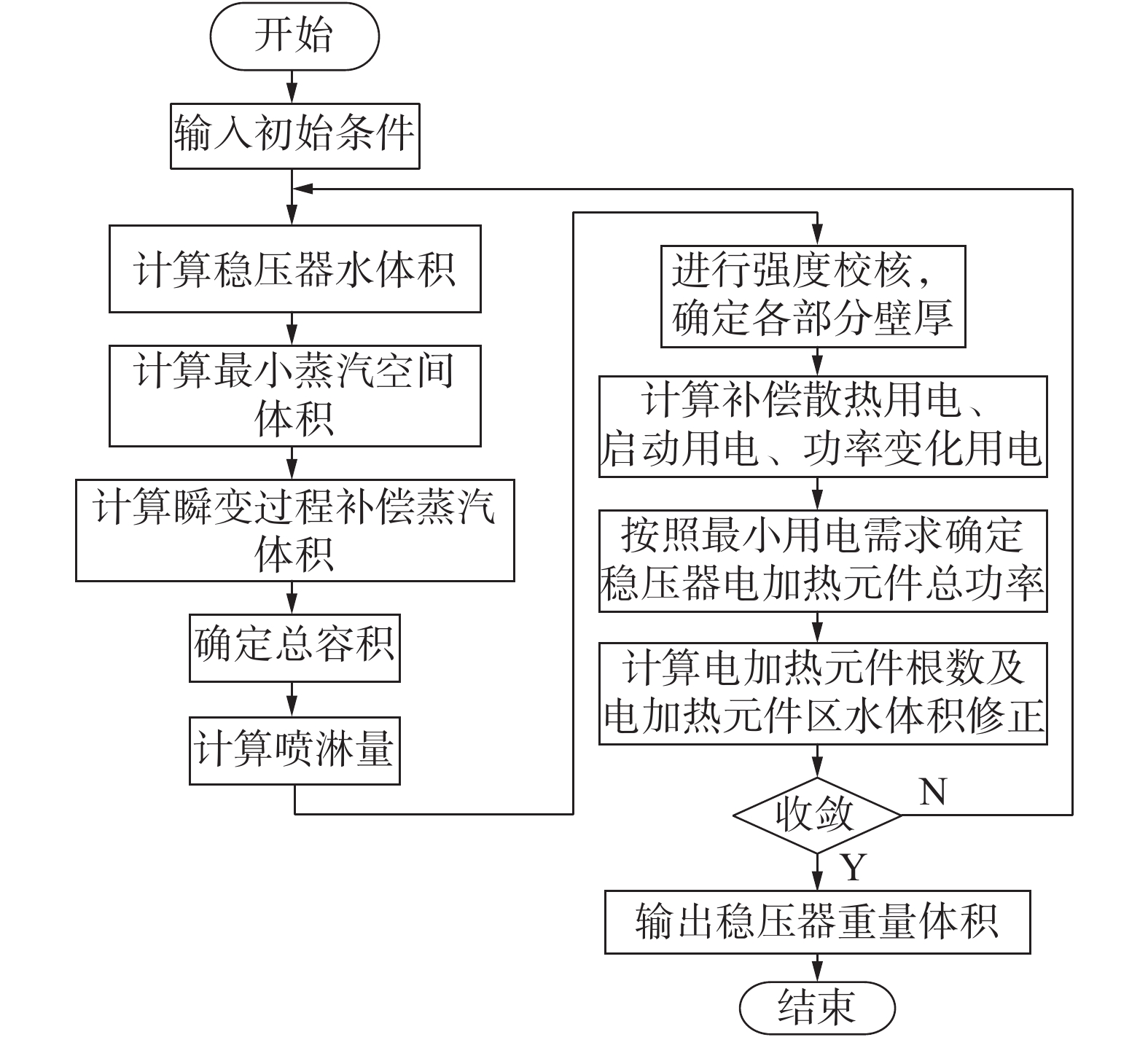
稳压器的总体设计流程可参见图2。
|
Download:
|
| 图 2 稳压器设计计算流程 | |
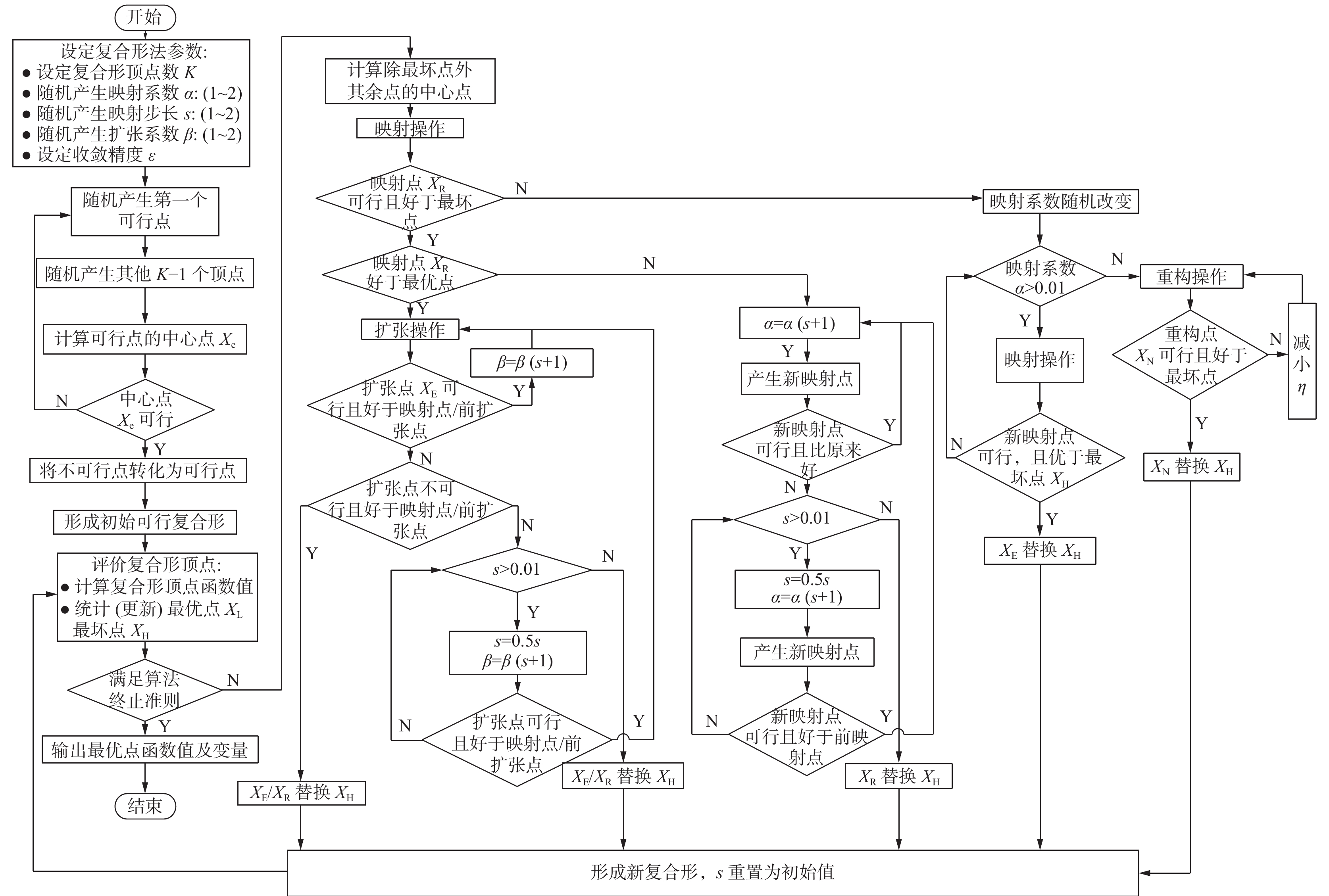
复合形法[6]是可用来求解约束优化问题的一种直接解法,其基本思路是在可行域内构造一个具有k个顶点(对应不同方案)的初始复合形,通过比较各顶点对应的目标函数值,按一定规则确定目标函数值既有优化、又满足约束条件的新顶点,利用新顶点代替最坏点,更新复合形,不断重复计算,使复合形不断向“最优点”移动和收缩,直至达到预定的收敛精度。由复合形算法的计算思路可知,一旦复合形算法的初始顶点确定,其最终优化结果也唯一确定,算法本身容易陷入局部最优。为此,文献[7]提出了对复合形算法的改进方案。在文献[7]基础上,本文借鉴进化类算法的思想,在复合形算法的扩张、收缩、映射操作中引入随机性,以解决复合形算法容易陷入局部最优的问题。改进复合形算法的计算流程如图3所示。
|
Download:
|
| 图 3 改进复合形算法流程 | |
遗传算法(genetic algorithm,GA)最早是由J. Holland于1975年受生物进化的启发而提出的一种启发式优化算法,遗传算法已被广泛应用于核动力设备的优化设计中[8-11]。遗传算法的主要操作包括复制(选择)、交叉、变异等,在本文所采用的遗传算法中,选择轮盘赌方式进行复制操作,其计算流程如图4所示。

|
Download:
|
| 图 4 遗传算法计算流程 | |
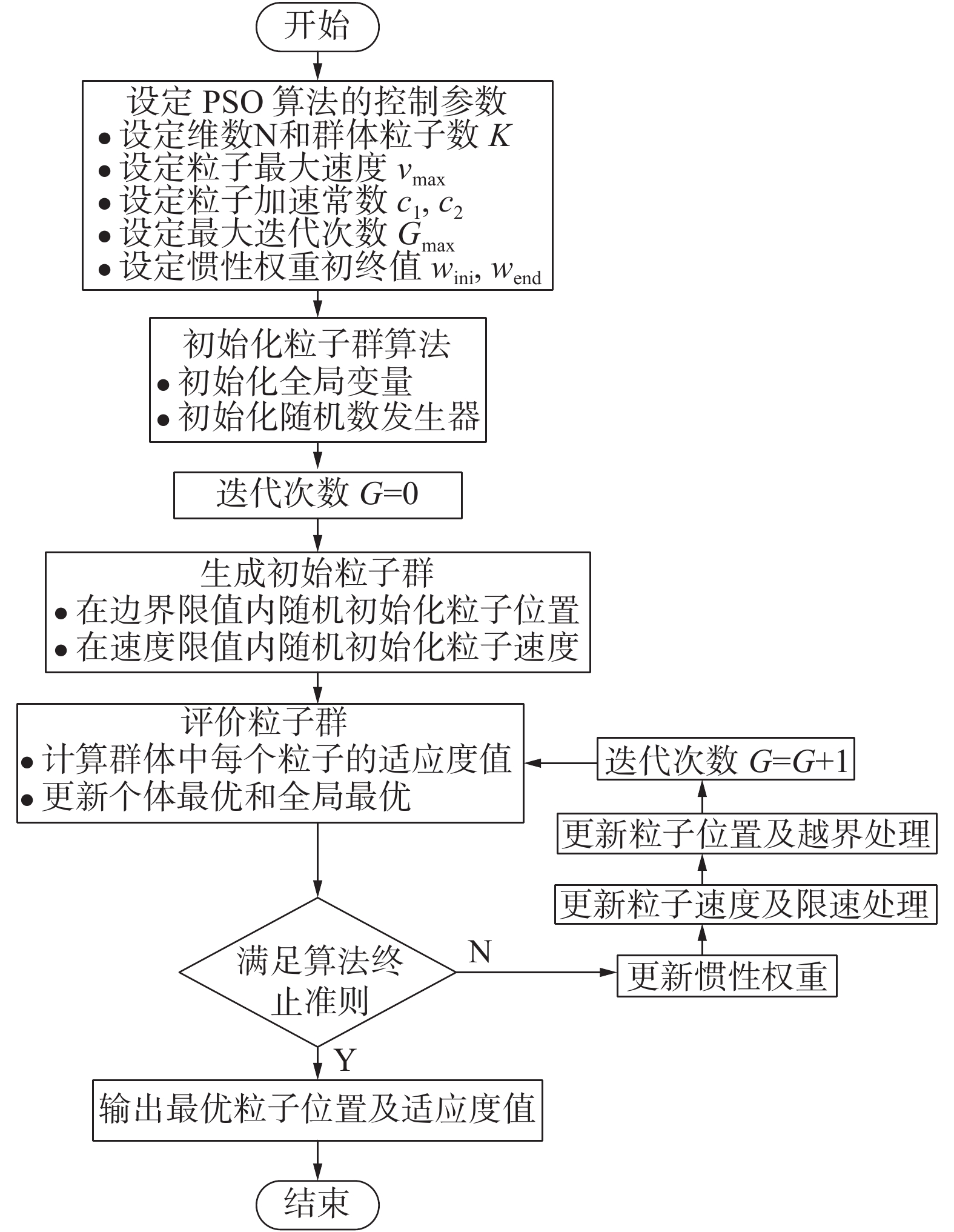
粒子群优化算法(particle swarm optimization,PSO)[12-13]是由Kennedy和Eberhart于1995年最早提出的,PSO算法主要模拟了鸟群飞行觅食的行为,通过借鉴鸟之间的集体协作觅食来实现使群体达到最优的目的。粒子群优化算法具有控制参数少、计算简单、容易实现等优点,并且不需对函数求导,只需利用目标函数的取值信息,具有很强的通用性。粒子群算法的寻优主要依赖对现有个体自身信息和群体信息的综合处理,其计算流程如图5所示。
|
Download:
|
| 图 5 粒子群算法流程 | |
本文以稳压器重量的最小化为目标开展优化计算。其数学描述可表示为寻找由优化变量构成的设计向量Xopt,使得:
| $ {{M}}({{{X}}_{{\rm{opt}}}}) = \min [M({{X}})],\forall {{X}} \in { R} $ | (3) |
式中:M表示稳压器的重量,R表示由设计变量的可行区间构成的设计向量空间。
在开展稳压器重量优化实例分析时,还需要满足功能性和工程性约束条件,本文采用的主要约束条件包括:1)反应堆输出功率不低于设计值;2)稳压器的高度应不超过允许限值;3)稳压器的高径比在要求范围内;4)当发生正波动时,喷淋水量不应使压力下降到系统正常工作压力以下;5)正波动蒸汽体积可保证系统压力不至于下降到压力下限以下;6)其他热工设计准则。
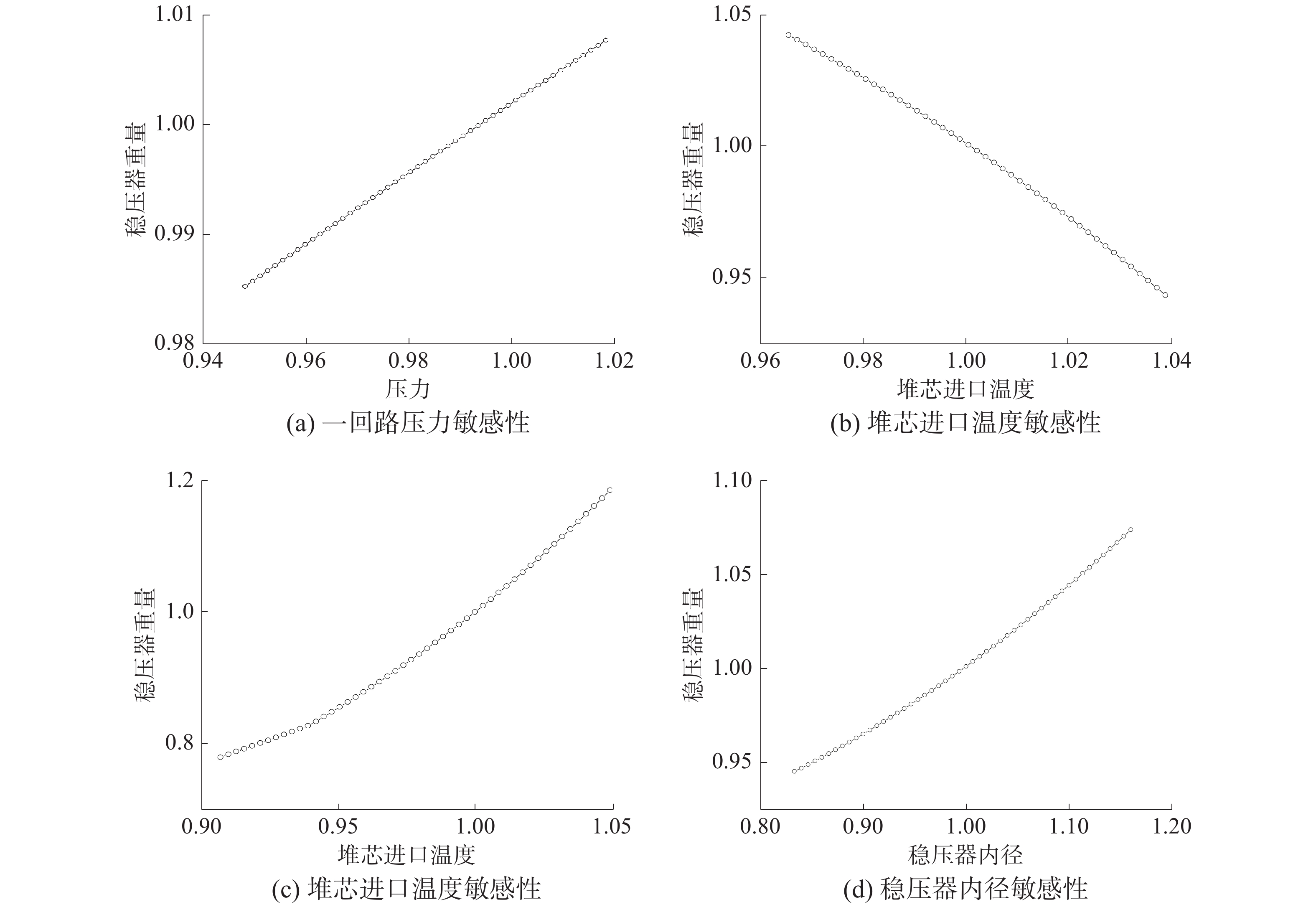
4 结果与讨论 4.1 敏感性分析为了确定不同参数变化时,稳压器重量指标的变化规律,本节以参考母型参数为基准,选取系统运行压力、堆芯冷却剂进口温度、堆芯出口冷却剂温度以及稳压器内径作为敏感性分析所要研究的参数,采用前文所述评价程序对稳压器重量随各参数的变化规律进行计算,结果示于图6。
|
Download:
|
| 图 6 敏感性分析结果(图中数据均经过归一化处理) | |
计算结果表明,在所研究参数范围内,当一回路运行压力提升时,稳压器的重量随之升高。容易理解,随着压力的提升,稳压器筒体、上下封头等所需要的壁厚均增加,这使得稳压器的重量有增加趋势。在堆芯出口温度不变时,随着堆芯进口温度的升高,堆芯进出口温差降低,使得一回路的冷却剂流量上升,一回路正负瞬变时的水体积变化减小,这将使稳压器容积和重量有减小趋势。此外,稳压器容积的减小使得所需要的电加热功率降低,从而减少电加热元件的数量,这也会使稳压器的重量下降。在堆芯进口温度不变时,随着堆芯出口温度的升高,堆芯进出口温差变大,堆芯的冷却剂流量下降,一回路正负瞬变时的水体积变化增大,这将使稳压器容积增加,进而使稳压器的重量有增长趋势;在保持其他条件不变时,当稳压器内径增加时,稳压器各部分承压壁厚均会增加,这将使得稳压器重量增加。
4.2 优化计算结果比较由4.1节中结果可以看出,在所研究参数范围内,稳压器重量与运行压力、反应堆进口温度、反应堆出口温度以及稳压器内径关系密切。为此,本节分别采用遗传算法、粒子群算法和改进复合形算法,对稳压器进行重量最小化优化设计,其中优化变量表示为
|
|
表 1 3种算法计算结果比较 |
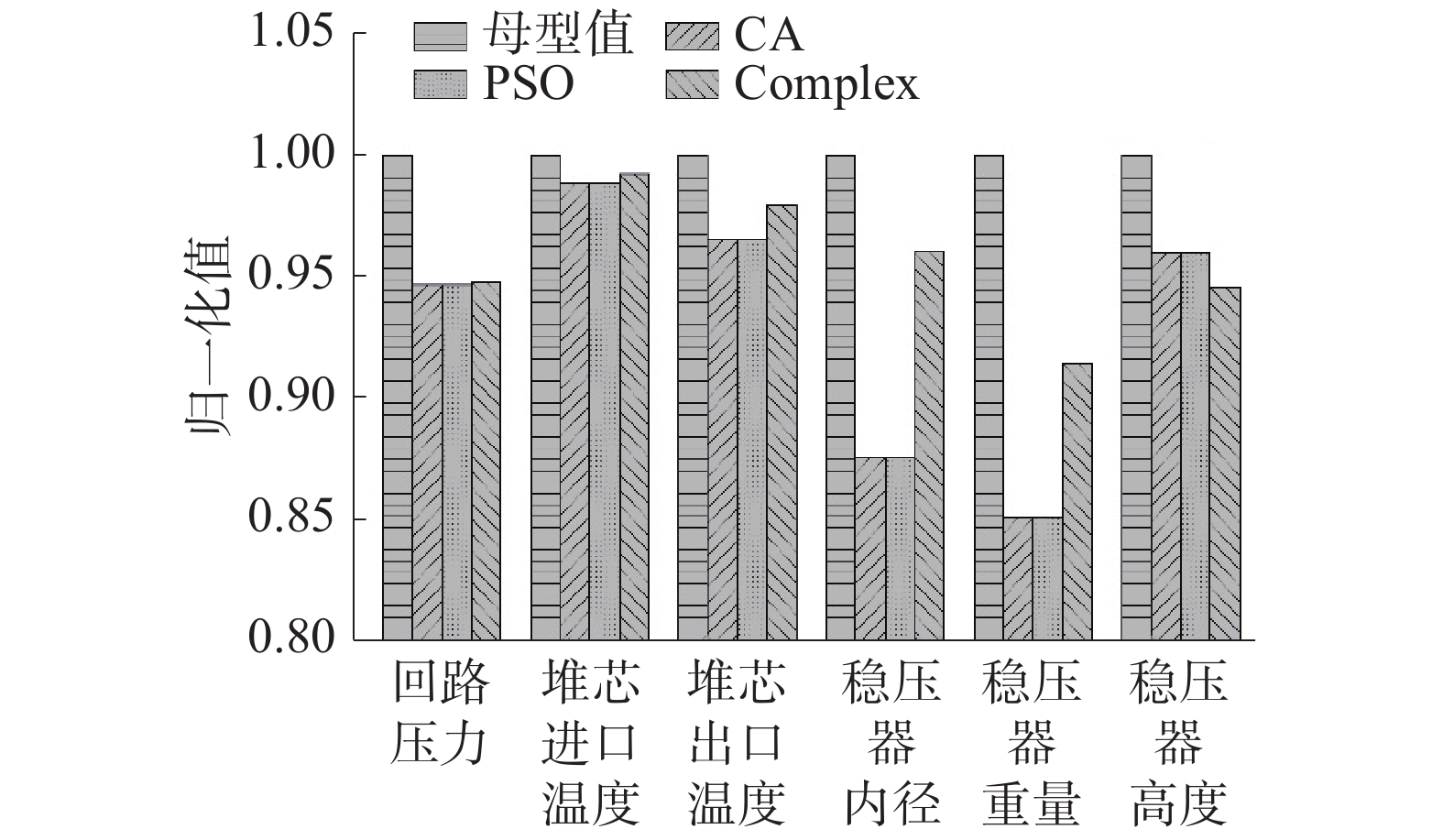
由计算结果可知,从算法收敛速度和计算效率角度看,改进复合形算法的表现最好,对同一问题所需的计算时间最短;粒子群算法与遗传算法则表现出了良好的全局性,即优化得到的稳压器重量比改进复合形算法所找到的最优值更好,且2种算法求解得到的优化变量向量完全一致,其中粒子群算法的计算效率优于遗传算法。图7则显示出了3种算法给出的优化变量与母型之间的对比情况,其中GA表示遗传算法,PSO代表粒子群算法,Complex则指改进复合形算法。结合表1和图7中所示结果可以发现,对于稳压器重量优化设计这类单一核动力设备最优化设计问题,采用粒子群算法或遗传算法均能保证收敛解的全局性,可以在进一步的案例研究中验证测试。
|
Download:
|
| 图 7 不同算法优化结果与母型参数对比 | |
本文建立了核动力装置一回路系统中的重要设备——稳压器的静态设计评价模型,给出了改进复合形算法、粒子群算法和遗传算法的计算流程,并利用3种优化算法对稳压器进行了重量最小化优化设计计算,对比了3种算法的性能。通过本文研究,得到如下结论:
1)对于稳压器重量最小目标的优化设计,改进复合形算法的计算效率最高,但存在初值依赖问题;
2)对于稳压器重量最小目标的优化设计,粒子群算法与遗传算法表现出良好的一致性,这2种算法均能在全局范围内找到优化解;
3)综合来看,粒子群算法是最适用于稳压器重量最小目标的优化设计方法,可在单一核动力设备优化设计中推广应用。
| [1] |
贺士晶, 阎昌琪, 王建军, 等. 稳压器容积的优化设计[J]. 原子能科学技术, 2010, 44(3): 320-324. ( 0) 0)
|
| [2] |
孙中宁. 核动力设备[M]. 哈尔滨: 哈尔滨工程大学出版社, 2003: 101-135.
( 0) 0)
|
| [3] |
贺士晶. 核动力装置参数优化设计[D]. 哈尔滨: 哈尔滨工程大学, 2010.
( 0) 0)
|
| [4] |
马秉骞. 椭圆形封头和碟形封头强度计算公式的应用条件[J]. 石油和化工设备, 2008, 11(1): 27-28. DOI:10.3969/j.issn.1674-8980.2008.01.007 ( 0) 0)
|
| [5] |
朱齐荣. 核电厂机械设备及其设计[M]. 北京: 原子能出版社, 2000: 53-110.
( 0) 0)
|
| [6] |
孙靖民, 梁迎春. 机械优化设计[M]. 北京: 机械工业出版社, 2006: 130-135.
( 0) 0)
|
| [7] |
王盟, 王建军, 贺士晶, 等. 一种解决复合形局部最优及加速计算的方法[J]. 计算机应用与软件, 2011, 28(2): 277-278, 289. DOI:10.3969/j.issn.1000-386X.2011.02.083 ( 0) 0)
|
| [8] |
刘成洋, 阎昌琪, 王建军. 基于改进遗传算法的冷凝器优化设计[J]. 原子能科学技术, 2012, 46(4): 457-462. ( 0) 0)
|
| [9] |
李贵敬, 阎昌琪, 王建军, 等. 映射交叉遗传算法在核动力设备优化设计中的应用[J]. 原子能科学技术, 2013, 47(7): 1212-1216. DOI:10.7538/yzk.2013.47.07.1212 ( 0) 0)
|
| [10] |
LAPA C M F, PEREIRA C M N A, DE A. MOL A C. Maximization of a nuclear system availability through maintenance scheduling optimization using a genetic algorithm[J]. Nuclear engineering and design, 2000, 196(2): 219-231. DOI:10.1016/S0029-5493(99)00295-2 ( 0) 0)
|
| [11] |
周明, 孙树栋. 遗传算法原理及应用[M]. 北京: 国防工业出版社, 1999: 4-7.
( 0) 0)
|
| [12] |
刘波. 粒子群优化算法及其工程应用[M]. 北京: 电子工业出版社, 2010: 1–2.
( 0) 0)
|
| [13] |
PEREIRA C M N A, LAPA C M F, MOL A C A, et al. A particle swarm optimization (PSO) approach for non-periodic preventive maintenance scheduling programming[J]. Progress in nuclear energy, 2010, 52(8): 710-714. DOI:10.1016/j.pnucene.2010.04.009 ( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


