2. 哈尔滨工程大学 动力与能源工程学院,黑龙江 哈尔滨 150001
2. College of Power and Nuclear Engineering, Harbin Engineering University, Harbin 150001, China
非能动安全壳冷却系统(PCCS)是能够在核电站发生严重事故,壳内充满大量高温、高压和放射性蒸汽的情况下,依靠换热器内冷却水的自然循环过程,持续不断地使壳内蒸汽发生凝结,从而维持安全壳的完整性的非能动安全系统。与常规电站换热器(即冷凝器)的运行状态不同,PCCS内换热器需要考虑安全壳固有空间内存在的大量空气以及燃料包壳在高温下与蒸汽发生锆水反应所产生的氢气对蒸汽冷凝换热过程的影响。因此,为分析PCCS内换热器的运行特征和优化换热器结构,建立能够模拟水平管内含不凝性气体的蒸汽对流冷凝换热过程的理论模型和计算程序具意义重大。
在以往PCCS换热器设计之中,通常使用竖直管外冷凝的方式带走热量,相关的理论研究也对集中于此方面[1-5]。而在后续研究中为提升换热器功率,部分学者选择在水平管内进行冷凝换热,以获得更低的换热热阻。但相比于竖直管来说,水平管内因素更多、过程更为复杂,已有成果相对较少,并多为国外研究[6-11]。在理论研究方面,目前缺少气液两相较高流速差异状态下的局部换热系数预测模型,并且在计算精度上仍存在一定改进空间。
为更清楚地认识水平管内含不凝性气体的凝结换热过程和特性,本研究基于Peterson[12]提出的扩散层模型,通过进行一定假设和简化,将水平管内含不凝性气体的强制对流冷凝分为显热和潜热两大部分,并分别建立了对应的数学模型,同时整合了伴随蒸汽凝结同时出现的其他物理现象对换热特性的影响,最终得到了可以模拟管内冷凝换热物理过程的计算程序。为考察本文所提出程序的计算精度,针对以往研究所获实验结果,将模型计算结果与实验数据进行了大量的比对工作。与此同时,在建模过程中,探讨了含不凝性气体的冷凝换热过程中各换热过程的渐变和差异。
1 冷凝换热计算程序建立有不凝性气体存在的蒸汽冷凝换热过程的典型特点是,不凝性气体不断在气液界面处聚集,始终以类似于气层的形式覆盖在凝液表面,阻碍蒸汽接触冷壁面发生凝结,最终削弱整个冷凝换热过程的热量传递强度。由此可知,如若蒸汽发生凝结,需先以扩散的方式穿透不凝性气体层,随即释放气化潜热,凝结为液态水。
除此之外,在强制对流冷凝换热过程之中,主流气体与凝液之间存在对流换热过程。高温的主流混合器将释放显热,携同蒸汽冷凝释放的潜热,一同通过凝液与换热管内壁面之间的对流换热穿过换热管壁,最终被管外的冷却剂带走。
综上所述,换热管内的含不凝性气体的蒸汽冷凝换热过程由3部分组成:凝液与换热管内壁面间的对流换热过程、凝液表面的凝结换热以及主流气体的对流换热。由此可知:
| $q = {h_{\rm{f}}}({T_{\rm{i}}} - {T_{{\rm{wi}}}}) = ({h_{\rm{c}}} + {h_{\rm{s}}})({T_{\rm{b}}} - {T_{\rm{i}}})$ | (1) |
式中:q为管内总换热过程热流密度;hf、hc和hs分别为凝液与换热管内壁面间的对流换热系数、凝液表面的凝结换热和主流气体的对流换热系数;Tb、Ti和Twi分别为主流气体温度、凝液表面温度和换热管内表面温度。
1.1 凝液与换热管内壁面间的对流换热系数hf计算水平管与竖直管的典型区别为,竖直管内液膜沿换热管周向均匀分布,管内气液两相将一直呈现环状流状态;而水平管内凝液受重力影响将出现环状流、波状流、分层流甚至弹状流。不同流型条件下,凝液热阻的大小差异明显,同时导致其他换热过程变化迥异。针对管内气液两相流型的变化,选择合适的经验关联式计算hf对整个换热模型的预测精度十分重要。
通过对比适用于环状流、波状流和分层流条件下的计算hf的不同经验关系式与实验数据,最终选择计算精度最高,适用范围最广的关联式计算hf[13]:
| ${h_{\rm{f}}} = \frac{{470.71{x^{0.081}}Re_{{\rm{in}}}^{0.011(x - {x_0})}P_{{\rm{red}}}^{0.746}J{a^{ - 1.095}} \times {\lambda _{\rm{l}}}}}{{{D_{\rm{i}}}}}$ |
式中:x为蒸汽质量含气率;Rein为蒸汽入口雷诺数;Pred为临界压力比;Ja为雅各布数;λl为凝液导热系数,W·m−1·K−1,Di为换热管内径,m。
1.2 凝结换热系数hc与主流气体对流换热系数hs计算参考PCCS内换热器运行工况可知,主流气体入口流速较高,湍流程度较大。虽然随着蒸汽逐渐凝结,主流气体流速降低,但由于作为主流气体组成部分的不凝性气体并不发生凝结,因此主流气体仍可维持较高流速,相应的湍流程度也相应较高。结合流态分析结果,最终选择Dittus-Boelter公式计算主流气体与凝液表面的对流换热系数:
| $N{u_{{\rm{s,0}}}} = 0.023Re_{\rm{m}}^{0.8}Pr_{\rm{m}}^{0.33}$ |
式中:Nus,0为主流气体与凝液表面的对流换热努赛尔数;Rem为混合气体Reynold数;Prm为混合气体普朗特数。
在稳态条件下,主流混合气内各组分气体在气液界面上的扩散过程可描述如下:
| ${m_{\rm{v}}}^{\prime \prime } = - \rho {D_{\rm{v}}}\frac{{\partial {w_{\rm{v}}}}}{{\partial y}} + {w_{\rm{v}}}{m_{\rm{m}}}^{\prime \prime }$ | (2) |
| ${m_{\rm{a}}}^{\prime \prime } = - \rho {D_{\rm{a}}}\frac{{\partial {w_{\rm{a}}}}}{{\partial y}} + {w_{\rm{a}}}{m_{\rm{m}}}^{\prime \prime }$ |
| ${m_{{\rm{He}}}}^{\prime \prime } = - \rho {D_{{\rm{He}}}}\frac{{\partial {w_{{\rm{He}}}}}}{{\partial y}} + {w_{{\rm{He}}}}{m_{\rm{m}}}^{\prime \prime }$ |
| ${m_{\rm{m}}}^{\prime \prime } = {m_{\rm{v}}}^{\prime \prime } + {m_{\rm{a}}}^{\prime \prime } + {m_{{\rm{He}}}}^{\prime \prime }$ |
式中:w和D分别为各组分气体在混合气中的质量分数和扩散系数,m2·s−1;m″为气体质量流速,kg·m−2·s−1;ρ为主流气体密度,kg·m−3;下标m、v、a和He分别代表混合气、混合气中的蒸汽、空气和氦气。由于氦气与氢气相对分子质量相同,物理性质相似,因此在后续模型建立中使用氦气代替氢气进行分析。
考虑到不凝性气体只会在凝液表面聚集,这意味着其无法通过气体边界层扩散达到气液界面。于是有
| ${m_{\rm{v}}}^{\prime \prime } = - \rho {D_{\rm{v}}}\frac{{\partial {w_{\rm{v}}}}}{{\partial y}} + {w_{\rm{v}}}{m_{\rm{v}}}^{\prime \prime }$ |
同时可知:
| ${m_{\rm{v}}}^{\prime \prime } = \frac{{\rho D}}{\delta }\ln (\frac{{1 - w_{\rm{v}}^{\rm{i}}}}{{1 - w_{\rm{v}}^{\rm{b}}}}){\rm{ = }}\frac{{\rho D}}{\delta }\ln \frac{{w_{{\rm{nc}}}^{\rm{i}}}}{{w_{{\rm{nc}}}^{\rm{b}}}}$ | (3) |
式中:上标i和b分别表示气液界面处和主流气体处;下标nc代表不凝性气体;δ为凝结液膜的厚度,m。
在假设主流气体中各组分气体均为理想气体的情况下,根据Clapeyrom方程可得到:
| $\dfrac{{P_{{\rm{nc}}}^{\rm{i}}}}{P} = \dfrac{{\dfrac{{w_{\rm{a}}^{\rm{i}}}}{{29}} + \dfrac{{w_{{\rm{He}}}^{\rm{i}}}}{2}}}{{\dfrac{{w_{\rm{v}}^{\rm{i}}}}{{18}} + \dfrac{{w_{\rm{a}}^{\rm{i}}}}{{29}} + \dfrac{{w_{{\rm{He}}}^{\rm{i}}}}{2}}} = \dfrac{{\dfrac{{w_{\rm{a}}^{\rm{i}}}}{{29}} + \dfrac{{\alpha w_{\rm{a}}^{\rm{i}}}}{2}}}{{\dfrac{{1 - \left( {1 + \alpha } \right)w_v^{\rm{i}}}}{{18}} + \dfrac{{w_{\rm{a}}^{\rm{i}}}}{{29}} + \dfrac{{\alpha w_{\rm{a}}^{\rm{i}}}}{2}}}$ |
| $w_{{\rm{nc}}}^{\rm{i}} = \dfrac{{58\left( {1 + \alpha } \right)\dfrac{{P_{_{{\rm{nc}}}}^{\rm{i}}}}{P}}}{{\left[ {36\left( {1 - \dfrac{{P_{_{{\rm{nc}}}}^{\rm{i}}}}{P}} \right) + 522\alpha \left( {1 - \dfrac{{P_{_{{\rm{nc}}}}^{\rm{i}}}}{P}} \right) + \dfrac{{58P_{_{{\rm{nc}}}}^{\rm{i}}}}{P}\left( {1 + \alpha } \right)} \right]}}$ |
式中:
这里定义对数平均空气质量分数
| $w_{{\rm{nc}}}^{{\rm{lm}}} = \dfrac{{w_{{\rm{nc}}}^{\rm{i}} - w_{{\rm{nc}}}^{\rm{b}}}}{{\ln \left(\dfrac{{w_{{\rm{nc}}}^{\rm{i}}}}{{w_{{\rm{nc}}}^{\rm{i}}}}\right)}}$ |
将
| ${q_{\rm{c}}} = {i_{{\rm{fg}}}}{m_{\rm{v}}}^{\prime \prime } = \frac{{{i_{{\rm{fg}}}}\rho D}}{\delta }\frac{{(w_{{\rm{nc}}}^{\rm{i}} - w_{{\rm{nc}}}^{\rm{b}})}}{{w_{{\rm{nc}}}^{{\rm{lm}}}}}$ |
式中ifg为蒸汽汽化潜热,J·kg−1。
根据上述推导结果,可以获得气液界面处凝结换热系数hc:
| ${h_{\rm{c}}} = \frac{{{q_c}}}{{{T_{\rm{b}}} - {T_{\rm{i}}}}} = \frac{{{m_{\rm{v}}}^{\prime \prime }{i_{{\rm{fg}}}}}}{{{T_{\rm{b}}} - {T_{\rm{i}}}}} = \frac{{{i_{{\rm{fg}}}}\rho D}}{\delta }\frac{{(w_{{\rm{nc}}}^{\rm{i}} - w_{{\rm{nc}}}^{\rm{b}})}}{{w_{{\rm{nc}}}^{{\rm{lm}}}}}\frac{1}{{{T_{\rm{b}}} - {T_{\rm{i}}}}}$ | (4) |
将式(4)进行无量纲化可知:
| $N{u_{{\rm{c,0}}}} = S\!{h_m}\left(\frac{{w_{{\rm{nc}}}^{\rm{i}} - w_{{\rm{nc}}}^{\rm{b}}}}{{w_{{\rm{nc}}}^{{\rm{lm}}}}}\right)\frac{{P{r_{\rm{m}}}}}{{S\!{c_{\rm{m}}}}}\frac{1}{{J{a_{\rm{m}}}}}$ |
式中:
气液表面由于发生蒸汽凝结,会形成局部的低压区,其与主流气体间的压差会促进蒸汽进一步向凝液表面运动,从而增强了局部冷凝换热能力,即抽吸效应。本文选取Kuhn[14]模型确定修正因子计算结果,通过加入此抽吸效应修正因子,在本文模型中引入抽吸效应对冷凝换热能力的影响。
对于含空气条件来说有:
| $ \begin{aligned} f{({\beta _{\rm{m}}})_{\rm{a}}} = & 1 + 0.046{( - {\beta _{\rm{m}}})^{2.49}} =\\ & 1 + 0.046{\left( - \frac{{m_{\rm{v}}^{''}}}{{0.021Re_{\rm{m}}^{ - 0.2}S\!c_{\rm{m}}^{ - 0.5}\rho {u_{\rm{m}}}}}\right)^{2.49}} \end{aligned} $ |
对于含氦气条件来说有:
| $ \begin{aligned} f{({\beta _{\rm{m}}})_{{\rm{He}}}}=& 1 + 0.126{( - {\beta _{\rm{m}}})^{2.49}} = \\ & 1 + 0.126{\left( - \frac{{m_{\rm{v}}^{''}}}{{0.021Re_{\rm{m}}^{ - 0.2}S\!c_{\rm{m}}^{ - 0.5}\rho {u_{\rm{m}}}}}\right)^{2.49}} \end{aligned} $ |
考虑到空气与氦气共存的情况,采用通用公式确定抽吸效应修正因子:
| $f({\beta _{\rm{m}}}) = {\left( {\frac{{{X_{\rm{a}}}}}{{f{{({\beta _{\rm{m}}})}_{\rm{a}}}}} + \frac{{{X_{{\rm{He}}}}}}{{f{{({\beta _{\rm{m}}})}_{{\rm{He}}}}}}} \right)^{ - 1}}$ |
式中Xa和XHe分别为空气和氦气的体积分数。
1.4 凝液非均匀效应因子计算水平管内冷凝换热的最典型特征即为凝液沿换热管周向的非均匀分布规律。在以往的换热模型建立过程中,通常忽略液膜厚度周向变化对局部换热能力的影响。本模型基于凝液微元的动量方程,提出了凝液非均匀效应因子ft。
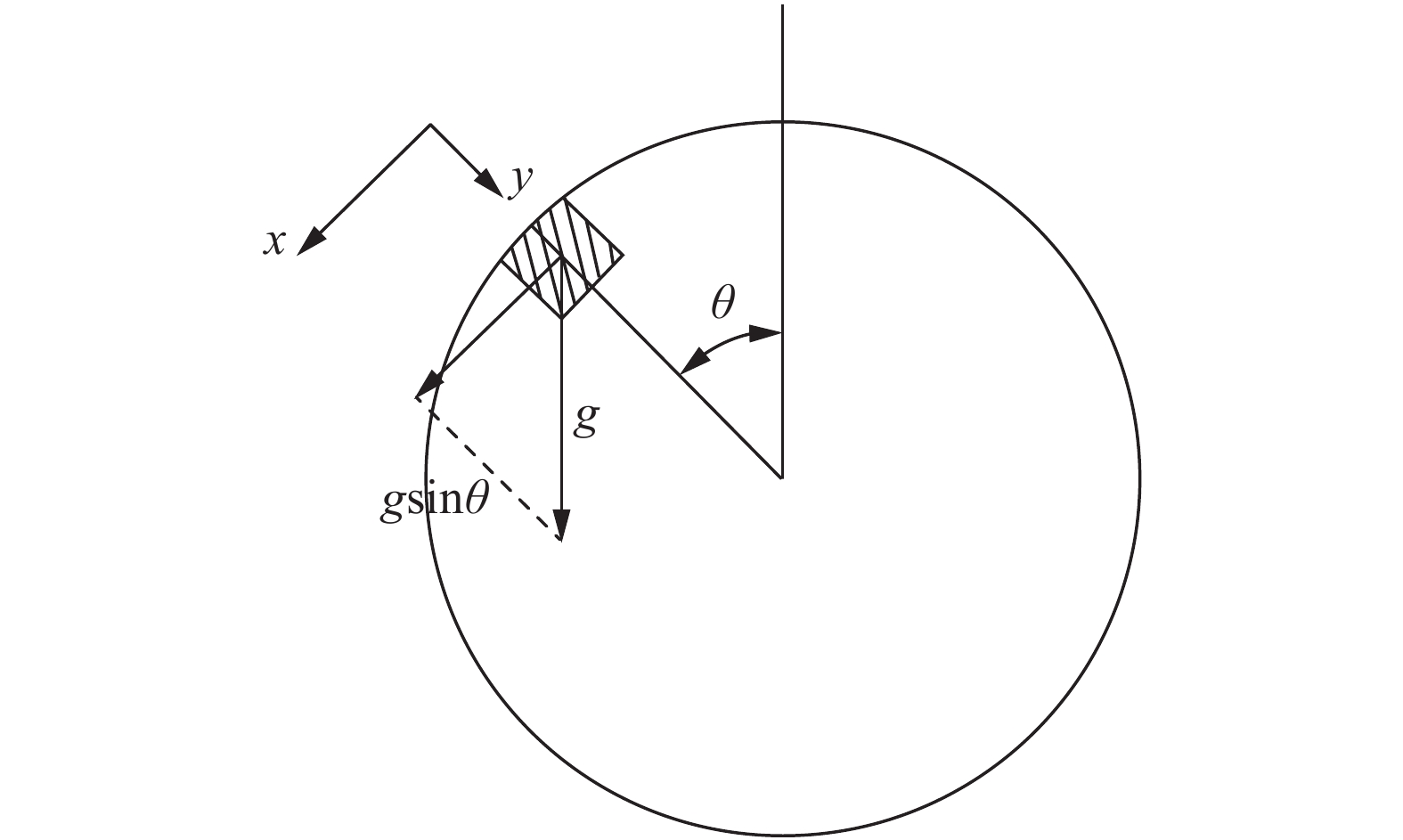
主流气体进入换热管l处的凝液受力情况如图1所示。此时凝液微元的动量方程可以表示为:
| ${\rho _{\rm{l}}}(u\frac{{\partial u(\theta )}}{{\partial x}} + v\frac{{\partial u(\theta )}}{{\partial y}}) = - \frac{{{\rm{d}}p}}{{{\rm{d}}x}} + {\rho _{\rm{l}}}g\sin \theta + {\mu _{\rm{l}}}\frac{{{\partial ^2}u(\theta )}}{{\partial {y^2}}}$ |
|
Download:
|
| 图 1 换热管内径向截面凝液受力 | |
在忽略液膜惯性力时可知:
| ${\rm{0}} = - {\rho _{\rm{m}}}g\sin \theta + {\rho _{\rm{l}}}g\sin \theta + {\mu _{\rm{l}}}\frac{{{\partial ^2}u(\theta )}}{{\partial {y^2}}}$ | (5) |
对式(5)进行积分可以得到:
| $u(\theta ) = \frac{{\left( {{\rho _{\rm{l}}} - {\rho _{\rm{m}}}} \right)g\sin \theta }}{{{\mu _{\rm{l}}}}}\left( {\delta y - \frac{1}{2}{y^2}} \right)$ | (6) |
对式(6)再进行转变和积分可获得轴向l处、换热管横截面θ角位置上内壁面上液膜的质量流量:
| ${M_{\rm{l}}}\left( {l,\theta } \right) = \int_0^{\delta \left( \theta \right)} {{\rho _{\rm{l}}}u(\theta ){\rm{d}}y} = \frac{{{\rho _{\rm{l}}}\left( {{\rho _{\rm{l}}} - {\rho _{\rm{m}}}} \right)g\sin \theta \delta {{\left( \theta \right)}^3}}}{{3{\mu _{\rm{l}}}}}$ | (7) |
这里认为冷凝换热过程中,自换热管顶部至底部,总热流密度随换热管横截面圆心角呈线性变化。于是有:
| ${\rm{d}}{M_{\rm{l}}}\left( {z,\theta } \right)\left| {_{z = l}} \right. = \left( {{q_{{\rm{top}}}}\left( l \right) - \dfrac{{\dfrac{1}{2}\left[ {{q_{{\rm{top}}}}\left( l \right) - {q_{{\rm{bot}}}}\left( l \right)} \right]\theta {D_{\rm{i}}}}}{{\dfrac{1}{2}{\text{π}}{D_{\rm{i}}}}}} \right)\dfrac{1}{{{i_{{\rm{fg}}}}}}{\rm{d}}z$ |
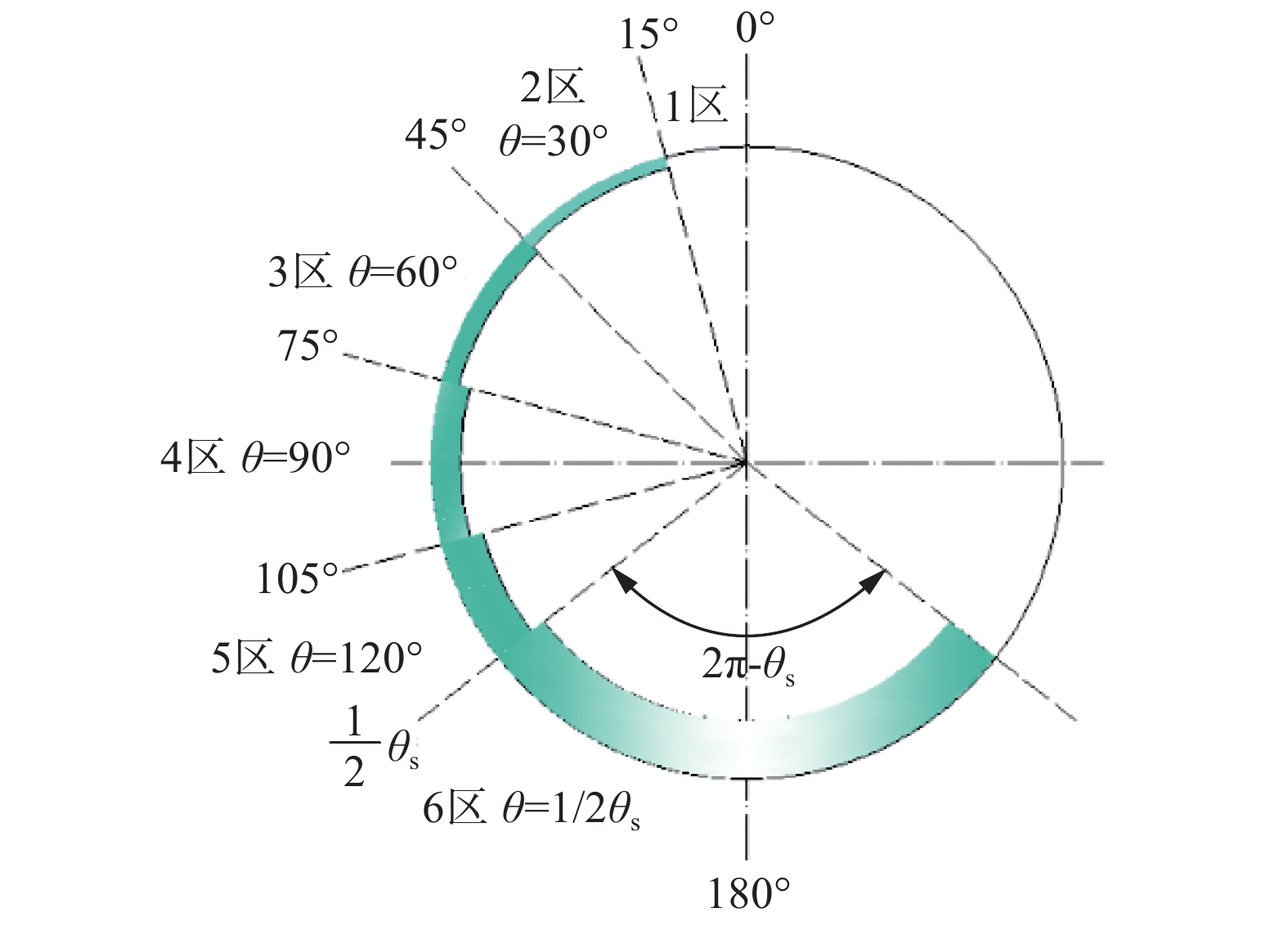
结合Thome模型[15],将换热管内半侧凝液分为6个子区间(如图2所示),假设每个子区间内凝液厚度一致,并且换热管顶部,即1区内不被凝液所覆盖,使用Thome模型可以获得换热管横截面上液膜覆盖区间,即图2中θs角的大小:
| $\begin{aligned} {\theta _{\rm{s}}} \!= & 2{\text{π}} \!- \!2\left\{ {{\text{π}}\left( {1 - \alpha } \right) \!+ \!{{\left( {\frac{{3{\text{π}}}}{2}} \right)}^{\frac{1}{3}}}\!\left[ {1 - 2\left( {1 - \alpha } \right) + {{\left( {1 - \alpha } \right)}^{\frac{1}{3}}} - {\alpha ^{\frac{1}{3}}}} \right] \!- } \right. \\ & \left. {\frac{{\alpha \left( {1 - \alpha } \right)}}{{200}}\left[ {1 - 2\left( {1 - \alpha } \right)} \right]\left[ {1 + 4\left( {{{\left( {1 - \alpha } \right)}^2} + {\alpha ^2}} \right)} \right]} \right\} \\ \end{aligned} $ |
式中α为任意处的截面含气率,由Grahan公式[16]计算:
| $\alpha = 1 - \exp \left\{ { - 1 - 0.3\ln (Ft) - 0.0328{{\left[ {\ln (Ft)} \right]}^2}} \right\}$ |
其中
|
Download:
|
| 图 2 换热管内凝液分布示意 | |
结合实验结果分析可知,换热管内凝液质量流量的增量
| $\frac{{{\rm{d}}{M_{\rm{l}}}\left( {z,\theta } \right)}}{{{\rm{d}}z}} = {{a}}{z^2} + {{b}}z + {{c}}$ | (8) |
通过对全部实验数据进行整理和统计,可确定式(8)中a、b、c各常数项数值,结合式(7)可以确定换热管截面上各分区内液膜厚度,由此定义液层非均匀因子ft为:
| ${f_{\rm{t}}} = \dfrac{{\dfrac{{\text{π}}}{6}\left( {\dfrac{1}{{{\varepsilon _2}}} + \dfrac{1}{{{\varepsilon _3}}} + \dfrac{1}{{{\varepsilon _4}}}} \right) + \left( {\dfrac{1}{2}{\theta _{\rm{s}}} - \dfrac{7}{{12}}{\text{π}}} \right)\dfrac{1}{{{\varepsilon _5}}} + \left( {{\text{π}} - \dfrac{1}{2}{\theta _{\rm{s}}}} \right)\dfrac{1}{{{\varepsilon _6}}}}}{{\dfrac{1}{\varepsilon }}}$ |
式中εn为各区间对应的凝结液膜厚度。
1.5 气液界面粗糙度修正因子计算在强制对流冷凝条件下,主流气体与凝液之间存在较大流速差异。在主流气体对凝液的剪切作用力下,气液界面粗糙度增加,甚至会出现明显的波浪起伏,这会使得凝液表面上的不凝性气体层内出现较强扰动,相应的蒸汽在其中的扩散阻力得到降低,换热能力得到增强。为描述气液界面粗糙度对冷凝换热的影响,这里引入Siddique[17]基于大量实验所提出的修正因子fc对本文换热模型进行优化:
| ${f_{\rm{c}}} = {\left\{ {\dfrac{{0.079Re_{_{\rm{m}}}^{ - 0.25}}}{{1.375 \times {{10}^3}\left[ {1 + 21.544{{\left( {\dfrac{{{\varepsilon _0}}}{{{D_{\rm{i}}}}} + \dfrac{{100}}{{R{e_{\rm{m}}}}}} \right)}^{1/3}}} \right]}}} \right\}^{P{r^{0.36}}}}$ |
式中ε0为凝液平均厚度,m。
1.6 换热模型计算流程综合以上分析,在考虑各项因素对模型进行修正的情况下,将凝液与换热管内壁面间的对流换热系数、凝结换热系数与主流气体与凝液之间的对流换热系数分别带入式(1)中,可得到计算水平管内局部冷凝换热系数计算公式为:
| $ \begin{aligned} {h_{{\rm{cal}},{\rm{0}}}} = & \dfrac{1}{{{h_{\rm{f}}}}} + \dfrac{1}{{{h_{\rm{s}}} + {h_{\rm{c}}}}} = \\ & S\!{h_{\rm{m}}}\left(\left(\dfrac{{w_{{\rm{nc}}}^{\rm{i}} - w_{{\rm{nc}}}^{\rm{b}}}}{{w_{{\rm{nc}}}^{{\rm{lm}}}}}\right)\dfrac{{P{r_{\rm{m}}}}}{{S\!{c_{\rm{m}}}}}\dfrac{1}{{J{a_{\rm{m}}}}} \times f\left( {{\beta _{\rm{m}}}} \right) \times \right.\\ & \left. f\left( {{f_{\rm{c}}},{f_{\rm{t}}}} \right) + {\left(\dfrac{{P{r_{\rm{m}}}}}{{S{c_{\rm{m}}}}}\right)^{0.33}}\right){\lambda _{\rm{m}}}/{D_{\rm{i}}} + \dfrac{1}{{{h_{\rm{f}}}}} \end{aligned}$ |
为便于计算,将凝液非均匀分布因子与气液界面粗糙度因子进行了整合,得到综合修正公式f (fc, ft)为:
| $f\left( {{f_{\rm{c}}},{f_{\rm{t}}}} \right) = 0.795f_{\rm{c}}^{2.442}f_{\rm{t}}^{0.78}$ |
已知主流气体总压力、温度、空气和氦气质量分数和换热管内壁面温度后,使用MATLAB编程迭代计算后最终可得到管内局部冷凝换热系数的计算值[18]。
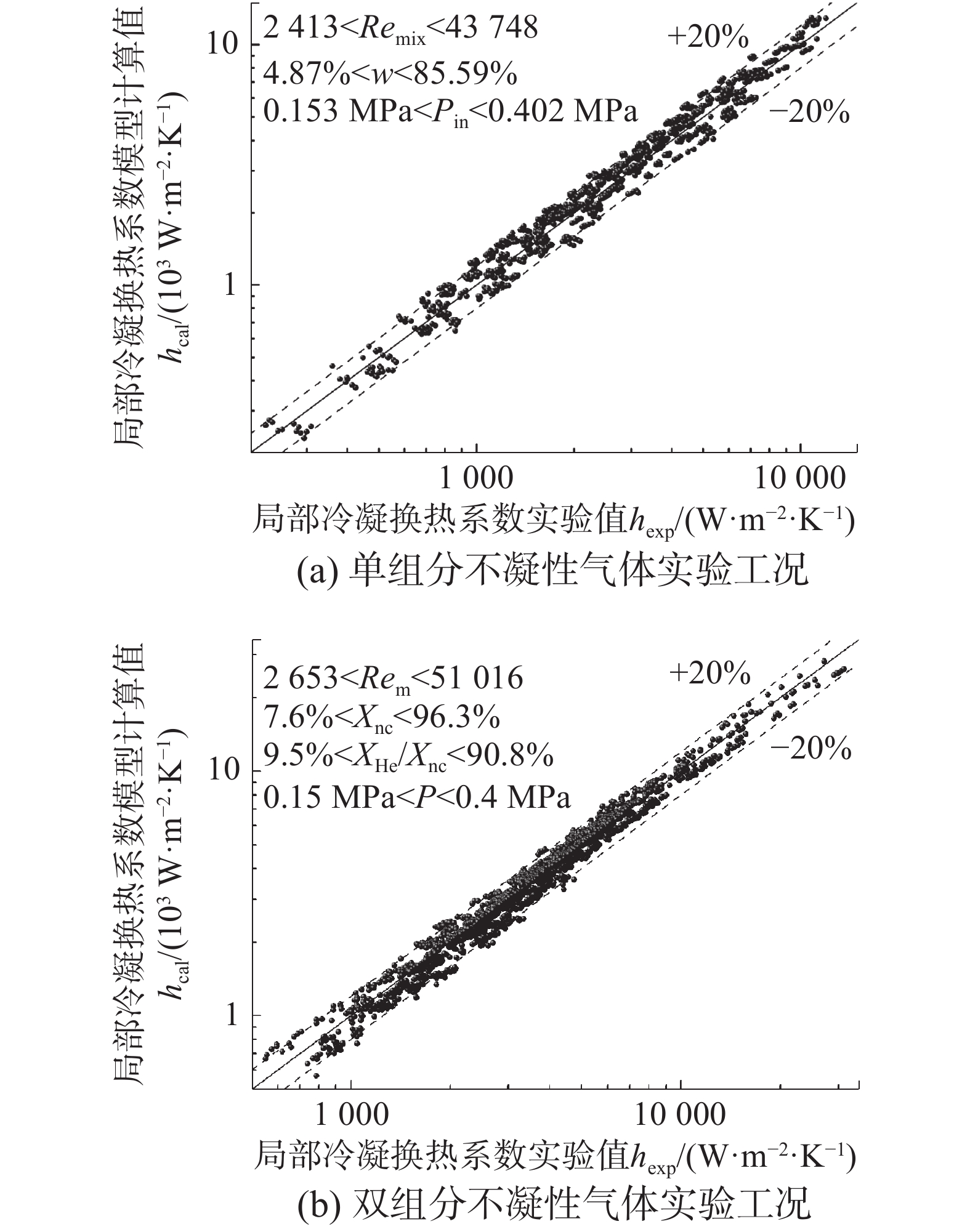
2 模型计算结果分析为考察本文所提出换热模型的计算准确性,结合以往研究成果中的实验数据,分别针对含单组分不凝性气体(空气)和含多组分不凝性气(空气、氦气)条件下,总计1 279和1 990的实验点对应的管内局部冷凝换热系数,使用本文所提模型进行计算,并与实验数据相比较,结果如图3所示。结果显示,对于含空气工况来说,平均偏差为13.26%;对于含空气和氦气工况来说,平均偏差为8.62%。全部数据点的计算值与实验值之间的相对偏差基本处于±24%以内。以上结果证实在充分考虑水平管内含不凝性气体冷凝换热的典型特点和正确选择各换热环节的计算方法后,本文所提出的冷凝换热模型能够很好地模拟管内冷凝换热过程,并较为准确地预测局部冷凝换热系数。
|
Download:
|
| 图 3 局部冷凝换热系数模型计算结果与实验数据对比 | |
为分析在不凝性气体存在条件下,总换热过程中各子过程的热交换能力变化,以此判断影响总换热能力的关键环节,以便后续有针对性的采取强化换热手段,最终提升PCCS换热的整体换热功率,使用本文所提出的换热程序,分别计算出不同主流气体流速条件下,凝液与换热管内壁面间的对流换热系数hf、凝结换热系数hc与主流气体与凝液之间的对流换热系数hs随局部不凝性气体质量分数的变化规律,结果如图4所示。由图4可知,主流气体与凝结液膜之间的对流换热系数相比于其他环节来说,其换热强度基本可以忽略不计。凝结液膜与换热管壁的对流换热系数和凝结换热系数的下降梯度逐渐随局部不凝性气体含量的增加趋于平缓。在局部不凝性气体含量增加到一定程度时,凝液对流换热系数将高于凝结换热系数,在此之前,二者之间呈相反的高低关系。

|
Download:
|
| 图 4 不同主流气体流速下,各换热环节换热系数对比 | |
产生以上结果的主要原因在于,在冷凝换热起始阶段,气液界面处不凝性气体含量较低,其对冷凝换热的消极影响相对较弱,因此伴随相变过程的凝结换热能力十分强烈,远高于凝液的对流换热过程。随着蒸汽逐渐凝结,一方面不凝性气体在气液界面不断聚集,蒸汽向凝液表面的扩散过程受阻不断增加,从而导致凝结换热系数逐渐降低;另一方面,主流气体流速逐渐降低,不凝性气体层内部扰动效果减弱,使得层内蒸汽扩散能力随之降低。这两方面的物理过程变化使得局部不凝性气体含量达到一定程度时,凝液对流换热系数将超过凝结换热系数。由此可知,在管内整个换热过程之中,主要热阻由凝液侧对流换热热阻逐渐转变为凝结换热热阻。因此出现如图4所示情况,总换热系数先靠近凝液换热系数,后靠近凝结换热系数的变化规律。
针对上述管内换热能力的变化规律,可以在靠近换热管前端的换热管壁面上增加强化肋或螺旋扰丝,以增强凝液侧换热能力;在接近换热管中段,可增高强化肋的高度使之能够穿出凝液表面,增加凝液表面不凝性气体层内的扰动,强化凝结换热能力。通过两方面的改进,最终实现强化整体换热能力的效果,以此增强PCCS换热器的换热功率。
4 结论基于Petererson的边界层扩散模型,通过分解管内总换热过程,并分别选择对应传热传质模型及公式进行推导,得到了可以模拟管内冷凝换热物理过程的计算程序。结合模拟结果,得到以下主要结论:
1)在模型计算精度方面,通过分析程序计算结果与大量实验数据的相对偏差,可知计算结果的偏差值不超过24%。对于含单组分不凝性气体工况,二者平均偏差为13.26%;对于含多组分不凝性气体工况,二者平均偏差为8.62%。由此可证实当前换热计算程序在预测精度方面具有较大提升。
2)在模型建立之中考虑凝结液膜的周向非均匀分布、气液表面粗糙度以及抽吸效应的影响对于提升计算模型预测精度和模拟冷凝换热的实际物理过程有重要意义。
3)在管内冷凝过程中,伴随蒸汽不断凝结,不凝性气体在气液表面逐渐聚集,管内换热过程的主要热阻将在局部不凝性气体含量达到某一程度时,由液膜热阻逐渐转变为凝结热阻。相应的管内总换热系数先近似于液膜对流换热系数,随后接近凝结换热系数。
| [1] |
AL-SHAMMARI S B, WEBB D R, HEGGS P. Condensation of steam with and without the presence of non-condensable gases in a vertical tube[J]. Desalination, 2004, 169(2): 151-160. DOI:10.1016/j.desal.2003.11.006 ( 0) 0)
|
| [2] |
OH S, REVANKAR S T. Effect of noncondensable gas in a vertical tube condenser[J]. Nuclear engineering and design, 2005, 235(16): 1699-1712. DOI:10.1016/j.nucengdes.2005.01.010 ( 0) 0)
|
| [3] |
LEE K Y, KIM M H. Effect of an interfacial shear stress on steam condensation in the presence of a noncondensable gas in a vertical tube[J]. International journal of heat and mass transfer, 2008, 51(21/22): 5333-5343. ( 0) 0)
|
| [4] |
DEHBI A A. Analytical and experimental investigation of the effects of non-condensable gases on steam condensation under turbulent natural convection conditions[D]. US: MIT, 1990.
( 0) 0)
|
| [5] |
LIU H, TODREAS N E, DRISCOLL M J. An experimental investigation of a passive cooling unit for nuclear plant containment[J]. Nuclear engineering and design, 2000, 199(3): 243-255. DOI:10.1016/S0029-5493(00)00229-6 ( 0) 0)
|
| [6] |
CARUSO G, DI MAIO D V, NAVIGLIO A. Condensation heat transfer coefficient with noncondensable gases inside near horizontal tubes[J]. Desalination, 2013, 309: 247-253. DOI:10.1016/j.desal.2012.10.026 ( 0) 0)
|
| [7] |
CARUSO G, DI MAIO D V, NAVIGLIO A. Film condensation in inclined tubes with noncondensable gases: an experimental study on the local heat transfer coefficient[J]. International communications in heat and mass transfer, 2013, 45: 1-10. DOI:10.1016/j.icheatmasstransfer.2013.04.010 ( 0) 0)
|
| [8] |
WU Tiejun, VIEROW K. Local heat transfer measurements of steam/air mixtures in horizontal condenser tubes[J]. International journal of heat and mass transfer, 2006, 49(15/16): 2491-2501. ( 0) 0)
|
| [9] |
CHATO J C. Laminar condensation inside horizontal and inclined tubes[J]. ASHRAE journal, 1962, 4(2): 52-60. ( 0) 0)
|
| [10] |
REN Bin, ZHANG Li, XU Hong, et al. Experimental study on condensation of steam/air mixture in a horizontal tube[J]. Experimental thermal and fluid science, 2014, 58: 145-155. DOI:10.1016/j.expthermflusci.2014.06.022 ( 0) 0)
|
| [11] |
CAVALLINI A, CENSI G, DEL COL D, et al. Condensation inside and outside smooth and enhanced tubes— a review of recent research[J]. International journal of refrigeration, 2003, 26(4): 373-392. DOI:10.1016/S0140-7007(02)00150-0 ( 0) 0)
|
| [12] |
PETERSON P F, SCHROCK V E, KAGEYAMA T. Diffusion layer theory for turbulent vapor condensation with noncondensable gases[J]. Journal of heat transfer, 1993, 115(4): 998-1003. DOI:10.1115/1.2911397 ( 0) 0)
|
| [13] |
徐慧强, 孙秋南, 谷海峰, 等. 水平管内含空气蒸汽流动冷凝局部换热特性[J]. 化工学报, 2015, 66(7): 2456-2463. ( 0) 0)
|
| [14] |
KUHN S Z, SCHROCK V E, PETERSON P F. An investigation of condensation from steam–gas mixtures flowing downward inside a vertical tube[J]. Nuclear engineering and design, 1997, 177(1/2/3): 53-69. ( 0) 0)
|
| [15] |
THOME J R, EL HAJAL J, CAVALLINI A. Condensation in horizontal tubes, part 2: new heat transfer model based on flow regimes[J]. International journal of heat and mass transfer, 2003, 46(18): 3365-3387. DOI:10.1016/S0017-9310(03)00140-6 ( 0) 0)
|
| [16] |
GRAHAM D, CHATO J C, NEWELL T A. Heat transfer and pressure drop during condensation of refrigerant 134a in an axially grooved tube[J]. International journal of heat and mass transfer, 1998, 42(11): 1935-1944. ( 0) 0)
|
| [17] |
SIDDIQUE M, GOLAY M W, KAZIMI M S. Local heat transfer coefficients for forced-convection condensation of steam in a vertical tube in the presence of a noncondensable gas[J]. Nuclear technology, 1993, 102(3): 386-402. DOI:10.13182/NT93-A17037 ( 0) 0)
|
| [18] |
XU Huiqiang, GU Haifeng, SUN Zhongning. Forced convection condensation of steam in the presence of multicomponent noncondensable gases inside a horizontal tube[J]. International journal of heat and mass transfer, 2017, 104: 1110-1119. DOI:10.1016/j.ijheatmasstransfer.2016.09.031 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


