高光谱遥感技术是基于多光谱遥感技术的基础，并在20世纪80年代开始发展的一种新兴遥感技术，其明显的优势在于拥有丰富的地物光谱波段。光谱分辨率较高，因此可以解决许多在全色和多光谱遥感中无法解决的难题。高光谱图像不仅可以很好地表现图像的空间信息，还可以表示地物的光谱信息。但是，由于遥感图像中的单个像元所对应的实际空间范围比较大，因此在一个像元中可能会出现多于一种的地物类别，这种现象称之为像元混合^[1−2]。这种现象是遥感成像空间尺度有限性和自然界地物复杂程度的无限性之间矛盾的体现。如果像元出现混合将会严重影响高光谱遥感技术的广泛使用。因此，如何解决遥感图像中的像元混合问题，是当前遥感图像处理领域一个较为热门的研究方向之一。

处理像元混合问题^[3−6]需要建立合适的模型^[7]。模型主要有两种选择，一种是线性，另外一种是非线性。依据线性混合模型的结论，构成混合像元的地物光谱曲线之间是以线性比例组成的。这种模型成立的理论依据是：太阳光子在空间传播的过程中只能与一种物质发生电磁相互作用，而不能在多种物质之间发生多重的电磁相互作用，否则模型就是非线性的。因为非线性混合模型需要将太阳光子和地物之间的多重电磁相互作用包含在内，而这种因素本身比较难以表达。因此它的物理意义理解起来相对来说比较困难，求解起来比较复杂。与非线性模型相比，线性模型^[8]不需要考虑光子与物质之间的多重电磁相互作用，相对来说比较简单。因此，大多数光谱分解算法都是依据线性模型而编写的。在使用线性光谱混合模型对遥感图像中的混合像元进行处理之前，首先需要弄清楚遥感图像中所包含的地物总数以及它们所属的光谱曲线；然后将所有的光谱曲线组成一个完整的端元集；最后将得到的端元集作用于图像中的像元。经过上述几个步骤之后，将会得到端元集中的每种地物光谱曲线在像元中所占的比例。端元可以从对应的光谱库中提取或经过实地测量得到，还可以利用N−FINDR、PPI、IEA等端元提取算法从指定的高光谱图像中提取。在没有考虑端元光谱曲线的变异之前，代表某种地物的端元光谱曲线一般只有一条，然后利用这些端元光谱曲线组成的端元集去处理混合像元。但是这样做会对分解结果造成不良的影响。由于成像光谱仪所覆盖的实际地域范围比较广，因此同一种地物有可能出现因为光照条件不均匀等因素而引起端元光谱曲线扰动的现象，这种现象被称为光谱变异。在这种情形下，已经不再适合用一个单一且固定的端元去表示某种地物的端元了。在那些需要准确知道每个端元在混合像元中所占比例的应用中，以前的基于单个端元线性模型会造成较大的分解误差。针对这个不足，Roberts等^[9−11]采用了一种新型的高光谱图像混合像元分解方法，该方法考虑到端元的光谱和空间变化，并迭代地调整端元的数量和类型。对于高光谱图像中的每一个像元，这种方法需要对不同地物之间的端元进行排列组合，并将排列组合后的结果作为图像中每个像元的候选端元集合；然后使用这个端元集合去处理图像中的每一个像素；最后根据重构误差最小准则从这个端元集合中选择出最佳的端元组合。该方法能够将光谱变异的情况考虑在内，分解效果较好。这种方法的主要缺点是当图像中包含的端元数量比较多时，产生的计算量将变得非常大。为此，赵春晖等^[12]提出一种基于分层的多端元高光谱分解算法，该算法最终的计算量相对较小，分解效果与多端元光谱混合分析算法相差不大。

分层算法虽然能够降低多端元光谱混合分析算法所产生的计算量，但是由于噪声的存在，如果在一个混合像元中某些地物所占的比例比较小，那么在最终的结果中这些地物的所占比例可能会被记为0。因此，对于小丰度地物的检测效果可能不是很好。本文提出了一种基于分组寻优的多端元高光谱分解方法，该方法能够克服遥感图像中噪声的影响，对小丰度目标的检测有较好的效果。

1 光谱混合模型及反演理论

混合像元的分解^[13]有赖于具体模型的建立。研究人员必须根据具体情况选择合适的模型。目前，可供参考的模型主要有线性和非线性之分，这两种模型所代表的物理意义有很大不同。

如果太阳光子在到达成像光谱仪之前只与一类地物发生电磁相互作用，但在地物之间没有发生电磁相互作用，那么这种模型称之为线性的。与之相反的是，非线性模型是由于太阳光子与同一场景内多种地物之间发生电磁相互作用，根据这种过程所建立的模型是非线性的。由于建立和求解非线性模型相对困难，因此对于非线性模型研究相对较少。然而，由于线性模型的概念清晰，物理意义简单，对其研究的相对较多。本文正是在线性模型的基础上对高光谱图像中的混合像元进行研究。

光谱分解技术作为混合像元处理的最主要技术，目的就是要求得每个端元在其中所占的比例。这是一种更为精确的分类技术。

1.1 线性混合模型

如果一幅高光谱图像中共有n个像元，地物的种类为p，光谱维度为B，则线性光谱混合模型（linear spectral mixing model，LSMM）可以表示为

${{{r}}_{{i}}} = \sum\limits_{j = 1}^{\rm{p}} {{\alpha _{ij}}{{{e}}_{{j}}} + {{{\varepsilon }}_{{j}}}} $

(1)

式中：α_ij是端元 ${{{e}}_{{j}}}$ 在像元 ${{{r}}_{{i}}}$ 中的比例，称之为丰度； ${{{\varepsilon }}_{{j}}}$ 代表了由环境噪声引起的误差。

如果将式（1）中的向量排列成矩阵，可以得到线性混合模型的矩阵形式：

${{R}} = {{E}}{{{A}}^{\rm{T}}} + {{\varepsilon}} $

式中：R代表的是一个图像矩阵，其每列表示一个像元，维度为B；E表示地物端元矩阵，它的每列表示一个端元；A表示丰度矩阵；ε表示误差矩阵。相应地，式（1）为线性光谱混合模型的向量表示形式。

1.2 丰度反演算法

将各种地物在混合像元中所占的比例计算出来的方法就是混合像元分解技术。常用的丰度计算方法是最小二乘法，假设一幅高光谱图像中包含有p个端元，那么端元矩阵为 ${{E}} = [{e_1},{e_2}, \cdots ,{e_p}]$ ，丰度向量为 ${{\alpha}} = [{\alpha _1},{\alpha _2}, \cdots ,{\alpha _p}]$ ，n为噪声项。将高光谱图像中的任意混合像元x表示为p个端元在丰度值 ${\alpha _1},{\alpha _2}, \cdots ,{\alpha _p}$ 下的线性组合，即

$ {{x}} = {{E\alpha}} + {{n}} $

(2)

若将式（2）视为方程组，由于高光谱图像中波段的数目比较多，那么在式（2）中将会出现独立方程个数大于未知参数的个数的情况，此时可以通过最小二乘法求解，将式（2）表示为最小二乘误差问题，可得

$\mathop {\min }\limits_{{\alpha}} \left\{ {{{\left( {{{x}} - {{E\alpha}} } \right)}^{\rm{T}}}\left( {{{x}} - {{E\alpha}} } \right)} \right\}$

由于各个端元在像元中所占的比例是非负的、且将各个端元对应的比例相加满足和为1的条件。因此可以在传统的最小二乘法中加入合理的约束，就能够得到更加符合实际情况的最终结果。根据对丰度施加约束的情况，可以将最小二乘法分为4种，具体地描述如下所示。

1.2.1 没有任何约束的最小二乘法

在没有加入任何约束的情况下，仅用最小二乘算法求解式（2），可得到无约束的解为

${\hat \alpha _{{\rm{UCLS}}}}\left( {x} \right) = {\left( {{{{E}}^{\rm{T}}}{{E}}} \right)^{ - 1}}{{{E}}^{\rm{T}}}{{x}}$

1.2.2 和为1约束最小二乘法

当考虑各个端元在某个混合像元中的丰度系数之和为1时，式（2）可以表示为：

$\left\{ \begin{array}{l} \mathop {\min }\limits_{{\alpha}} \left\{ {{{\left( {{{x}} - {{E\alpha}} } \right)}^{\rm{T}}}\left( {{{x}} - {{E\alpha}} } \right)} \right\} \\ {\rm{s}}{\rm{.t}}{\rm{. }}\displaystyle\sum\limits_{j = 1}^p {{\alpha _j} = 1} \\ \end{array} \right.$

在和为1的约束条件下，可得式（2）在部分约束下的解为

$ \mathop {{\alpha _{{\rm{SCLS}}}}\left( x \right) = \left[ {{{{I}}_m} - \frac{{{{\left( {{{{E}}^{\rm{T}}}{{E}}} \right)}^{ - 1}}{{\bf{1}}^{\rm{T}}}}}{{{{\bf{1}}^{\rm{T}}}{{\left( {{{{E}}^{\rm{T}}}{{E}}} \right)}^{ - 1}}{\bf{1}}}}} \right]}\limits^{} {\hat \alpha_{{\rm{UCLS}}}}\left( x \right) + \\ \frac{{{{\left( {{{{E}}^{\rm{T}}}{{E}}} \right)}^{ - 1}}{\bf{1}}}}{{{{\bf{1}}^{\rm{T}}}{{\left( {{{{E}}^{\rm{T}}}{{E}}} \right)}^{ - 1}}{\bf{1}}}} \\ $

式中： ${{{I}}_m}$ 为 $m$ 阶单位矩阵； ${\bf{1}} = {[1,1, \cdots ,1]^{\rm{T}}}$ 为全1的 $m$ 维列向量。

1.2.3 非负约束最小二乘法

在非负约束条件下，可将式（2）表示为：

$\left\{ \begin{array}{l} \mathop {\min }\limits_{{\alpha}} \left\{ {{{\left( {{{x}} - {{E\alpha}} } \right)}^{\rm{T}}}\left( {{{x}} - {{E\alpha}} } \right)} \right\} \\ {\rm{s}}{\rm{.t}}{\rm{. }}\quad {\alpha _j} \geqslant 0 \\ \end{array} \right.$

(3)

1.2.4 完全约束最小二乘法

为了使混合像元的分解结果更符合实际情况，可以在式（3）的基础上加上和为1的约束条件。此时，完全约束最小二乘法可以表示成：

$\left\{ \begin{array}{l} \mathop {\min }\limits_{{\alpha }} \left\{ {{{\left( {{{x}} - {{E\alpha} }} \right)}^{\rm{T}}}\left( {{{x}} - {{E\alpha} }} \right)} \right\}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;{\alpha _j} \geqslant 0且\left( {\displaystyle\sum\limits_{j = 1}^p {{\alpha _j} = 1}} \right) \end{array} \right.$

2 高光谱图像的分层算法

Roberts等^[9]提出的算法并不是针对每个像元都使用相同的端元集进行处理，而是为每个像元迭代生成一个特定的端元集。在这个算法中每个像元对应的端元类别和数量是变化的，分解效果较好。但是需要人工迭代端元的所有可能组合，在光谱库很大的情况下，所需的计算量将变得非常大。假定一幅高光谱图像中总的地物种类为M，第 $i$ 类地物包含 ${N_i}$ 条类内光谱曲线，则M端元组合数为 $\prod\nolimits_i^M {{N_i}} $ ，随着 ${N_i}$ 的增大，组合数会大量增加，若再考虑2，3， $ \cdots $ ， $\left( {M - 1} \right)$ 端元组合，那么总的端元组合数量可能会更大。文献[12]采用分层的思想，将比较困难的问题转化成较为简单的步骤来实现。因为高光谱图像包含的全部端元不可能都出现在图像的每一个像元中。因此，每个像元所对应的最佳端元组合应该是M端元组合的一个子集，通过分层能够确定最佳的类内光谱以及端元数量。分层算法在第1层将所有的端元作用于某个混合像元，会得到一个丰度向量。然后将每类地物所对应的丰度系数进行排列，并将每类地物中丰度系数最大的值所对应的那条光谱曲线挑选出来，将它作为这种地物在这个像元中唯一的光谱曲线。与多端元光谱混合分析方法相比，M端元组合个数从 $\prod\nolimits_i^M {{N_i}} $ 骤降到1。当算法运行到第二层的时候，将会对第一层所得到的类内光谱曲线进行从2到 $\left( {M - 1} \right)$ 之间的端元组合过程。然后将这些端元组合作用于同一个混合像元，并将这些端元组合与对应的丰度系数进行重构，计算重构值与该混合像元之间的光谱角距离，将每一层得到的光谱角距离集中起来进行比较，从中选择出光谱角距离的最小值，该最小值所对应的端元组合以及对应的丰度系数就是最终的结果。下面通过举例说明该方法的实施过程。

假设有4类地物分别包括3条、2条、2条、2条类内光谱变异曲线，则端元集可以表示为E = $ \left\{ {{A_1},{A_2},{A_3},{B_1},{B_2},{C_1},{C_2},{D_1},{D_2}} \right\}$ 。在第1层中，假设通过计算之后确定某个混合像元 $y_{{\rm{pixel}}}^k$ 中包含总的地物类别的类内光谱 ${M_k} = \left\{ {{A_1},{B_1},{C_1},{D_1}} \right\}$ ，接下来分别计算端元 $\left\{ {{A_1}} \right\}$ 、 $\left\{ {{B_1}} \right\}$ 、 $\left\{ {{C_1}} \right\}$ 、 $\left\{ {{D_1}} \right\}$ 与像元 $y_{{\rm{pixel}}}^k$ 光谱角距离。假定最佳的匹配端元为 ${A_1}$ ，在第2层可以确定的所有两端元组合有 $\left\{ {{A_1}{B_1}} \right\}$ 、 $\left\{ {{A_1}{C_1}} \right\}$ 、 $\left\{ {{A_1}{D_1}} \right\}$ ，然后利用与第1层相同的方法假定最佳匹配的端元组合为 $\left\{ {{A_1}{B_1}} \right\}$ ；在第3层需要验证的端元组合则是 $\left\{ {{A_1}{B_1}{C_1}} \right\}$ 和 $\left\{ {{A_1}{B_1}{D_1}} \right\}$ ，假定通过计算后所确定的最佳匹配的端元组合为 $\left\{ {{A_1}{B_1}{C_1}} \right\}$ ，那么在第4层唯一需要确定的端元组合就是 $\left\{ {{A_1}{B_1}{C_1}{D_1}} \right\}$ ；最后通分别使用端元组合 $\left\{ {{A_1}} \right\}$ 、 $\left\{ {{A_1}{B_1}} \right\}$ 、 $\left\{ {{A_1}{B_1}{C_1}} \right\}$ 和 $\left\{ {{A_1}{B_1}{C_1}{D_1}} \right\}$ 对混合像元 $y_{{\rm{pixel}}}^k$ 进行处理，得到它们各自所对应的丰度值，并将相应的端元组合和丰度进行重构，根据重构误差确定重构结果与 $y_{{\rm{pixel}}}^k$ 之间的差别，选择误差最小所对应的丰度作为最终的结果。

3 基于分组寻优的多端元高光谱解混方法

分组寻优的思想与分层思想相似但有所不同。鉴于高光谱图像中存在噪声，对于那些小丰度值地物的检测效果不理想。因为这些地物在对应像元中所占的比例较小，在处理的过程中很容易受到噪声的干扰而被过滤掉，这样会使最终的分解效果不理想。本文方法可以将每种地物所对应的端元在混合像元中的存在充分扩大，即使是丰度较小的端元在检测过程中也不会因为噪声的影响而被忽略掉，因此对小概率目标的检测效果较好。分组寻优的多端元高光谱分解算法主要包括以下几个步骤：

1）使用各类地物所对应的端元对混合像元分别进行处理，并使用根均方误差（RMSE）确定每类地物中的最佳端元；

2）对步骤1）得到的根均方误差按大小顺序进行排列，将每类地物中具有最小根均方误差所对应的端元作为基准，与步骤2）中确定的其他最佳端元分别组合构成若干个两端元组合模型；

1）重复步骤1）和2）；

4）将每一步所得到的最小根均方误差进行比较，找出最小的根均方误差所对应的端元组合即是最佳的端元组合，它所对应的丰度即是最终结果。

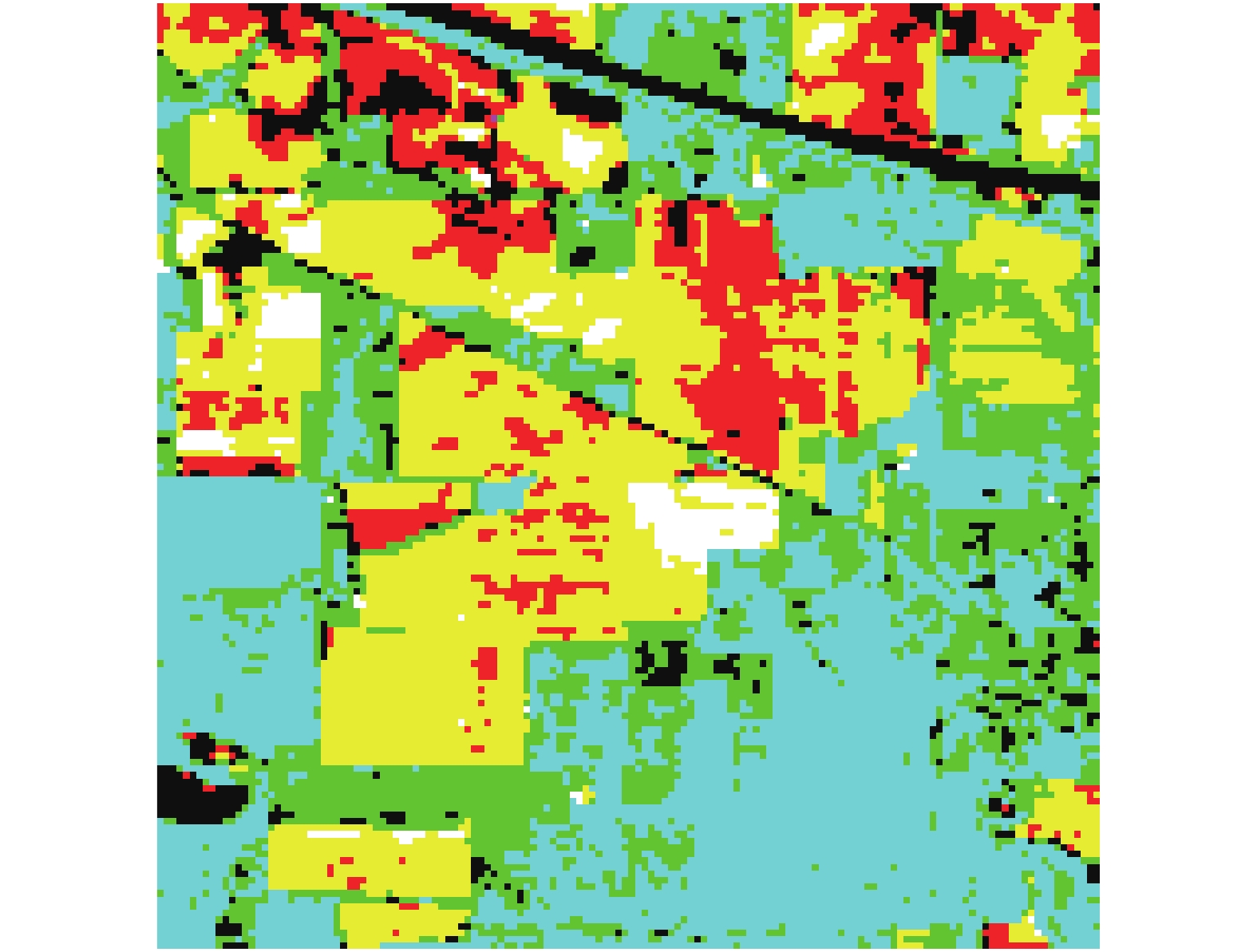
4 实验结果与分析

本次实验采用的是美国印第安纳州试验田高光谱数据，它真实图像如图1所示，图像大小为144×144，有100个波段。

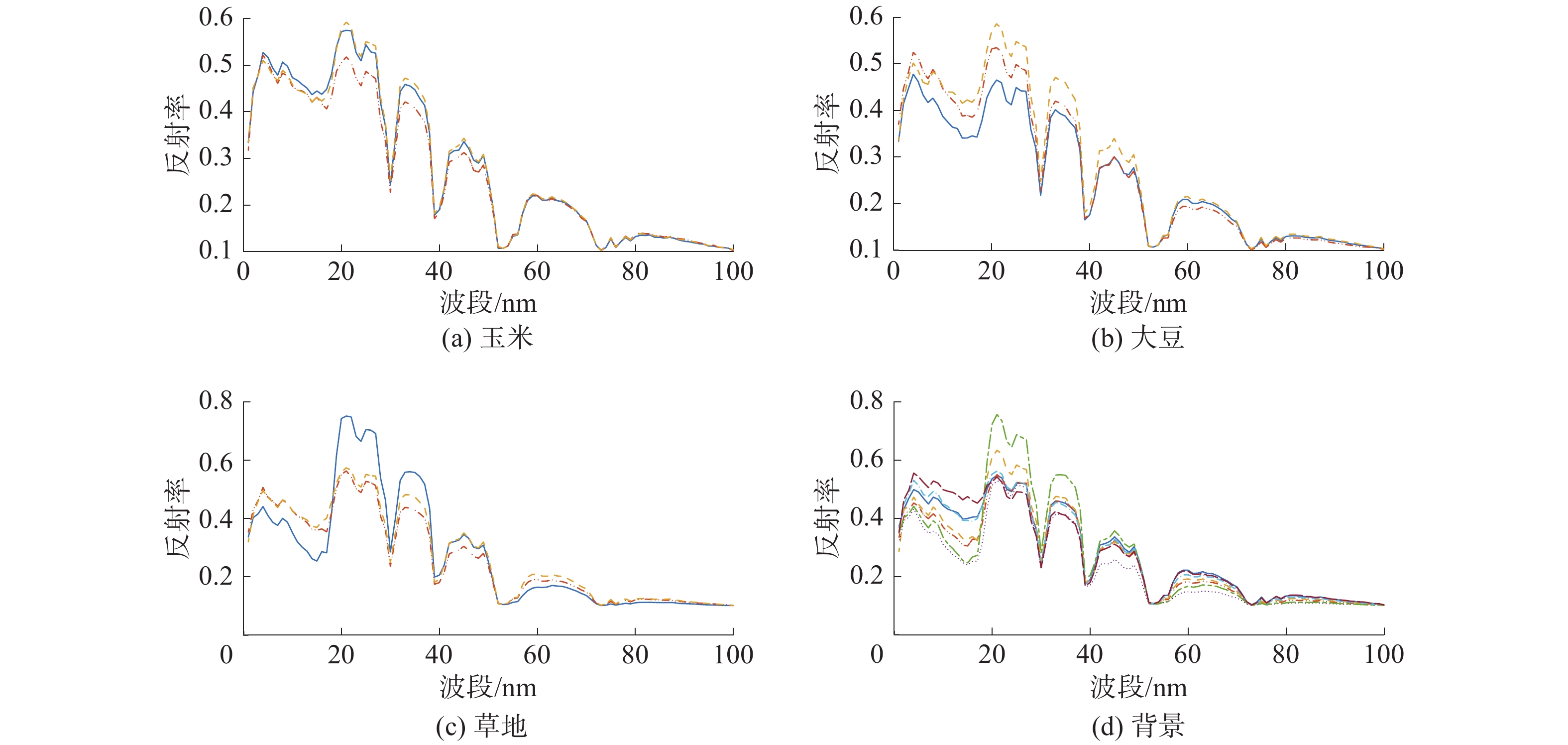
本次实验中共选用了4组端元，分别是玉米、大豆、草地和背景，每组的端元个数分别是3、3、3和7，具体的端元波谱图如图2所示。

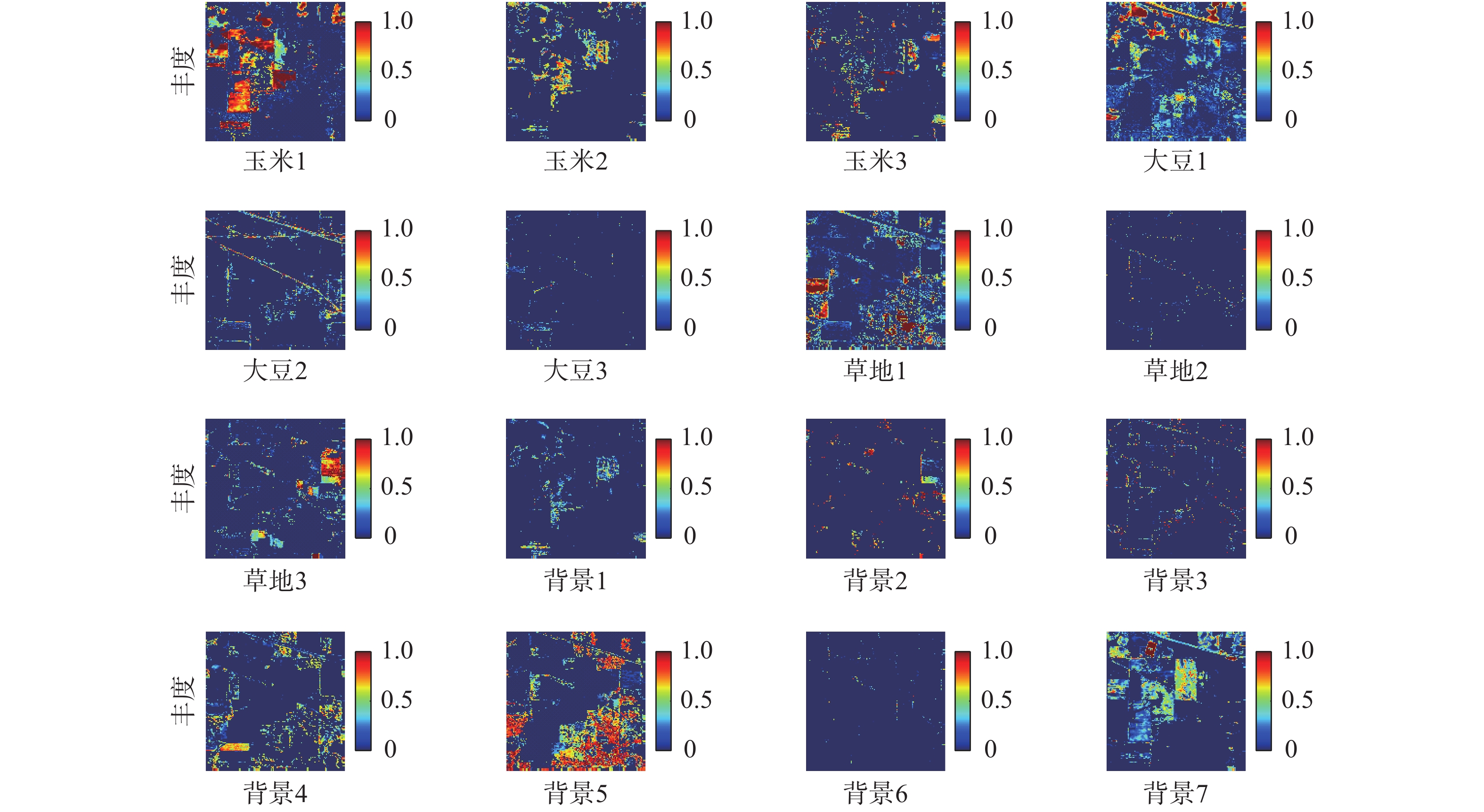
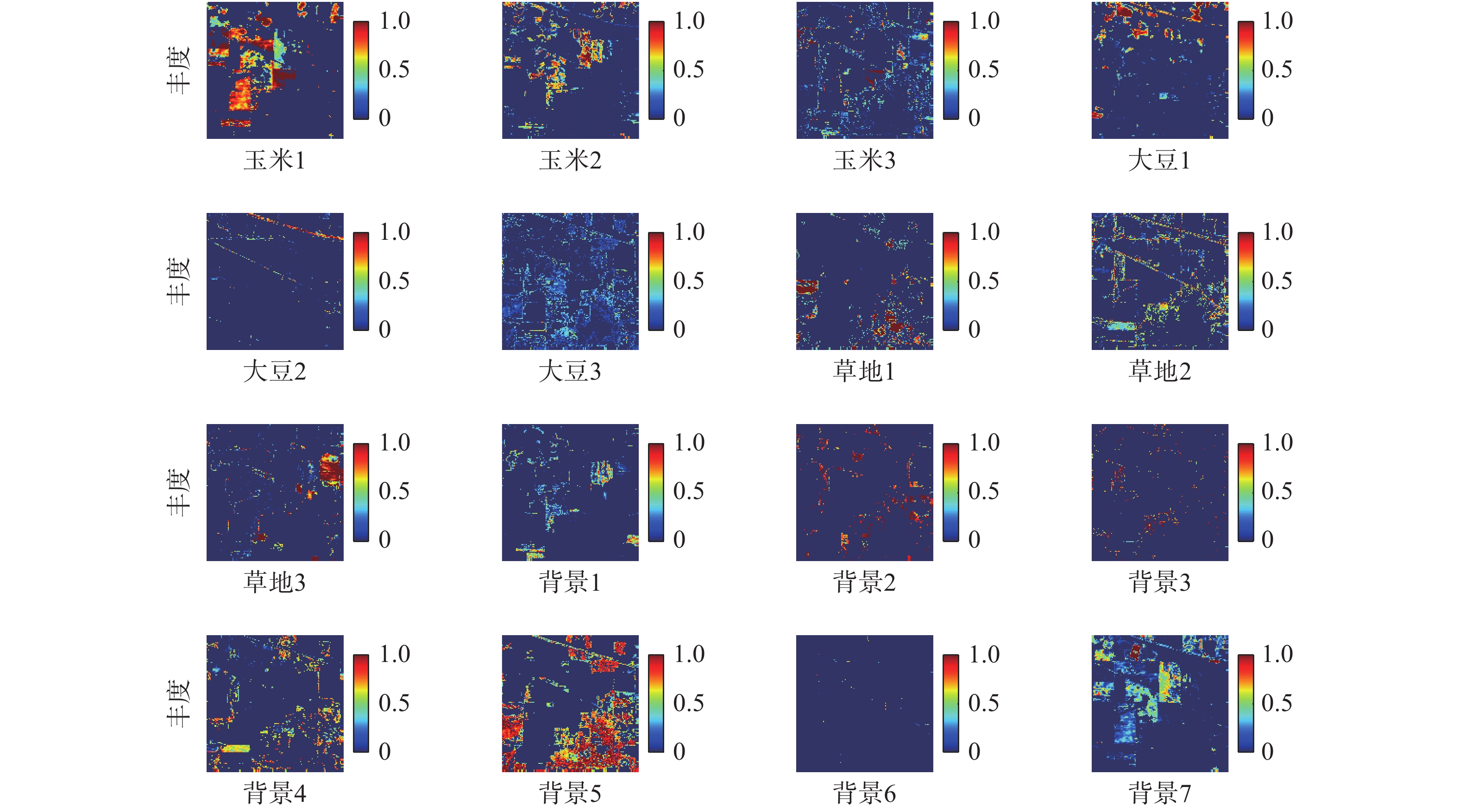
本次实验结果如图3、4所示，从图中可以看出本文所提出的算法和基于分层的解混算法的最终效果大致相当，但基于分组的多端元高光谱解混算法的解混结果更符合真实图像中的地物分布，甚至在某些地物的解混结果上还要优于基于分层的解混算法，具体的评价指标如表1所示。

5 结论

1）基于分组寻优的多端元高光谱解混算法在解混精度和解混时间上与分层高光谱图像的分层解混算法相当；

2）由于采用分组寻优的策略使得迭代次数大大减少，比基于分层的多端元高光谱解混算法少了将近2 000；

3）计算复杂度大大降低，且在某些小丰度目标的检测效率上要高于基于分层多端元高光谱解混算法。在未来的研究中，要注意使用不同类型的数据进行试验，以证明该算法的有效性。