灰色系统理论由邓聚龙教授在20世纪70年代末提出,经过30多年的发展壮大,已经广泛应用于工业、农业、经济等诸多领域[1]。灰色预测模型是灰色系统理论的主要研究内容之一,GM(1, 1)模型作为其核心,因应用的广泛性受到了极大的关注。至今为止,许多学者针对GM(1, 1)模型预测精度的不稳定性做了大量的研究,分析表明模型背景值与预测精度息息相关。谭冠军[2-4]阐述了背景值构造方法不当是引发GM(1, 1)模型预测误差过大的主要原因,并给出了背景值新的构造方法。王正新等[5]证明了离散指数函数的累加性质,基于非齐次指数函数拟合一次累加生成序列,推导出优化背景值的新方法。WANG等[6]提出一种背景值和初始项优化的组合方法对无偏指数分布的序列进行预测,阐述证明了新信息优先原则和GM(1, 1)模型中初始项的合理性。李凯等[7]提出Simpson公式与牛顿插值公式相结合的组合插值法构造背景值,将灰作用量加在原始建模数据序列前,使得第一个数据参与GM(1, 1)模型建模过程。徐宁等[8]讨论了真实背景值与发展系数之间的关系,并建立新的灰微分方程,突破了发展系数[-2,2]的限制,最终使得背景值同时具有无偏性和最小误差性。蒋诗泉等[9]从积分几何意义出发构建灰色动态序列预测模型,并基于函数逼近思想结合复化梯形公式提出背景值优化方法。谭冠军等[10]分析高增长指数序列建模产生滞后误差的原因,在保持GM(1, 1)模型计算仍比较简单的情形下重构背景值,使得GM(1, 1)模型同时对低、高增长序列具有良好的适应性。江艺羡等[11]利用黎曼积分思想以不规则梯形面积逼近曲边梯形面积,同时验证了新模型具有白指数律重合性。沈艳等[12]基于数值分析中的逼近思想,采用数值积分中的Newton-Cotes公式和Gauss-Legendre公式对背景值进行修正求积以建立改进GM(1, N)模型,实例结果表明了模型在拟合与预测方面的优越性。胡攀[13]从GM(1, 1)幂模型指数连续性着手,将背景值转化为相邻序列点的确定性函数建立改进模型。
文章基于GM(1, 1)模型背景值构造方式所带来的误差,提出采用三、四阶Newton-Cotes公式与灰色动态序列预测模型结合的优化方法重构GM(1, 1)模型背景值,提升其预测精度。结果表明,改进后的GM(1, 1)模型有效降低了模型预测误差,有着非常重要的理论研究价值及意义。
1 GM(1, 1)模型建模机理定义1[1] 在灰色GM(1, 1)预测模型中,假设原始非负序列:
| $ {X^{(0)}} = \left( {{x^{(0)}}(1),{x^{(0)}}(2), \cdots ,{x^{(0)}}(n)} \right) $ |
| $ {x^{(0)}}(k) \ge 0(k = 1,2, \cdots ,n) $ |
对应的1-AGO序列:
| $ {X^{(1)}} = \left( {{x^{(1)}}(1),{x^{(1)}}(2), \cdots ,{x^{(1)}}(n)} \right) $ |
| $ {x^{(1)}}(k) = \sum\limits_{i = 1}^k {{x^{(0)}}} (i)\quad (k = 1,2, \cdots ,n) $ |
设Z(1)为X(1)的紧邻均值生成序列,亦称其为GM(1, 1)预测模型的背景值序列。
| $ {Z^{(1)}} = \left( {{z^{(1)}}(1),{z^{(1)}}(2), \cdots ,{z^{(1)}}(n)} \right) $ |
| $ {z^{(1)}}(k) = 0.5\left( {{x^{(1)}}(k) + {x^{(1)}}(k - 1)} \right) $ |
其中k=2, 3, …, n,称灰色微分方程
| $ {x^{(0)}}(k) + a{z^{(1)}}(k) = b $ | (1) |
为GM(1, 1)模型的基本形式。其中称-a为发展系数,b为灰作用量。
定理1[1] 若[a, b]T为参数列,且:
| $ \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {{x^{(0)}}(2)}\\ {{x^{(0)}}(3)}\\ \vdots \\ {{x^{(0)}}(n)} \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - {z^{(1)}}(2)}&1\\ { - {z^{(1)}}(3)}&1\\ \vdots & \vdots \\ { - {z^{(1)}}(n)}&1 \end{array}} \right] $ |
则GM(1, 1)模型的最小二乘估计参数列满足:
| $ \hat a = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $ |
定义2[1] 设X(0)为非负序列,X(1)为X(0)的一阶累加生成序列,Z(1)为X(1)的背景值序列,则称
| $ \frac{{{\rm{d}}{x^{(1)}}(t)}}{{{\rm{d}}t}} + a{x^{(1)}}(t) = b $ | (2) |
为GM(1, 1)模型的白化微分方程。
定理2[1] GM(1, 1)模型的时间响应序列为
| $ {\hat x^{(1)}}(k) = \left( {{x^{(0)}}(1) - \frac{b}{a}} \right){{\rm{e}}^{ - a(k - 1)}} + \frac{b}{a} $ |
还原值:
| $ \begin{array}{*{20}{l}} {{{\hat x}^{(0)}}(k) = {{\hat x}^{(1)}}(k) - {{\hat x}^{(1)}}(k - 1) = }\\ {\left( {1 - {{\rm{e}}^a}} \right)\left( {{x^{(0)}}(1) - \frac{b}{a}} \right){{\rm{e}}^{ - a(k - 1)}} + \frac{b}{a}} \end{array} $ |
其中k=1, 2, …, n。
2 GM(1, 1)模型背景值误差分析根据GM(1, 1)预测模型的构建过程,可以得出参数a、b影响着GM(1, 1)模型预测精度,而背景值z(1)(k)又决定着参数a、b的取值,故背景值z(1)(k)是制约GM(1, 1)模型预测精度的一个至关重要的因素。
对式(2)在[K-1, K]上积分,得:
| $ {x^{(0)}}(k) + a\int_{k - 1}^k {{x^{(1)}}} (t){\rm{d}}t = b $ |
与式(1)比较,得:
| $ {z^{(1)}}(k) = \int_{k - 1}^k {{x^{(1)}}} (t){\rm{d}}t $ | (3) |
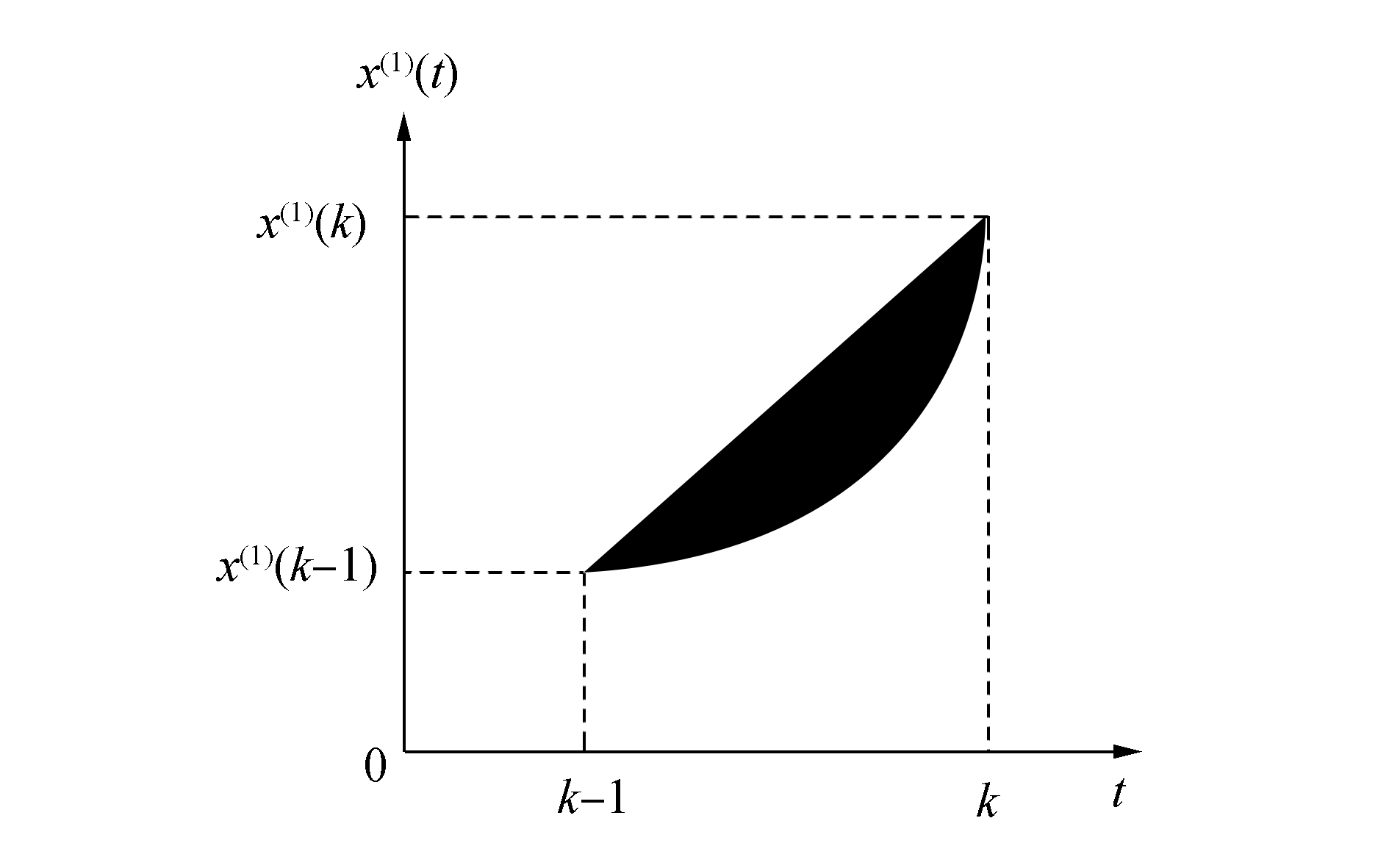
GM(1, 1)模型中背景值采用梯形公式构造,而实际背景值则是曲线x(1)(t)在区间[k-1, k]上与t轴围成的一个曲边梯形面积,即式(3)。
3 重构背景值优化方法建立现从背景值的几何意义考虑GM(1, 1)模型的优化方法。如图 1所示,阴影面积即为传统背景值与真实背景值之间的差值,即为GM(1, 1)模型的背景值构建方式所产生的误差来源。文中采用Newton-Cotes求积公式与灰色动态序列预测模型结合改进背景值构建方式。
|
Download:
|
| 图 1 背景值误差来源 | |
定理3[9] 设GM(1, 1)模型中原始非负序列:
| $ {X^{(0)}} = \left\{ {{x^{(0)}}(1),{x^{(0)}}(2), \cdots ,{x^{(0)}}(n)} \right\} $ |
| $ {x^{(0)}}(i) > 0\quad (i = 1,2, \cdots ,n) $ |
设其1-AGO序列:
| $ {x^{(1)}}(k) = A{{\rm{e}}^{\alpha (k - 1)}} + B $ |
则有:
| $ \alpha = \ln \frac{{{x^{(0)}}(k)}}{{{x^{(0)}}(k - 1)}} $ |
| $ A = \frac{{{x^{(0)}}(k)}}{{{{\left( {\frac{{{x^{(0)}}(k)}}{{{x^{(0)}}(k - 1)}}} \right)}^{k - 1}}\left( {1 - \frac{{{x^{(0)}}(k)}}{{{x^{(0)}}(k - 1)}}} \right)}} $ |
| $ \begin{array}{*{20}{c}} {B = {x^{(0)}}\left( {{k_1}} \right) - A = }\\ {{x^{(0)}}\left( {{k_1}} \right) - \frac{{{x^{(0)}}(k)}}{{{{\left( {\frac{{{x^{(0)}}(k)}}{{{x^{(0)}}(k - 1)}}} \right)}^{k - 1}}\left( {1 - \frac{{{x^{(0)}}(k)}}{{{x^{(0)}}(k - 1)}}} \right)}}} \end{array} $ | (4) |
称x(1)(t)=Aeα(t-1)+B(t≥1)为灰色动态序列预测模型。
3.2 基于Newton-Cotes求积公式重构背景值文中基于背景值误差来源,采用Newton-Cotes求积公式与灰色动态序列预测模型相结合重构背景值z(1)(k),达到提升GM(1, 1)模型预测精度的目的。
定义3[14] 将积分区间[K-1, K]=[a, b]划分为n等份,选取等距节点xk=a+kh(k=0, 1, 2, …, n),步长
| $ {I_n} = (b - a)\sum\limits_{k = 0}^n {C_k^{(n)}} f\left( {{x_k}} \right) $ | (5) |
称为Newton-Cotes求积公式,式中Ck(n)称为Cotes系数。引进变换x=a+th得到:
| $ \begin{array}{*{20}{l}} {C_k^{(n)} = \frac{h}{{b - a}}\int_0^n {\prod\limits_n {\frac{{t - j}}{{k - j}}} } {\rm{d}}t = }\\ {\frac{{{{( - 1)}^{n - k}}}}{{nk!(n - k)!}}\int_0^n {\prod\limits_n {(t - j)} } {\rm{d}}t} \end{array} $ |
当n=3时,得三阶Newton-Cotes公式:
| $ {N_3} = \frac{{b - a}}{8}\left[ {f\left( {{x_0}} \right) + 3f\left( {{x_1}} \right) + 3f\left( {{x_2}} \right) + f\left( {{x_3}} \right)} \right] $ |
| $ {x_k} = a + kh $ |
| $ h = \frac{{b - a}}{3} $ |
当n=4时,得四阶Newton-Cotes公式:
| $ \begin{array}{*{20}{c}} {{N_4} = \frac{{b - a}}{{90}}\left[ {7f\left( {{x_0}} \right) + 32f\left( {{x_1}} \right) + 12f\left( {{x_2}} \right) + } \right.}\\ {\left. {32f\left( {{x_3}} \right) + 7f\left( {{x_4}} \right)} \right]} \end{array} $ |
| $ {x_k} = a + kh $ |
| $ h = \frac{{b - a}}{4} $ |
分别依据三、四阶Newton-Cotes求积公式重构背景值,结合GM(1, 1)模型建模机理,得到如下背景值计算公式:
| $ z_3^{(1)}(k) = \frac{1}{8}\left( {{x^{(1)}}(k - 1) + 3\left( {{x^{(1)}}\left( {k - \frac{2}{3}} \right) + {x^{(1)}}\left( {k - \frac{1}{3}} \right) + {x^{(1)}}(k)} \right)} \right) $ |
| $ z_4^{(1)}(k) = \frac{1}{{90}}\left( {7{x^{(1)}}(k - 1) + 32{x^{(1)}}\left( {k - \frac{3}{4}} \right) + 12{x^{(1)}}\left( {k - \frac{1}{2}} \right) + 32{x^{(1)}}(k)\left( {k - \frac{1}{4}} \right)} \right) $ |
以基于三阶Newton-Cotes求积公式的优化方法为例:
1) 依据原始数据序列{x(0)(k)}(x(0)(k)>0)及其累加生成序列建立灰色动态序列预测模型;
2) 利用灰色动态序列预测模型,计算区间[k-1, k]上插值节点x(1)(k-
3) 利用Newton-Cotes求积公式重构背景值:
| $ z_3^{(1)}(k) = \frac{1}{8}\left( {{x^{(1)}}(k - 1) + 3\left( {{x^{(1)}}\left( {k - \frac{2}{3}} \right) + {x^{(1)}}\left( {k - \frac{1}{3}} \right)} \right) + {x^{(1)}}(k)} \right) $ |
4)根据z3(1)(k)求得参数a和b并代入定理2中的还原值公式,计算预测值
分别称经两种优化方法建立的模型为NC-3-GM(1, 1)、NC-4-GM(1, 1)模型,统称为NC-GM(1, 1)模型。
4 NC-GM(1, 1)模型适用范围分析GM(1, 1)模型中发展系数-a反映着
已知在-a>1时,不适宜采用GM(1, 1)模型;当0.8 < -a≤1时,应采用残差修正GM(1, 1)模型。所以文中针对0 < -a≤0.8的情形,分别选取-a=0.1, 0.2, …, 0.8进行模拟预测,并取k=0, 1, …, 16,由xi(0)(k+1)=e-ak可得如下数列[1]:
| $ \begin{array}{*{20}{c}} { - a = 0.1,X_1^{(0)} = (1,1.105,1.221, \cdots ,4.953)}\\ { - a = 0.2,X_2^{(0)} = (1,1.221,1.492, \cdots ,24.533)}\\ \cdots \\ {a = 0.8,X_8^{(0)} = (1,2.226,4.953, \cdots ,362217.450)} \end{array} $ |
以上述8组序列作为原始数据构建GM(1, 1)模型,分别采用GM(1, 1)模型以及NC-3-GM(1, 1)、NC-4-GM(1, 1)模型进行预测,最后将得到的预测数据与真实数据比较,相对误差比较结果见于表 1。
|
|
表 1 发展系数不同取值误差比较结果 |
可得结论:在0 < -a≤0.7时,GM(1, 1)模型不大于18.320%,而NC-3-GM(1, 1)、NC-4-GM(1, 1)模型误差分别不超过3.734%、3.660%,其预测精度达到96%以上。与此同时,NC-4-GM(1, 1)模型预测误差明显低于NC-3-GM(1, 1)模型预测误差,预测效果更好。
在上述基础上,分析3种预测模型在发展系数不同取值下的一步、两步、五步、十步预测误差。统计结果如表 2~5所示。
|
|
表 2 一步预测误差比较结果 |
|
|
表 3 两步预测误差比较结果 |
|
|
表 4 五步预测误差比较结果 |
|
|
表 5 十步预测误差比较结果 |
以GM(1, 1)模型10%的预测误差为预测模型合格标准,将-a取值范围划分为:0 < -a≤0.4和0.4 < -a≤0.8。由上述4种表格结果,可得到结论:
1) 五步预测之内
a) 当0 < -a≤0.4时,GM(1, 1)模型预测误差最大为9.059%,NC-3-GM(1, 1)模型预测误差最大为1.731%,而NC-4-GM(1, 1)模型预测误差最大为1.617%;
b) 当0 < -a≤0.8时,预测效果最好的当属NC-4-GM(1, 1)模型,五步预测时最高误差为9.908%,预测精度达到了90%以上。而此时GM(1, 1)模型和NC-3-GM(1, 1)模型预测误差最高分别是43.748%、10.047%,属于不合格预测模型。
说明在短期预测中,上述3种预测方法中,NC-4-GM(1, 1)模型预测效果最好。
2) 十步预测之内
a) 在0 < -a≤0.4时,NC-3-GM(1, 1)模型、NC-4-GM(1, 1)模型的预测误差最高是1.736%、1.616%,与GM(1, 1)模型最大预测误差分别相差7.326%、7.446%。NC-3-GM(1, 1)模型、NC-4-GM(1, 1)模型的预测精度均达到98%以上,说明当0 < -a≤0.4时在中长期预测中,采用NC-3-GM(1, 1)模型、NC-4-GM(1, 1)模型做数据预测是可行的。
b) 当0 < -a≤0.8时,发现0 < -a≤0.6范围内,两种优化方法预测精度超过93%。在0.6 < -a≤0.8内,两种优化方法预测精度小于90%。
因此在0 < -a≤0.6范围内,两种优化方法都适合于中长期预测,打破了GM(1, 1)模型在适用范围上的局限性。
5 应用实例总人口数预测是最原始的人口预测内容,也是现今人口预测不可缺少的组成部分[15]。文中以2000—2013年全国年末总人口数据为原始建模数据构建GM(1, 1)模型,预测2014—2016年全国年末总人口数。表 6为2000—2016年全国年末总人口实际数据。
|
|
表 6 年末总人口数据表 |
采用GM(1, 1)、NC-3-GM(1, 1)、NC-4-GM(1, 1)模型进行预测,分析三者相对误差差异。在GM(1, 1)模型建模过程中,求得发展系数-a=0.005 < 0.1,依据上节适用范围分析得到,能够采用NC-GM(1, 1)模型预测年末总人口数。表 7~8为预测结果比较。
|
|
表 7 GM(1, 1)模型预测结果 |
|
|
表 8 NC-GM(1, 1)模型预测结果 |
根据表 7~8可得结论:GM(1, 1)模型预测平均相对误差为0.173%,而NC-3-GM(1, 1)、NC-4-GM(1, 1)模型预测平均相对误差分别是0.068%、0.066%,分别较GM(1, 1)模型预测误差降低了0.105%、0.107%,说明NC-3-GM(1, 1)、NC-4-GM(1, 1)模型有效提升了GM(1, 1)模型预测精度。
6 结论文中所做主要工作如下:1)提出采用三、四阶Newton-Cotes求积公式结合灰色动态序列预测模型重构GM(1, 1)模型背景值的优化方法;2)探究比较了改进模型和GM(1, 1)模型的适用范围差异;3)通过实际算例对改进模型进行了有效性和可行性分析。结果表明,文中提出的优化方法显著提升了GM(1, 1)模型的预测精度,打破了GM(1, 1)模型适用范围上的局限,在理论和实用上有着重要的意义及参考价值。
| [1] |
刘思峰, 党耀国, 方志耕, 等. 灰色系统理论及其应用[M]. 第8版. 北京: 科学出版社, 2017: 1-168.
( 0) 0)
|
| [2] |
谭冠军. GM(1, 1)模型的背景值构造方法和应用(Ⅰ)[J]. 系统工程理论与实践, 2000, 20(4): 98-103. DOI:10.3321/j.issn:1000-6788.2000.04.019 ( 0) 0)
|
| [3] |
谭冠军. GM(1, 1)模型背景值构造方法和应用(Ⅱ)[J]. 系统工程理论与实践, 2000, 20(5): 125-132. DOI:10.3321/j.issn:1000-6788.2000.05.024 ( 0) 0)
|
| [4] |
谭冠军. GM(1, 1)模型的背景值构造方法和应用(Ⅲ)[J]. 系统工程理论与实践, 2000, 20(6): 125-127. ( 0) 0)
|
| [5] |
王正新, 党耀国, 刘思峰. 基于离散指数函数优化的GM(1, 1)模型[J]. 系统工程理论与实践, 2008, 28(2): 61-67. DOI:10.3321/j.issn:1000-6788.2008.02.008 ( 0) 0)
|
| [6] |
WANG Yuhong, LIU Qin, TANG Jianrong, et al. Optimization approach of background value and initial item for improving prediction precision of GM(1, 1)model[J]. Journal of systems engineering and electronics, 2014, 25(1): 77-82. DOI:10.1109/JSEE.2014.00009 ( 0) 0)
|
| [7] |
李凯, 张涛. 基于组合插值的GM(1, 1)模型背景值的改进[J]. 计算机应用研究, 2018, 35(10): 2994-2999. DOI:10.3969/j.issn.1001-3695.2018.10.026 ( 0) 0)
|
| [8] |
徐宁, 党耀国, 丁松. 基于误差最小化的GM(1, 1)模型背景值优化方法[J]. 控制与决策, 2015(2): 283-288. ( 0) 0)
|
| [9] |
蒋诗泉, 刘思峰, 周兴才. 基于复化梯形公式的GM(1, 1)模型背景值的优化[J]. 控制与决策, 2014(12): 2221-2225. ( 0) 0)
|
| [10] |
谭冠军, 檀甲友, 王加阳. 灰色系统预测模型GM(1, 1)背景值重构研究[J]. 数学的实践与认识, 2016, 45(15): 267-273. ( 0) 0)
|
| [11] |
江艺羡, 张岐山. GM(1, 1)模型背景值的优化[J]. 中国管理科学, 2015, 23(9): 146-152. ( 0) 0)
|
| [12] |
沈艳, 孙红影, 李丽萍. 优化GM(1, N)模型在交通噪声预测中的应用和精度分析[J]. 中国安全生产科学技术, 2012, 8(11): 27-32. ( 0) 0)
|
| [13] |
胡攀. 优化背景值的GM(1, 1)幂模型及其应用[J]. 数学的实践与认识, 2017, 47(19): 99-104. ( 0) 0)
|
| [14] |
李庆扬, 王能超, 易大义. 数值分析[M]. 第5版. 北京: 清华大学出版社, 2008: 20-125.
( 0) 0)
|
| [15] |
李晓梅. 人口预测模型研究及应用[M]. 成都: 西南财经大学出版社, 2011: 1-125.
( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


