2. 东南大学 电子信息工程学院, 江苏 南京 211189
2. School of Electronic Science and Engineering, Southeast University, Nanjing, 211189, China
在当前的航天推进系统研究中,液体火箭发动机的故障检测与分类是迫切需要解决的关键技术问题[1]。收集故障样本较为困难,缺乏故障诊断经验,知识更新不及时等都是液体火箭发动机的故障诊断存在的难题。同时,对诊断的实时性、准确性和完整性提出了更高的要求[2-3]。为了解决这些困难,一般将液体火箭发动机的检测与诊断方法归纳为三大类[1]:1)基于直接测量及信号处理的方法;2)基于模型的方法;3)基于人工智能的方法。
近年来,随着人工智能技术的发展与革新,基于人工智能的方法被大量应用于各类系统的故障诊断中。徐宗本等[4]提出了一种用于空间推进系统的方法,该方法将神经网络与云理论相结合,是一种静态网络的故障诊断方法;黄强等[5]采用类似神经网络的方法实现了液体火箭发动机的故障诊断。但是,训练神经网络需要大量的样本和训练时间,难以满足故障诊断的实时性要求。彭小辉[6]等构建出云分类器,将液体火箭发动机的故障问题变为模式分类问题,与神经网络相比,该方法的结构和参数具有明显的物理含义,能够挖掘到数据样本中的深层含义,但对数据样本的依赖程度太强,需要训练数据中具有完整的故障模式。
本文提出的贝叶斯网络分类器的判别类条件网络模型,是由类条件贝叶斯网络模型经过对数形式重新参数化得到的。然后,通过改进粒子群算法对其优化求解,得到各节点的概率,完成分类任务。改进后的分类器对训练样本要求较少,且分类器的训练效率高,算法收敛速度快,分类准确率高。
1 贝叶斯网络分类器的参数学习 1.1 贝叶斯网络分类器贝叶斯网络B=〈G, Θ〉是由结构G(一个有向无环图,其中每个节点表示一个变量Zi)和一组参数Θ组成的,其中,Θ是与贝叶斯网络相关的参数集,这些参数可以量化结构内的依赖关系。变量Y=Z0表示类别,变量X1=Z1, X2=Z2, …, Xn=Zn,称为属性,其中,n表示属性的数量。参数Θ由结构G中的每个节点的一组表示局部条件概率分布的参数θz0|∏0(x)和θzi|y, ∏i(x)组成。
若给定某一数据实例x=〈x1, x2, …, xn〉,则贝叶斯网络的联合概率分布为
| $ {P_B}(y,x) = {\theta _{y\left| {{\Pi _0}(x)} \right.}} \cdot \prod_{i = 1}^n {{\theta _{{x_i}|y,{\Pi _i}(x)}}} $ | (1) |
式中:y∈Y,表示类变量的取值,与z0相同。
根据贝叶斯定理,相应的条件概率分布PB(y|x)为
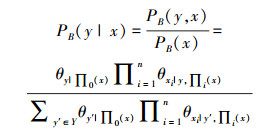
|
(2) |
本文直接通过最大化条件对数似然函数(conditional log-likelihood,CLL)来优化P(y|x)。这种方法直接优化了从样本特征到类标签的映射,因此对分类问题更加高效。
根据贝叶斯定理,本文将条件对数似然函数定义为
| $ \begin{array}{*{20}{c}} { CLL (B) = \frac{1}{N}\sum\limits_{j = 1}^N {\log } {P_B}\left( {{y^{(j)}}|{x^{(j)}}} \right) = }\\ {\frac{1}{N}\left[ {\sum\limits_{j = 1}^N {\left( {\log {P_B}\left( {{y^{(j)}},{x^{(j)}}} \right) - \log \sum\limits_{y'}^{\left| y \right|} {{P_B}\left( {y',{x^{(j)}}} \right)} } \right)} } \right] = }\\ {\frac{1}{N}\left[ {\sum\limits_{j = 1}^N {\left( {\log {\theta _{y\left( j \right)\left| {\prod\nolimits_0 {\left( {x\left( j \right)} \right)} } \right.}} + \sum\limits_{i = 1}^n {\log {\theta _{{x_i}\left( j \right)\left| {\prod\nolimits_i {\left( {x\left( j \right)} \right)} } \right.}}} } \right)} - } \right.}\\ {\left. {\log \left( {\sum\limits_{y'}^{\left| y \right|} {{\theta _{y'\left| {\prod\nolimits_0 {\left( {x\left( j \right)} \right)} } \right.}}} \prod\limits_{i = 1}^n {{\theta _{{x_i}\left| {y',\prod\nolimits_i {\left( {x\left( j \right)} \right)} } \right.}}} } \right)} \right]} \end{array} $ | (3) |
将Roos等[7]提出的定义稍作修改:
定义1 对具有严格正参数集θB*的网络B*,若从属性集(X1, X2, …, Xn)到类变量Y上的分布的所有函数集合采用式(2)的形式,则称这类基于网络B*的条件分布集合为类条件贝叶斯网络模型,记为MB*。
1.3 判别类条件贝叶斯网络模型根据Roos等[7]提出的贝叶斯网络,将判别类条件贝叶斯网络定义如下。
定义2 对类条件贝叶斯网络,若将式(2)以β=log θ的形式重新参数化,同时通过最大化条件对数似然函数得到参数β,则称为判别类条件贝叶斯网络模型,记为MdB*。
重新定义式(2)中的P(y|x):
| $ {P_B}(y|x) = \frac{{\exp \left( {\log {\theta _y} + \sum\nolimits_{i = 1}^n {\log {\theta _{{x_i}|y,{\Pi _i}(x)}}} } \right)}}{{\sum\nolimits_{y'}^{\left| y \right|} {\exp \left( {\log {\theta _{y'}} + \sum\nolimits_{i = 1}^n {\log {\theta _{{x_i}|y',{\Pi _i}(x)}}} } \right)} }} $ | (4) |
根据定义2,重新定义式(4)中与每个参数θ相关联的参数β:
| $ \log {\theta _y} = {\beta _y},\log {\theta _{{x_i}|y,\prod\nolimits_i {(x)} }} = {\beta _{y,{x_i}}},{\Pi _i} $ |
现在式(4)变为
| $ {P_B}(y|x) = \frac{{\exp \left( {{\beta _y} + \sum\nolimits_{i = 1}^n {{\beta _{y,{x_i},{\Pi _i}}}} } \right)}}{{\sum\nolimits_{y' = 1}^{\left| y \right|} {\exp \left( {\sum\nolimits_{y'} {{\beta _y}} + \sum\nolimits_{i = 1}^n {{\beta _{y',{x_i},{\Pi _i}}}} } \right)} }} $ | (5) |
根据定义2,由MdB*优化的CLL为
| $ \begin{array}{l} \log {P_B}(y|x) = \left( {{\beta _y} + \sum\limits_{i = 1}^n {{\beta _{y,{x_i}}}} ,{\Pi _i}} \right) - \\ \log \left( {\sum\limits_{y' = 1}^{|y|} {\exp } \left( {{\beta _{y'}} + \sum\limits_{i = 1}^n {{\beta _{y,{x_i}}}} ,{\Pi _i}} \right)} \right) \end{array} $ | (6) |
由于式(6)没有封闭形式的解,本文将采用基于改进粒子群的迭代优化方法对其进行优化求解。
2 基于频率确定搜索范围的粒子群优化算法 2.1 算法的主要思想文献[8]认为,每个蝙蝠在位置xi, d具有随机飞行速度vi, d,同时蝙蝠有不同的频率Qi和脉冲发射率r。如果蝙蝠追踪到食物,则蝙蝠改变频率、脉冲发射率,选择最优方案,直到算法满足终止条件。
根据上述思想,任意粒子i,j在一定的范围内具有不同的频率Qi、Qj,这样能够保证每个粒子不被其他粒子发出的声波所干扰。粒子通过自身的频率范围确定下一步的步长。其数学描述为:
| $ {Q_i} = {Q_{\min }} + \left( {{Q_{\min }} - {Q_{\max }}} \right) \times {\rm{rand}} $ | (7) |
式中:Qmax和Qmin是最高频率和最低频率。
粒子的更新公式为
| $ v_{i,d}^{t + 1} = \omega v_{i,d}^t + {Q_i}\left( {p_{i,d}^t - x_{i,d}^t} \right) + {c_2}{r_2}\left( {p_{g,d}^t - x_{i,d}^t} \right) $ | (8) |
| $ x_{i,d}^{t + 1} = x_{i,d}^t(t){Q_i} + v_{i,d}^{t + 1} $ | (9) |
粒子在高维空间中运动时,为了避免算法在局部最优解处收敛,本文将采用式(10)衡量多样性度量:
| $ D(t) = \frac{{\sum\nolimits_{i = 1}^N {\sqrt {\sum\nolimits_{d = 1}^D {{{\left( {x_{i,d}^t - {p_d}} \right)}^2}} } } }}{{NL}} $ | (10) |
式中:D为空间的维数;t为迭代次数;L为空间的最大长度;pd为粒子在第d维的平均值;N为种群的规模。D(t)减小,则种群集中,种群的多样性减小。
计算种群多样性D(t)后,如果D(t) < ε,则调整种群的多样性:提供脉冲发射率r,比较r与rand的大小,并按照式(11)对粒子当前位置进行调整:
| $ {x_{i,d}} = \left\{ {\begin{array}{*{20}{l}} {{p_{g,d}} + 0.01 \times {\rm{ randn }} (1,D),\quad {\rm{ rand }} < r}\\ {{p_{g,d}},\quad 其他} \end{array}} \right. $ | (11) |
本文设置的终止条件为迭代次数大于104或由
综合上文所述算法的主要思想,算法的具体实现步骤如下。
procedure BAPSO
for each particle i
Initialize vi, d and xi, d for particle i
Evaluate particle i and set pi=xi, d
Set Qmin,Qmax
end for
pg=min{pi}
while(termination condition)
for i = 1 to N
Calculate Qi by Eq.7
Update vi, d and xi, d by Eq.8 and Eq.9
Calculate D(t) by Eq.10
if(D(t) < ε)
set r
if(r < rand)
xi, d=pg, d+0.01×randn(1, D)
else
xi, d=pg, d
Evaluate particle i
if fit(xi, d) < fit(pi)
pi=xi, d
if fit(pi) < fit(pg)
pg=pi
end for
end while
print pg
end procedure
3 实例分析与验证Weka系统是由新西兰Waikato大学开发的一个开放源码的机器学习及数据挖掘系统。
3.1 数据的预处理本文采用的数据样本是某大型氢氧发动机36次仿真试车数据,通过建立大型氢氧液体火箭发动机的数学模型,对该型号的液体火箭发动机可能发生的各类故障进行多次仿真,得到了仿真数据。其中30次为正常数据,6次为故障数据,共7 500个样本。6组故障数据分别是:发生器氢副控阀泄露、氢涡轮出口燃气泄露、氧稳压阀出口泄露、发生器氧副控阀泄露、氧涡轮入口燃气泄露及氧泵后泄露。
本文从易发故障部分组件选择相应属性参数,共22个。同时,由于实际数据变化较大,数据的数量级有可能差别很大,为了提高分类及优化效率,本文采用式(12)对数据进行归一化处理:
| $ D = \frac{{\left( {{X_{ij}} - {X_j}} \right)}}{{{X_j}}} $ | (12) |
式中:Xij为第i个样本中第j个属性的值;Xj为数据样本中第j个属性的均值。
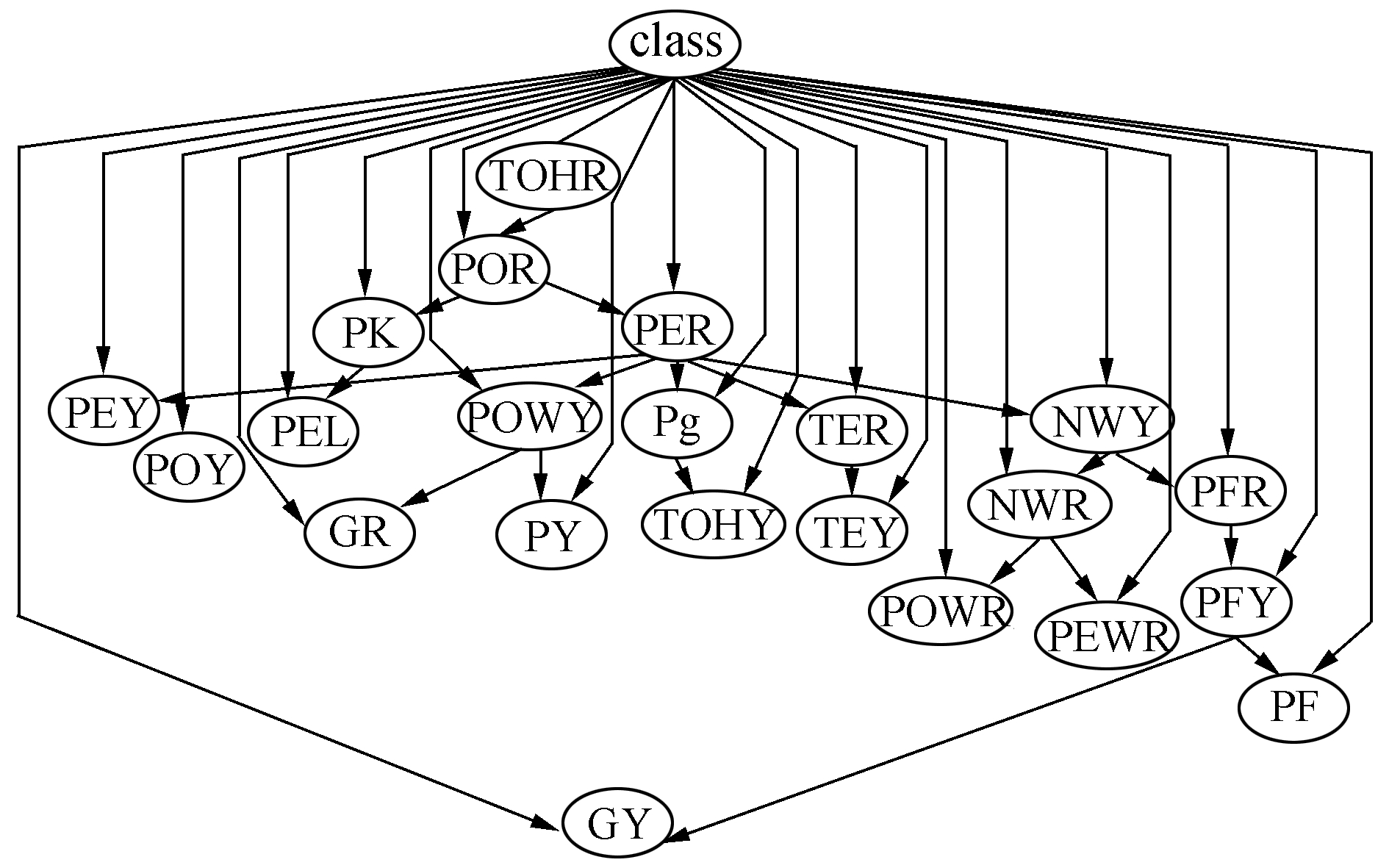
3.2 故障诊断与分类 3.2.1 TANd分类器的构建及故障诊断方法将判别类条件贝叶斯网络模型与TAN分类器相结合,通过最大化条件对数似然函数,获得各节点的参数。将新的分类器记为TANd分类器。液体火箭发动机的各参数之间并非完全相互独立,因此,采用TANd分类器时,各属性参数之间存在一定的联系。TANd分类器通过计算不同属性之间的条件互信息函数,能够在属性间添加弧,建立一个有向无环图。
3.2.2 第1次仿真数据的故障诊断结果利用生成的TANd分类器对仿真数据集1进行故障诊断与分类。
根据样本集训练生成的TANd分类器结构如图 1所示。
|
Download:
|
| 图 1 TANd网络模型 | |
仿真数据集1的分类结果用错分矩阵表示,如表 1所示。
|
|
表 1 仿真数据集1的故障诊断结果 |
表 1、2给出了分类结果和各项评价指标。可以看出,判别类条件贝叶斯网络模型应用于TAN分类器时,进一步提高了模型精度,分类效果很好。改进的分类器对于故障诊断与分类的正确率较高,且误分类率很低,在查全率和查准率上也有较好表现。另外,各种故障类型的F-Measure指标均接近于1,表明该算法对故障诊断具备相当高的可靠性。
|
|
表 2 仿真数据集1的故障分类评价指标 |
为了进一步验证TANd分类器的分类性能,证明其在样本数据的属性变量及类变量的数量增加时,依然能够保持较高的分类精度,本文通过对液体火箭发动机模型多次仿真,得到了第2次仿真数据集,共有76个属性变量。从这些数据中,选择10类故障数据:发生器氢副控阀泄露、氢涡轮出口燃气泄露、氧稳压阀出口泄露、发生器氧副控阀泄露、氧涡轮入口燃气泄露、氧泵后泄露、氧主文氏管后泄露、氧涡轮出口燃气泄漏、氢涡轮入口燃气泄露及氧稳压阀入口泄露,再从每一类故障数据中选择1 000个样本,共计10 000个数据样本。为了标记方便,将这10类故障类型记为Fault1~Fault10。
在进行分类任务前,依照前面所述方法对数据进行归一化处理。同时采用最小描述长度离散化方法对连续数据离散化。
利用生成的TANd分类器对仿真数据训练集进行故障分类,分类结果如表 3、4。
|
|
表 3 仿真数据集2的故障分类结果 |
|
|
表 4 仿真数据集2的故障分类指标统计 |
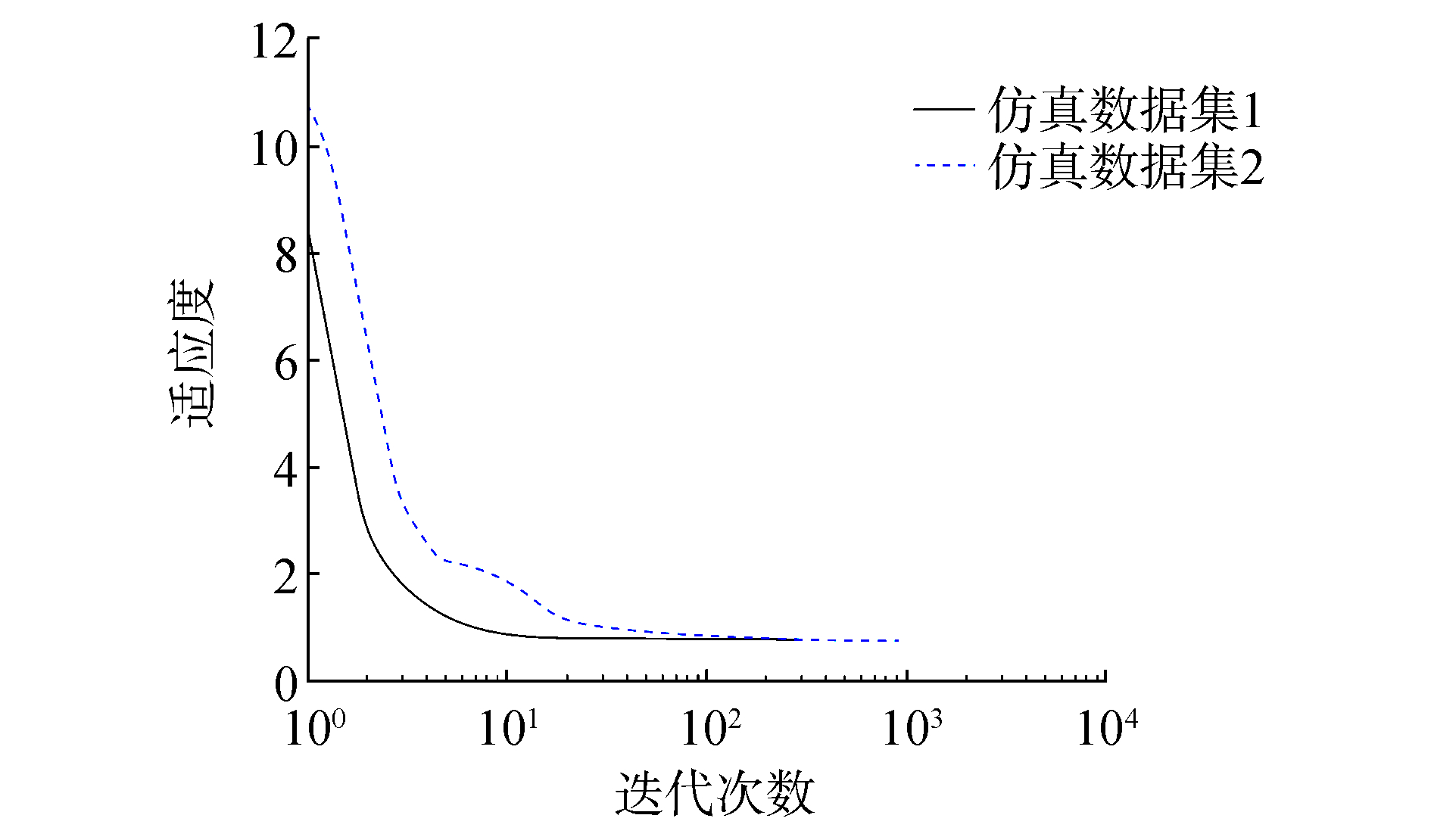
设置算法的参数,令Qmax=1,Qmin=0。设置种群规模。当由算法给出的适应度值的改进小于10-32时,算法终止。图 2是2次仿真数据集的目标函数采用负对数似然函数(negative-log-likelihood,LL)形式的收敛性比较。
|
Download:
|
| 图 2 TANd分类器在不同数据集上的演化曲线 | |
图 2的演化曲线的x轴采用了对数刻度。由图可以看出,算法通过引入粒子的频率,使得算法能够快速逼近问题的最优解,收敛速度比较快。此外,在仿真数据集1的优化过程中,算法能够极快地逼近最优解,在大约10次迭代之后,就会限制粒子的频率,围绕最优解进行搜索,且没有陷入局部极值。与第1次仿真数据相比,第2次仿真数据中包含的类变量和属性变量增加,分类器模型更复杂,目标函数变为多峰函数。但在优化过程中,算法能够在陷入局部极值点时,通过改变粒子的频率,快速摆脱出来,并且逼近全局最优解。
4 结论1) 针对液体火箭发动机的故障诊断问题,本文基于贝叶斯网络的参数学习,将判别类条件贝叶斯网络模型与TAN分类器结合,构建TANd分类器,并根据贝叶斯定理和最大后验概率原则对训练集进行分类,判断是否属于故障数据,或者是故障中的哪一类。
2) 改进的分类器对数据量需求较少,分类精度很高,适用于液体火箭发动机这类数据样本收集困难的对象。
3) TANd分类器放宽了贝叶斯网络的独立性假设条件,能够反映出不同属性之间的联系。增加训练集的样本数量,并增加属性变量和类变量,分类器依然能够保持分类精度。但目标函数较为复杂,因此算法优化过程中的迭代次数增加。
| [1] |
张振鹏. 液体发动机故障检测与诊断中的基础研究问题[J]. 推进技术, 2002, 23(5): 353-359. DOI:10.3321/j.issn:1001-4055.2002.05.001 ( 0) 0)
|
| [2] |
YANG H, JIANG B, COCQUEMPOT V, et al. Spacecraft formation stabilization and fault tolerance:a state-varying switched system approach[J]. Systems & control letters, 2013, 62(9): 715-722. ( 0) 0)
|
| [3] |
ZHANG X, TANG L, DECASTRO J. Robust fault diagnosis of aircraft engines:A nonlinear adaptive estimation-based approach[J]. IEEE transactions on control systems Technology, 2013, 21(3): 861-868. DOI:10.1109/TCST.2012.2187057 ( 0) 0)
|
| [4] |
徐宗本, 樊忠泽. 基于云神经网络的空间推进系统故障检测与诊断[J]. 兵工学报, 2009, 30(6): 727-732. DOI:10.3321/j.issn:1000-1093.2009.06.013 ( 0) 0)
|
| [5] |
黄强, 吴建军. 基于云-神经网络的液体火箭发动机故障检测方法[J]. 国防科技大学学报, 2010, 32(1): 11-15. DOI:10.3969/j.issn.1001-2486.2010.01.003 ( 0) 0)
|
| [6] |
彭小辉, 刘垠杰, 程玉强, 等. 基于云分类器的液体火箭发动机故障诊断方法[J]. 国防科技大学学报, 2013(6): 15-19. DOI:10.3969/j.issn.1001-2486.2013.06.003 ( 0) 0)
|
| [7] |
ROOS T, WETTIG H, GRUNWALD P, et al. On discriminative Bayesian network classifiers and logistic regression[J]. Machine learning, 2005, 59(3): 267-296. ( 0) 0)
|
| [8] |
YANG Xinshe. A new metaheuristic bat-inspired algorithm[M]. Nature Inspired Cooperative Strategies for Optimization. Berlin: Springer-Verlag, 2010: 65-74.
( 0) 0)
|
| [9] |
PERNKOP F, BILMS J A. Efficient heuristics for discriminative structure learning of Bayesian network classifiers[J]. Journal of machine learning research, 2010, 11: 2323-2360. ( 0) 0)
|
| [10] |
HU M, WU T, WEIR J D. An adaptive particle swarm optimization with multiple adaptive methods[J]. IEEE transactions on evolutionary computation, 2013, 17(5): 705-720. DOI:10.1109/TEVC.2012.2232931 ( 0) 0)
|
| [11] |
MARTINEZ A, CHEN S, WEBB G I, et al. Scalable learning of Bayesian network classifiers[J]. Journal of machine learning research, 2016, 17: 1-35. ( 0) 0)
|
| [12] |
WEBB G I, BOUGHTON J R, Zheng F, et al. Learning by extrapolation from marginal to full-multivariate probability distributions:decreasingly naive Bayesian classification[J]. Machine learning, 2012, 86(2): 233-272. DOI:10.1007/s10994-011-5263-6 ( 0) 0)
|
| [13] |
ZAIDI N A, WEBB G I, CARMAN M J, et al. Efficient parameter learning of Bayesian network classifiers[J]. Machine learning, 2017, 106(9): 1289-1329. ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


